Networks of influence and infection: parental choices and childhood disease

Abstract

Clusters of unvaccinated individuals are at risk of outbreaks of infection. When an individual's decision to choose vaccination is influenced by the choices of his social group, such clusters can readily arise. However, when the interactions that influence decision-making and those that permit the transmission of infection are different—for instance, when parents make vaccination decisions on behalf of their children—it is unclear how large the impact of this social influence will be. Here we use a modelling approach to represent social influence within a network of parents and the transmission of infection through a network of children. We show that the effect of social influence depends on the amount of overlap between the two different networks; large overlap means that clusters of parents who choose not to vaccinate are likely to have interacting children, generating clusters of unvaccinated children. Spatially local connections can further increase the impact of social influence. Outbreaks are most likely when parents who do not vaccinate have children who interact.

1. Introduction

Mass vaccination is a widely used method of disease control, particularly for common childhood infections such as measles (Anderson & May 1991; Grenfell et al. 2001). When a population mixes at random it is straightforward to calculate a threshold level of vaccination that will provide herd immunity to the population and prevent outbreaks of infection (Anderson & May 1991). However, if there are clusters of susceptible individuals the picture becomes more complex since, even with extremely high levels of vaccination, outbreaks can occur within such clusters (Hanratty et al. 2000; van den Hof et al. 2002; May & Silverman 2003; Stewart-Freedman & Kolvalsky 2007; Richard et al. 2008; Schmid et al. 2008). Analysis of recent outbreaks of measles in populations with high vaccination coverage suggests that such clustering exists, arising in many instances from belief systems within some communities regarding vaccination (Hanratty et al. 2000; Stewart-Freedman & Kolvalsky 2007; Henderson et al. 2008; Schmid et al. 2008). To anticipate future outbreaks of infection, it is necessary to understand the generation and impact of clusters of unvaccinated individuals.

A recent report described a model to generate clustering of attitudes regarding vaccination (Salathé & Bonhoeffer 2008). The model allowed attitudes to be influenced by underlying social networks, such that individuals tended to share the attitudes of their contacts (May & Silverman 2003; Leask et al. 2006; Abbasi 2008; Henderson et al. 2008); the emergence of heterogeneous vaccine coverage increased the likelihood of outbreaks. The model assumed that individuals who might become infected made decisions about their own vaccination uptake, and that the network of social influence for opinion formation was the same as the network of contacts through which infection spreads. For many infections of interest, the primary risk group is young children while decisions about vaccination are taken by their parents (May & Silverman 2003; Leask et al. 2006; Abbasi 2008; Heathcock & Watts 2008; Henderson et al. 2008); thus, the populations relevant to vaccine choice and infection transmission are different. Furthermore, the social networks that influence vaccine opinion and infection transmission are likely to have different characteristics.

Data suggest that the spread of childhood infections is predominantly spatially localized (Grenfell et al. 2001; van den Hof et al. 2002; Richard et al. 2008; Schmid et al. 2008). Children report more social interactions than adults (Mossong et al. 2008), and we might anticipate that adults' contacts have greater spatial reach. However, it is unclear precisely how social contacts relate to either contacts that might lead to transmission of infection or contacts that influence opinions about vaccination.

We explore a simple model combining opinion formation among parents and infection transmission between their offspring. We consider the amount of overlap between the networks of opinion and transmission and the spatial properties of interactions; we investigate how these influence the likelihood of an outbreak.

2. Methods

We model two populations, parents and children, and two processes: opinion formation among parents and infection spreading between children. We assume that opinion formation is influenced by the parents' social contacts and that infection is transmitted between offspring through their social network. Our methods build on those of Salathé & Bonhoeffer (2008).

2.1. Networks

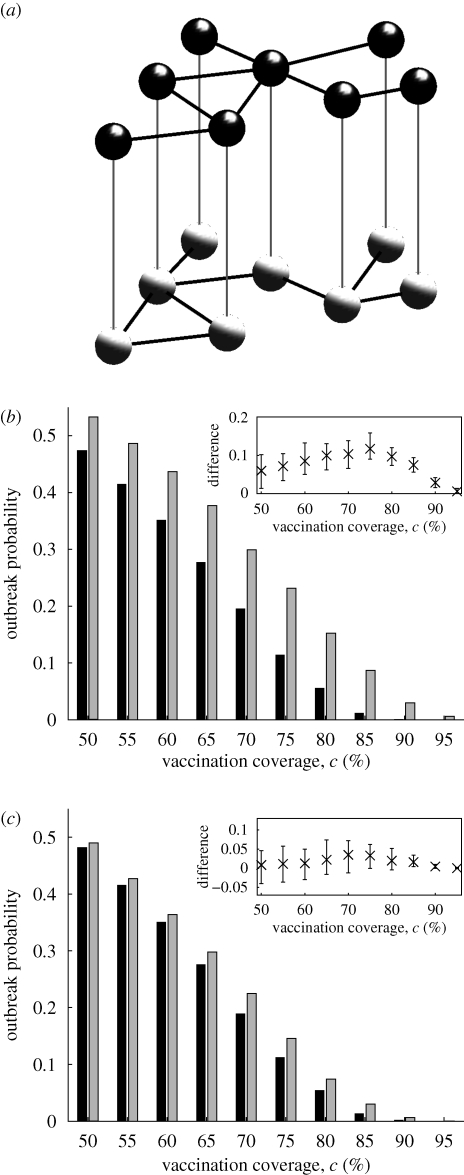
For simplicity, we assume that parent and child populations are both of size N, every parent having exactly one child. Each individual is located at random within a 1 × 1 square; offspring share their parent's location, which can be thought of as representing the household location.

Links are formed between parents: two parents are picked at random and their separation distance, s, calculated. If they are not already linked, a link is created between them with a probability depending on s. The process is repeated until the parent population has the desired number of links. To explore the impact of overlap between the networks of parents and offspring, we control the number of the parental links that are shared by the offspring (i.e. if two parents are linked then their children are also linked). The remaining links between offspring are formed similarly to parental links (figure 1a). We define F as the fraction of links in the offspring network that also appear in the parental network.

Figure 1.

(a) The model population consists of a network of parents (black, above) and a network of children (grey, below); in both networks, links (black lines) are formed locally. Each parent has exactly one child, who shares his spatial location (illustrated by grey vertical lines). Not all links between parents correspond to links between their offspring. (b) Outbreak probability with (Ω = 1, grey) and without (Ω = 0, black) opinion formation for varying vaccination coverage. The parent and offspring networks share all connections (i.e. F = 1); T = 0.2. The inset box shows how the difference in outbreak probability for Ω = 1 and Ω = 0 varies across the different stochastically generated networks (bars from 5th to 95th percentiles, with the mean shown as a cross). (c) As given in (b), but F = 0.2.

The probability of forming a link equals 0.1 if s is below a ‘local threshold’ T (which may differ for the parent and offspring networks) and zero otherwise, allowing generation of networks with varying degrees of localness.

2.2. Vaccination choice

Parents are given an initial opinion about vaccination (For or Against), with a fraction c of the parental population For vaccination. In reality, c will be determined by multiple factors, including government information campaigns and beliefs about a vaccine's safety and effectiveness.

Vaccination opinion is then updated: a parent is randomly selected and changes opinion with probability Ω × d, where d is the fraction of that parent's contacts with a different opinion and Ω represents the strength of opinion formation (ranging from 0 to 1); if this parent changes opinion (from For to Against, say) then, to keep c unchanged, a second parent is chosen to change opinion in the opposite direction (from Against to For): this second parent is chosen randomly from current ‘Against’ parents and changes opinion with probability Ω × d—second parents are chosen until a balancing opinion change takes place (Salathé & Bonhoeffer 2008).

Once the above updating process has taken place N times, the offspring of parents who are For vaccination are vaccinated.

We measure opinion clustering within the parental network by calculating the probability that two connected parents have the same vaccination opinion, A (without opinion formation, A = c² + (1 − c)²). We can increase A by altering the probability that opinion change takes place to make parents with larger d more likely than previously to choose to agree with their contacts. Further details appear in the electronic supplementary material.

2.3. Transmission

Offspring are susceptible, infected or recovered/vaccinated (immune to further infection). The epidemic is updated at every timestep δ; at each timestep each susceptible offspring becomes infected with probability 1 − e^−βiδ (where β is the transmission rate and i his number of infected neighbours) and each infected individual recovers with probability gδ. After vaccination, infection is seeded by infecting one randomly chosen susceptible individual. An outbreak is defined as any epidemic that infects more than 10 individuals. To aid comparison with Salathé & Bonhoeffer (2008), unless stated otherwise N = 2000, g = 1, β = 0.05 and δ = 1, and both parents and offspring average 10 contacts in their respective networks.

For each parameter set, 20 networks are formed; for each network the opinion formation process is carried out 10 times (the same 20 networks are used for each value of Ω), and for each of these vaccinated networks 50 epidemics are seeded.

3. Results

If parent and offspring networks are identical (F = 1) our results confirm the observation of Salathé & Bonhoeffer (2008) that the opinion formation process described influences outbreak likelihood (figure 1b). The precise network used does not affect the conclusion (figure 1b, inset). Clustering of vaccination introduced by the decision-making process among parents corresponds to a clustering of unvaccinated offspring and more outbreaks. The same effect is still apparent, though much less dramatic, when the parent and offspring networks share only 20 per cent of their contacts (figure 1c).

To quantify the impact of opinion clustering, we measure the difference between the outbreak probabilities with and without opinion formation. We define the effect of opinion clustering, Δ, as

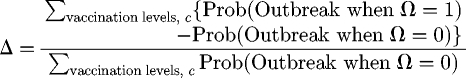that is, the relative height difference between the black and grey bars in figure 1b or 1c.

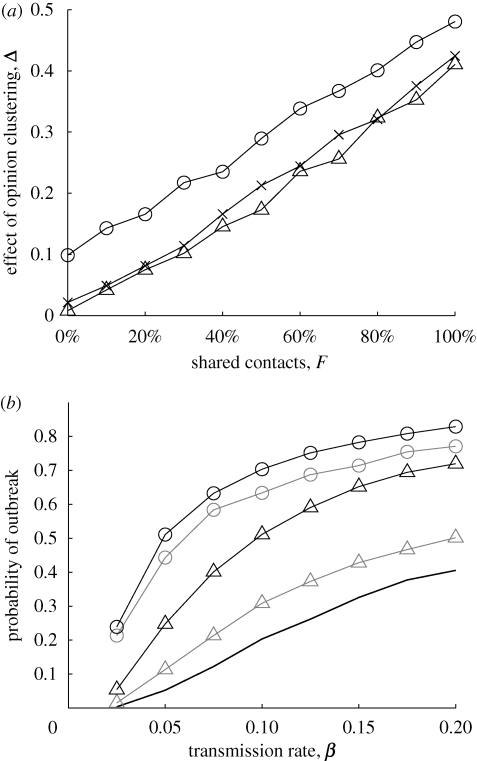
Increased overlap between the two networks increases Δ (figure 2a). Δ is larger in more localized networks; here, connected offspring may have unconnected parents whose mutual contacts result in them being part of an non-vaccinating cluster. Similar results arise if offspring and parents have different numbers of contacts (electronic supplementary material, fig. 1). Including long-distance connections in the parental network can negate the local clustering effect (electronic supplementary material, fig. 2), but, unless the comparison is between extremely local and long distance, the difference is minimal, and the impact of opinion formation can be predicted by the overlap between the networks.

Figure 2.

(a) Impact of shared contacts, F, on the effect of opinion clustering, Δ. Results are shown for different local thresholds: T = 0.1 (circles), T = 0.2 (crosses), T = unlimited (triangles). (b) Impact of amount of agreement between parents; c = 80 per cent and β is varied. Shown is the probability of an outbreak for F = 0.2 (grey) and F = 1 (black) and for agreement between parents of 0.68 (i.e. random vaccination, solid line), 0.75 (triangles) and 0.85 (circles); T = 0.2.

Greater agreement between parents corresponds to more clusters of unvaccinated children and therefore increases the likelihood of an outbreak (figure 2b).

4. Discussion

Clusters of susceptible individuals present a problem for infection control; they offer infection a safe haven from intervention, and a foothold into otherwise well-protected populations. An important consideration is that, often, the individuals who are at a risk of infection do not make vaccine decisions. Parents determine the protection their children receive. Thus, it is important to know the relationship between the networks of transmission and the networks of influence. The simple model presented here allows questions about the impact of parental vaccination choices on outbreaks of infection in children to be explored.

We have seen that the effect of opinion clustering among parents is stronger when there is more overlap between the networks of parents and those of their children. When the two networks share many contacts, clustering of opinion among parents can cause a large increase in the risk of an outbreak. This effect is increased when interactions are spatially local; in closely knit communities, two parents may have the same attitudes even if they do not directly influence each other. Therefore, we would expect clustered opinion to have the greatest impact when additional social factors, such as schools that serve particular religious communities (Hanratty et al. 2000; May & Silverman 2003; Schmid et al. 2008), result in large interacting groups of unvaccinated children.

Unvaccinated children are unlikely to form clusters unless their parents are also clustered; however, clustering of parents need not lead to clustering of offspring. It is important to understand the influences on parental choice—social contacts, healthcare providers, government information—and consider groups of parents who might decline vaccination; if their children are expected to interact, then surveillance should focus on them, since such groups can sustain infection outbreaks. The model presented here allows different degrees of opinion clustering among parents; simple surveys designed to measure agreement between pairs of socially connected parents would help to parameterize the model and to determine the extent to which social influences affect vaccination decisions.

We have assumed that the social networks influencing parental vaccination choices operate independently of infection; realistically, we might expect that the presence of infection in the offspring of parents' friends or neighbours would motivate vaccination of their own offspring. Thus, when there is more infection in the parents' community there would be a greater chance of choosing vaccination. We would expect this to have an impact if the parent and offspring networks overlap, but only if such reactive vaccination decisions operate rapidly enough to allow children to become immunized before exposure to infection. Greater benefits might accrue if infection within a school prompted additional vaccination uptake in nearby schools; here, the spread of information between parents of children in different schools would be important and thus the non-overlapping links between the parental and offspring networks could be key to enabling vaccination to outrun transmission.