Thermo- and Mesostabilizing Protein Interactions Identified by Temperature-Dependent Statistical Potentials

Abstract

The goal of controlling protein thermostability is tackled here through establishing, by in silico analyses, the relative weight of residue-residue interactions in proteins as a function of temperature. We have designed for that purpose a (melting-) temperature-dependent, statistical distance potential, where the interresidue distances are computed between the side-chain geometric centers or their functional centers. Their separate derivation from proteins of either high or low thermal resistance reveals the interactions that contribute most to stability in different temperature ranges. Thermostabilizing interactions include salt bridges and cation-π interactions (especially those involving arginine), aromatic interactions, and H-bonds between negatively charged and some aromatic residues. In contrast, H-bonds between two polar noncharged residues or between a polar noncharged residue and a negatively charged residue are relatively less stabilizing at high temperatures. An important observation is that it is necessary to consider both repulsive and attractive interactions in overall thermostabilization, as the degree of repulsion may also vary with temperature. These temperature-dependent potentials are not only useful for the identification of meso- and thermostabilizing pair interactions, but also exhibit predictive power, as illustrated by their ability to predict the melting temperature of a protein based on the melting temperature of homologous proteins.

Introduction

The evaluation and rational modification of protein thermal stability is an important challenge in molecular biology, and the number of studies focusing on this issue has been largely increasing during the past few years. However, although the amount of experimental data has grown and the theoretical approaches have improved, the exact rules that underlie protein thermostability remain basically unresolved.

The main reason for the intensification of experimental and theoretical research on protein thermostability is that an understanding of the mechanics involved would make possible a wide range of affordable and accessible new applications. The ability to rationally modify the thermal stability of a protein would allow the optimization of different bioprocesses (like starch blenching, or detergent depollution), as well as the design of new processes using proteins that remain stable and functional at the temperature that optimizes the process (1,2).

The complexity of the protein thermostability issue can be attributed to the high level of sequence and structure similarity between proteins of different thermal resistance (3), the lack of theoretical knowledge about the temperature dependence of the interactions that stabilize protein structures, and the diversity of ways to achieve the thermal resistance of a protein. Several studies comparing protein homologs with different melting temperatures or which come from organisms of different thermophilicity suggest a series of thermostability-influencing factors (4–12). For instance, salt bridges have repeatedly been shown to promote thermal resistance (3,7,8,11,12). However, many of the factors that have been pinpointed do not seem to be universal but depend on the protein family. Lately, an explanation of these discrepancies has been suggested that involves two kinds of thermal adaptation: a structure adaptation undergone by proteins coming from archaea, and a sequence adaptation undergone by proteins coming from mesophilic organisms that have recolonized hot biotopes (13).

It seems useful to recall briefly the differences between the thermal and thermodynamic stabilities of proteins. Thermodynamic stability is evaluated by the folding free energy at a given temperature, generally room temperature, and is usually in the 5–10 kcal/mol range. This weak free energy difference between folded and unfolded states reflects the subtle balance between the forces that tend to stabilize the unfolded state (essentially conformational entropy) and those that stabilize the folded conformation (the hydrophobic effect, and specific interactions such as H-bonds, salt bridges, cation-π, or π−π). In contrast, thermal stability refers to the temperature range where the folding free energy is negative, between the cold and hot denaturation (melting) temperatures. Usually, thermodynamic and thermal stabilities of proteins are correlated—the more thermodynamically stable at room temperature, the more thermally stable—but this is not always true (14). The basic reason for this is that the relative strengths of the different forces that stabilize the native fold depend on the temperature.

There is also a functional reason for the small folding free energy values. A protein has to be stable enough to avoid the loss of its structure and flexible enough to perform its biological activity near the functioning temperature (15–17). Generally, indeed, higher flexibility implies lower stability, although locally the converse may be true (19). This imposes a stability/activity balance and implies that the temperatures of optimal thermodynamic stability and optimal functioning may be very different. For example, human ubiquitin has a melting temperature of 91°C (20), whereas its functioning temperature is ∼37°C (21). This large temperature difference may be due to evolution, but might also indicate that some specific level of flexibility is required for the active site to fulfill its biological function in an optimal way.

A possible way to investigate these issues is to study theoretically the influence of temperature on the different entropic and enthalpic forces that play a role in the folding and stabilization of proteins. Another possibility is to rely on experimental data about the stability of proteins, and to derive rules from these data. We give preference here to the latter option, through the derivation of statistical mean force potentials from data sets of known protein structures. Such potentials are commonly used to predict protein structure and stability, because they are able to deal with low-resolution models and take the solvent implicitly into account. They have been shown to reflect the characteristics of the data set from which they are derived, such as protein length (22) or melting temperature (23). We exploited this property here to evaluate the temperature dependence of different kinds of amino acid pair interactions. For this purpose, we developed a statistical amino acid pair potential that takes into account the sequence and size adaptation of proteins to different thermal biotopes, and derived it from two subsets of proteins of known structure and melting temperature, one subset grouping mesostable and the other thermostable proteins. This technique allowed us to evaluate in an objective way the temperature dependence of various amino acid pair interactions, such as aromatic, salt-bridge, cation-π, H-bond, polar, and hydrophobic interactions.

Methods

Protein data set

We designed a protein data set that contains 166 proteins with an x-ray structure of good quality (resolution ≤2.5 Å) and known melting temperature, T_m. Only monomeric proteins were included in the data set, as identified by the Protein Quaternary Structure server (24). Indeed, the denaturation of multimeric proteins is usually not a one-step mechanism, and the exact meaning of the measured T_ms is not always precisely defined: do the T_ms correspond to the separation of the multimers into monomers or to complete denaturation?

The 166 entries were collected from the literature and from the ProTherm database (25) and were manually checked, on the basis of the original articles, to ensure the good quality of the data set. If several T_m measures were performed for a given protein, the one with a pH closest to 7 was kept. If more than one experience was driven under the same conditions, the mean T_m was computed.

This protein data set was divided into two subsets of 83 proteins each, one set referred to as mesostable, containing the entries with the lowest T_ms (T_m < 64°), and the other called thermostable, containing the entries with the highest T_ms (T_m > 64°). These two subsets were refined, using the protein-culling server PISCES (26), to avoid the presence of proteins of similar sequence in a data set, which would lead to a bias in our computations. In each subset, protein pairs showing >25% sequence identity were identified. In the mesostable group, the protein with the lowest T_m was kept, while the other was removed and in the thermostable group, the protein with the highest T_m was kept. This procedure leads to an increase in the difference between the average T_ms (${\overline{T}}_{\text{m}}$) of the two sets. The same refinement was performed on the complete data set, which is used as a reference set. In this case, when two proteins showed >25% sequence identity, the one with a T_m closest to the ${\overline{T}}_{\text{m}}$ was kept. The characteristics of each data set and their amino acid compositions are given in Table S1 and Table S2 of the Supporting Material. A detailed table including the list of all proteins in each data set and their characteristics is given in Table S3 and Table S4.

Statistical residue-residue potentials

Statistical amino acid pair potentials are derived from the relative frequency of observing residue pairs separated by a certain spatial distance in a set of known protein structures. These frequencies are assimilated to probabilities and converted into folding free energies using the Boltzmann law (27,28). To evaluate the temperature dependence of different kinds of residue-residue interactions, we previously formulated a statistical potential that takes into account the sequence adaptation of thermoresistant proteins. Here, we designed a modified version of this potential that is more adapted to compare sets of meso- and thermostable proteins and reads as follows:

$$\Delta W(s,s\prime ,d,{\overline{T}}_{\text{m}})=-kT\text{ln}\frac{P(s,s\prime ,d,{\overline{T}}_{\text{m}})}{P(s,s\prime )P(d,{\overline{T}}_{\text{m}})}\cong -kT\text{ln}\frac{F(s,s\prime ,d,{\overline{T}}_{\text{m}})}{F(s,s\prime )F(d,{\overline{T}}_{\text{m}})},$$ (1)

where F(s,s′,d,${\overline{T}}_{\text{m}}$) is the relative frequency of a pair of amino acids of types s and s′ separated by a spatial distance, d, in a data set of average melting temperature, ${\overline{T}}_{\text{m}}$; F(s,s′) is the relative frequency of pairs of residues, s,s′, in the complete data set, independent of the spatial distance that separates them ; F(d,${\overline{T}}_{\text{m}}$) is the relative frequency of distances, d, independent of the type of residues in a given subset of average melting temperature, ${\overline{T}}_{\text{m}}$; k is the Boltzmann constant; and T is the absolute temperature. The reason we consider F(d,${\overline{T}}_{\text{m}}$) instead of F(d) × F(${\overline{T}}_{\text{m}}$) in the denominator is to wipe out the effect of protein size. Indeed, the size has an influence on the distance distribution (22), and we want to avoid taking this effect into account, because we assume that the size distribution in each subset is not related to the thermo-/mesostability. In contrast, we assume that the overall composition of amino acids was adjusted through evolution to optimize thermal stability and thus consider F(s,s′) rather than F(s,s′,${\overline{T}}_{\text{m}}$) in the denominator.

We focused on nonlocal interactions along the polypeptide chain, and dismissed all pairs of residues separated by fewer than eight positions along the sequence. The spatial interresidue distance, d, was computed in two different ways: either between the geometrical centers of the heavy side-chain atoms, named C_μ (29), or between a new side-chain descriptor, referred to as C_ν, located near the characteristic functional group of the side chain to better account for the chemical properties of the residue. In the case of aromatic residues (Phe, His, Tyr, and Trp), the C_ν coordinates are defined as the average of the coordinates of all atoms of the aromatic rings. The C_ν of negatively charged amino acids (Glu and Asp) is located at the geometrical center of the COO⁻ group. The geometrical center of the CO-NH₂ moiety defines the C_ν pseudoatoms of Asn and Gln, and the center of CNH₂-NH₂⁺ defines the C_ν of Arg. The C_ν coordinates of Cys, Lys, Ser, and Thr are located on the S, N, O, and O atoms, respectively, of their side chains. For all other amino acids, the C_ν is identical to the C_μ.

Distances, d, between 3.0 Å and 8.9 Å were grouped into 55 overlapping bins of 0.5-Å width, each shifted by 0.1 Å; two additional bins describe distances <3.0 Å and >8.9 Å. This procedure ensures both a sufficient number of observations in each bin and a good resolution of the potentials, due to the bin width of 0.5 Å and their 0.1-Å shift, respectively. Yet, when the number of occurrences of an amino acid pair in a bin was <15, the energy value computed on this bin was considered to be insignificant and was excluded from our analysis. Note that although it is known to be an important parameter (28), we did not make the distinction between core and surface in computing the potentials, as the amount of data was too limited.

T-dependent protein folding free energy

The folding free energy ΔW of a protein of sequence S (consisting of amino acids of type s) and conformation C (represented by all interresidue distances, d) can be evaluated using our statistical potentials as

$$\Delta W(S,C,{\overline{T}}_{\text{m}})=\sum _{i,j\text{=}1;i+8<j}^N\Delta W(s_i,{s\prime }_j,d,{\overline{T}}_{\text{m}}),$$ (2)

where s_i and s′_j are the amino acid types at positions i and j along sequence S, and N is the length of S. The folding free energy, ΔW, depends on the ${\overline{T}}_{\text{m}}$ s of the proteins from which the potentials are derived. Using the potentials derived from the thermostable, mesostable, and reference sets (Table S1), we computed three folding free energies, denoted ΔW_thermo, ΔW_meso, and ΔW_ref, for each protein. In the next section, we argue that this ${\overline{T}}_{\text{m}}$-dependent potential actually represents a T-dependent potential.

Results

To systematically analyze the impact of temperature on the different types of residue-residue interactions, we developed the statistical potential defined in Eq. 1, which evaluates the contribution of each amino acid pair interaction to the protein folding free energy as a function of the melting temperature and the spatial distance separating the two amino acids, in the context of a mean protein environment. Two alternative definitions of the interresidue distance were used: the distance between the side chain centroids, C_μ, or that between the pseudoatoms, C_ν, that carry the main side-chain functional group (see Methods). The two novelties of this potential are the use of the C_νs and the estimation of the temperature dependence of pair interactions taking into account the protein adaptation across evolution in terms of sequence composition.

Given the limited amount of available data, we chose to limit the ${\overline{T}}_{\text{m}}$ dependence of the potentials to two discrete values of ${\overline{T}}_{\text{m}}$, corresponding to the average T_ms of the proteins belonging to the mesostable and thermostable subsets (see Methods and Table S1). Hence, for each of the 210 possible amino acid pairs, two potentials were obtained: one corresponding to proteins of high T_m, and the other to proteins of low T_m. When many more proteins with known structure and T_m become available, it will be possible to derive potentials on the basis of more than two discrete values of ${\overline{T}}_{\text{m}}$ and thus obtain a much more precise—even almost continuous—T_m dependence.

In the following discussion, we assume that this ${\overline{T}}_{\text{m}}$ dependence reflects a genuine T dependence of the pair interactions, and we use both terms without distinction. To do so, we must take into consideration that protein thermostability is achieved not only by having a larger number of stabilizing interactions, but also—at least in part—by an increased occurrence of interactions that are more resistant to temperature. Indeed, it is known that the free energy contributions of all amino acid interactions (such as salt bridges and hydrophobic forces) depend on the temperature, and that this T dependence differs according to the type of interaction. As a consequence, the potentials corresponding to T-resistant interactions will be computed as more favorable in proteins of high T_m, since they occur on average more frequently in such proteins. The ${\overline{T}}_{\text{m}}$ dependence of our potentials is therefore directly related to the T dependence of the residue-pair interactions, although the quantitative correspondence between T and ${\overline{T}}_{\text{m}}$ is not obvious to establish.

The energy profiles of the 210 potentials derived from thermostable proteins were compared to the corresponding potentials derived from mesostable proteins. To objectivize the comparison, a similar analysis was conducted on 1000 random pairs of subsets, with a view to assessing the statistical significance of the observed differences. According to the criteria listed in Appendix S2 and Fig. S1 of the Supporting Material, we found 36 amino acid pairs for which significant differences were observed between the potentials derived from the meso- and thermoresistant subsets, that is, for which the probability of finding similar differences in random pairs of subsets is small, and which are thus likely to play a role in the temperature resistance of proteins. Among those, nine appear to be more favorable at low temperatures, whereas the other 27 provide a more efficient stabilization at higher temperatures.

Unfortunately, the number of proteins whose melting temperatures have been experimentally measured is relatively limited. Some energy profiles are hence strongly affected by the noise resulting from the lack of data, and on the basis of our significance criteria, a number of amino acid pairs are not selected, even though they may be important with respect to temperature adaptation. To deal with this issue, we also derived effective potentials that involve the groups of similar amino acids defined in Appendix S1 and Table S5. In addition to the 36 residue-residue potentials that fulfill the statistical significance criteria, we also identified 43 potentials involving a single amino acid and an amino acid group, and eight potentials involving two amino acid groups. The results obtained with single amino acids and with groups are complementary: the latter yield a global, coarse-grained view of the effect of temperature on a given type of interaction to add to the finer analysis of the specificities of each amino acid type.

The pair potentials that successfully satisfy our statistical significance criteria are given in Tables 1 and 2, and are described in detail in the next subsections. The details of all pairs of amino acids and amino acid groups that satisfy our statistical significance criteria are presented in Table S6.

Table 1.

Thermostabilizing interactions

Thermostabilizing interactions	Interaction∗	Ptotal (%)†Cμ-Cμ	Ptotal (%)†Cν-Cν	Pmin (%)†‡Cμ-Cμ	Pmin (%)†‡Cν-Cν
Salt bridges	DE-KR	0.7	1.7	0.6 (3)	1.2 (1)
	D-KR	5.5	—	3.1 (2)	—
	E-KR	1.4	6.1	1.1 (1)	8.5 (2)
	DE-R	2.4	4.6	3.4 (3)	2.4 (2)
	D-R	8.6	5.5	4.6 (1)	6.3 (1)
	E-R	2.6	2.5	1.1 (2)	1.9 (5)
	E-H	—	2.7	—	3.7 (1)
Cation-π interactions	KR-FWY	3.7	2.8	3.1 (4)	1.6 (3)
	R-FWY	6.4	8.4	3.1 (2)	5.0 (3)
	KR-W	3.6	2.9	1.9 (3)	0.3 (1)
	KR-Y	3.6	3.5	1.2 (2)	1.3 (3)
	K-F	—	0.3	—	0.8 (2)
	K-Y	8.9	—	3.1 (2)	—
	R-W	1.8	—	7.3 (1)	—
	R-Y	0.5	1.5	0.8 (2)	0.7 (4)
	H-F	2.6	—	0.8 (1)	—
Aromatic interactions	F-FWY	8.0	8.2	7.5 (1)	9.4 (1)
	F-W	1.5	2.3	2.2 (2)	4.2 (2)
Negatively charged-Y or -W	DE-W	4.1	1.2	2.6 (5)	0.7 (2)
	DE-Y	3.3	6.1	1.2 (4)	1.1 (2)
	D-W	6.0	—	1.4 (1)	—
	D-Y	8.5	—	0.8 (5)	—
Small-charged	AG-KR	1.2	1.4	0.7 (1)	0.3 (2)
	G-KR	3.1	1.1	5.8 (2)	<0.1 (2)
	AG-R	0.4	4.0	0.7 (3)	0.6 (1)
	G-H	9.1	5.8	8.1 (1)	6.1 (1)
	G-R	2.8	5.7	0.5 (5)	0.4 (1)
	AG-E	8.2	—	6.8 (1)	—
	A-E	0.8	—	0.4 (2)	—
Cysteine-uncharged	C-AILV	9.7	—	5.7 (3)	—
	C-AG	—	7.8	—	9.1 (3)
	C-G	2.4	5.6	9.0 (2)	2.6 (4)
	C-FWY	0.4	0.8	0.2 (2)	0.4 (3)
	C-NQST	7.8	—	9.7 (2)	—
Isoleucine-hydrophobic or -small	I-AILV	1.0	0.8	2.1 (2)	0.9 (1)
	I-I	0.2	0.2	0.1 (4)	0.1 (5)
	I-AG	2.6	1.9	3.0 (2)	6.1 (3)
	I-A	0.1	0.1	1.7 (2)	1.8 (2)
	I-FWY	—	4.1	—	1.2 (3)
	I-W	5.6	4.2	0.7 (1)	0.6 (1)
	I-Y	3.7	3.8	4.6 (2)	4.3 (1)
Methionine-charged, aromatic, or -small	M-KR	3.7	1.2	4.4 (1)	4.5 (2)
	M-DE	—	3.5	—	4.9 (3)
	M-FWY	7.6	6.3	7.0 (2)	5.1 (1)
	M-Y	6.60	6.10	2.2 (1)	2.6 (1)
	M-A	1.1	1.2	2.1 (3)	1.7 (3)
Others	Y-AILV	5.7	3.5	5.7 (1)	4.9 (1)
	Y-V	9.3	—	1.8 (3)	—
	R-KR	6.2	—	6.7 (1)	—
	E-N	—	4.1	—	6.0 (2)
	R-N	2.1	—	1.5 (3)
	V-KR	9.4	—	3.6 (2)	—
	F-P	7.9	3.1	8.8 (1)	3.0 (3)
	N-P	5.0	—	1.4 (2)	—
	T-Y	—	3.9	—	3.2 (1)

^∗Italic indicates unfavorable interactions, for which the folding free energy is always positive.

^†P_total and P_min are the probabilities (%) that a similar difference in free-energy profile will be observed in random protein subsets. P_total is defined with respect to the global surface area between ΔWs from thermostable and mesostable subsets, and P_min is defined with respect to the surface area around the free-energy minima (see Appendix S2 in the Supporting Material and Fig. S1). A dash means that the statistical significance criterion (P_total < 5% and P_min < 10% in the case of pairs of amino acid groups, and P_total < 10% and P_min < 20% in the case of single amino acids) is not satisfied.

^‡Number of local minima considered is given in parentheses.

Table 2.

Mesostabilizing interactions

Mesostabilizing interactions	Interaction∗	Ptotal (%)†Cμ-Cμ	Ptotal (%)†Cν-Cν	Pmin (%)†‡Cμ-Cμ	Pmin (%)†‡Cν-Cν
Aliphatic- or small-noncharged polar	AILV-NQST	1.0	<0.1	0.5 (2)	0.2 (2)
	AG-NQST	0.3	0.2	0.1 (2)	0.5 (2)
	A-NQST	1.6	1.7	1.4 (3)	0.8 (4)
	G-NQST	0.8	1.3	0.1(2)	0.5(1)
	L-NQST	0.3	1.2	0.4 (4)	0.5 (3)
	AILV-N	3.2	5.9	2.7 (1)	4.6 (2)
	AILV-Q	7.8	5.1	8.5 (2)	1.9 (2)
	AG-S	4.8	5.8	4.0 (3)	1.9 (1)
	AILV-T	3.5	7.5	3.3 (2)	5.6 (2)
	AG-T	0.1	0.4	0.9 (3)	<0.1 (3)
	A-T	1.5	1.2	0.5 (3)	0.3 (4)
	G-S	2.6	—	1.4 (3)	—
	G-T	5.4	9.4	<0.1 (1)	<0.1 (2)
Noncharged polar-noncharged polar	NQST-NQST	0.1	0.1	0.1 (1)	0.1 (1)
	N-NQST	<0.1	0.8	<0.1 (2)	<0.1 (3)
	Q-NQST	<0.1	<0.1	<0.1 (2)	<0.1 (3)
	S-NQST	4.8	1.2	2.7 (1)	0.6 (1)
	T-NQST	6.3	—	0.9 (1)	—
	S-N	—	5.9	—	2.6 (2)
Negatively charged-noncharged polar	DE-NQST	4.5	—	0.9 (1)	—
	D-NQST	0.2	0.2	0.4 (3)	2.6 (3)
	DE-T	1.0	3.2	0.5 (3)	4.1 (3)
Small-small	G-AG	2.1	2.3	1.6 (1)	1.6 (1)
	A-G	5.1	4.5	1.4 (1)	1.1 (2)
Leucine-other	L-FWY	—	4.5	—	3.7 (1)
	L-F	5.9	—	8.1 (2)	—
	L-D	8.6	—	6.3 (2)	—
	L-G	1.9	1.9	1.9 (3)	1.8 (3)
Negatively charged-F	DE-F	9.3	—	1.5 (1)	—
	E-F	—	9.2	—	6.5 (1)

See Table 1 footnotes.

Thermostabilizing interactions

As shown in Table 1, several kinds of amino acid pair interactions are significantly more frequent and stabilizing in the subset of thermostable proteins than in the set of mesostable proteins. These involve salt bridges, cation-π interactions, aromatic interactions, and some types of H-bond and hydrophobic interactions. Note that we use the term “thermostabilizing interactions” in a relative sense, to indicate interactions that are more favorable (or less unfavorable) at higher temperatures compared to the other interactions.

Salt bridges

Salt bridges are established between a residue carrying a negative charge (D or E) and a residue carrying a positive charge (K or R). Histidine (H) can be positively charged or neutral in physiological conditions, and is thus also capable of forming salt bridges in some protein environments. Several previous studies have pointed at salt bridges as being particularly important in the thermostabilization of proteins, on the basis of analyses of homologous protein families (3,7,8,11,12), physicochemical considerations (30), or statistical potentials (23). In agreement with this, we find that several pair potentials involving oppositely charged residues are identified as significantly more favorable at high temperatures in comparison with other interactions. In particular, for the DE-KR potential (Fig. 1, A and B), the probability of observing similar differences in random sets is <1% for the C_μ-C_μ potential and slightly higher than 1% for the C_ν-C_ν potential (Table 1).

Figure 1.

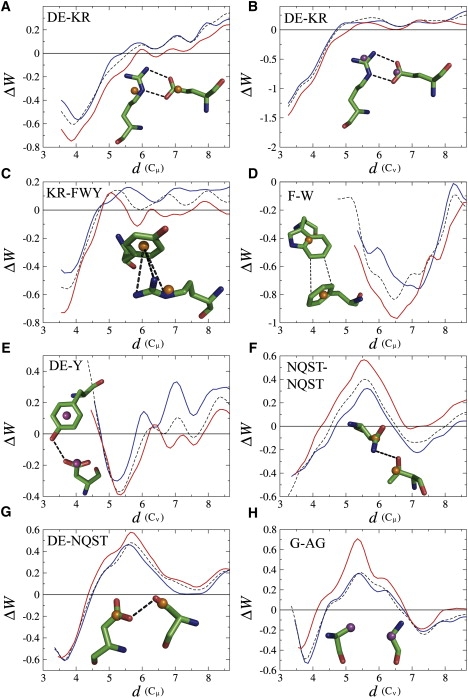
Folding-free-energy contribution, ΔW (kcal/mol), as a function of the distance, d, between side-chain descriptors for the thermoresistant protein subset (red), the mesoresistant subset (blue), and the reference subset (dashed line). The molecular structures drawn correspond to examples of the interactions DE-KR (A), DE-KR (B), KR-FWY (C), F-W (D), DE-Y (E), NQST-NQST (F), DE-NQST (G), and G-AG (H). Plots designed with PyMol and XmGrace (38,39). The side-chain descriptor is the C_μ pseudoatom in A, C, D, F, and G, and the C_ν pseudoatom in B, E, and H.

The comparison between the amino acid pair potentials and the potentials involving amino acid groups indicates subtle differences among salt bridge interactions. First the stabilization at high temperatures appears to be stronger for salt bridges involving R than for those involving K. Indeed, the latter are selected by our significance criteria only when R and K are grouped. This may be related to the fact that the side chain of K is longer and possesses more entropic degrees of freedom and/or that the positive charge of R is delocalized on the guanidinium group. Second, H residues also form thermostabilizing salt bridges with E, but the statistical significance of this observation is less pronounced, which is obviously due to the fact that not all histidines are positively charged in physiological conditions. Third, the observed impact of temperature is slightly more significant for salt bridges involving E than for those involving D, whereas the free-energy minimum is deeper for salt bridges involving D. This may be related to the shorter side chain of D relative to E. Overall, we thus observe that among salt bridges, the amino acid pairs E-R and D-R are the most influential with respect to thermostabilization.

It is interesting to note that the absolute minimum of the salt bridge potential, at distances of 3–4 Å, is much deeper in the C_ν-C_ν potential (∼−1.5 kcal/mol) than in the C_μ-C_μ potential (∼−0.6 kcal/mol). This can be attributed to the fact that the C_ν pseudoatoms represent more accurately the position of the charges and, thus, that the distance between the C_νs of amino acids forming a salt bridge is much more constant than the distance between their C_μs. The C_μ-C_μ salt bridge potentials E-R and D-R show a second minimum at inter-C_μ distances of ∼5–7 Å (Fig. S1, Fig. S6, and Fig. S7), which corresponds to another kind of side-chain geometry, as shown earlier (23). This second minimum is absent in the potentials involving amino acid groups, as it is defined by different inter-C_μ distances (minus the side-chain radii; see Appendix S1 in the Supporting Material) for each amino acid of the groups. It is also absent in the C_ν-C_ν potential because all salt bridge geometries, for all amino acid pairs, are represented by the same inter-C_ν distances and thus are all included in the first free-energy minimum; this somehow explains why this minimum is so much deeper in the C_ν-C_ν potential.

Cation-π interactions

Cation-π interactions in proteins are defined as an aromatic amino acid (F, W, Y) interacting with a positively charged residue (K, R) located above it. The C_μ-C_μ and C_ν-C_ν potentials both present a deep minimum at short interresidue distances, supporting the importance of cation-π interactions in stabilizing folded proteins (Fig. 1 C). Note that our results also show that the contribution of these interactions to stability is higher at elevated temperatures relative to the contribution of other interactions, as suggested previously (31,32). Indeed, most pair potentials corresponding to cation-π interactions successfully pass our statistical significance criteria, and are identified as thermostabilizing interactions whether they involve individual amino acids or amino acid groups. The most thermostabilizing cation-π interactions are established between R and Y or W. The higher thermostabilizing effect of R compared to K may be related to the fact that its guanidinium group makes stacking interactions with the aromatic moiety, in addition to electrostatic interactions. The H-F interaction also satisfies our significance criteria, but it mixes aromatic π-π stacking and cation-π interactions when the histidine is charged (32).

Note that the related interaction, called amino-π, between an aromatic moiety (F, Y, or W) and a group carrying a partially charged (amino) group (Q or N) located above it, is not identified as being thermostabilizing.

Aromatic interactions

Aromatic amino acids are not very abundant in proteins, and it is hence not easy to accurately determine their influence on protein stability in different temperature ranges (33). It has previously been shown that the occurrences of such interactions are sometimes—but not always—more frequent in thermoresistant proteins than in their mesoresistant homologs (3–8).

Here, due to our ability to group the three aromatic amino acids in a single class, we were able to reach a sufficient number of occurrences and to show the generally thermostabilizing tendency of aromatic interactions (Table 1 and Fig. 1 D).

Negatively charged-aromatic (Y or W)

Another type of interaction that appears to be more favorable at higher temperatures links a negatively charged residue (D or E) to an aromatic residue (Y or W); the interaction involving Y is especially thermostabilizing. Note that the potential between D/E and F, the third aromatic residue, shows the opposite behavior: the effective folding free energies are more favorable when derived from the set of mesostable proteins (see Table 2). This indicates that the aromatic character of Y, W, and F is not determining—as far as thermostability is concerned—when these residues interact with D or E. The characteristics of Y and W, compared to F, are their larger polarity and their ability to form H-bonds. Inspection of the geometries of DE-YW interactions that contribute to the folding free energy minimum shows that the D or E side chains are in the aromatic plane of the Y or W side chains, where there is a lack of electrons, and, moreover, that they form an H-bond with the alcohol group of Y (O_η atom) or the amine group of W (N_ɛ1 atom). We can thus conclude that this type of H-bond is quite resistant to temperature.

Small-charged

Our results also indicate that a small amino acid (A or G) interacts more favorably with a charged amino acid (D, E, K, or R) in thermoresistant proteins. In fact, these interactions are not particularly stabilizing: the free-energy minimum corresponding to these interactions is not very deep and in some cases remains positive at all interresidue distances. This means that relative to other interactions, this type of interaction is less detrimental to protein stability at higher temperatures. The rationale behind this observation is difficult to establish: charged amino acids are known to be more frequent in thermostable proteins, but residues such as A and G are less frequent (Table S2).

Isoleucine-, cysteine-, or methionine-involving interactions

In some cases, the thermostabilizing character of a pair potential is mostly driven by one of the residues that form the interaction. This is the case for I-, M-, and C-involving interactions. All three amino acids are more frequent in our set of thermostable proteins than in the set of mesostable proteins, which partly explains why the interactions involving these amino acids appear to be more thermoresistant.

As shown in Table 1, the interaction between I and hydrophobic or small amino acids has a high thermal resistance, as reported previously (23). Curiously, although their chemical properties are very similar, L and V amino acids present a very different behavior with respect to temperature (Table 2). Note that for these three aliphatic amino acids, the variations in composition between mesostable and thermostable proteins seem to be correlated with their side-chain hydrophobicity. Indeed, according to most hydrophobicity scales (34,35), I is more hydrophobic than V, and V is more hydrophobic than L. In a similar way, as shown in Table S2, the frequency of I is higher in thermoresistant than in mesoresistant proteins, the frequency of V is basically identical in the two sets, and the frequency of L is lower in thermoresistant proteins. This finding can be taken to mean that a higher hydrophobicity is beneficial to thermal stability, which may be rationalized as follows: side chains with more hydrophobic groups experience a higher entropic penalty in the unfolded state due to their solvation, and thus tend to increase the stabilility of the folded state. This suggests that the replacement of L or V by I tends to increase the thermal stability of proteins by stabilizing their hydrophobic core.

The interaction between C and an uncharged residue also appears as thermostabilizing. C is significantly more frequent in thermostable proteins, which probably results from the fact that some proteins rely on disulfide bridges to ensure a sufficient temperature resistance (3). The reason the C-C pair potential does not come out among thermostabilizing interactions, which would be direct proof of the thermal resistance of disulfide bridges, is that C is quite a rare amino acid and this poses statistical significance problems.

Other interactions

The last rows of Table 1 contain the other pairs of amino acids selected by our procedure. Some correspond to interactions that do not bear a clear physical meaning, and are isolated in the sense that no similar amino acid pairs are selected. Therefore, it is likely that some of these pairs correspond to artifacts attributable to the relatively limited number of proteins of known melting temperature. Other pair potentials probably correspond to interactions whose thermoresistance and/or statistical significance is relatively limited.

However, some of these other interactions may be relevant and come out more clearly when larger data sets become available. In particular, the totally unfavorable R-KR interaction, between positively charged residues, appears less unfavorable in proteins of high melting temperature. This finding again shows the power of our procedure: it identifies not only favorable interactions that are more or less thermoresistant but also unfavorable ones that are more or less repulsive according to the temperature. It is the balance of these different repulsive and attractive interactions that defines the thermal resistance of a protein.

Mesostabilizing interactions

Proteins from psychrophilic microorganisms are able to perform their biological functions at temperatures around, or even below, 0°C (3,15). In such proteins, it is difficult to find a compromise between stability and flexibility (18), and they are thus particularly interesting to study. Unfortunately, our data set of proteins contains very few psychrostable proteins. Indeed, the lowest melting temperature in our data set is 39.45°C, and the average for the mesostable protein subset is 51.8°C. We are thus able to analyze only the interactions that are more stabilizing in this range of temperatures. It is possible that psychroresistance is achieved through different, as yet unidentified, interactions.

The pair potentials identified as being more resistant at lower temperatures, according to our statistical significance criteria, are listed in Table 2 and Fig. 1, F–H (see also Figs. S57–S86 in the Supporting Material). They are discussed in detail in what follows. Note that we use the term mesostabilizing interactions in a relative sense, to indicate interactions that are more favorable (or less unfavorable) at lower temperatures compared to the other interactions.

Noncharged polar-noncharged polar

Interactions between noncharged polar residues appear to be relatively more stabilizing at low than at high temperatures. For some pairs of groups, such as NQST-NQST, the probability of similar differences being observed in random sets is as low as 0.1%. In addition, the influence of temperature is found to be equivalent for all subgroups of NQST, and is identified as significant with both the C_μ- and C_ν-based potentials. Inspection of the geometries corresponding to the first free-energy minimum, at distances of ∼3–4 Å, shows an H-bond between the amide moieties of N (atoms O_δ1 and N_δ2) and Q (atoms O_ɛ1 and N_ɛ2) and the alcohol groups of S (atom O_γ) and T (atom O_γ1). These observations strongly support the idea that H-bonds between noncharged polar residues are more stabilizing at low temperature relative to other interactions.

These results are in accordance with the differences in amino acid composition between the two subsets of proteins corresponding to different ${\overline{T}}_{\text{m}}$ values (Table S2). Indeed, the number of polar residues N, Q, S, and T in our thermostable protein subset is slightly lower than in our mesostable subset. This is possibly also related to the deamidation tendency of N and Q residues at higher temperatures, and to the fact that S and T residues seem to facilitate this deamidation process (36). The difference in composition may thus result from the temperature adaptation of the proteins.

Negatively charged-noncharged polar

Our results show that noncharged polar residues (N, Q, S, and T) also interact with negatively charged residues (D and E), and that these interactions are less favorable at higher temperatures. The potential curves present a deep minimum at interresidue distances of ∼3–4 Å. This minimum corresponds to the formation of an H-bond between the amide moieties of N (atoms O_δ1 and N_δ2) and Q (atoms O_ɛ1 and N_ɛ2) or the alcohol groups of S (atom O_γ) and T (atom O_γ1) and the carboxyl group of D (atoms O_δ1 and O_δ2) or E (atoms O_ɛ1 or O_ɛ2).

Negatively charged-F

Whereas negatively charged residues interact with aromatic residues Y or W in a way that promotes thermal resistance, as described above, their interaction with F is more stabilizing at lower temperatures, probably because of the incapacity of F to form H-bonds and/or its higher hydrophobicity. The only favorable geometry occurs when the charged group is in the aromatic plane of F, where there is a lack of electrons. However, the contribution of this interaction is not very stabilizing (ΔW ≈ −0.1 kcal/mol).

Aliphatic- or small-noncharged polar

The interactions between noncharged polar residues and aliphatic or small residues are also relatively more stabilizing at lower temperatures. These interactions are only moderately stabilizing (ΔG values of ∼−0.2 to −0.4 kcal/mol) and exhibit two clear minima, one at interresidue distances of ∼4 Å and another at ∼7 Å; both minima are visible in both the C_μ-C_μ and C_ν-C_ν potentials. Inspection of the geometries of these interactions shows that they consist mostly of nonspecific packing, and that the polar residues are generally located at the protein surface or involved in specific interactions, such as H-bonds, with other residues in the vicinity.

Small-small

The interactions between small residues also appear to be more stabilizing in mesostable proteins than in thermostable ones. In fact, closer inspection of the shape of the potentials indicates that finding two small residues separated by ∼5 Å—that is, not directly interacting—is much less unfavorable in mesostable proteins. This observation is difficult to interpret and is expected to come from a mixture of several indirect effects, such as the incapacity of small amino acids to form specific side-chain interactions, their main-chain flexibility (especially in the case of glycine), and their small entropy loss upon folding (37).

Leucine-other

We reported above that interactions involving I present a strong thermal resistance. In contrast, we find here that interactions with L appear to be preferred in mesostable proteins. This results essentially from the lower frequency of leucine in the thermostable subset, whereas I is more frequent. As discussed above, this may be related to the lower hydrophobicity of L compared to V and I.

Prediction of thermostability within homologous protein families

To probe the predictive power of our T-dependent potentials, we apply them to evaluate the T_m of a protein belonging to a given homologous family on the basis of the T_ms of the other proteins in the family. For that purpose, we retrieve from our complete set of 166 proteins of known structure and T_m eight homologous protein families containing at least three members. These families are summarized in Table 3 and described in detail in Table S6. The folding free energy of each of these proteins is evaluated by means of Eq. 2, using the potentials derived from the thermostable, mesostable, and reference protein sets. This yields three types of folding free energy for each protein, ΔW_thermo, ΔW_meso, and ΔW_ref (see Methods).

Table 3.

Linear correlation coefficients between folding free energies and melting temperatures in eight protein families

Protein family	Number of members	r (Tm, ΔWref)	r (Tm, ΔWthermo − ΔWmeso)
Acyclophosphatase	3	−0.96	−0.96
Adenylate kinase	5	−0.54	−0.78
α-Amylase	4	−0.97	−0.95
Endoglucanase 12	4	−0.41	−0.88
Cold shock protein	3	+0.99	−0.99
Cytochrome P450	5	+0.40	−0.80
Lysozyme	4	−0.58	−0.97
Myoglobin	3	+0.97	−0.88
Average		−0.14	−0.90

r, linear correlation coefficient; ΔW, folding free energy; T_m, melting temperature.

If thermodynamic and thermal stability were perfectly correlated, we would expect to find a good linear anticorrelation between the T_m and ΔW_ref values of the proteins belonging to a given family. As seen in Table 3 and Table S6, this is true for certain families, but not for all families: we observe an almost perfect anticorrelation for one family, with a linear correlation coefficient, r, of −0.97, whereas we find an almost perfect correlation (r = +0.99) for another. On average, the correlation coefficient is negative but quite close to zero (r = −0.14).

To analyze whether our T-dependent potentials perform better than the T-independent ones, we compare the T_ms of the proteins belonging to a homologous family with their folding-free-energy differences, ΔW_thermo − ΔW_meso. We thus focus now only on the interactions that are more or less stabilizing in thermostable proteins than in mesostable proteins, and correlate the presence of these interactions with the melting temperature. As shown in Table 3 and Table S6, there is a clear anticorrelation between ΔW_thermo − ΔW_meso and T_m: the linear correlation coefficients, r, are between −0.78 and −0.99, with an average of −0.90. This anticorrelation can thus be used to predict the T_m of a new protein of the family.

These results clearly show the importance of introducing a T dependence in the potentials to identify the interactions in a protein that are important for ensuring thermal stability, and for predicting, for example, the T_m of a protein based on the T_ms of homologous proteins. This predictive power will be thoroughly exploited in further analyses.

Conclusion

The goal of this study was to carry out an automatic and systematic analysis of the temperature dependence of the amino acid pair contributions to the protein folding free energy. For this purpose, we designed two subsets of proteins of known structure that differ with respect to their thermostability, a statistical distance potential specifically designed to monitor temperature dependence, and an automated method for analyzing the statistical significance of the observed dependence. We also introduced a different potential where the distances are computed between C_ν pseudoatoms, which represent more accurately the location of the side-chain functional groups such as aromatic cycles, carboxylic groups, alcoholic groups, and amine groups. This potential gives information complementary to that provided by the C_μ-C_μ potential, where the distances are computed between side-chain geometric centers. For salt-bridge potentials in particular, the C_ν representation appeared to be slightly superior (Table 1, Fig. S2, Fig. S3, Fig. S4, Fig. S5, Fig. S6, Fig. S7, and Fig. S8).

The conclusions that can be drawn from our analysis are summarized as follows:

• 1.Salt bridges, cation-π interactions, and H-bonds involving a negatively charged residue and an aromatic residue, all of which involve electrostatic interactions, are more stabilizing at high temperatures relative to other interactions. In a similar way, repulsive interactions between positively charged residues appear to be relatively more favorable (less unfavorable) at high temperatures.
• 2.H-bonds between two polar noncharged residues, or between a polar noncharged residue and a negatively charged residue, are relatively less stabilizing at high temperatures. Note, however, that this property may be indirectly due to the deamidation tendency of N and Q at higher temperatures and to the facilitation of this process by S and T.
• 3.Interactions between aromatic residues, which involve π-π stacking (when they are parallel), electrostatic interactions (in T-shape), and hydrophobic packing appear to be more stabilizing at high temperatures relative to other interactions. In a similar way, cation-π interactions involving arginine, where the positive charge is delocalized on the guanidinium group and which engender π-π stacking interactions with the aromatic moiety, are more thermostabilizing than cation-π interactions involving lysine, which are of a purely electrostatic nature.
• 4.Hydrophobic packing of aliphatic residues appears to be equally stabilizing at all temperatures when valine is involved, thermostabilizing when isoleucine—the most hydrophobic aliphatic residue—is included, and mesostabilizing when leucine—the least hydrophobic residue—is involved. Thermoresistance thus seems to be favored by highly hydrophobic residues, for which the solvation penalty in the unfolded state is highest.
• 5.Disulfide bridges appear to be thermally stabilizing, though the rarity of cysteine residues makes it difficult to reach a definite conclusion.
• 6.Some interactions appear as not (or not very) stabilizing, but rather less detrimental to protein stability in either the thermo- or the mesostable protein subsets. In some cases, this effect seems to result from the properties of only one of the interacting partners. In particular, the greater occurrence of small-charged interactions among thermostabilizing pairs, and of small or aliphatic-noncharged polar interactions among mesostabilizing pairs, can probably be credited to the thermostabilizing nature of charged residues and the mesostabilizing nature of noncharged polar residues, respectively. The fact that interactions between small residues appear to be mesostabilizing is also probably due to the character of small amino acids and the incapacity of their side chains to form specific interactions.

Some of these conclusions are somewhat tentative and should be confirmed when more data become available. In an attempt to further support the reliability of these conclusions, we performed a similar analysis with contact potentials, defined in the same way as the distance potentials of Eq. 1, except that only two distance ranges were considered, in which d is either smaller or larger than a threshold distance D. Two threshold distances were considered, D = 6 Å and D = 8 Å, calculated either between C_μs or C_νs; the former threshold is better suited for small residues and the latter for large residues. These contact potentials were derived from the mesostable and thermostable protein subsets, and the results were in agreement with those obtained using the distance potentials. For all mesostable interactions listed in Table 2, the contact potentials turned out to be more favorable (or less unfavorable) when derived from the mesostable protein subset, for both distance thresholds and independent of the use of C_μs or C_νs (Table S8). In a similar way, for all thermostable interactions listed in Table 1, the contact potentials were more favorable when derived from the thermostable protein subset, for both distance thresholds and C_μ-C_ν definition in almost all cases, and in all cases for at least one of these.

We would furthermore like to stress that there are two distinct ways for increasing thermal resistance: by stabilizing the structure both thermodynamically and thermally, or by stabilizing it thermally while keeping the thermodynamic stability unchanged. Increasing the number of stabilizing interactions will increase both types of stabilities, whereas replacing some interactions by different ones allows the modulation of the thermal stability only. Our approach aims at identifying the factors whose effect is specific to the thermal stability. However, distinguishing between both ways of reaching thermal resistance is far from obvious and would only be possible by comparing sets of proteins of equivalent thermodynamic stability but different thermal stability.

Another interesting observation that results from our analysis is that instead of focusing on stabilizing interactions only, it is necessary to look also at repulsive interactions, which may be more or less repulsive according to the temperature, and thus also contribute to the overall thermal stability of a protein. This is especially true given that our potentials are mean force potentials, which mix enthalpic and entropic contributions from charges, partial charges, permanent or induced dipoles or quadrupoles, hydrophobic forces, aromatic stacking, conformational entropy, etc. Many more data will be necessary to unravel precisely all these contributions and the effects of the protein environment.

However, even if we have not yet elucidated all details of protein thermal stability, the C_μ-C_μ and C_ν-C_ν potentials we derived from the thermoresistant and mesoresistant protein sets can be directly incorporated in algorithms aiming at predicting protein thermal stability changes upon mutation. These are expected to outperform the existing algorithms, which mostly consist of inferring thermal stability from thermodynamic stability. A first analysis firmly supports these expectations: in eight families of homologous proteins, T_m was shown to have a clear anticorrelation with the difference in folding free energy, ΔW_thermo − ΔW_meso (<r> = −0.90), whereas with the usual T-independent potentials, the anticorrelation between T_m and ΔW_ref values was very bad (<r> = −0.14).

Supporting Material

Amino acid groups, statistical criteria to identify differences among potentials, eight tables, and 86 figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01724-X.