TEM-1 Backbone Dynamics—Insights from Combined Molecular Dynamics and Nuclear Magnetic Resonance

Abstract

Dynamic properties of class A β-lactamase TEM-1 are investigated from molecular dynamics (MD) simulations. Comparison of MD-derived order parameters with those obtained from model-free analysis of nuclear magnetic resonance (NMR) relaxation data shows high agreement for N-H moieties within α- and β-secondary structures, but significant deviation for those in loops. This was expected, because motions slower than the protein global tumbling often take place in loop regions. As previously shown using NMR, TEM-1 is a highly ordered protein. Motions are observed within the Ω loop that could, upon substrate binding, stabilize E166 in a catalytically efficient position as the cavity between the protein core and the Ω loop is partially filled. The rigidity of active site residues is consistent with the enzyme high turnover number. MD data are also shown to be useful during the model selection step of model-free analysis: local N-H motions observed over the course of the trajectories help assess whether a peptide plan undergoes low or high amplitude motions on one or more timescales. This joint use of MD and NMR provides a better description of protein dynamics than would be possible using either technique alone.

Introduction

The dynamics of a protein refers to its internal motions (1). These take place on a wide range of timescales, from sub-picosecond bond vibrations to events lasting seconds or days, such as the folding or unfolding of a domain. Some of these structure fluctuations directly influence ligand binding and catalytic events. Our research group previously carried out an investigation of TEM-1 backbone dynamics using nuclear magnetic resonance (NMR) relaxation experiments analyzed within the model-free formalism (2). TEM-1 hydrolyzes various penicillin substrates, including ampicillin. It is the commonest β-lactamase in Gram-negative bacteria and a model enzyme. Describing dynamics events related to catalysis in TEM-1 furthers our understanding of β-lactam resistance and provides information to assist in the rational design of new antibiotics. Here, we present the results of molecular dynamics simulations of β-lactamase TEM-1 and compare backbone dynamics parameters with those obtained from NMR. We use MD trajectories as a tool for validating and refining NMR results.

TEM-1 is a 263-residue protein (28.9 kDa) that consists of two domains: the first is α/β, and is comprised of a five-stranded β-sheet and three α-helices. The second is all α, and contains eight helices. The active site is located at the domain interface and comprises five residues: S70 (the catalytic serine), K73, S130, E166, and K234. The Ω loop, a common feature of class A β-lactamases, borders the active site, spanning residues 161–179, including helix H7 (168–170) and catalytic E166. β-Lactam hydrolysis happens in two steps: acylation to catalytic S70, followed by deacylation and antibiotic release (3). The mechanism of the first step is still controversial with regard to the nature of the S70-activating general base, warranting further investigation into TEM-1 catalytic properties at the atomic level (4,5). With at least 160 known variants with various substrate specificities (6), TEM β-lactamases display an exceptional adaptability. TEM-1 structure and dynamics were studied extensively by x-ray diffraction (7–9), NMR spectroscopy (2,10), and computational methods such as molecular dynamics (MD) and semiempirical quantum mechanics/molecular mechanics (3,4,11–13). For reviews of β-lactam resistance and serine β-lactamases, see the literature (14,15).

The analysis of NMR relaxation measurements by the model-free approach (16,17) yields generalized squared order parameters (S²) and local correlation times (τ). S² is interpreted as the degree of spatial restriction of a chemical bond vector. The value τ is the vector rate (timescale) of motion. The vectors investigated are usually the N-H bonds in the amide of the peptide planes. In a previous work (2), we reported that TEM-1 is a highly ordered protein with an unusually high average S² of 0.901. The Ω loop and active site were highly ordered on the picosecond-to-nanosecond timescale, although slow motions were detected on the microsecond-to-millisecond timescale. These slow motions might be related to catalysis. Protein-scale motions (such as domain unfolding) were found to be very limited.

However, dynamics parameters derived from NMR relaxation experiments cannot be easily interpreted in terms of precise physical motion, and they probe timescales faster than the protein global tumbling time. In contrast, MD simulations provide precise descriptions of the dynamics at the atomic level and are not limited by the protein global tumbling. Recently, MD has been used to study the dynamics of many proteins, including model systems such as lysozyme and ubiquitin, for which simulated dynamics reproduced experimental (NMR spectroscopy) results very well (18,19). Such simulations are useful to validate and compare force fields and verify the accuracy of simulations of a given biological system. Combined approaches using both NMR and MD have been used to study protein dynamics and their contribution to molecular recognition (20). Using MD simulations, we confirm that TEM-1 is a rigid protein and show that high amplitude motions take place in the Ω loop bordering the active site, whereas the latter is kept rigid by a network of hydrogen bonds. Model-free model selection is a delicate process due to the risks of under- and overfitting, and it is sometimes impossible to discriminate among two or more models that each fit experimental data just as well; we show that the motions observed in MD simulations allow the elimination of some models on the basis of physical criteria, leading to an improved analysis procedure.

Methods

Computational methods

The CHARMM program (21), Ver. c31b2, was used to build the system and perform the simulations. Initial coordinates were taken from wild-type TEM-1 crystallographic structure 1XPB (1.9 Å resolution) (9). Solvated system contains 32,862 atoms. Simulations were carried out in the NPT ensemble using the CHARMM22 force field (22) and periodic boundary conditions. The first 5 ns of simulation were considered equilibration time. Total system energy, backbone root mean-square deviation (RMSD), surface accessibility, and solvent-protein interaction energy were stable after ∼2 ns (graphs shown in the Supporting Material). Three 25-ns trajectories were recorded. Twenty nanoseconds of each of these were analyzed.

Two methods were used for peptide N-H bonds S² parameter calculation. In the first approach, global tumbling was removed by a root mean-square minimizing superposition of the C_α of residues involved in secondary structures. By doing so, a fixed reference frame is obtained where only local motions take place. The autocorrelation function C_I(t) is computed for each trajectory (approximating the ensemble using the last 20 ns of simulation) for t < 10 ns. Convergence to a plateau value was visually verified. S² is the mean C_I(t) value past convergence point. When a function did not converge, S² was estimated as the average of the last 500 ps. This first method is referred to as M₁ in the following sections. The second method combines trajectories to obtain better conformational space sampling. Global tumbling is removed as in method M₁, and all structure snapshots from the three trajectories are combined and randomized. The correlation function decays to its plateau value immediately after C_I(0). The S² estimate therefore takes into account 60 ns of simulation time. This method is referred to as M₂ in the next sections. Function convergence has no meaning within M₂, but the convergence information provided by M₁ gives clues as to whether there is sufficient statistical sampling of a given conformational space. To the best of our knowledge, this is the first time multiple trajectories are combined in such a way to improve S² computations.

Exhaustive methodology for system generation, molecular dynamics simulations, order parameters calculations, and essential dynamics, along with detailed S² parameters, convergence information, and plots showing simulation stability are given as Supporting Material.

Reanalysis of NMR data

¹⁵N spin relaxation data for TEM-1 were previously analyzed using the model-free formalism with the ModelFree program, Ver. 4.15 (2). To take advantage of recent developments in model-free analysis (23–26) and improve our comparison of MD- and NMR-derived order parameters, we decided to reanalyze published data using two different protocols. Complete methodology, detailed results, and their discussion are available as Supporting Material and summarized below.

In the first protocol, the conceptual approach of Mandel et al. (27) was used as in the original analysis, but we used it with ModelFree, Ver. 4.20, to assess the influence of improvements related to termination criteria, simulated distribution of F-statistic error, parameter bounds, and the Levenberg-Marquardt algorithm (25). Except for a few residues, the resulting model-free parameters are similar to those obtained from the original analysis.

The second reanalysis uses a modified version of the analytical protocol of d'Auvergne and Gooley (26,28) with the relax program, as described elsewhere (29). Extracted model-free parameters are slightly different from those originally published. However, the general trends are the same: TEM-1 is a highly ordered protein with slow μs-ms motions present in the vicinity of the active site.

Results and Discussion

Order parameters comparison

Average backbone S² values determined from MD simulations (three 20-ns trajectories, two calculation methods) and relaxation experiments (relax analysis) are given in Table 1. Values from initial model-free analysis (ModelFree, Ver. 4.15) are also included (2). Separate averages are given for various residue sets (depending on secondary structure or correlation function convergence in MD). For α-helices and β-strands, S² computed for each simulation using M₁ are comparable among themselves and also to those obtained using M₂ (mean values range from 0.853 to 0.866 for residues in α-helices, and from 0.894 to 0.902 for those in β-strands; Table 1). This indicates simulations are long enough to obtain statistically significant sampling of the conformational space of these residues. This was expected for these highly structured elements as TEM-1 undergoes little global fluctuations. A greater variation between the three simulations is observed for loop residues (mean values range from 0.796 to 0.819) and particularly the Ω loop (mean values range from 0.705 to 0.755), indicating estimates from each individual simulation are hindered by the limited length of the trajectory. RMSD between MD datasets, presented in Table S1 along with RMSD between MD and experimental S², further demonstrates that loop dynamics vary considerably among the simulations. Combining conformations from the three simulations using calculation method M₂ is absolutely necessary, as individual simulation results for loop residues vary just as much among themselves as they do compared to experimental values.

Table 1.

Average S² from NMR spectroscopy and MD

Technique	NMR		MD
Analysis method	MF∗	relax	M1†			M2‡
Simulation			1	2	3
All residues§	0.901	0.886	0.854	0.853	0.866	0.853
α-helices¶	0.921	0.904	0.894	0.899	0.902	0.896
β-strands‖	0.893	0.877	0.875	0.876	0.890	0.876
Loops∗∗	0.883	0.869	0.803	0.796	0.819	0.797
Ω loop††	0.898	0.901	0.705	0.755	0.746	0.748
Converged residues			0.868	0.876	0.874
Unconverged residues‡‡			0.833	0.820	0.844

^∗Original ModelFree analysis (2).

^†Internal autocorrelation, individual simulations.

^‡Internal autocorrelation by randomization of all simulations.

^§Except N-terminus (H26) and 12 prolines for MD: 27, 62, 67, 107, 145, 167, 174, 183, 219, 226, 252, and 257. For NMR spectroscopy, this also excludes residues that could not be analyzed and residues whose model-free model does not involve an S².

^¶There are 12 α-helices in the structure: H1, 26–40; H2A, 69–71; H2B, 72–85; H3, 109–111; H4, 119–128; H5,132–142; H6, 145–154; H7, 168–170; H8, 183–195; H9, 201–212; H10, 221–224; and H11, 272–288.

^‖There are five β-strands (in one sheet) in the structure: S1, 56–60; S2, 43–50; S3, 259–266; S4, 244–251; and S5, 230–237.

^∗∗Including the Ω loop.

^††The Ω loop spans residues 161–179.

^‡‡Fourteen residues are unconverged in all three simulations: E64, S70, V159, T160, L169, N170, N175, D176, E177, R191, L193, L194, L198, and A202.

When comparing MD-derived S² parameters to those obtained from NMR relaxation experiments, discrepancies are expected for two main reasons. The first and most important one is the difference between the timescales probed by each technique. MD order parameters take into account motions happening from the picosecond timescale up to the order of the trajectory length. Although NMR can probe fast subpicosecond motions, it is limited on the other range of the spectrum by protein global tumbling, which cannot be decoupled from local motions (16). Therefore, motions whose timescales are comparable to TEM-1 global tumbling time (τ_m ≈ 12.3 ns) are not reflected in experimental analysis. The result is that MD will yield lower order parameters for very flexible regions and other regions where slow motions take place. To reconcile NMR- and MD-derived S² for slowly moving regions, global tumbling in simulations must be recoupled with local motions (19); this would require trajectories of an order of at least 10 times τ_m, and simulations that accurately reproduce protein global motions. The second reason for NMR/MD S² differences is that finite MD trajectories do not sample perfectly the conformational space of all residues. Motions that happen at a frequency in the same order of magnitude as the trajectory length, but faster than global tumbling (on the 10-ns timescale for the present system), still contribute to NMR S², but may not show up in a given MD simulation. MD S² values are then overestimated. Nonconvergence of C_I(t) is an indication of that problem.

MD starting structure was recently shown to influence simulated dynamics, and therefore MD-determined S² parameters, particularly in feebly structured regions such as solvent-exposed loops (30). To minimize initial structure influence, we use three simulations and compute S² using method M₂. The improved agreement between experiment and simulation when using M₂ over M₁ is obvious for the Ω loop, the most flexible region of the protein according to MD results: RMSDs to experimental results are significantly smaller for M₂ than for M₁, as shown in Table S1. For other loops, improvements are not statistically significant. A worse agreement between experimental and simulation results for loop residues (without regard for the calculation method used) than for helices and sheets was expected as motions on the ≈10-ns timescale happening in the most flexible regions of the protein remain imperfectly sampled due to limited simulation time. However, the fact that S² RMSD between MD datasets is of the same order of magnitude as RMSD between MD and NMR results shows that the difference between MD and NMR S² is within the MD reproducibility. As the agreement between MD and NMR datasets cannot be better than the reproducibility limit of the simulations, this validates the use of MD results as a guide in NMR data analysis.

The average S² for the whole sequence, computed from MD simulations using M₂, is significantly lower than what is seen in relax analysis (0.853 vs. 0.886; Table 1). However, agreement between the simulations and the experiment is good for highly structured residues inside α-helices or β-strands. The small differences between simulated and experimental parameters are likely due to MD limitations. Discrepancies between simulated and experimental S² thus lie mostly within loops, where order parameters are significantly lower in MD results than in NMR (0.797 vs. 0.869 for relax). The influence of secondary structure on S² agreement is readily seen in Fig. 1, a and b, which shows S² and |ΔS²| (absolute value of MD/NMR S² difference) along sequence. The most important differences between experimental and simulated parameters are observed between helices H2 and H3, in the loop following helix H6, in the Ω loop, and between helix H9 and strand S5. Correlation between MD- and NMR-derived order parameters according to secondary structure is shown in Fig. 1, c–f. For residues in α-helices (Fig. 1 d), S² ratios are clustered around the ideal value of 1.0. A similar pattern is observed for residues in β-strands (Fig. 1 e). For residues in loops (Fig. 1 f), however, the ratio distributions are centered on 0.925, indicating systematically higher experimental values. Differences are very important for residues in the Ω loop (Fig. 1 a), which exemplifies the difference-of-timescales problem discussed previously. NMR-derived order parameters for the Ω loop (and possibly other flexible regions) are misleading as they suggest residues in the Ω loop are as constrained as those in α-helices. MD results show this is clearly not the case.

Figure 1.

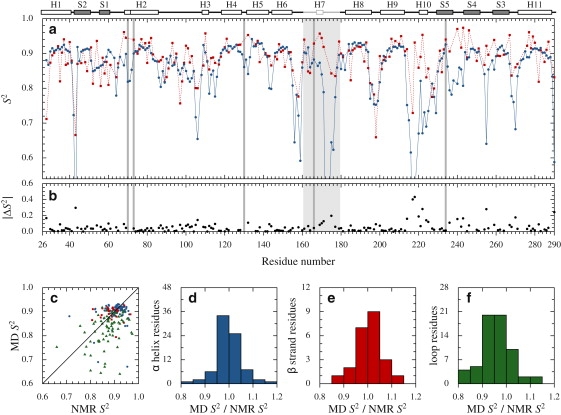
S² parameters from NMR spectroscopy and MD simulations along the TEM-1 sequence and their correlation. (a) S². MD results (calculation method M₂) are blue circles and solid line; relax analysis results are red squares and dashed line. (b) |ΔS²|. Between MD and relax. (a and b) Catalytic residues (S70, K73, S130, E166, and K234) are indicated with gray lines, the Ω loop with a light gray box. Above panel a is the TEM-1 sequence; α-helices are white boxes, β-strands gray boxes; the Ω loop is in light gray; a vertical bar in H2 indicates the bend between H2A and H2B. (c) MD against relax S². Residues in α-helices are blue circles; those in β-strands are red squares; those in loops are green triangles. (d–f) Ratio of MD and relax S² for residues in α-helices (d), β-strands (e), and loops (f).

Regions where |ΔS²| discrepancies are notable are mainly located near the active site (see Fig. S5). Weak phosphate binding to the active site (from 25 mM NaPO₄ buffer, data not shown) could influence the dynamic properties of residues near the active site when measured using NMR spectroscopy and contribute to the observed differences. Also, as mentioned above, order parameters report on the picosecond-nanosecond timescale in the model-free formalism because of the protein global tumbling. Hence, slower motions do not influence NMR-derived S² values, provided that an R_ex parameter is appropriately included to fit the resulting exchange contribution to the transverse spin-relaxation rate. In contrast, slower motions will generally yield lower MD-derived S². Residues with experimental and simulated order parameters that vary substantially are also seen at the end of β-strands and in the loop bordering the β-sheet.

Globally, average S² values >0.85 for structured regions in MD confirms NMR results: β-lactamase TEM-1 is a highly structured protein with little global fluctuation. Slow motions in the Ω loop are observed in simulations (as in NMR experiments), and will be discussed latter.

Improving model selection using MD motions

Given the generally good agreement between MD and NMR order parameters, we decided to further compare experimental and simulated dynamics, this time from a qualitative point of view, by relating the model-free abstract models to the N-H bond motions observed in simulations. This comparison was carried out systematically for each residue and allowed to further refine relax analysis. Although there is no simple correspondence between a given model-free model and a particular motion observed in MD, some motions can definitely be judged compatible (or incompatible) with specific models. Detailed improved dynamic models and parameters resulting from the comparison of MD and NMR data are given as Supporting Material and summarized below; amide N-H bond local motions observed in MD simulations (for all residues with an N-H moiety) are also included as Supporting Material.

Of the 177 residues fitted using relax, 144 have model-free abstract models that are compatible with N-H bond motions observed in MD simulations. A typical example involves catalytic K73 (Fig. 2 d), located in helix H2. This residue sampled a restricted conformational space, leading to high S². It was fitted with one of the simplest models in model-free analysis: m1, involving only an S² parameter. Experimental and simulated S² are 0.94 and 0.90, respectively. Another typical example involves R43, located at the N-terminal end of strand S2. This residue was fitted using model m5, which corresponds to a two-timescale motion. This motion was clearly observed in MD simulations (jump between two cones, Fig. 2 b): fast motions are associated to bond oscillation inside the densely populated cones, whereas slow motions correspond to transitions between these two conformations. Experimental and simulated S² values are 0.67 and 0.37, respectively. Finally, D214 (Fig. 2 i) illustrates the slow conformational space sweeping associated with μs-ms timescale motions; in model-free analysis, the residue was fitted to m3, which involves an R_ex parameter (4.73 ± 0.84 s⁻¹). Experimental and simulated S² values are 0.91 and 0.75, respectively.

Figure 2.

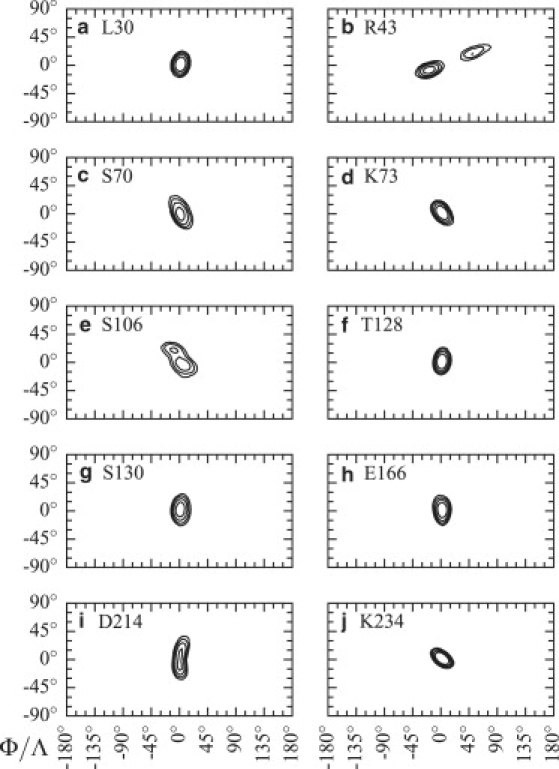
Amide N-H bond local motions in MD simulations. For each snapshot in all simulations, the orientation of the selected residue N-H amide bond (in the local reference frame used for M₁ and M₂) is plotted on a cylindrical map projection (latitude (ϕ) versus longitude (Λ)). Isolines follow vector orientation density in rad⁻²ns⁻¹; they are: 50, 100, 200, and 400. Mean orientation is centered at the origin.

From the 33 residues fitted to models incompatible with motions observed in MD, the two methods were reconciled in 14 cases by selecting a different, more compatible model with a similar AICc score. (AICc, the small-sample corrected Akaike information criteria, is used in model selection; it measures the goodness of fit of each abstract model. See detailed protocol in Supporting Material.) L30, in helix H1, is a good example of model-free overfitting. The residue was fitted to m5, a two-timescale motion model. However, MD results suggested a single-timescale motion that would be compatible with models m1 and m2 (Fig. 2 a). AICc scores for m5 and m1 were 19.9 and 20.0, respectively. Eliminating m5 on the basis of incompatibility with simulations improved model-free analysis, and led to selecting m1 with a similar level of statistical confidence.

S106, in a solvent-exposed loop, exemplifies model-free underfitting. The m2 model was selected from relax analysis. However, MD results suggest two-timescale motions that could be described in NMR either through an R_ex or two S² parameters (Fig. 2 e). AICc criterion for m5, the “statistically second-best” model for that residue, is 26.0, compared to 24.1 for m2. Eliminating m2 on the basis that it does not fit the simulated physical motions leaves m5 as the best description of that residue's dynamics.

Theoretical studies have used synthetic relaxation datasets and MD simulations to analyze and assist model selection for fitting relaxation data (31). This article is the first instance, to our knowledge, of using N-H vector motions from MD simulations to refine model-free analysis of real relaxation data. Combining MD and NMR results to obtain a better global picture of protein dynamics is particularly important in light of the fact that model-free analysis deals only with abstract models that have no direct or easily understandable physical interpretation. Moreover, model-free derived motional models are limited by experimental data and their associated error, both affecting model selection. MD, on the other hand, provides detailed atomic knowledge of physical motions. This information can be used to produce simulated dynamic parameters, and also to complement NMR results and facilitate model-free analysis.

Still, NMR and MD data did not reconcile for 19 residues. There are many possible explanations for this. First, model-free analysis is prone to overfitting and, although relax analysis is less affected by that problem than the original ModelFree analysis, this remains an important methodological limitation. Additionally, R_ex parameters can arise from motions near an N-H vector but without actual movement of that vector, as conformational exchange R₂ modulation proceeds from fluctuations in magnetization as a result from either movement of the vector itself or of its surrounding environment (32). That possibility complicates MD/NMR comparisons as such conformational exchange would be sensed by NMR but invisible to MD using the current analysis procedures that look at the details of isolated N-H moieties. T128, at the C-terminal end of H4, could be an example of this: although the presence of an R_ex parameter seems very clear from model-free analysis, MD motions (Fig. 2 f) are similar to those observed for residues fitted with models m1 and m2. Also, nonconvergence of autocorrelation functions from MD trajectories could be responsible for some model incompatibilities. When comparison suggests a different model, we ensure that function convergence is observed for that residue; this can be limiting in the case of highly flexible residues. Finally, although force fields for MD simulations of proteins are well established, they still have their limits. For instance, a recent MD/NMR comparison shows that modern classical force fields tend to overestimate the flexibility of backbone N-H vectors in loops and at the borders of secondary structure elements (33).

Essential dynamics (ED)

Essential dynamics (ED) (or principal component analysis of MD simulations) reduces the dimensionality of a trajectory by using eigenvectors (the principal components) to represent the variance of atomic position (34). The ED of our trajectories shows similar motions in all three simulations. Movies of the first five eigenvectors described below are given as Supporting Material.

The first eigenvector (Fig. 3) represents a concerted deformation and rotation. In the α/β domain, helix H11 bends, with its extremities pulling away from the β-sheet. This is accompanied by the twisting of strands S2 and S3. The α-domain undergoes a rotational motion with regard to the rest of the protein. This motion is most pronounced in the region spanning helices H2B, H3, and H4. The main hinges are located at the domain-domain interface (M69-S70) and in the second loop connecting the two domains (L224-P225). The axis of rotation passes near strand S5 of the β-sheet; observed angle of rotation is 12°. These motions affect helix H7; its translation in turn induces conformational changes in the Ω loop. The second and third eigenvectors correspond to protein “breathing”. In the second mode, helix H1 and the C-terminal portion of the Ω loop are the most affected regions. The Ω loop also moves in the third mode, but to a lesser extent. The fourth motion mode is made of concerted, small-amplitude movements in the backbone of solvent-exposed residues in the loops and helix caps of the α-domain. Although it is at the protein surface, helix H7 is not involved here. The Ω loop, particularly residue A172, is also moving in this mode. Motions in the fifth eigenvector are mainly those of solvent-exposed side chains.

Figure 3.

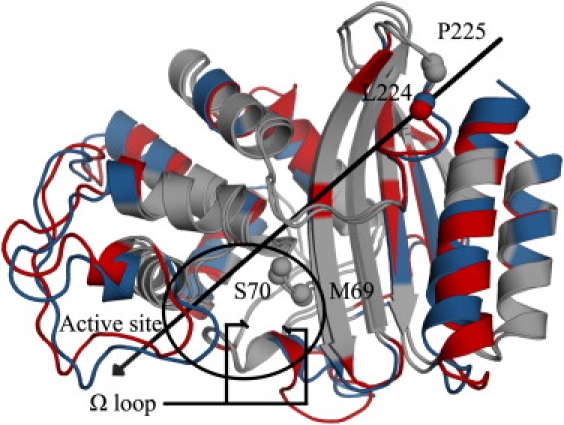
Essential dynamics first component. Minimal and maximal eigenvector projections observed in the first simulation are superposed. Colored residues are the most mobile ones (blue and red for the minimum and maximum projections, respectively). The α-domain rotates clockwise around the axis (black arrow). The α-carbons of hinge residues M69, S70, L224, and P225 are shown as spheres. The active site and Ω loop extremities are shown (black circle and lines). Movies showing the five principal components are supplied as Supporting Material.

These results show that the domains move relatively to each other. Of great interest are the motions in the Ω loop: ED reveals these are concerted with global-scale movements in the protein, supporting the hypothesis of induced fit (2,35). Given its relevance to catalysis, the Ω loop is further analyzed below.

Dynamics of the Ω loop

The Ω loop is common to all class A β-lactamases. It forms a wall of the active site and bears catalytic E166 (involved in both acylation and deacylation reactions (11,36)). Slow motions in the loop (potentially allowing induced fit) were suspected from crystallographic structures (35), then confirmed by NMR (2). In the definition used here, the Ω loop spans residues 161–179, and includes helix H7 (168–170) and catalytic E166. The loop can be divided into three independent regions. The first one (Ω_R1) stretches from R161 (start of the loop) to W165 and is highly structured. C_α RMSFs (Fig. 4) for these residues are ∼0.5 Å, and their average S² is 0.891. That loop portion is stabilized through interactions with helix H6, except for W165, whose side chain makes hydrophobic contacts with that of L139 (in helix H5). The second region (Ω_R2) includes residues 166–170, and exhibits a limited flexibility (higher RMSF, especially for P167, and an average S² of 0.865) that might allow E166 to position its catalytic side chain upon substrate binding. N170, the C-terminal end of H7, exhibits little fluctuation (C_α RMSF of ∼0.6 Å) and clearly delimitates the second region from the third (Ω_R3), which comprises residues 171–179. Ω_R3 is the region where motions are the most important; some residues have C_α RMSF that go above 1.5 Å and the average S² is 0.661. This last region can be further divided into two subregions that display concerted motions. The N-terminal subregion (Ω_R3N) includes E171, A172, and I173; the C-terminal one (Ω_R3C) comprises the rest of the loop (P174–D179).

Figure 4.

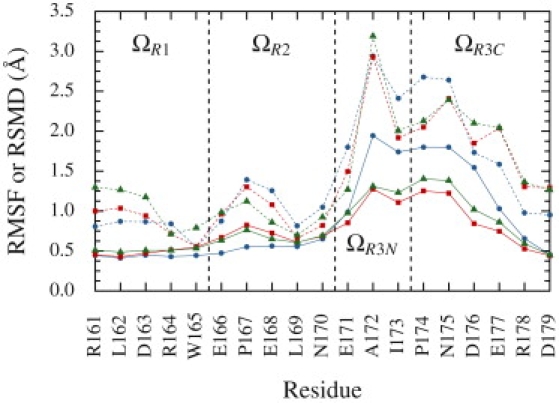
Ω Loop flexibility. Solid lines are C_α RMSF to the average structure. Dashed lines are time-averaged C_α RMSD to the crystallographic structure. Blue circles, red squares, and green triangles refer to the first, second, and third simulation, respectively. Vertical dashed lines separate Ω loop regions as described in the text.

Abrupt changes in ϕ and ψ torsion angles of the three Ω_R3N residues result in conformational changes in this portion of the loop. A K-means clustering analysis of main chain torsion angles showed three principal conformations (referred to as A, B, and C). Clustering based on C_α positions, however, suggested four conformations—one being substantially visited only during the first simulation. Visual inspection showed two of these four conformations are in fact the same (C) and differ mainly because of a translational motion arising from Ω_R2 (though torsion angles also show limited variation). All four Ω_R3N conformations (A, B, C₁, and C₂) can be seen in Fig. 5. Conformation A is similar to the crystallographic structure. In conformations B and C, the loop moves away from the protein core. A timeline of the visited conformations is shown in Fig. 5. As there are relatively few transition events (12 in all simulations), their sampling is limited.

Figure 5.

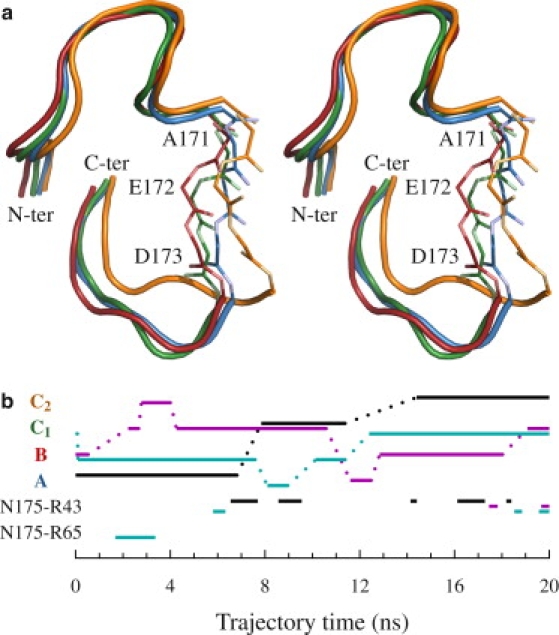
Ω Loop conformations. (a) Structure with Ω_R3N conformations. The whole Ω loop is in cartoon representation, except for residues E171, A172, and I173 (Ω_R3N) which are shown as sticks (along with atoms C_O and O_C from N170 and atoms C_O, O_C, and N_H from P174). Conformations A, B, C₁, and C₂ are in blue, red, green, and orange, respectively. Oxygen and nitrogen atoms in stick representation are paler than other atoms. Stereoscopic figure. (b) Simulation timeline. (Upper portion) Ω_R3N conformations. (Lower portion) Interactions between N175 O_δ and R43 N_η and between N175 O_δ and R65 N_η in Ω_R3C (cavity-filling motions). Conformations and interactions are labeled on the left. Black, magenta, and cyan lines refer to the first, second, and third simulation, respectively. Interaction cutoffs are 3.0 Å distance and 90° angle for the hydrogen bond between N175 O_δ and R43 N_η, and 4.0 Å distance for the R65 side-chain motion that brings N175 O_δ and R65 N_η closer.

From the trajectories, the Ω_R3C subregion of the Ω loop sweeps its conformational space slowly and with no abrupt change in conformation. Its position is impacted by Ω_R3N conformation. With Ω_R3N in the A or B conformation, Ω_R3C remains far from the protein core, as in the crystallographic structure, and even farther. Distance between N175 N and R65 O is 7.3 Å in the crystallographic structure, and varies from 6.0 Å to 9.1 Å when Ω_R3N is in the A conformation. With Ω_R3N in the B conformation, that distance varies from 6.6 Å to 11.0 Å. When Ω_R3N enters the C conformation, however, the distance varies from 5.2 Å to 8.8 Å. This move toward the protein core is not enough to allow formation of hydrogen bonds between main-chain atoms as is reported in another MD study (13), but does allow the formation of an H-bond (2.7 Å distance) between N175 O_δ and R43 N_η. This interaction partially fills the cavity between the Ω loop and the protein core, as shown in Fig. 6, a and b. This interaction is observed in all simulations. The H-bond forms and then breaks as the side chains move away from each other. The timeline of the interaction is shown in Fig. 5.

Figure 6.

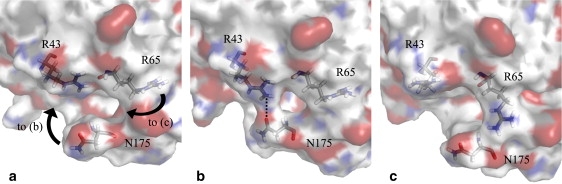
Cavity-filling motions in the Ω loop. Residues R45, R65, and N175 are shown as sticks. (a) Crystal structure 1XPB (simulation starting point). (b) N175 approaches the protein core; a hydrogen bond is formed between N175 O_δ and R43 N_η; first simulation, at 9.0 ns. (c) R65 side chain rotates toward the cavity, partially filling it; third simulation, at 3.0 ns.

Interestingly, in the third simulation, R65 side chain changes conformation and enters the cavity between the Ω loop and protein core. R65 side chain is usually packed against the loops between H6-H7 and H7-H8. Conformational changes (mainly for χ₁ and χ₄ dihedral angles) bring it above N175 (Fig. 6, a–c). However, Ω_R3C being in the B conformation at that time (see Fig. 5), the N175 side chain is too far to establish a strong H-bond and R65 eventually goes back to its previous conformation. Longer simulations might allow the stabilization of R65 in the Ω loop/protein core cavity with Ω_R3C in the C conformation.

Upon substrate binding, these two cavity-filling motions are expected to have a structuring effect on the active site by anchoring the Ω loop to the rest of the protein, thereby stabilizing E166. This effect, however, would certainly be less pronounced than if N175 N_H and R65 O_C established a strong, high occupancy hydrogen bond as reported in a 5-ns MD simulation (13). Differences in the Ω loop dynamics between our simulations and those of Roccatano et al. (13) could result from the use of different starting structures (1XPB (9) here versus 1BTL (35)), as starting structure has been shown to influence dynamics in another system (30). This is speculative, however, especially since the Ω loop has the same conformation in both crystal structures. The current simulations are more consistent with experimental data since the μs-ms timescale motions observed in NMR spectroscopy cannot be explained by a strong interaction that would tether the Ω loop to the protein core and considerably limit the amplitude of its movements. The slow sweeping observed here fits better the conformational exchange model suggested by NMR experiments. The only way to reconcile results from Roccatano et al. with experimental observations would be to assume that the Ω loop would have eventually moved back to a fully solvated position had their simulation been longer.

Dynamics of active site residues

TEM-1 active site is located at the interface of its two domains and is formed by the junction of four structural elements. Helix H2 provides catalytic residues S70 and K73 and forms the bottom of the groove. The SDN loop (between helices H4 and H5) bears S130 and forms the first side of the active site. Strand S5 forms the second side of the groove and provides the K234 side chain. Finally, the N-terminal portion of the Ω loop (providing E166) forms the third side. Simulations show that, in absence of substrate, the active site is a rigid body stabilized by a network of hydrogen bonds involving catalytic residue side chains. High S² parameters (0.82, 0.90, 0.86, 0.88, and 0.93 for S70, K73, S130, E166, and K234, respectively) and simple local motions (see Fig. 2, c, d, g, h, and j) confirm backbone rigidity. A detailed description of the active site interactions observed in MD is given as Supporting Material. Rigid active sites have been reported in many other biological systems, such as serine proteases (37) (that use a catalytic mechanism similar to that of class A β-lactamases) and, more recently, T7 DNA polymerase (38).

These results are consistent with experimental data indicating that TEM-1 active site is highly structured. We posit that the strict positioning of catalytic residues is optimized to allow TEM-1 to react immediately with its substrate upon binding. With some class A β-lactamase kinetics (including TEM-1) being diffusion-controlled for their specific substrates (39) (k_cat/K_m ≈ 10⁸ M⁻¹ s⁻¹), molecular dynamics simulations of lengths comparable to the current ones can provide insights on catalysis-related motions. For such “perfect” enzymes, almost all turnover time is dedicated to substrate binding and product release. Therefore, though the complete catalytic cycle takes up to 1 ms, active site dynamic events happening on the nanosecond timescale are relevant to catalysis.

Conclusion

TEM-1 dynamics were described at an atomic resolution using MD simulations. Simulated backbone order parameters were compared to those previously determined using NMR spectroscopy relaxation experiments and model-free analysis. Improvements upon original model-free analysis were obtained using the alternative relax program, which implements recent theoretical developments.

Simulations were shown to accurately reproduce dynamics of highly structured elements such as α-helices and β-sheets, but conformational sampling of solvent-exposed loops is insufficient to adequately reproduce experimental results for these flexible regions. Nonetheless, a partial atomic description of the motions taking place in the Ω loop was presented, showing that this catalytically important element is not solidly anchored to the protein core as suggested in previous, much shorter simulations. The Ω loop undergoes a variety of motions. Its N-terminal portion is packed on helix H6, whereas its central part acts as a flexible hinge that makes its C-terminal portion sweep a large conformational space. The last part of the loop is completely solvated in general, but does exhibit transient interactions with the protein core. This is consistent with experimental data, as the presence of R_ex parameters in that region suggests conformational changes on the μs-ms timescale. ED has shown that Ω loop motions are correlated to global-scale fluctuations in the protein, supporting the hypothesis of induced fit. ED studies also show that the α-domain undergoes a rotational motion with regard to the α/β domain. Active site dynamics were well characterized as all residues are highly structured due to a network of hydrogen bonds between catalytic side chains. Being highly constrained allows catalytic residues to perform their role immediately upon substrate binding. High experimental S² for catalytic residues support these results.

Combining molecular dynamics simulations and model-free analysis gives a powerful analysis framework for protein dynamics. The two techniques are complementary. Using MD insights during the abstract model selection process helped correct mistakes caused by the over- and underfitting of relaxation data. Final NMR relaxation analysis results are thus more reliable. Future work will focus on further bridging MD and NMR to develop improved dynamics analysis protocols.

Supporting Material

Additional text, six figures, six tables, and five movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01561-6.