Primary Changes of the Mechanical Properties of Southern Bean Mosaic Virus upon Calcium Removal

Abstract

The mechanical properties of viral shells are crucial determinates for the pathway and mechanism by which the genetic material leaves the capsid during infection and have therefore been studied by atomic force microscopy as well as by atomistic simulations. The mechanical response to forces from inside the capsid are found to be relevant, especially after ion removal from the shell structure, which is generally assumed to be essential during viral infection; however, atomic force microscopy measurements are restricted to probing the capsids from outside, and the primary effect of ion removal is still inaccessible. To bridge this gap, we performed atomistic force-probe molecular dynamics simulations of the complete solvated icosahedral shell of Southern Bean Mosaic Virus and compared the distribution of elastic constants and yielding forces on the icosahedral shell for probing from inside with the distribution of outside mechanical properties obtained previously. Further, the primary effect of calcium removal on the mechanical properties on both sides, as well as on their spatial distribution, is quantified. Marked differences are seen particularly at the pentamer centers, although only small structural changes occur on the short timescales of the simulation. This unexpected primary effect, hence, precedes subsequent effects due to capsid swelling. In particular, assuming that genome release is preceded by an opening of capsomers instead of a complete capsid bursting, our observed weakening along the fivefold symmetry axes let us suggest pentamers as possible exit ports for RNA release.

Introduction

Animal and plant viruses generally consist of a protein shell with an icosahedral symmetry, protecting the genetic material inside. Most icosahedral capsids are constructed from fivefold and sixfold morphological units, the centers of which are located at the five- and threefold symmetry axes, respectively. These shells are built up from 12 pentamers and 10 × (T-1) hexamers, where the triangulation (T-) number describes the shell geometry and determines the number of subunits comprising the complete capsid (1). Until now, the role of pentamers and hexamers during viral maturation (2) and cell infection has remained unclear (3). One of the major challenges in understanding the structural and dynamical differences of these capsomers is the investigation of their mechanical properties (4). In particular, the spatial distribution of mechanical properties such as elastic constants or yielding forces on the viral shell and their atomistic correlates is unknown, but essential for our picture of viral assembly, shell fracture, and RNA/DNA release.

To this aim, many different viruses have been probed by atomic force microscopy measurements to image their capsid structure (5–7) and to investigate their elastic behavior during deformation (8–13). A heterogeneous distribution of elastic constants was found for different viruses. Remarkably, the mechanical properties varied for mature and immature capsids (2,14). In addition, the failures of viruses under external force (15–19), as well as the distribution of rupture forces and stresses (20), are crucial properties in understanding viral disassembly, but the question of how (and where) the genetic material leaves the capsid during infection, remains elusive.

Release of the genetic material from the capsid is preceded by a transition of the mature viral shell to a structure that is able to release the DNA/RNA. A uniform swelling of the capsid with subsequent burst of the viral shell was proposed by Tama and Brooks (21,22) as a possible scenario for RNA release. Alternatively, swelling may be accompanied by a subsequent change of mechanical properties of the capsid, allowing an opening of only part of the shell, e.g., a port on the viral surface, to release the genetic material (20). Here we address possible changes of mechanical properties of the capsid by atomistic force-probe molecular-dynamics simulations of a complete viral shell solvated in water. As a typical representative of T = 3 viruses, we have chosen southern bean mosaic virus (SBMV). Its shell consists of 60 subunits, each composed of three almost identical proteins (Fig. 1 a) (23,24). The mature capsid contains 180 bound Ca²⁺ ions, three per subunit, with each of the ions located at the interface of adjacent proteins within a subunit. Removal of these Ca²⁺ ions induces swelling of the complete capsid and, thus, the viral infection cycle (25–28). The details of how Ca²⁺ removal changes the mechanical properties of the capsid, and how these changes are linked to subsequent RNA release, remain unknown.

Figure 1.

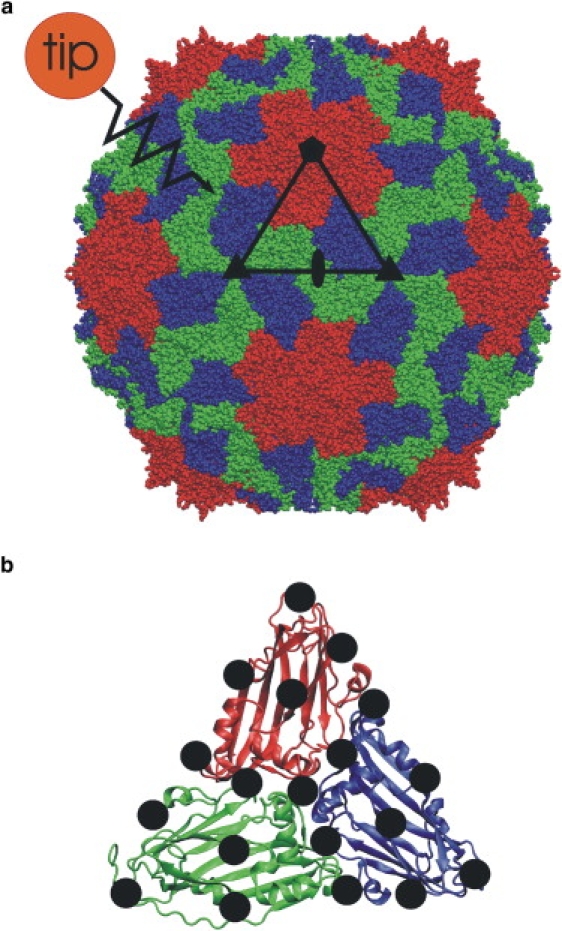
Force-probe simulations of southern bean mosaic virus (SBMV) capsid. (a) SBMV is built up from 60 subunits, each of which is composed of protein A (red), protein B (blue), and protein C (green). Black symbols mark the five-, three- and twofold symmetry axes referred to in the text. The black triangle depicts one of the 60 subunits. The approaching tip-sphere (red sphere) was initially located close to the surface and attached to a virtual spring that pushed the tip-sphere toward the viral shell. (b) Nineteen equally distributed positions (black circles) were chosen on the surface of one of the 60 subunits. During each of the 152 force-probe simulation runs, the tip-sphere was pushed with constant velocity against one of these grid points, and the force exerted by the tip-sphere onto the capsid surface is recorded. From the obtained force-distance curves, respective elastic constants and yielding forces were derived.

Two simulation systems were investigated: the solvated SBMV x-ray structure with bound Ca²⁺ ions, and a partially relaxed capsid after Ca²⁺ removal. In our simulations, the mechanical properties of both systems were characterized and compared. To this end, a Lennard-Jones (LJ) sphere (i.e., a tip-sphere) was used as a simple model for the atomic force microscopy (AFM) tip and pushed with a constant velocity and at various positions toward and into the surface of the viral capsid as described in Zink and Grubmüller (29). A tight grid of indentation positions (see Fig. 1 b) was chosen to obtain a spatially resolved elasticity map. Both the outer and inner surface of the capsid was probed, as well as the effect of calcium removal on the elasticity and on the force needed to cause fracture. Each simulation system contained >4,500,000 particles.

Methods

System setup and molecular-dynamics simulations

The simulation setup and equilibration of the ion-bound southern bean mosaic virus (SBMV) capsid was already described in Zink and Grubmüller (29). Additionally, a simulation system for a calcium-free capsid was set up. This section first summarizes the simulation details of the ion-bound capsid for convenience of the reader. Subsequently, we will describe the setup for the ion-free system.

All molecular-dynamics simulations were carried out with the GROMACS-3.3.1 simulation software package (30) in an NpT ensemble, using the OPLS-AA force field (31). The x-ray structure of the SBMV capsid (23,24), including 180 calcium ions, was taken from the Protein Data Bank (PDB code: 4sbv) and VIPER data bank (32,33) and put in a rhombic dodecahedral box of 366 × 366 × 372 ų with box vector angles of 60° × 60° × 90°. After adding hydrogen atoms to the crystal structure of the protein with the GROMACS tool pdb2gmx, the protein was solvated, using the TIP4P water model (34). A total of 2576 sodium and 2936 chloride ions were added, corresponding to a 150 mM physiological ion concentration. The simulation system contained 564,000 protein atoms, including 180 Ca²⁺ ions, and ∼1,000,000 water molecules, totaling 4,500,000 particles.

The system was energy-minimized and equilibrated for ∼20 ns as described in Zink and Grubmüller (29). For the production runs, the protein and the solute were separately coupled to an external temperature bath (35) with coupling times τ_T = 0.1 ps. An isotropic Berendsen barostat with τ_p = 1.0 ps and a compressibility of 4.5 × 10⁻⁵ bar⁻¹ was used to keep the pressure at 1.0 bar (35). LJ and van der Waals interactions were explicitly calculated within a cutoff distance of 0.9 nm, and long-range electrostatic interactions were calculated using the particle-mesh Ewald method (36) with a grid spacing of 0.12 nm. Integration steps of 2.0 fs were used, with all bonds constrained using the LINCS algorithm (37).

To study the effect of calcium removal, we obtained a Ca²⁺ ions-free viral capsid by removing the 180 Ca²⁺ ions present in the x-ray structure from the ion-bound simulation system after 1-ns equilibration. The salt concentration was adapted to neutralize the system at 150 mM NaCl concentration. Subsequently, the system was energy-minimized with 300 steepest decent steps and further equilibrated for 32 ns using the same simulation parameters as described above for the simulation system with Ca²⁺.

During all simulations, the root mean-square deviation (RMSD) to the two initial structures of the capsid with and without Ca²⁺ ions was recorded, as well as the radii of gyration.

Force-probe molecular-dynamics simulations

All force-probe molecular-dynamics (FPMD) simulations were carried out as described in Zink and Grubmüller (29), except where noted otherwise. Briefly, all FPMD simulations were carried out with the GROMACS 4.0 CVS version from July 4, 2007 (38,39). To obtain a spatially resolved elasticity map of the viral surface, an LJ sphere (tip-sphere) (LJ parameter σ = 5.0 nm, ɛ = 0.001 kJ/mol) served as a model of a very sharp AFM tip. The tip-sphere was pushed with constant velocity of 0.01 nm/ps against and through the viral shell (Fig. 1, a and b). The capsid was probed at 19 different grid points evenly distributed on one of the 60 identical subunits. From the force acting onto the tip-sphere during each force-probe simulation, the elastic constant and yielding force of the respective capsid region was obtained as described in Zink and Grubmüller (29). In contrast to the FPMD simulations reported before, here we probed the mechanical properties of the capsid from inside, which is obviously impossible for AFM. To this aim, the tip-sphere was placed within the water inside the capsid and subsequently pushed against the inner surface of the shell toward the outside, i.e., toward the same 19 grid points as reported, but in opposite directions. Further, here the primary change of elastic properties of the capsid upon calcium removal was probed. To this end, a similar FPMD simulation protocol, for both the inside and the outside of the capsid structure without calcium, was carried out.

Accordingly, four sets of simulations were performed in total: two sets probing the calcium-bound and calcium-free capsid from outside, and two sets indenting these two systems from inside. To rule out anecdotal events and to access the amount of stochastic scatter of elastic constants and yielding forces, all force-probe simulations were performed at least twice. The first run of FP simulations including calcium ions was started from structures extracted after 12 ns of the equilibration run, and the second run from structures taken after 13 ns. For the Ca²⁺-free capsid, the first run was performed after an equilibration of the structure for 14 ns, and the second run after 15 ns. Thus, a total of 152 indentation simulations for the four simulation series was carried out, each containing 38 simulations. All molecular-dynamics and force-probe simulations were carried out on an SGI Altix 4700 using 64 processor cores.

Analysis

Elastic constants from capsid indentations were calculated from the linear regime in each of the force-distance plots using linear regression. The start and end points of the linear regimes were determined manually. Yielding forces were obtained from the maximum force in each of the force-distance plots.

To graphically represent the distribution of elastic constants and yielding forces on the surface of the viral shell and subunit, the obtained values from the 19 grid points were used and interpolated to the position of all atoms of the subunit, using Gaussian functions as described in Zink and Grubmüller (29). Subsequently, the corresponding values were added to the capsid PDB file as b-factors and color-coded for the distribution of b-factors with the software VMD (40).

Results

Equilibration

To study the mechanical properties on the surface of SBMV, the simulation system including the calcium ions was first solvated and equilibrated for 13 ns. For the second simulation system, the Ca²⁺ ions were removed from SBMV, which was then equilibrated for 32 ns. During the equilibration phase, the RMSD and the radius of gyration of the viral shell were recorded and compared to the initial (minimized) structures. For the system including calcium ions, the RMSD rose from 2.0 Å at 1.0 ns to 2.5 Å at 10 ns and remained nearly constant such that we consider the system sufficiently equilibrated for the mechanical properties studied here. The radius of gyration remained constant at 131.5 ± 0.5 Å, which is the value of the x-ray structure.

After removal of calcium, the RMSD increased from 1.7 Å at 1.0 ns to 2.3 Å at 10 ns, 2.5 Å after 15 ns and leveled off at 2.7 Å for the remaining 7 ns of the 32-ns equilibration phase. Although the RMSD did not fully converge after 15 ns (see the Supporting Material), we used that 15-ns equilibrated simulation system as the initial structure for our 152 force-probe molecular-dynamics simulations.

Additional control force-probe simulations were performed using the structure with calcium after 19.5 ns and without Ca²⁺ ions extracted after 32 ns of equilibration. The obtained values for the mechanical properties were within the error bars of the results found from force-probe simulations after a 13-ns equilibration phase for the calcium-bound structure and after a 15-ns equilibration for the ion-free viral shell (see below).

In contrast to the swelling of the capsid seen in experiments after Ca²⁺ removal, the radius of gyration of the capsid without calcium decreased slightly by 0.2 Å during equilibration. No swelling was observed on the necessarily short simulation timescale. Although here the RMSD leveled off after the 15-ns equilibration phase, it is clear that the calcium-free capsid is not fully equilibrated, because no significant capsid swelling was observed. Therefore, this study focuses on the primary effect of Ca²⁺ removal, which enables us to separate it from the effect of subsequent structural changes. These are expected to further change the mechanical properties; these changes, however, are outside the scope of this study.

An RMSD of 2.3 ± 0.3 Å between the equilibrated structures with and without calcium was found. This difference is mainly due to the flexibility of the loops, whereas the β-barrel structures remained stable and no structural changes after Ca²⁺ removal were observed.

Deformation of the capsid

To study the spatial distribution of elastic properties on the shell of SBMV, we defined a grid of 19 evenly distributed points on the triangular surface of subunit (SU) 12 (Fig. 1 b), which covered the complete subunit and the directions along the five-, three- and twofold symmetry axes. The tip-sphere was pushed toward each grid point with a constant probe-velocity of 0.01 nm/ps (Fig. 1). Four simulation series, each containing two simulations for every grid point, and totaling 152 simulations, were performed:

• 1.SBMV with calcium ions included in the shell structure; the tip-sphere was pushed from outside against the outer capsid surface.
• 2.SBMV with calcium; the tip-sphere was pushed from the inside of the virus against the inner capsid surface.
• 3.SBMV without calcium; the tip-sphere was pushed against the outer surface.
• 4.SBMV without calcium; the tip-sphere was pushed against the inner surface.

At the beginning of each simulation, the tip-sphere was positioned within the bulk solvent close to the viral surface, and subsequently pushed through the solvent and against the viral shell. During the force-probe simulations, the force acting on the tip-sphere was recorded, thus obtaining force-distance curves used for subsequent analysis. For each force-probe simulation, the linear force increase in the force-distance curve served to determine the elastic constant of the shell at the position toward which the tip-sphere was pushed.

Elastic constants

From the four simulation series of 38 simulations each during which the tip-sphere was pushed against the 19 evenly distributed grid points on SU 12 of SBMV, four heterogeneous distributions of elastic constants were obtained with values ranging from 1.65 N/m to 4.33 N/m (Fig. 2 a and the Supporting Material). The elastic constant map obtained from simulations in which the tip-sphere penetrated the calcium-bound capsid from outside was described in detail before in Zink and Grubmüller (29) and are summarized here for later reference. The largest elastic constant (4.33 N/m) was found at the fivefold symmetry axis at the center of the pentamer, followed by the two threefold symmetry axes (center of hexamers, 3.42 N/m and 3.53 N/m, respectively). The weakest point, i.e., the most flexible position of the shell, was seen at the subunit center with an elastic constant of 1.82 N/m, followed by the elastic constant along the twofold symmetry axis (1.89 N/m). The elastic constants at the grid points between the subunits (SU 11-12, SU 12-28) were consistently larger at the grid points where the A-proteins meet (2.46 N/m and 2.61 N/m) than between B and C proteins (2.17 N/m and 2.28 N/m, respectively). In addition to the subunit center, all elastic constants near the center of SU 12 were found to be in the range of 2.29–2.45 N/m, also at the interfaces of the subunit proteins A, B, and C. When the tip-sphere was pushed from the capsid inside against the inner surface of SBMV with Ca²⁺ ions, the distribution of elastic constants changed, whereas inside SU 12 the values of the elastic constants were very similar to the value obtained on the outer surface within a deviation of 0.17 N/m (Fig. 2 b and the Supporting Material). The subunit center was also the weakest and most flexible point of the subunit (1.65 N/m). The elastic constants at the interfaces of the subunits, where A-A and B-C proteins meet, were smaller, and no significant differences in the values for A-A and B-C protein intersections were seen. Here, the fivefold symmetry axis lost its rigidity and an elastic constant of 2.01 N/m was found, 2.32 N/m weaker than against indentations from outside. The threefold symmetry axes also became weaker and more pliable, and the elastic constants dropped to 2.45 N/m and 2.31 N/m, respectively. The only region which turned out to be stiffer was the twofold symmetry axis; the elastic constant rose to 2.87 N/m, compared to 1.89 N/m from outside. In fact, the twofold symmetry axis turned out to be the stiffest region on the inner surface of the shell.

Figure 2.

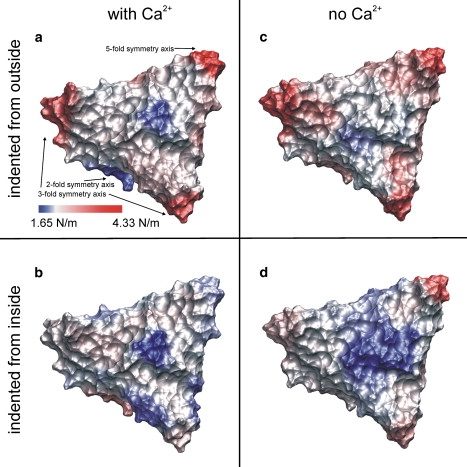
Distribution of elastic constants on a viral subunit. Color-coded distribution of elastic constants on the surface of subunit 12 of the SBMV capsid (soft, blue; stiff, red). The viral shell was indented from the outside (a) with and (b) without calcium ions in the structure and (c and d) from the inside.

Next, the elastic constants of the capsid of SBMV were determined after removal of the calcium ions from the viral structure (Fig. 2 c and the Supporting Material). When the outer surface of the capsid was probed, the largest elastic constants were seen at the pentamer center (3.56 N/m) and at the hexamer centers (3.34 N/m and 3.27 N/m, respectively), as already seen for the same positions with bound Ca²⁺ ions. The elastic constants obtained at the grid points between the subunits where A-A proteins meet (2.54 N/m and 2.56 N/m, respectively) were also slightly larger than those between B-C proteins (2.28 N/m and 2.40 N/m, respectively). In contrast to the Ca²⁺ bound case, the subunit center (2.23 N/m) and the twofold symmetry axis (2.64 N/m) became stiffer after Ca²⁺ removal, rendering the interfaces of protein A, B, and C within SU 12 as the softest region (2.10 N/m, 2.10 N/m, and 2.07 N/m, respectively). Interestingly, this is the Ca²⁺ binding region. The centers of the three proteins were strengthened, and the elastic constants increased by ∼0.6 N/m to 2.79 N/m (protein A), 2.89 N/m (protein B), and 2.31 N/m (protein C).

Finally, the tip-sphere was pushed against the 19 grid points from inside, and again calcium was removed (Fig. 2 d and the Supporting Material). Similar to the behavior of the Ca²⁺-bound structure which was indented from outside, the largest elastic constant was seen at the pentamer center (3.31 N/m), followed by the hexamer centers (2.65 N/m and 2.51 N/m, respectively). However, overall the respective values were much smaller compared to the Ca²⁺-bound case. The subunit exhibited the softest point at its center (1.88 N/m). The elastic constants inside SU 12 were comparable to that found from outside indentations in the calcium-free structure. The value at the twofold symmetry axis (2.35 N/m) was reduced by 0.29 N/m.

As an estimate for the standard deviation of the elastic constants due to the stochasticity of the process, for each of the four force-probe simulation series the 19 differences to the respective mean values were calculated and found to be between 0.1 and 0.3 N/m.

Yielding forces

In addition to the elastic constants, we determined the yielding forces F_max for each grid point from the four simulation series, each comprising 38 FP simulations toward the 19 grid points of SBMV described before. As can be seen from all 152 simulations (Fig. 2, a–d, and Fig. 3, a–d, and the Supporting Material), the distribution of F_max was less heterogeneous than that of the elastic constants, with F_max values between 1.80 nN and 3.80 nN.

Figure 3.

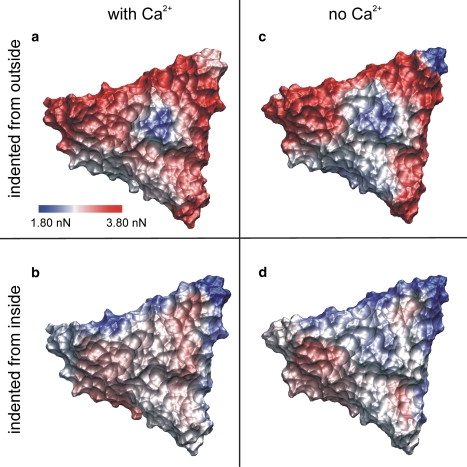
Distribution of yielding forces on a viral subunit. Color-coded distribution of yielding forces on the surface of subunit 12 of the SBMV capsid (low stability, blue; high stability, red). The viral shell was indented from the outside (a) with and (b) without calcium ions in the structure and (c and d) from the inside.

For probing the calcium-bound capsid from the outside (29), the largest yielding forces were seen at the subunit interfaces (SU 12-11 and SU 12-28) between the subunits where two A-proteins meet (3.80 nN and 3.75 nN, respectively) and between B-C proteins (3.47 nN and 3.27 nN, respectively) (Fig. 3 a and the Supporting Material). Smaller yielding forces were found at the interface of subunit 12-3 (2.75 nN and 2.79 nN) and along the twofold symmetry axis (2.68 nN). A yielding force of 2.96 nN was seen for the center of the pentamer, and 3.36 nN and 3.40 nN, respectively, for the two hexamer centers. Close to the subunit center, F_max values ranged from 2.99 nN to 3.31 nN, whereas the subunit center turned out to be the weakest region (2.16 nN).

For the simulations probing the inner shell of the Ca²⁺-bound capsid, the distribution of yielding forces changed drastically (Fig. 3 b and the Supporting Material). In particular, the yielding force at the pentamer center dropped to 1.80 nN, rendering this the weakest region of the subunit surface. In addition, the forces at the hexamer centers dropped to 2.73 nN and 2.59 nN, respectively. Only along the twofold symmetry axis (3.10 nN) was a slight strengthening seen. The interfaces of SU 12 to its adjacent subunits 11 and 28 became weaker, with an average yielding force decrease of >1.0 nN. Inside SU 12, the yielding forces were found to be similar to the values obtained on the outer surface of the calcium-bound subunit.

Overall, the most dramatic change after Ca²⁺ removal for the outside yielding forces was seen at the fivefold symmetry axis. Here, a nearly 50% larger value was obtained for the Ca²⁺-bound capsid (2.96 nN vs. 2.04 nN, respectively; see Fig. 3, a and c, Fig. 4, and the Supporting Material), such that after calcium removal the pentamer center became the weakest region of the subunit. The yielding forces on the other grid points were nearly unaffected by calcium removal, and were also similar to those obtained for the outer surface of the Ca²⁺-bound capsid.

Figure 4.

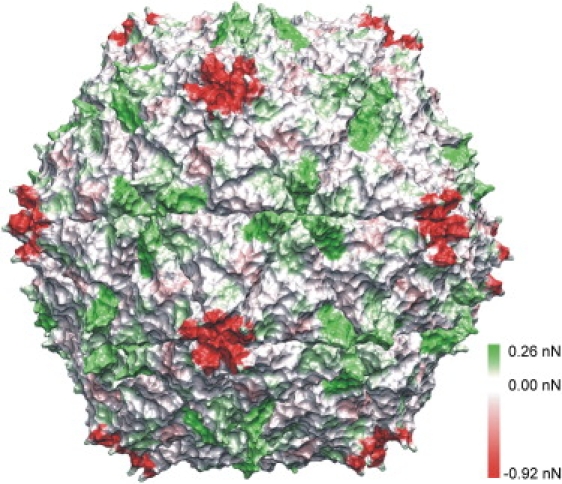
Changes of yielding forces after Ca²⁺ removal, mapped onto the complete capsid. Major differences are seen at the pentamer centers. Here, yielding forces dropped by 0.92 nN from 2.96 nN to 2.04 nN (red). (White) Unaffected regions. (Green) Regions with increased stability.

The distribution of yielding forces on the inner surface of SBMV after Ca²⁺ removal was found to be similar to that on the inner surface of the calcium-bound capsid (Fig. 3 d and the Supporting Material). The yielding force at the subunit center was slightly reduced by 0.35 nN to 2.45 nN, and the weakest region was the pentamer center (2.03 nN), as was already found for the Ca²⁺-bound viral shell. The estimated standard deviation, determined from all 152 simulations, ranged from 0.1–0.3 nN.

Discussion and Conclusion

As has been shown by AFM experiments (2), the transition from the assembled virus to a structure that is able to release the genetic material is accompanied by changes of its mechanical properties, as a prerequisite for rupture of the shell or the opening of a port. Without these changes, the mature virus structure would remain stable, and only harsh external forces or strong interactions with the environment could cause shell opening. The icosahedral shell of SBMV was shown to become infectious after removal of calcium from the capsid structure (28). Swelling of up to 44% in volume (28,41) was identified as a primary step in cell infection. To reveal the mechanical determinants of Ca²⁺ removal, our extensive set of force-probe simulations, totaling ∼150 ns, provided an atomistically resolved map of both elastic constants and yielding forces at the inner and outer surfaces of the capsid with bound Ca²⁺, and after calcium removal. Because swelling of the capsid occurs at much larger timescales (minutes) than those accessible to MD simulations, here we have focused on the primary effect of Ca²⁺ removal, with nearly unchanged structure of the shell. Subsequent changes of mechanical properties, indirectly caused by structural changes of the shell, lie outside the scope of this article.

No RNA was included within the simulation system due to lack of structural information. Thus, only capsid-intrinsic properties were studied here, and structural effects induced by the pressure exerted by the RNA onto the capsid are not seen. Generally, the pressure exerted by the RNA inside virions is much smaller than that for DNA viruses or, e.g., bacteriophage ϕ29 (42), due to the much smaller persistence length of RNA. Further, the observation of empty capsids suggests that no dramatic structural changes are caused by the pressure exerted by the RNA. Finally, this approach allows the separation of the intrinsic mechanical properties of the capsid from the additional effects of internal pressure.

During equilibration, as well as after calcium removal, the structure of SBMV capsid remained nearly unchanged, as documented by an RMSD of 2.3 ± 0.3 Å, which is a typical value for thermal fluctuations. The main result of the work is that, quite unexpectedly, the mechanical properties of the capsid changed markedly after Ca²⁺ removal even though the structure did not. These changes, therefore, are independent of and precede the known swelling of the capsid. Although pH-induced softening without marked capsid swelling was already observed for cowpea chlorotic mottle virus (CCMV) (16), it is surprising that the large changes of the mechanical properties observed here arise from structural changes that are very small even when viewed at the atomic scale (which was inaccessible to the above CCMV study). Additionally, recent AFM experiments with CCMV in the group of C. Schmidt corroborate our findings by obtaining a marked softening of the capsid before a subsequent swelling (Christoph Schmidt, Georg-August-Universität Göttingen, III. Physikalisches Institut, Göttingen, Germany, personal communication, 2009).

Taken together, the 152 force-probe simulations reveal a highly heterogeneous distribution of both elastic constants and yielding forces on the SBMV capsid surface. The calcium-bound shell exhibited the smallest elastic constants and yielding forces (1.82 N/m and 2.16 nN, respectively) at the subunit center when probed from outside. The most stable parts of the shell turned out to be the pentamer centers, with a stiffness of 4.33 N/m and a yielding force of 2.96 nN, respectively.

Tama and Brooks (22) predicted the pentamer amino acids of SBMV with bound calcium ions to have a higher flexibility and propensities to move freely compared to hexamer amino acids. If a higher flexibility of amino acids translates into a larger elastic deformability and thus, a smaller elastic constant—which would contribute our findings of a higher stiffness along the fivefold symmetry axis of the ion-bound capsid—is difficult to answer.

The distribution, upon being probed from inside (which is not possible by AFM experiments), revealed quite different mechanical properties. Although the same grid points were probed from inside and outside, the obtained elastic constants and yielding forces on the same capsid positions varied. As the main cause, we suggest the markedly different secondary structure arrangement. In particular, deformation of the single β-strands due to the penetrating tip-sphere was very different when probed from inside or outside. Although the β-sheet, upon indentation from the outside tended to be compressed, forces exerted from the inside turned out to stretch and expand the β-sheets. This quite different behavior can explain the differential mechanical response. Notably, no correlation was seen for the variations and distributions of elastic constants and yielding forces, respectively, as they describe largely independent material properties.

In contrast to the capsomer centers, within the subunit, similar elastic constants and yielding forces were found for the inner and outer subunit surface, as these were hardly affected at all by Ca²⁺ removal. The only exception was seen at the subunit center. Here, different elastic constants were seen for the inner and outer surface, which also changed after calcium removal. Furthermore, in most of the simulations, this turned out to be the weakest and most flexible spot of the capsid.

When the tip-sphere was pushed against the subunit center on the outer surface (for both the calcium-bound and calcium-free capsid), this region always exhibited a low stability. When the tip-sphere approached this position from inside the virus, the stability increased for the structure with Ca²⁺ compared to the capsid without ions. Remarkably, after calcium removal, the greatest weakening of the capsid (i.e., the largest drop of yielding forces) was seen for the pentamer center.

Assuming that fracture of viral shells occurs at weak capsid regions, i.e., those for which small yielding forces are observed, we propose two possible scenarios for RNA release from the obtained yielding force distributions. In the first scenario, the internal pressure exerted by the RNA contributes to overcome the gating barrier for release through thermal activation. In this case, the slight reduction of yielding forces seen for the twofold symmetry axis after calcium removal suggests this region as a possible release port. However, this relatively small decrease of yielding forces by only 0.2 nN is probably not large enough to cause a sufficient weakening of viral stability and thus enable RNA release. Furthermore, yielding forces obtained on the five- and threefold symmetry axes on the inner surface of the ion-free capsid are smaller and thus, more likely for RNA release, even when no weakening after calcium removal was observed at these positions. Therefore, we prefer the second scenario for genome release based on changing yielding forces with calcium removal.

In this scenario, the pentamer centers would act as possible ports for RNA release, for which a marked decrease of stability is observed after calcium removal. Such a capsid breakage and subsequent RNA release could, for example, be triggered or driven by interactions of the outer capsid surface with the cell membrane (2,43). In particular, these perturbations might result in additional weakening—or even in a tearing open—of the capsid, with the RNA pressure from inside overcoming the remaining gating barrier. Contrary to what might be expected at first sight, the large elastic constants seen for this region both for the inner and outer calcium-free capsid surface corroborate this scenario, because these imply smaller deformations and, accordingly, lower energies required for capsid rupture. In contrast, larger energies are needed for capsid rupture at positions with smaller elastic constants because here much larger elastic deformation can occur without resulting fracture. Within the harmonic approximation, e.g., the deformation energy scales as E = 1/2 kx² with deformation x (with elastic constant k), whereas the force scales linearly, F = kx. Combining the two equations, one obtains E = F²/k, as is claimed above.

Our findings are in line and could explain previous suggestions for RNA and DNA release of other viruses. For human rhinovirus 14, an icosahedral T = 3 virus with very similar positions of the C_α atoms and tertiary fold of the main protomer proteins compared to the structure of SBMV (44), Giranda et al. (45) proposed that pentamers could act as a port and open to release the genetic material during infection. A similar mechanism was suggested by Mosser et al. (46) for poliovirus type 3.

Our simulation results render other SBMV capsid positions unlikely for RNA release during infection. Yielding forces obtained at the three- and twofold symmetry axes on the outer surface, for example, are larger than those seen for the surrounding subunit surface and the pentamer center. Therefore, primary capsid breakage along these symmetry axes is not expected.

Small elastic constants and yielding forces were also found at the subunit center for both the calcium-bound and the calcium-free capsid. If the subunit center acts as a port for RNA release, then the already mature virus structure would be infectious even before calcium removal (which is not observed (28,41)).

The mechanical properties and the yielding of the viral shell against both forces from outside (e.g., interaction with membranes) and from inside (e.g., pressure exerted by the viral RNA) will likely be crucial for the primary steps of viral infection. By providing access to both, our simulations link the former (which can be measured) to the latter, which are so far inaccessible to experiment. The unexpectedly large heterogeneity seen for the mechanical properties suggests that the process of RNA release might be more complex than previously expected.

Supporting Material

Eleven figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01720-2.