An Analytic Solution of the Cable Equation Predicts Frequency Preference of a Passive Shunt-End Cylindrical Cable in Response to Extracellular Oscillating Electric Fields

Abstract

Under physiological and artificial conditions, the dendrites of neurons can be exposed to electric fields. Recent experimental studies suggested that the membrane resistivity of the distal apical dendrites of cortical and hippocampal pyramidal neurons may be significantly lower than that of the proximal dendrites and the soma. To understand the behavior of dendrites in time-varying extracellular electric fields, we analytically solved cable equations for finite cylindrical cables with and without a leak conductance attached to one end by employing the Green's function method. The solution for a cable with a leak at one end for direct-current step electric fields shows a reversal in polarization at the leaky end, as has been previously shown by employing the separation of variables method and Fourier series expansion. The solution for a cable with a leak at one end for alternating-current electric fields reveals that the leaky end shows frequency preference in the response amplitude. Our results predict that a passive dendrite with low resistivity at the distal end would show frequency preference in response to sinusoidal extracellular local field potentials. The Green's function obtained in our study can be used to calculate response for any extracellular electric field.

Introduction

The neurites of nerve cells can be subjected to extracellular electric fields either physiologically or artificially. Physiologically, for instance, it has been shown that the extracellular potential recorded from the stratum lacnosum-moleculare in the CA1 region oscillates with a 180° difference in phase compared to the potentials in the stratum oriens (1,2) and during hippocampal θ-activity. In such a situation, the dendrites of the pyramidal cells experience oscillatory extracellular electric fields. It has been proposed that the electric fields produced by neurons may modify the activities of nearby neurons (3,4). Artificially, electric stimulation is used to activate excitable cells in clinical and laboratory settings (5,6). Efforts have been made at gaining an understanding of how the membrane potential of neurites behaves in response to extracellular fields (7–16).

Most neurites have complex electric properties because of there being various voltage-gated ion-channels along branched dendrites. Therefore, it would be necessary to take all morphological and electrophysiological properties into account to enable us to fully understand the electric behavior of neurites in electric fields. Before considering the impact of active properties and morphology, however, we need to get a fundamental understanding of the behavior of simple passive finite cables exposed to extracellular electric fields. Tranchina and Nicholson (15) provided steady-state solutions for the cable equation in which an extrinsic electric field was applied to a uniform passive cylindrical cable. The transient response of passive cables to extracellular stimulation was studied by Cartee and Plonsey (7). By numerically solving the cable equation, they showed that the rate of rise is faster for shorter cables than for longer ones. For increasingly longer cables, they showed that the responses approach that of an infinite cable, namely error functions.

The behavior of the membrane potential of hippocampal pyramidal neurons in response to extrinsically applied weak direct current (DC) step fields has been experimentally investigated either by using conventional whole-cell recording techniques (17,18) or by using a fast voltage-sensitive dye imaging technique (19). If the dendrites of the cells can be considered as finite cables with uniform passive parameters such as membrane resistivities, intracellular resistivities, and membrane capacitance, then Cartee and Plonsey's study (7) suggests that the rate of rise in the membrane potential for a DC step extracellular field should be faster than that for current injection because the electrotonic length of pyramidal cells has been estimated to be shorter than a few space constants (20–23). Contrary to expectations, the rate of rise near the soma was slow (19). In addition to this, a peculiar membrane response, a reversal in polarization during DC step field stimulation, was recorded from the distal part of the apical dendrites (17,18). Because it has been shown that low threshold voltage-gated ion channels such as A-type K⁺ channels and T-type Ca²⁺ channels, and hyper-polarization-gated ion channels such as hyper-polarization-activated nonselective cation channels (I_h channels) are present in the distal part of the dendrites, the actions of those channels can conceivably be responsible for the discrepancy. However, there is another possibility. Recent experimental studies suggested that the membrane resistivity of the distal apical dendrites of cortical and hippocampal pyramidal neurons may be significantly lower than that of the proximal dendrites and the soma (24–27). A theoretical study by Svirskis et al. (14) claimed that the analytic solution of a passive cable with a significantly large shunt at one end shows a reversal in the membrane potential response at the shunt end and a slow rise at the tight end in response to a DC step applied field. Thus, it is possible that the slow rise and response reversal in pyramidal cell dendrites are due to the low membrane resistivity at distal apical dendrites.

We are interested in investigating the electric responses of a passive finite dendritic cable with a significant shunt at one end in response to oscillating extracellular electric fields. For this purpose, we obtained the Green's function of a passive finite cable for an extracellular field. Analytic solutions for a passive finite uniform cable in an extracellular DC step field confirmed the numerical solutions for finite cables previously reported by Cartee and Plonsey (7). The solutions for a shunt-attached finite cable were identical to the ones reported by Svirskis et al. (14) showing a response reversal at the shunt end and a slow rise at the tight end. We obtained analytic solutions for a shunt-attached cable in an extracellular sinusoidal electric alternating-current (AC) field by using the Green's function. At the end with no shunt, the amplitude of the change in membrane potential decays as the frequency of the field increases, whereas at the other end where the shunt is attached, the amplitude of the response shows a frequency preference.

Several studies have shown frequency preferences in responses that were induced by alternating current injection through recording electrodes to central nervous system (CNS) neurons, and the frequency preference has been shown to be dependent on voltage-sensitive membrane conductances (28–32). Our results show that CNS neurons with leaky membrane resistivity at distal dendrites may show a frequency preference because of their passive membrane properties when they are in an oscillating extracellular electric field.

Theory

Cable equation

Let us consider a finite cylindrical cable that has resistive intracellular and extracellular media as shown in Fig. 1 A. The spatial-temporal variation of the membrane potential along the cylindrical cable is described by the well-known cable equations (33)

$$\tau \frac{\partial V_{\text{m}}\left(x,t\right)}{\partial t}={\lambda }^2\frac{{\partial }^2{V}_{\text{m}}\left(x,t\right)}{\partial x^2}-V_{\text{m}}\left(x,t\right),$$ (1)

where V_m is the membrane potential in mV, a difference between intracellular and extracellular potentials. The values λ and τ are the space constant in cm and time constant in ms, respectively, defined by

$$\lambda =\sqrt{\frac{r_{\text{m}}}{r_{\text{e}}+r_{\text{i}}}}\text{and}\tau =r_{\text{m}}{c}_{\text{m}},$$

where r_i and r_e are the intracellular resistance (in Ω/cm) and extracellular resistance (in Ω/cm). The values r_m and c_m are the membrane resistance (in Ω/cm) and membrane capacitance (in F/cm), respectively.

Figure 1.

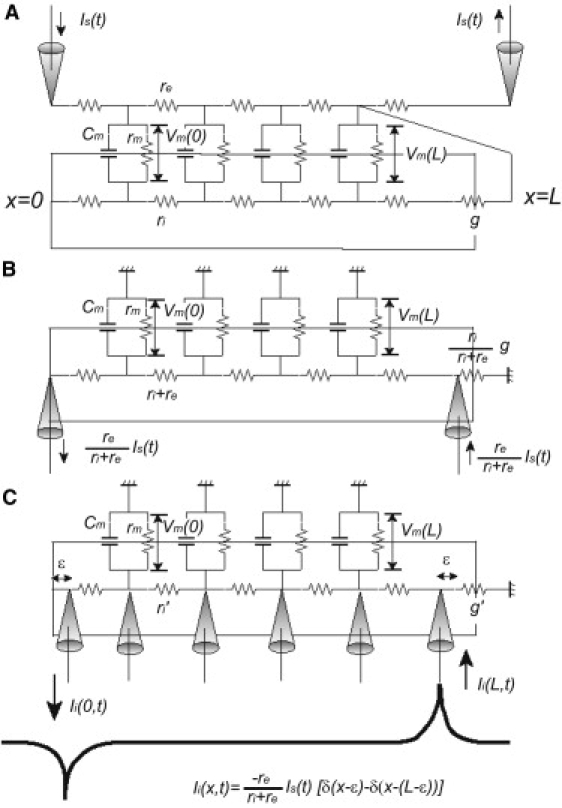
(A) A finite length cable with extracellular stimuli applied by a pair of electrodes. The dendrite subjected to extracellular electric fields is idealized as a finite cylindrical cable, which has resistive intracellular and extracellular media denoted by resistances, r_i and r_e, stimulated by extracellular currents, I_s(t) and − I_s(t) with an anode and a cathode located at cable ends. Stimulus current flows from the anode to the cathode via the intracellular and extracellular media. To capture effects of the nonuniform membrane resistivity of the dendrite, the shunt conductance g is attached to one end at x = L. The values r_m, c_m, and V_m are the membrane resistance, membrane capacitance, and membrane potential, respectively. (B) An equivalent system with intracellular stimuli given by a pair of current injections. Through variable reduction of the cable system (A) to the cable equation (Eq. 1) and for boundary conditions (Eq. 3) based on the membrane potential, the cable system (A) can be transformed into the equivalent system with grounded extracellular medium and a current pair injected into both ends of the cable. In this equivalent system, the intracellular resistance r′_i is r_i + r_e, the shunt conductance g′ attached at x = L is $r_{\text{i}}/r_{\text{i}}+r_{\text{e}}g$, and intracellular stimulus currents at x = 0 and x = L become $I_{\text{s}}^{\prime }\left(t\right)=-\frac{r_{\text{e}}}{r_{\text{i}}+r_{\text{e}}}{I}_{\text{s}}\left(t\right)\mathrm{and}-I_{\text{s}}^{\prime }\left(t\right)=\frac{r_{\text{e}}}{r_{\text{i}}+r_{\text{e}}}{I}_{\text{s}}\left(t\right),$ respectively. (C) Instead of injecting I′_s(t) and − I′_s(t) at x = 0 and x = L, current density I_i(x, t) = I′_s(t)[δ(x − ɛ) − δ(x − (L − ɛ))] is given along the cable. The value ɛ is an infinitesimal distance. The injected current does not flow through the very end of the cable, hence Eq. 6. Through this transformation, we can derive analytic solutions for any extracellular stimulus.

Boundary conditions for extracellular electric fields

A finite-length cable subjected to extracellular electric fields can be represented as an equivalent system with extracellular stimulations of an anode and cathode pair located at the cable ends (7), as shown in Fig. 1 A. Stimulus current flows from the anode to the cathode via the intracellular and extracellular media. The finite-length cable with sealed ends at x = 0 and a shunt g (in pS) attached at x = L (in cm) stimulated with such an electrode pair can be formulated as cable equation (Eq. 1) with the following boundary conditions (7),

$${\frac{\partial V_{\text{e}}\left(x,t\right)}{\partial x}|}_{x=0}=-r_{\text{e}}{I}_{\text{s}}\left(t\right),{\frac{\partial V_{\text{e}}\left(x,t\right)}{\partial x}|}_{x=L}=-r_{\text{e}}{I}_{\text{s}}\left(t\right),$$

$${\frac{\partial V_{\text{i}}\left(x,t\right)}{\partial x}|}_{x=0}=0,\frac{\partial V_{\text{i}}\left(x,t\right)}{\partial x}{|}_{x=L}=r_{\text{i}}g\left(V_{\text{i}}-V_{\text{e}}\right),$$ (2)

where V_i and V_e are the intracellular and extracellular potential, and the extracellular currents at x = 0 and x = L are I_s(t) and − I_s(t) pA, respectively. In this case, there is no current flow through the sealed ends; thus the intracellular current is zero at x = 0. At x = L, some current flows through the shunt; thus the intracellular current is not zero. By subtracting the boundary conditions for the intracellular potential from those for the extracellular potential, we derive the boundary conditions for the membrane potential, V_m:

$${\frac{\partial V_{\text{m}}\left(x,t\right)}{\partial x}|}_{x=0}=r_{\text{e}}{I}_{\text{s}}\left(t\right),$$

$${\frac{\partial V_{\text{m}}\left(x,t\right)}{\partial x}|}_{x=L}=r_{\text{e}}{I}_{\text{s}}\left(t\right)+r_{\text{i}}g{V}_{\text{m}}\left(L,t\right)\text{.}$$ (3)

If g = 0, then the cable is sealed at both ends and symmetrical.

Although the cable equation (Eq. 1) with the boundary conditions (Eq. 3) describes the situation shown in Fig. 1 A, V_i and V_e are no longer explicitly included. As mentioned in Cartee and Plonsey (7) and Svirskis et al. (14), the boundary conditions (Eq. 3) are formally equivalent to current injection into both ends of the cable. This is because the cable equation (Eq. 1) with the boundary conditions (Eq. 3) can be interpreted as a cable system with grounded extracellular medium and current pair injected into both ends of the cable, as shown in Fig. 1 B. Here, the intracellular resistance r′_i is r_i + r_e, the extracellular resistance r′_e is 0, the shunt conductance g′ is $r_{\text{i}}/r_{\text{i}}+r_{\text{e}}g$, and the intracellular stimulus currents at x = 0 and x = L become

$$I_{\text{s}}^{\prime }\left(t\right)=-\frac{r_{\text{e}}}{r_{\text{i}}+r_{\text{e}}}{I}_{\text{s}}\left(t\right)\mathrm{and}-I_{\text{s}}^{\prime }\left(t\right)=\frac{r_{\text{e}}}{r_{\text{i}}+r_{\text{e}}}{I}_{\text{s}}\left(t\right),$$

respectively. The boundary conditions in this situation are as follows (Eq. 4), and are the same as Eq. 3. Note that the direction of the injecting current is inward at the anode and outward at the cathode:

$${\frac{\partial V_{\text{m}}\left(x,t\right)}{\partial x}|}_{x=0}=-{r^{\prime }}_{\text{i}}{I^{\prime }}_{\text{s}}\left(t\right),$$

$${\frac{\partial V_{\text{m}}\left(x,t\right)}{\partial x}|}_{x=L}=-{r^{\prime }}_{\text{i}}{I^{\prime }}_{\text{s}}\left(t\right)+{r^{\prime }}_{\text{i}}g\prime V_{\text{m}}\left(L,t\right)\text{.}$$ (4)

This alternative interpretation of the situation may help us understand the behavior of the solution. Still, there is a serious problem. Generally, it is difficult to mathematically treat such time-varying boundary conditions depending on the stimulus current, I′_s(t). In fact, analytic solutions have so far been derived only for the case of a DC step input, (g = 0 (7); g ≠ 0 (14)). To go around this difficulty, we derived a slightly modified cable equation (Eq. 5) and boundary conditions (Eq. 6) for a physically equivalent situation (Fig. 1 C). In this situation, instead of injecting I′_s(t) and −I′_s(t) at x = 0 and x = L, current density I_i(x, t) = I′_s(t)(δ(x − ɛ) − δ(x − L + ɛ)) is given along the cable. Here, δ(t) is the Dirac δ-function and ɛ is an infinitesimal distance along the cable. The injected current does not flow through the very end of the cable, hence the boundary condition (Eq. 6):

$$\tau \frac{\partial V_{\text{m}}\left(x,t\right)}{\partial t}={\lambda }^2\frac{{\partial }^2{V}_{\text{m}}\left(x,t\right)}{\partial x^2}-V_{\text{m}}\left(x,t\right)+{\lambda }^2{r^{\prime }}_{\text{i}}{I}_{\text{i}}\left(x,t\right),$$ (5)

$$\frac{\partial V_{\text{m}}\left(x,t\right)}{\partial x}{{|}_{x=0}=0,\frac{\partial V_{\text{m}}\left(x,t\right)}{\partial x}|}_{x=L}={r^{\prime }}_{\text{i}}g\prime V_{\text{m}}\left(L,t\right)\text{.}$$ (6)

The system is expressed as a cable equation with boundary conditions independent of the stimulus current, consisting of the reflecting boundary condition at x = 0 and the leaky boundary condition at x = L. Through this transformation, we can derive analytic solutions for any extracellular stimulus current, I_s(t), as follows.

Derivation of the Green's function

Shunt-end case

The eigenvalues and eigenfunctions of the cable equation (Eq. 1) satisfying the boundary conditions (Eq. 6) are given by the following expressions (14,33–35):

$${\mathit{\mu }}_{\text{n}}\tan \left({\mathit{\mu }}_{\text{n}}L\right)=r_{\text{i}}g;n=0,1,2,\dots ,$$ (7)

$${\mathit{\varphi }}_{\text{n}}\left(x\right){\theta }_{\text{n}}\left(t\right)=\cos \left({\mathit{\mu }}_{\text{n}}x\right)\exp \left(-t/{\mathit{\kappa }}_{\text{n}}\right),$$ (8)

$${\mathit{\kappa }}_{\text{n}}=\frac{\tau }{1+{\mathit{\mu }}_{\text{n}}^{\text{2}}{\lambda }^2},$$ (9)

where the eigenvalues, μ_n, obey the transcendental equation (Eq. 7).

Here, we calculate the inner products between the eigenfunctions,

$${\mathit{\alpha }}_{\text{n},\text{m}}=\langle {\mathit{\varphi }}_{\text{n}}\left(x\right),{\mathit{\varphi }}_{\text{m}}\left(x\right)\rangle ={\int }_0^{\text{L}}dx\cos \left({\mathit{\mu }}_{\text{n}}x\right)\cos \left({\mathit{\mu }}_{\text{m}}x\right),$$

and then we obtain

$${\mathit{\alpha }}_{\text{n},\text{m}}=\left[\frac{L}{2}+\frac{r_{\text{i}}g}{2}{\left(\frac{\cos \left({\mathit{\mu }}_{\text{n}}L\right)}{{\mathit{\mu }}_{\text{n}}}\right)}^2\right]{\mathit{\delta }}_{\text{n},\text{m}},$$ (10)

where δ_{n, m} is the Krönecker δ. Because the set of orthogonal eigenfunctions, {ϕ_n(x)}, is complete (36), the δ-function can be expanded in a series of these eigenfunctions:

$$\mathit{\delta }\left(x-x\prime \right)=\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathit{\varphi }}_{\text{n}}(x\prime ){\mathit{\varphi }}_{\text{n}}\left(x\right)}{{\mathit{\alpha }}_{\text{n},\text{n}}}\text{.}$$ (11)

This enables us to derive the Green's function of the cable equation (Eq. 1) with asymmetric boundary conditions (Eq. 6):

$$G\left(x,x\prime ,t-t\prime \right)=\frac{1}{\tau }\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathit{\varphi }}_{\text{n}}(x\prime )}{{\mathit{\alpha }}_{\text{n},\text{n}}}{\mathit{\varphi }}_{\text{n}}\left(x\right)\exp \left(-\frac{t-t\prime }{{\kappa }_{\text{n}}}\right),$$ (12)

where x is the observation point for an impulse response, and x′ and t′ are the position and time of an impulse input, respectively. A detailed explanation of the derivation is given in the Appendix.

Sealed-end case

When g = 0, the eigenvalues and eigenfunctions expressed in Eqs. 7 and 8 become

$${\mathit{\mu }}_{\text{n}}=\frac{n\pi }{L}\text{and}{\mathit{\alpha }}_{\text{n},\text{m}}=\frac{L}{2}{\mathit{\delta }}_{\text{n},\text{m}}\text{.}$$ (13)

Therefore, the Green's function derived here includes the conventional Green's function for sealed ends (37–39).

Response to extracellular stimulus

The advantage to using the Green's function method is that it enables us to obtain analytic solutions of responses to any extracellular stimulus current, I_s(t). According to the transformation into the equivalent system described in Eqs. 5 and 6, by convolving the Green's function (Eq. 12) with the current density I_i(x, t) in Eq. 5, we can obtain a solution for the cable response to the extracellular stimulus, I_s(t), as

$$V_{\text{m}}\left(x,t\right)=\sum _{n=0}^{\mathrm{\infty }}{A}_{\text{n}}\left(x\right){\int }_0^{\text{t}}dt\prime \exp \left(-\frac{t-t\prime }{{\kappa }_{\text{n}}}\right)I_{\text{s}}(t\prime ),$$ (14)

$$A_{\text{n}}\left(x\right)=\frac{r_{\text{e}}{\lambda }^2}{\tau {\mathit{\alpha }}_{\text{n,n}}}\left({\mathit{\varphi }}_{\text{n}}\left(L\right)-{\mathit{\varphi }}_{\text{n}}\left(0\right)\right){\mathit{\varphi }}_{\text{n}}\left(x\right)\text{.}$$ (15)

This equation means that a finite length cable perturbed by extracellular stimuli can be expanded in a series of first-order lag elements, as in the case of intracellular stimuli (14,33–35). Namely, it is equivalent to a parallel circuit consisting of a set of first-order lag elements with different time constants, κ_n (n = 0, 1, 2, ···).

Equation 14 can be separated into the following two terms:

$$V_{\text{m}}\left(x,t\right)=\frac{r_{\text{e}}{\lambda }^2}{\tau }\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathit{\varphi }}_{\text{n}}\left(L\right)}{{\mathit{\alpha }}_{\text{n},\text{n}}}{\mathit{\varphi }}_{\text{n}}\left(x\right){\int }_0^{\text{t}}dt\prime \exp \left(-\frac{t-t\prime }{{\kappa }_{\text{n}}}\right)I_{\text{s}}(t\prime )-\frac{r_{\text{e}}{\lambda }^2}{\tau }\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathit{\varphi }}_{\text{n}}\left(0\right)}{{\mathit{\alpha }}_{\text{n},\text{n}}}{\mathit{\varphi }}_{\text{n}}\left(x\right){\int }_0^{\text{t}}dt\prime \exp \left(-\frac{t-t\prime }{{\kappa }_{\text{n}}}\right)I_{\text{s}}(t\prime )\text{.}$$ (16)

Here, the first term corresponds to a response to the injection current, $\frac{r_{\text{e}}}{r_{\text{i}}+r_{\text{e}}}{I}_{\text{s}}\left(t\right)$, into the shunt end (x = L), and the second term is equal to that to the injection current, $-\frac{r_{\text{e}}}{r_{\text{i}}+r_{\text{e}}}{I}_{\text{s}}\left(t\right)$, into the sealed end (x = 0). Consequently, the difference between the two responses to the intracellular stimuli at both ends of the cable is equal to the response to the extracellular stimulation.

Results

Numerical calculation and parameters

To solve Eq. 1 numerically with the boundary conditions (Eq. 3), we employed the implicit method (40).

The eigenvalues μ_n obeying Eq. 7 were calculated with the Newton's method (40). Moreover, for the numerical calculations of Eq. 14, we approximated the infinite series composing Eq. 14 as a finite series until n = 1000. In this case, the error ratio is 0.382%. Here, the error ratio we used is defined as the difference between the steady solution of Eqs. 1 and 3 in response to the DC stimulus calculated by the implicit method and that of the finite series until n = 1000 normalized to the former solution.

We used the parameter values suggested for the hippocampal CA1 pyramidal neuron: specific membrane capacitance C_m = 1.5 (μF/cm²) (25), specific membrane resistivity R_m = 30 (kΩcm²) (25,41,42), specific intracellular resistivity R_i = 200 (Ω-cm) (22,42), diameter of the cable d = 1.2 (μm) (22), and length of the cable L = 700 (μm) (22). The parameters for determining the electric characteristics per unit length of cable were calculated as r_m = R_m/(πd), r_s = R_s/(πd), r_i = 4Ri/(πd²), and c_m = C_mπd. The extracellular resistance was set to be r_e = 20 (Ω-cm) (39).

The inhomogeneous membrane resistance of the dendrite, which has been reported by Stuart and Spruston (27), Inoue et al. (25), Golding et al. (24), and Omori et al. (26), has been modeled by assuming that its effect can be approximated by the effect of the shunt g attached to the uniform cable at x = L. In Figs. 2–4, we used g = 880 pS. If one-tenth of the cylindrical cable whose whole length is 700 μm is leakier than other nine-tenths of the cable, the membrane resistance per unit length of the leakier part corresponding to g = 880 pS becomes 7.96 MΩ-cm. When the diameter of the cable is 1.2 μm, the specific membrane resistivity is 3 kΩcm², which is one-tenth of the specific membrane resistivity we used.

Figure 2.

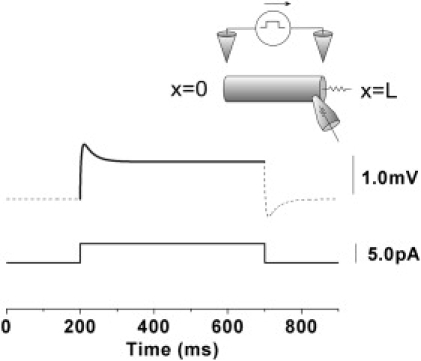
Biphasic response at the shunt end (x = L) to DC step extracellular stimulus. The resistor sticking out of the cable at the x = L end represents the shunt and the truncated cone with a resistor inside it represents a recording electrode. In the upper plots, the dashed line is a numerical solution to the cable equation using the implicit method, and the solid line is the theoretical solution from Eq. 18. The lower trace shows a DC step extracellular stimulus current. These solutions show slower hyperpolarization after rapid depolarization, i.e., a biphasic change. Here, g = 880 pS.

Figure 3.

Cable with a shunt shows a frequency preference in response to a ZAP extracellular stimulus. (A-1) AC extracellular stimulus current with an increasing frequency, i.e., ZAP current. (A-2) Frequency of the ZAP current as a function of the time t. The frequency of the ZAP current used here exponentially increases from 0 Hz to 200 Hz obeying $freq=200/(\exp \left(1\right)-1)\left[\exp \left(t/1000\right)-1\right]$. (B-1) The trace is the numerically obtained ZAP responses at the x = L end of the cable with a shunt (g = 880 pS). The arrowhead in panel B-1 indicates the maximum point of the amplitude responses at the shunt end of the cable with the shunt to the ZAP extracellular stimulus. (B-2) The trace is the numerically obtained ZAP responses at the x = L end of the cable without shunt (g = 0 pS). AC extracellular stimuli do not cause the frequency preference in the cable without the shunt. (C and D) The traces in panels C and D show numerically obtained responses at the shunt end (x = L) to ZAP injection currents into the shunt end (x = L) and the sealed end (x = 0), respectively. A subtraction of the numerical solution in panel D from that in panel C is equal to the response in panel B-1. The amplitudes responses to the ZAP injection current only into one end monotonically decrease with increasing frequency, in contrast with the frequency preference in response to the ZAP extracellular stimulus.

Figure 4.

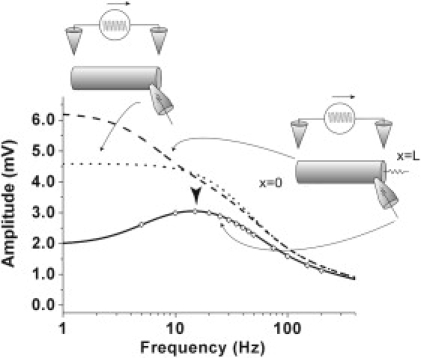
Comparison of amplitude-frequency characteristics in the cables with and without a shunt. The long broken line and solid line, respectively, denote amplitude-frequency characteristics of the cable with a shunt (g = 880 pS) at the sealed end (x = 0) and the shunt end (x = L) in response to the AC extracellular stimuli. The dotted line denotes amplitude-frequency characteristics of the cable without shunt (g = 0 pS). These results were obtained from Eq. 22. The dots show the amplitude-frequency responses of the cable equation with the shunt at the shunt end (x = L) obtained by the implicit method in the sinusoidal steady state. Only the leaky part of the cable with the shunt shows a frequency preference. The amplitude of the frequency response at the sealed end of the cable with the shunt is larger than that of the cable without the shunt.

Response to DC step extracellular stimulus

First, we consider the case of a DC step current input, I_s(t) = I_cu(t) where

$$u\left(t\right)=\{\begin{array}{ll}1\hfill & \left(t\ge 0\right),\hfill \\ 0\hfill & \left(t<0\right)\text{.}\hfill \end{array}$$ (17)

According to Eq. 14, the response to the DC step stimulus is

$$V_{\text{m}}\left(x,t\right)=\sum _{n=0}^{\mathrm{\infty }}{A}_{\text{n}}\left(x\right)I_{\text{c}}{\kappa }_{\text{n}}\left(1-\exp \left(-\frac{t}{{\kappa }_{\text{n}}}\right)\right)\text{.}$$ (18)

This solution is formally similar to that of Svirskis et al. (14). Note that in the strict sense, the model used here is not identical to the one of Svirskis et al., which neglected the resistive extracellular medium. Their model is classified as a Rattay's model (13), assuming that the potential gradients in the extracellular space are uniform.

When g = 0, applying a Laplace transform to the solution Eq. 18 yields

$${\tilde{V}}_{\text{m}}\left(x,s\right)=\frac{r_{\text{e}}{I}_{\text{c}}\lambda }{s\sqrt{\tau s+1}}\frac{\sinh \left(\frac{\sqrt{\tau s+1}\left(2x-L\right)}{2\lambda }\right)}{\cosh \left(\frac{\sqrt{\tau s+1}L}{2\lambda }\right)}\text{.}$$ (19)

Moreover, according to the final value theorem, the steady solution becomes

$$V_{\text{m}}\left(x,\mathrm{\infty }\right)=2r_{\text{e}}{I}_{\text{c}}\lambda \frac{\sinh \left(\frac{2x-L}{2\lambda }\right)}{\cosh \left(\frac{L}{2\lambda }\right)}\text{.}$$ (20)

These results are equal to Eq. 47 in Cartee and Plonsey (7).

Fig. 2 superimposes the theoretical solution of the cable with a shunt at one end on the numerical simulation of Eqs. 1 and 3. Both solutions show slow hyperpolarization after rapid depolarization, i.e., a biphasic change, as previously reported (14,19,26).

Response to AC extracellular stimulus

Next, we consider the case of an AC input current, I_s(t) = I_c sin(ωt). The value ω is the angular frequency of the AC extracellular stimulus. Here, we elucidate the frequency dependence of the cable with a shunt at one end in response to an AC extracellular stimulus. After enough time passes, the frequency response converges to

$$V\left(x,t\right)=B\left(x,\omega \right)I_{\text{c}}\sin \left(\omega t+\Phi \left(x,\omega \right)\right),$$ (21)

where the amplitude, B(x, ω), and the phase, Φ(x, ω), are

$$B\left(x,\mathit{\omega }\right)=\sqrt{{\left(\sum _{n=0}^{\mathrm{\infty }}\frac{1}{1+{\mathit{\kappa }}_{\text{n}}^2{\mathit{\omega }}^2}{A}_{\text{n}}\left(x\right)\right)}^2+{\left(\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathit{\kappa }}_{\text{n}}\mathit{\omega }}{1+{\mathit{\kappa }}_{\text{n}}^2{\mathit{\omega }}^2}{A}_{\text{n}}\left(x\right)\right)}^2},$$ (22)

$$\Phi \left(x,\mathit{\omega }\right)=-{\tan }^{-1}\frac{{\sum }_{n=0}^{\mathrm{\infty }}\frac{{\mathit{\kappa }}_{\text{n}}\mathit{\omega }}{1+{\mathit{\kappa }}_{\text{n}}^2{\mathit{\omega }}^2}{A}_{\text{n}}\left(x\right)}{{\sum }_{n=0}^{\mathrm{\infty }}\frac{1}{1+{\mathit{\kappa }}_{\text{n}}^2{\mathit{\omega }}^2}{A}_{\text{n}}\left(x\right)}\text{.}$$ (23)

Fig. 3 B-1 shows the frequency response at the shunt end (x = L) obtained by a numerical simulation for the ZAP stimulus. The frequency of the ZAP stimulus obeys the following equation:

$$freq=\frac{200}{\exp \left(1\right)-1}\left[\exp \left(\frac{t}{1000}\right)-1\right]\text{.}$$

As denoted by the arrowhead in Fig. 3 B-1, the amplitude was maximized at ∼10 Hz. On the other hand, as shown in Fig. 3 B-2, in contrast with the frequency preference of the cable with the shunt end, the amplitude response of the cable without the shunt end monotonically decreases as the frequency of the stimulus increases.

As previously mentioned, the extracellular stimulations with the anode and cathode were formally equivalent to current injection into both ends of the cable. Fig. 3, C and D, shows the frequency response at the shunt end (x = L) to an intracellular stimulus at one side of the cable ends (x = 0 and x = L) (see the inset in Fig. 3, C and D). Subtracting the numerical solution in Fig. 3 D from that of Fig. 3 C is equal to the response to the extracellular stimulation shown in Fig. 3 B-1. As shown in Fig. 3, C and D, the amplitudes of the responses to the ZAP intracellular stimulus only at one end monotonically decrease with increasing frequency, in contrast with the frequency preference in response to the ZAP extracellular stimulus as shown in Fig. 3 B-1.

Fig. 4 shows the amplitude-frequency characteristics in the cables with and without a shunt. In contrast with the frequency preference of the shunt end (x = L), the amplitude response at the sealed end (x = 0) of both the cables with and without a shunt monotonically decreases as the frequency of the stimulus increases. Therefore, only the leaky part of the cable shows a frequency preference in response to an AC extracellular stimulus. Furthermore, as shown in Fig. 4, we can clearly see that the amplitude of the frequency response of the cable at the sealed end (x = 0) with a shunt, is larger than that of the cable without a shunt in low frequency range.

As shown in Fig. 5, A and D, the amplitude of the frequency response at the sealed end becomes larger as the shunt conductance g and the membrane time constant τ increase.

Figure 5.

Parameter dependence of the frequency response. (A) Amplitude-frequency characteristics in the sealed end (x = 0) depending on the shunt conductance g. (B, 1 and 2) Amplitude-frequency characteristics and normalized characteristics in the shunt end (x = L), depending on g. Here, the membrane time constant τ = 45 ms. (C) Preferred frequency maximizing the amplitude response at the shunt end (x = L) depending on g and τ. (D) Amplitude at 0 Hz in the sealed end (x = 0) depending on g and τ. (E) Amplitude maximized at the preferred frequency in the shunt end (x = L) depending on g and τ. These results were obtained from Eq. 22. Depending on these parameters, the preferred frequencies at x = L vary from δ- to β-bands. The dominant frequencies inducing large amplitudes are mainly in δ- and θ-bands. On the other hand, the amplitude of the frequency response at x = 0 becomes larger as g and τ increase.

Fig. 5, B-1, B-2, C, and E, shows the parameter dependence of the preferred frequency maximizing the amplitude response at the shunt end (x = L) to the AC extracellular stimulus. Depending on the shunt conductance g and the membrane time constant τ, the preferred frequencies varied from the δ- to the β-bands (1–30 Hz). The dominant frequencies inducing large amplitudes are mainly in δ- and θ-bands (1–12 Hz).

Discussion

To understand the behavior of dendrites subjected to time-varying extracellular electric fields, we analytically solved cable equations for finite cylindrical cables with and without a leak conductance attached to one end by employing the Green's function method. Analytic solutions have previously been derived only in the case of the DC step stimulus (sealed case (7); shunted case (14)) because it is difficult to mathematically treat time-variable boundary conditions in Eq. 3. To address this problem, we transformed the cable stimulated by an extracellular electrode pair (Fig. 1 A) into an equivalent system with grounded extracellular medium and the current density

$$I_{\text{i}}\left(x,t\right)=-\frac{r_{\text{e}}}{r_{\text{i}}+r_{\text{e}}}{I}_{\text{s}}\left(t\right)\left[\right(\mathrm{\delta }\left(x-\varepsilon \right)-\mathrm{\delta }(x-(L-\varepsilon ))]$$

along the cable (Fig. 1 C), where ɛ is an infinitesimal distance. Through this transformation, the boundary conditions (Eq. 3) are transformed into the boundary conditions consisting of the reflecting boundary condition and the leaky boundary condition in Eq. 6. Thus, we can derive analytic solutions for a general extracellular stimulus by employing the Green's function method. As a consequence of this analysis, we can picture the behavior of a cable subjected to extracellular electric fields as responses to intracellular stimuli at both ends of the cable, and this can help us imagine the behavior of dendrites in time-varying extracellular electric fields. Moreover, our theoretical framework makes it possible for us to understand the modifications of neural activities caused by extracellular electric fields, and thus, it has the potential for a new understanding of nonsynaptic interactions of nerve cells via extracellular electric fields.

Whereas the Green's function of finite cables sealed at both ends was given in Tuckwell (38) and Koch (39), there was no clear description for cables with asymmetric boundary conditions consisting of a reflecting and leaky one. For such cables, analytic solutions for intracellular DC step stimuli have been obtained by using the separation of variables method and Fourier series expansion (33–35). On the other hand, for the finite cable with symmetric sealed ends and nonuniform membrane resistivity, the Green's function for intracellular stimuli was given in London et al. (43). For extracellular DC step stimuli, Svirskis et al. (14), derived solutions here again by using the separation of variables method and Fourier series expansion. For AC intracellular or extracellular stimuli, however, no analytic solution has been derived for such cables. To our knowledge, our study is the first attempt to obtain the Green's function of finite cable with asymmetric boundary conditions perturbed by general intracellular/extracellular stimuli. Our solution for extracellular DC step stimuli (Eq. 18) is formally equivalent to that of Svirskis et al. (14).

As revealed in Fig. 1 C, we can picture the behavior of a cable subjected to extracellular electric fields as responses to intracellular stimuli at both ends of the cable. To elucidate the mechanism of the unique behaviors induced by extracellular stimuli, we plotted the responses to intracellular stimuli in Fig. 6. Fig. 6, A and B, shows responses to DC step stimuli in the cables without and with a shunt at x = L. By comparing these figures, we can see a clear distinction between electric spread speed from x = 0 to x = L in these cables. The arrowhead in Fig. 6 B denotes a delayed response, which is unique to the cable with a shunt. The main reason for the biphasic response is the slow spread of potential from the sealed end to the shunt end (25,26).

Figure 6.

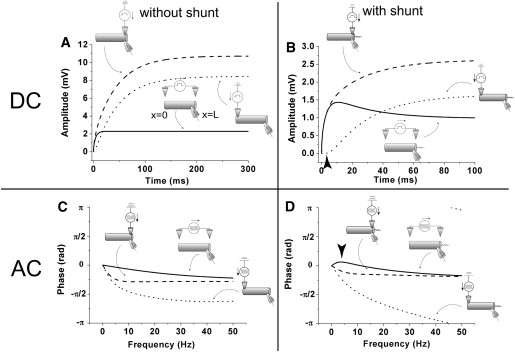
Mechanism of the unique behaviors induced by extracellular stimuli. (A and B) The dotted and broken lines denote responses at the x = L end to DC step intracellular stimulus at x = 0 and x = L, respectively. These lines were numerically obtained from the first and second terms of Eq. 16. The solid lines are responses to a DC extracellular stimulus, and they were obtained from Eq. 18. (A) Responses in the case without shunt (g = 0 pS). (B) Responses in the case with a shunt (g = 880 pS). A delayed response denoted by the arrowhead in panel B, which is unique to the shunt case, is the main reason for the biphasic response. (C and D) The dotted and broken lines denote phase-frequency characteristics in response to AC currents injected into x = 0 and x = L, respectively. The solid lines are phase-frequency characteristics in responses to an AC extracellular stimulus. These lines were obtained from Eq. 23. (C) Responses in the case without shunt (g = 0 pS). (D) Responses in the case with a shunt (g = 880 pS). The relative phase between the dotted and broken lines in panel D quickly becomes larger than that in panel C as the frequency of stimuli increases. The balance between the increment of the relative phase and the attenuation of the amplitude with increasing frequency of stimuli is the main reason for the frequency preference. The arrowhead in panel D shows the phase advance around the preferred frequency.

Fig. 6, C and D, shows phase-frequency characteristics in response to AC stimuli in cables without and with a shunt at x = L. Whereas in both cables the phase in responses to AC intracellular stimuli becomes monotonically delayed as the frequency of stimuli increases, the phase of the cable with the shunt advances in response to AC extracellular stimuli, as denoted by the arrowhead in Fig. 6 D. By comparing these figures, we can see a clear distinction between the relative phases of the two frequency responses to intracellular stimuli in these cables. The relative phase of the cable with the shunt (Fig. 6 D) quickly becomes larger than that of the cable without the shunt (Fig. 6 C) as the frequency of stimuli increases. As mentioned previously, the difference between two sinusoidal waves of the membrane potentials induced by the AC intracellular stimuli at both ends of the cable is equal to the wave induced by the AC extracellular stimulus. If the two waves are in phase, then they will tend to cancel out. Conversely, if the two waves are out of phase, then the resultant wave will have a large amplitude. Note that the polarity of the second term of Eq. 16 is negative. Thus, amplitude of the resultant wave becomes larger as the relative phase of the two waves become out of phase. On the other hand, as shown in Fig. 3, C and D, the amplitudes of the responses to the AC intracellular stimulus only at one end monotonically decrease with increasing frequency. Consequently, the main reason for the frequency preference is the balance between the increment of the relative phase and the attenuation of the amplitude with increasing frequency of stimuli. Because the quick increment of the relative phase reflects the slow electric spread from the sealed end to the shunt end, it is appropriate to say that the biphasic response in the DC step extracellular stimulation and the frequency preference in the AC extracellular stimulation share the same mechanism.

Several studies have shown frequency preference of responses that were induced by applying an AC current through recording electrodes to CNS neurons, and the frequency preference has been shown to be dependent on voltage-sensitive membrane conductances (28–32). Our theoretical results show that CNS neurons with leaky membrane resistivity at distal dendrites may show a frequency preference when they are in an oscillating extracellular electric field. Recently, estimates of the nonuniform distribution of the dendritic membrane resistance have been obtained using either a combination of double whole-cell patch clamping and simulations or voltage imaging and simulations, and the distal dendrite was found to be more leaky than the proximal dendrite in both cortical layer V pyramidal neurons (27) and hippocampal CA1 pyramidal neurons (24,26,44). Thus, there is a possibility that both neuron types show a frequency preference for oscillating extracellular electric fields.

As shown in Fig. 5, depending on the shunt conductance attached to one end and the membrane time constant, the preferred frequency varied from δ- to β-bands. Particularly if the membrane time constant is ∼20 ms, the finite cable can tune in the preferred frequency from 0 Hz to 20 Hz through modulation of the shunt conductance. This result raises the possibility that CNS neurons show a wide range of frequency preference depending on the leaky membrane resistivity at distal dendrites. For example, in an EEG recording, the hippocampus shows a characteristic 4–12 Hz oscillation, the θ-rhythm. As mentioned above, the leaky distal part of the dendrite may cause a sensitive tuning of hippocampal CA1 pyramidal neurons in a θ-oscillating extracellular electric field.

In Fig. 4 and Fig. 5 D, we have shown that the response amplitude at the sealed end of a cable with a shunt is greater than that of the cable with no shunt in low-frequency range. This is because the extracellular stimulating current caused a larger voltage drop across the sealed membrane than the shunt membrane. This fact implies that the response at the sealed end of a cable can be amplified by introducing a shunt to the other end of the cable. If voltage-gated ion channels for inward current such as Na channels or Ca channels are located at the sealed end of the cable, then those channels are more likely to be activated by applying extracellular current when the other end has a shunt. The cell body or the initial segment of a neuron with leaky dendrites may have higher sensitivity to the extracellular field than those without leaks.

Appendix: Derivation of the Green's Function

Because the set of eigenfunctions {ϕ_n(x) = cos(μ_nx)} is complete, the Green's function of the finite-length cable equation (Eq. 1) with the boundary conditions (Eq. 6) and the δ-function representing the impulse input can be expressed as a series of eigenfunctions as follows:

$$G\left(x,x\prime ,t-t\prime \right)=\frac{1}{2\pi }\sum _{n=0}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d\mathit{\omega }\overline{G}\left(n,\mathit{\omega },x\prime \right){\mathit{\varphi }}_{\text{n}}\left(x\right)\exp \left(i\mathit{\omega }\left(t-t\prime \right)\right),$$ (24)

$$\mathit{\delta }\left(x-x\prime \right)\mathit{\delta }\left(t-t\prime \right)=\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d\mathit{\omega }\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathit{\varphi }}_n(x\prime ){\mathit{\varphi }}_{\text{n}}\left(x\right)}{{\mathit{\alpha }}_{\text{n},\text{n}}}\exp \left(i\mathit{\omega }\left(t-t\prime \right)\right)\text{.}$$ (25)

Here, the time components of these functions are represented by the inverse Fourier transform. $\overline{G}(n,\mathit{\omega },x^{\prime })$ denotes the frequency transfer function of this system.

The Green's function satisfies the following equation:

$$\tau \frac{\partial G\left(x,x\prime ,t\right)}{\partial t}-{\lambda }^2\frac{{\partial }^{2}G\left(x,x\prime ,t\right)}{\partial x^2}+G\left(x,x\prime ,t\right)=\mathit{\delta }\left(x-x\prime \right)\mathit{\delta }\left(t-t\prime \right)\text{.}$$ (26)

Substituting Eqs. 24 and 25 into Eq. 26, one can determine the frequency transfer function as

$$\overline{G}\left(n,\mathit{\omega },x\prime \right)=\frac{\frac{{\mathit{\varphi }}_{\text{n}}(x\prime )}{{\mathit{\alpha }}_{\text{n,n}}}}{i\mathit{\omega }\tau +{\mathit{\mu }}_{\text{n}}^2{\mathit{\lambda }}^2+1}\text{.}$$ (27)

Thus, the Green's function becomes

$$G\left(x,x\prime ,t-t\prime \right)=\frac{1}{2\pi }\sum _{n=0}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d\mathit{\omega }\frac{\frac{{\mathit{\varphi }}_{\text{n}}(x\prime )}{{\alpha }_{\text{n},\text{n}}}}{i\mathit{\omega }\tau +{\mathit{\mu }}_{\text{n}}^2{\mathit{\lambda }}^2+1}{\mathit{\varphi }}_{\text{n}}\left(x\right)\exp \left(i\mathit{\omega }\left(t-t\prime \right)\right)\text{.}$$ (28)

The inverse Fourier transform for the time domain gives

$$G\left(x,x\prime ,t-t\prime \right)=\frac{1}{\tau }\sum _{n=0}^{\mathrm{\infty }}\frac{{\mathit{\varphi }}_{\text{n}}(x\prime )}{{\mathit{\alpha }}_{\text{n},\text{n}}}{\mathit{\varphi }}_{\text{n}}\left(x\right)\exp \left(-\frac{{\mathit{\mu }}_{\text{n}}^2{\mathit{\lambda }}^2+1}{\tau }\left(t-t\prime \right)\right)\text{.}$$ (29)