A factorial analysis of timed and untimed measures of mathematics and reading abilities in school aged twins

Abstract

The present study examined the phenotypic and genetic relationship between fluency and non-fluency-based measures of reading and mathematics performance. Participants were drawn from the Western Reserve Reading and Math Project, an ongoing longitudinal twin project of same-sex MZ and DZ twins from Ohio. The present analyses are based on tester-administered measures available from 228 twin pairs (age M=9.86 years). Measurement models suggested that four factors represent the data, namely Decoding, Fluency, Comprehension, and Math. Subsequent quantitative genetic analyses of these latent factors suggested that a single genetic factor accounted for the covariance among these four latent factors. However, there were also unique genetic effects on Fluency and Math, independent from the common genetic factor. Thus, although there is a significant genetic overlap among different reading and math skills, there may be independent genetic sources of variation related to measures of decoding fluency and mathematics.

Reading is associated with mathematics, especially when the math problem requires linguistic effort (see Jordan, 2007). For example, if a child has difficulty recognizing and understanding individual words, then understanding the syntax of a mathematical word problem would be hard, even before any computation occurs. Quantitative genetic methodology allows for an examination of the overlap and independence of etiological influences on reading and mathematics. Twin studies estimate the proportion of variance in a trait that is influenced by additive genetic effects, or heritability (the combined effect of all genes which influence an outcome; h²), shared environmental effects (c², those influences that make family members more similar) and nonshared environmental effects (e², those influences that make family members less similar; see Plomin, DeFries, McClearn, & McGuffin, 2008).

Although the quantitative genetic literature suggests that there is substantial genetic overlap between reading and mathematics (Petrill & Plomin, 2007), there is also evidence for unique genetic effects on mathematics, distinct from other cognitive abilities such as reading (Plomin & Kovas, 2005). For example, Hart, Petrill, Thompson, and Plomin (2009) reported that after accounting for genetic covariance among general cognitive ability, reading and mathematics, there were still significant independent genetic influences on mathematics. Similarly, Kovas, Harlaar, Petrill, and Plomin (2005) found independent genetic effects for mathematics outside common influences shared among general cognitive ability, reading and math.

Historically, quantitative genetic analyses of the relationship between reading and mathematics have used global achievement tests (Thompson, Detterman, & Plomin, 1991). Recent work has begun to examine theoretically-derived measures of the skills important for overall reading and mathematics performance; for example measures of rapid automatized naming (RAN) and decoding as measures of “reading”, and calculation, fluency and problem solving as measures of “mathematics” (Hart et al., 2009). This initial analysis suggested that measures which were timed, such as RAN and math fluency, shared significant genetic overlap. Measures which were not timed, namely word decoding and calculation, did not have significant shared genetic effects. Moreover, research has suggested the independent genetic effects seen in general factors of mathematics may be driven by measures of math fluency only (Petrill & Hart, 2009). These results in total would suggest that there may be a relationship between timed measures which is a different relationship than untimed measures. However, the association has yet to be directly tested.

The goal of this present report is to better understand the relationship between components of mathematics and reading performance, from both a measurement perspective and a quantitative genetic perspective. The literature is just beginning to identify the component processes of mathematical performance, as well as how these processes are associated with reading (e.g., Fuchs & Fuchs, 2002; Geary et al., 2000). Therefore, we will first examine a series of theoretically motivated latent factor models to provide greater insight into the relationship among the components of reading and math performance. Hart et al. (2009) served as a preliminary survey of the association between specific reading and mathematics measures, and did not use latent factors representing various constructs. For example, there is debate as to the extent of the similarity between timed measures versus untimed measures of reading, especially when both require word level decoding skills (e.g., Wolf & Bowers, 1999). Moreover, the Hart et al. (2009) study did not examine specific component processes within reading, instead only using measures of decoding.

We propose to move through a series of measurement models which represent the most general theories of cognition to more specific hypotheses within construct. Therefore, we will first test a domain general hypothesis (e.g., Fodor, 1983), followed by a model which tests the hypothesis of specific cognitive abilities. Following these, the specific cognitive ability factors will be broken up into more precise components, representing the ideas of reading decoding being separate from comprehension, and fluency being distinct from each (e.g., Hoover & Gough, 1990). After determination of the best-fitting measurement model, quantitative genetic methodology will be used to study the genetic and environmental etiology among the factors.

1. Method

1.1. Participants

Participants were drawn from the Western Reserve Reading and Math Project (WRRMP), an ongoing longitudinal twin project based in Ohio (further details of the sample may be found in Petrill, Deater-Deckard, Thompson, DeThorne, & Schatschneider, 2006). Twins are assessed across seven annual home visits. The present analyses are based on the fifth home visit, which includes the intensive measurement of both mathematics and reading performance. Twins were approximately 10 years old (M=9.86 years, SD=.89 years, range=7.42–12.25 years). Parent education levels varied widely, although slightly higher than the population average, and were similar for fathers and mothers: 14% high school or less, 16% some college, 38% bachelor's degree, 24% some post-graduate education or degree, 4% not specified. Most families were two-parent households (93%) and nearly all were White (91% of mothers, 94% of fathers). Data collection is currently ongoing, but presently 228 pairs of monozygotic (MZ; N=94) and same-sex dizygotic (DZ; N=134) are available for analysis. To date, 13 families (5% of total sample) have failed to complete a wave 5 home visit but had completed all other home visits previously.

1.2. Procedure and measures

Each twin was assessed by a separate tester during the annual visit. Test sessions were conducted in the twins' home in separate rooms, and lasted about 3 h. Families received $100 and the twins $5 each, for participation in the home visit.

1.2.1. Reading measures

Six reading-related measures were administered. Word Attack is a test of phonological decoding from the Woodcock Reading Mastery Tests (WRMT; Woodcock, 1987). It requires the participant to pronounce nonsense words using appropriate phonological rules. Word Identification (Word ID) is a test of whole word decoding from the WRMT, where the child must recognize and correctly pronounce real words (Woodcock, 1987). Published split-half reliabilities for these two tests are .94 and .95, respectively, for children in the fifth grade (Woodcock, 1987). Reading fluency was represented by a mean score from two subtests of the Test of Word Reading Efficiency (TOWRE): sight word efficiency and phonemic decoding efficiency (Torgesen, Wagner, & Rashotte, 1999). Sight word efficiency was measured by the number of real words accurately read in 45 s, whereas phonemic decoding efficiency was measured by the number of pronounceable nonwords read in 45 s. Test–retest reliability for both subtests of the TOWRE for children aged 10–18 years is .88. Fluency was also assessed via a mean score of the Oral Reading subtests from the Dynamic Indicators of Basic Early Literacy Skills (DIBELS; Good & Kaminski, 2002). These tests require the student to read out loud a story in paragraph form as fast and accurately as possible within 1 min. Scoring is based on the total number of words read accurately within the time limit based on grade-specific versions of the test. Test–retest reliability is published for elementary students as a range from .92–.97 (Good & Kaminski, 2002). The fifth test was the Passage Comprehension subtest of the Woodcock Reading Mastery Tests (WRMT; Woodcock, 1987). This test is a cloze format (i.e., fill in the blank) test of comprehension, where participants read a short passage and identify a missing key word that makes sense in the context of that passage. Published median reliability for the test is .83 in children. Finally, the Reading Comprehension subtest of the Peabody Individual Achievement Test (PIAT; Markwardt, 1997) was included. Participants read a sentence and then select the picture from four choices that best represents the meaning of the sentence. Test–retest reliability for 10-year-old children is .93.

1.2.2. Math measures

All math measures were subtests from the Woodcock–Johnson III Achievement test (Woodcock, McGraw, & Mather, 2001). Applied Problems measures the ability to analyze and solve applied math word problems. Quantitative Concepts tests the knowledge of mathematical concepts, symbols, and vocabulary, without any calculations required. Fluency measures a participant's ability to answer addition, subtraction, and multiplication problems in a 3-minute time limit. Calculation measures a child's ability to complete questions of addition, subtraction, multiplication, division, within an open time limit. Published median reliabilities of these tests are .92, .90, .89 and .85, respectively, in children.

1.2.3. Analysis plan

Analyses begun with a descriptive examination of each measured variable. This included a correlations matrix which allowed for the initial assessment of the variance and covariance structure of the data. Following this, a series of theoretically motivated confirmatory factor analyses was conducted to determine the factor structure of the data. Model fit indices were used to select the best model to represent the data at the phenotypic level. Quantitative genetic modeling was then applied to the data. First, descriptive univariate models were examined for each measured variable, allowing for an initial understanding of the genetic and environmental effects on each. Finally, the univariate quantitative genetic models were expanded into a multivariate analysis, allowing for a genetic and environmental breakdown of the variance and covariance of the best-fitting phenotypic model.

2. Results

Descriptive statistics for all measures are presented in Table 1. In order to provide comparison between the current sample and the larger population of children, standardized scores, age normed with a population mean of 100 and standard deviation of 15, are provided where available. In general, descriptive statistics suggest a slightly higher mean and lower standard deviation than population average. Consistent with prior publications, all further analyses were conducted with raw scores which had been age and sex standardized through a regression procedure. Pearson correlations between all measures were significant (see Table 2).

Table 1.

Means, standard deviations (SD), minimums and maximums for all reading and mathematics performance measures.

Variable	Mean	SD	Minimum	Maximum	n
WRMT Word Attacka	107.81	12.25	62.00	159.00	405
WRMT Word Identificationa	107.05	10.08	80.00	130.00	442
TOWREb	103.71	11.80	74.00	130.50	446
DIBELSc	122.21	35.02	31.00	209.33	443
WRMT Passage Comprehensiona	103.74	11.03	68.00	134.00	411
PIAT Reading Comprehensiond	106.38	11.44	79.00	144.00	442
WJ Applied Problemse	107.92	11.49	61.00	144.00	392
WJ Quantitative Conceptse	105.20	12.94	73.00	145.00	294
WJ Calculatione	106.06	13.24	71.00	152.00	436
WJ Fluencye	100.90	14.57	62.00	154.00	432

^aWoodcock Reading Mastery Tests (WRMT).

^bMean score of Test of Word Reading Efficiency Sight Word Efficiency and Decoding Efficiency (TOWRE).

^cDynamic Indicators of Basic Early Literacy Skills (DIBELS).

^dPeabody Individual Achievement Test (PIAT).

^eWoodcock–Johnson III (WJ).

Table 2.

Pearson correlations between all reading and mathematics performance measures.

Variable	WRMT Word Attacka	WMRTWord Identificationa	TOWREb	DIBELSc	WRMT Passage Comprehensiond	PIAT Reading Comprehensione	WJ Applied Problemsa	WJ Quantitative Conceptsa	WJ Calculationa	WJ Fluencya
WRMT Word Attacka	1.00
WRMT Word Identificationa	.78*	1.00
TOWREd	.72*	.72*	1.00
DIBELSe	.51*	.53*	.72*	1.00
WRMT Passage Comprehensiona	.52*	.67*	.55*	.56*	1.00
PIAT Reading Comprehensionb	.50*	.63*	.53*	.50*	.61*	1.00
WJ Applied Problemsc	.44*	.52*	.44*	.48*	.55*	.48*	1.00
WJ Quantitative Conceptsc	.36*	.42*	.33*	.36*	.47*	.34*	.70*	1.00
WJ Calculationc	.39*	.44*	.35*	.34*	.39*	.33*	.64*	.62*	1.00
WJ Fluencyc	.34*	.33*	.43*	.42*	.29*	.23*	.46*	.48*	.52*	1.00

Note. Only one child from the twin pair was used for these analyses.

^aWoodcock Reading Mastery Tests (WRMT).

^bMean score of Test of Word Reading Efficiency Sight Word Efficiency and Decoding Efficiency (TOWRE).

^cDynamic Indicators of Basic Early Literacy Skills (DIBELS).

^dPeabody Individual Achievement Test (PIAT).

^eWoodcock–Johnson III (WJ).

^*p<.05.

2.1. Evaluation of measurement models

Confirmatory factor analyses were conducted to ascertain the best-fitting measurement model for the data (see Table 3). Models were estimated using the structural equation modeling program Mx (Neale, Boker, Xie, & Maes, 2006) with all available age and sex standardized raw data. Modeling as such was conducted by an iterative process using full-information maximum likelihood (FIML) in order to minimize the negative log-likelihood (−2LL) function, providing the maximum likelihood estimates for the effects of interest. An index of goodness of fit between the model and the data was quantified using the Akaike Information Criterion (AIC; Akaike, 1987) and the sample-size adjusted Bayesian Information Criterion (BIC; Raftery, 1995). Lower AIC and BIC values identify a better fit of the model to the data, suggesting that it best reproduces the observed variances and covariances with as few unknown estimated parameters as possible. This fit index also compensates for the effect of model complexity by taking into account the degrees of freedom (Hu & Bentler, 1998; Marsh, Balla, & Hau, 1996). Also, for these analyses, only one member of the twin pair was randomly selected for modeling to counter non-independence.

Table 3.

Model fit statistics for phenotypic confirmatory factor analysis (best-fitting model in boldface).

Model	−2LL	df	AIC	BIC
Model 1	4796.38	2055	686.38	94.04
1 factor
Model 2	4646.57	2054	538.57	20.26
2 factors [Reading + Math]
Model 3	4618.36	2052	514.36	8.39
3 factors[Word Recognition + Comprehension + Math (Math Fluency)]
Model 4	4587.80	2049	489.80	−3.52
4 factors[Decoding + Fluency (math Fluency) + Comprehension + Math]
Model 5	4567.40	2049	469.40	−13.72
4 factors[Decoding + Fluency + Comprehension + Math (math Fluency)]

Note. Only one child from the twin pair was used for these analyses. AIC=Akaike Information Criterion. BIC=sample-size adjusted Bayesian Information Criterion Model 1 contains one factor, representing all available measures grouped as a domain general factor. Model 2 contains two factors, representing a Reading (WRMT Word Attack, Word Identification and Passage Comprehension, PIAT Reading Comprehension, the DIBELS and the TOWRE) and Math (WJ Applied Problems, Quantitative Concepts, Calculation and math Fluency).Model 3 represents three factors, incorporating Word Recognition (WRMT Word Attack and Word Identification, the DIBELS and the TOWRE), Comprehension(WRMT Passage Comprehension and PIAT Reading Comprehension) and finally all Math measures (WJ Applied Problems, Quantitative Concepts, Calculation and math Fluency). Model 4 contains four factors, Decoding (WRMT Word Attack, Word Identification), Fluency (the DIBELS, the TOWRE and WJ math Fluency), Comprehension (WRMT Passage Comprehension and PIAT Reading Comprehension), and Math (WJ Applied Problems, Quantitative Concepts and Calculation). Finally, Model 5 also contain four factors, Decoding (WRMT Word Attack, Word Identification), Fluency (the DIBELS and the TOWRE), Comprehension (WRMT Passage Comprehension and PIAT Reading Comprehension), and Math (WJ Applied Problems, Quantitative Concepts, Calculation and math Fluency).

Five measurement models were tested to determine the best fit for the data ahead of quantitative genetic modeling. Model 1 examined whether the measures could be best represented by a single domain general factor (e.g., Fodor, 1983). In Model 2, the domain general factor was separated into two specific factors, with all reading measures set to load on a reading factor (Reading) and all math measures set to load on a math factor (Math).

Model 3 separated the reading measures into two factors (e.g., Chall, 1983). The education literature distinguishes between decoding (word recognition) and comprehension as distinct factors within the construct of reading (Hoover & Gough, 1990). Given this, a Word Recognition factor and a Comprehension factor were created. The mathematics field has yet to come to an agreement on the constructs underlying mathematical outcomes, so there is less of a theoretical background from which to choose factors from compared to the reading literature. Therefore, we elected to maintain a factor structure of mathematics which had been identified through previous exploratory factor analyses of these data (Petrill & Hart, 2009).

Model 4 further separated the Word Recognition factor into timed and untimed measures of decoding. There have been studies in the educational literature that have separated timed measures of reading from untimed measures (Fuchs, Fuchs, Hosp, & Jenkins, 2001; Wolf & Bowers, 1999). Recent analyses using these data have suggested that the math Fluency measure may be more similar to other timed measures of cognitive processing than other untimed mathematics measures (Hart et al., 2009). The timed nature of the reading and math fluency batteries may serve to make them more analogous than to the specific cognitive skill they purportedly measure. Therefore, Model 4 allowed for the math fluency measure to be on the Fluency factor, rather than the Math factor.

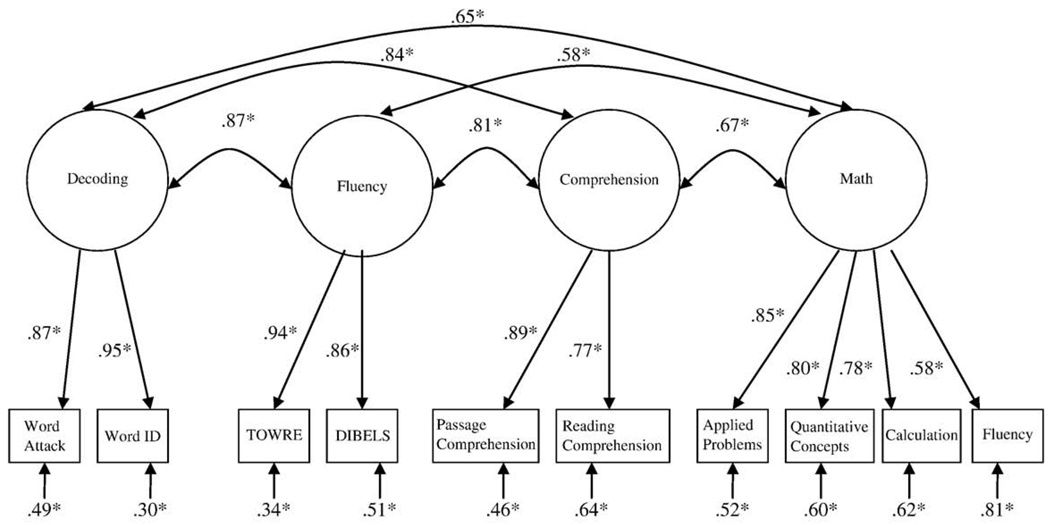
Model 5 tested the same four-factor model as Model 4, but with the math Fluency measure loaded on the Math factor (see Fig. 1). Model 5 resulted in the best fit for the data. This was determined by all fit indices suggesting a better model fit (i.e., lowest) for the degrees of freedom (−2LL=4567.40, AIC=469.40, BIC=−13.72, df=2049). All factor loadings, residuals, and correlations between the latent factors for the model can be seen in Fig. 1.

Fig. 1.

Best-fitting phenotypic model, consisting of a four-factor solution representing Decoding, Fluency, Comprehension, and Math, with factor correlations and standardized factor loading scores and residuals. Note. Only one child from the twin pair was used for these analyses. *p<.05.

2.2. Univariate genetic analyses

Following the confirmatory factor analysis, a quantitative genetic analysis was conducted. Genetic effects (h²) are implicated if MZ twins are more similar than DZ twins. Furthermore, shared environmental effects (c²) are indicated if the MZ twins are less than twice as similar as the DZ twins. Finally, nonshared environmental influences (e²; plus error) are suggested if the MZ twins are not completely the same (Neale & Cardon, 1992). Therefore, univariate estimates of genetic and environmental influences on each measured variable were calculated using the structural equation modeling program Mx (Neale et al., 2006). These latent factors representing genetic and environmental effects are also commonly called biometric factors, to differentiate them from latent factors derived from measured variables. All available raw data from each twin was used for each measure. Significance of the point estimates was ascertained via 95% confidence intervals (see Table 4). In total, results suggested all estimates of heritability were moderate to high, and significant (h²=.34–84). Significant shared environmental effects were only implicated for Applied Problems, Calculation and Fluency (c²=.37–.46). Finally, all measures indicated significant nonshared environmental estimates, including error (e²=.17–.42).

Table 4.

Univariate variance components estimates of heritability (h²), shared environment (c²) and nonshared environment (e²) for all reading and mathematics performance measures [95% confidence intervals].

Variable	Variance components estimates
	h2	c2	e2
WRMT Word Attacka	.74 [.52–.92]	.00 [.00–.00]	.27 [.20–.37]
WRMT Word Identificationa	.80 [.54–1.00]	.03 [.00–.29]	.17 [.13–.23]
TOWREb	.84 [.63–1.02]	.00 [.00–.00]	.17 [.13–.24]
DIBELSc	.82 [.58–.99]	.00 [.00–.23]	.17 [.13–.23]
WRMT Passage Comprehensiona	.79 [.57–.99]	.00 [.00–.16]	.26 [.19–.36]
PIAT Reading Comprehensiond	.68 [.30–.77]	.00 [.00–.21]	.42 [.32–.56]
WJ Applied Problemse	.41 [.15–.71]	.37 [.09–.63]	.22 [.16–.31]
WJ Quantitative Conceptse	.49 [.17–.90]	.32 [.00–.66]	.19 [.13–.29]
WJ Calculatione	.35 [.10–.63]	.39 [.13–.64]	.25 [.19–.34]
WJ Fluencye	.34 [.13–.57]	.46 [.22–.70]	.19 [.14–.26]

^aWoodcock Reading Mastery Tests (WRMT).

^bMean score of Test of Word Reading Efficiency Sight Word Efficiency and Decoding Efficiency (TOWRE).

^cDynamic Indicators of Basic Early Literacy Skills (DIBELS).

^dPeabody Individual Achievement Test (PIAT).

^eWoodcock–Johnson III (WJ).

2.3. Multivariate genetic analysis of latent factors

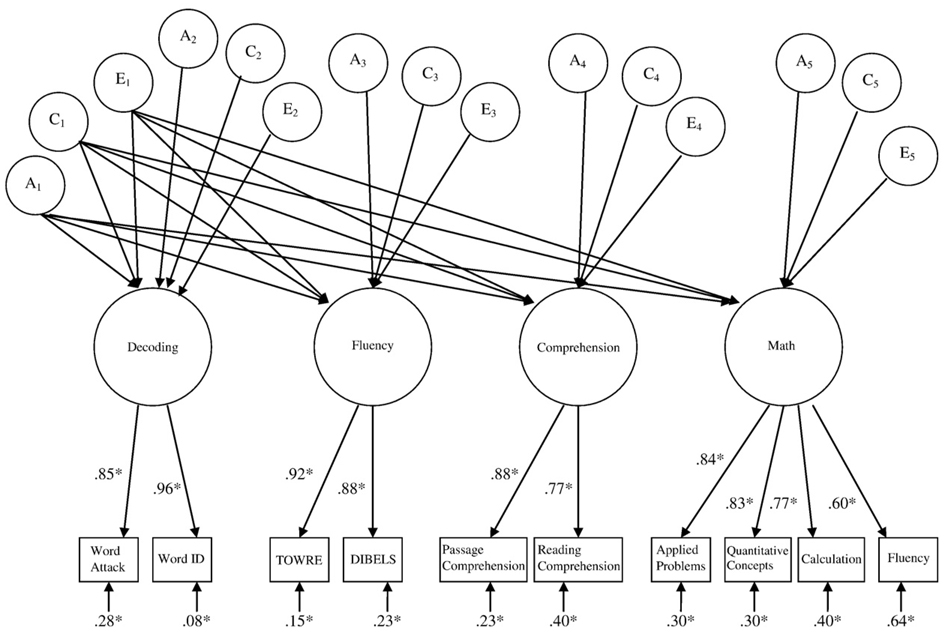
Next, we conducted a multivariate genetic analysis using the best-fitting model from Table 3 (Model 5). These analyses are an extension of the univariate biometric analyses presented in Section 2.2, examining all the measures together in one model in an expanded test rather than individually. An independent pathway model was utilized, allowing for an examination of the genetic and environmental effects on Model 5 (Neale & Cardon, 1992). This model was used because of previous evidence of a unitary etiology among specific cognitive abilities (Plomin & Kovas, 2005), with some factors suggesting further unique significant effects (Hart et al., 2009; Petrill & Hart, 2009). The independent pathway model estimates a single common genetic (represented by “A₁”), shared environmental (represented by “C₁”) and nonshared environmental (represented by “E₁”) biometric factor underlying all the latent factors (see Fig. 2). After the common effects are modeled, each of the latent factor's specific variance is partitioned into genetic (A₂, A₃, A₄ and A₅), shared environmental (C₂, C₃, C₄ and C₅), and nonshared environmental (E₂, E₃, E₄ and E₅) effects. In this case, the subscripts 2 to 5 represent the variance associated with each of the specific latent factors. For example, “2” characterizes the Decoding factor, “3” the Fluency factor, and so on.

Fig. 2.

The best-fitting phenotypic model with a biometric independent pathway model, with variances and covariances among the factors decomposed into genetic (A), shared environment (C) and nonshared environmental (E) influences, as well as standardized factor loading scores and residuals. *p<.05.

Table 5 presents the standardized path estimates from the independent pathway model. Significant path estimates are represented by 95% confidence intervals which do not encompass zero. The parameters emanating from the A₁ factor suggest significant genetic overlap, or a common genetic etiology, among all four of the factors, Decoding, Fluency, Comprehension, and Mathematics. This can be seen in Table 5, with the path estimate of .86 under the common A₁ factor representing the significant genetic effects specifically associated with Decoding, the .82 representing significant genetic effects on Fluency, etcetera. The shared environment path estimates, fromC₁, also indicate significant overlap, or a common shared environmental etiology, among all the factors. The nonshared environmental estimates, represented by E₁, implied overlap between Decoding and Fluency only. The second set of biometric factors, A₂, C₂, and E₂, represent the unique genetic and environmental influences on the Decoding factor. None were statistically significant. The third set of biometric factors (A₃, C₃, and E₃) measure the unique effects on the Fluency factor. Significant unique genetic effects were indicated (A₃=.40). The fourth set of biometric estimates, examining the effects on Comprehension alone, was non-significant. Finally, the last set of biometric estimates measured the genetic and environment effects on the Math factor. The genetic estimate (A₅=.50) was significant.

Table 5.

Latent factor modeling of genetic and environmental influences on the best-fitting phenotypic model, including the factors of Decoding, Fluency, Comprehension, and Math [with 95% confidence intervals].

	A1	A2	A3	A4	A5
Decodinga	.86 [.77–.93]	.22 [.00–.38]
Fluencyb	.82 [.73–.89]		.40 [.18–.51]
Comprehensionc	.86 [.75–.94]			.28 [.00–.42]
Mathd	.45 [.30–.60]				.50 [.31–.65]
	C1	C2	C3	C4	C5
Decodinga	.29 [.08–.46]	.17 [.00–.34]
Fluencyb	.29 [.09–.46]		.16 [.00–.37]
Comprehensionc	.39 [.19–.56]			.10 [.00–.36]
Mathd	.74 [.51–.86]				.00 [.00–.45]
	E1	E2	E3	E4	E5
Decodinga	.29 [.15–.39]	.11 [.00–.29]
Fluencyb	.23 [.12–.35]		.00 [.00–.21]
Comprehensionc	.11 [.00–.26]			.11 [.00–.31]
Mathd	.02 [.00–.13]				.00 [.00–.21]

^aDecoding: WRMT Word Attack and WMRT Word Identification.

^bFluency: TOWRE and DIBELS.

^cComprehension: WRMT Passage Comprehension and PIAT Reading Comprehension.

^dMath: WJ Applied Problems, WJ Quantitative Concepts, WJ Calculation and WJ math Fluency.

3. Discussion

The present study examined the genetic and environmental contributions to latent factors of reading and mathematics performance. Results suggested a four-factor model including reading Decoding, reading Fluency, reading Comprehension, and Math. Further quantitative genetic analysis suggested that a common genetic factor is important to the covariance among phenotypically distinct latent factors (e.g., Plomin & Kovas, 2005). However, Fluency and Math factors were also influenced by unique genetic influences, independent from the general genetic factor.

Interestingly, the two factors with unique genetic influences are the only ones to contain measures of timed performance, or fluency. Previous work has suggested that there are large and significant effects due to heritability on measures of reading fluency (h²=.65–.67; Harlaar, Spinath, Dale, & Plomin, 2005), and mathematics fluency (h²=.63; Hart et al., 2009). It is possible that the fluency components in each of these factors are important for explaining the unique genetic effects on both. Importantly, these genetic effects are outside of the substantial genetic overlap between reading and math. Hart et al. (2009) suggested that measures which were timed in nature were more similar to each other genetically than untimed measures. Measures which have a timed component are influenced by additional genetic effects, more so than those measures which are not timed. Notably, there is no genetic overlap between the factors which contain fluency-based measures, outside of the general genetic overlap among all the latent factors. That, as well as the comparison of phenotypic models 4 and 5 in Table 3, suggests that the genetic influences of reading fluency are not the same as the genetic influences of mathematics fluency, although both are strongly independently influenced by genes. Reading fluency has been highlighted to be a major component of reading ability and disability (Wolf & Bowers, 1999). Less work has been done concerning the role of mathematics fluency. These results suggest that mathematics fluency may have an influential role in mathematics ability and disability, which has yet to be fully explored.

It is also interesting to note the shared environmental overlap among all the factors. Instruction in this age-group is typically for the skills represented by these factors (e.g., Chall, 1983). This would serve to influence these processes through the shared environment, especially given that for most students in the early elementary years, academic skill exposure and learning are a function of what is taught in school. Moreover, in the case of twins, they also share the same rearing environment. This overlap is of note as it is shared between all mathematics and reading factors, suggesting that whether it is school- and/or family-level influences, there is a common environmental etiology underlying academic difficulties. This can have ramifications in how academic skill-based interventions are conceptualized.

There are limitations to this study. First, we were somewhat limited in our ability to examine the factor structure of math. The math literature sometimes separates math into components of computation and problem solving. Our findings in the current study and others (Petrill & Hart, 2009) suggest that the data were best represented by one latent factor. However, all measures of math are based on the Woodcock–Johnson, which may be serving to make them more similar. Another potential limitation is there may be a power limitation in our ability to detect significance for some of the independent pathway estimates. However, the effect sizes of the non-significant estimates of genetic independence in our study are small in comparison to the magnitude of the significant genetic overlap. This indicates that if they were truly significant with more power, they would be minor in explaining the total variance of the model. Related to this issue, although the shared environmental influences on math are higher than those on reading, this difference cannot be directly tested statistically. Additionally, gene–environment correlations may be inflating the genetic and/or shared environmental estimates. A final limitation is that the measures of fluency included here are tied to reading or math academic outcomes, as opposed to cognitive neuroscience measures, such as reaction time measures.

Future quantitative genetic research should concentrate on the measurement issues raised by these limitations. More specific cognitive process measures (e.g., number line estimation), would allow for greater insight into the etiology of the cognitive underpinnings of mathematics performance in children. Unlike the similar domains of language and reading, the field of mathematics is still emerging, with fundamental questions concerning how to define mathematics skills, the etiology of such skills, and how these skills develop in children (Gersten, Jordan & Flojo, 2005). Also important, the mathematics processes which are both overlapping to other domains and unique to mathematics may be shown to also be at work within disabilities in these areas. From this, quantitative genetic methodology can be used to examine the relationship among these mathematics component processes. Examining genetic and/or environmental overlap and uniqueness among the components is most important to the question of the extent to which mathematics and reading disability share the same underlying etiology.

In sum, the results suggest that there are some common genetic and environmental factors that connect reading and mathematics performance. At the same time, there also appear to be independent genetic effects for reading fluency and for mathematics. Although requiring further study, these findings may suggest that the overlap in reading and mathematics performance may be due to both genes and the shared environment whereas the discrepancy between math and reading may be genetically mediated. This has ramifications for our understanding of math and reading difficulties. Independent genetic effects may be serving to make math disability and reading disability distinct, and differentially prevalent. On the other hand, the extent to which they are comorbid in some children, common genes and environments may be affecting the outcomes.