Detectors for single-molecule fluorescence imaging and spectroscopy

Abstract

Single-molecule observation, characterization and manipulation techniques have recently come to the forefront of several research domains spanning chemistry, biology and physics. Due to the exquisite sensitivity, specificity, and unmasking of ensemble averaging, single-molecule fluorescence imaging and spectroscopy have become, in a short period of time, important tools in cell biology, biochemistry and biophysics. These methods led to new ways of thinking about biological processes such as viral infection, receptor diffusion and oligomerization, cellular signaling, protein-protein or protein-nucleic acid interactions, and molecular machines. Such achievements require a combination of several factors to be met, among which detector sensitivity and bandwidth are crucial. We examine here the needed performance of photodetectors used in these types of experiments, the current state of the art for different categories of detectors, and actual and future developments of single-photon counting detectors for single-molecule imaging and spectroscopy.

1. Introduction

Single-molecule detection by optical methods, pioneered in the late 80s - early 90s (1, 2) has experienced an exponential development over the last decade and a half. Several reasons explain the rapid adoption of this novel toolkit by researchers in fields as diverse as photochemistry, polymer physics, biophysics and biology, to name just a few in a still expanding list. The first and foremost is that there is a lot of information to gain from overcoming the technical complications of single-molecule detection, as we briefly discuss in the next section. Another reason of this early adoption is that the technical requirements are now easily met by most laboratories already utilizing fluorescence microscopy techniques, thanks to an understanding of the critical parameters of single-molecule detection, as we will discuss in section 2.2. In addition, fully integrated commercial products incorporating analysis software are beginning to address the needs of laboratories that have little interest in device integration and software development. A third and related reason for the rapid success of single-molecule techniques is that efficient detectors having almost ideal properties for the recording of weak and brief signals of single-molecules have become commercially available during the past decade, as reviewed in Section 3. As the field reaches maturity and sophisticated analysis methods are developed, the case for even more powerful detectors has become reinforced, and will be discussed in the final section, in relation to our own efforts to build a time- and space-resolved single-photon counting detector.

2. Single-molecule imaging and spectroscopy

2.1. Single-molecule versus ensemble measurements

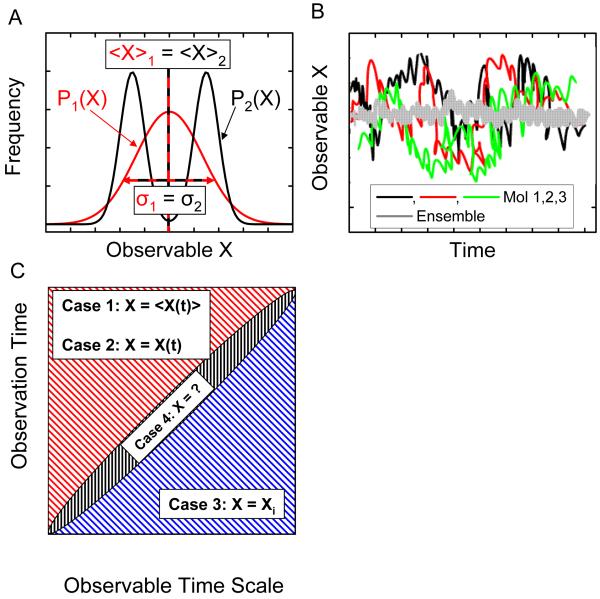
Although textbook pictures of molecular systems represent them as isolated units, experimental science has been dominated until recently by measurements done on macroscopic samples comprising an astronomical number of molecules. This type of measurement results in so-called ensemble averages, that is, only the first few moments of an observable (mean value and, in some special cases, standard deviation) can be extracted, hiding the wealth of information that could potentially be uncovered at microscopic and mesoscopic scales. Over the past fifteen years, methods to study single molecules have become important experimental tools, advancing several scientific disciplines, such as molecular biology, biophysics, and material science, precisely because they give access to the full distribution of an observable. In particular, single-molecule approaches permit to detect and quantify both static and in certain conditions, dynamic heterogeneities in a sample. Static heterogeneity refers to the existence of two or more molecular species characterized by different values (or distributions) of the measured observable (Fig. 1A) Dynamic heterogeneity characterizes samples consisting of identical molecules evolving asynchronously, in which an observable is always averaged out at any point in time in ensemble measurements (Fig. 1B). Obviously, single-molecule measurements will be able to characterize the molecular evolution only if the time during which a single molecule is observed is significantly longer than the typical time scale of the dynamic, and its temporal resolution is shorter than the typical rate of change (Fig. 1C). In this case, the ergodicity theorem even indicates that the average value of any observable obtained in an ensemble measurement will be equivalent to the time average of this observable over a single-molecule time trajectory. On the contrary, discrepancy between the two measurements will indicate a breakdown of the hypothesis of ergodicity for the system under study. For systems involving static or dynamic heterogeneity, single-molecule methods directly give access to the distributions of static properties and the dynamics of interconversion between different states of the system at equilibrium, without the need to synchronize or trigger the interconversion. This ability is crucial in many biological contexts, where: (i) triggering is not possible, and/or (ii) stochastic movements of molecular ensembles on complex reaction landscapes result in rapid loss of the coherence of molecules, allowing only for their time-averaged behavior to be observed. When the molecular system of interest can be synchronized, single-molecule methods allow the observation of non-equilibrium trajectories of individual reacting species.

Figure 1.

Single-molecule measurements give access to information hidden in ensemble measurements. A. Two distributions of an observable X are represented. The first distribution, P₁(X), is a simple Gaussian corresponding for instance to a single species of molecule, or a single state. The second distribution, P₂(X), is the sum of two Gaussians, corresponding to two different species, or two different possible states of a molecule. Both distributions have the same mean and standard deviation, and would result in indistinguishable ensemble measurements, whereas single-molecule experiments have the potential to give the complete distribution by separately observing molecules with different X values, revealing the static heterogeneity of sample 2. B. In a sample characterized by dynamic heterogeneity, molecules in an ensemble have non-synchronized evolutions, and any measurement will only give the average value of the observable. Single-molecule experiments, by giving access to the temporal evolution of individual molecule, or by allowing capturing snapshots of many different molecules, allow the full phase space to be recovered. C. The dynamic of single molecules can be captured if and only if the duration of the observation exceeds the typical time scale of the dynamic to be observed (upper left part of the graph). Two limit cases are possible. Case 1: the duration of the experiment is long enough to encompass different molecular states, but the experimental time resolution is not fast enough to capture them: the measured observable is a time average of the observable, <X(t)>, over the minimum integration time; Case 2: if the time resolution is sufficient, the measurement will give access to the full temporal dynamic, X(t), allowing to observe equilibrium fluctuations or non-equilibrium trajectories. If, on the other hand, the duration of the observation is shorter than the typical dynamic time scale, the measurement can only capture a snapshot, X_i, of the observable (case 3, lower right). In between these two regimes (case 4), the resolution will be too long to capture snapshots of the molecular state, and to short to properly average out the observable, resulting in hard to analyze fluctuating data

Although we will introduce the basic concepts of single-molecule spectroscopy and imaging needed to follow our arguments, this article is in no way a review on single-molecule techniques. We refer the reader unfamiliar with the literature on single-molecule spectroscopy to recent reviews for an introduction and an overview of its applications (3-15).

2.2. Single-molecule optical spectroscopy and microscopy: signal, background and noise

The ability to detect, visualize or manipulate single-molecules is not limited to photonic techniques, and certainly did not start with them. For instance, electron microscopy is able not only to visualize single molecules (and even allow to reconstruct the 3-dimensional structure of proteins with sub-nm resolution in the case of cryo-EM (16)), but also single atoms. Atomic force microscopy (AFM) too, among other scanning probe microscopy techniques, allowed observing single atoms and molecules, and manipulating them, several years before single-molecules were detectable optically (17). X-ray microscopy has recently made significant progresses and allows the observation of details below 20 nm in hydrated cells (18). These methods are however far from innocuous for the observed sample, since vacuum and metal coating is required for EM, freezing for cryo-EM and X-ray microscopy, and direct contact with a tip is unavoidable in scanning probe microscopies. Optical methods using far-field optics (scanning near-field optical microscopy, or SNOM, rather qualifies as a scanning probe technique, even though it uses photons as its source of signal) on the other hand, allow observation of live samples in three dimensions non-invasively, but have lesser imaging resolution due to the diffraction limit of light. Recent efforts to beat this diffraction limit in fluorescence microscopy using clever structured illumination, detection and reconstruction tricks have however in large part filled this resolution gap, although at the price of additional sophistication and acquisition time (19).

Different contrast mechanisms (phase contrast, differential interference contrast, Hoffman contrast, etc) or spectroscopies (Raman, fluorescence, coherent anti-Stokes Raman, second harmonic generation, etc) can be employed in optical microscopy, most of which can be also used to detect single molecules, provided signal, background, and noise are carefully optimized.

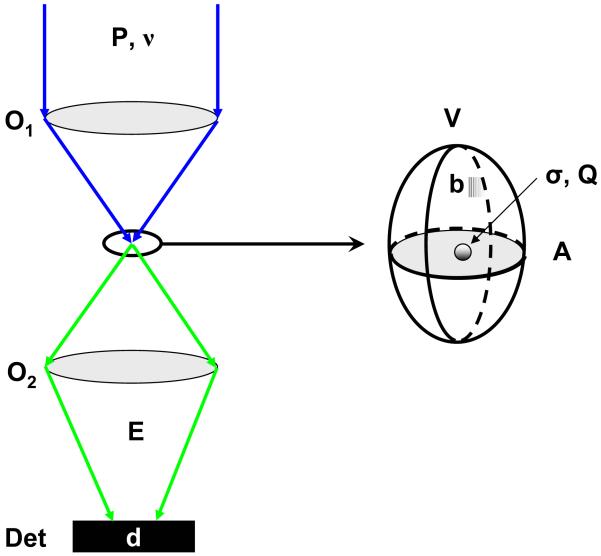
Fig. 2 illustrates simple principles involved in single-molecule optical excitation and detection. Whatever contrast mechanism is employed, the process resulting in photon “emission” by the sample can be characterized by a cross-section σ and an emission quantum yield Q (number of emitted photons per “absorbed” photon). A different expression would be used for processes involving two- or more photon absorption such as two-photon fluorescence excitation or second harmonic generation and beyond, but conclusions would be similar. For the sake of illustration, we will henceforth focus on fluorescence.

Figure 2.

Signal-to-noise ratio in single-molecule microscopy and spectroscopy. A: In a single-molecule spectroscopic experiment, excitation light (power P, frequency ν) is focused on the sample through an optical element O₁ (objective lens, fiber tip, etc), exciting a volume of cross-section A, represented by an ellipsoid in the expanded view. The absorption process is characterized by an absorption cross-section σ and the emission by a quantum yield Q. The background contribution per watt of incident power is b, whereas the detector has a dark count rate d. The signal is collected by an optical element O₂ (possibly identical to O₁) to the detector, with an overall efficiency E.

The excitation arm of the optical setup is characterized by an excitation power P at a frequency ν, resulting in a signal rate:

$$s=EQ\sigma P∕Ahv,$$ (1)

expressed in counts per second (cps or Hz). This rate is proportional to P/A where A is the cross-section of the excitation beam in the plane of the molecule. On the emission arm, the setup can be characterized by a global collection efficiency E. The environment of the single molecule can add a background contribution modelled by a rate b per unit-volume and unit-excitation power (for instance due to remnant Raman or Rayleigh scattering, fluorescence of the substrate or of the detection optics, etc). Similarly, the detector will in general contribute a dark count rate d₁ to the detected signal. From these definitions, the signal-to-background ratio (SBR) can be calculated as:

$$\begin{array}{cc}\hfill \mathit{SBR}& =\frac{s\tau }{bVP\tau }\hfill \\ \hfill & =\frac{EQ\sigma }{bVAhv},\hfill \end{array}$$ (2)

where V is the intersection between the excitation and the detection volume. The readout electronics of non photon-counting detectors generally contributes a Gaussian noise with standard deviation σ_R per detection element, which is independent of the integration time, and is added in quadrature to the sources of shot noise. Some detectors amplify the incoming signal S (= sτ) before readout, introducing a gain G in the measured signal (and a second stage of dark count contribution, d₂). Since the amplification process is itself statistical, the resulting standard deviation component is not obtained simply as the square root of the amplified signal G.S, but depends on the amplification process (e. g., amplification before accumulation, such as in intensified CCD camera or ICCD; or amplification after accumulation, such as in electron-multiplying CCD camera or EMCCD). In practice, the shot noise component of the incoming signal is itself multiplied by the gain G, and a correction factor F, called the excess noise factor (20):

$${\sigma }_{\mathit{amp}}=FG{\sigma }_{\mathit{in}},$$ (3)

where σ_in represents the standard deviation of the input signal and σ_amp that of the amplified signal. For a detector without gain (such as a CCD camera), or for photon-counting detectors, G = 1 and F = 1. The gain will depend on the camera model and can usually be adjusted experimentally, whereas the excess noise factor depends on the amplification technology and the actual gain (21, 22). Typical values for various actual detectors are reported in Table 1.

Table 1.

Typical characteristics of different detectors used in single-molecule spectroscopy and imaging. QE: Quantum Efficiency; PC: Photocathode; ROS: Readout Stage. Except for the SPAD, the gain is expressed in counts per photo-electron, where “counts” is the number of electrons generated at the end of the photon conversion and photo-electron amplification processes. In other words, this is the number of electrons to be readout by the Analog-to-Digital Converter (ADC) of the detector. In a SPAD, millions of secondary charge carriers per avalanche can be generated, but they are all read as a single “count”

Detector Type	QE @ 600 nm (%)	Gain (cts/photon)	PC Dark Count (d1) (e−/pixel/s)	ROS Dark Count (d2) (e−/pixel/s)	Readout Noise (e−/pixel/s rms)	Excess Noise Factor†	Model
CCD	95	1	0	0.002	5 @ 100 kHz 12 @ 2 MHz	1	PIXIS 512B, Roper Scientific
ILT CCD	62	1	0	0.05	6 @ 10 MHz 8 @ 20 MHz	1	CoolSnap HQ, Roper Scientific
ICCD Gen III	46	1,500	0.04	30	20 @ 1 MHz 32 @ 5 MHz	1.8	I-Pentamax, Roper Scientific
EMCCD	92	1,000	0.5	0	45 @ 5 MHz 60 @ 10 MHz	1.4	Cascade 512B, Roper Scientific
EBCCD/EBAPS	29	100	0.04	50	40 @ 54 MHz	1.1	NightVista E1100, Intevac
Photon Counting	68	1 (106)	100	0	0	1	SPCM-AQR-14, Perkin-Elmer

^†Excess noise factor value for maximum gain.

The resulting signal-to-noise ratio (SNR) can thus be expressed generally as:

$$\begin{array}{cc}\hfill \mathit{SNR}=& \frac{Gs\tau }{\sqrt{\{F^2{G}^2(s+bVP+n{d}_1)+n{d}_2\}\tau +n{\sigma }_R^2}}\hfill \\ \hfill & =\frac{s\tau }{\sqrt{F^2\left\{s+bVP+n\left(d_1+\frac{d_2}{F^2{G}^2}\right)\right\}}\tau +\frac{n{\sigma }_R^2}{G^2}},\hfill \end{array}$$ (4)

where n is the number of pixels involved in the collection of the signal (Fig. 3). The denominator is the root mean square of all contributions to the noise. The SNR obviously increases at larger integration time τ . From the last expression, the advantage of having a large amplification of the signal before readout is obvious, as it can in practice suppress the contribution of the readout noise to the overall SNR. In practice, changes in SNR saturate rapidly with gain (for a given signal), and it is therefore important to adapt the gain to the type of signal that is looked for, as any gain increase is compensated by a reduction in dynamic range (ratio between the maximum and minimum signals that can be accumulated). For negligible dark count rates (which is the case if the detector is cooled) and negligible readout noise component (which is the case for large gains),

$$\mathit{SNR}=\frac{\sqrt{s\tau }}{F\sqrt{1+1∕\mathit{SBR}}}.$$ (5)

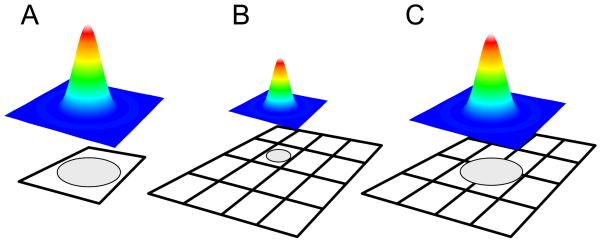
Figure 3.

Relation between PSF and detector size. A: For point detectors (SPAD, PMT), the image PSF should fit within the sensitive area of the detector, in order to detect as much of the collected photons. B-C: For pixilated wide-field detectors, the best SNR (Eq. (4)) is obtained when the PSF image fits within a single pixel (case B). For PSF localization however, it is preferable to chose a magnification that lead to oversampling (as defined by the Nyquist criteria) of the PSF image (case C),

As expected, a large SBR results in an optimal SNR, which will then depend only on the count rate s and integration time τ. A poor SBR reduces the SNR compared to this optimal value.

Both ratios can be increased by improving the collection efficiency E, either by using better filters, anti-reflection coated optics or higher quantum efficiency detectors. Unfortunately, the potential gains in these three areas are somewhat limited. Although a direct experimental comparison between detectors is somewhat difficult, it is at least theoretically possible to compare the SNR for a single-molecule signal detected by different devices. Even in this case, one has to remember that the collection efficiency of an optical setup designed for point detection (such as a confocal setup, see Section 2.4) may differ from that of a setup designed for wide-field detection (such as an epifluorescence setup, ibidem), therefore, even though one may look at the same sample and excite it with the same power, the signal reaching the detector will depend on the specific optical arrangement. When using point detectors, one will in general try to adjust the total magnification such that the integrality of the single-molecule image (i.e. its point-spread-function or PSF) is contained within the sensitive area of the detector (Fig. 3A). This will ensure that all collected photons will get a chance to be detected. Using a pixilated wide-field detector, one can maximize the SNR by limiting the PSF size to one pixel (n = 1 in Eq. (4), Fig. 3B), or trade it off to increase the localization accuracy by expanding its image over several pixels (Fig. 3C) (23). Increasing the number of pixels sampling the PSF has a particularly adverse effect on the SNR for detector without gain such as CCD’s. For intensified detectors, part of the benefit of amplification on readout noise reduction is lost by the increased number of pixel (last term in the denominator of Eq. (4)) and for detectors in which there is a significant amplified dark count d₁ (such as EMCCD’s) a similar reduction of the SNR occurs. Fig. 4A-C summarizes the SNR performances of current detectors as a function of incoming photon flux (per single molecule) on the detector, and Fig. 4D a few choices of pixel numbers (over which the PSF is imaged) for one wide-field detector (a CCD without amplification). The issue of imaging resolution will be discussed in more details in a later section.

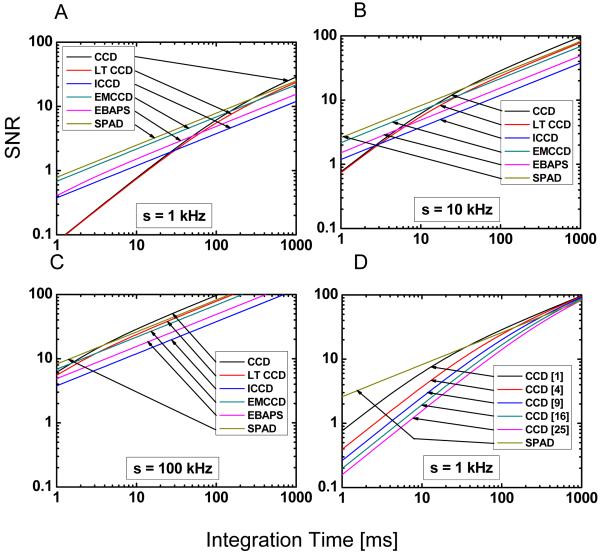
Figure 4.

SNR calculated according to Eq. (4) and Table 1. A-C: SNR for different photon fluxes reaching the detector, assuming that the signal is concentrated in a single pixel. D: effect of oversampling the PSF on the SNR for a detector without amplification (CCD). This effect turns out to be negligible in most cases for detectors with amplification (ICCD, EMCCD, EBAPS). In comparison, the SNR for a SPAD collecting the total signal is shown.

The SBR can be improved separately by decreasing the excitation volume V, but for in vitro experiments, where the experimentalist has a complete control on sample preparation, background can be reduced to negligible levels. In particular, buffer components or solvents in which samples are observed need to be properly filtered and optical components (including the glass coverslip constituting the bottom part of the sample) carefully chosen or treated to remove fluorescent impurities. In general, a larger excitation power or a longer integration time will improve the SNR without changing the SBR, but some emission processes (such as fluorescence) exhibit saturation, in which case increasing the excitation power beyond a certain value will in fact degrade the SNR.

Let us consider a typical confocal fluorescence microscopy signal (see Section 2.4 for a description of this geometry) to get an idea of actual numbers encountered in experiments: that of freely-diffusing fluorescein isothiocyanate (FITC) molecules in water, using a single-photon avalanche photodiode detector (SPAD) to collect the signal. Typically, the global detection efficiency is low, due to the combination of filters and loss in the optics, and a worst case value would be E = 5 %. The quantum yield and the absorption cross-section of FITC are: Q = 0.85, σ = 2.8.10⁻¹⁶ cm², and the effective cross-section of the excitation beam (λ = 525 nm) at the focus is of the order of A = 1 μm². Common values of background and dark count rate are: bV = 100 Hz/μW and d = 100 Hz for a SPAD. With an excitation power of 100 μW and a 1 ms integration time, a count rate of 314 counts/ms can be obtained, of which 10 come from the background sources, leading to a SNR ~ 17 and SBR ~ 31.

Although these are good figures, they have to be balanced by the fact that single molecules have a finite life span. Single molecules in an oxygen-rich environment typically emit on the order of 10⁶-10⁸ photons before irreversible degradation (photobleaching). With the above parameters, this amounts to a total emission of ~ 160 ms-16 s. This time is long enough to observe freely diffusing molecules during their transit time of a few hundred μs. For an immobilized molecule however (see next section), it sets a stringent limit on the total duration of a single-molecule observation, and all efforts are put on increasing the detection efficiency in order to be able to use lower excitation intensity.

Besides working on improving experimental setups, a significant part of the efforts of the single-molecule community has been invested in probe development and optimization, in order to maximize the number of photons that can be extracted from a molecule. In particular, fluorescent semiconductor quantum dots have recently come to the forefront due to their exceptional brightness and stability, making them ideal probes for a number of single-molecule fluorescence studies (for a recent review, see for instance ref. (24)).

2.3. Single-photon time-stamping

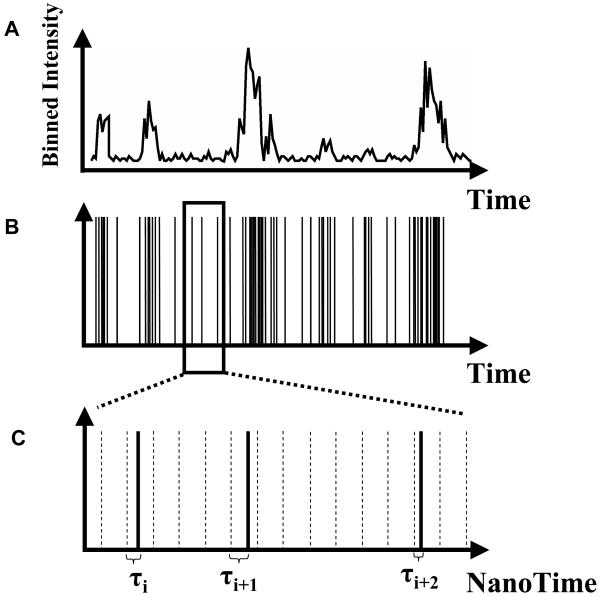
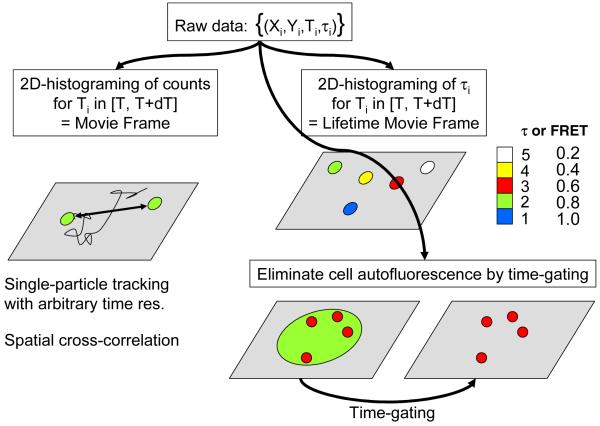
In the previous section about SNR and SBR analysis, we have considered only the total signal emitted by a molecule, or the number of photons detected during a specified integration time. This is perfectly adapted for single-molecule experiments using cameras (charge-coupled devices (CCD), intensified CCD (ICCD) or silicon intensified target (SIT) detectors) that inherently accumulate photons over a pre-defined integration time. Experiments employing point-detectors such as single-photon avalanche photodiodes (SPAD), on the other hand, do not directly provide such information. Counting electronics and software are needed to bin photons collected by these detectors over a user-specified interval (typically 100 μs – 10 ms) (Fig. 5A). The binning process obviously reduces the information content of the detected photon stream. Alternatively, it is possible to stamp each detected photon with its arrival time with respect to the preceding and following photons, or the beginning of the experiment (the macro-time). We thus preserve the information lost by time binning, but at the price of a larger disk storage space. Fig. 5A shows a hypothetical, binned photon stream versus the non-binned, original photon count data (Fig. 5B) originating from fluorescence bursts of diffusing molecules in solution. Different schemes have been developed to acquire and utilize such macro-time information in single-molecule experiments (25-28). Fluorescence correlation spectroscopy, photon-counting histograms and other related analyses are extremely powerful tools for analyzing molecular interactions and we refer the reader to the literature for details (29-33). One principal advantage of these approaches is that even when shot noise severely limits the usefulness of time traces at short time scales (where < 20 photons are counted on average), keeping the time stamp information of each photon allows correlation methods to reveal fluorescence dynamics at the ensemble level. Fluorescence correlation spectroscopy (FCS) and its variants essentially histogram time separation between successive fluorescence photons from thousands of separate individual molecules, allowing the recovery of time scales and amplitudes of processes resulting in variations in the photon emission rate. In other words, whereas it is impossible to observe fluctuations of fluorescence intensity occurring at time scales too short to obtain a decent signal-to-noise ratio by simple binning, there is information hidden in the photon stream that can be extracted by statistical analysis of the distribution of macro-times of a large number of bursts (34).

Figure 5.

Binning and Time-stamping of photons. A: Most detectors accumulate the signal (photo-electrons, amplified or not) during a fixed, user-selectable duration (integration time), then transfer, digitize and store this information, and resume the whole cycle. B: Photon-counting detectors usually output a short voltage pulse each time a photon is detected. The voltage pulses can be counted and/or time-stamped, resulting in a pulse-train that can be further processed, for instance to yield binned time-traces as shown in A. C: For photons emitted in a process triggered by pulsed laser excitation, it can be useful to measure not only the photon arrival time since the beginning of the experiment (as in B), but also the arrival time of the photon with respect to the previous excitation laser pulse (nanotime τ).

2.4. Pulsed excitation and nanotiming

When pulsed excitation is utilized, new timing information can be added to the simple macro-time introduced before. In addition to time-stamping each photon with respect to the beginning of the experiment, the arrival time of the photon with respect to the laser pulse that excited the molecule (the nanotime) can be measured using a Time-to-Amplitude Converter (TAC) (Fig. 5C). By histograming these nanotimes τ_i, the fluorescence lifetime of the fluorophore can be extracted. In the simplest encountered case, their distribution is a decaying exponential characterized by a lifetime τ typical of each species. This lifetime is extremely sensitive to the molecule’s environment, due to non-radiative decay channels opened for instance by the presence of neighboring molecules. An example is fluorescence resonance energy transfer (FRET), a process taking place between a donor molecule (D) and a nearby acceptor molecule (A) having its absorption spectrum overlapping with the donor emission spectrum (35). The presence of the acceptor has a measurable effect on the lifetime of the donor molecule, which decreases according to:

$${\tau }_{D\left(A\right)}={\tau }_0(1-E),$$ (6)

where τ₀ is the donor lifetime in the absence of any perturbation and τ_D(A) the donor lifetime in the presence of an acceptor molecule A. E, the FRET efficiency, is related to the distance R between dyes by the well-known equation derived by Förster (36):

$$E={\left(1+{\left(\frac{R}{R_0}\right)}^6\right)}^{-1}.$$ (7)

R₀ is the Förster radius, a measurable characteristic of the dye pair, and is in the range of a few nm. Measuring the fluorescence lifetime of the donor only is thus sufficient to estimate the distance between the two dyes. By comparison, an alternative way of measuring the FRET efficiency can be obtained from the detected donor signal, D, and the detected acceptor signal, A:

$$E=\frac{A}{A+\gamma D},$$ (8)

where:

$$\gamma =\frac{{\eta }_A{\Phi }_A}{{\eta }_D{\Phi }_D}$$ (9)

is the product of two ratios: that of the acceptor and donor detection efficiencies (η) and that of their quantum yield (Φ). These ratios are not easily determined and therefore, the fluorescence lifetime estimation of FRET efficiency is a much more robust one (there are however reliable ways to measure γ, see ref. (37)). Similarly, a process such as electron transfer, which results in a decrease of the lifetime of the donor with an exponential dependence on the distance R between electron donor and acceptor:

$$\frac{1}{\tau }=\frac{1}{{\tau }_0}+k_0{e}^{\frac{R}{R_0}},$$ (10)

where R₀ is of the order of 1 Angström, is more easily characterized by lifetime measurement than donor intensity fluctuation measurements. Recent work on electron transfer between two residues of a single enzyme using ultrafast SPAD’s has taken advantage of this dependence to study the conformational dynamics of individual enzymes from sub-ms to seconds time scales (38, 39), and is a beautiful illustration of this phenomenon observed at the single-molecule level.

In addition to providing information on the environment of the molecule, fluorescence lifetime measured in conjunction with the polarization of the emission gives access to the depolarization dynamics of the fluorescence. This dynamics is essentially due to the rotational diffusion of the dye, and is therefore a proxy of its rotational freedom. Dyes can also be attached rigidly to a molecule, in which case the depolarization dynamics directly reports on molecular tumbling or internal dynamics. Applications to single-molecule experiments range from monitoring the rotational dynamics of proteins or nucleic acids (40), to identification of single molecules (41) and proper calculation of FRET efficiencies (42).

2.5. Fluorescence Lifetime Imaging Microscopy (FLIM)

Measuring fluorescence lifetime by single-photon counting is not only useful for single-molecule spectroscopy. It is also the foundation of fluorescence lifetime imaging microscopy (FLIM), which measures it on each point of a sample to map out the environment of a molecular probe, monitor the presence or absence of a species by its effect on the lifetime of a molecular probe, or distinguish between different species having well separated lifetimes (43-48). This latter application is for instance useful to distinguish spectrally similar green fluorescent protein (GFP)-tagged proteins, which cannot be easily separated spectrally (49, 50).

FLIM can be performed in two different ways: using time-domain measurement, or frequency-domain measurements (43, 44, 51). The time-domain approach can be implemented using a time-correlated single-photon counting (TCSPC) confocal setup, which requires raster-scanning the sample to build an image. Another possibility is to use a time-gated ICCD in either a multifoci excitation configuration (52) or a wide-field one (53). In the first case, the scanning process is time-consuming while in the latter, the camera detects only photons emitted during a fixed time-window after the laser pulse, losing the remaining photons. In particular, this last technique can only distinguish between fluorophores of well-separated lifetimes and necessitates acquiring two sets of images for that purpose. The frequency domain approach is no-less complicated and is based on radio-frequency (RF) modulation of the laser intensity and of the image intensifier gain, either in phase (homodyne) or out-of-phase (heterodyne). The acquisition of several images acquired at different phase differences allow the calculation of an apparent lifetime and concentration for each pixel of the image, but this process can be extremely time-consuming (several minutes) (54) and for this reason, suffers from photobleaching of the fluorescent dyes. Several lifetimes can be recovered using global analysis (55). For all these wide-field techniques, which do not have a built-in optical cross-sectioning capability as in confocal microscopy, 3D-deconvolution can be applied to a z-series of images to obtain vertical spatial resolution (56). A similar effect can be obtained with less computationally intensive processing using structured illumination (57). Applications to live intracellular Ca²⁺ imaging (54) or of receptor phosphorylation events (58-60) have illustrated the power of this imaging technique where spectral information is of little use. These approaches still remain time-consuming both for acquisition and data analysis and would definitely benefit from a detector combining the advantage of the time-domain technique (optimal use of all detected photons) and of a 2D detector, as demonstrated by preliminary results using a 1D detector (61), a very low-resolution 2D detector (62) and recently a full 2D detector with low counting rate capability (63).

2. 6. Timing resolution

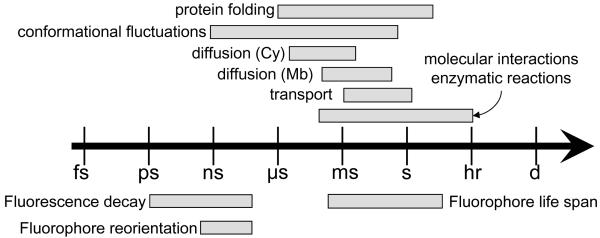
The previous sections did not mention the resolution of either the macro-time or the nanotime measurements. The time resolution needs only to be sufficient to tackle the fastest time scale in the experiment. Fig. 6 summarizes typical orders of magnitude for various molecular phenomena. Typical lifetimes of fluorophores used in single-molecule spectroscopy vary from a few ns (dyes) to several hundred ns (quantum dots), or even μs to ms (lanthanides). These values, however, correspond to isolated fluorophores in a pure solvent or buffer. As mentioned previously, the fluorescence lifetime is affected by the proximal environment of the fluorophore, and is decreased by any non-radiative process. As a result, it might become important to be able to measure lifetime (and therefore nanotime) much shorter than the natural lifetime of the fluorophore used in the experiment. Usually, timing electronics is not the limiting factor, with typical TAC resolution of the order of a few ps for time-windows of a few dozen ns. The main limitation comes from either the excitation source (laser pulse widths can vary from 100 fs to 100 ps depending on the technology and model) or the detector time response. We will address the latter in a later section.

Figure 6.

Time scales relevant for single-molecule studies. Fluorescence is ideally suited to study a variety of biophysical phenomena such as protein folding, conformational fluctuation, diffusion in the cytoplasm (Cy) or in the membrane (Mb), transport by molecular motors, protein interactions or enzymatic dynamics to name a few. The short lifetimes of fluorophores gives access to fast fluctuations due to its sensitivity to various non-radiative decay channels (FRET, ET), whereas slower evolving processes can be followed by correlation methods, intensity fluctuations or imaging. The time windows are approximate, each fluorophore, biomolecule or reaction having its own situation-dependent time scales

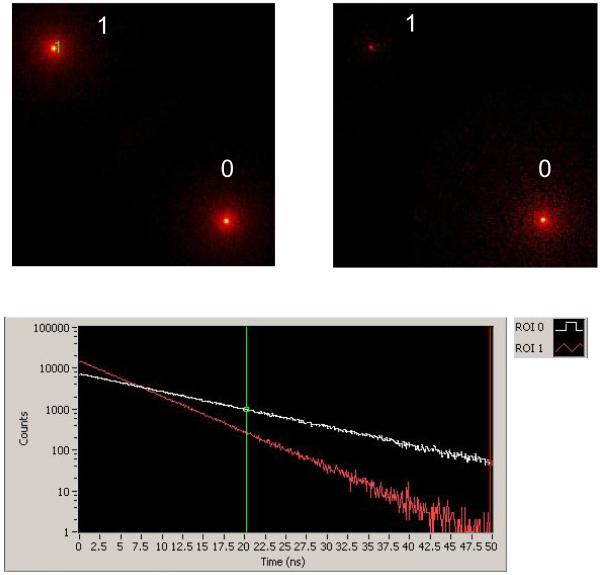
The duration (pulse width) of the excitation pulse needs naturally to be taken into account, but is in general not accessible directly. In practice, the only useful information is the instrument response function (IRF) of the whole apparatus, which combines all elements of the excitation and detection chain (including the detector). It is best measured using a sample with ultra short fluorescence lifetime (< 100 ps) emitting in the wavelength range used during the experiment. Deconvolution methods, or fitting approaches that incorporate the knowledge of the instrument response function, then allow fluorescence lifetime to be measured with resolution equal to a fraction of the IRF’s width (64).

Another way to take advantage of fast timing electronics, even in the absence of pulsed excitation, consists in studying the photon arrival statistics at sub-ns time scales, extending the range of standard FCS techniques. As mentioned before, time-correlation methods mostly employ photon-counting detectors, which are the only one to provide sub-μs time-resolution. Two types of correlations can then be considered: auto-correlation of a single signal, or cross-correlation of two (or more) signals. Although there is a lot to learn from autocorrelation of a single photon stream, the minimum time scale accessible is set by the dead-time of the detector, which is of the order of 40 ns for SPAD’s (autocorrelator cards or counting electronics can in principle handle counts at 80 MHz or more). A standard way to go around this limitation consists in splitting the incoming signal in two streams with a beam splitter and use two detectors. In this Hanburry Brown-Twiss geometry (65), the time separation between photon counts on one detector and the other is measured by a TAC, allowing the detection of photons arriving at the beam splitter within intervals shorter than the deadtime of the two detectors. This approach permits to demonstrate the phenomenon of photon antibunching in the fluorescence of single molecules (66, 67), i.e. the null probability to observe simultaneous emission of two photons from a single emitter, observable as a dip down to zero in the inter-photon delay histogram at time scales shorter than the fluorescence lifetime (< ns). This very short time scale corresponds to that of rapid fluctuations of small protein modules or nucleic acids and is therefore of fundamental interest. In particular, it is the only way to access perturbation of a fluorophore environment at the ns time scale (68). Integrated TAC and counting electronics have recently been commercialized that make this type of analysis accessible to non-specialists (69, 70).

2.7. Imaging versus non-imaging geometries

With this basic understanding of what a single-molecule detection experiment consist of, we will now briefly describe the main excitation and detection geometries used in the laboratory, with the purpose of defining the type of photon detectors that are required for various single-molecule spectroscopy or imaging applications.

Fig. 7 describes three geometries revolving around the same microscope design, based on: (i) a high numerical aperture (NA) objective lens (typically NA = 1.2 for water immersion and NA = 1.4-1.45 for oil immersion); (ii) a dichroic mirror and (iii) a tube lens. Samples are usually liquid and enclosed between ~170 μm thick (also referred to as number 1.5) glass coverslips. Microscope objective lenses are designed to account for this standardized thickness and achieve optimal illumination and collection in their presence.

Figure 7.

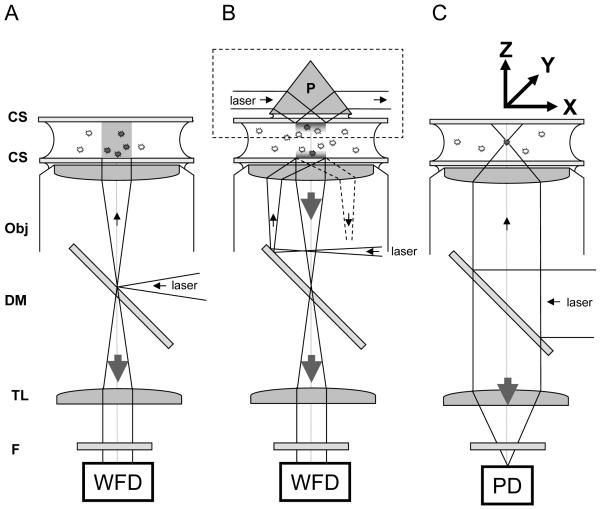
Typical excitation/detection geometries utilized in single-molecule fluorescence microscopy. A, Epifluorescence: in epi-illumination, a laser beam or broadband source (lamp) is focused at the back focal plane of the objective lens (Obj), resulting in a collimated output beam, which illuminates the whole sample. The emitted light is collected by the same objective and imaged at the focal plane of the tube lens (TL) of the microscope on a wide-field detector (WFD). The role of the dichroic mirror (DM) is to reflect excitation light only and transmit the Stokes-shifted fluorescence light only. An additional emission filter (F) is used in front of the detector to reject background and residual excitation light. B: in Total Internal Reflection (TIR) excitation, a similar approach can be used (bottom part: objective TIR), but the focus beam is shifted off the optical axis, resulting in a tilted incidence on the object plane. At a critical angle, the incident light undergoes total internal reflection, leaving only an evanescent wave on the sample side of the coverslip (CS), with a typical penetration depth of a few hundred nm. An alternative approach (upper part, dashed box: prism TIR) uses a prism (P) to bring a laser beam at the critical angle on the top coverslip, resulting in an evanescent wave on inner, upper side of the sample. In both cases, the fluorescence of molecules within 100 nm of the coverslip (usually adherent molecules only) is collected by the objective and tube lenses as in the case of epifluorescence, with the advantage that little fluorescence (background) is excited away from the coverslip. C: in confocal microscopy, a collimated laser beam is sent into the back focal plane of the objective lens, resulting in a diffraction-limited excitation volume within the sample. This point can be raster-scanned throughout the sample using a scanning stage to move the sample around (XYZ arrows). The emitted light is collected by the objective and tube lenses, and focused on a point detector (PD). Alternatively, a pinhole is placed at the focal point of the TL, and a relay lens images it on a PD, in order to reject out-of-focus light (not shown).

In all drawings, the filled and empty circles between the coverslips represent fluorescent molecules that are excited or not, respectively. The small arrows represent the excitation path, the large arrows indicting the path followed by the emitted light. The Figure is not to scale.

In the case of fluorescence, the excitation source is usually a laser line. Both continuous wave (CW) and pulsed lasers can be used, although the latter can only be taken complete advantage of with a subset of the detectors that will be discussed next. The laser line is reflected off the dichroic mirror (DM) through the objective lens into the sample. Fluorescence light emitted by the sample is usually collected by the same lens and transmitted through the dichroic mirror to the tube lens and imaged at the tube lens image focal plane. An emission filter is intercalated before the detector in order to reject background from the excitation or Raman scattering, or simply to select part of the spectrum, when different fluorophores are used. By focusing the laser beam on the back focal plane of the objective lens, a collimated beam of light is sent to the sample, illuminating a large area. This is the simplest configuration, termed epi-illumination geometry (Fig. 7A). Its main disadvantage is to excite the whole sample thickness, therefore resulting in background signal coming from out-of-focus regions and bleaching of out-of-focus regions.

By shifting the excitation beam off axis, one obtains a collimated beam exiting the objective lens at an angle, until a critical angle is reached, at which total internal reflection (TIR) occurs, leaving only an evanescent wave exciting the first few hundred nm above the coverslip (Fig. 7B, center). This has the considerable advantage of not exciting the rest of the sample, thus allowing weak signals close to the surface of the coverslip to be detected almost background-free. An alternative way to obtain such an effect uses a prism in direct contact with the upper coverslip, as described in Fig. 7B (dashed box). In this case, the objective lens is used only for the collection of fluorescence and needs to be focused on the upper coverslip (71).

In all three previous cases, the image of the sample is sent to infinity by the objective lens, and formed by the tube lens of the microscope at its image focal plane, where a wide-field detector can be placed for recording.

A different illumination is obtained when a collimated and expanded beam is sent into the back focal plane of the objective (Fig. 7C). This focuses the excitation light into a diffraction-limited excitation spot at the focal point of the objective lens (the excitation point spread function or PSF) within the sample, which can then be raster-scanned in 3 dimensions in the sample to acquire a voxel-by-voxel image. Usually, this raster scanning is performed as a series of 2-dimensional scans, providing stacks of 2D images similar to those obtained in the previous geometries. Although the excitation volume is small (approximately an elongated 3D Gaussian of waist λ/2 and height 2λ), fluorescence is not excited at a single point, and therefore it is customary to reject as much of out-of-focus light as possible using a pinhole having a diameter of the order of the imaged PSF size placed at the tube lens focal point, or of a relay lens. The light emerging from the pinhole is then relayed to one or more point detectors. In some cases, the detection area of the point detector is small enough to dispense of a pinhole, the detector placed at the focal point of the tube lens playing the role of a spatial filter. The rejection of out-of-focus light is at the origin of the name “confocal” given to this geometry, as the detector placed at the focal point of the tube lens collects only the light emitted at the focal point of the objective lens (72).

The previous descriptions of the wide-field epifluorescence and TIR geometries are in fact not specific to single-molecule setups: essentially any commercial microscope can be used, provided the optics elements and filters are optimized. The confocal geometry described here is however specific of most single-molecule setups, in the sense that images are obtained by scanning the sample (rather than the beam), and the excitation and detection path are axial and designed to minimize losses and be flexible rather than to be compact (unlike a commercial system). In particular, point-detectors used for single-molecule detection are different from those used for brighter sample imaging for which commercial confocal microscopes are mostly used, as discussed in the next section.

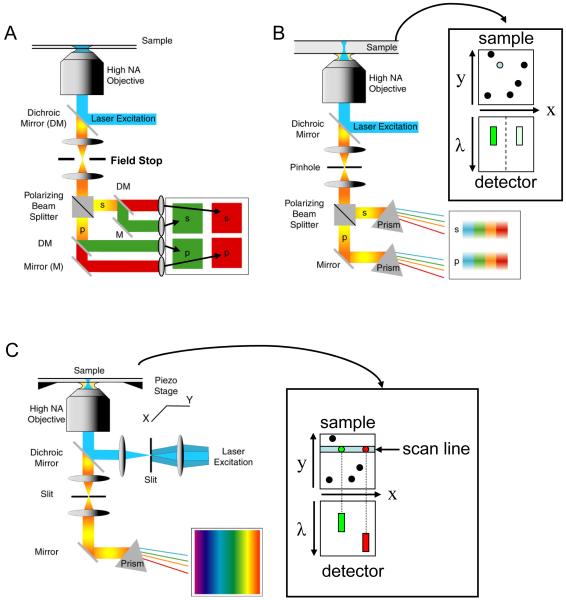
Fig. 8 illustrates further refinements on the previous experimental setups. Using a wide-field geometry (e.g. TIR), the image can be split according to polarization and/or color (as illustrated in Fig. 8A) and each component imaged on four/two separate quadrants of a wide-field detector (73, 74). This geometry is adapted to single-molecule measurements in which two colors are involved, such as in fluorescence resonance energy transfer between two fluorescent dye molecules (11, 12). The measurement of the polarization of the emitted signal gives access to the polarization anisotropy of each dye molecule, which reports on its rotational freedom and/or orientation (75). The large field of view provided by the wide-field detector allows the simultaneous recording of the fluorescence of many molecules. This becomes critical when one is interested in transient and irreversible phenomena, where a conformational change is triggered by addition of a reagent (for a recent example studying RNA transcription initiation, see ref. (76)).

Figure 8.

Some fluorescence detection schemes utilizing a wide-field detector. A: dual-color and dual-polarization layout. Using a field-stop at the focal plane of the tube lens, the imaged field-of-view can be made to fit in a quarter of the wide-field detector. Using a polarizing beamsplitter (or a Wollaston prism), the image is first decomposed in its two polarization components. Each resulting image can then be spectrally decomposed in two color images using a dichroic mirror. Mirrors and lenses are used to direct each component image to a different quadrant of the detector. B: Instead of a wide-field illumination, a confocal geometry can be used. As the PSF image is small compared to the detector area, a more complete spectral decomposition (for instance using dispersion by a prism as shown) can be afforded. The schematic on the side illustrates the situation where the excitation beam is located on a green, partially polarized emitter: the detector sees two spectra centered in the green region of the spectrum. C: To use the detector area more efficiently, a line excitation geometry can be used. Here, we illustrate a detection scheme where no polarization selection is performed. The schematic on the right illustrates a situation where the line excitation hits two green and red emitters, resulting in two distinct spectra on the detector side. In B & C, the image is formed by scanning the sample along 2 or 1 dimension respectively.

Similar spectroscopic analyses can be performed in the confocal geometry, as illustrated on Fig. 8B. Here, the light emitted from the excitation volume is first split according to polarization (e.g. using a Wollaston prism or a polarizing beam-splitter), and then dispersed spectrally (e.g. using a prism). The two resulting extended strips of light can be imaged on two separate linear detectors, or on two distinct areas of a wide-field detector (77) (see also ref. (78, 79) for examples of spectrally-resolved single-molecule detection). A more efficient use of the wide-field area of the detector is described in Fig. 8C, where a diffraction limited line (instead of a spot) is excited in the sample, and confocality is ensured using a slit. In this case, one dimension encodes the spectral information, and the other represents one dimension of the image. Of course a hybrid between the scheme of Fig. 8B and Fig. 8C can be implemented too.

This brief discussion with no pretension to exhaust the topic of optical arrangements permitting single-molecule detection, imaging or spectroscopy, has introduced 3 types of detector geometries: (i) point detectors, (ii) linear detectors (1D) and (iii) wide-field detectors (2D), but most importantly, has illustrated the fact that point detectors can be used for imaging applications (scanning confocal microscopy) and wide-field detectors for spectroscopy, and vice versa. In other words, there is a significant flexibility in the detection arm of a single-molecule setup, and the choice of detector will be dictated by the requested performance of the overall acquisition setup. The next section will now examine these characteristics.

2.8. Spatial resolution

Spatial resolution issues were briefly discussed in the perspective of maximizing the SNR of a single-molecule imaged by a pixilated detector in Section 2.2. Other considerations may take precedence when imaging single molecules, in particular (i) localization accuracy and (ii) imaging resolution. Any object, no matter how small, will be imaged by a conventional optical system as a finite size spot, with a minimum dimension obtained for point-like objects (such as single molecules) approximately equal to the wavelength of light, λ, multiplied by the optical magnification M and divided by the numerical aperture, NA (80). The radius of this so-called point-spread-function (PSF) can be used as a convenient criterion to define an upper limit (the Rayleigh criterion) to the minimum distance below which two nearby objects in the object plane cannot be distinguished. This imaging resolution issue has been tackled and somewhat overturned by different microscopy techniques: (i) using non conventional optics (near-field optics (81) or negative refraction index lenses (82, 83)), it is possible to obtain images with finer details, but at the expense of considerable complexity and limited to local, surface observations; (ii) deconvolution of fluorescence images using the knowledge of the PSF (or not) allows to attain superresolution (84); (iii) structured illumination (85), non-linear effects in fluorescence (86, 87) or both (88) can also be employed to obtain higher imaging resolution. These approaches yield exquisite images, but are still rather complex to implement, and oftentimes require a very photostable sample to collect enough photons. A related but different problem is that of measuring the distance between individual nano-objects. In this distance resolution problem, what matters is the ability to precisely pinpoint the location of each individual object, in order to be able to measure their distance. There are of course quite a few subtleties even in this simpler problem, but in practice the diffraction limited size of the PSF is not really the issue: instead, what matters is the PSF sampling (pixel size versus PSF size) and its contrast (signal-to-noise ratio, SNR, and signal-to-background ratio, SBR) (23, 89-91).

In summary, for a fixed optical magnification and image pixel size, it is possible to compute the required SNR needed to achieve a given single-molecule spatial resolution. In general, this will entail adjusting the integration time to reach a sufficient signal. Inversely, if the magnification can be adjusted, the knowledge of the pixel size and the available signal are sufficient to maximize the spatial resolution by a proper adjustment of the magnification, leading to an optimal sampling of the image PSF. In other words, the pixel size of imagers is not a critical parameter as far as the achievable resolution is concerned.

Notice that in the case of confocal imaging, the image pixel size as well as the number of pixels in an image can be adjusted instead of the optical magnification, which therefore does not play a prominent role.

3. Current detectors

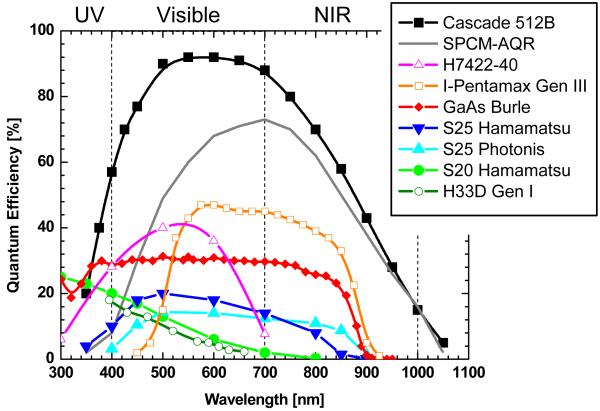
Photodetectors that are relevant for single-molecule spectroscopy rely on the photoelectric effect (e.g. multi-alkali photocathodes) or generation of an electron-hole pair in a semiconductor. Detectors relying on other phenomena, such as bolometers (92), frequency up-conversion (93), thermoelectric effect (94) and others may indeed become relevant at later stage of their development, but do not represent realistic alternatives at this time. In detectors relying on the photo-electric effect, a photon impinging on a photocathode deposited as a thin film on a glass window in a vacuum tube has a finite probability (quantum efficiency, or QE) to extract an electron from the photocathode material. In a semiconductor-based detection, absorption of a photon promotes an electron of the valence to the conduction band, leaving behind a vacancy (hole) in the valence band. The minimum energy needed to extract an electron from the photocathode depends on the photo-sensitive material, resulting in different spectral sensitivity. Various material compositions that can be used as photocathodes, as well as their QE at different wavelengths are shown on Fig. 9 (see also ref. (95)).

Figure 9.

Quantum efficiency of different photocathode materials. Data were obtained from detector manufacturer’s specification sheets or measurements performed at the Space Sciences Laboratory. Cascade: back-illuminated Si EMCCD camera manufactured by Photometrics, Tucson, AZ; SPCM-AQR-14: reach-through Si SPAD manufactured by Perkin-Elmer Optoelectronics, Fremont, CA; H7422-40: GaAsP/MCP photon-counting PMT manufactured by Hamamatsu Photonics, Bridgewater, NJ; I-Pentamax: GaAs/MCP based intensified CCD camera manufactured by Princeton Instruments, Trenton, NJ. H33D Gen I: time-resolved position-sensitive photon-counting detector developed by ourselves (see text).

In the case of low-light levels encountered in single-molecule spectroscopy, the total number of photons reaching the detector (and hence generated photoelectrons) is generally very low (100-10,000), and can be emitted in a short amount of time (1 ms-100 ms). As we have already seen in a previous section, there are three main strategies to deal with these low-light level conditions: (i) accumulate the photo-electrons over a time sufficient to obtain a signal that overcomes the different sources of noise; (ii) amplify the signal in order to reduce the influence of these sources of noise even in the case of a small number of accumulated photo-electrons; (iii) detect each individual photo-electron. These strategies can be implemented in imaging (2D or 1D) detectors or point detectors, as discussed next.

3.1. Current single-molecule imaging detectors

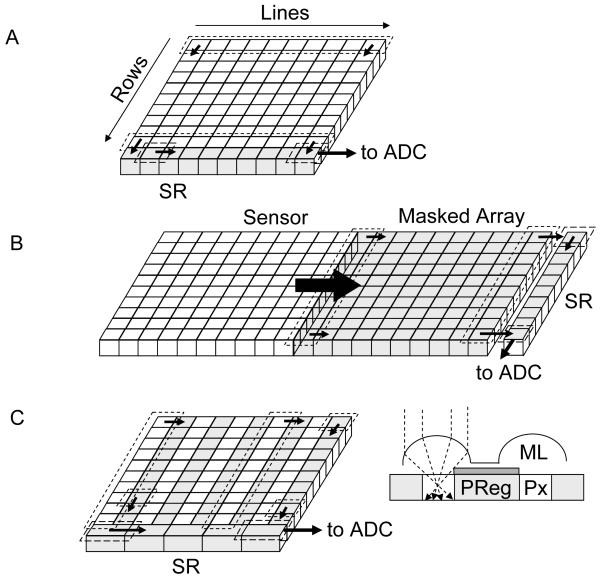
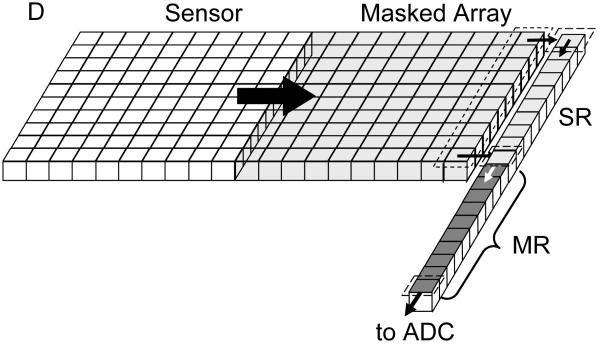
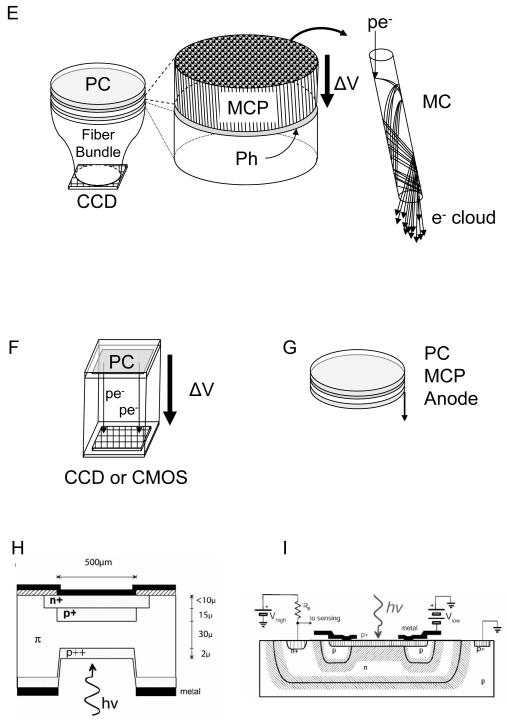
The first strategy (accumulation without any significant amplification) is used in silicon charge-coupled devices (CCD), in which photoelectrons generated in a silicon layer are stored locally in potential wells (pixels) before being sequentially readout and converted to digital information (Fig. 10A-C). Different implementations of readout schemes result in different performance and trade-offs between detection efficiency, cost and readout speed. In standard CCD (Fig. 10A), whose highest QE is obtained when back-thinned and back-illuminated, all rows of pixels are shifted in parallel one step towards the so-called shift register in a few μs per step. The shift register pixel contents are digitized sequentially and transferred to on-board or computer memory. The main disadvantage of this approach is that, since the whole array digitization process may last several ms, photons can still be accumulated in pixels during the row shifting process, unless a shutter is employed, potentially resulting in image blurring. This problem was partially solved by the frame transfer CCD design (Fig. 10B), in which the whole exposed pixel array is first rapidly (< 1 ms) transferred into a masked array, which is then readout as in a standard CCD. An alternative design, the interline transfer CCD (Fig. 10C), uses masked pixel columns interspersed in the array, such that each column of exposed pixels is first transferred within a few 10’s μs into its neighboring masked column. A standard CCD readout process is then used to digitize each row of pixel sequentially. One major drawback of this design is that the effective sensitive area of the detector is reduced by a factor of two. This is generally compensated by a system of micro-lenses, but their overall QE is generally smaller than that of other back-thinned CCD’s. In all these designs, any information on the photon arrival times is obviously lost, and low level signals (few photo-electrons per pixels) are irreparably contaminated by readout noise (several electrons rms, see Table 1). Even using pixel binning or restricting data transfer to small regions of interest, the maximum frame rate of these technologies hardly goes beyond 1 KHz.

Figure 10.

Principle of some detectors used in single-molecule spectroscopy and imaging. A-C: CCD, frame-transfer CCD and interline-transfer CCD cameras. In all designs, the limiting factor is the sequential digitization of the pixel accumulated charges. However the frame-transfer design (B) improves on the full-frame design (A) by allowing using the exposed array of pixels, while the stored array is being digitized. In the interline-transfer design (C), the storage process is even faster, as a single column shift is needed. However, the lower fill-factor of the sensitive area of the CCD requires the use of a micro-lens array to direct as much light as possible to the small sensitive area. The detection efficiency of these devices is therefore inferior to the two previous designs. (D) The electron-multiplying CCD adds a series of small charge amplification stages before conversion to a voltage and digitization. SR: shift register, MR: multiplication register, ADC: analog to digital converter, ML: microlens, PReg: pixel register, Px: pixel. E-F: Photocathode-based imagers. Intensified CCD’s (E) use a photocathode (PC) deposited under vacuum on a window, which is proximity-focused on a microchannel plate (MCP) or a stack thereof. The MCP amplifies the photo-electron up to 10⁶ times by a cascade of wall material ionization and acceleration of the resulting electrons. The electron cloud emerging from a microchannel impacts a proximity-focused phosphorescent screen (Ph), resulting in emission of 100’s photons. This amplified optical signal is then transmitted through a fiber bundle to a standard CCD camera for readout. Electron-bombarded cameras use a similar photocathode to that of ICCD’s, but directly accelerate photo-electrons towards the final imager (CCD or CMOS). Upon impact, 100’s electrons are created locally, amplifying the initial signal accordingly. G-I: Non-imaging detectors. High QE photomultipliers (G) are based on a design similar to that of the ICCD described in (E), and output a fast (ns) current pulse for each amplification event. Silicon-based single-photon counting avalanche photodiode can have two typical structures: reach-through (H) or more recently, planar (I). In both cases, a large amplification of the number of charge carriers (electrons and holes) is generated in an avalanche process upon photo-creation of an e-/h pair when the p-n junction is biased above its breakdown voltage. Whereas the sensitive area of PMT’s can reach mm, SPAD’s have much smaller sensitive areas of the order of 10’s μm. H: reproduced with permission from ref. (102); I: reproduced with permission from ref. (104).

The second strategy is implemented with image intensifiers (silicon intensified target (SIT) tubes, microchannel plates (MCP)) coupled with a CCD or a CMOS sensor as the position detection device (Fig. 10E-F), or using a series of electron-multiplying registers before digitization of the collected pixel signal (EMCCD, Fig. 10D). In all cases, the timing of each photon arrival is evidently lost, except in time-gated models of intensified camera (e.g. PicoStar camera, LaVision Gmbh, Germany) which are however very inefficient in the usage of emitted photons, due to their very principle. This principle consists of accumulating intensified photoelectrons on an ICCD whose intensifier is gated (turned on) at a predefined time and for a predefined duration after the laser pulse. The camera thus records photons emitted during a short (200 ps – 1 ns) time window of the fluorescence decay. To reconstruct the full decay, a succession of time windows is needed, therefore necessitating several images acquired with different time-gates. In this approach where photons are accumulated for a fixed period of time long enough to get a good SNR, only the nano-time is preserved, and then only with a resolution as good as the time-window size. In addition, when a time-gate is selected, all photons hitting the photocathode outside of this time-window are lost, resulting in a very inefficient use of the emitted signal. Intensified cameras used in this time-gated mode are thus definitely unable to detect single-molecules and are mentioned here uniquely for their ensemble fluorescence lifetime imaging capabilities. Notice that other approaches using the principle of time-gating can also be used (e.g. ref. (96)). It is also worth noting that a different approach to measuring the fluorescence lifetime can be employed with intensified camera, using a high-frequency modulated light source. In this case, the emitted fluorescence is modulated as well, and the phase and amplitude contain information on the different lifetime components and their amplitude (44). In practice, these can be recovered by modulating the intensifier of the camera at different frequencies or at different dephasing. This frequency-domain FLIM technique is thus in principle more photon-efficient that the time-gated approach and might be sensitive enough to perform single-molecule fluorescence imaging, although to our knowledge, this has not been reported yet.

For the sake of completeness, we will also mention streak cameras (97, 98), which allow time-resolved spectroscopy to be performed, using deflection by an electric field to displace each photo-electron proportionally to its arrival time. Used in a confocal line-scanning geometry as described in Fig. 8C, it provides ps-resolution fluorescent lifetime measurement capabilities. This technique also only provides with the microscopic arrival time of the emitted photons, and does not currently have enough sensitivity to study single-molecules. Line CCD cameras can naturally be used in a similar manner for non time-resolved line-confocal imaging, as recently introduced in a product commercialized by Zeiss.

The choice of wide-field detector from the previous list depends on many factors. Fig. 4 and the corresponding discussion of Section 2.2 indicate that the best SNR is obtained for cooled back-thinned slow-scan CCD camera for long integration time (or large signal, both being obviously interdependent), EMCCD’s being a close second. The main problem with slow-scan cameras is their limited frame rate, and very logically, EMCCD’s have become the detectors of choice among single-molecule imagers. Their cost is however still high (although generally less than the older ICCD technology), and in some circumstances, an affordable interline-transfer CCD camera can do surprisingly well at moderate frame rates. The recently commercialized electron-bombarded CCD (or now CMOS) technology has a lower QE than its silicon counterpart, but is expected to be competitive in terms of cost. Like interline-transfer cameras, it may find niche-applications (for instance using IR sensitive photocathodes where silicon has no sensitivity) or photon-flux regimes where it will be sufficient to image single molecules with a sufficient signal-to-noise ratio.

3.2. Current single-molecule point detectors

Point detectors are detectors which do not provide position information, but are not necessarily of small dimension. For instance, most single-photon avalanche photodiodes used in SMS have a sensitive area with a diameter of a few dozen to a couple hundred micrometers, whereas photomultipliers have typically diameters of several millimeters. This has some practical consequences for collection efficiency and design of the detection path. As discussed in Section 2.7, point detectors are mostly used in a confocal setup to detect photons emitted from a small volume excited in the sample. The smaller the sensitive area, the lower the magnification of the collection optics needed to focus the collected light onto this sensitive area, and the more difficult the alignment of the detector for maximum detection efficiency.

As was just mentioned, there are two general types of point-detectors used for single-molecule applications: photomultiplier tubes (PMT) (99) and single-photon avalanche photodiodes (SPAD) (100). In both kinds of devices, each detected photon is first converted into a charge carrier/s (photo-electron or electron-hole pair), which is/are then amplified by several orders of magnitude in a rapid avalanche process. PMT’s relevant for single-molecule detection are based on the same photocathode + MCP technology (Fig. 10G) as used in ICCD’s (Fig. 10E) (20, 64, 101). Instead of the phosphor screen used in image intensifiers, the electron cloud impacts an anode, and a simple circuitry transforms this signal into a small ns-wide voltage pulse output. This output then needs to be amplified and fed to a constant fraction discriminator (CFD) before being time-stamped using for instance a time-to-digital converter (TDC). In practice, only GaAsP (70) and GaAs (2) photocathodes have a sufficient QE to be of any use in SMS, even though some of the very first single-molecule fluorescence detection experiments were performed using PMT’s with multi-alkali photocathodes (99).

Notice that the same amplification technology can be used to create “linear” and “pixelated” detectors using a segmented anode instead of a monolithic one. Such a linear, 32 pixel-anode PMT has been used recently to demonstrate spectrally- and time-resolved single-molecule spectroscopy (79). Following the same principle, a 10 × 10 multianode PMT has recently been commercialized by Hamamatsu Photonics, although no single-molecule application has been reported yet (model R4110U-74-M100B). One major problem with these devices is the complexity of the required external electronics, since each anode segment requires a separate preamplifier and timing electronics to process the incoming pulses. Currently, this type of PMT offers a time resolution of the order of 250-300 ps (70, 79).

Avalanche photodiodes (AP) work on a similar amplification principle, except that the generated carriers are electron-hole pairs and their accessible gain is limited to a few thousands (102). SPAD’s are based on an entirely different principle, whereby the number of secondary charge carriers is no more proportional to the incoming photon flux. In this regime, the voltage bias is set slightly above the breakdown level and the diode functions as a bistable device. The device has no current circulating in the absence of photon conversion, and a constant current level circulating after an avalanche has been generated. The onset of this current is very rapid, and can be recorded with an onboard circuitry generating a fast voltage output (fast NIM or TTL signal). However, the device needs to be reset below the breakdown voltage after each detection, a process that results in dead-time of 30-40 ns, limiting the counting rate without loss to a few MHz. Two types of SPAD architectures are currently commercially available: the reach-through architecture initially developed at RCA using dedicated ultra-low doped p-silicon wafers (Fig. 10H) and the planar technology using low-doped p-silicon wafers compatible with CMOS process commercialized by several companies (Fig. 10I) (103-105). The interested reader is referred to the excellent review by Cova et al. on the different merits of both architectures (102). Briefly, the reach-through architecture results in a higher QE in the red and NIR region of the spectrum (> 60 % from 600 nm to 750 nm (106) vs < 30 % above 600 nm for the planar technology (104)), whereas the planar technology, due to its thinner depletion layer results in better timing resolution (~ 350 ps for reach-through vs ~ 50 ps for planar). Notice however that reach-through SPAD’s can have similar timing resolution with the addition of a dedicated electronic circuit (107).

In practice, most current single-molecule confocal experiments are performed with reach-through SPAD due to their higher QE in the 500-750 nm wavelength range in which most organic fluorophores emit. Some gain of QE can be obtained in the planar technology by increasing the overvoltage over breakdown (104). This comes at a cost, namely increased dark count rate. For instance, ref. (104) shows a two orders of magnitude increase of dark count rate (70 Hz to 5 kHz) upon increase of the overvoltage from 5 V to 10 V, for a gain of 5 % QE from 500 to 700 nm. Returning to the example presented in Section 2.2, we see that such a high dark count level has a negligible effect on the SNR of a typical signal of a few 100 kHz obtained from a single molecule diffusing in solution, suggesting that the overvoltage might be a parameter users could be interested to have access to and modify depending on their applications.

The better time resolution of planar technology SPAD’s is certainly attractive but might not be necessary for most applications. As discussed in ref. (64), the timing resolution of TCSPC techniques is not limited (only) by the instrument response function (IRF) of the detection system (and therefore the detector’s response), but mainly by the number of photons used to fit the recorded nanotime histogram with a model decay curve convolved with the IRF. In other words, extraction of decay times much shorter than the IRF width can be obtained with a sufficient number of collected photons, in analogy to the way the localization of a single-molecule can be performed with sub-pixel resolution (and even arbitrary resolution), provided that enough photons are collected for this task (23). In experiments such as that of ref. (39) in which estimation of very short lifetime was performed with a small number of photons to get access to fast time scale fluctuations (down to ~ 100 μs), such detectors are definitely needed. As the planar technology is also much easier to industrialize and results in better production yields, one can hope that, with the help of competition between different manufacturers, the cost of individual detectors will drop, making them very attractive alternatives to reach-through SPAD’s. More importantly, this technology is amenable to the production of dense arrays of SPAD’s, a perspective that will be discussed below.

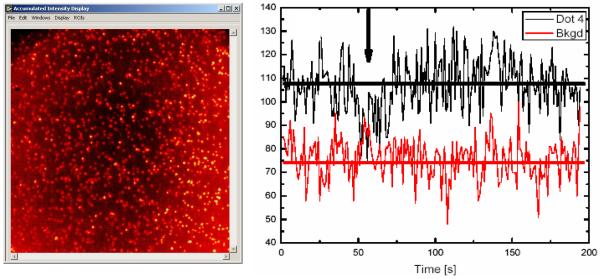
Point-detectors are invaluable for the burst analysis of diffusing molecules in a confocal geometry, or of immobilized molecules. Most importantly, they provide exquisite temporal resolution, which allows FCS, antibunching and time-resolved analysis to be performed from sub-ns time scale upwards. In addition, the absence of readout noise and negligible dark count let them outperform all other types of detectors at short acquisition time (Fig. 4). The problem is that point-detection approaches are low-throughput. In FCS or related approaches, thousands or even millions of molecules might well be analyzed in a single experiment, but a complete confocal microscope and its associated detectors is monopolized for a single sample at a time. In the analysis of immobilized molecules, a single molecule at a time (possibly for several minutes in a row) can be studied. And when such a setup is used for raster-scanning imaging, the typical minimum dwell-time of a few ms per pixel necessary to acquire a sufficient SNR results in very low acquisition rate (for instance, a 512 × 512 image at 1 ms per pixel would take over 4 min to acquire (while the transfer rate of a comparable image acquired by a fast EMCCD is ~ 30 ms). Multiplexing the acquisition of single-molecule data in solution has recently been attempted using multiple excitation schemes and several detectors (108), but with significant technical issues and no real prospect to extend this to a truly high-throughput regime.

4. Recent and future developments

The obvious conclusion of the two previous sections is that current imaging detectors lack temporal resolution, and point-detectors, which possess the required temporal resolution giving access to the complete photon information, cannot be used efficiently for high-throughput studies. An ideal detector for single-molecule imaging and spectroscopy would thus combine the advantages of both types of detectors. This conclusion led us several years ago to propose a new type of detector based on a palette of existing technologies, which will be described in the next section. Meanwhile, steady progresses in SPAD planar technology have made it clear that there are alternatives to our proposal, and we will briefly discuss expected progresses in this area. As single-molecule imaging and spectroscopy matures and extends its fields of application, it will certainly attract more talents eager to improve its performance and capabilities, potentially giving rise to entirely novel detector concepts (see for instance ref. (109-111)).

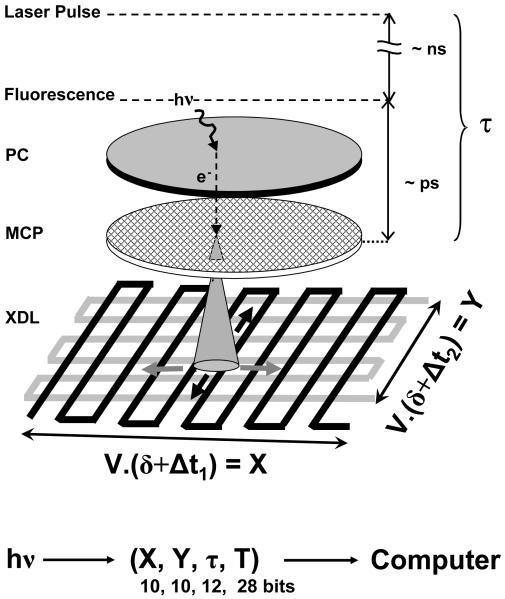
4.1. The H33D detector

Combining the characteristics of imagers and point detectors practically means building a wide-field time-resolved position-sensitive photon-counting detector. Non time-resolved wide-field photon detectors have been actively developed for decades by the astronomical community, who had to deal with low light levels long before single-molecule spectroscopists (112). Historically, one-dimensional (1D) (113-115) and two-dimensional (2D) (116-118) detectors allowing the determination of the position of the secondary electrons of an amplifying MCP without intermediate storage can be traced back to the 70’s. Developed for astrophysical observations, these MCP-based position-sensitive detectors (PSD) were later extended to the visible spectrum with astrophysics and geophysics application in mind (119-121), and finally used for spectroscopic applications (122). Several approaches have been used for the purpose of detecting the position of the electron cloud generated at the anode. They can be subdivided in two different categories depending on which principle they rely upon to analyze the collected charges (116): analysis of the pulse shape and timing (propagative and delay line anodes) or of the pulse amplitudes (charge-division anodes). Each of these principles can be used in different geometries (quadrant anode (116, 123), multianode array (117), wedge- and-strip (124, 125), delay line (126, 127) or pixelated (128) geometries for instance).

MCP’s are characterized by a fast response time of a few tens of ps (129-131), which makes them useful intensifiers for detectors used in time-correlated spectroscopic applications. Coupled with a PSD, they form a powerful time-resolved position-sensitive detector as first demonstrated in ion detection experiments (132). This type of functionality was later on applied to time-resolved spectroscopy (133-137). This latter application has given rise to at least four commercial products (Mepsicron 2601B, Quantar Technology, Inc., Santa Cruz, CA; TSCSPC detector, Europhoton Gmbh, Germany; PIAS detector model C1822-06, Hamamatsu Corp., USA –discontinued; and IPD425, Photek, UK) which have been used to perform time-resolved spectroscopic studies (61, 77, 138-144) and lifetime imaging using either a slit detector (61, 143), a prototype 4×4 pixel division (62) and finally a true 2-dimensional detection (145). These detectors are characterized by a time-resolution of a few tens of picoseconds, but a relatively low maximum count-rate of a few kHz and rely on classical semi-transparent photocathodes having a relatively low QE, which makes them rather poor detectors for SMS. The only demonstrated single-molecule application can be found in ref. (144), which does not seem to have been followed by any further work.

Building on this previous work, we have proposed a concept for a High temporal, High spatial resolution, High throughput 3-dimensional detector (2 spatial, 1 temporal), or in short, a H33D detector (pronounced “heed” detector) (146-148). The general architecture is presented in Fig. 11 and is based on a photocathode proximity focused on a three-MCP stack for the photo-detection and signal amplification, and a position-sensitive anode mounted ~ 6 mm behind the MCP’s for position registration. The nanotime of each event is measured as the delay between the MCP voltage pulse (time jitter < 100 ps) and the next laser pulse. In our first prototype, the photocathode, deposited on a fused-silica window (sensitive area: ~ 27 mm diameter), is a S20 type (multi-alkali: Na₂KSb:Cs (20)) with limited sensitivity in the red part of the spectrum (4 % at 600 nm) (146). The anode has a cross delay line architecture (XDL), and is made of alumina substrate with metal coatings on both sides. The delay line pattern is built up onto the conductor to provide a cross finger ~ 30 × 30 mm active area, with delay lines for X and Y. The zig-zag pattern has a ~ 0.5 mm period and give a signal propagation delay of < 1 ns/mm and pulse widths of less than 5 ns, which is sufficient to achieve <100 μm FWHM resolution for single-photon events using high resolution timing electronics. The electronics used in this first prototype consists of a custom designed module for the delay lines (SOHO TDC, (149)) and a commercial one for the nanotime measurement (TDC model 7072T, FastComtec). Their outputs are integrated by a Field Programmable Gate Array (FPGA) (Spartan II, Xilinx), which also counts the number of laser pulses since the beginning of the experiment, thus providing a macrotime information for each detected photon. The final information (2 × 32 bits per event) is sent asynchronously to the computer and handled by a custom-made software. The maximum throughput of this system (~ 500 kHz) is mainly limited by the timing electronics (deadtime of the SOHO TDC ~ 1.2 μs), but the MCP gain also limits the local count rate to ~ 10 kHz over a 100 μm diameter area. We emphasize that, like a SPAD, this is an event driven data transfer process: in the absence of signal, no readout is performed, and photon information is transferred for each photon as soon as it is acquired.

Figure 11.

Principle of operation of the H33D detector. Pulsed laser excitation is used to excite the fluorescence of a sample. A fluorescence photon emitted a few ns after the excitation pulse is collected by the imaging optics and interacts with the photocathode (PC), creating a photoelectron with a wavelength-dependent probability QE. The photoelectron is amplified by an apposed MCP stack, generating an electron cloud (cone shape). The measurement of the delay between the charge pulse at the back of the MCP and the laser pulse (nanotime τ) is performed with a TDC. A position-sensitive anode determines the position of the cloud. Here a cross-delay line anode (as implemented in our first prototype) is represented: the charges propagate through the lines and are collected at both ends of each line. A timing electronics converts the differences in arrival time into position information (X, Y). A laser-pulse counter built in the readout electronics provides a 4^th coordinate, the macrotime T. The 4 coordinates of each photon (10 bits per spatial coordinate, 12 bits for the nanotime, 28 bits for the macrotime and 4 control bits) are then asynchronously sent to a computer for storage and processing. δ: fixed time delay. V > 1 mm/ns: signal propagation velocity.

Fig. 12 outlines basic operations permitted by the software, given the train of photon coordinates. Similarly to a point detector, the raw data consists in a train of time-stamped photons, with the additional information of the photon impact position. A possible way of treating the data is to form a series of images (a movie) by building 2-dimensional histograms of the number of photons per “pixel” per integration time dT (fixed by the user). Strictly speaking, there are no defined pixels for this detector, but with the position information being digitized on 10 bits per axis, there is effectively a fixed number of possible positions, which we call pixels for convenience. This data treatment makes the connection with the wide-field imagers discussed previously, with the subtle difference that the value of the integration time dT is entirely up to the user. The main difference however is that each “pixel” of an “image” now contains a precise recording of the arrival time of each photon (macrotime and nanotime). The macrotime information can be used for instance to perform FCS on the signal emitted by a moving single molecule tracked from frame to frame. Simultaneously, the nanotime information can be used to build fluorescence decay histograms for each pixel in each frame, or for each identified particle (or region of interest) in each frame. Standard fluorescence lifetime fitting procedures can be used (for instance, maximum likelihood estimation – MLE – of single lifetimes (150), or non-linear least-square fitting of multiple lifetime or stretched exponentials) to extract one or more numerical value per pixel. In the simple case where a single lifetime is extracted, this information can be color-coded and represented as a new, fluorescence lifetime image (in addition to the intensity image obtained initially) or a FRET efficiency image if the observed signal is that of a donor molecule in a FRET pair. Contrary to TCSPC FLIM methods, which require a dwell time per pixel that results in a sufficient SNR, and whose image acquisition time is proportional to the number of pixels, the acquisition time for the H33D detector will be fixed by the minimum SNR desired in the image, or in other words, the equivalent dwell time of the TCSPC approach (145).

Figure 12.

Principle of operation of the H33D detector data visualization. Individual photons are tagged with 4 numbers: 2 spatial coordinates X, Y and 2 temporal ones τ, T. Intensity images are obtained by forming 2D-histograms of the recorded counts during user selectable periods, using the macrotime information. Starting from these images, it is possible to use the nanotime information to display the fluorescence lifetime information obtained from each pixel by maximum likelihood estimation or non-linear least-square fitting. It is also possible (and easier) to form intensity images with photons arriving with a certain delay with respect to the laser excitation (time gating).

Yet another way to exploit the nanotime information consists of digitally rejecting photons arriving in a user-specified time window, that is, form an image using photons arriving only after a specified delay after each laser pulse. As demonstrated in ref. (151) using TCSPC confocal imaging, this can be used to reject most of the fast-decaying autofluorescence background, while enhancing the contrast of objects with longer lifetimes such as quantum dots in live cells (146). Fig. 13 illustrates this idea with the simulation of two spots of equal brightness corresponding to objects with lifetime 5 ns and 10 ns respectively. These values correspond to the measured lifetimes of fluorescent beads filled with Nile Red dye molecules (Invitrogen, Carlsbad, CA), and yellow nanocrystals respectively. The measured lifetime histograms corresponding to regions of interest including these two spots are shown in the lower panel. A time-gate of 20 ns (indicated as a green vertical line) is applied to obtain the time-gated image shown on the right, in which all photons arriving within 20 ns of each laser pulse are omitted. The spot corresponding to the 5 ns species has disappeared from the image, while the quantum dot signal is still visible, its SNR decreasing only by a factor 3. In practice, this approach will be interesting to track single quantum dots in the cytoplasm of live cells, where background reducing techniques such as TIR cannot be used. The detectability of individual quantum dots by our first generation H33D detector is demonstrated in Fig. 14, where yellow quantum dots deposited on a glass coverslip were imaged in TIR microscopy. Although the low QE of the S20 photocathode prevents us from obtaining a large SNR at short integration time, residual blinking dynamic can be observed in a time trace with 1 s integration.

Figure 13.

Left image: simulation of two spots of equal brightness corresponding to objects with lifetime 5 ns (upper left) and 10 ns (lower right). The simulation is performed within IdefiX, the software used for the actual data acquisition, and analysis is performed as it would be in an actual experiment. The measured lifetime histograms are shown in the lower panel (screen capture of the Lifetime Histograms panel of IdefiX). A time-gate of 20 ns (indicated as a green vertical line) is applied to obtain the time-gated image shown on the right. The spot corresponding to the 5 ns species has disappeared from the image.

Figure 14.

Left: Accumulated image (3 min) of a spin-cast sample of 565 nm emitting qdots excited in TIR mode by 2 mW @ 488 nm. Image size: 130 × 130 μm. Right: Black curve: Time-trace corresponding to one of the dots in the image (1 s resolution). Red curve: local background. Despite the low SNR, a clear blinking event can be observed (arrow), indicating that a single qdot was observed. Notice that these quantum dots exhibited very little blinking when observed in similar conditions using an ultra-sensitive EMCCD.

Our current H33D prototype has already significantly better performances than similar detectors developed in the past or currently commercialized. Nevertheless, it is not sensitive enough to be a good single-molecule detector, and it still has limited throughput (mainly due to the limitation of the delay line electronics). There are several ways we intend to improve it.

1. higher QE: as shown in Fig. 9, S25 photocathodes (20) have notably better sensitivity in the red part of the spectrum than the S20 used here. Even better are GaAs photocathodes (~ 30% QE from 400 to 800 nm) and GaAsP photocathodes (~ 45 % QE from 450 nm to 650 nm, see Fig. 9). Recent technological developments have decreased the response time of these photocathodes down to ~ 250 ps, which is sufficient for most single-molecule and FLIM applications. Future H33D detectors will therefore use one of these materials.

2. higher throughput: although faster timing electronics could be used to measure the time delay of the XDL, a better alternative anode technology used by the Space Sciences Laboratory for several years is the crossstrip anode architecture (152). The cross strip (XS) anode concept employs many of the physical design techniques used for the XDL anodes. However the XS anode works completely differently than delay-line anodes, to achieve much higher resolution and speed, while using gain that is several orders of magnitude lower. It is however more challenging in terms of electronics, requiring application specific integrated circuits (ASIC) working in parallel. Count rates of up to 5 MHz are expected with currently existing ASIC’s.

3. local throughput: secondary electron emission process in the microchannels of MCP’s is limited and a finite recovery time is required before a channel recovers its typical response. At the high gain used in the generation 1 H33D detector to provide sufficient signal to the XDL, this results in a maximum local count rate of ~ 10 kHz per 100 μm diameter. The use of a XS anode instead of a XDL anode allows using lower gains while achieving similar position resolution. This should allow achieving local count rates of up to 100 kHz (H33D Gen II).

4. multihit: the current design of the H33D detector cannot handle two or more quasi-simultaneous photon impacts on the photocathode. On one hand, the strategy employed to measure the time delay between each end of the delay lines does not allow to detect multihit events. This is true during the duration of the propagation of the charges (< 50 ns), but also during the deadtime of the nanotiming electronics (~ 1.2 μs). The latter can be shortened down to ~ 300 ns with more recent TDC electronics, or by having more than one TDC. Other XDL architectures and readout electronics schemes have been proposed to obviate the anode deadtime problem (153), although they would not address the second issue. Indeed, in our current design, the nanotime information is obtained from the voltage pulse generated on the back of the MCP after each amplification event. This voltage pulse has a finite width of a few ns for single photons and can be timed precisely if isolated (<100 ps in the Gen I detector, < 250 ps in future generations). In the case of multihit (either simultaneous impacts, or separated by less than the width of a single-photon MCP pulse, or during the deadtime of the electronics), the current strategy will not be able to measure the nanotime of each impact. Sophisticated signal treatment can be employed to deal with such bursts of impacts (154), but we propose instead to segment the back of the MCP and the anode in order to perform the nanotime measurement and position determination separately for different regions of the photocathode (155). Although this strategy would still not allow to address simultaneous and colocalized photon impacts, it would allow increasing the throughput accordingly, by mirroring the MCP back segmentation at the anode and anode readout electronics. A four quadrant geometry would thus allow a 20 MHz global count rate and to handle 4 simultaneous hits in separate regions of the detector (H33D Gen III).

Table 2 compares the theoretical performances of the H33D detector (current generation, Gen I, or future Gen III) with others discussed previously. The definition of a maximum local and global count rate for standard imager is a bit artificial, but can be done with a basic set of assumptions. Here we define the maximum global count rate as the maximum local count rate times the number of pixels. The maximum local count rate is defined as the maximum number of photons that can be accumulated while using the maximum detector gain, divided by the minimum full frame readout duration. For non-intensified CCD’s, this pretty much define the maximum photon flux supported by the camera before saturation would occur. For intensified CCD’s (ICCD and EMCCD), the choice of a maximum gain improves the signal-to-noise ratio (which is what is needed for single-molecule sensitivity), at the expense of the dynamic range. In practice, the optimal SNR can be obtained before the maximum gain is attained. Therefore these local and global count rates are lower bounds provided as orders of magnitude only. The main interest of this comparison with standard imagers is to show that photon counting detectors are currently intended for low light level imaging only. It is also interesting to contemplate the colossal data-throughput that a photon-counting detector competing with imagers would need to achieve. With at least 8 bytes of information per photon, the many GHz counting rates of imagers would translate into Gb/s of data, imposing a severe constraint in data transfer bandwidth, storage and analysis.

Table 2.

Comparison of performance of different types of detectors. The following detector specifications were used: reach-through SPAD: SPCM AQR-14 (Perkin Elmer Optoelectronics, Fremont, CA, USA); epitaxial SPAD: PDM 50CTC (Micro Photon Devices, Bolzano, IT); GaAsP PMT: H7422-40 (Hamamatsu Photonics, Bridgewater, NJ, USA); CCD: CoolSnap HQ (Photometrics, Tucson, AZ, USA), ICCD: I-Pentamax (Princeton Instruments, Trenton, NJ, USA); EMCCD: Cascade 512B (Photometrics)

	H33D		Single-Photon Counting Detectors			Imagers
	Gen I	Gen III	Reach-through SPAD	Epitaxial SPAD	GaAsP PMT	CCD	ICCD	EMCCD
Technology	Vacuum	Vacuum	Solid State	Solid State	Vacuum	Solid State	Vacuum + Solid State	Solid State
Photon Counting	+	+	+	+	+	−	−	−
Sensitive material	S20	GaAs	Si	Si	GaAsP	Si	GaAs	Si
QE (@ 600 nm)	4%	35-40%	70%	30%	40%	60%	45%	90%
Time Resolution	100 ps	250 ps	300 ps	50 ps	400 ps	100 ms†	60 ms†	34 ms†
Global Rate*	500 kHz	20 MHz	N/A	N/A	N/A	217 GHz	315 MHz	12 GHz
Local Rate*	10 kHz	100 kHz	10 MHz	10 MHz	10 MHz	150 kHz	1.2 kHz	46 kHz
Nb of Pixels	π 1282	π 2562	1	1	1	1392 ×1040	512 × 512	512 × 512
Pixel Size	100 μm	35 μm	170 μm	50 μm	5 mm	6.5 μm	15 μm	16 μm
Max Frame Rate‡	1 kHz	1 kHz	¼ frame/min	¼ frame/min	¼ frame/min	10 Hz	15 Hz	29 Hz

^*For imagers, the local count rate is replaced by the pixel well capacity divided by the maximum gain (electrons per photon) divided by the maximum frame rate. Using the minimum gain would allow obtaining higher count rates, but would result in worse single-molecule detection (lower SNR) because of the larger influence of the readout noise.

^†Better timing resolution (down to a few ms) can be achieved by limiting the acquisition to a small number of pixels, or by binning pixels. Notice also that ICCD’s can in some case be gated to obtain ~ 200 ps nanotime-resolution (see text).

^‡Frame rates for point detectors are calculated for a raster-scanned image of 512 × 512 pixels, and assuming a dwell-time of 1 ms/pixel.

Photon-counting detectors are indeed principally adapted to single-molecule applications, where very localized high count rates (up to ~ 100 kHz) are encountered, and a few dozen to a few hundred single-molecules are present at the same time in the field of view. Even though we described this detector as an imager, it can therefore also be seen as equivalent to an array of point detectors, each providing up to 100 kHz of throughput. Applications such as multiplexed analysis of diffusing single-molecules could evidently take advantage of this type of detector.

4.2. SPAD arrays

Reach-through SPAD discussed in Section 3.2 would constitute ideal pixels of a H33D detector. With the appropriate electronics, they can reach <100 ps timing resolution, have a deadtime of <50 ns and a quantum efficiency almost as good as that of CCD cameras, while sustaining MHz readout rate. Unfortunately, the production yield of these devices is very low and therefore producing them as matrices of individual detectors is currently unrealistic. SPAD’s made in the planar technology on the other hand are manufactured much more reproducibly, and the technology is flexible enough to allow a variety of array geometries. As they are made using a CMOS process, their associated control electronic can be embedded in the chip design. Small arrays (from 2 × 2 to 32 × 32) have already been produced by several groups (108, 156-159) with demonstrated applications ranging from single-molecule FCS (reach-through SPAD, (108)), to adaptive optics (158) and 3D imaging (157, 160). Although they are all arrays of single-photon counting elements, several issues need to be solved before they truly qualify as time-resolved photon-counting wide-field detectors.

1. fill factor: each sensitive SPAD element occupies a very small amount of the detector area (<25 %), which therefore results in a significant loss of photons. Solutions based on arrays of lenslets (microlenses) matching the SPAD array layout and focusing the impinging light onto the sensitive area have been proposed (158) (159) but the final collection efficiency remains unknown. Added to the reduced QE of planar technology SPAD’s, the final sensitivity might be at best comparable to GaAs or GaAsP based H33D designs.

2. signal output: although arbitrary large arrays could in principle be built, a technological obstacle is the output of each SPAD signal to the external processing electronics and close packaging of the latter (timing or counting, depending on the application), while avoiding cross talk especially if fast timing is planned.

3. processing electronics: the question of how to time-stamp or count incoming photons on arrays of SPAD’s has received very diverse solutions. Fast timing has been performed either sequentially (one SPAD at a time) on large size arrays (157) or in parallel (160). Counting-only applications (where each photon is associated with macrotime and position information) have been limited to small arrays (108). In another case, the electronics was designed to count incoming photons per individual SPAD, but the data sent to the computer memory was the number of counts per SPAD integrated (binned) over a finite period of time. A promising though very complex architecture based on “bridge-bonding” an array of timing electronics directly to the array of SPAD was recently illustrated with a 32 × 32 array (160).

In summary, where and how to build the photon counting and time-stamping electronics remains an open question. By analogy with the design of the H33D detector presented in the previous section, SPAD arrays (SPADA) for single-molecule applications may not necessarily need as many counting and time-stamping electronic modules as there are pixels. Since single-molecule signals are spatially sparse and faint, architectures relying on multiplexing for signal processing might be perfectly adapted and simpler to implement. In addition, imaging arrays may not be the best niche market for this technology: linear arrays for spectroscopy (79), or fiber-coupled arrays (159) for high-throughput single-molecule analysis of diffusing molecules (108) might turn out to be easier applications to tackle in a first step.

5. Conclusion

We have described the characteristics of signals generated in single-molecule fluorescence experiments, and reviewed the suitability of different types of detectors to these characteristics. We have also briefly described new developments in wide-field photon-counting detectors as well as SPAD arrays, which may in the near future provide the community of single-molecule spectroscopists with powerful tools to devise new experimental protocols. As the list of bibliographic references indicates, these characteristics are in fact common to many other scientific fields, further justifying research and development in this domain. Recent developments in signal processing electronics (autocorrelator modules, multichannel TCSPC electronics, etc) will also help transform this research area. Even though SMS has not yet fully exploited all the potential of current detectors and techniques, it is exciting to see that several promising developments may transform the field even further in the future.