Prehension synergies: trial-to-trial variability and hierarchical organization of stable performance

Abstract

We studied multi-digit synergies as relations among digit forces and points of their application across multiple repetitions of a static prehensile task. The task required holding a grasped object (14.9 N) against different external torques. Subjects (n=6) performed 25 trials for each torque condition: −1.0, −0.5, 0, +0.5 and +1.0 Nm. In spite of the variability of individual forces and points of their application, stable performance was achieved. Individual performance variables were organized into two subsets. Variables within each subset highly correlated with each other (the coefficients of correlation were close to ±1.0) while there was no correlation among variables from different subsets. The two subsets were associated with two components of the prehension task: grasp control (preventing an object from slipping out of the hand) and torque control (maintaining a desired object orientation).

Introduction

A prehension synergy is defined as a conjoint change of finger forces and moments during multi-finger prehension tasks (Zatsiorsky et al. 2003a). To study prehension synergies researchers have employed different experimental techniques: (a) inflicting external perturbations (Cole and Abbs 1987, 1988), (b) recording correlations among output variables in single trials of long duration (Santello and Soechting 2000; Vaillancourt et al. 2002), and (c) varying the task parameters, in particular the object geometry, resisted torque and/or load (Zatsiorsky et al. 2002a, b, 2003a). Cole and Abbs (1986), who studied rapid pinch movements of the index finger and the thumb from an open-hand position, found that the finger and the thumb are not controlled independently, but rather behave synergistically as a single unit. Santello and Soechting (2000) discovered that individual normal finger forces oscillate synchronously and hence are determined by a common multi-finger synergy. Zatsiorsky et al. (2003a) recorded both the normal and tangential finger forces and reported consistent conjoint adjustments of digit forces to changes in task parameters. Trial-to-trial variability in prehension tasks with fixed task parameters has not been addressed.

High trial-to-trial variability in such tasks would imply that the CNS does not optimize for a unique solution for the apparently redundant problems, but rather organizes a pattern of co-variation of elemental variables that satisfies the task constraints (behavioral goals). Such a modus operandi should lead to relatively high variability at the level of elemental variables and relatively low variability at the level of performance variables. In mathematical parlance, a completely compensated variability would mean that the CNS specifies not a unique solution but a null-space of elemental variables (for a description of null spaces in human movement see Zatsiorsky 2002). In static prehension tasks, the null space indicates all sets of finger forces that correspond to a fixed combination of the resultant force and moment exerted on the hand-held object. This theory is similar to the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2002a), which assumes that the controller specifies a sub-space (a manifold, UCM) in the state space of elemental variables and restricts the variability of the elemental variables to the UCM. While the existence of a compensated component of motor variability in static force production tasks seems almost certain (Latash et al. 2001, 2002b; Scholz et al. 2002), earlier studies have been limited to pressing tasks in which only normal forces were analyzed.

One of the main issues addressed in the current study is whether there exists only one null space or two (several) uncorrelated null spaces in static prehension tasks. In robotics, the principle of superposition has been recently suggested for control of prehension (Arimoto and Nguyen 2001; Arimoto et al. 2001). The principle allows for decoupling the control: an entire manipulation task is divided into subtasks such that independent controllers specify different subsets of control parameters. The commands from the controllers, for instance the ‘torque’ and ‘force’ commands to the fingers, superpose such that their effects are added without interfering with each other. Such a control sharply decreases computation time. In human motor control the principle has not been addressed.

If the principle of superposition is valid for human prehension, we should expect the existence of two (or more) null spaces: the elemental variables are included in different null subspaces such that the variables from one subspace compensate for each other’s effects on the corresponding performance variable but not for the variables from another subspace. For instance, it is well established that the normal forces exerted on the object are coordinated to prevent the slipping of the object from the hand (reviewed in Johansson 1996). The normal forces of the thumb and the virtual finger change in synchrony (Santello and Soechting 2000); they are modulated by the weight of the object (Hager-Ross et al. 1996), gravity changes during parabolic flights (Hermsdorfer et al. 1999), abrupt vertical load perturbations (Eliasson et al. 1995), tangential pulling forces (Burstedt et al. 1999), friction conditions (Edin et al. 1992; Cole and Johansson 1993), and dynamic forces acting during fast movements (Flanagan and Wing 1997; Weeks et al. 2002). A question arises whether changes in the normal forces (’grip control’ intended to prevent the slipping) correlate with changes in the moment that these forces produce (’torque control’). If they do not correlate, we deal with two null spaces representing the grip and torque control, respectively. Such a finding would support the principle of superposition.

Both theoretical analyses (Cutkosky and Howe 1990; Mackenzie and Iberall 1994; Iberall 1997; Yoshikawa 1999) and experimental evidence (Santello and Soechting 1997; Baud-Bovy and Soechting 2001, 2002; Zatsiorsky et al. 2003a) suggest that prehension is controlled in a hierarchical fashion. The hierarchical approach is based on the idea of a virtual finger (VF), which is an imaginable finger that generates the same mechanical effect as a set of actual fingers (AF). At a higher level of control (the VF level), the forces exerted by the thumb and the VF are coordinated. At a lower level (the AF level) the individual finger forces are determined.

This study explores the trial-to-trial (intra-subject) variability of finger forces in a planar static task at the two hypothesized levels of the control hierarchy. Two main topics are addressed: (a) trial-to-trial variability—its magnitude, dependence on the task and similarity/dissimilarity between subjects, and (b) the correlation, or in other words compensation, among the experimental variables. We are specifically interested in whether the observed correlations are completely determined by the task mechanics or whether they represent a subject’s preference to perform the task in a given manner. Due to the novelty of the problem we did not formulate formal hypotheses to test; this is an exploratory study. Still, we expected to find that (a) the variability of the elemental variables is larger than the variability of the main performance variables (and, hence, the UCM hypothesis is, in principle, correct), (b) not all correlations are necessitated by the mechanics of the task—some of them represent subject’s preferences, and (c) there is more than one null space in prehension tasks, meaning that the principle of superposition is valid for human prehension. We expected to find positive correlations among individual finger forces (the reasons for this anticipation will be explained later in the text; also see Rearick and Santello 2002; Rearick et al. 2003). Contrary to the expectations, the correlations were either close to zero or negative.

Materials and methods

To explore the problems formulated above it was essential to find a task that was sufficiently complex to manifest a variety of correlations among the experimental variables but was also simple enough such that the basic task mechanics could be described with uncomplicated equations. We chose a planar static task with a prismatic grip involving three fingers located symmetrically with respect to the thumb.

Equipment

Four six-component transducers (Nano-17, ATI Industrial Automation, Garner, NC, USA) were attached to an aluminum handle to which an aluminum beam (5.0×85.0×0.6 cm) was affixed, Fig. 1. The center of mass of the unloaded handle was determined by suspending the handle at different points. A load was attached to the beam with an eyehook that could be moved horizontally along a slot in the beam. Sliding the weight along the beam produced different torques on the handle system. A level was positioned at each end of the beam so that subjects could monitor and avoid rotation of the handle and beam. Each end of the beam was positioned inside a narrow slot of a vertical rack (Fig. 1) so that the handle and beam would not rotate about a vertical axis.

Fig. 1.

Experimental ‘inverted-T’ handle/beam apparatus and subject position during the experiment. The force components in the X and Y directions are called normal and tangential forces, respectively. The black rectangles represent the sensors. Subjects maintained the handle statically in the upright position using minimal forces. The figure is not drawn to scale

The index and ring finger sensors were positioned 30 mm above and below the middle finger sensor, respectively. The thumb sensor was placed at the same level as that for the middle finger. The grip width, which is the shortest distance between the contact surfaces of thumb and middle finger sensors, was 68 mm. To increase the friction between contacting digits and transducers, 100-grit sandpaper was placed on the contact surface of each transducer. The finger pad-sandpaper static friction coefficient was approximately 1.4–1.5 (previously measured; Zatsiorsky et al. 2002a).

A total of 24 analog signals from the sensors (4 sensors × 6 components) were routed to a 12-bit analog-digital converter (PCI-6031, National Instrument, Austin, TX, USA) and processed in a microcomputer (Gateway AMD800, North Sioux City, SD, USA).

Subjects

Six right-handed males served as subjects (age: 27.3±3.2 years, weight: 70.9±2.7 kg, height: 177.8±5.3 cm, hand length: 20.2±2.9 cm, hand width: 9.3±1.1 cm). The hand length was measured between the middle fingertip and the distal crease of the wrist with the hand extended. The subjects had no previous history of neuropathy or trauma to the upper limbs. All subjects gave informed consent according to the procedures approved by the Office for Research Protections of The Pennsylvania State University.

Experimental Procedure

Subjects washed their hands with soap and warm water to normalize the skin condition. The subjects were given a familiarization session to the experimental procedure and devices to ensure that they were able to accomplish the experimental tasks.

The subjects sat on a chair and positioned their right upper arm on a wrist-forearm brace that was fixed to a table. The forearm was held stationary with Velcro straps and the wrist in the brace was locked in its flexion, extension, and abduction. The upper arm was abducted approximately 45° in the frontal plane and flexed 45° in the sagittal plane. The forearm was aligned parallel to the sagittal axis of the subject. When the subjects held the handle, the angle of the beam attached to the bottom of the handle with the frontal plane was approximately 45°. The horizontal location of the center of mass of the handle without the load was measured and the top of the handle above the center of mass was connected to the rack using a cotton thread. The handle was suspended approximately 5 cm below a natural holding position. During the trials, the subjects grasped the handle and lifted it to a natural holding position. The subjects released the handle after each trial.

A load of 0.5 kg was suspended from the beam at five different positions that generated five different external torques (−1.0, −0.5, 0.0, +0.5, and +1.0 Nm) in both clockwise (CW, negative torques) and counterclockwise (CCW, positive torques) from the subject’s perspective. The total weight of the handle, beam, transducers, and suspended load was 14.9 N. During testing, subjects were instructed to hold the handle with minimal force exertion. Hyperextended joint configurations were not allowed for any phalangeal joints of the hand. The task was constructed and instructions were given in attempts to achieve a stable trial-to-trial performance: the forearm, wrist, and hand positions were fixed and the instructions to the subjects were to grasp the handle in the same way by placing the fingertip centers at the centers of the sensors and to always apply a minimal effort.

Twenty-five trials were performed for each load condition for a total of 125 trials for each subject. Signals from all 24 channels were zeroed before each trial. When the subjects reported that they were holding the handle comfortably, data recording started. The data collection was performed at a sampling frequency of 50 s⁻¹ for 3 s. A minimum 20-s rest interval was given to the subjects between trials, and between torque conditions a rest interval of 10 min was given in order to avoid fatigue effects. The order of torque conditions was randomized and balanced.

Data analysis

The recorded force data were averaged over 3-s periods. Positions of the points of digit force application along axis Y with respect to the sensor center were solved as y = −M_Z = F_X where M_Z is the moment of force about axis Z and F_X is the normal force component.

Model

The model employed in this study was similar to that used previously (Zatsiorsky et al. 2003a). The only difference between the models was that the number of digits changed from five to four. This was done to make both the task and the analysis simpler.

Consider a hand-held object grasped by a prismatic precision grip in which the tips of the fingers and the thumb oppose each other, as seen in Fig. 2. We limit the consideration to planar static tasks. We assume that friction at the digit-object interface is sufficiently large to prevent the object from slipping for all exerted digit forces.

Fig. 2.

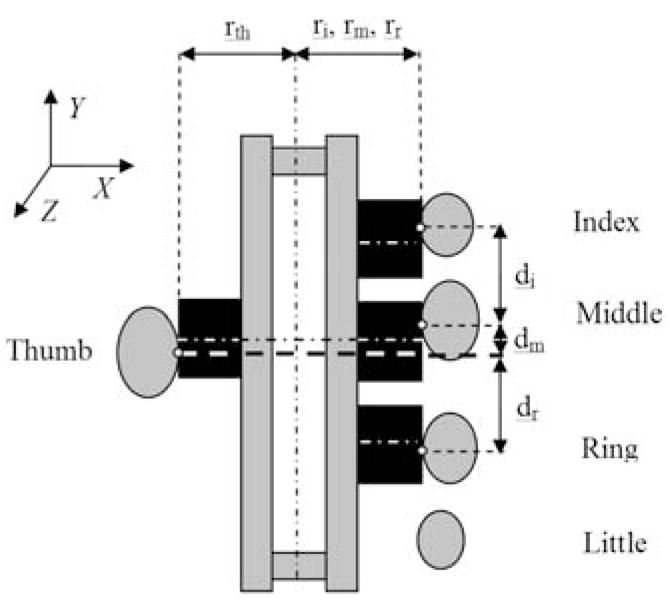
Prismatic precision grip. r_th, r_i, r_m, and r_r are the moment arms of thumb, index, middle, and ring tangential forces, respectively (|r_th|=|r_i|=|r_m|=|r_r|). d_i, d_m, and d_r are the moment arms of index, middle, and ring normal forces, respectively. The latter moment arms are partially dependent on the position of the point of application of the thumb normal force along axis Y

For the system to be at rest, the sum of all forces and the sum of all moments acting on the handle should be equal to zero. Hence, the following three requirements should be satisfied:

1. The sum of the normal forces of the three fingers equals the normal force of the thumb

   $$F_{th}^n=F_i^n+F_m^n+F_r^n=\sum _{f=1}^3{F}_f^n$$ (1)

2. The sum of the digit tangential forces equals the weight (L) of the hand-held object

   $$L=F_{th}^t+F_i^t+F_m^t+F_r^t$$ (2)

3. The total moment produced by the digit forces M is equal and opposite to the external torque exerted on the objects. It equals

   $$\begin{array}{l}M=\underset{\text{Moment}\text{of}\text{the}\text{normal}\text{forces}\equiv M^n}{\underbrace{F_{th}^n{d}_{th}+F_i^n{d}_i+F_m^n{d}_m+F_r^n{d}_r}}\\ +\underset{\text{Moment}\text{of}\text{the}\text{tangential}\text{forces}\equiv M^t}{\underbrace{F_{th}^t{r}_{th}+F_i^t{r}_i+F_m^t{r}_m+F_r^t{r}_r}}\end{array}$$ (3)

where the subscripts th, i, m, and r refer to the thumb, index, middle, and ring finger, respectively; the superscripts n and t stand for the normal and tangential force components, respectively; and coefficients d and r stand for the moment arms of the normal and tangential force with respect to a pre-selected center, respectively.

The moment of the normal finger forces Mⁿ about the point of force application of the thumb (selected as a pivot) is

$$M^n=\sum F_f^n{d}_f=F_v^{n}D$$ (4)

where the subscript f designates individual fingers (the index, middle, or ring), $F_v^n$ is the normal virtual force (the resultant normal force exerted by the three fingers) and D is the moment arm of the resultant force with respect to the pivot point. The location of D may vary due to changes in the sharing percentage of $F_v^n$ among the fingers and/or due to the displacement of the points of finger force application with respect to the sensor centers. Note that the index and ring fingers work as positive and negative moment producers, respectively, while the direction of the moment produced by the middle finger normal force $F_m^n$ depends on its relative position with respect to the force application point of thumb.

The moment of the tangential forces M^t is proportional to the difference between the total tangential force of the three fingers combined (the tangential virtual force) and the tangential force of the thumb. Hence, the following equation is also valid

$$M^t=(\sum _{f=1}^3{F}_f^t-F_{th}^t)r$$ (5)

Equations 1–3 impose three constraints on the 12 variables (four normal and four tangential finger force components and four coordinates of the points of force application in the vertical direction). Therefore, there are nine degrees of freedom (DoF) that can be manipulated by the performer in different ways. There are also two inequality constraints: (1) the fingers can only push but not pull on the sensors and (2) the sum of the normal finger forces should be sufficiently large to prevent slip. These constraints, however, do not change the number of DoF.

Virtual forces and moments

The virtual finger (VF) is an abstract representation of all three fingers that act as a functional unit to produce a force and a moment with respect to the thumb. The VF tangential force and VF normal force were computed as the sums of the tangential and normal forces of the three fingers, respectively. The moment of the tangential forces was computed from Eq. 5. The moment of the normal forces was computed with respect to the point of application of the thumb force (see Eq. 4). The moment arm of the normal VF was computed from the Varignon theorem

$$D=\frac{\sum F_f^n{d}_f}{\sum F_f^n}$$ (6)

where $F_f^n$ is the normal force of finger f (f = 1, 2, 3) and df is the moment arm of the finger force with respect to the point of application of the thumb force (a projected distance from the point of application of a finger force to the point of application of the thumb force).

Accuracy of measurements

The error propagation and uncertainty of indirect measurements were estimated from the data reported by the producer for individual sensors. The propagation of uncertainty in the elemental errors u_i to the uncertainty of the result u_R was computed as (Taylor 1997; Figliola and Beasley 2000):

$$u_R=\pm \sqrt{\sum _{i=1}^n{\left(\frac{\partial R}{\partial x_i}{u}_i\right)}^2}$$ (7)

where the partial derivatives of the result variable R with respect to an elemental variable x_i characterize the sensitivity of R to changes in x_i, and n is the number of elemental variables involved in a given calculation. The uncertainty estimates are presented in Table 1. The moment arms of normal forces and the moments of normal forces are computed with respect to the point of application of the thumb force.

Table 1.

Uncertainty of the measurements (standard deviations of the errors)

	Thumb	Index	Middle	Ring	Virtual
Tangential force, N	0.0370	0.0132	0.0166	0.0142	0.0255
Normal force, N	0.0538	0.0219	0.0195	0.0211	0.0362
Point of force application, cm	0.0044	0.0043	0.0035	0.0042	–
Moment arm of normal force, cm	0.0073	0.0082	0.0079	0.0085	0.0814
Moment of normal force, Ncm	0.1259	0.0448	0.0637	0.0590	0.0977
Moment of tangential force, Ncm	0.0865	0.0476	0.0622	0.0756	0.1088

The uncertainty of measurement of the normal and tangential forces (the elemental variables) has been computed from the calibration protocols provided by the manufacturer. Then, Eq. 6 was used to compute the propagation of the uncertainty to the computed points of force application, moment arms of normal force, and the moment of normal and tangential forces.

Oscillation of the handle (tremor) was not recorded in this experiment. However, the forearm, wrist, and the proximal half of the hand were supported to reduce hand shaking. In addition, averaging the data over a 3-s period would reduce oscillatory effects.

Statistics

To determine whether the trial-to-trial variability was affected by the factors: TASK (5 levels) and SUBJECTS (6 levels), Levene’s homogeneity test was performed on 15 variables (four normal forces, four tangential forces, four displacements of the digit force application, virtual normal and tangential forces, and point of application of the virtual normal force). Two-factor MANOVAs were then performed using the TASK and SUBJECTS as factors. Two separate MANOVAs were carried out, on the VF variables and on the AF forces. The two-factor ANOVAs (in total 15) were then performed on each of the outcome variables mentioned above.

Pearson coefficients of correlation were computed where necessary and then corrected for noise. The uncertainty affects the values of coefficients of correlation: when the error increases, the values of the coefficients decrease. A general relation between the coefficients of correlation computed for the variables measured with and without noise is

$$\frac{r_x}{r_{x+n}}=\sqrt{\left(1+\frac{{\sigma }_{n1}^2}{{\sigma }_{x1}^2}\right)\left(1+\frac{{\sigma }_{n2}^2}{{\sigma }_{x2}^2}\right)}$$ (8)

where r_x is a coefficient of correlation between the variables x₁ and x₂ measured without errors (a ‘true’ coefficient), r_x+n is the coefficient of correlation between these variables when they are measured with errors (noise), σ_n1and σ_n2 are the standard deviations of the errors (noise) of the first and second variables, respectively, and σ_x1and σ_x2 are the standard deviations of the first and second variables measured without errors.

The true coefficients of correlations (with the effects of error eliminated) were computed from Eq. 8 using the data presented in Table 1. For the computation, the true values of the standard deviations σ_x1 and σ_x2 were estimated from the relation ${\sigma }_x^2={\sigma }_{x+n}^2-{\sigma }_n^2$. At n=25, the critical values of significance for the empirical coefficients of correlation equal 0.396 for P=0.05 and 0.505 for P=0.01. To average the coefficients of correlation they were first z-transformed.

Results

All subjects were able to maintain a stable handle position without visible oscillations. Nevertheless, the recorded finger forces values varied among the trials. Levene’s homogeneity test showed that the trial-to-trial variability of all the 15 investigated variables was affected by the task (P<0.001). The variability was also different in various subjects (P<0.001). While the observed non-homogeneity makes the MANOVA and ANOVA application questionable, we took the liberty to perform these analyses and found that the average data for task-subject combinations were influenced by both TASK and SUBJECTS. If non-homogeneity was neglected, the results would be highly significant (P<0.001) for all tested variables. In general, we may conclude that people do not perform the same static task in an identical way: the magnitude of the trial-to-trial variability in finger force parameters is substantial and hence the task stability is achieved by the compensated changes of the controlled variables (i.e., finger forces and the points of their application).

The experimental data are presented below in downward sequence: from a higher level of the control hierarchy to the actual finger forces.

The VF level

At this level of analysis, only the thumb and the VF forces, as well as the moments generated by them, are considered.

Variability

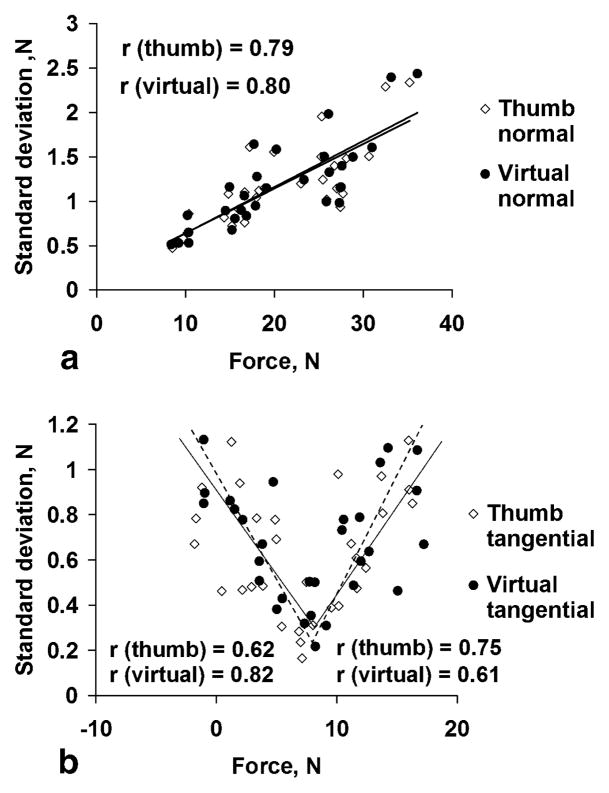
The trial-to-trial variability of the normal forces increased with force magnitude (Fig. 3a). For the tangential forces, V-like relations were observed: the variability increased both at the large and small forces (Fig. 3b). At the lower force magnitudes, the standard deviations were larger than the average force, indicating that both positive (upward) and negative (downward) forces were produced.

Fig. 3.

a, b Variability of the thumb and virtual forces versus the force magnitude. The data for individual subjects are pooled. a Normal forces. b Tangential forces. The coefficients of correlation are determined separately for the left and right branches of the curves for b

Inter-relations among the forces

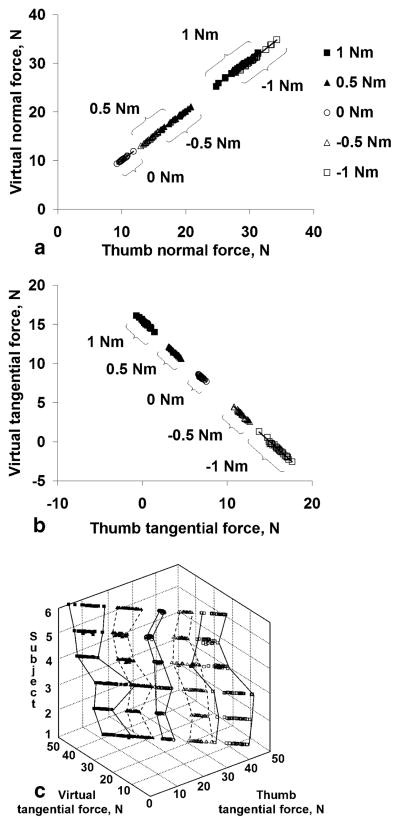
The relations between the virtual finger forces are presented in Fig. 4. As follows from Fig. 4a, in each trial the virtual normal force equals the normal force of the thumb. This finding was expected from Eq. 1. Note that from a purely mechanical standpoint the normal forces can vary broadly provided that the forces are sufficiently large to prevent the object from slipping.

Fig. 4.

a–c Relationships among forces at the VF level. a Normal forces of the virtual finger and the thumb for a representative subject. The data for both the clockwise and counterclockwise torques are shown. All coefficients of correlation were 1.00. b Tangential forces of the thumb versus tangential forces of the virtual finger for the same subject. The coefficients of correlation ranged from −0.95 to −1.00, while all error-corrected coefficients of correlation were −1.00. c Tangential forces of the thumb versus tangential forces of the virtual finger for all six subjects. Note the differences among the subjects in the location and the width of the clusters

Perfect negative correlation between the tangential forces (Fig. 4b) is a direct consequence of the constraints imposed by Eq. 2: to maintain equilibrium in the vertical direction, the sum of the virtual tangential force and the thumb tangential forces must be equal to the supported load and, consequently, their values should be positioned on a straight line. Along the line, the data for different tasks are organized in separate clusters. The evident differences among the subjects in the position of the clusters (average values) and their width (variability) were seen in Fig. 4c. These differences should be expected from the results of the statistical analyses described previously (MANOVA/ANOVA and Levene’s test). The data support a hypothesis that the variability of the elemental variables is larger than the variability of the main performance variables: tangential forces of the VF and thumb vary substantially among the trials while their sum remains constant.

Moments of the virtual forces

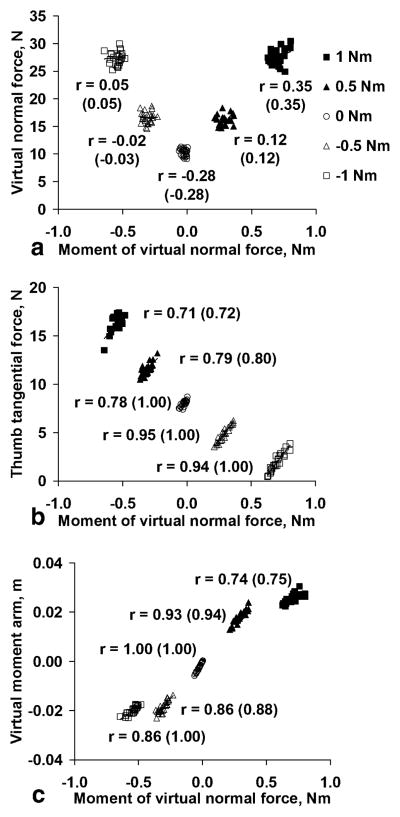
The moments of the normal forces Mⁿ did not correlate with the force magnitude but they did highly correlate with both the tangential forces and the moment arm of the virtual normal force D (Fig. 5). Without the principle of superposition hypothesis, the lack of correlation of Mⁿ with the normal force would be surprising because the Mⁿ is simply a product of the normal force and its moment arm. We conclude that the trial-to-trial changes of the virtual normal force are not associated with trial-to-trial changes of the moment that this force produces. To fine-tune a moment production in a set of trials, people do not vary the magnitude of the total normal force, rather they re-distribute the force among the fingers and possibly displace the points of finger force application.

Fig. 5.

a–c Relationships between the moments of the virtual normal force Mⁿ and (a) the virtual normal force, (b) the thumb tangential force, and (c) the moment arm of the virtual normal force D for a representative subject. Corrected coefficients of correlation are shown in parentheses

A significant correlation between the thumb tangential force $F_{th}^t$ and the point of application of the resultant normal force D w as found in all tasks in four subjects of six (Fig. 6). In subject 4, two coefficients were not significant at the torques of −1.0 and −0.5 Nm, while the coefficients at 0, +0.5, and +1.0 Nm were significant (r = 0.72, 0.85, and 0.85, respectively). In subject 5, the coefficients were not significant at −1.0 and 0 Nm while the coefficients at −0.5, +0.5, and +1.0 Nm were significant (r = 0.57, 0.85, and 0.71, respectively).

Fig. 6.

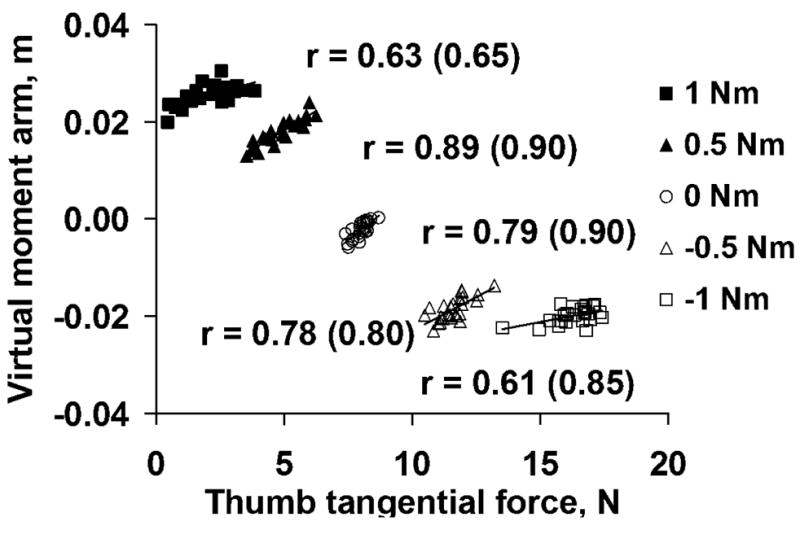
Relationships between the tangential force of the thumb $F_{th}^t$ and the moment arm of the normal virtual force D for a representative subject. Corrected coefficients of correlation are shown in parentheses

The moments of the tangential forces M^t completely depended on the magnitude of the thumb and VF tangential force (with coefficients of correlation close to 1.0), as was expected from Eqs. 5 and 3.

The AF level

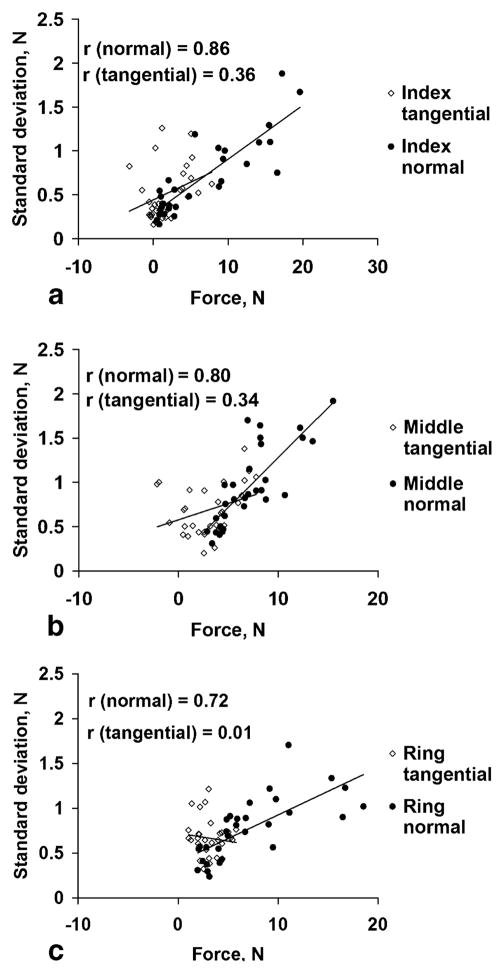
The variability of the normal forces increased with the force magnitude while the variability of the tangential forces either did not depend on the force magnitude (the ring finger) or depended only slightly, Fig. 7.

Fig. 7.

a–c Variability of the normal and tangential finger forces versus the force magnitude of (a) index finger, (b) middle finger, and (c) ring finger for all six subjects

Correlation with the Mⁿ

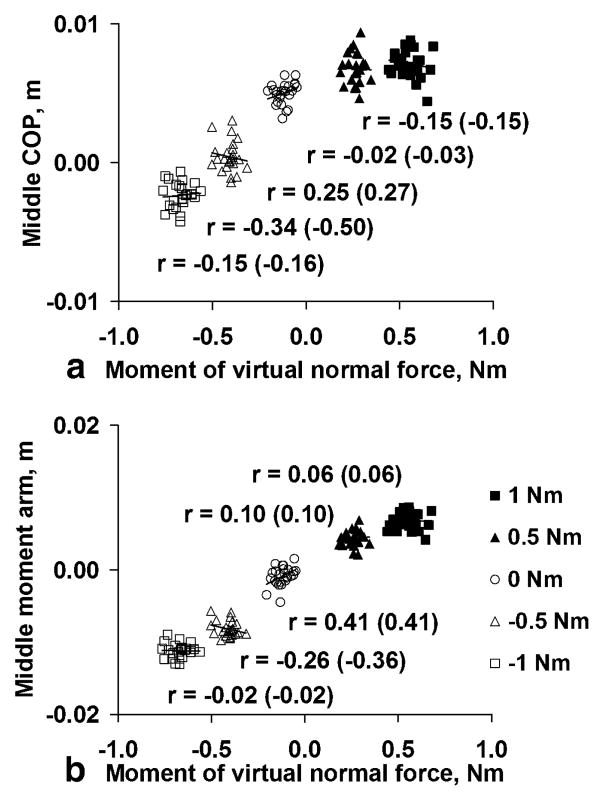
In individual tasks, there was no correlation—as a rule—between the displacements of the points of finger force application from the center of the sensors and Mⁿ (Fig. 8a). The same was valid for the moment arms, i.e., the projected distance between the point of force application of the thumb and the point of force application of a finger (Fig. 8b). However, among the tasks differences in both the position of the point of force application and the finger moment arms were evident.

Fig. 8.

a Points of finger force applications with respect to the sensor center (CoP center of pressure). b The moment arms of the finger normal force versus the moment of the virtual normal force. The moment arms are computed as a projected distance between the points of force application of the thumb and a finger. A representative subject. Middle finger. Corrected coefficients of correlation are shown in parentheses

Interrelations among the individual finger forces

The coefficients of correlation among the individual finger forces are presented in Table 2. Note the negative correlations between the tangential forces and the low, mainly negative, correlation between the normal forces of the index and ring fingers in all tasks.

Table 2.

Coefficients of correlations among the finger forces

External torque		1.0 Nm	0.5 Nm	0.0 Nm	−0.5 Nm	−1.0 Nm
Tangential force, N	IM	−0.68 (−0.85, −0.45)	−0.52 (−0.75, −0.28)	−0.50 (−0.79, −0.29)	−0.27 (−0.72, 0.19)	−0.13 (−0.30, 0.27)
	MR	−0.31 (−0.69, 0.05)	−0.29 (−0.67, 0.22)	−0.31 (−0.73, 0.47)	−0.63 (−0.90, −0.10)	−0.35 (−0.65, 0.08)
	RI	−0.12 (−0.43, 0.13)	−0.26 (−0.72, 0.12)	−0.29 (−0.73, 0.11)	−0.61 (−0.92, −0.04)	−0.23 (−0.57, 0.15)
Normal force, N	IM	−0.11 (−0.78, 0.36)	−0.21 (−0.60, 0.04)	−0.16 (−0.60, 0.57)	0.11 (−0.28, 0.55)	0.04 (−0.33, 0.15)
	MR	0.32 (0.00, 0.54)	0.40 (−0.22, 0.57)	0.14 (−0.22, 0.57)	−0.42 (−0.84, −0.51)	−0.55 (−0.86, −0.33)
	RI	−0.10 (−0.57, 0.24)	−0.13 (−0.45, 0.26)	0.01 (−0.45, 0.26)	−0.06 (−0.56, 0.48)	0.01 (−0.42, 0.40)

Group averages and the minimal-maximal values (in parentheses) are shown. I index finger, M middle finger, R ring finger

Discussion

The discussion addresses the following topics: (a) trial-to-trial variability, (b) the compensation among the variables and the task mechanics, (c) the principle of superposition—one or two null spaces?, (d) the null spaces versus optimization approach, and (e) local versus global fine-tuning on the AF level.

Trial-to-trial variability

In spite of all the efforts to assure consistent performance of the task (such as forearm fixation, hand support, instruction, etc.), the variability of finger forces among the trials was substantial. The accuracy and stability of static force production has been the object of many research efforts (Fullerton and Carttell 1892; Michon 1967; Newell et al. 1984). In the present experiment, where the forces were relatively small, the variability of the normal force of the virtual finger increased with the force magnitude (Fig. 3a), as could be expected from earlier studies (Newell et al. 1984; Slifkin and Newell 1999), while the variability of the tangential force showed a V-shape dependence on the force magnitude (Fig. 3b).

The increase of force variability at low force values is a rather unusual phenomenon that has not been previously reported in the literature. Studies with ramp force production (Latash et al. 2002b; Shinohara et al. 2003) showed no decrease in variability of the normal finger forces at low force levels. The atypical increase in force variability at low forces (Fig. 3b) can be explained by the task mechanics. Because the sum of the thumb and VF tangential forces must be constant (Eq. 2), the VF force in each trial should correspond to the thumb force: the larger one force, the smaller another and vice versa. At large values of the resisted torque, the moment of the tangential forces M^t is also large and, hence, the difference between the tangential forces of the VF and the thumb increases. If the thumb force increases, its trial-to-trial variability is expected to increase as well. Trial-to-trial variations in the thumb tangential force have to be matched by trial-to-trial co-variations of the VF tangential force. In other words, force variabilities of both the thumb and VF are expected to be similar although the force exerted by the latter is low. As a result, in some prehension tasks, the positive relation between the force magnitude and its variability can break down.

Compensation among the variables and the task mechanics

If people cannot precisely control individual finger forces (see Fig. 3a, b), how do they manage to precisely control prehension tasks that involve several digits? As follows from Fig. 4, they achieve this by fine adjustments of forces across digits. In spite of the evident variability of individual forces and their points of application, the performance was highly reproducible. These observations are similar to those reported in studies of multi-finger ramp force production in young subjects, elderly, and persons with Down’s syndrome (Latash et al. 2002b, c; Shinohara et al. 2003). In these studies, variance profiles of the individual finger forces and of the total force were computed across trials. The variances of individual finger forces increased with the total force, while the variance of the total force stayed low and unchanged over much of the force range.

Some of the observed relations are mechanically necessitated; the task cannot be performed in a different way. Other relations represent a choice made by the CNS. In the present research all 12 relevant mechanical variables were recorded. The variables were inter-related by three elementary equations. As a result, we can separate relations that are necessitated by the task mechanics from those that represent solutions preferred by the CNS.

Relations/facts necessitated by the task mechanics

At the VF level the following three relations are determined by the task mechanics (see Figs. 4 and 5b):

1. High positive correlations (approaching r =1.0) between the normal forces of the thumb and the VF (predicted by Eq. 1), see Fig. 4a.

2. High negative correlations (approaching r = −1.0) between the tangential forces of the thumb and the VF (predicted by Eq. 2), see Fig. 4b.

3. The relations between the tangential forces and the moment produced by the normal forces, Fig. 5b. The relation arises from the following chain effects (cf. Zatsiorsky et al. 2003a): (a) Because the sum of the tangential forces of the thumb and VF is constant, one of these forces dictates another (Eq. 2 and Fig. 4b). → (b) The difference between the tangential forces of the thumb and the VF defines the moment generated by them (Eq. 5). → (c) Because the sum of the moments of the normal and tangential forces is constant (Eq. 3), the moment of the normal forces is uniquely defined by the tangential force of the thumb.

The relatively low values of the coefficients of correlation in Fig. 5b can be explained by the uncertainty of the measurements (Table 1). When corrected for uncertainty, the coefficients of correlations increased.

Facts/relations not necessitated by the task mechanics

Three facts attract attention: (a) different locations of the clusters of tangential forces of the thumb and VF along the force-force lines in various tasks (Figure 4b) and in different subjects (Fig. 4c); (b) the lack of correlation between the total normal force and the moment that the force generates (Fig. 5a); and (c) a significant correlation between the thumb tangential force and the point of application of the normal VF force (Fig. 6).

The positions of the individual clusters along the force-force lines, as well as their ‘width’ (i.e., the variability of finger forces), are not prescribed by the task mechanics. Mechanically, tangential forces can be of any value provided that their sum equals the load. The different locations of the clusters along the force-force lines are indicative of the difference between the tangential forces of the thumb and VF, and hence —according to Eq. 5—the moment of the tangential force M^t. Since the sum of M^t and Mⁿ must be constant (Eq. 3), the different cluster location signifies different percentage contributions of M^t and Mⁿ to the total torque production (cf. Zatsiorsky et al. 2002a, 2003a). Data presented in Fig. 4c, as well as the ANOVA results, support the assertion that different subjects have preferred patterns of distribution of the total moment between the tangential and normal forces.

The lack of correlation between the normal force $F_v^n$ and the moment that the force generates (Fig. 5a) suggests that the CNS does not use all mechanically possible options to control the moment of VF normal force Mⁿ; rather, it employs only some of them. Mechanically, the trial-to-trial tuning of the Mⁿ can be achieved by variations of the $F_v^n$ (i.e., by proportional changes of all normal finger forces, see Eq. 4) but the CNS does not use this option. Instead, it mainly controls the moment arm D (see Fig. 5c) by changing the sharing pattern of finger forces (but not by displacing the location of the points of finger force application, Fig. 8). Because (a) the moment of the tangential forces is controlled by the difference in the tangential forces of the thumb and VF (Eq. 5) and (b) the fine tuning of the moment of the normal VF forces is controlled by adjustments of D; correlation between $F_{th}^t$ and D is also observed (Fig. 6). As a result, the sharing pattern of the normal finger forces represented by the parameter D depends on the tangential forces to a much larger extent than on the total normal force.

Null spaces and the principle of superposition

The high interdependence among variables at the VF level of control is evident from Figs. 4 and 5b, c. Due to the static nature of the task, the relationships are very strong (with coefficients of correlation close to ±1.0) and the compensations are transparent in the sense that variations in an elemental variable are nearly perfectly matched by variations in another variable(s) such that a functional performance variable is stabilized. On the whole, the data show that elemental variables are organized in null spaces and thus support the UCM hypothesis. Note, however, that while the normal VF and thumb forces highly correlate with each other (Fig. 4a), their correlation with other variables does not reach the level of statistical significance (see Fig. 5a as an example). In contrast, variables such as the tangential forces of the thumb and VF, as well as the moments of the tangential and the normal forces, highly correlate among themselves (Figs. 4b and 5b). We can conclude that control of prehension can be described by two null spaces that represent two subsets of the experimental variables. The first subset includes normal forces of the thumb and VF. The second subset includes five variables: tangential forces of the thumb and VF, the moments produced by the tangential and normal forces, and the moment arm of the normal force D. The compensated variations within each of the two null spaces are necessitated by the task mechanics. Although relations between the two subsets of variables are mechanically possible, they are not realized. Conjoint variations of the variables of the first subset prevent the object from slipping out of the hand and from movement in the horizontal direction. Conjoint variations among the variables of the second subset maintain the torque magnitude constant and prevent the object from movement in the vertical direction.

The discovery of two null spaces supports the principle of superposition for human prehension (Arimoto and Nguyen 2001; Arimoto et al. 2001). In particular it supports an assertion that the prehension synergy is organized as two sub-synergies realizing correspondingly grasp control (preventing an object from slipping out of the hand) and torque control (maintaining a desired object orientation). It is worth mentioning that an overwhelming majority of the research on grasping dealt only with the first sub-synergy (Burstedt et al. 1997; Cole et al. 1999; Flanagan et al. 1999) while the second one has typically been overlooked.

The obtained data on the existence of the two null spaces in static prehension agree with the principle of superposition but they do not provide a decisive proof. Such proof requires that the torque and load should be independently varied in the experiment. When this manipulation was performed, the obtained results agreed with the principle of superposition (see Zatsiorsky et al. 2002b, Figs. 2 and 4 on p. 53; Zatsiorsky et al. 2003b). In particular, in Zatsiorsky et al. (2003b) study the effects of LOAD and TORQUE factors on the finger forces were highly significant (P<0.001). Conversely, the effects of the interaction LOAD×TORQUE were not significant (P>0.6). The lack of the statistically significant interaction effects signifies the additive action of the LOAD and TORQUE commands.

The observed ‘dissociation’ between the grasp control (preventing an object from slipping out of the hand) and the torque control (maintaining a desired object orientation) in static tasks may be a part of a broader picture. As an example, Flanagan and Wing (1995), who studied the coordination of grip force and load during brisk cyclic arm movements, found dissociation between the gain of the relation between grip force and load and the grip force offset. Increases in frequency lead to an increase in the offset but a decrease in gain. The authors concluded that these two parameters are under independent high-level control. Nowak et al. (2001) observed changes in the magnitude of the grip force under digital anesthesia without changes in the pattern of anticipatory changes in the digit forces associated with vertical movement of a hand-held object.

The purpose of our exploratory study was to document and analyze correlations among behavioral variables. Hence the concepts of ‘null spaces’ and ‘uncontrolled manifolds’ have been used to describe the findings, while their possible relations to neurophysiological structures are beyond the scope of the study. Currently, there is no clear evidence that would relate the ‘null spaces’ to particular supraspinal or spinal structures. Also, the role of sensory feedback loops in the observed phenomena is unknown: Studies of steady-state performance allow ample time for the action of feedback loops based on proprioceptive signals.

Null spaces vs. optimization

The data on the null spaces provoke a question on the applicability of numerous optimization models that have been used to solve the problem of motor redundancy (Nelson 1983; Hogan 1984; Uno et al. 1989; Prilutsky and Zatsiorsky 2002). It is evident that the CNS does not use the same solutions for the same task. In spite of all the efforts to perform the task in the same way, the variability of the performance variables was substantial. Hence, if the CNS uses some kind of optimization to solve the motor redundancy problem, i.e., to find a better solution among the myriad existing solutions, in multi-finger prehension (as can be concluded from Zatsiorsky et al. 2002b), the optimization does not specify the solution precisely. It identifies only a fitting subspace of solutions (a UCM), while other mechanisms are responsible for the fine motor adjustment of the motor variables to the task requirements. This idea is very close to one expressed recently by Todorov and Jordan (2002) in their theory of optimal feedback control.

The AF level

In general, the large differences in the behavior of the virtual and actual forces support the hypothesis on the hierarchical control of prehension (Mackenzie and Iberall 1994; Iberall 1997; Baud-Bovy and Soechting 2001, 2002; Zatsiorsky et al. 2003a).

As previously mentioned, we expected to find positive correlations between pairs of finger forces. In particular, we expected that the index and ring finger that are positioned symmetrically with respect to the thumb would show positive co-variation of the moments they generate with respect to the point of thumb contact: if in a given trial one finger generates a moment higher than average, the second finger is expected to compensate for that by exerting a larger moment in the opposite direction. Therefore, we expected a positive correlation between the normal forces of these two fingers. The expectation was also based on the reported data (Santello and Soechting 2000) obtained in continuous trials of long duration where significant positive correlations between the normal finger forces were observed (in these experiments the external torque was either zero or very small). Contrary to the expectations, the paired trial-to-trial correlations among the forces were mainly negative and small.

We also expected to find positive correlations between the tangential finger forces. An idea was that the tangential forces arise from the passive resistance provided by the finger structures (TC Pataky, ML Latash, VM Zatsiorsky, Tangential load sharing among fingers during prehension, submitted for publication). In such a case, the resistance (force) depends only on the elastic properties (stiffness) of the fingers in the shear direction and on the magnitude of the total load supported by all three fingers: the load is distributed proportionally to the stiffness as in passive statically indeterminate structures (Rumann 1991). The discovered negative correlations suggest that the tangential finger forces were actively controlled.

The reported low correlations among individual finger forces do not mean that the forces were completely independent from each other. For non-correlated random variables the sum of the variances should be equal to the variance of the sum (the Bienaimé Equality theorem). In the present experiment, the sum of the variances of the individual finger forces was in most cases larger than the variance of the total force (cf. Li et al. 1998; Latash et al. 2002c; Shinohara et al. 2003); this finding indicates a predominantly negative correlation (compensation) among the finger forces. This pattern was observed in 23 cases of 30 for the normal forces and in 29 cases of 30 for the tangential forces. Such a tendency suggests that the CNS prefers a global solution: a deviation of one finger force from the average is compensated by changes of normal and tangential forces of all the fingers. This conclusion agrees with previously reported findings (Zatsiorsky et al. 2003a) that were obtained in experiments in which the object geometry was varied: changes in one variable were associated with the conjoint adjustments in many variables. It is also in a good correspondence with a conclusion made by Bernstein (1967) about half a century ago that a synergy never reacts to a small local change with another small local change, but with changes in all its elemental variables.

The current study is only an initial step towards a comprehensive analysis of prehension synergies. It has a number of limitations. In particular, only a limited subgroup of prehensile tasks was studied, the subjects were not allowed to select different positions of the digits, and they were asked “to apply minimal effort”. It remains to be seen whether the conclusions reached in this study generalize to other prehensile tasks and to control strategies that are less constrained by instruction.