Age-related changes in multifinger synergies in accurate moment of force production tasks

Abstract

The purpose of this investigation was to document and quantify age-related differences in the coordination of fingers during a task that required production of an accurate time profile of the total moment of force by the four fingers of a hand. We hypothesized that elderly subjects would show a decreased ability to stabilize a time profile of the total moment of force, leading to larger indexes of moment variability compared with young subjects. The subjects followed a trapezoidal template on a computer screen by producing a time profile of the total moment of force while pressing down on force sensors with the four fingers of the right (dominant) hand. To quantify synergies, we used the framework of the uncontrolled manifold hypothesis. The elderly subjects produced larger total force, larger variance of both total force and total moment of force, and larger involvement of fingers that produced moment of force against the required moment direction (antagonist moment). This was particularly prominent during supination efforts. Young subjects showed covariation of commands to fingers across trials that stabilized the moment of total force (moment-stabilizing synergy), while elderly subjects failed to do so. Both subject groups showed similar indexes of covariation of commands to the fingers that stabilized the time profile of the total force. The lack of moment-stabilizing synergies may be causally related to the documented impairment of hand function with age.

Aging is accompanied by well-documented changes in manual dexterity and strength that can have a negative effect on the activities of daily living (2, 13, 18, 21, 22, 35). This decline in hand function has been attributed to both peripheral changes, such as a drop in the number of motor units, an increase in their average size, and general slowing down of their contractile properties (5, 10, reviewed in Ref. 25) and changes at the level of central commands to the motoneuronal pool (8, 9, 42).

Earlier studies have revealed age-related differences in indexes of finger interaction during multifinger force production tasks. On average, elderly individuals produce lower maximal voluntary contraction (MVC) force and show changed indexes of finger interaction (42, 43). These findings have been interpreted as evidence for a neural origin of age-related changes in finger coordination (42, 43).

Most studies of finger coordination have focused on force production during pressing (43, 44) and grasping tasks (6 – 8). Much less attention has been paid to the ability to produce an accurate rotational hand action, which is essential for many daily activities, such as drinking from a glass, writing with an implement, or using a hand-held tool (reviewed in Refs. 28, 51). A number of studies investigated rotational actions but with the focus on grip force production by the thumb and index finger during a pinch grip (20, 23). The main purpose of the present study has been to document and quantify changes in indexes of finger interaction during tasks that required the production of an accurate time profile of the moment of force (rotational action) by the four fingers of the hand.

The pressing task used in the present study may be viewed as reflecting control processes at one of the two hypothetical levels involved in hand action (1, 32). The two levels are as follows: 1) distributing the task between the thumb and the “virtual finger” (VF; an imagined finger whose mechanical action is equivalent to the combined action of a set of actual fingers); and 2) distributing the action of the VF among the actual fingers. A series of earlier studies of prehensile tasks with a rotational component have addressed synergies at the thumb-VF level (39, 40, 49; reviewed in Ref. 51), including one study of elderly individuals (41). The latter study has demonstrated deficits in synergies involved in the rotational hand action at the thumb-VF level. Our present study addresses multifinger synergies involved in stabilizing the rotational action of the VF at the lower level of the hierarchy that does not involve the thumb.

To quantify multifinger synergies, we used the framework of the uncontrolled manifold (UCM) hypothesis (37). The UCM hypothesis assumes that the controller acts in the space of elemental variables and limits variability of these variables across trials to a subspace corresponding to a desired value of an important performance variable. The hypothesis allows multidigit synergies involved in both pressing and rotational finger action to be quantified (26, 27, 36).

Based on an earlier study (53), we hypothesized that young subjects would show high indexes of stabilization of the moment of force, while elderly subjects were expected to show a decreased ability to stabilize the rotational multifinger action. We also hypothesized that elderly subjects would produce relatively larger forces by fingers that generate moments of force directed against the required moment direction (cf. Ref. 41). Such a strategy may be viewed as adaptive, that is, less economical but assuring higher stability of performance by an increase in the peripheral resistance of the hand to possible rotational perturbations.

A couple of secondary issues were addressed in the study. These include stabilization of the total force produced by the fingers in such tasks. Earlier studies have documented lower indexes of multifinger synergies stabilizing the total force in elderly (42–44), but only in tasks that involved the production of a time profile of the total force. Based on those studies, we expected elderly subjects to show lower indexes of force stabilization in tasks that required the production of a time profile of the moment of force. We also addressed the contribution of the fingers with the longer moment arm (index and little fingers) to the supination (SU) and pronation (PR) moments. The “mechanical advantage hypothesis” proposes that, when multiple effectors act together to produce moment of force, those with the longer moment arms contribute more to the total task (4, 15, 34, 41, 48). Based on this idea, we hypothesized that the moment produced by index and little fingers would exceed 50% of the PR and SU moments, respectively. In addition to that, we also explored possible differences in the ability of the elderly to produce stable rotational actions in PR and in SU.

METHODS

Subjects

Twelve young (26 ± 3 yr old) and twelve elderly (77 ± 4 yr old) subjects volunteered to participate in the study. Both groups consisted of six men and six women. The average height and weight were, respectively, 171.0 ± 9.5 cm and 69.5 ± 16.6 kg for the young subjects, and 167.9 ± 10.2 cm and 72.2 ± 15.5 kg for the elderly subjects. All subjects were healthy and right-handed, according to their preferential hand use during writing and eating. The elderly subjects were recruited from a local retirement community and passed a screening process that involved a cognition test (mini-mental status exam ≥24 points), a depression test (Beck depression inventory ≤20 points), a quantitative sensory test (monofilaments ≤3.22), and a general neurological examination. We purposefully selected for the study elderly subjects who exercised regularly and were in generally good physical shape (self-reported). We also purposefully set the tasks to be easier for the elderly group to avoid possible effects related to fatigue (see later). All subjects gave informed consent according to the procedures approved by the Office for Research Protection of The Pennsylvania State University.

Apparatus

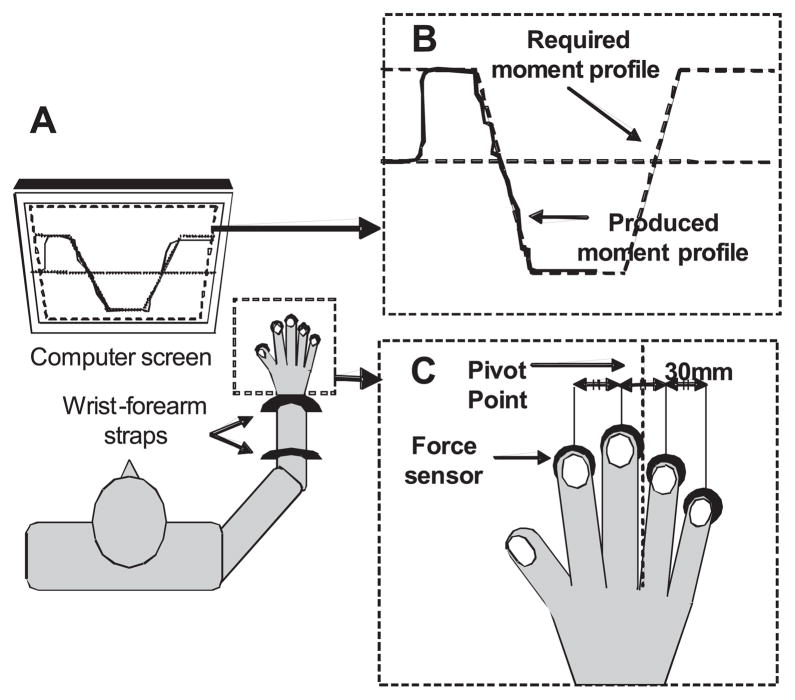
Figure 1 displays the experimental setup. Four piezoelectric sensors (model 208A03, PBC Piezotronics, Depew, NY) amplified by AC/DC conditioners (M482M66, PBC Piezotronics) were used to measure the vertical forces generated by the fingers. Cotton pads were attached to the surface of the sensors to increase friction and prevent possible effects of skin temperature. The sensors were placed in a metal frame sitting in a grove on a wooden board. The sensors were mediolaterally spaced 3.0 cm apart and could be adjusted in the forward-backward direction within 6.0 cm to fit each subject’s hand anatomy. Once the appropriate position of the sensors had been determined, double-sided tape was placed under the bases of the sensors to prevent them from moving from that position.

Fig. 1.

A: schematic illustration of the experimental setup. B: the experimental task shown on the computer screen. C: finger and force sensor configuration.

During the experiment, the subjects sat in a chair facing the testing table with the right shoulder at ~45° of abduction and flexion, and the elbow flexed ~135°. Metacarpophalangeal joints were flexed ~20°, and all interphalangeal joints were slightly flexed such that the hand formed a dome. A wooden piece, shaped to fit comfortably under the subject’s palm, helped maintain a constant configuration of the hand and fingers. The forearm was attached to the board with Velcro straps. A 17-in. computer monitor, located ~65 cm away in front of the subject, displayed the task (a target total moment time profile) and the actual total moment. A LabVIEW-based program was used for data acquisition. For the elderly subjects, the data were collected at 1,000 Hz with a 12-bit resolution; the data were collected at 200 Hz for the young subjects. The difference in the sampling rate is due to the fact that electromyographic signals were collected in the elderly subjects; however, in this paper we do not describe those data.

Experimental Procedure

Before each trial, the subject sat relaxed with the fingers of the right hand resting on the sensors. The computer generated two beeps, and a cursor showing the total force (F_tot) or the total moment of force (M_tot) generated by the task fingers started to move across the screen. The experimental protocol consisted of two tasks: a F_tot production task (from now on referred to as “force task”), and an accurate M_tot production task (“accurate moment task”). The force task had two conditions: maximal force production with instructed finger(s) and single-finger force ramp production. The accurate moment task had only one condition: accurate production of a total moment profile. During all of the tests, the forces produced by all four fingers were collected. In the force task, MVC force of each finger pressing separately (I, index; M, middle; R, ring; L, little) and all four fingers pressing together (IMRL) was first measured. In these trials, subjects were asked to press “as hard as possible” with the instructed finger(s). Subjects were given 3 s to reach peak force. The intervals between the trials were at least 30 s. Two MVC trials were recorded for each of the tasks, and the trial with the highest magnitude of the task force was used to set up other tasks.

The second force task condition involved subjects to produce single-finger force ramps. The subjects were asked to produce a ramp pattern of force from 0 to 25% of each finger’s MVC over 5 s by pressing down with an instructed finger; different fingers were instructed in separate trials. An oblique blue line was shown on the screen, and the participant’s task was to trace this line in time with the cursor representing the force of the instructed finger. These data were used to generate linear estimates of the relations between changes in commands to individual fingers and change in the F_tot during multifinger tasks (the Jacobian; Ref. 36). These relations are nontrivial because of the phenomenon of enslaving (24a, 29, 30, 52). In both of the control sets, subjects were instructed not to pay attention to possible force production by the noninstructed fingers of the hand and not to lift any finger off its sensor at any time.

The accurate moment task required the subjects to follow a trapezoidal template on the screen by producing a time profile of the M_tot computed with respect to a horizontal axis passing between the M and R fingers while pressing with all four fingers (see Fig. 1). Pressing down with the I and M fingers produced a positive PR moment, while pressing down with the R and L fingers produced a negative SU moment. The initiation of each trial was indicated by two beeps generated by the computer, and a line appeared on the screen showing M_tot computed online using the finger force signals:

$${\text{M}}_{\text{tot}}={\text{d}}_{\text{I}}{\text{F}}_{\text{I}}+{\text{d}}_{\text{M}}{\text{F}}_{\text{M}}-{\text{d}}_{\text{R}}{\text{F}}_{\text{R}}-{\text{d}}_{\text{L}}{\text{F}}_{\text{L}}$$ (1)

where subscripts I, M, R, and L stand for the index, middle, ring, and little finger, respectively, and d stands for the lever arms (d_I = d_L = 4.5 cm, d_M = d_R = 1.5 cm). This approximation assumes that the points of force application on the sensor surfaces do not move in the mediolateral direction.

To follow the template, the subjects had first to produce a constant level of PR moment over 3 s, then to change from PR to SU moment over a 3-s interval, maintain the SU moment for 2 s, then change from SU to PR moment over 3-s interval, and maintain the PR moment for 3 s. Each trial lasted 14 s, but only the middle 10 s were used for the data analysis. Maximal levels of PR and SU moments were set at 5% of the maximal moment produced by the I finger for elderly subjects but at 10% of that value for young subjects (computed as 5 and 10% of d_IMVC_I). During pilot tests, we noticed that elderly subjects could have problems with producing SU moments of a large magnitude (see results). This may be related to a relatively small decrease in the I finger force with age compared with the R and L finger forces (42). We selected the two magnitudes for the main task to make the task comparably challenging for the two subject groups. Note that between-group comparisons were performed in units normalized to the magnitude of the task (see the next section). Young subjects performed 25 trials within a series, while elderly subjects performed only 20 trials. This was done to minimize chances of fatigue in elderly subjects. Five practice trials were given before the collection of the data, and trials were repeated during the series if the experimenter or the subject noticed an obvious mistake, for example producing a wrong constant-force level, taking a finger off its sensor, “giving up” in the middle of a trial, etc. On average, less than one trial per series was repeated.

Data Analysis

The data were processed offline using MatLab 7.0, Excel, and SPSS. In the MVC tasks, peak forces were measured when the instructed finger force reached its maximum.

During the experiment, the maximal moment a subject was required to reach was set for elderly subjects as 5% of that subject’s I finger MVC multiplied by its moment arm (d_IMVC_I = 4.5 cm × MVC_I), and at 10% of d_IMVC_I for young subjects. This was done because, during a pilot study, it became apparent that the elderly subjects could have problems with the task set at 10% d_IMVC_I, particularly during SU efforts. For across-subjects comparisons, the force data were normalized by 5 or 10% of MVC_I (for elderly and young subjects, respectively), while the moment data were normalized by 5 or 10% of d_IMVC_I (for elderly and young subjects, respectively). In other words, across-subjects comparisons were done in “task units”.

At each point in time, the following variables were computed for each subject across the trials of the accurate moment task: 1) the average F_tot, its standard error, and variance (V_F); 2) the average M_tot, its standard error, and variance (V_M); 3) the average moment produced by the I finger force (M_I), the average total PR moment (M_PR = M_I + M_M), and their proportion (M_I/M_PR); 4) the average moment of the L finger force (M_L), the average total SU moment (M_SU = M_R + M_L), and their proportion (M_L/M_SU); and 5) the average total agonist and total antagonist moment (M_Ag and M_Ant). M_Ag was defined as the moment produced by fingers that acted in the direction corresponding to the task requirement, while M_Ant was the moment produced by fingers that acted against the required moment direction. When subjects were required to produce PR moment, moments generated by the I and M fingers contributed to M_Ag, while the moments generated by the R and L fingers produced M_Ant. When the subjects had to produce SU moment, I and M fingers produced M_Ant, while R and L fingers produced M_Ag.

Statistics

The data in the text and Figs. 3–8 are presented as means and SE. After the data had been “trimmed” to 10 s, each trial was divided into five time intervals: “prepronation” (PR_pre; 1–1,000 ms); “pronation-supination” (PR-SU; 1,001–4,000 ms); “supination” (SU; 4,001–6,000 ms); “supination-pronation” (SU-PR; 6,001–9,000 ms); and “postpronation” (PR_post; 9,001–10,000 ms) (see Fig. 2).

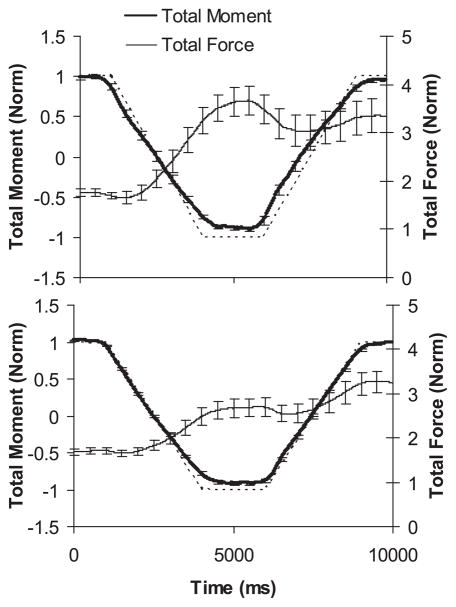
Fig. 3.

Typical performance of an elderly female subject (A) and a young male subject (B) during the moment production task. Thick solid lines represent average total moment of force (M_tot) (left Y-axis) across trials with SE bars; thin solid lines show average total force (F_tot) (right Y-axis) across trials with SE bars; and the dotted line shows the target template.

Fig. 8.

Average profiles of change in variance (ΔV) indexes computed for stabilization of the total force (ΔV_F) and total moment (ΔV_M) at each time sample with SE bars. A–D: ΔV_M of elderly and young subjects and ΔV_F of elderly and young subjects, respectively. Dotted lines show the experimental task. Note that ΔV_M of elderly subjects (A) fluctuates around zero, while ΔV_M of young subjects (B) is consistently positive.

Fig. 2.

The template and the five time intervals. PR, pronation; SU, supination; PR_pre, prepronation; PR_post, postpronation.

For the force task, the effect of age (young vs. elderly) on forces produced by individual fingers (I, M, R, L) and by the four fingers together (IMRL) was analyzed with a two-way ANOVA with repeated measures and one-way ANOVA, respectively.

For the accurate moment task, the effect of age across three steady-state time intervals (PR_pre, SU, PR_post) on the F_tot and M_tot were analyzed with repeated-measures two-way ANOVAs. In a similar fashion, the effects of age across all five time intervals (PR_pre, PR-SU, SU, SU-PR, PR_post) on the V_F and V_M were analyzed with repeated-measures two-way ANOVAs.

To test the hypothesis of a larger M_Ant production by the elderly subjects, we compared the effects of age and torque (PR vs. SU) across time intervals on the magnitude of M_Ant produced. Due to the symmetry of the moment template (see Fig. 1), repeated-measures three-way ANOVAs on two indexes, M_Ant1 and M_Ant2, were used. Each trial was first divided into two 5,000-ms parts (1–5,000 ms and 5,001–10,000 ms), and then each of them was divided into 500-ms intervals. M_Ant1 represented the first half of the trials, with the moment changing from PR to SU, and M_Ant2 described the second half, with the moment changing from SU to PR.

To test the effects of age on the contribution of individual digits to the total PR and SU moments, M_I/M_PR and M_L/M_SU, across two time intervals (PR and SU), two repeated-measures two-way ANOVAs were used. Multiple comparisons with Bonferroni corrections were used as post hocs to analyze significant effects. The level of significance was set at P = 0.05.

UCM Analysis

Further analysis was done using the framework of the UCM hypothesis (37; reviewed in Ref. 27). The description below applies to the analysis of forces, but a similar procedure was used when moments of force were analyzed; the only difference was in the linear equations that link the performance variables to individual finger forces (F_tot = F_I + F_M + F_R + F_L; M_tot = d_IF_I + d_MF_M − d_RF_R − d_LF_L). The UCM hypothesis assumes that the controller organizes covariation among elemental variables to stabilize a certain value of a performance variable (here F_tot or M_tot). Individual finger forces cannot be manipulated independently by the controller because of the phenomenon of enslaving, i.e., unintended force production by fingers when other fingers of the hand produce force (24a, 30). Hence, the first step was to convert the data sets from time series of finger forces to time series of elemental variables, force modes.

Force modes were defined similarly to previous studies (26, 36). Briefly, single-finger force ramp trials were used to compute the enslaving matrix E for each subject. The entries of the E matrix were computed as the ratios of the change in the force of each finger to the change in the F_tot over the ramp duration. The E matrix was used to compute changes in the vector of hypothetical commands to fingers (force modes, m) based on force changes.

Further analysis was done across repetitive trials performed by a subject within the main series at different time slices over the duration of the task. According to the UCM hypothesis, more variance in the m space per dimension is expected within the manifold (UCM), corresponding to a constant value of F_tot (M_tot) than in an orthogonal complement to the UCM. For each subject and for each time, t_i, the average across trials mode vector m_av was computed. Then, for each trial j, deviations (Δm_j) between m_j and m_av were computed. Variance of the Δm_j data set was then computed along a direction orthogonal to the UCM computed for the average value of F_tot (M_tot) observed across trials at that particular time slice. We will refer to this index as V_ort. This was done using the Raleigh fraction:

$${\text{V}}_{\text{ort}}=\frac{{\mathbf{J}}_{\text{m}}cov(\mathbf{m}){\mathbf{J}}_{\text{m}}^{\text{T}}}{{\mathbf{J}}_{\text{m}}{\mathbf{J}}_{\text{m}}^{\text{T}}}=\frac{\mathbf{J}{\mathbf{E}}^{-1\text{T}}{\mathbf{E}}^{-1}cov(\mathbf{f}){\mathbf{E}}^{-1\text{T}}{\mathbf{E}}^{-1}{\mathbf{J}}^{\text{T}}}{\mathbf{J}{\mathbf{E}}^{-1\text{T}}{\mathbf{E}}^{-1}{\mathbf{J}}^{\text{T}}}$$ (2)

where J is the Jacobian matrix relating small changes in modes (J_m) or forces (J) to changes in the F_tot, cov(m) is the covariance matrix in the mode space, cov(f) is the covariance matrix in the finger force space, and T is the sign of transpose. For F_tot, J = [1, 1, 1, 1], while for M_tot, J = [4.5, 1.5, −1.5, −4.5]; J_m = JE^−1T.

The difference between the total amount of variance (V_tot) and V_ort corresponds to variance that does not affect the average value of the performance variable. We will address this variance as V_UCM (variance within the UCM; cf. Ref. 26): V_UCM = V_tot − V_ort. Note that the finger mode space is four-dimensional, V_ort lies along a one-dimensional subspace, while V_UCM is three-dimensional. To compare the amounts of variance per dimension the following index was used:

$$\mathrm{\Delta }\text{V}=\frac{({\text{V}}_{\text{UCM}}/3)-{\text{V}}_{\text{ort}}}{{\text{V}}_{\text{tot}}/4}$$ (3)

where ΔV is the difference in variance. Normalization by the V_tot per dimension (V_tot/4) was used to compare the data across subjects who could show different amounts of the total variance.

Note that positive values of ΔV correspond to proportionally more V_UCM, i.e., they are compatible with a constant value of F_tot (M_tot). Therefore, ΔV > 0 may be interpreted as a multimode synergy stabilizing F_tot (M_tot). If ΔV = 0, this means that the amount of variance per dimension is the same in directions that correspond to a change in F_tot (M_tot) and along directions that keep the variable unchanged. ΔV < 0 may be interpreted as covariation among changes in finger modes contributing to a change in F_tot (M_tot) or destabilizing it. For statistical purposes, the ΔV time profiles computed for F_tot (ΔV_F) and for M_tot (ΔV_M) were averaged over the duration of the test for each subject, and a one-group Student’s t-test was used to define if the ΔV value within each age group was, on average, different from zero. Furthermore, a two-way ANOVA was used to explore possible differences in the time profiles of ΔV indexes with the factor time (5 levels as described earlier).

RESULTS

Force Task

Individual and four-finger forces

In the single-finger force tasks, young subjects produced on average 18% larger forces with individual fingers than the elderly subjects, but this difference was under the level of significance, according to a two-way ANOVA with factors age and finger (factor age: F_1,22 = 1.11, P = 0.3). Statistical differences were, however, found in the performance of individual fingers (factor finger: F_3,66 = 49.41, P < 0.001). The I finger produced on average the largest force, then the M finger, followed by the R and L fingers. The forces produced by the R and L fingers were not different from each other (P = 0.28). In the four-finger task, no differences were found between the two age groups in a one-way ANOVA with factor age (F_1,22 = 1.19, P = 0.29). The results of the single-finger and four-finger force tasks are displayed in Table 1 as averages and SEs.

Table 1.

Single- and four-finger force task results

	Index	Middle	Ring	Little	IMRL
Elderly	41.46±4.60	30.95±2.89	19.93±1.76	19.09±2.08	81.68±9.02
Young	45.95±5.24	34.59±3.66	26.68±3.62	22.07±2.78	97.20±11.0

Values are means ± SE in newtons. IMRL, index, middle, ring, and little fingers together.

Accurate Moment Production Task

F_tot and total M_tot

The task of following the template with the signal corresponding to the M_tot produced with respect to the midpoint between the M and R fingers proved to be quite challenging for the subjects. All subjects were, however, able to produce the required time profile M_tot after the practice trials. Figure 3 shows the patterns of the F_tot and M_tot, averaged across trials for two representative subjects. Subjects of both age groups showed an increase in F_tot during the task, such that they produced more force to maintain the same level of PR moment at the end of the trials than at its start. Young subjects produced overall larger forces during the task than elderly subjects, increasing on average from 8.17 ± 1.07 to 15.80 ± 2.36 N over the trial duration compared with the 3.96 ± 0.76 and 6.96 ± 0.92 N forces in elderly subjects. The average peak target M_tot magnitude for the young subjects was significantly larger than for the elderly subjects (21.15 ± 2.48 vs. 10.36 ± 2.08 N·cm; P < 0.05). These differences were largely due to the differences in setting the magnitude of the peak target M_tot for the two groups. Therefore, the moment of force data were normalized by the magnitude of M_tot, and the force data were normalized by the percentage of the I finger MVC force that was used to set M_tot (see METHODS). From this point onward, we present and analyze normalized data.

Normalized F_tot and M_tot

Figure 4 shows the patterns of F_tot and M_tot averaged across subjects. The average M_tot profile matched the template (dotted lines) closely in both age groups. The similarity in the performance of M_tot of the two groups was confirmed by a two-way ANOVA with factors age and time (the data were averaged over time within the three intervals: PR_pre, SU, PR_post; see Fig. 2) that showed no effects of age (F_1,22 = 0.332, P = 0.57) or age × time interaction (F_1,22 = 3.749, P = 0.07), but significant effect of time (F_2,44 = 27.310, P < 0.001).

Fig. 4.

Average performance of elderly (top) and young (bottom) subjects, with SE bars during the moment production task. Thick solid lines represent average M_tot (left Y-axis), and thin solid lines average F_tot (right Y-axis). Dotted line shows the target template.

Similar to the nonnormalized data (Fig. 3), normalized F_tot nearly doubled over the duration of the task in both subject groups. In elderly subjects, F_tot increased from an average of 1.75 ± 0.25 in the PR_pre phase to 3.55 ± 1.00 in the SU phase, but dropped slightly to 3.34 ± 1.24 in the PR_post phase, while young subjects increased their F_tot gradually throughout the task (1.71 ± 0.23 in PR_pre; 2.65 ± 0.70 in SU; and 3.26 ± 0.84 in PR_post). A two-way ANOVA on F_tot with repeated measures, with factors age and time (three levels: PR_pre, SU, PR_post; see Fig. 2) showed a significant effect of time (F_2,44 = 39.22, P < 0.001) and a significant age × time interaction (F_2,44 = 3.16, P < 0.05). Multiple comparisons with Bonferroni correction revealed that, while the average values of F_tot during the PR_pre and PR_post phases were not different when the two groups were compared (P = 0.098 for PR_pre and P = 0.433 for PR_post), elderly subjects produced significantly larger force in the SU phase than did the younger ones (P < 0.05). In both groups, PR_pre phase differed from both SU and PR_post phases (P < 0.05), but SU and PR_post phases were not different from each other (P = 1.0 for elderly subjects and P = 0.127 for young subjects).

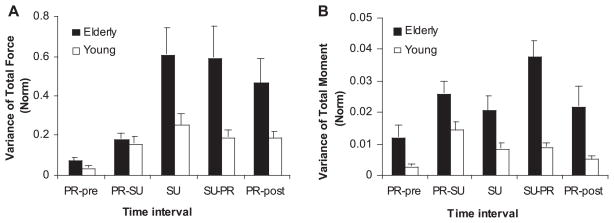
V_F and V_M

Time profiles of the variance of normalized F_tot (V_F) and M_tot (V_M) were computed across all trials for each of the subjects. V_F and V_M were then averaged over each of the five time intervals (PR_pre, PR-SU, SU, SU-PR, PR_post; see Fig. 2). Figure 5A shows V_F for the two age groups averaged across subjects with SE bars. The elderly subjects showed larger V_F than the young subjects within all time intervals, except in the PR-SU phase. In both age groups, V_F increased dramatically in the beginning of the task but then leveled off. In elderly subjects, V_F grew from PR_pre (0.07 ± 0.01) to PR-SU (0.19 ± 0.02) and to SU (0.611 ± 0.14) phases, leveled off in SU-PR phase (0.60 ± 0.15), and decreased significantly in the PR_post phase (0.47 ± 0.12). Young subjects showed a similar pattern of changes in V_F, but a significant difference was only found between the PR_pre phase (0.04 ± 0.01) and the other time phases (PR-SU, 0.16 ± 0.04; SU, 0.26 ± 0.05; SU-PR, 0.19 ± 0.03; and PR_post, 0.19 ± 0.03). This was confirmed by the significant effects of age (F_1,22 = 39.90, P < 0.05) and time (F_4,88 = 15.49, P < 0.01) and age × time interaction (F_4,88 = 4.878, P < 0.05) in a two-way ANOVA with repeated measures on V_F and multiple comparisons with Bonferroni corrections (P < 0.05).

Fig. 5.

A: average variance of the total force (V_F) during the five time intervals with SE bars. The data were averaged over each of the five time intervals and further across subjects. Elderly subjects are represented by solid bars, and young subjects by open bars. B: average variance of the total moment (V_M) during the five time intervals with SE bars. The data were averaged over each of the five time intervals and further across subjects. Elderly subjects are represented by solid bars, and young subjects by open bars.

Similar analyses of V_M showed substantially higher indexes of M_tot variability in the elderly subjects than in the young subjects. Figure 5B shows V_M for the two age groups averaged across subjects with SE bars. V_M was substantially larger for the elderly subjects than for the young subjects in all time intervals. In particular, the elderly subjects showed larger values of V_M during the two intervals where switching of the moment direction occurred (PR-SU and SU-PR). V_M was ~30% larger in the SU-PR phase compared with the PR-SU phase. Young subjects also showed larger V_M during the PR-SU phase, while V_M during the SU-PR phase was relatively modest. A two-way repeated-measures ANOVA on V_M with factors age and time (five levels: PR_pre, PR-SU, SU, SU-PR, PR_post) showed significant effects of age (F_1,22 = 13.99, P < 0.001), time (five levels: PR_pre, PR-SU, SU, SU-PR, PR_post; see Fig. 2) (F_4,88 = 14.77, P < 0.001), and age × time interaction (F_4,88 = 5.82, P < 0.001) in support of the mentioned differences.

M_Ag and M_Ant

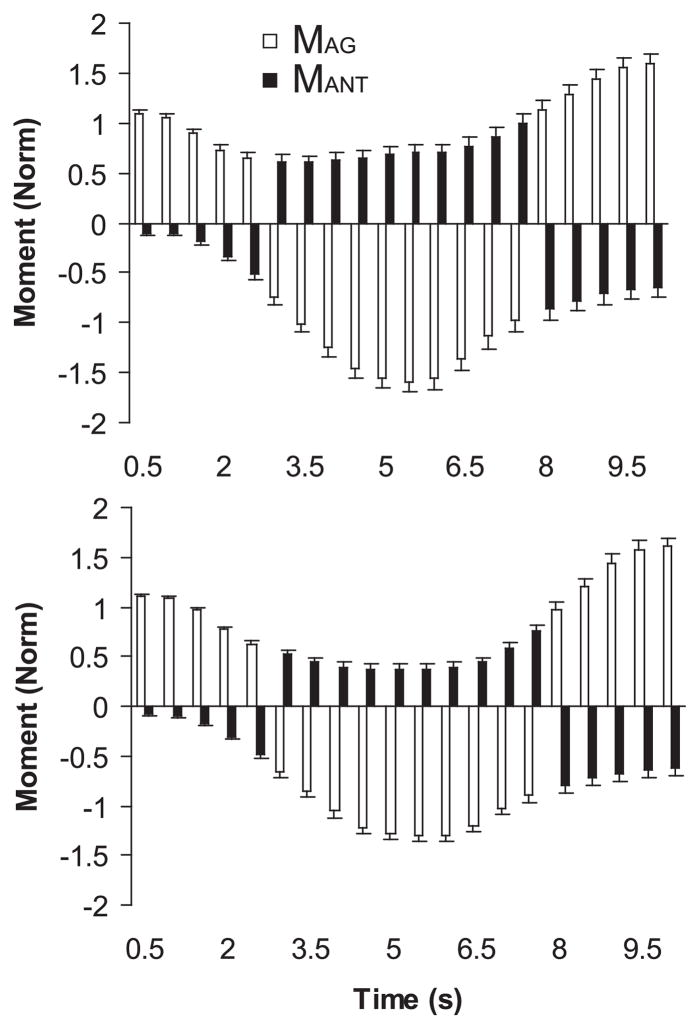
As described in METHODS, we define M_Ag as a moment produced in the direction that meets the current task requirements. M_Ag was produced by the I and M fingers when the task was required to produce PR moment, and it was produced by the R and L fingers when the task required production of a SU moment. M_Ant acted against M_Ag such that, during the PR portion of the task, it was produced by the R and L fingers, and during the SU portion of the task, it was produced by the I and M fingers. M_Ag and M_Ant were averaged over twenty 500-ms time intervals for each subject separately and further averaged across subjects. The time profiles of M_Ag (open bars) and M_Ant (solid bars) averaged across subjects with SE bars are shown for the elderly subjects in Fig. 6, top and for the young subjects in Fig. 6, bottom. Note the higher solid bars for the elderly subjects, particularly in the middle portion of the trial.

Fig. 6.

Average agonist (M_Ag, open bars) and antagonist moment (M_Ant, solid bars) of elderly (top) and young (bottom) subjects with SE bars. M_Ag and M_Ant were averaged over half-second intervals and further across subjects of each age group.

To compare the magnitudes of M_Ant during PR and SU efforts, when the task involved either a PR-SU change (1–5,000 ms) or a SU-PR change (50,001–10,000 ms), the M_Ant data were divided into two 5,000-ms parts (M_Ant1 and M_Ant2) that were analyzed separately using two three-way ANOVAs with factors age, torque, and time, where torque had two levels, PR (M_Ant is negative) and SU (M_Ant), and time had 10 levels, corresponding to the 500-ms intervals. For the first half of the task duration (M_Ant1), the ANOVA showed significant effects of age (F_1,22 = 4.90, P < 0.05), torque (F_1,22 = 45.55, P < 0.001), and time (F_4,88 = 44.69, P < 0.001), and all of their interactions except age × time (P = 0.15). Multiple comparisons with Bonferroni correction showed that the elderly subjects produced significantly larger M_Ant1 than the young subjects during SU (0.63 ± 0.06 vs. 0.42 ± 0.06; P < 0.05) but not during PR. In addition, in both age groups, M_Ant1 was significantly larger in SU than in PR (P < 0.01).

For the second half of the task (M_Ant2), the ANOVA showed only significant effects of time (F_4,88 = 75.65, P < 0.001), age × torque (F_1,22 = 15.96, P < 0.01), and torque × time (F_4,88 = 4.34, P < 0.05). Multiple comparisons with Bonferroni correction revealed that the elderly subjects produced larger M_Ant2 than the young subjects during SU (0.81 ± 0.07 vs. 0.51 ± 0.07; P < 0.01) but not PR (P = 0.783). Only in young subjects did M_Ant2 differ between SU and PR (P < 0.01).

Moments of force produced by individual fingers

The accurate moment task was set such that the moment arms of the I and L finger forces were three times longer than those of the M and R finger forces (4.5 vs. 1.5 cm). The mechanical advantage hypothesis states that, when multiple effectors (muscles or fingers) act together to produce a moment of force, those with longer moment arms contribute more to the total task compared with the ones with shorter moment arms (4, 15, 34, 41, 48). According to this hypothesis, the I and L fingers were expected to contribute significantly more than 50% to the respective PR and SU moments. We tested this hypothesis.

Figure 7 displays the shares of the I and L fingers in the PR and SU moments, respectively: M_I/M_PR (A) and M_L/M_SU (B) averaged over 1-s intervals and across subjects with SE bars. Figure 7, C and D, depicts further analysis where M_I/M_PR (C) and M_L/M_SU (D) have been averaged over the two steady-state PR intervals (bars 1 and 10 in A and B) and the two steady-state SU intervals (bars 5 and 6 in A and B). To test whether I and L fingers contributed proportionally more to the PR and SU moments than M and R fingers, a two-way ANOVA with repeated measures with factors age and time was run separately for M_I/M_PR and M_L/M_SU. Here, the time factor had two levels: PR and SU. Both indexes (M_I/M_PR and M_L/M_SU) for PR were calculated by first averaging them over time for each of the two 1,000-ms PR intervals (bars 1 and 10, A and B in Fig. 7) and then taking the average across them. For SU, the indexes were calculated in a similar way for each of the two 1,000-ms SU intervals (bars 5 and 6, A and B in Fig. 7) and then averaging across them. The I finger contributed between 72 and 80% of the total PR moment during both PR and SU efforts in elderly subjects. In young subjects, its contribution was ~80% during PR efforts (when it acted as an agonist), but dropped significantly to ~58% in SU (when it acted as an antagonist, P < 0.001). The two-way ANOVA on M_I/M_PR showed a significant effect of time (F_1,22 = 29.46, P < 0.001) and age × time interaction (F_1,22 = 8.41, P < 0.01).

Fig. 7.

Average proportion of the total PR moment produced by the index finger (A and C) and of the total SU moment (B and D) produced by the little finger for elderly (solid bars) and young subjects (open bars) with SE bars. A and B: data averaged over 1-s intervals. C and D: data further averaged over PR and SU intervals.

The L finger’s contribution to the total SU moment was in both age groups significantly larger during SU efforts (elderly, 66 ± 5%; young, 69 ± 5%) than during PR efforts (elderly, 56 ± 3%; young, 57 ± 3%) (P < 0.05), while no differences were found between the age groups. The two-way ANOVA on M_L/M_SU showed only a significant effect of time (F_1,22 = 16.68, P < 0.001), corresponding to an increase in the proportion M_L/M_SU over the trial duration (see Fig. 7B).

UCM analysis

The UCM analysis offers a method to quantify two components of the total variance in the space of commands to the fingers (modes) that correspond to keeping a potentially important performance variable (F_tot and M_tot in our study) unchanged (“good variability” or V_UCM) and contributing to its changes (“bad variability” or V_ort). We computed V_UCM and V_ort for F_tot and M_tot separately, at each time sample across trials for each subject. An index, ΔV, reflecting the difference in the magnitude of “good” and “bad” variability, was computed as described in methods. Positive ΔV values can be interpreted as multifinger synergies stabilizing that particular performance variable.

Figure 8 depicts the average ΔV_F and ΔV_M computed across subjects within each age group with SE bars. The data for the elderly subjects are shown in A (ΔV_M) and C (ΔV_F), while B (ΔV_M) and D (ΔV_F) show the data for the young subjects. Young subjects were able to stabilize the time profile of M_tot, reflected by positive ΔV_M values across the task duration (panel B, average 0.65 ± 0.2, P < 0.01), while elderly subjects failed to do so, as reflected by ΔV_M values that are not significantly different from zero (panel A, average 0.15 ± 0.47, P = 0.759). On the other hand, all subjects were able to stabilize the time profile of the F_tot as reflected by positive ΔV_F values across the task (panels C and D, on average 0.41 ± 0.13 for elderly and 0.53 ± 0.13 for young); ΔV_F showed a tendency to drop to less positive values over the duration of the task. A one-sample t-test on the average ΔV_F showed that, in both age groups, average ΔV_F was significantly above zero (P < 0.05).

A two-way ANOVA with repeated-measures run separately for ΔV_F and ΔV_M with factors age and time (five intervals: PR_pre, PR-SU, SU, SU-PR, PR_post; see Fig. 2) showed significant effects of time for both ΔV_F (F_4,88 = 9.05, P < 0.001) and ΔV_M (F_4,88 = 6.59, P < 0.001). ΔV_F generally decreased along the time intervals, but a statistical difference was only found between PR_pre and the other four intervals (P < 0.05). Note that ΔV_F drops from a higher level in young subjects compared with elderly subjects. ΔV_M decreased significantly during the intervals when the direction of M_tot changed: PR-SU and SU-PR (P < 0.05).

DISCUSSION

The goal of this study was to investigate age-related changes in finger coordination during tasks that require the production of accurate time profiles of moment of force. We hypothesized that elderly individuals would show lower indexes of synergies stabilizing both M_tot and F_tot. The former hypothesis received support in the experiment: the young subjects showed covariation of commands to fingers that stabilized the time profile of the moment of force, while the elderly subjects failed to do so. In contrast, there were no age-related changes in the ability of the subjects to stabilize the time profile of the F_tot: both subject groups showed covariation of commands to fingers that stabilized the F_tot, even though they were not specifically instructed to do so and got no visual feedback on the F_tot. These observations suggest that age may be associated with an impairment of rotational hand actions that goes beyond the documented impairment in the control of finger force (43, 44). It may contribute to failure at a variety of everyday tasks relying on rotational hand action, including spilling the contents of a mug, failing to turn the key to open the door lock, producing poorly legible handwriting, etc. In the remainder of the discussion, we address these and other issues, in particular those related to possible adaptive motor strategies seen in elderly persons leading to less economical but safer performance.

Age Effects on Force Production

With advancing age, the human muscle undergoes many physiological changes. The number of α-motoneurons declines (5, 16), larger motor units lose their resistance to fatigue (reviewed in Ref. 31), motor units decrease in number (5, 11) but increase in size (24), peak tension and length of the muscle twitch increases (10), and overall the muscles lose both mass and strength (12). For this study, we purposefully selected elderly individuals who were in an excellent physical condition. As a result, there were only marginal changes between the subject groups in their ability to produce finger force. The elderly subjects produced, on average, 18% lower peak forces during both one-finger and four-finger MVC trials, but these differences were not statistically significant. Elderly subjects showed significantly higher indexes of variability, despite the fact that their task was set to be easier than that of the younger subjects. The V_F was significantly larger for the elderly subjects in all time intervals, and particularly during the SU, SU-PR, and PR_post intervals. The finding of higher force variability in the elderly is in agreement with previous studies (14, 46). It is unlikely to reflect a difference in setting the tasks, since the tasks for the elderly required lower finger forces, and V_F has been shown to increase with force magnitude (33). Since the subjects did not receive any explicit feedback on the F_tot and were not instructed to pay attention to the force level, these results indicate that the differences in the reproducibility observed between the two age groups were not related to differences in their visual perception or in processing visual feedback information (38). As discussed further, we believe that the higher force variability in the elderly was a reflection of their worse force stabilizing synergies (cf. Ref. 41).

Contrary to our predictions, both age groups covaried commands to individual fingers to stabilize the F_tot over the duration of the main task, reflected in positive ΔV_F values. As can be seen from Fig. 8, the elderly subjects started from a lower level of ΔV_F than the young subjects and produced, on average, slightly lower ΔV_F. The results can thus be interpreted so that the elderly subjects were able to stabilize the F_tot but to a lesser level than the young subjects (cf. 43, 44). Nevertheless, the presence of force-stabilizing synergies in the present experiment is a very much nontrivial result, given that the subjects were not instructed with respect to the F_tot and had no visual feedback on its value.

Age Effects on Rotational Action by the Fingers

Only a handful of earlier studies used tasks that explicitly required accurate hand torque exertion. Several studies that have addressed hand rotational action have focused on grip force production by the thumb and I finger during a pinch grip (20, 23). Other studies had steady-state torque production as an implicit component required to keep a hand-held object vertical (50, 40, 15). A couple of recent studies have explored finger coordination during accurate isometric moment of force production by young adults (54). An earlier study explored effects of age on digit interaction during gripping tasks, with an implicit requirement to keep the orientation of the hand-held object unchanged (41).

The average performance in the main task was defined by the template, and all subjects could perform the task well. However, the time profiles of the variance (V_M) of the M_tot revealed significant differences between the two age groups: the elderly subjects produced larger V_M during all time intervals, but especially during the phases when the direction of the moment of force changed: PR-SU and SU-PR. Note that the time profile of V_M across the five time intervals is different from the time profile of V_F; in particular, in both groups, the highest values of V_F were seen during the steady-state production of SU moment of force, while the highest values of V_M were seen during the PR-SU and SU-PR time intervals. These results suggest that the differences in V_M characteristics were not simply by-products of differences in force characteristics between the subject groups, but likely reflected different coordination of commands to fingers with respect to force and moment of force production.

Both groups showed higher V_M values during the PR-SU and SU-PR intervals when the magnitude of the total moment was, on average, smaller compared with the other three intervals: PR_pre, SU, and PR_post. This observation contrasts the well-established force-force variability relations, which suggest an increase in force variability with an increase in the force magnitude (reviewed in Refs. 33, 45). Note that the F_tot, on average, showed a transient drop at the times when the moment of force changed its direction (Fig. 4). As such, force changes could not account for the increase in V_M over those time intervals. These results provide more support for the idea that the variability of the moment of force was not simply a reflection of variability of individual finger forces but was to a large degree defined by covariation of commands to fingers, that is, a moment-stabilizing synergy.

The transient increase in V_M during the switch of direction of the moment of force (53) may be due to the relatively high rate of change of the moment of force combined with an error in the timing of control signals (19). Since V_M was computed in relative units, the higher V_M values in elderly subjects during the PR-SU and SU-PR intervals suggest an increase in the timing error, which can include timing offset errors or errors in the timing parameter that define the rate of change of the moment of force. Errors in timing of motor acts have been shown to increase with age (47) in support of this hypothesis.

The higher variability in the moment of force produced by a set of fingers by elderly persons is a novel finding. It extends the early report on increased variability of the rotational action of the thumb and the VF with age (41). As mentioned, this phenomenon may have profound effects on a variety of activities of daily living.

An earlier study reported larger magnitudes of the moment produced by fingers acting against the required moment direction (M_Ant) by elderly persons in a static prehension task (41). Our results are partially in agreement with that observation: elderly subjects produced significantly larger M_Ant than the young subjects when the total moment was in SU. The higher M_Ant may be viewed as an adaptive strategy, increasing the resistance of the hand and fingers to possible rotational perturbations (cf. Ref. 41). It may represent a consequence of the weaker moment-stabilizing synergies in elderly persons.

The experimental task involved tracking a visual template, and, as such, it could be affected by age-related differences in visual tracking tasks. On the one hand, visual and manual tracking performance has been shown to suffer with age (3, 32a). These differences, however, are particularly pronounced during tracking unpredictable signals (3), while the template used in our study was always the same and perfectly predictable. On the other hand, elderly are known to rely more on visual information during accurate motor tasks (38). Given that all of our participants had vision corrected to normal and the task involved only predictable, not very quick actions, the nature of the task could be expected to favor elderly subjects.

Aging and the Principle of Mechanical Advantage

When several effectors contribute to a common mechanical effect while acting in the same direction, sharing patterns among the elements may be defined by optimization rules. The mechanical advantage hypothesis has been suggested as a principle that defines sharing patterns for multimuscle and muscle-digit actions (4, 34). The general idea is that effectors with larger lever arms should produce larger shares of the total moment because they have to produce relatively smaller forces per unit of M_tot. In our study, the I and L fingers had moment arms three times as large as those for the M and R fingers. According to the mechanical advantage principle, the I finger should contribute more than one-half of the total PR moment, and the L finger should contribute more than one-half to the SU moment. The young subjects showed modulation of the percentage of the total moment produced by the I and L fingers, such that the mechanical advantage hypothesis was true, but only when the fingers acted as agonists (produced M_AG); the hypothesis failed when the fingers produced M_Ant. In contrast, the elderly subjects did not show a comparable modulation of the percentage of the total moment produced by the I finger: they produced close to 80% of the total PR moment of force with that finger over the whole trial duration. This result may reflect the reduced flexibility in the control of the moment of force in the elderly, which may be a consequence of their weaker synergies. Note that one advantage of having strong synergies stabilizing a performance variable is in the possibility to use multiple, flexible solutions (17). The difference in the tasks was not expected to lead to such results, because the tasks were set at rather low values. For young persons, 4 N of force by the I finger are typically under 10% of its maximal force (see Table 1). Hence, the requirement to produce such a low force is not expected to be a limiting factor in using the I finger to produce required moment of force.

Changes in Multifinger Synergies With Age

The principle of abundance views synergies as neural organizations that provide for flexible families of solutions for motor tasks, based on apparently redundant sets of effectors (17). The UCM hypothesis (37) has formalized this principle and suggested that the purpose of synergies is to minimize variability along particular directions in the space of elemental variables (that change a desired value of an important performance variable, “bad variability”), while allowing variability in other directions. For example, if the controller tries to ensure accurate production of a particular value of the total moment produced by a set of fingers, it is expected to keep the variability of commands to fingers across trials mostly confined to a subspace (a UCM) in the finger mode space that does not lead to changes in that value. The index of synergy we used in this study (ΔV, see also Refs. 39, 44) was computed in such a way that its positive values corresponded to proportionally more variability within the corresponding UCM, which can be interpreted as a multifinger synergy stabilizing either F_tot or M_tot (ΔV_F and ΔV_M, respectively).

Consider the task of supporting a heavy object with two fingers (Fig. 9). If the forces of the two fingers vary independently, the object may be expected to move up and down and/or to tilt. If, however, the forces covary negatively, the F_tot may be expected to stay relatively unchanged (more variability confined to the UCM computed for the F_tot, ΔV_F > 0), but the M_tot will show large variations (more variability orthogonal to the UCM for the total moment, ΔV_M < 0). If the two forces covary positively, the total moment will be relatively stabilized (ΔV_M > 0), but the F_tot will not (ΔV_F < 0). The system of only two effectors illustrated in Fig. 9 is only marginally redundant (26) and cannot stabilize these two variables at the same time. The availability of four fingers in our tasks allowed simultaneous stabilization of both F_tot and M_tot.

Fig. 9.

Illustration of a system of two effectors (fingers F₁ and F₂) involved in the task of supporting an object (top). Bottom: two hypothetical distributions of data points over many trials. One of them corresponds to force covariation, stabilizing the total force but not the total moment (ΔV_F > 0, ΔV_M < 0). The other one corresponds to force covariation, stabilizing the total moment but not total force (ΔV_F < 0, ΔV_M > 0).

The main results of the study summarized in Fig. 8 show that both subject groups were able to covary commands to fingers to stabilize F_tot (ΔV_F > 0), while only young subjects stabilized M_tot (ΔV_M > 0). The former result is counterintuitive, since the subjects got no feedback on F_tot and were given no instruction about it. The latter result supports our main hypothesis and suggests that age is associated with a decrease in the ability to coordinate commands to digits to produce rotational actions.

Note that our task was designed to minimize possible involvement of the forearm, i.e., its radio-ulnar proximal and distal joints, into the moment production: the palm was supported by a wooden block and the forearm was attached to the board with Velcro strap. This was done purposefully to avoid possible changes in the moment due to forearm PR/SU. The task used in the study may be viewed as artificial and even odd, but it has allowed us to address the issue of synergies among commands to fingers that stabilize their combined rotational action. This action can be formally expressed as that by the VF (Refs. 1, 32, also see the Introduction). An earlier study (41) analyzed synergies at the higher level of the hypothetical control hierarchy, that is, at the level of coordinated action of the thumb and the VF. For example, during drinking from a glass, the thumb and combined finger (VF) actions have to be coordinated to stabilize the M_tot applied to the glass. Commands to individual fingers covary to stabilize the VF action. Taken together, the two studies emphasize the necessity to focus on the rotational hand action in both research and medical practice related to the aging hand.