Abstract
This study investigated a method to evaluate mediational processes using latent growth curve modeling. The mediator and the outcome measured across multiple time points were viewed as 2 separate parallel processes. The mediational process was defined as the independent variable influencing the growth of the mediator, which, in turn, affected the growth of the outcome. To illustrate modeling procedures, empirical data from a longitudinal drug prevention program, Adolescents Training and Learning to Avoid Steroids, were used. The program effects on the growth of the mediator and the growth of the outcome were examined first in a 2-group structural equation model. The mediational process was then modeled and tested in a parallel process latent growth curve model by relating the prevention program condition, the growth rate factor of the mediator, and the growth rate factor of the outcome.
Most prevention studies are based on theories that specify causal variables that have an effect on the outcome, and the prevention programs include the components designed to modify these causal variables to obtain the desired outcome. For example, a drug prevention program based on Social Learning Theory (Bandura, 1977) may include program components to teach adolescents refusal skills and correct their misperception of the prevalence of drug use, aiming to reduce the social environmental influences. A drug prevention program based on the Health Belief Model (Janz & Becker, 1984) may seek to increase adolescents’ perception of susceptibility to the negative effects of drugs. If the theory is correct, changing the causal variables, such as social environmental influence for Social Learning Theory and perceived susceptibility for Health Behavior Theory, will prevent drug use.
Despite the theoretical basis of prevention programs, most evaluation studies neglect the link between theory and evaluation (Judd & Kenny, 1981; MacKinnon & Dwyer, 1993). Until recently, the success of a prevention trial has been assessed only by the change in the outcome; that is, whether the treatment program reduced the harmful outcome or enhanced the desired outcome. Assessing a prevention trial only by the change in the outcome variable may provide a gross assessment of whether or not a program works, but may fail to identify the underlying mechanisms concerning how the program achieved or failed to achieve its effects. The evaluation of a program should involve more specific investigation by laying out program components and identifying causal links based on theory (Chen, 1990; Donaldson, Graham, & Hansen, 1994; MacKinnon, 1994).
Mediation analysis has been introduced as an appropriate method for theory-driven evaluation of prevention trials (MacKinnon & Dwyer, 1993; MacKinnon et al., 1991). Mediation analysis is important in that it allows researchers not only to assess the success of the program, but also to obtain more specific information on how the program succeeded or failed. Through mediation analysis, researchers can obtain information on whether the prevention program successfully changed the mediating variable and whether the change in the mediating variable was responsible for the change in the outcome (Baron & Kenny, 1986; MacKinnon & Dwyer, 1993). Furthermore, researchers can estimate and test the significance of the mediated effect (MacKinnon, 2000; MacKinnon & Dwyer, 1993; MacKinnon, Warsi, & Dwyer, 1995). For example, if adolescent drug use decreased in the group receiving a social influences based drug prevention program, researchers may want to explore whether the resistance skills enhanced by the prevention program were responsible for the success of the program. Such information may be more valuable when a prevention trial was not successful. If the treatment program did not work as expected, findings about which components were successful and which were not can provide valuable information for the design of future studies.
As the main goal of prevention trials is to change outcomes, using the appropriate methods to estimate the change has been a critical issue. Recently, researchers have pointed out the inadequacy of using pre- and postintervention measures to estimate the longitudinal change (Rogosa, 1988; Rogosa, Brandt, & Zimowski, 1982; Willett & Sayer, 1994). Measures at two time points contain only minimal information on individual change, and it may be misleading to specify individual changes over time with two data points when the trajectory follows a shape other than a straight line (e.g., quadratic or exponential) or when there is a fluctuation of scores between the two time points. Longitudinal growth modeling has been advocated as a better method for answering questions about individual change over time and individual differences in change (Rogosa, 1988; Rogosa et al., 1982; Willett & Sayer, 1994). In particular, the investigation of how each construct changes over time should precede the examination of the relation between the two constructs (Raudenbush, 2001; Rogosa, 1988), when the research question involves the long-term relation between two different constructs, such as a mediator and an outcome.
The purpose of this study is to illustrate how to carry out mediation analysis using latent growth modeling (LGM) in the case of longitudinal randomized prevention trials. Several studies (e.g., Muthén & Curran, 1997; Raudenbush, 2001; Willett & Sayer, 1994) have described methods for LGM, and studies evaluating the effect of prevention programs using LGM (e.g., Park et al., 2000; Taylor, Graham, Cumsille, & Hansen, 2000) have started to appear in scholarly journals. In this study, we expand the application of the LGM approach to mediation analysis. The modeling procedures are demonstrated by estimating a series of latent growth models using a data set from a longitudinal drug prevention study designed to reduce adolescent football players’ anabolic steroid use (Goldberg et al., 1996; Goldberg et al., 2000).
ESTIMATION AND TEST OF THE MEDIATED EFFECT
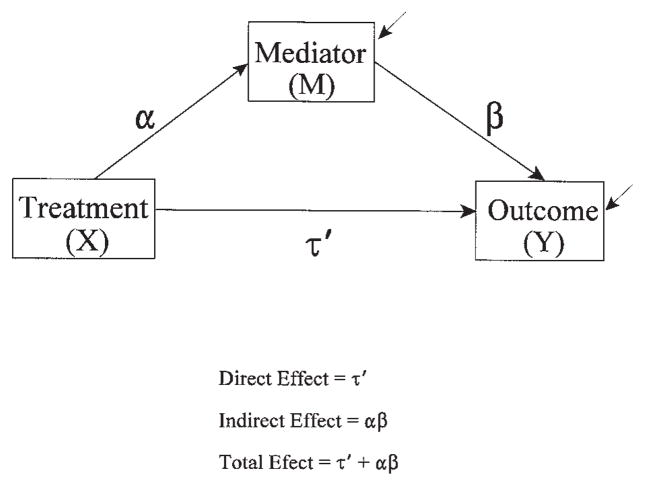
The basic single mediator causal model, on which the prevention trials are based, is illustrated in Figure 1. Here, the theory-based causal variables can be conceptualized as potential mediating variables (M) intervening in the relation between the prevention program (X) and the outcome variable (Y). The prevention program influences the outcome directly and also indirectly through the mediator. Chen (1990) used the term action theory to refer to the link between the treatment program and the mediating variables and the term conceptual theory to refer to the link between the mediating variables and the outcome variable.
FIGURE 1.
A single mediator model.
One of the most commonly used methods to obtain the point estimate of the mediated effect is the product of coefficients method (Aroian, 1947; Goodman, 1960; MacKinnon & Dwyer, 1993; MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002; MacKinnon et al., 1995; Sobel, 1982). In the product of coefficients method, the following regression equations are estimated to obtain the mediated effect:
| (1) |
| (2) |
In Equation 1, the potential mediator M is regressed on the prevention program X. In Equation 2, the outcome variable Y is regressed on the prevention program X and the potential mediator M. The coefficient α represents the effect of the prevention program on the potential mediator. The coefficient β denotes the effect of the potential mediator on the outcome after controlling for the effect of the prevention program. Similarly, the coefficient τ′ represents the effect of the prevention program on the outcome variable after controlling for the effect of the mediator. The constants β01 and β02 are the regression intercept terms and ε1 and ε2 are residuals in the two equations. The mediated effect is estimated by the product of the two regression coefficients for α and β, conveying that the mediated effect is determined by the extent to which the treatment program changes the mediator (α) and the extent to which the mediator, in turn, changes the outcome (β).
There are several ways to estimate the variance of the product of two coefficients (αβ), any of which can be used for estimation of the standard error of the mediated effect to conduct a significance test and to obtain confidence intervals (CIs) of the mediated effect (see MacKinnon, Lockwood, Hoffman, et al., 2002). One of the most commonly used formulas for the standard error of the product of two coefficients is based on the multivariate delta method (Sobel, 1982) or the first-order Taylor series as follows:
| (3) |
where α and σα are the regression coefficient and its standard error in Equation 1 and β and σβ are the regression coefficient and its standard error in Equation 2. For observed data, sample estimates of α, σα, β, and σβ are inserted in Equation 3. The significance test of the mediated effect is conducted by dividing the estimate of the mediated effect (αβ) by the estimated standard error (σαβ), which is compared to a standard normal distribution. The first-order solution method (Sobel, 1982) is widely used, being implemented in the SEM software programs such as LISREL and EQS; however, it was found to have low statistical power because the distribution of the product of the two random variables is not always normally distributed (MacKinnon, Lockwood, & Williams, 2002).
In an alternative method called the asymmetric CI method (MacKinnon, Lockwood, Hoffman, et al., 2002), both α and β coefficients are converted to z scores (i.e., zα = α/σα and zβ = β/σβ) and the critical values for the two z scores are found from the tables in Meeker et al. (1981) to construct the CI. Because the distribution of the product of αβ is often asymmetric, different values are used for the upper and lower critical values. Using these critical values, the lower confidence limits (LCLs) and upper confidence limits (UCLs) are computed by UCL = αβ + (upper critical value)*σαβ and LCL = αβ + (lower critical value)*σαβ. When the CI does not include zero, the mediated effect is considered statistically significant. According to an extensive simulation study (MacKinnon, Lockwood, Hoffman, et al., 2002), the asymmetric CI method has greater power compared to other methods for testing mediation.
LATENT GROWTH CURVE MODELING
Growth curve modeling is a way to investigate individual differences in change over time and explore the predictors of these individual differences. A growth curve model can be formulated in the multilevel modeling framework (Bryk & Raudenbush, 1992; Goldstein, 1995; Raudenbush, 2001) utilizing random coefficients modeling (Longford, 1993) and also in the structural equation modeling (SEM) framework (Meredith & Tisak, 1990; Muthén & Curran, 1997; Willett & Sayer, 1994). When growth curve modeling is carried out in the conventional SEM framework, the growth of a measured variable can be modeled in the measurement model as follows:
| (4) |
where Yi is a T × 1 vector of repeated measures of the variable Y for individual i over the T time points (t = 0, 1, 2, ···, T), νi is a T × 1 vector of the intercepts of the repeated measures, Λ is a T × J matrix of factor loadings on the growth factors, ηi is a J × 1 vector of J latent factors representing the growth parameters, and εi is a T × 1 vector of measurement errors.
The distinctive feature of latent growth curve model is in the Ληi term, where the growth factors and the growth trajectory shape are defined. For example, for a linear growth across six time points (T = 6) at equal intervals, Equation 4 can be rewritten in the following matrix form:
| (5) |
The latent factor η1i is the status factor, representing the true level at T = 0. In this example, η1i denotes the initial status at the first measurement occasion. The latent factor η2i is the growth rate factor, representing the rate of growth per unit time. Estimation of the average initial status can be achieved either by estimating the common intercept equated across six time points (ν1i = ν2i = ν3i = ··· = ν6i) while fixing the mean of η1i to zero or, alternatively, fixing the common intercept νis to zero while estimating the mean of the status factor η1i (see Khoo, 2001, for more details). The factor loadings on the growth rate factor, η2i, are specified to reflect the time intervals between measurements and the growth trajectory shape. Setting the loadings on η2i as [0 1 2 3 4 5] reflects the linear trajectory across six time points at equal intervals.
Modeling various shapes of the growth trajectory is fairly easy when LGM is carried out in the SEM framework (Du Toit & Cudek, 2001; Stoolmiller, 1995). If the growth trajectory is assumed to be other than a linear trajectory, the factor loadings on the growth rate factor can be specified accordingly. For example, when the growth trajectory is expected to show a positive growth at earlier measurement occasions followed by a stabilized plateau at later measurement occasions, the trajectory shape can be modeled by setting the loadings on the growth rate factor (η2i) to be [0 1 1 1 1 1]. Furthermore, the factor loadings on the growth rate factor do not have to be fixed across the measurement occasions. For example, when the trajectory is expected to depart from the stabilized level at a later time point (e.g., at Time 3) the factor loadings on the growth rate factor can be specified as [0 1 * 1 1 1] to freely estimate the growth at Time 3. The estimated loading smaller than 1 indicates a lower level at Time 3 than other posttest measurements. These specifications will be utilized in our example for illustration.
Individual differences in growth are captured in the variances of the initial status factor and the growth rate factor. When the variances of the growth factors are substantial, the latent growth factors can be regressed on individual background variables such as Xi as in the following:
| (6) |
For example, the initial status and the growth rate of drinking alcohol among college students might be related to how much the individuals were involved in problem behaviors in the past. This can be studied by regressing the growth factors of alcohol consumption on the problem behavior indicators (e.g., Harford & Muthén, 2001). Program effects in random experiments can also be assessed in this way. For example, adolescent alcohol use might increase over time in general, but the individuals in the treatment group might show a slower increase than those in the control group. Then the growth rate factor can be regressed on the prevention program condition to explain the different growth trajectories in the two groups (e.g., Taylor et al., 2000).
MEDIATION IN LGM
In a pretest–posttest situation, mediation is supported when the prevention program changes the level of the mediator and the change in the mediator, in turn, affects the level of the outcome. When both the outcome variable and the hypothesized mediating variable are measured repeatedly over time, the growth of the mediator and the growth of the outcome can be viewed as two distinctive processes. In such situations, the mediational process can be modeled as the prevention program influencing the growth of the outcome indirectly through its effect on the growth of the mediator. Mediation is supported when the prevention program significantly changes the trajectory of the mediator, which, in turn, affects the trajectory of the outcome.
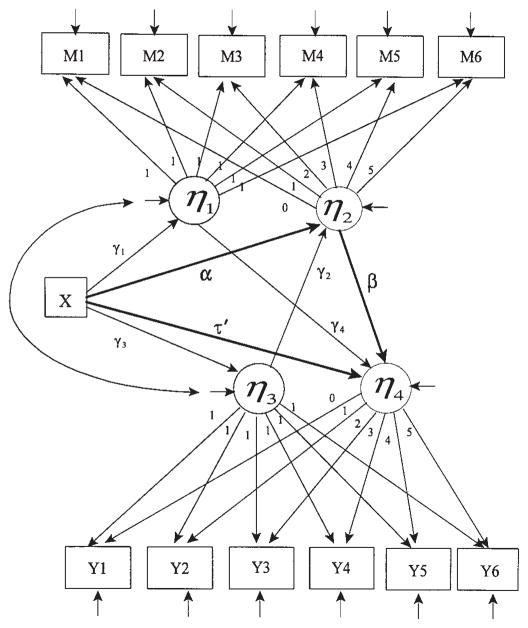
Evaluation of the mediational process in longitudinal studies can be carried out using the parallel process LGM. Figure 2 shows a parallel process growth curve model where the mediator and the outcome are measured across six time points and the growth of each process is modeled as linear. The upper half of Figure 2 represents the mediator process and the lower half represents the outcome process. The mediational process is modeled by relating the prevention program X and the latent growth factors of the two parallel processes.
FIGURE 2.
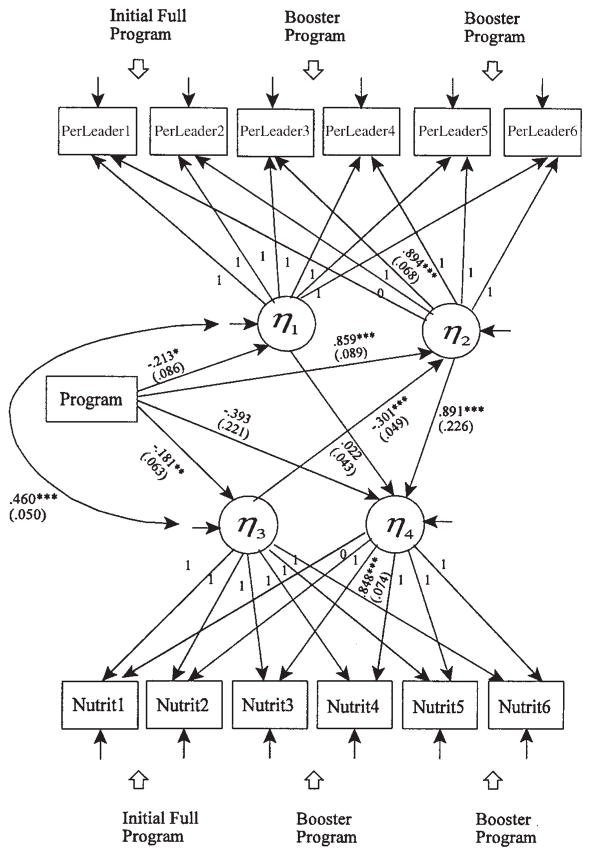
A parallel process latent growth model for mediation. X = treatment program condition; Y = outcome; M = mediator; η1 = initial status factor of mediator; η2 = growth rate factor of mediator; η3 = initial status factor of outcome; η4 = growth rate factor of outcome.
In parallel process latent growth curve models, the growth of the mediator process and the growth of the outcome process are modeled in the measurement model. Examining the growth of the mediator and the growth of the outcome separately, each process can be written as follows:
| (7) |
where the superscript (m) denotes the mediator process, Mi is a 6 × 1 vector of the repeated measures of the mediator, νi(m) is a 6 × 1 vector of the common intercepts of the mediator, Λ(m) is a 6 × 2 matrix of factor loadings on the two growth factors, ηi(m) is a 2 × 1 vector of the latent growth factors for the mediator, and εi(m) is a 6 × 1 vector of the measurement errors of the mediator.
| (8) |
where the superscript (y) denotes the outcome process, Yi is a 6 × 1 vector of the repeated measures of the outcome, νi(y) is a 6 × 1 vector of the common intercepts of the outcome, Λ(y) is a 6 × 2 matrix of factor loadings on the two growth factors, ηi(y) is a 2 × 1 vector of the latent growth factors for the outcome, and εi(y) is a 6 × 1 vector of the measurement errors of the outcome.
Once the growth of each process is satisfactorily modeled and the effects of the prevention program on the growth of each process is investigated, the two separate growth curve models are combined into one parallel process growth curve model. The mediation is modeled in the structural model by relating the prevention program condition, the growth factors of the mediator process, and the growth factors of the outcome process. The structural relations are expressed in terms of each latent factor (η1i, η2i, η3i, and η4i) as follows:
| (9) |
| (10) |
| (11) |
| (12) |
where η1i is the initial status factor of the mediator process, η2i is the growth rate factor of the mediator process, η3i is the initial status factor of the outcome process, and η4i is the growth rate factor of the outcome process.
Equations 9 and 11 model the relations between the prevention program Xi and the initial status factors (η1i and η3i) of the mediator process and the outcome process. In these equations, π0(m) and π0(y) denote the regression intercepts. The coefficients γ1 and γ3 represent the difference between the treatment group and the control group in the status factors of the mediator process and the outcome process, respectively. Equations 10 and 12 model the relations between the prevention program and the growth rate factors and the relations among the latent factors of the two processes. In these equations, π1(m) and π1(y) denote the regression intercepts. Equation 10 models the regression of the growth rate factor of the mediator process (η2i) on the prevention program condition (Xi) and the initial status factor of the outcome process (η3i). The coefficient α represents the mean difference in the average growth rate between the two groups and a significant α coefficient suggests that the prevention program is effective in changing the growth trajectory of the mediator process. Similarly, Equation 12 models the regression of the growth rate factor of the outcome process (η4i) on the prevention program (Xi), the initial status of the mediator process (η1i), and, more important, the growth rate factor of the mediator process (η2i). A significant β coefficient indicates a significant association between the growth rate of the mediator process and the growth rate of the outcome process.
The point estimate of the mediated effect can be obtained by taking the product of the coefficients (αβ). Testing the significance of the mediated effect and obtaining the CI can be conducted as described in the previous section using the first-order solution method (Sobel, 1982) or the asymmetric CI test (MacKinnon, Lockwood, Hoffman, et al., 2002).
ILLUSTRATION OF LGM MEDIATION ANALYSIS
Adolescents Training and Learning to Avoid Steroids (ATLAS) Prevention Study
This study used part of the data from a longitudinal prevention study entitled ATLAS (Goldberg et al., 1996; Goldberg et al., 2000). The goals of the ATLAS project were to reduce high school football players’ use of anabolic androgenic steroids (AAS) and other drugs and to improve their health behaviors (e.g., eating a nutritional diet and strength training). The ATLAS program was designed to change a number of potential mediators based on health behavior theories. Based on Social Learning Theory (Bandura, 1977), the ATLAS program targeted to change social environmental influences: The program sessions were delivered by coaching staff and peer team leaders and the program activities consisted of small group projects and discussions. As suggested by Theory of Planned Behavior (Ajzen & Madden, 1986; Fishbein & Ajzen, 1975), the ATLAS program included several components to change norms, beliefs, and attitudes about AAS: The treatment group students discussed the reasons to use and not to use AAS, analyzed media advertisements on AAS effects, and developed an anti-AAS advertisement. The treatment group also received classroom sessions providing the alternatives to steroid use, such as nutrition and strength training. Furthermore, as suggested by Health Belief Model (Janz & Becker, 1984), the ATLAS program emphasized harmful effects of AAS and susceptibility to these negative effects. More details regarding the ATLAS program and the primary research findings can be found elsewhere (Goldberg et al., 1996; Goldberg et al., 2000; MacKinnon et al., 2001).
ATLAS design
The ATLAS project lasted for 4 years beginning in 1994. A total of 31 high school football teams in Oregon and Washington states were randomly assigned to the treatment group or the control group. The participants were followed until they graduated from high school and a new cohort of participants was added in each study year.
The prevention program was delivered in full length in the first year and the shortened version of the booster program was delivered in the following years. There were a total of eight measurement occasions over the 4 project years. This study included the first six measurement occasions: baseline measurement (Time 1), posttest after the initial full prevention program (Time 2), 1-year follow-up (Time 3), posttest after the first booster program (Time 4), 2-year follow-up (Time 5), and posttest after the second booster program (Time 6). The intervals between the two measurements before and after the program delivery (Time 1 and Time 2, Time 3 and Time 4, Time 5 and Time 6) were about 2 months, whereas the intervals between posttests and the 1- and 2-year follow-up measures (Time 2 and Time 3, Time 4 and Time 5) were about 10 months.
Measures
In this study, nutrition behaviors (Nutrit) was used as an outcome variable. Perceived importance of team leaders as an information source (PerLeader) was used as a mediator. The high school football players in the treatment group participated in the discussions on drug prevention and healthy alternatives to drug use led by the team leaders. It was hypothesized that these program activities would increase the perception of team leaders as a valid information source about diet, and this, in turn, would improve nutrition behaviors.
There were seven items measuring nutrition behaviors on 7-point Likert type scales that consisted of Over the last few months I have tried to improve my diet, I eat a diet that has no more than 30% calories from fat, I am aware of the calorie content of the foods I eat, I set goals for my nutrition, I keep track of the calories I eat, I keep track of the protein I eat, and I choose healthy foods when I eat at a fast food restaurant. The mean score of these seven items was used for analyses. Higher scale scores reflected better nutrition behaviors. In the prior analyses for the scale development, these seven items were found to constitute one factor in exploratory factor analysis. The Cronbach’s α at baseline measurement was .810.
Perceived importance of team leaders as an information source was measured with three items on 7-point Likert type scales: My team leaders help me learn about drug prevention, My team leaders help me learn about sports nutrition, and My team leaders help me learn about weight lifting. The mean score of these three items was used for analyses. Higher scores represented greater perception of peer team leaders as a valid information source. The Cronbach’s α for these items measured at baseline was .844.
A dummy variable was created to represent group membership. The treatment group was coded as 1 and the control group as 0.
Sample
The participants included in this study were the first cohort of high school football players who participated in the ATLAS study from 1994 to 1996. There were 1,506 participants (Control N = 804; Treatment N = 702) at baseline in 1994. Among those, 1,339 participants (Control N = 730; Treatment N = 609), who were present at both baseline and at least one of the follow-up assessments, were included in the analysis. The main sources of missing data were graduation, quitting the football team, injury during the football season, and absenteeism on the assessment day. The attrition rate was consistent with the estimated rate of students’ quitting the football team during the season (20%). The attrition rate from the study was actually less than the nominal high school dropout rate in the area (28%). The analyses in this study were conducted adjusting for missing data.
General Steps of Modeling and Testing Mediational Process in LGM Framework
Conducting mediation analysis using parallel process LGM method involves several steps. First, the growth trajectory shape of each process is investigated. The main goals of this step are to test whether the hypothesized trajectory shape fits the data and to examine whether the growth rates are different in the treatment and the control groups. In the second step, the two latent growth curve models investigated in the first step are combined to one parallel process model and the hypothesized relations among the prevention program and the growth factors of the two processes are modeled. Finally, the estimates of the mediated effect and the estimated standard error are calculated to test the significance of the mediated effect and to construct the CI. The analyses were conducted using the Mplus 2.0 (Muthén & Muthén, 2001) SEM program. The programs used in this article are available by writing to JeeWon Cheong or at the Web site (http://www.public.asu.edu/~davidpm/ripl).
Investigation of Growth Trajectory and Assessment of Program Effects
When the prevention program is effective, the growth of the mediator and the growth of the outcome are expected to be different in the treatment group and the control group. In the ATLAS study, the initial full prevention program implemented in the first year was expected to increase the football players’ nutrition behaviors (Nutrit) and perceived importance of team leaders as a valid information source (PerLeader). In addition, the booster programs delivered in the later years were expected to recover and maintain the program effect achieved by the full prevention program, when and if there was a decay of effects. Thus, the factor loadings on the growth rate factor of the mediator and the outcome were specified as [0 1 * 1 1 1]. We specified the status factor to represent the initial status, the true level at baseline. By setting the loadings on the growth rate factor for Time 2, Time 4, Time 5, and Time 6 to be 1, we hypothesized that the effects achieved by the initial full prevention program would be recovered and maintained at the same level by the booster programs. The factor loading of the Time 3 measure was freely estimated to examine the decay of program effect before the booster programs. If there was a decay of program effect, this factor loading would be smaller than 1.
Because the significant shift in the mediator process and the outcome process was expected only for the treatment group, it was examined whether the aforementioned specification of the trajectory shape was appropriate for both groups. The trajectory of the mediator process and the trajectory of the outcome process were examined separately in a two-group model. The factor loadings on the latent factors were specified to be equal across the two groups. The residual variances of the repeated measure at each measurement occasion were also equated across groups. The covariance between the initial status factor and the growth rate factor was freely estimated and allowed to be different across the two groups. The common intercept was estimated and the status factor mean of the control group was set to 0 to capture the mean difference in the initial status between the two groups in the status factor mean of the treatment group. Given the specification of the growth trajectory, the overall model fit would indicate the appropriateness of using the current specification for both groups and, thus, justify combining the two groups and using the program group membership as a causal variable for the different trajectory shapes.
The program effects on the growth of the mediator process and the outcome process were assessed by comparing the means of the growth rate factors between the two groups. With the current data, the mean and the variance of the growth rate factor for the control group were found to be nonsignificant for both perceived importance of team leaders and nutrition behaviors. In light of this, the means and the variances of the growth factors were constrained to be 0 for the control group. Thus, the mean of the growth rate factor estimated for the treatment group was the estimated program effect (i.e., the shift of growth rate due to the ATLAS program).
Table 1 shows the sample covariances and means by each group estimated with the Maximum Likelihood (ML) method adjusting for missing data. The results from the two-group SEM are reported in Table 2. The overall fit of the two-group model was reasonable. Due to the large sample size (N = 1,339), the χ2 statistics were significant; however, root mean square error of approximation (RMSEA) estimate was acceptable for both perceived importance of team leaders, χ2(39) = 155.204, p < .001, RMSEA = .067 with 90% CI = (.056, .078), and nutrition behaviors, χ2(39) = 123.035, p < .001; RMSEA = .057 with 90% CI = (.046, .069).
TABLE 1.
Estimated Covariances and Means by Group
| Perceived Importance of Team Leaders as an Information Source |
||||||
|---|---|---|---|---|---|---|
| PerLeader1 | PerLeader2 | PerLeader3 | PerLeader4 | PerLeader5 | PerLeader6 | |
| PerLeader1 | 1.196 | .882 | .683 | .705 | .541 | |
| PerLeader2 | .839 | .894 | .772 | .618 | .329 | |
| PerLeader3 | .835 | 1.085 | 1.141 | 1.063 | 1.253 | |
| PerLeader4 | .330 | .565 | 1.227 | .942 | .916 | |
| PerLeader5 | .550 | .848 | 1.399 | .925 | 1.486 | |
| PerLeader6 | .796 | .807 | .892 | 1.140 | 1.383 | |
| Variance | 2.381 | 2.563 | 2.698 | 2.464 | 2.658 | 3.119 |
| 2.464 | 2.350 | 2.493 | 2.529 | 2.167 | 3.071 | |
| M | 4.357 | 5.398 | 5.135 | 5.286 | 5.178 | 5.269 |
| 4.566 | 4.427 | 4.586 | 4.916 | 4.794 | 4.948 | |
| Nutrition Behaviors |
||||||
|---|---|---|---|---|---|---|
| Nutrit1 | Nutrit2 | Nutrit3 | Nutrit4 | Nutrit5 | Nutrit6 | |
| Nutrit1 | .658 | .633 | .622 | .480 | .560 | |
| Nutrit2 | .714 | .594 | .589 | .482 | .532 | |
| Nutrit3 | .659 | .848 | .819 | .742 | .781 | |
| Nutrit4 | .642 | .750 | .803 | .708 | .792 | |
| Nutrit5 | .607 | .776 | .947 | .861 | .941 | |
| Nutrit6 | .752 | .635 | .996 | .734 | 1.097 | |
| Variance | 1.328 | 1.354 | 1.435 | 1.433 | 1.636 | 1.850 |
| 1.260 | 1.064 | 1.220 | 1.259 | 1.367 | 1.491 | |
| M | 3.878 | 4.367 | 4.092 | 4.227 | 4.195 | 4.121 |
| 4.049 | 4.029 | 4.075 | 4.094 | 3.944 | 4.030 | |
Note. Treatment group in regular font; control group in italic. The covariances and the means are the estimates of the sample covariances and means estimated using the Maximum Likelihood method to adjust for the missing data. Nutrit1–Nutrit6 = Nutrition behaviors measured from Time 1 to Time 6; PerLeader1–PerLeader6 = Perceived importance of peer team leaders as an information source measured from Time 1 to Time 6.
TABLE 2.
Growth Process of Peer Team Leaders as an Information Source and Nutrition Behaviors by Group
| Peer Team Leaders as an Information Source (PerLeader) | |||||
|---|---|---|---|---|---|
| χ2(39)=155.204, p < .001; RMSEA=.067, 90% CI: .056, .078 | |||||
| Control Group (n = 730) | Treatment Group (n = 609) | ||||
| Initial Status | Growth Rate | Initial Status | Growth Rate | ||
| Factor loadings on growth factors | |||||
| PerLeader 1 | 1a | 0a | 1a | 0a | |
| PerLeader 2 | 1a | 1a | 1a | 1a | |
| PerLeader 3 | 1a | .874 (.071)b | = | 1a | .874 (.071)b |
| PerLeader 4 | 1a | 1a | 1a | 1a | |
| PerLeader 5 | 1a | 1a | 1a | 1a | |
| PerLeader 6 | 1a | 1a | 1a | 1a | |
| Intercept | 4.587 (.044)b | = | 4.587 (.044)b | ||
| Growth factors | M | Variance | M | Variance | |
| Initial status | 0a | 1.030 (.132)b | −.233 (.077)b | .954 (.177)b | |
| Growth rate | 0a | 0a | .947 (.071)b | .590 (.203)b | |
| Covariance between growth factors | |||||
| −.058 (.076)b | −.224 (.172)b | ||||
| Residual variances | |||||
| PerLeader 1 | 1.443 (.113)b | = | 1.443 (.113)b | ||
| PerLeader 2 | 1.501 (.084)b | = | 1.501 (.084)b | ||
| PerLeader 3 | 1.507 (.090)b | = | 1.507 (.090)b | ||
| PerLeader 4 | 1.709 (.128)b | = | 1.709 (.128)b | ||
| PerLeader 5 | 1.421 (.110)b | = | 1.421 (.110)b | ||
| PerLeader 6 | 2.131 (.209)b | = | 2.131 (.209)b | ||
| Nutrition Behaviors (Nutrit) | |||||
|---|---|---|---|---|---|
| χ2 (39) = 123.035, p < .001; RMSEA = .057, 90% CI: .046, .068 | |||||
| Control Group (n = 730) | Treatment Group (n = 609) | ||||
| Factor loadings on growth factors | Initial Status | Growth Rate | Initial Status | Growth Rate | |
| Nutrit 1 | 1a | 0 | 1a | 0a | |
| Nutrit 2 | 1a | 1 | 1a | 1a | |
| Nutrit 3 | 1a | .636 (.097)b | = | 1a | .636 (.097)b |
| Nutrit 4 | 1a | 1 | 1a | 1a | |
| Nutrit 5 | 1a | 1 | 1a | 1a | |
| Nutrit 6 | 1a | 1 | 1a | 1a | |
| Intercept | 4.041 (.033)b | = | 4.041 (.033)b | ||
| Growth factors | M | Variance | M | Variance | |
| Initial status | 0a | .632 (.065)b | −.171 (.058)b | .667 (.084)b | |
| Growth rate | 0a | 0a | .423 (.044)b | .108 (.079)b | |
| Covariance between growth factors | |||||
| −.008 (.037)b | .039 (.069)b | ||||
| Residual variances | |||||
| Nutrit 1 | .662 (.045)b | = | .662 (.045)b | ||
| Nutrit 2 | .516 (.032)b | = | .516 (.032)b | ||
| Nutrit 3 | .563 (.035)b | = | .563 (.035)b | ||
| Nutrit 4 | .584 (.046)b | = | .584 (.046)b | ||
| Nutrit 5 | .753 (.056)b | = | .753 (.056)b | ||
| Nutrit 6 | .852 (.085)b | = | .852 (.085)b | ||
Note. = parameter equated across groups.
Parameter fixed in the model.
Parameter estimate with the standard error of estimate in parentheses.
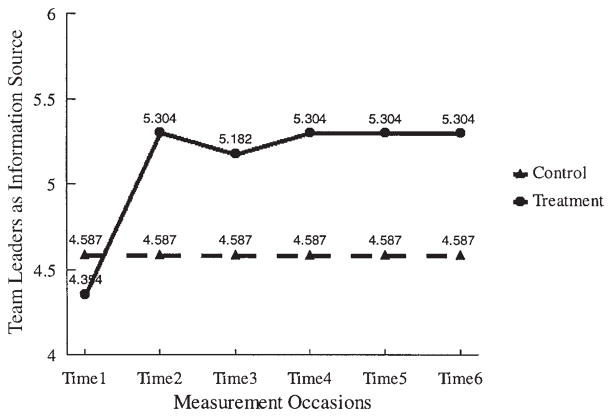
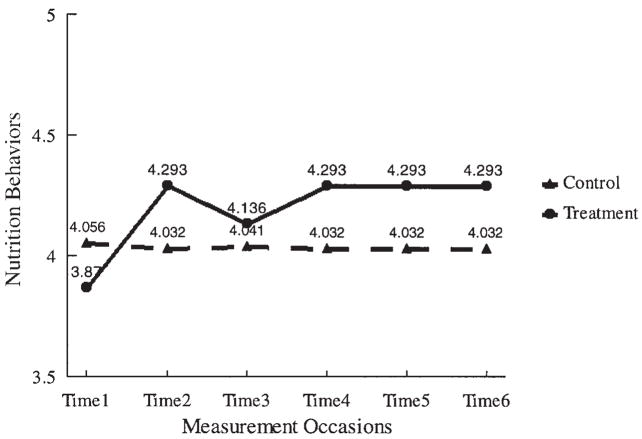
Comparing the average growth rates between the treatment and the control groups, the average growth rate for the treatment group was positive and statistically significant for both perceived importance of team leaders and nutrition behaviors, whereas the growth rates for the control group were not significant. The difference in the growth rate between the two groups was .947 (SEgrowth rate = .071, p < .001) for perceived importance of team leaders and .423 (SEgrowth rate = .044, p < .001) for nutrition behaviors. These results indicate that the treatment group’s growth trajectory of perceived importance of team leaders and growth trajectory of nutrition behaviors were shifted upward due to the ATLAS prevention program, whereas the control group stayed at the same level as baseline. In addition, there was a significant difference in the average initial status between the treatment and the control groups. The initial status of the treatment group was lower than the control group for both importance of team leaders (Mstatus = 4.354 for treatment group, Mstatus = 4.587 for control group; p < .01) and nutrition behaviors (Mstatus = 3.870 for treatment group, Mstatus = 4.041 for control group; p < .01). However, the difference in the initial status is unlikely to be attributable to the different treatment conditions because the initial status was the true level at baseline, which took place before the delivery of the program.
The variance of the growth rate factor for the treatment group was significant for importance of team leaders, Var (Growth RatePerLeader) = .590, SE = .203, p < .01, indicating that although the treatment program increased the perceived importance of peer team leaders on average, the increment was different across individuals. The variance of the growth rate factor for nutrition behaviors was not significant for the treatment group, Var (Growth RateNutrit) = .108, SE = .079, ns. The covariance between the initial status and the growth rate factors was negative but was not statistically significant for both groups for both processes. Figures 3 and 4 show the estimated means of perceived importance of team leaders and nutrition behaviors across time for the treatment and control groups.
FIGURE 3.
Model-based change in peer team leaders as an information source over six measurement time points.
FIGURE 4.
Model-based change in nutrition behaviors over six measurement time points.
As expected, there was a slight decay of program effect at Time 3 (1-year follow-up). The factor loading of Time 3 on the growth rate factor was slightly smaller than 1 but significantly different from 0 for both importance of team leaders, λ32(m) = .874, SE = .071, p < .001, and nutrition behaviors, λ32(y) = .636, SE = .097, p < .001. These results suggest that the program effect achieved by the initial full prevention program could deteriorate in time without the booster programs.
Assessment of Mediation
The latent growth model for the mediator process and the latent growth model for the outcome process were combined into one parallel process latent growth model. The trajectory shape was specified as in the previous step. Now that the treatment and the control groups were found to be different in their average growth rates, the variable coding the group membership was introduced as a covariate to explain the group differences in growth trajectory.
As an intermediate step, the two growth curve models for the mediator and the outcome processes were combined as parallel processes influenced only by the treatment program and the relations among growth factors of the two processes were not estimated. The model fit of this intermediate model yielded a χ2 of 487.427 with 76 df (p < .001) and the RMSEA estimate of .064 with 90% CI = (.058, .069). Following the estimation of the intermediate model, the relation between the growth factors of the two processes was added (Figure 5). The model shown in Figure 5 fits the data well, χ2(72) = 317.298, p < .001; RMSEA = .050 with 90% CI = (.045, .056). The chi-square difference between the intermediate model and the final model was statistically significant, Δχ2(4) = 170.131, p < .001, indicating that modeling the relations among the latent growth factors improves the model fit significantly and thus justifies inclusion of the mediational process in the model.
FIGURE 5.
A parallel process latent growth model for mediation: Program effect on the growth of nutrition behaviors via the growth of perceived importance of peer team leaders as an information source. Program = prevention program condition; Nutrit = nutrition behaviors (outcome); PerLeader = team leaders as an information source (mediator); η1 = initial status factor of PerLeader; η2 = growth rate factor of PerLeader; η3 = initial status factor of Nutrit; η4 = growth rate factor of Nutrit.
The main interest in the parallel process growth curve model in Figure 5 is in the relations among the prevention program and the growth rate factors of the two processes. The estimates of these relations are shown in Figure 5 and the more detailed results are reported in Table 3. The effect of the treatment program on the growth rate factor of importance of team leaders was significant (α = .859, SE = .089, p < .001) and the effect of the growth rate factor of importance of team leaders on the growth rate factor of nutrition behaviors was also significant (β = .891, SE = .226, p < .001). This implies a mediational process in such a way that the exposure to the ATLAS program led to positive change in perceived importance of team leaders over time, which, in turn, led to positive change in nutrition behaviors over time. The estimated mediated effect (αβ) was .765 and the estimated standard error of the mediated effect (σαβ) based on the first-order solution was .210, indicating a significant mediated effect (zαβ = 3.643, p < .001). The mediated effect tested based on the asymmetric CI method was also significant, 95% CI = (.372, 1.196).
TABLE 3.
Parameter Estimates in the Parallel Process Latent Growth Curve Model for Mediation
| χ2 (38) = 122.648, p < .001; RMSEA = .058, 90% CI: .046, .069 | |||
|---|---|---|---|
| Mediator process: Peer team leaders as an information source (PerLeader) | |||
| Factor loadings on growth factors | Initial Status | Growth Rate | Residual Variances |
| PerLeader 1 | 1a | 0a | 1.421 (.077)b |
| PerLeader 2 | 1a | 1a | 1.472 (.088)b |
| PerLeader 3 | 1a | .894 (.068)b | 1.504 (.084)b |
| PerLeader 4 | 1a | 1a | 1.718 (.128)b |
| PerLeader 5 | 1a | 1a | 1.430 (.110)b |
| PerLeader 6 | 1a | 1a | 2.078 (.204)b |
| Intercepts | |||
| PerLeader 1–6 | 4.564 (.058)b | ||
| Initial status(p) | 0a | .997 (.069)b | |
| Growth rate(p) | .033 (.060)b | .224 (.069)b | |
| Outcome process: Nutrition behaviors (Nutrit) | |||
| Factor loadings on growth factors | Initial Status | Growth Rate | Residual Variances |
| Nutrit 1 | 1a | 0a | .430 (.069)b |
| Nutrit 2 | 1a | 1a | .583 (.036)b |
| Nutrit 3 | 1a | .848 (.074)b | .507 (.032)b |
| Nutrit 4 | 1a | 1a | .578 (.045)b |
| Nutrit 5 | 1a | 1a | .759 (.057)b |
| Nutrit 6 | 1a | 1a | .843 (.084)b |
| Intercepts | |||
| Nutrit 1–6 | 4.052 (.042)b | ||
| Initial status(n) | 0a | .868 (.077)b | |
| Growth rate(n) | −.049 (.061)b | .067 (.041)b | |
| Group | M .455 (.014)b | Variance .248 (.010)b | |
| Mediational process | |||
| Group → Growth rate(p) | .859 (.089)b | ||
| Growth Rate(p) → Growth rate(n) | .891 (.226)b | ||
| Group → Growth rate(n) | −.393 (.221)b | ||
| Initial Status(p) →Growth rate(n) | .022 (.043)b | ||
| Initial Status(n) → Growth rate(p) | −.301 (.048)b | ||
| Group → Initial status(n) | −.181 (.063)b | ||
| Group → Initial status(p) | −.213 (.086)b | ||
Note. Initial status(p) = status factor of PerLeader; Growth rate(p) = growth rate factor of PerLeader; Initial status(n) = status factor of Nutrit; Growth rate(n) = growth rate factor of Nutrit.
Parameter fixed in the model.
Parameter estimate with the standard error of estimate in parentheses.
DISCUSSION
Procedures for applying latent growth curve modeling to the examination of program effects and mediation effects were outlined in this study. An example from a prevention study, entitled ATLAS, was used to illustrate the method. First, the growth trajectory of the mediator process and the growth trajectory of the outcome process were investigated, followed by assessing the program effect on the growth trajectories. The growth trajectory across six measurement occasions was modeled to reflect the program effect achieved by the full prevention program, a slight decay of effect, and a program effect recovered and maintained by the booster programs. Because the prevention programs were delivered only to the treatment group, it was examined whether this specification was appropriate to describe the data from both groups. Using the two-group SEM technique, the appropriateness of the specification of the growth trajectory was assessed by the overall model fit and the program effect on the growth trajectory was evaluated by comparing the means of the growth rate factors between the treatment and the control groups. Alternatively, the investigation of different trajectory shapes between the two groups can be carried out by examining each group’s trajectory separately. When the trajectory form is found to be appropriate for both treatment and control groups, two groups can be combined and the latent growth factors can be regressed on the group membership to account for the trajectory differences between the groups. The coefficient of the growth rate factor on the group membership represents the program effect; that is, the mean shift in the growth rate due to the prevention program.
It appears that the ATLAS prevention program shifted the growth trajectory of the mediator and the growth trajectory of the outcome upward. Perceived importance of team leaders increased and nutrition behaviors improved for the treatment group after the full prevention program was implemented in the first year. A slight decay of the program effect was found during the long period between the full prevention program and the 1-year follow-up assessment; however, this decay was recovered and maintained by the booster programs delivered in the later years. These results suggest not only the effectiveness of the ATLAS prevention program but also the importance of booster programs. The program effect achieved by the full prevention program could deteriorate in time and the booster programs may be needed to maintain the program effects.
The mediation was modeled and estimated using the parallel process LGM method. In this approach, mediation is defined such that the treatment program influences the growth of the outcome process indirectly by influencing the growth of the mediator process. Thus, the presence of significant mediation depends on whether the treatment program changes the growth trajectory of the mediator and whether the change of the growth trajectory of the mediator, in turn, is related to the change in the growth trajectory of the outcome variable. In this study, it was found that the ATLAS prevention program significantly increased both perceived importance of the team leaders (mediator) and nutrition behaviors (outcome) over time. Furthermore, the growth trajectory of perceived importance of team leaders was significantly related to the growth trajectory of nutrition behaviors such that the greater the increase in perceived importance of team leaders over time, the greater the improvement in nutrition behaviors over time. The test of mediation indicates that the ATLAS program shifted the growth trajectory of the nutrition behaviors upward by changing the growth trajectory of the positive peer influence (i.e., perceiving that the team leaders are a valuable information source about healthy diet, strength training, and drug prevention).
Although growth curve modeling is beginning to appear in the context of mediation analysis (e.g., Muthén & Curran, 1997), parallel process latent growth curve modeling has been applied in only a few studies investigating mediation (e.g., Cheong, MacKinnon, & Khoo, 2001; Sandler, Tein, Mehta, Wolchik, & Ayers, 2000). In our previous study (Cheong et al., 2001), we investigated the possibility of applying the parallel process LGM to mediation analysis for randomized prevention trials. Sandler et al. (2000) modeled three latent growth processes and examined the relations among the growth process of independent variable, the growth process of the mediator, and the growth process of the outcome. However, Sandler et al. (2000) did not include a randomized treatment group situation.
There are several advantages of the parallel process LGM method for mediation analysis. This approach allows for estimation of the individual differences in growth over time. In real life situations, there are considerable individual differences in development and modeling the individual differences is more representative of the reality. Another advantage of the parallel process LGM method is that the growth of the mediator and the growth of the outcome can be modeled simultaneously and the change in the mediator can be related to the change in the outcome variable in the structural model. This provides a superior method for investigating mediational processes in longitudinal studies. Furthermore, the flexibility of SEM is allowed in the parallel process LGM method for assessing mediation. For example, the growth curve of the mediator and the outcome can be modeled to reflect various trajectory shapes, including a linear or a curvilinear trajectory. Also, the trajectory shape of the mediator can be modeled differently from the trajectory of the outcome. The growth curve of the mediator can be a straight line, whereas the growth curve of the outcome is a stabilized plateau after the initial shift, as modeled in this study.
When the group membership variable represents random assignment to treatment or control groups, the interpretability of the mediation model is improved because the effect of the program on the growth of the mediator and the growth of the outcome can be attributed more confidently to the program assignment. Under random assignment, the counterfactual trajectory, the trajectory that would have been obtained if the individuals had been assigned to the other condition, is missing completely at random. Thus, the difference in the mean trajectories of the two groups can be used as an unbiased estimate of the average treatment effect (Raudenbush, 2001). On the other hand, the relation between the growth of the mediator process and the growth of the outcome process is more complicated. Although the explicit modeling of longitudinal growth in the mediator and the outcome makes it a better test of this relation than the cross-sectional data because multiple measurements are used to estimate true long-term change, a causal statement regarding the relation between the growth rate factors of the two processes should be based on strong theory. Without strong theory, the relation between the growth rate factors of the two processes may only be interpreted as correlational because the mediator and the outcome variables were measured simultaneously on each occasion and levels on the mediator were not randomly assigned.
As the number of measurement occasions increases, more complex models can be estimated. For example, the growth across time can be evaluated in two different phases by using piecewise growth models (e.g., Khoo, 2001). In the two-phase piecewise models, the growth at the earlier phase and the growth at the later phase can be modeled simultaneously in one model. One of the benefits of the two-phase parallel process model is that the change in one process at the earlier phase can be modeled to predict the change in the other process at the later phase. This would provide a more convincing test of the mediational hypothesis because the change in the mediator preceding the change in the outcome may be investigated.
There are a few issues to be considered in the present study. One issue is the influence of attrition. In the ATLAS study, participants who graduated from high school or quit the football team were no longer available for follow-up measurements. To adjust for the missing data, we used the ML method. The ML estimates adjusting for missing data are less biased than the estimates obtained by pairwise or listwise deletion, even when the assumption of missing at random is not strictly satisfied (Arbuckle, 1996; Little & Rubin, 1989; Muthén, Kaplan, & Hollis, 1987). Also, the ML estimates are slightly more efficient than the estimates obtained by Multiple Imputation when the sample size is reasonably large (Schafer & Olsen, 1998). However, it is not clear how the use of these methods and the amount of attrition affect the accuracy of growth curve models. Another issue is the nesting of individuals within school teams. In this study, data were analyzed at the individual level because the theories on which the ATLAS prevention program was based were conceptualized at the individual level and the intraclass correlations (ICC) at the baseline assessment were small (ICC = .03 for nutrition behavior; ICC = .02 for perceived importance of team leaders). However, other nonparametric methods such as the bootstrapping method can be used to estimate the standard errors and construct CIs or multilevel modeling can be incorporated when the magnitude of the ICCs is substantial.
There are at least two future directions for this research. First, simulation studies can be conducted. Although applications of parallel process LGM have begun to appear in the substantive research, little is known about how accurately the parameters are recovered. Researchers can set the parameter values of the population model for the parallel process and investigate the conditions under which an accurate representation of the true population model is reproduced. In addition, Type I error rates and statistical power can be investigated. Second, more applications of the parallel process growth model are needed to understand practical issues. For example, researchers can probe questions such as whether the mediated effect estimated with this approach is statistically significant or how accurately the growth trajectories can be identified across different substantive areas. In any case, latent growth curve models for the investigation of the mediational process show considerable promise.
Acknowledgments
This project was supported by Grants R01–DA07356 and R01–DA09757–04 from the National Institute on Drug Abuse.
Contributor Information
JeeWon Cheong, Department of Psychology, State University of New York at Albany.
David P. MacKinnon, Department of Psychology, Arizona State University
Siek Toon Khoo, Department of Psychology, Arizona State University.
References
- Ajzen I, Madden TJ. Prediction of goal-directed behavior: Attitudes, intentions, and perceived behavioral control. Journal of Experimental Social Psychology. 1986;22:453–474. [Google Scholar]
- Arbuckle JL. Full information estimation in the presence of incomplete data. In: Marcoulides GA, Schumacker RE, editors. Advanced structural equation modeling: Issues and techniques. Mahwah, NJ: Lawrence Erlbaum Associates, Inc; 1996. pp. 243–277. [Google Scholar]
- Aroian LA. The probability function of the product of two normally distributed variables. Annals of Mathematical Statistics. 1947;18:265–271. [Google Scholar]
- Bandura A. Social learning theory. Englewood Cliffs, NJ: Prentice Hall; 1977. [Google Scholar]
- Baron RM, Kenny DA. The moderator–mediator distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bryk AS, Raudenbush SW. Hierarchical linear models for social and behavioral research: Applications and data analysis methods. Newbury Park, CA: Sage; 1992. [Google Scholar]
- Chen H-T. Theory-driven evaluations. Newbury Park, CA: Sage; 1990. [Google Scholar]
- Cheong J, MacKinnon DP, Khoo ST. A latent growth modeling approach to mediation analysis [Abstract] In: Collins L, Sayer A, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 390–392. [Google Scholar]
- Donaldson SI, Graham JW, Hansen WB. Testing the generalizability of intervening mechanism theories: Understanding the effects of adolescent drug use prevention interventions. Journal of Behavioral Medicine. 1994;17:195–216. doi: 10.1007/BF01858105. [DOI] [PubMed] [Google Scholar]
- Du Toit SHC, Cudeck R. The analysis of nonlinear random coefficient regression models with LISREL using constraints. In: Cudeck R, Du Toit SHC, Sörbom D, editors. Structural equation modeling: Present and future. Lincolnwood, IL: Scientific Software International; 2001. pp. 259–278. [Google Scholar]
- Fishbein M, Ajzen I. Beliefs, attitude, intention, and behavior: An introduction to theory and research. Reading, MA: Addison-Wesley; 1975. [Google Scholar]
- Goldberg L, Elliot D, Clarke GN, MacKinnon DP, Moe E, Zoref L, et al. Effects of a multidimensional anabolic steroid prevention intervention: The Adolescents Training and Learning to Avoid Steroids (ATLAS) program. Journal of the American Medical Association. 1996;276:1555–1562. [PubMed] [Google Scholar]
- Goldberg L, MacKinnon D, Elliot D, Moe E, Clarke G, Cheong J. The ATLAS program: Preventing drug use and promoting health behaviors. Archives of Pediatric and Adolescent Medicine. 2000;154:332–338. doi: 10.1001/archpedi.154.4.332. [DOI] [PubMed] [Google Scholar]
- Goldstein H. Multilevel statistical models. 2. New York: Wiley; 1995. [Google Scholar]
- Goodman LA. On the exact variance of products. Journal of the American Statistical Association. 1960;55:708–713. [Google Scholar]
- Harford TC, Muthén BO. Alcohol use among college students: The effects of prior problem behaviors and change of residence. Journal of Studies of Alcohol. 2001;62:306–312. doi: 10.15288/jsa.2001.62.306. [DOI] [PubMed] [Google Scholar]
- Janz NK, Becker MH. The health belief model: A decade later. Health Education Quarterly. 1984;11:1–47. doi: 10.1177/109019818401100101. [DOI] [PubMed] [Google Scholar]
- Judd CM, Kenny DA. Process analysis: Estimating mediation in treatment evaluations. Evaluation Review. 1981;5:602–619. [Google Scholar]
- Khoo ST. Assessing program effects in the presence of treatment–baseline interactions: A latent curve approach. Psychological Methods. 2001;6:234–257. doi: 10.1037/1082-989x.6.3.234. [DOI] [PubMed] [Google Scholar]
- Little RJA, Rubin DB. The analysis of social science data with missing values. Sociological Methods and Research. 1989;18:292–326. [Google Scholar]
- Longford N. Random coefficient models. Oxford, England: Clarendon; 1993. [Google Scholar]
- MacKinnon DP. Analysis of mediating variables in prevention intervention studies. In: Cazares A, Beatty LA, editors. Scientific methods for prevention intervention research. NIDA research monograph 139. Washington, DC: U.S. Government Printing Office; 1994. pp. 127–153. DHHS Pub. Number 94-3631. [PubMed] [Google Scholar]
- MacKinnon DP. Mediating variable. In: Smelser NJ, Baltes PB, editors. International encyclopedia of the social and behavioral sciences. New York: Elsevier; 2001. pp. 9503–9507. [Google Scholar]
- MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Evaluation Review. 1993;17:144–158. [Google Scholar]
- MacKinnon DP, Goldberg L, Clarke GN, Elliot DL, Cheong J, Lapin A, et al. Mediating mechanisms in a program to reduce intentions to use anabolic steroids and improve exercise self-efficacy and dietary behavior. Prevention Science. 2001;2:15–28. doi: 10.1023/a:1010082828000. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP, Johnson CA, Pentz MA, Dwyer JH, Hansen WB, Flay BR, et al. Mediating mechanisms in a school-based drug prevention program: First-year effects of the Mid-western prevention project. Health Psychology. 1991;10:164–172. doi: 10.1037//0278-6133.10.3.164. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Williams J. Confidence limits for the indirect effect: Distribution of the product and resampling methods. 2002 doi: 10.1207/s15327906mbr3901_4. Manuscript submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Warsi G, Dwyer JH. A simulation study of mediated effect measures. Multivariate Behavioral Research. 1995;30:41–62. doi: 10.1207/s15327906mbr3001_3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meredith W, Tisak J. Latent curve analysis. Psychometrika. 1990;55:107–122. [Google Scholar]
- Muthén BO, Curran PJ. General longitudinal modeling of individual differences in experimental designs: A latent variable framework for analysis and power estimation. Psychological Methods. 1997;2:371–402. [Google Scholar]
- Muthén BO, Kaplan D, Hollis M. On structural equation modeling with data that are not missing completely at random. Psychometrika. 1987;52:431–462. [Google Scholar]
- Muthén BO, Muthén L. Mplus user’s guide. Los Angeles: Author; 2001. [Google Scholar]
- Park J, Kosterman R, Hawkins JD, Haggerty KP, Duncan TE, Duncan SC, et al. Effects of the “preparing for the drug free years” curriculum on growth in alcohol use and risk for alcohol use in early adolescence. Prevention Science. 2000;1:125–138. doi: 10.1023/a:1010021205638. [DOI] [PubMed] [Google Scholar]
- Raudenbush SW. Comparing personal trajectories and drawing causal inferences from longitudinal data. Annual Reviews of Psychology. 2001;52:501–525. doi: 10.1146/annurev.psych.52.1.501. [DOI] [PubMed] [Google Scholar]
- Rogosa D. Myths about longitudinal research. In: Schaie KW, Campbell RT, Meredith W, Rawlings SC, editors. Methodological issues in aging research. NewYork: Springer; 1988. pp. 171–205. [Google Scholar]
- Rogosa D, Brandt D, Zimowski M. A growth curve approach to the measurement of change. Psychological Bulletin. 1982;90:726–748. [Google Scholar]
- Sandler IN, Tein JY, Mehta P, Wolchik S, Ayers T. Coping efficacy and psychological problems of children of divorce. Child Development. 2000;71:1099–1118. doi: 10.1111/1467-8624.00212. [DOI] [PubMed] [Google Scholar]
- Schafer JL, Olsen MK. Multiple imputation of multivariate missing-data problems: A data analyst’s perspective. Multivariate Behavioral Research. 1998;33:545–571. doi: 10.1207/s15327906mbr3304_5. [DOI] [PubMed] [Google Scholar]
- Sobel ME. Asymptotic confidence intervals for indirect effects in structural equation models. In: Leinhard S, editor. Sociological methodology 1982. Washington, DC: American Sociological Association; 1982. pp. 290–312. [Google Scholar]
- Stoolmiller M. Using latent growth curve models to study developmental processes. In: Gottman JM, editor. The analysis of change. Mahwah, NJ: Lawrence Erlbaum Associates, Inc; 1995. pp. 103–138. [Google Scholar]
- Taylor BJ, Graham JW, Cumsille P, Hansen WB. Modeling prevention program effects on growth in substance use: Analysis of five years of data from the adolescent alcohol prevention trial. Prevention Science. 2000;1:183–197. doi: 10.1023/a:1026547128209. [DOI] [PubMed] [Google Scholar]
- Willett JB, Sayer AG. Using covariance structure analysis to detect correlates and predictors of individual change over time. Psychological Bulletin. 1994;116:363–381. [Google Scholar]