Abstract
We have been developing force fields designed for the eventual simulation of peptides and proteins using the Kirkwood-Buff (KB) theory of solutions as a guide. KB theory provides exact information on the relative distributions for each species present in solution. This information can also be obtained from computer simulations. Hence, one can use KB theory to help test and modify the parameters commonly used in biomolecular studies. A series of small molecule force fields representative of the fragments found in peptides and proteins have been developed. Since this approach is guided by the KB theory, our results provide a reasonable balance in the interactions between self-association of solutes and solute solvation. Here, we present our progress to date. In addition, our investigations have provided a wealth of data concerning the properties of solution mixtures, which is also summarized. Specific examples of the properties of aromatic (benzene, phenol, p-cresol) and sulfur compounds (methanethiol, dimethylsulfide, dimethyldisulfide) and their mixtures with methanol or toluene are provided as an illustration of this kind of approach.
Keywords: KB theory, molecular simulation, force fields, KBFF, alcohols
Introduction
Protein force fields (FFs) assume that a protein behaves as a sum of its parts and that the interactions between these parts, or functional groups, are the same as between the isolated functional groups themselves [1,2]. For example, serine is one of the amino acids found in proteins. The side chain of serine contains the CH2OH functional group. Hence, the parameters adopted for serine side chains are often determined by reproducing the properties of methanol molecules in the gas phase. In some cases, the accuracy of the parameters would be further tested by determining the properties of pure methanol solutions [3]. This type of approach has resulted in several FFs capable of studying a variety of biomolecular systems [4–7]. Burgeoning computational power has ensured a reduction of sampling issues and led to more quantitative comparisons between simulations and experiments. These advancements have created a pressing need for increasingly accurate FFs.
In our opinion, a serious drawback with the above approach is that mixtures of the required functional groups in water are rarely studied to validate the FFs. It is generally assumed that the properties of aqueous solutions of these solutes are adequately reproduced, even though the parameterization typically relies on studies of pure liquids and little attention is given to reproducing the solutes’ properties in mixtures over the full composition range. Indeed, many properties of solution mixtures (e.g., densities, dielectric constants, and compressibilities) are usually well reproduced, but others (e.g., diffusion constants and the enthalpy of mixing) are more problematic [8]. The diffusion constants are often very sensitive to small errors in the density, and both experimental diffusion and enthalpy of mixing data in aqueous solutions are not always available for all the functional groups observed in proteins. Hence, the results obtained for the latter data are of usually of minor concern.
More recently, biomolecular FFs have used free energies or free enthalpies of solvation data for a series of solutes [9,10]. This helps to probe solute-solvent interactions, although only at infinite dilution, but does not provide a check of solute-solute interactions. To our knowledge, arguably the most important thermodynamic property of solution mixtures, the solute activity, is never tested during the development of biomolecule FFs. Since solute activity is a measure of the balance between solute-solute and solute-solvent interactions in mixtures, the only way to ensure a correct description of the microscopic structure of solution mixtures is to accurately reproduce the changes in solute activity with solute concentration [11]. We believe that the ability to reproduce solute activities should be a key feature of a force field if it is to be considered reliable. In principle, the solute chemical potential could be determined by thermodynamic integration, but the free energy changes are often small and require a high degree of precision [12].
Our major goal is the development of improved FFs for biomolecules using changes in solute activity as a guide. However, some previous FFs developed for other uses have also included data related to chemical potentials. The most noticeable example is the TraPPE FFs of Siepmann and coworkers [13,14]. Here, the quantitative agreement with vapor-liquid coexistence curves ensures that the chemical potentials (vapor pressures) of both components are correctly reproduced as a function of temperature. In contrast, most biomolecule FFs would be expected to reproduce solute activities as a function of concentration close to ambient temperatures. Ideally an accurate FF should do both. However, this is unlikely with current models. We doubt the FFs optimized at ambient temperatures can quantitatively reproduce the coexistence curves because these curves span a broad range of temperatures. It is also not clear to what extent the TraPPE FFs reproduce activity changes with composition at a fixed temperature. The KB approach has the advantage that one can easily study nonvolatile solutes.
Recently, we have studied the properties of a variety of solution mixtures obtained using common biomolecule FFs available in the literature [15–17]. In particular, changes in the solute activity were determined and compared with experiment with the use of Kirkwood-Buff (KB) theory. In most cases the currently available FFs do not accurately reproduce the changes in activity, and therefore do not provide a reliable description of the molecular distributions suggested by experiment. Consequently, we have embarked on a series of studies to generate more accurate force fields for computer simulation of liquid mixtures where the solute activity is reasonably well reproduced. Our eventual aim is a full protein force field. Here, we summarize our results to date. Furthermore, we investigate the properties of mixtures of hydrophobic groups (benzene, toluene, methanethiol, dimethylsulfide, dimethyldisulfide) with alcohols (methanol, phenol, p-cresol), especially at low alcohol mole fractions, as provided by these new models in an effort to illustrate the power of this approach.
Overview
Our focus has been the use of Kirkwood-Buff theory to gain insight into the solute activity and intermolecular distributions for solution mixtures. KB theory provides a direct link between the radial distribution functions (rdfs) observed for all molecular pairs and the thermodynamic properties of the solution. The central quantities of interest are the KB integrals (KBIs) between species i and j given by [11,18],
| (1) |
where gij is the corresponding center of mass based rdf. The above integral relates the distribution of j molecules around a central i molecule. The KBIs can be determined from molecular simulation or from appropriate experimental data as outlined below.
KB theory can be used to study any multicomponent solution Ref. Our focus is on binary solutions of both volatile and nonvolatile solutes. Application of KB theory to a binary solution of solvent (1) and solute (2) provides the following relationships for the derivatives of the chemical potential or activity of the cosolvent (μ2 or a2) with respect to molarity (ρ) or mole fraction (x), the partial molar volumes V̄ and the isothermal compressibility (κT) at a given temperature (T) and pressure (P) [18],
| (2) |
| (3) |
| (4) |
| (5) |
where
| (6) |
and β = 1/RT, with R being the Gas constant.
For binary mixtures there are three KBIs to be determined for each composition to be studied. The KBIs can be calculated from the simulated rdfs by simple integration to a point where g(r) approaches unity. The corresponding experimental KBIs can be extracted from data characterizing the changes in solute activity, solution density, and solution compressibility with composition [19] through the relationships outlined in Equations 2–5. The above expressions (Equations 2–5) are exact. Hence, an accurate force field for the description of solute-solvent mixtures should reproduce the experimental KBIs and thereby ensure a reasonable description of the solute activity.
Unfortunately, early studies of a variety of solute FFs indicated that the experimental KBIs were not, in general, well reproduced [15,20–22]. In fact, the agreement with experiment was often very poor. This implies an incorrect balance between solute-solute self association (G22) and solute solvation (G21). This imbalance must arise from inappropriate intermolecular potentials i.e., inaccurate FF parameters. To solve this problem we have been developing FFs for small solutes specifically designed to reproduce the experimental KBIs. Hence, we have labeled this the Kirkwood-Buff derived force field (KBFF) approach. In the following section we outline our results to date and how they have improved our understanding of solutions. In particular, we focus on hydrophobic solutes in alcohol solvents and comment on the similarities in the clustering of alcohol molecules, a feature observed across different systems for low alcohol mole fractions. The microscopic view of these alcohol solutions is intriguing because, although alcohols are macroscopically homogeneous and disordered, we see that they exhibit heterogeneity and local order on the microscopic scale. Significant efforts are being taken to understand the relationship among the liquid microstructure observed from computer simulations, statistical solution theories, experimental correlation functions obtained from spectroscopy, and experimental solution thermodynamics [23–26]. For example, our KB derived approach essentially implies that, while a number of force fields are able to produce many thermodynamic properties of solutions, these are necessary, but not sufficient, conditions for accurate descriptions of solutions. Information on the microstructure e.g., the KBIs, is of key importance as well.
Simulation Details
Here we provide a brief description of the typical simulation conditions used in the development of the new FFs. More details can be found in our recent studies [27,28]. All mixtures are simulated via classical molecular dynamics techniques using the Gromacs program (version 3.3) [29]. The simulations are performed in the isothermal-isobaric NpT ensemble at the temperature and pressure of interest using Berendsen thermostats and barostats [30]. All solute and solvent bonds are constrained using the LINCS algorithm [31]. A 2 fs time step is used for integration of the equations of motion. Electrostatic interactions are evaluated using the particle-mesh-Ewald technique [32] with cutoff distances of 1.2 nm and of 1.5 nm for the real space electrostatic and van der Waals interactions, respectively. The SPC/E water model is adopted for all aqueous simulations [33].
The KBIs have to be truncated in closed systems. We have discussed this issue in detail [20,21,27]. Typically, the integral is truncated after several solvation shells (1–1.5 nm) depending on the size of the solute and solvent. To eliminate statistical variations we have averaged the integral values over a small range of integration distances, typically corresponding to one solvation shell. The accuracy of this truncation procedure can be checked by determining the simulated partial molar volumes and compressibility using other approaches, and comparing with the values obtained from Equations 4 and 5 [27]. Error estimates are typically obtained from multiple 1–5ns block averages.
The simulations presented here involve a series of solutes and solvents. The force fields for methanol and sulfur compounds were taken from the literature [27,28]. The force fields for aromatic compounds have been recently developed and will be submitted for publication shortly [34]. The nonbonded parameters for these aromatic molecules are: q = −0.13, ε = 0.33, σ = 0.381 for aromatic carbons; q = 0.13, ε = 0.088, σ = 0.158 for aromatic hydrogens; and q = 0.0, ε = 0.8672, σ = 0.3742 for united atom methyls. The σ and ε parameters for the hydroxyl oxygen and hydrogen in phenol and p-cresol were taken from our previous study of methanol, with a modified charge distribution of qc = 0.270, qo = −0.738, qH = 0.468. The simulations were performed for cubic systems of L = 6nm, or L = 10nm (for the sulfur systems), and for at least 10ns of production starting from random initial configurations followed by 1–2ns of equilibration.
Results
Amino acid side chains include both polar and nonpolar functional groups. Using the KBIs as a guide, a series of models for simple polar solutes in water have been developed. More recently, nonpolar solutes have been studied by switching the solvent of interest to methanol [28,34]. This then assumes that reasonable FFs for solutes in methanol should provide good models for solutes in water as long as one has an accurate model for methanol and water mixtures. Indeed, it is hoped that the properties of any binary liquid mixture will be well reproduced.
The KBFF models are simple nonpolarizable classical force fields. The Lennard-Jones 6–12 potential is used for the van der Waals interactions, together with a simple Coulomb potential for electrostatic interactions which are evaluated using Ewald sums. The general approach taken during the parameterization procedure is to focus on the effective charge distributions for solutes. The primary goal is to mimic condensed phase polarization effects. A variety of charge distributions are typically investigated and the one that provides the closest agreement with experiment for the KBIs is adopted in the model. A complete list of solutes studied to date, and the relevant amino acid side chains or cosolvent, is provided in Table 1. The list does not include the nonpolar side chains of Ala, Ile, Leu, Pro, and Val. In our opinion, the parameters previously used to model these groups are less questionable as these groups do not display large polarization effects even in polar solvents such as water. Hence, our hydrocarbon parameters have been taken from previous studies [35].
Table 1.
Functional groups for which KBFF models have been developed.
| Solute | Solvent | Relevant species | Reference |
|---|---|---|---|
| acetone | Water | cosolvent | [20] |
| urea | Water | cosolvent | [21] |
| nacl | Water | cosolvent | [42] |
| guanidinium chloride | Water | cosolvent, arg | [43] |
| amides | Water | asn, gln, peptide group | [36] |
| methanol | Water | ser, thr, tyr | [27] |
| thiols, sulfides | Methanol | met, cys, disulfide | [28] |
| aromatics, aromatic alcohols | Methanol | phe, tyr | [34] |
| amine salts, carboxylates | Water | lys, asp, glu, termini | [44] |
In developing the above FFs a large body of information concerning the behavior of solution mixtures and our ability to reproduce their properties has been provided. We summarize what we have learned in the following six points:
It cannot be assumed that existing FFs for solutes reproduce the KBIs for solution mixtures. In most cases too much self association of solute molecules is observed [8,20,22,36]. Therefore, in our opinion, the simulated KBIs provide an excellent approach to determine the quality of a FF.
While the KBIs are defined for open systems, reliable values can also be obtained in closed systems by truncating the integral in Equation 1. However, this requires the simulation of systems with a length significantly larger than twice the truncation distance. Unfortunately, the truncation distance is unknown before the system has been simulated.
Both the experimental and simulated Gij values display significant uncertainty as the concentration of either i or j approaches zero.
Finding a reasonable effective solute charge distribution that mimics solution phase polarization effects over the full composition range appears to be the major problem. In this regard it is the charge distribution that is the crucial issue, not the solute polarity (dipole moment) [17].
Creating a solute FF that reproduces the experimental KBIs does not require a sacrifice of agreement between traditionally reproducible solution properties (diffusion constants, relative permittivity, etc.) [21].
The properties of binary solutions of a solute and solvent affect the interactions between the solute and additional solutes in ternary systems [17,37,38].
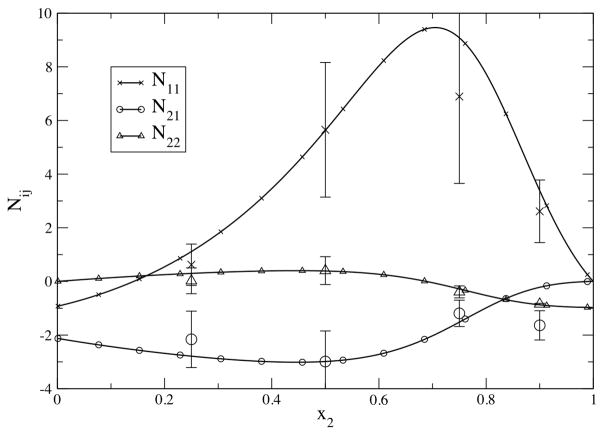
As an example of the insight that can be obtained from this kind of approach, we present some of our more recent unpublished data concerning mixtures of the sulfur solutes (2) with methanol (1), and for mixtures of alcohols (1) with aromatics (2) such as benzene and toluene [28,34]. Our simulations reproduce the interesting general features of these systems that are observed experimentally and it is these properties we investigate further here. The experimental and simulated KBIs for benzene and methanol mixtures are displayed in Figure 1 as excess coordination numbers, Nij = ρjGij. We prefer to display the data in this way, instead of displaying Gij values, for two reasons. First, the Nij values suppress the errors in both the experimental and simulated data at low ρj values. Second, the Nij’s have a simple physical interpretation, namely the excess number of j molecules around an i molecule in an open system above the number of j molecules observed within an equivalent volume of a bulk reference solution at the same chemical potentials. In developing the benzene force field the benzene charge distribution was adjusted until reasonable agreement with experiment for the KBIs was obtained [34]. Similar agreement was also observed for the other systems studied here.
Figure 1.
Excess coordination numbers for benzene (2) and methanol (1) mixtures at 308K. The solid lines represent a KB analysis of the experimental data [45,46], while the larger symbols indicate the simulation data obtained using the KBFF models for both molecules.
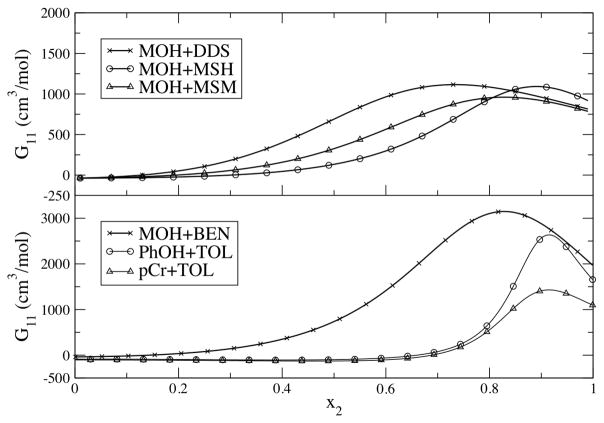
Not only can KB theory be used to provide additional data for the development of new and improved force fields, it can also provide valuable information on the properties of the mixtures themselves. This can be further illustrated using the simulation data. For example, a comparison of the experimental KBIs for a series of sulfur and aromatic solutes (2) in alcohol mixtures (1) is displayed in Figure 2. One observes a consistent picture for low alcohol compositions. Here, the G11 values all display a maximum at low alcohol compositions. The maxima display large G11 values of >1000 cm3/mol. This suggests a significant degree of self association between the alcohol molecules at these compositions. As this data is generally reproduced by the KBFF models, one can have a high degree of confidence that the simulations accurately represent the real solution distributions. The above mixtures have been simulated using our models for mole fractions of either x1 = 0.100 or 0.125. Analysis of the simulations indicates very similar types of alcohol microstructures. In particular, chains and rings of alcohol molecules of various sizes are clearly visible. This type of behavior has also been observed in other simulations [23,39,40]. However, the KB analysis of both the experimental and simulation data provides a clear quantitative description of the aggregation which can be related directly to the thermodynamics of the solution mixture. In our opinion, this is a significant advantage of the KB approach.
Figure 2.
Experimental KB integrals observed for binary solutions containing an alcohol (1) and various hydrophobic compounds (2). Top: KB integrals for a variety of methanol (1) and sulfur compounds (2). The data refer to solutions of dimethyldisulfide (DDS) at 311K, methanethiol (MSH) at 288K, and dimethylsulfide (MSM) at 288K in methanol (MOH). Bottom: KB integrals for a series of alcohols (1) and aromatic compounds (2). The data refer to mixtures of methanol and benzene (BEN) at 308K, phenol (PhOH) and toluene (TOL) at 333K, and p-cresol (pCr) and toluene at 333K. Experimental data was taken from references [45,46].
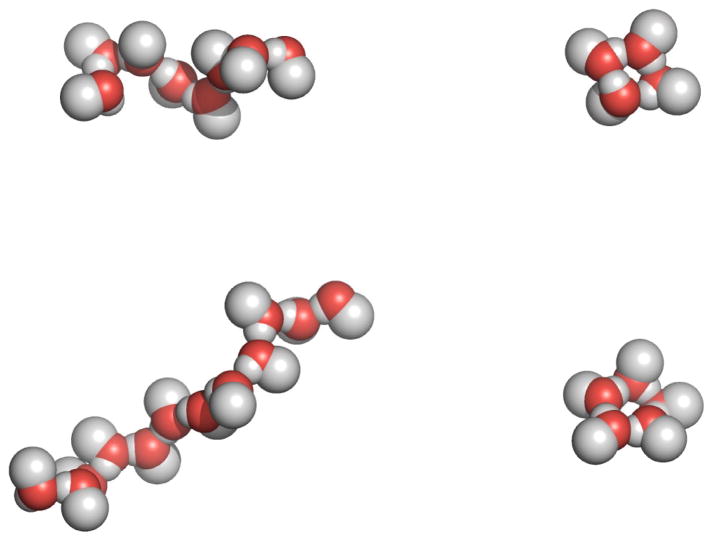
Some of the structures observed during the simulations of methanol solutions are presented in Figure 3. The cyclic structure is not the dominant species according to our simulations; however, we will not provide a rigorous statistical analysis of the structures observed in this work. This small proportion of cyclic structures, along with the number of methanol molecules per cycle and their spatial orientations in the ring, all agree with previous liquid phase simulation and experimental results [41]. Cyclic structures, though entropically less favorable than similar size chain structures, have the advantage of an additional hydrogen bond. In addition, cyclic structures mimic an inverse micelle where the hydroxyl groups are relatively buried while the methyl groups are exposed to the nonpolar solute molecules. Hence, we would expect to see these types of structures for most nonpolar solutes in the presence of low concentrations of methanol. The clustering should eventually disappear, for simple entropic (dilution) reasons, as the alcohol approaches infinite dilution.
Figure 3.
Representative snapshots of methanol structures observed in the simulations of methanol mixtures containing high concentrations of benzene (xMOH = 0.1 at 308K) or methanethiol (xMOH = 0.125 at 288K). The formation of long chains of molecules (left) and cyclic four and five member rings structures (right) was observed during both simulations.
The effect does not seem to be limited to methanol solutions. Similar configurations for other alcohols are also observed in the presence of nonpolar solutes. Figure 4 includes sample structures of phenol and p-cresol molecules observed in mixtures with toluene at low alcohol mole fractions. Again, both chain and ring structures are observed, although these aromatic alcohols displayed a higher percentage of ring structures. It is possible that the steric interactions between the aromatic rings in chain structures significantly reduce the chain entropy and therefore favor ring structures. However, a proof of this would require a more detailed analysis and is beyond the scope of the current study.
Figure 4.
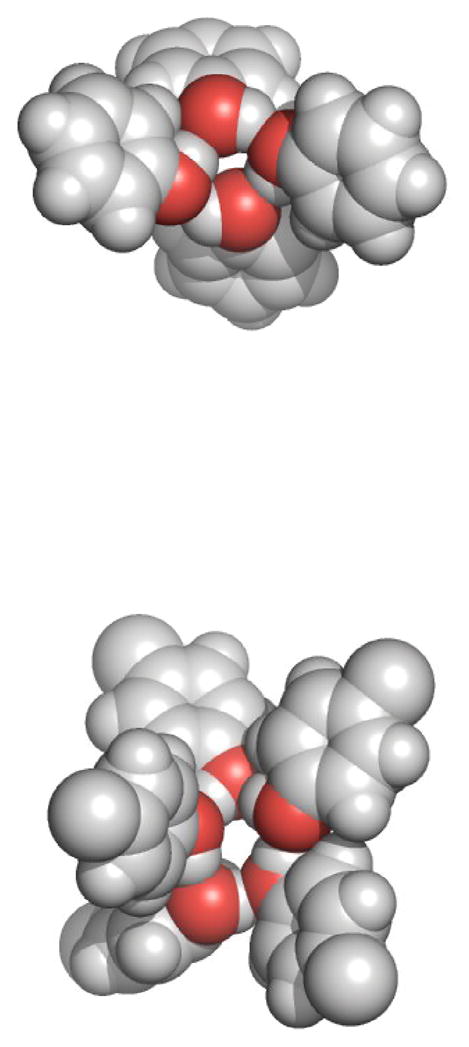
Representative snapshots of phenol (top) and p-cresol (bottom) structures observed in the simulations of mixtures containing high concentrations of toluene (xTOL = 0.9 at 333K). The formation of four and five member cyclic rings structures was observed during both simulations.
Conclusions
A new approach for the development of FFs for the study of solution mixtures has been presented. The approach uses the experimental KBIs as target data and thus ensures a reasonable approximation of the solute activity. Our final goal is a complete protein force field capable of providing a balanced description of the interactions between the various functional groups, and between the functional groups and water. During these studies a variety of information has been obtained concerning the properties of solution mixtures and our current ability to mimic their behavior.
The primary advantages of the present approach include the use of additional data for testing of the FF and the ability to extract information on the solute activity. Furthermore, the KBIs appear to be sensitive to relatively small changes in the charge distributions and therefore provide a stern test of the FF quality. The primary disadvantages are the need to simulate larger systems than usual for longer times to ensure the KBIs have converged. In addition, the effective solution phase charge distributions are currently obtained by trial and error. This makes the approach rather slow compared to traditional gas phase or pure liquid based studies. Nevertheless, we feel that FFs capable of reproducing the experimental KBIs are vital to provide realistic insights into the behavior of solution mixtures.
Acknowledgments
The project described was supported by Grant Number R01GM079277 from the National Institute of General Medical Sciences. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of General Medical Sciences or the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Brooks BR, et al. Journal of Computational Chemistry. 1983;4:187. [Google Scholar]
- 2.Weiner SJ, et al. Journal of the American Chemical Society. 1984;106:765. [Google Scholar]
- 3.Jorgensen WL. Journal of Physical Chemistry. 1986;90:1276. [Google Scholar]
- 4.Case DA, et al. Journal of Computational Chemistry. 2005;26:1668. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. Journal of Physical Chemistry B. 2001;105:6474. [Google Scholar]
- 6.MacKerell AD, et al. In: The Encyclopedia of Computational Chemistry. Schleyer PvR., editor. John Wiley & Sons; Chichester: 1998. [Google Scholar]
- 7.Scott WRP, et al. Journal of Physical Chemistry A. 1999;103:3596. [Google Scholar]
- 8.Chitra R, Smith PE. Journal of Chemical Physics. 2001;115:5521. [Google Scholar]
- 9.Oostenbrink C, Villa A, Mark AE, van Gunsteren WF. Journal of Computational Chemistry. 2004;25:1656. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- 10.Xu ZT, Luo HH, Tieleman DP. Journal of Computational Chemistry. 2007;28:689. doi: 10.1002/jcc.20560. [DOI] [PubMed] [Google Scholar]
- 11.Ben-Naim A. Molecular Theory of Solutions. Oxford University Press; New York: 2006. [Google Scholar]
- 12.Kokubo H, Rosgen J, Bolen DW, Pettitt BM. Biophysical Journal. 2007;93:3392. doi: 10.1529/biophysj.107.114181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Potoff JJ, Siepmann JI. AIChE Journal. 2001;47:1676. [Google Scholar]
- 14.Chen B, Potoff JJ, Siepmann JI. Journal of Physical Chemistry B. 2001;105:3093. [Google Scholar]
- 15.Chitra R, Smith PE. Journal of Physical Chemistry B. 2000;104:5854. [Google Scholar]
- 16.Chitra R, Smith PE. Journal of Chemical Physics. 2001;114:426. [Google Scholar]
- 17.Weerasinghe S, Smith PE. Journal of Chemical Physics. 2003;118:5901. doi: 10.1063/1.1768938. [DOI] [PubMed] [Google Scholar]
- 18.Kirkwood JG, Buff FP. Journal of Chemical Physics. 1951;19:774. [Google Scholar]
- 19.Ben-Naim A. Journal of Chemical Physics. 1977;67:4884. [Google Scholar]
- 20.Weerasinghe S, Smith PE. Journal of Physical Chemistry B. 2003;118:10663. [Google Scholar]
- 21.Weerasinghe S, Smith PE. Journal of Physical Chemistry B. 2003;107:3891. [Google Scholar]
- 22.Perera A, Sokolic F. Journal of Chemical Physics. 2004;121:11272. doi: 10.1063/1.1817970. [DOI] [PubMed] [Google Scholar]
- 23.Zoranic L, Sokolic F, Perera A. Journal of Chemical Physics. 2007;127:024502. doi: 10.1063/1.2753482. [DOI] [PubMed] [Google Scholar]
- 24.Zoranic L, Mazighi R, Sokolic F, Perera A. Journal of Physical Chemistry C. 2007;111:15586. [Google Scholar]
- 25.Kaatze U, Brai M, Menzel K. Berichte der Bunsen-Gesellschaft-Physical Chemistry Chemical Physics. 1994;98:1. [Google Scholar]
- 26.Hetu D, Perron G. Journal of Solution Chemistry. 1991;20:207. [Google Scholar]
- 27.Weerasinghe S, Smith PE. Journal of Physical Chemistry B. 2005;109:15080. doi: 10.1021/jp051773i. [DOI] [PubMed] [Google Scholar]
- 28.Bentenitis N, Cox NR, Smith PE. Journal of Physical Chemistry B. 2009;113:12306. doi: 10.1021/jp904806f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lindahl E, Hess B, van der Spoel D. Journal of Molecular Modeling. 2001;7:306. [Google Scholar]
- 30.Berendsen HJC, et al. Journal of Chemical Physics. 1984;81:3684. [Google Scholar]
- 31.Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. Journal of Computational Chemistry. 1997;18:1463. [Google Scholar]
- 32.Darden T, York D, Pedersen L. Journal of Chemical Physics. 1993;98:10089. [Google Scholar]
- 33.Berendsen HJC, Grigera JR, Straatsma TP. Journal of Physical Chemistry. 1987;91:6269. [Google Scholar]
- 34.E. A. Ploetz and P. E. Smith, to be submitted.
- 35.Schuler LD, Daura X, van Gunsteren WF. Journal of Computational Chemistry. 2001;22:1205. [Google Scholar]
- 36.Kang M, Smith PE. Journal of Computational Chemistry. 2006;27:1477. doi: 10.1002/jcc.20441. [DOI] [PubMed] [Google Scholar]
- 37.Kang M, Smith PE. Fluid Phase Equilibria. 2007;256:14. [Google Scholar]
- 38.Chitra R, Smith PE. Journal of Physical Chemistry B. 2001;105:11513. [Google Scholar]
- 39.Stubbs JM, Siepmann JI. Journal of Physical Chemistry B. 2002;106:3968. [Google Scholar]
- 40.Lanshina LV, Abramovich AI. Russian Journal of Physical Chemistry. 2005;79:608. [Google Scholar]
- 41.Buck U, Huisken F. Chemical Reviews. 2000;100:3863. doi: 10.1021/cr990054v. [DOI] [PubMed] [Google Scholar]
- 42.Weerasinghe S, Smith PE. Journal of Chemical Physics. 2003;119:11342. doi: 10.1063/1.1768938. [DOI] [PubMed] [Google Scholar]
- 43.Weerasinghe S, Smith PE. Journal of Chemical Physics. 2004;121:2180. doi: 10.1063/1.1768938. [DOI] [PubMed] [Google Scholar]
- 44.M. B. Gee and P. E. Smith, to be submitted.
- 45.Wilson GM. Journal of the American Chemical Society. 1964;86:127. [Google Scholar]
- 46.Klauck M, et al. Industrial & Engineering Chemistry Research. 2008;47:5119. doi: 10.1021/ie070957b. [DOI] [PMC free article] [PubMed] [Google Scholar]