On the importance of preserving the harmonics and neighboring partials prior to vocoder processing: Implications for cochlear implants

Abstract

Pre-processing based noise-reduction algorithms used for cochlear implants (CIs) can sometimes introduce distortions which are carried through the vocoder stages of CI processing. While the background noise may be notably suppressed, the harmonic structure and∕or spectral envelope of the signal may be distorted. The present study investigates the potential of preserving the signal’s harmonic structure in voiced segments (e.g., vowels) as a means of alleviating the negative effects of pre-processing. The hypothesis tested is that preserving the harmonic structure of the signal is crucial for subsequent vocoder processing. The implications of preserving either the main harmonic components occurring at multiples of F0 or the main harmonics along with adjacent partials are investigated. This is done by first pre-processing noisy speech with a conventional noise-reduction algorithm, regenerating the harmonics, and vocoder processing the stimuli with eight channels of stimulation in steady speech-shaped noise. Results indicated that preserving the main low-frequency harmonics (spanning 1 or 3 kHz) alone was not beneficial. Preserving, however, the harmonic structure of the stimulus, i.e., the main harmonics along with the adjacent partials, was found to be critically important and provided substantial improvements (41 percentage points) in intelligibility.

INTRODUCTION

The performance, in terms of speech understanding, of cochlear implant (CI) users is known to degrade in noisy conditions. Over the years, many researchers have shown that the use of noise-reduction (NR) algorithms as a pre-processing step is an effective approach to improve speech recognition in noisy listening conditions for unilateral cochlear-implant listeners (Hochberg et al., 1992; Weiss, 1993; Yang and Fu, 2005; Loizou et al., 2005; Hu et al., 2007) as well as for bilateral implant users and CI users wearing two microphones (van Hoesel and Clark, 1995; Hamacher et al., 1997; Wouters and Berghe, 2001; Kokkinakis and Loizou, 2008). Hochberg et al. (1992) used the INTEL noise-reduction algorithm to pre-process speech and presented the processed speech to ten Nucleus implant users fitted with the F0∕F1∕F2 and MPEAK feature-extraction strategies. Consonant-vowel-consonant words embedded in speech-shaped noise at signal to noise ratios (SNRs) in the range of −10 to 25 dB were presented to the CI users. Significant improvements in performance were obtained at SNRs as low as 0 dB. The improvement in performance was attributed to more accurate formant extraction, as the INTEL algorithm reduced the errors caused by the feature-extraction algorithm. Yang and Fu (2005) evaluated the performance of a spectral-subtractive algorithm using subjects wearing the Nucleus-22, Med-El, and Clarion devices. Significant benefits in sentence recognition were observed for all subjects with the spectral-subtractive algorithm, particularly for speech embedded in speech-shaped noise. Loizou et al. (2005) evaluated a subspace noise-reduction algorithm which was based on the idea that the noisy speech vector can be projected onto “signal” and “noise” subspaces. The clean signal was estimated by retaining only the components in the signal subspace and nulling the components in the noise subspace. The performance of the subspace reduction algorithm was evaluated using 14 subjects wearing the Clarion device. Results indicated that the subspace algorithm produced significant improvements in sentence recognition scores compared to the subjects’ daily strategy, at least in continuous (stationary) noise.

All the above methods were based on pre-processing the noisy signal and presenting the “enhanced” signal to the CI users. Pre-processing techniques, however, can introduce distortions which will be subsequently carried out and introduced in the vocoder stages of processing. Pre-processing can notably suppress the background noise, but can distort the harmonic structure and∕or spectral envelope of the signal. The present study focuses on the development of techniques aimed at alleviating the negative effects of pre-processing. In particular, it investigates the potential of preserving the signal’s harmonic structure present primarily in voiced segments (e.g., vowels). Both the masking noise and noise-reduction algorithm can degrade the harmonics structure, as most noise-reduction algorithms are designed to recover the spectral envelope, while paying little attention to the harmonics. The present study maintains the hypothesis that preserving the harmonic structure of the clean signal is crucial for subsequent vocoder processing. The implications of preserving either the main harmonic components or the main harmonics along with adjacent partials are investigated in the present study. This is done by first pre-processing noisy speech with a conventional noise-reduction algorithm, regenerating the harmonics, and vocoder processing the stimuli with eight channels of stimulation in steady speech-shaped noise at 0–6 dB SNR. The experiments in this study were designed to assess the importance of preserving the signal’s harmonic structure prior to vocoder (CI) processing.

EXPERIMENT: NOISE REDUCTION AND HARMONICS REGENERATION

Methods

Subjects

Seven normal-hearing native speakers of American English participated in this experiment. All subjects were paid for their participation, and all of them were undergraduate and graduate students at the University of Texas-Dallas.

Stimuli

The target speech materials consisted of sentences from the IEEE database (IEEE, 1969) and were obtained from Loizou (2007). The IEEE corpus contains 72 lists of ten phonetically balanced sentences produced by a male speaker and recorded in a double-walled sound-attenuation booth at a sampling rate of 25 kHz. Further details about the speech recordings can be found in Loizou (2007). The estimated F0 values of the male speaker ranged from 75 to 250 Hz with a mean of 127.57 Hz and a standard deviation of 21.16 Hz.

The masker was steady speech-shaped noise and had the same long-term spectrum as the sentences in the IEEE corpus. Speech-shaped noise was selected as its stationarity minimizes the confounding effect of the accuracy of noise estimation algorithms.

Signal processing

The experiments were designed to evaluate the benefits of harmonics regeneration when used in a pre-processing stage to vocoder (cochlear-implant) processing. Figure 1 shows the block diagram of the overall system. A total of six processing conditions were used for this purpose. The first condition was designed to simulate the cochlear-implant processing. As the first step, a pre-emphasis filter with 2000 Hz cutoff and 3 dB∕octave rolloff was applied to the signal. An eight-channel noise-excited vocoder was utilized (Shannon et al., 1995). The speech signal was bandpassed into eight frequency bands between 80 and 6000 Hz using sixth-order Butterworth filters. For the specified frequency range, the equivalent rectangular bandwidth (ERB) filter spacing (Glasberg and Moore, 1990) was used to allocate the eight frequency channels (the channel allocation is shown in Table 1). The envelopes of the bandpassed signals were obtained by full-wave rectification followed by low-pass filtering using a second-order Butterworth filter with a 400 Hz cut-off frequency. This cut-off frequency was chosen to preserve F0 modulations in the envelopes. The extracted temporal envelopes were modulated with white noise, and bandpass filtered through the same analysis bandpass filters. The resulting (narrow-band filtered) waveforms in each channel were finally summed to generate the stimuli. The level of the synthesized speech signal was scaled to have the same root mean square value as the original speech signal.

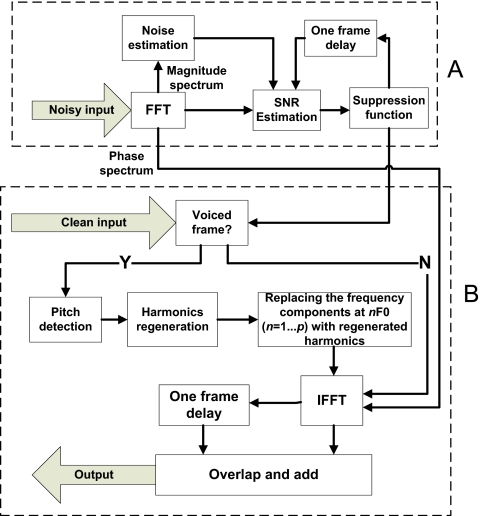
Figure 1.

Block diagram of the overall system.

Table 1.

Low and high cut-off frequencies (at −3 dB) for the eight channels used in the vocoding stage.

Channel	Low (Hz)	High (Hz)
1	80	221
2	221	426
3	426	724
4	724	1158
5	1158	1790
6	1790	2710
7	2710	4050
8	4050	6000

The other five conditions involved two pre-processing steps prior to vocoding processing (see Fig. 1). The first processing condition involved a NR algorithm based on the minimum mean square error log-spectral amplitude estimation (LogMMSE) proposed by Ephraim and Malah (1985). The LogMMSE algorithm was chosen as this noise-reduction method performed well in both speech quality and speech intelligibility studies (Hu and Loizou, 2007a, 2007b). The same noise estimation algorithm as in Hu and Loizou (2007a, 2007b) was used for estimating∕updating the masker spectrum. Fast Fourier transform (FFT) based frame processing was used in the implementation of the LogMMSE algorithm. Speech signals were segmented into 50% overlapping frames using a sliding 20-ms Hanning window. Figure 2 shows the block diagram for the processing. A 8192-point FFT (by zero padding) with a frequency bin resolution of 3.05 Hz was utilized.

Figure 2.

Block diagrams for the combined harmonics-regeneration stage (shown in block B) and noise-reduction stage (shown in block A).

The second pre-processing step was designed to evaluate the benefits of harmonics regeneration performed after the noise-reduction stage (see Fig. 2). As mentioned earlier, the rationale for this step is to alleviate any distortions introduced by the noise-reduction algorithm. The majority of phonetic segments are voiced segments (Mines et al., 1978) which can be approximately modeled by harmonic spectra. The harmonics appear at integer multiples of F0.

In order to establish an upper bound and evaluate the potential of the harmonics regeneration stage when combined with noise reduction, we assumed an ideal operating environment. That is, we estimated the F0 from the clean speech signal and regenerated the signal’s harmonics with prior knowledge of the clean speech spectrum. More specifically, an F0-detection algorithm based on the autocorrelation function (Kondoz, 1999, Chap. 6) was used to obtain the F0 in each frame. The number of regenerated harmonics was then calculated by p=⌊CF∕F0⌋, where CF is the cut-off frequency below which harmonics are included, and ⌊⋅⌋ is the floor operator. Two cut-off frequency values, 1000 and 3000 Hz, were evaluated. To compensate for the possible inaccuracy of the F0 detector, harmonics were regenerated by extracting the local peaks in a 30-Hz range around nF0, where n=1,…,p. The extracted harmonics had a quantization error of roughly 1.53 Hz (half of the FFT frequency resolution). Figure 2 shows the block diagram for the combined noise-reduction (block A) and harmonics-regeneration (block B) stages.

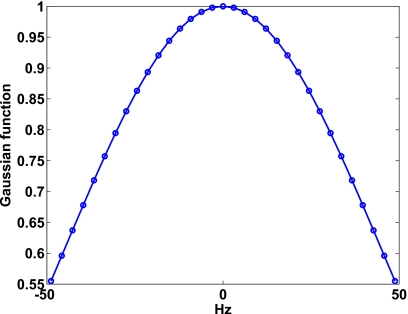
The magnitude spectra of voiced phonetic segments (e.g., vowels) possess a harmonic structure. The harmonics are evident at multiples of F0. In addition, sideband components or partials, falling between the main harmonic components (which occur primarily at multiples of F0), are also present in voiced magnitude spectra. To assess the importance of preserving the harmonic structure of voiced segments, two conditions were created. In the first condition, only the main harmonic amplitudes were included (the partials were left noise-suppressed), while in the second condition, both the main harmonics and neighboring partials were included. We denote the first condition as Main-xkHz, where x denotes the cut-off frequency (1 or 3 kHz) up to which harmonics are included, and the second condition in which both the main harmonics and neighboring partials are included as PartH-xkHz. The main harmonic amplitudes were extracted from the clean magnitude spectrum based on the estimated F0 value. The partials were not extracted from the clean spectra. Instead, a simple approach was taken to generate the neighboring partials. This was done by multiplying the main harmonic amplitudes by a Gaussian-shaped function (see Fig. 3) and sampling the Gaussian function at 16 discreet frequencies to the left and right of the main harmonics. Note that the FFT resolution was 3 Hz; hence the Gaussian function spanned a total bandwidth of 100 Hz. This bandwidth was chosen to accommodate the F0 of the male speaker. The Gaussian function was derived heuristically by inspecting the magnitude spectra of several frames of voiced segments. More complex algorithms could alternatively be used to generate the Gaussian function; however, we chose the function shown in Fig. 3 for its simplicity and practical implications. In a realistic implementation, the partials do not need to be estimated from the noisy signal, only the main harmonics need to be estimated.

Figure 3.

Gaussian-shaped function used for generating partials adjacent to the main harmonics.

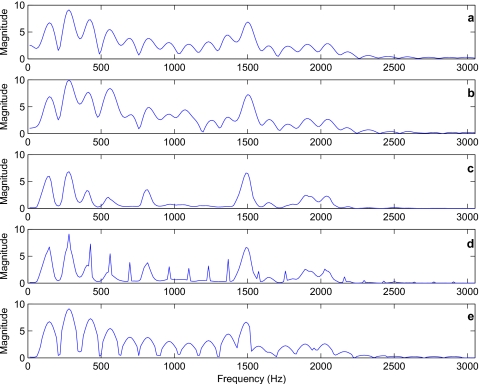
Figure 4 shows example plots of the FFT magnitude spectra of the clean, noisy, and enhanced signals, as well as signals with harmonics regenerated. As can be seen from panel (c), although the noise-reduction algorithm suppressed the background noise, the harmonics structure was degraded. Panel (d) in Fig. 4 shows the spectra with only the main harmonics regenerated, and panel (e) shows the spectrum with both the main harmonics and partials regenerated. Clearly, the spectrum shown in panel (e) resembles closer to the clean spectrum (panel a) than the output spectrum (panel c) produced by the noise-reduction algorithm.

Figure 4.

Example FFT magnitude spectra (displayed in linear units) of a voiced segment extracted from a sentence (for better clarity, only the spectrum spanning the frequency range 0–3 kHz is displayed). The top panel shows the clean speech spectrum. The second panel shows the noisy speech spectrum (SNR=0 dB) and the third panel shows the enhanced speech spectrum after applying the logMMSE noise-reduction algorithm. The fourth panel shows the harmonics-regenerated speech spectrum based only on the main harmonics occurring at multiples of F0. The bottom panel shows the harmonics-regenerated speech spectrum based on both the main harmonics and adjacent partials.

Procedure

The listening tests were conducted using a personal computer connected to a Tucker-Davis system 3. Stimuli were played monaurally to the subjects through Sennheiser HD 250 Linear II circumaural headphones at a comfortable listening level. The subjects were seated in a double-walled sound-attenuation booth (Acoustic Systems, Inc.). To familiarize each subject with the stimuli, a training session was administrated prior to the formal testing, and each subject listened to vocoded speech stimuli. The training session typically lasted about 15–20 min. During the testing session, the subjects were instructed to write down the words they heard. In total, there were 18 testing conditions (=3 SNR levels×6 processing methods). For each condition, two lists of sentences were used, and none of the lists was repeated across the testing conditions. The conditions were presented in random order for each subject. The subjects were allowed to take breaks whenever they wanted and no feedback was provided after each testing condition.

Results

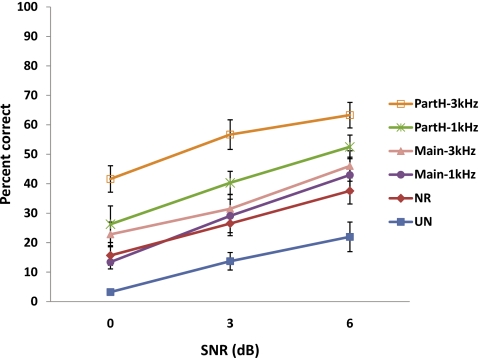
The mean percent correct scores for all conditions are shown in Fig. 5. Performance was measured in terms of percent of words identified correctly (all words were scored). The scores were first converted to rational arcsine units (RAU) using the rationalized arcsine transform proposed by Studebaker (1985). To examine the effect of cut-off frequency (1 kHz vs 3 kHz) and type of harmonic structure (main harmonics only vs main harmonics plus partials) preserved, we subjected the scores to statistical analysis using the transformed score as the dependent variable, and the SNR levels, cut-off frequency, and type of harmonic structure as the three within-subjects factors. Analysis of variance with repeated measures indicated significant effects of SNR levels [F(2,12)=20.72, p<0.001], significant effects of cut-off frequency [F(1,6)=102.80, p<0.001], and significant effects of type of harmonic structure [F(1,6)=73.14, p=0.002]. There were no significant between-factor interactions except the one between cut-off frequency and type of harmonic structure [F(1,6)=63.13, p=0.039]. Results indicated that a higher cut-off frequency and inclusion of partials provided additional benefits compared to those obtained using the noise-reduction algorithm alone.

Figure 5.

Mean percent correct scores as a function of SNR level. The error bars denote ±1 standard error of the mean.

Multiple paired comparisons, with Bonferroni correction, were run between the scores obtained with the corrupted (unprocessed, denoted as UN) and NR algorithm, NR and PartH-1 kHz, NR and PartH-3 kHz, and PartH-3 kHz and PartH-1 kHz at various SNR levels. The Bonferroni corrected statistical significance level was set at p<0.0125 (α=0.05). The results are shown in Table 2. The comparisons indicated statistically significant differences between the UN and NR scores at all three SNR levels, suggesting that the NR algorithm used in this study can provide benefit for vocoded speech in steady-state noise. The scores obtained with the PartH-1 kHz stimuli at lower SNR levels (0 dB) were not significantly higher (p=0.1) than those obtained with the NR scores but were significantly better (p=0.005) at higher SNR levels (3 and 6 dB), suggesting that maintaining the signal’s harmonics structure below 1000 Hz can further improve the benefits with noise-reduction methods at higher SNR levels. The scores obtained with the 3000 Hz cut-off frequency were significantly higher than those obtained with the 1000 Hz cut-off frequency at higher SNR levels (p<0.01), but they did not differ at 0 dB (p=0.02), indicating additional benefits when using a higher harmonics-regeneration cut-off frequency.

Table 2.

Multiple paired comparisons between the scores obtained in the various conditions.

	0 dB	3 dB	6 dB
NR vs UN	**a	**	**
PartH-1 kHz vs NR		**	**
PartH-3 kHz vs NR	**	**	**
PartH-3 kHz vs PartH-1 kHz		**	**

^aBonferroni corrected p<0.0125, α=0.05.

GENERAL DISCUSSION AND CONCLUSIONS

The above results and analysis clearly indicate that significant improvement in intelligibility, relative to NR processing alone, can be obtained when the harmonic structure of the input signal is preserved prior to vocoder processing. In particular, the scores obtained in the PartH-1 kHz and PartH-3 kHz conditions yielded the largest improvements. This was not surprising, since clean harmonic amplitudes spanning the range of 0–1 kHz or 0–3 kHz were used during the voiced segments of the corrupted signal. Performance obtained in the PartH-3 kHz condition was significantly higher than that obtained in the PartH-1 kHz condition owing to the fact that the stimuli in the PartH-3 kHz condition preserved to some degree formant frequency (F1 and F2) information. In contrast, the stimuli in the PartH-1 kHz condition preserved primarily F1 information. In effect, the stimuli in PartH- 1 kHz and PartH-3 kHz conditions provided glimpsing1 of the F1 and F2 information present in the voiced segments (e.g., vowels and semivowels) and thus enabled listeners to identify more words in the otherwise noisy speech stream (unvoiced segments were left corrupted). The PartH-1 kHz outcome is consistent with the outcomes from our prior studies (Li and Loizou, 2007, 2008) that indicated that glimpsing in the low-frequency region (<1000 Hz) can bring substantial benefits to speech intelligibility since listeners had a clear access to the voiced∕unvoiced landmarks, which are posited to facilitate syllable∕word segmentation (Stevens, 2002).

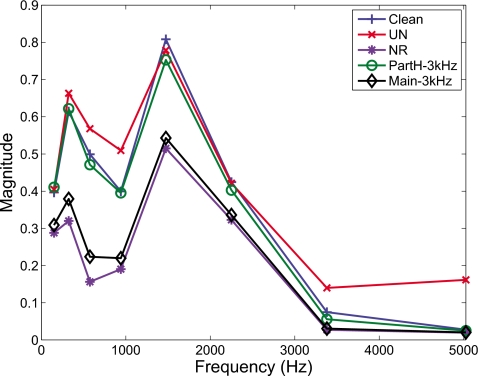
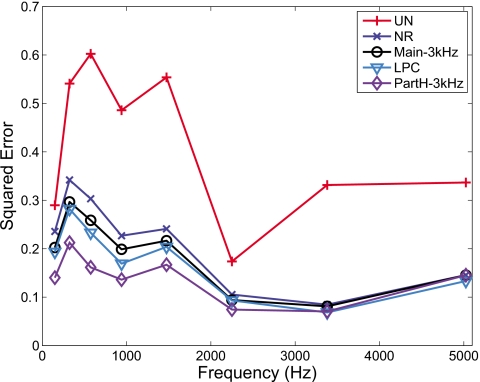
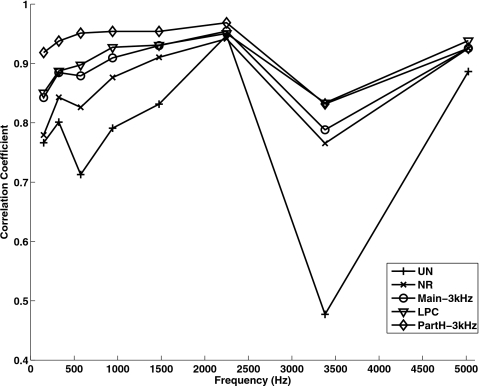
The most interesting finding from this study is the outcome that performance in the PartH-3 kHz condition was significantly higher than performance in the Main-3 kHz condition. The stimuli in both conditions contained the clean signal’s harmonic components spanning the range 0–3 kHz (see example in Fig. 4). The fact that the scores in the Main-3 kHz condition (which only preserved the main harmonic components of the clean signal) did not yield an improvement in intelligibility, relative to the NR condition, suggests that preserving only the main harmonics (i.e., harmonics occurring at multiples of F0) is not sufficient or beneficial, at least in the context of vocoder processing. The introduction of partials [see Fig. 4, panel (e)] adjacent to the main harmonics was found to be necessary to yield substantial improvements in intelligibility. This is because, in the context of vocoder processing, the inclusion of partials (adjacent to the harmonics) yielded channel envelope amplitudes closer to those of the clean signal’s envelope amplitudes. This is demonstrated in the example shown in Fig. 6. The accuracy in envelope amplitude estimation is quantified in Fig. 7, in terms of the squared error2 between the envelope amplitude values of the clean and processed signals. The smallest squared error value (i.e., amplitudes closest to the clean envelope amplitudes) was obtained with the PartH-3 kHz processed signals. Note that the resulting channel envelope amplitudes (following vocoder processing) of the Main-3 kHz stimuli were closer in value to those in the NR stimuli, despite the preservation of the main harmonic components in the Main-3 kHz stimuli. This was consistent with the rather equitable intelligibility scores observed (see Fig. 5) in the Main- 3 kHz and NR conditions. In addition to the use of squared error, we also quantified the fidelity of envelope reconstruction using the metric3 developed in Sheft et al. (2008). The resulting correlation coefficients for each band are shown in Fig. 8. As can be seen, higher correlation coefficient (hence, better envelope reconstruction) is obtained with the PartH-3 kHz processed signals, consistent with the outcome shown in Fig. 7. In summary, preserving both the main harmonics and adjacent partials results in envelope amplitudes closer in value to those obtained by vocoding the clean signal.

Figure 6.

The vocoded spectra of a voiced segment (same as that used in Fig. 4) processed in the various conditions.

Figure 7.

Plots of the squared error between the clean envelope and processed envelopes in the various conditions. The squared error was obtained by averaging, across ten IEEE sentences, the band squared error of processed envelopes.

Figure 8.

Plots of the band correlation coefficients of the clean envelopes and processed envelopes.

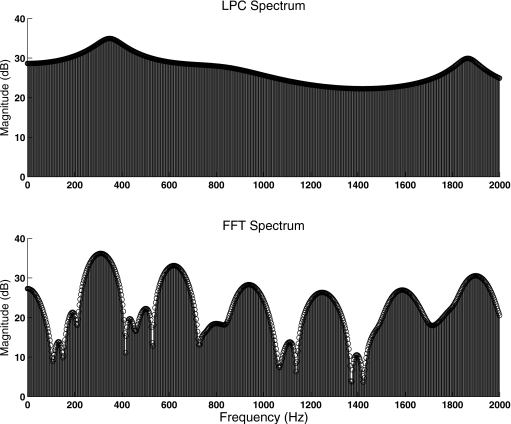
It is also interesting to note that the spectral envelopes of the stimuli in the Main-3 kHz and PartH-3 kHz conditions were identical (see Fig. 4). Yet, maintaining the spectral envelope of the clean signal alone (during voiced segments) was not found to be sufficient, at least in the context of vocoder processing. A different way of demonstrating this is to consider preserving the linear predictive coding (LPC) spectrum rather than the harmonic spectrum (see example in Fig. 9). The LPC spectrum preserves the spectral envelope of the signal but lacks the harmonic structure (see Fig. 9) present in voiced speech segments such as vowels. As shown in Figs. 78, preserving the LPC spectrum resulted in poorer envelope reconstruction compared to preserving the harmonic spectrum. In brief, preserving the harmonic structure of the stimulus, and, in particular, preserving the main harmonics along with the adjacent partials, was found to be critically important for vocoder processing. As shown in Fig. 4, the introduction of the partials adjacent to the harmonics provided a better spectral representation of the valleys, and alleviated to some degree spectral distortions introduced by the NR algorithm [see panel (c) vs panel (e)].

Figure 9.

Top panel shows the LPC spectrum of a voiced segment and bottom panel shows the corresponding FFT spectrum. Segment was taken from a sentence produced by a female speaker. Only the 0–2000 Hz region is shown for better visual clarity.

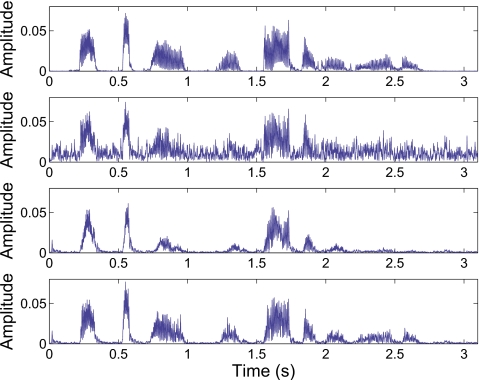
Figure 10 shows example plots of the vocoded temporal envelopes of channel 2 (center frequency=324 Hz). It is clear that the noise-reduction algorithm preserved the envelope peaks and deepened the envelope valleys, therefore effectively increasing the envelope dynamic range within each channel. However, as shown in the third panel (from top), the harmonics structure existing in the clean speech voiced segments was severely distorted following the noise-reduction stage. Harmonics-regeneration techniques can partly restore the harmonics structure (see bottom panel in Fig. 10) and provide a better envelope representation of the voiced segments.

Figure 10.

An example plot of the vocoded speech at channel 2 (center frequency=324 Hz). The top panel shows the temporal envelope of the vocoded clean speech. The second panel shows the temporal envelope of the vocoded noisy speech at SNR=0 dB. The third panel shows the temporal envelope of the vocoded speech after noise reduction. The bottom panel shows the temporal envelope of the vocoded speech in the PartH-3 kHz condition which preserved the main harmonics along with the adjacent partials.

In summary, regenerating harmonics can improve the spectral representation and temporal envelopes of vocoded speech and can provide substantial intelligibility benefits, relative to NR processing alone.

Practical implementation

The present study demonstrated the full potential, in terms of intelligibility improvement, of preserving the signals’ harmonic structure prior to vocoder processing. For that, we assumed we had access to the clean harmonic amplitudes and accurate F0 values. In practice, the F0 needs to be estimated from the noisy signal. Accurate F0 detection algorithms exist that can operate at the SNR levels tested in this study. The algorithm in Zavarehei et al. (2007), for instance, produced 13% and 7% pitch estimation errors at 5 and 10 dB babble noise, and 11% and 6% errors at 5 and 10 dB train noise. There exist several techniques for estimating, or rather regenerating, the harmonic amplitudes from a noisy signal. Such techniques can potentially be used as a pre-processing step in vocoder processing (see Fig. 1). Harmonics regeneration can be implemented using adaptive comb filtering (Nehorai and Porat, 1986) techniques, nonlinear functions (Plapous et al., 2006), and codebook-based techniques that capitalize on the fact that the harmonic amplitudes are highly correlated (Chu, 2004; Zavarehei et al., 2007). Once the harmonic amplitudes are estimated, it is straightforward to estimate the partials adjacent to the main harmonics using the Gaussian model shown in Fig. 3. The two additional steps (i.e., noise reduction and harmonics generation) will no doubt introduce additional complexity; however, the intelligibility benefits (see Fig. 5) clearly outweigh the additional computational load.

Implications for cochlear implants

The results from the present study suggest that the noise-reduction algorithm (Ephraim and Malah, 1985) alone, when used in a pre-processing stage to vocoder processing (see Fig. 1), can bring significant improvements in intelligibility (approximately 10–15 percentage points). This improvement is comparable to that obtained with other pre-processing algorithms (Yang and Fu, 2005) applied to cochlear implants. The implementation of the noise-reduction algorithm used in the present study can be easily integrated with existing speech coding strategies (e.g., ACE strategy) that rely on FFT processing rather than on filterbank processing to derive the channel envelopes. The added complexity is low, as it only involves SNR estimation (see Fig. 2) followed by the multiplication of the noisy FFT magnitude spectrum by a suppression function (which depends on the estimated SNR in each FFT bin). Further, and more substantial, improvements in intelligibility can be realized with the use of the proposed harmonics-regeneration technique, which in turn requires F0 estimation (during voiced segments) and harmonic amplitude estimation. Real-time F0 estimators suitable for CI processing have been demonstrated in Zakis et al. (2007); hence the F0 estimation does not pose a problem. The improvement in intelligibility, at least for the type of masker (steady noise) examined in this study, were quite substantial (41 percentage points), making the harmonics-regeneration stage worth incorporating in future speech coding strategies for cochlear implants.