It pays to have a spring in your step

Abstract

A large portion of the mechanical work required for walking comes from muscles and tendons crossing the ankle joint. By storing and releasing elastic energy in the Achilles tendon during each step, humans greatly enhance the efficiency of ankle joint work far beyond what is possible for work performed at the knee and hip joints.

Summary

Humans produce mechanical work at the ankle joint during walking with an efficiency two to six times greater than isolated muscle efficiency.

INTRODUCTION

Human walking mechanics have long been described using an inverted pendulum analogy (1, 4). The body center of mass travels in an arc trajectory such that it rises and slows down during the first half of stance, and lowers and speeds up during the second half of stance, similar to an inverted pendulum. By coupling two inverted pendulums together, a simple passive model can reproduce the basic movement and energy patterns of human walking (11, 17). Despite their simplicity, passive pendular models make a number of key predictions about the energetics of bipedal walking. First, energy can be conserved by exchanging kinetic and gravitational potential energy during the stance phase of each step. Second, leg swing can be purely passive under the right initial conditions. Third, the major source of energy loss during walking is the foot-ground collision (12). At the step to step transition, the center of mass must be redirected from moving downward and forward to moving upward and forward. This redirection requires mechanical work to maintain steady speed walking dynamics (12).

Simple models also provide insight into how the mechanical energy lost in the foot-ground collision is replaced by positive work performed by the legs. One way to perform the work is to generate an impulsive pushoff along the trailing limb right before the leading limb collides with the ground. An alternative way to power level walking in the model is to use active hip torque (11). Either of these methods could be done solely with active power production or by supplementing active power production with the return of some collisional energy stored in elastic elements.

The potential benefits of elastic energy storage and return have been established for bouncing gaits (i.e. hopping, running spring-mass model) (1, 2, 4) but have received much less attention in walking gaits. It has often been accepted that the longer stance times and asymmetric joint mechanical power outputs during walking limit the possibility for efficient energy storage and return by compliant tendons. This limitation has been challenged in recent models that extend the inverted pendulum concept by allowing the stance limb to compress and recoil, with dynamics similar to a stiff spring (7). With the appropriate leg stiffness, simple spring-loaded inverted pendulum models can generate walking dynamics that better match the trajectory of the center of mass (i.e. a non-circular arc) and the double peak shape of the ground reaction force compared to a rigid inverted pendulum model. The spring-like behavior of the stance limb in this model suggests that there may be substantial elastic energy storage and return in walking. Thus, muscles may not be the primary source of positive mechanical work at all the joints during human walking.

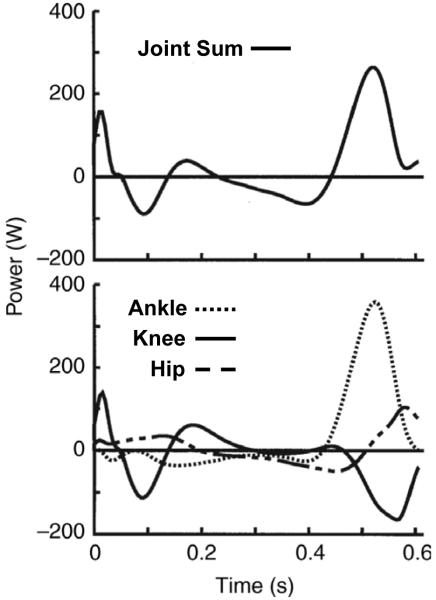
Inverse dynamics analyses can give insight into the possible sources of mechanical power generation of the lower limb joints during human walking. Data indicate, that similar to the trailing limb impulse used in a simple model (11), healthy young humans tend to rely a great deal on ankle pushoff at the end of stance to power walking. In fact, for preferred walking speeds on level ground (1.2 -1.5 m/s), the ankle joint produces 35-45% of the summed ankle, knee, and hip positive mechanical work during each stride (23, 26). When viewing the stance phase only, the ankle joint performs 60% (30 J out of 50 J) of the summed ankle, knee, and hip positive mechanical work (5) (Figure 1). There is a period of ankle joint negative work preceding the positive work at pushoff, a condition conducive for elastic energy storage and return. It is possible that some of the ankle joint positive work is transferred to the ankle from muscles that do not cross the ankle via biarticular muscles (e.g. gastrocnemius). In this case, negative work performed at other joints could be used as a relatively cheap means to store elastic energy in the Achilles tendon. A great deal of research has focused on the contribution of the role of sensory feedback in producing sustained ankle extensor muscle forces, but the potential contribution of Achilles tendon elastic recoil to help ankle muscles (primarily soleus and gastrocnemius) power walking has only recently been considered.

Figure 1. Stance limb mechanical power during walking.

Bottom panel shows the instantaneous rate of mechanical energy production (Watts) for each of the lower limb joints (ankle, knee and hip) of a single limb over the stance phase of level walking at 1.52 m/s. Positive values indicate energy generation and negative values indicate energy absorption. Top panel is the sum total power produced by the ankle, knee and hip. The ankle joint generates a large portion of the positive mechanical power during stance. Figure is adapted from Devita et al. (5).

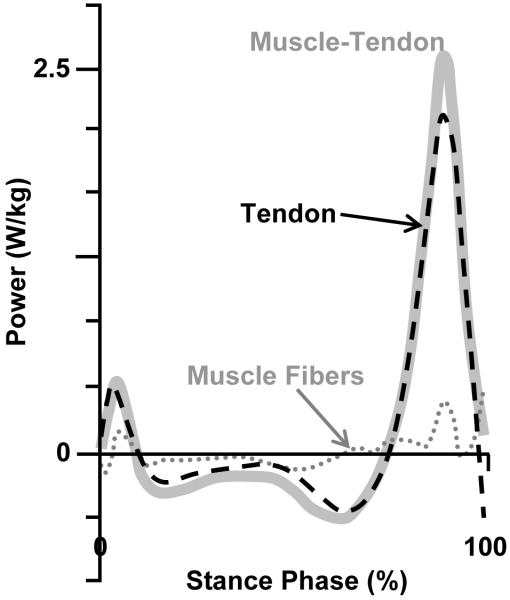
Ultrasound imaging has allowed for quantitative assessment of the mechanisms for elastic energy storage and return at the ankle joint in vivo during human walking. Essentially, the plantar flexor muscles and their long compliant tendon act like a catapult. The Achilles tendon slowly stores elastic energy during the majority of stance, releasing it at just the right moment to produce a rapid recoil with very high pushoff peak power output (9, 15). One important feature of the ankle ‘catapult mechanism’ is that the stretch and recoil of Achilles tendon allows muscle fibers to remain nearly isometric producing high forces with very little mechanical work (Figure 2). Muscles spend much less metabolic energy to produce force isometrically when compared to shortening (positive work) contractions (20). Thus, the elastic contribution at the ankle joint could save a significant amount of metabolic energy during walking. These in vivo ultrasound imaging data have revealed the mechanics of the spring in the human walking step, but the metabolic benefits of tendon recoil have proven more difficult to expose. To address this, we recently completed a series of studies estimating the efficiency of positive mechanical work performed at the ankle joint in vivo during human walking (22-24).

Figure 2. Ankle joint ‘catapult mechanism’ during walking.

Ultrasound imaging data from humans walking shows the instantaneous rate of mechanical energy production (W/kg) for gastrocnemius muscle fibers and Achilles tendon separately. The muscle-tendon power (bold gray) is the sum of the gastrocnemius muscle power (dotted gray) and the Achilles tendon power (black dashed). Positive values indicate energy generation and negative values indicate energy absorption. The muscle fibers contribute very little to total muscle tendon mechanical power output but the Achilles tendon stores and returns a significant amount of mechanical energy. Figure is adapted from Ishikawa et al. (9).

ROBOTIC ANKLE EXOSKELETON STUDIES

We constructed a robotic ankle exoskeleton that could assist human walking. It has a carbon fiber and polypropylene shell with an artificial pneumatic muscle (Figure 3). The exoskeleton uses a proportional myoelectric controller so that the wearer’s nervous system is in direct control of when and how much assistance is provided by the exoskeleton artificial pneumatic muscles.

Figure 3. Ankle joint powered exoskeleton hardware and control.

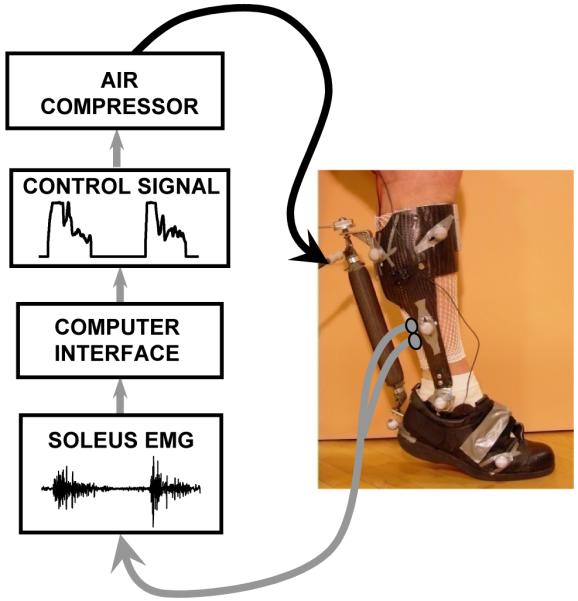
Light weight carbon fiber bilateral ankle-foot orthoses (i.e. exoskeletons) designed to drive ankle plantar flexion with artificial pneumatic muscles during walking. Exoskeletons were controlled using the subjects’ own soleus surface electromyography with proportional myoelectric control. Figure is adapted from Sawicki and Ferris (23).

When naïve subjects walk with the powered exoskeleton on one leg, they quickly adapt their muscle activation patterns to substitute exoskeleton work for the combined muscle and tendon work at the ankle joint. Gordon and Ferris found that after two 30-minute training sessions, walking kinematics were nearly identical for powered and unpowered walking (8). The user’s nervous system reduced the soleus muscle activity with the added assistance, allowing the exoskeleton to replace positive mechanical work that would normally be performed by the biological muscle-tendon unit. Activation of other lower limb muscles showed no differences between unpowered and powered walking conditions (8). This result suggests that the exoskeletons only affected the local muscle-tendon dynamics at the ankle.

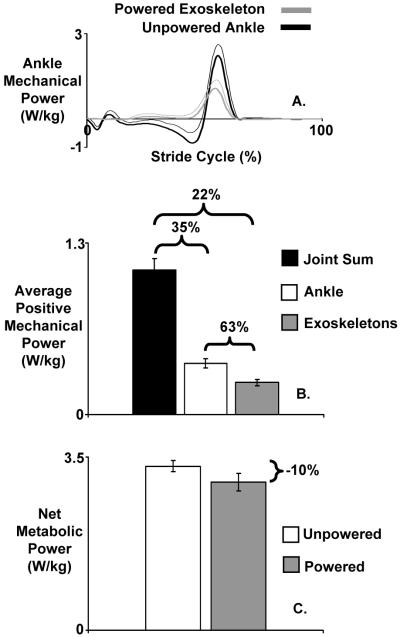
Sawicki and Ferris (22-24) examined the effects of using two robotic ankle exoskeletons on the metabolic cost of walking. By measuring oxygen consumption and mechanical work produced by the bilateral exoskeletons, we could calculate the apparent efficiency of the positive mechanical work at the ankle joint (23). The metabolic energy expenditure decreased with practice when walking with the robotic ankle exoskeletons. In healthy naïve subjects, changes in metabolic cost and exoskeleton mechanics during powered walking reached a steady state after three 30-minute training sessions. At the end of the third session, exoskeletons were replacing 22% of the summed joint lower limb positive work and subjects reduced their metabolic energy consumption by 10% while walking with exoskeletons powered when compared to walking with exoskeletons unpowered (Figure 4) (23).

Figure 4. Mechanical power and net metabolic cost during powered walking at 1.25 m/s.

Top panel (A) shows mean (thick black) and one standard deviation (thin black) mechanical power delivered by the ankle joint over the stride from heel-strike (0%) to heel-strike (100%). The mean contribution of the exoskeleton mechanical power (thick gray) + 1 standard deviation (thin gray) is overlaid. Mechanical power is computed as the product of exoskeleton torque and ankle joint angular velocity and is normalized by subject mass. Positive power indicates energy transferred to the user and negative power indicates energy absorbed from the user. Middle panel (B) shows the mean positive mechanical power delivered by the sum of the ankle, knee and hip joints (black) and ankle joint (white) during unpowered walking and the exoskeletons (gray) during powered walking. Error bars are standard error of the mean. Brackets indicate the percentage contribution comparison between bars (right to left). For example, the exoskeleton average positive mechanical power was 63% of the ankle joint average positive mechanical power over the stride. Bottom panel (C) shows the mean net metabolic power during unpowered (white) and powered (gray) walking. Error bars are standard error of the mean. Right bracket indicates the change in net metabolic power as a percentage difference from unpowered walking (−10%). Mechanical and metabolic power values are normalized by subject mass. Figure is adapted from Sawicki and Ferris (23).

For level walking, we found that the ankle joint apparent efficiency was approximately 61% (23). That is, for every joule of mechanical energy the biological ankle joint produced, it required ~1.6 J of metabolic energy. This efficiency was much higher than would be expected if muscle alone produced all of the ankle joint positive work. Reports have found that vertebrate skeletal muscles have a positive mechanical work efficiency of 10%-25%. Isolated muscles from rats and mice perform positive mechanical work in vitro with an efficiency of 10%-19% (25). In whole human studies, the efficiency of walking up a steep slope is approximately 25% (16). The ankle joint apparent efficiency we found using our robotic exoskeleton (61%) was 2.4 to 6 times greater than the numbers suggested by previous studies. These findings strongly suggest that the ‘catapult mechanism’ substantially enhances the efficiency of ankle joint mechanical work and reduces the metabolic energy consumed during walking. Thus, the ‘spring in your step’ has clear energetic benefits.

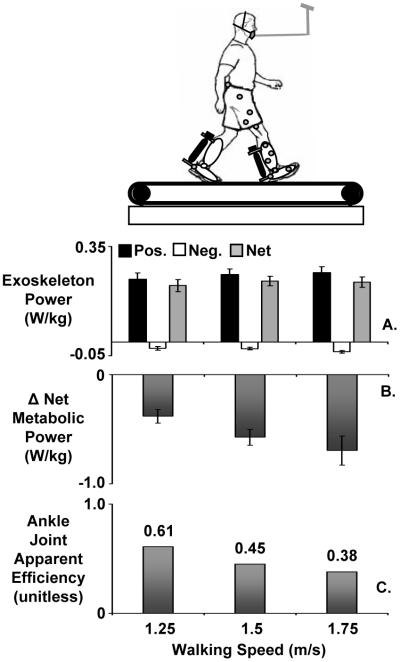
The apparent efficiency of ankle mechanical work was much lower for walking at fast speeds (24) (Figure 5) and on uphill inclines (22). Both perturbations greatly increased the amount of positive mechanical work required from the ankle joint. We found an ankle joint apparent efficiency of 38% for 15 degree incline walking and 38% for walking at 1.75 m/s (Figure 5). In both cases, the lowest values (38%) were still greater than those that would be predicted from isolated muscle studies (10%-19%). This suggests that even in walking tasks that require a large mechanical workload from the muscle fibers, the Achilles tendon still enhances ankle joint mechanical efficiency.

Figure 5. Exoskeleton mechanical power, net metabolic cost and ankle joint apparent efficiency with increasing walking speed.

Bars indicate nine subject mean (A) exoskeleton average positive (black), negative (white) and net (gray) mechanical power over a stride for powered walking, (B) change in net metabolic power (powered - unpowered) due to powered assistance from bilateral ankle exoskeletons, and (C) ankle joint apparent efficiency. Apparent efficiency is computed as the ratio of average exoskeleton positive mechanical power to the resulting reduction in net metabolic power and assumes that artificial muscle work directly replaces biological muscle work. For all panels, walking speed increases from left (1.25 m/s) to right (1.75 m/s). All metabolic power values are normalized by subject mass. Error bars are standard error of the mean. Figure is adapted from Sawicki and Ferris (24).

NOT ALL JOINTS ARE CREATED EQUAL

The major joints of the lower limbs have different mechanical functions during human walking. Their geometric location, anatomical range of motion, and the architecture of the muscles crossing them help to define their mechanical roles. Because of these different roles, there are likely large contrasts in how ankle, knee, and hip dynamics influence the metabolic cost of locomotion.

While the ankle joint is a major producer of positive work, the knee joint primarily yields negative work during walking. During early stance, the knee joint functions as a shock absorber, flexing to cushion weight bearing onto the leading leg. During the pushoff phase of late stance, the knee joint is flexing in preparation for the swing phase but resists the flexion with muscle activity. In both cases, the direction of net muscle moment and joint angle motion are opposite in direction. This results in power absorption rather than power production. The magnitude of the knee work is relatively small compared to the magnitude of the work at the ankle and hip joints. Negative muscle work also has approximately five times the efficiency of positive muscle work (16). As a result of the small magnitude of work and the efficiency of negative muscle work, the relative effect of knee joint musculature on metabolic energy expenditure is probably very low.

Although the hip joint both absorbs and produces power, the positive power far outweighs the negative power. During early stance, the hip performs positive work as it extends, assisting the torso to vault over the stance limb. There is a small amount of negative work at the hip just after midstance, when hip extension transitions to hip flexion. During the pushoff phase of late stance, the largest power burst of the hip occurs. As the thigh moves forward into flexion, the hip joint generates a significant amount of power, accelerating the swing leg. Given the large amount of positive work at the hip joint during human walking, it likely plays a substantial role in setting metabolic energy expenditure.

Though the ankle and hip both act to perform substantial positive work during walking, there are key differences in their muscle-tendon architecture. The plantar flexors have relatively short muscle fibers in a pennation arrangement with a long and compliant tendon that can store and return a considerable amount of energy (2). Pennation angles for the gastrocnemius and soleus range from 6.5 to 32 degrees (6). In contrast, the primary hip flexor and extensor muscles have small pennation angles (5 to 7.5 degrees) (6), large cross sectional areas, and relatively long fiber lengths (6). Importantly, the hip musculature does not possess long compliant tendons.

These specific differences in ankle and hip musculature in humans have been more generally described as the proximo-distal gradient for muscle-tendon architecture in legged animals (3). Proximal muscles in the legs tend to have long muscle fibers with low tendon elasticity. Distal muscles in the legs tend to have shorter muscle fibers with high pennation angles and long compliant tendons. Muscle mass is concentrated more proximally in the legs to reduce inertial costs during locomotion, particularly in humans and other large animals (3). As a result, larger proximal muscles are more likely to be sources of high muscular work output than distal muscles, which are generally better suited for storing and returning elastic energy during locomotion.

There are also likely to be differences in muscle efficiency for hip and ankle musculature due to their respective muscle fiber type compositions. Slow twitch fibers can perform work more efficiently than fast twitch fibers (20). The soleus is primarily slow twitch muscle fibers and the gastrocnemius is evenly split between fast and slow twitch fibers (10). In contrast, the fiber type composition of hip muscles has a larger percentage of fast twitch fibers (10).

Recent advances in biomechanical modeling and computer technology have allowed researchers to better simulate the complexity of muscle dynamics during human walking (27). These efforts have been very useful for investigating how individual muscles may contribute to the mechanical demands of locomotion such as supporting bodyweight or accelerating the leg into swing. The simulation studies have even begun to estimate the role of muscle-specific elastic energy storage and return at different walking speeds (18). While these studies are providing new insight into the biomechanics and energetics of human locomotion, it is important to remember that they are only one approach. Empirical studies are critical for independently testing assumptions and conclusions of biomechanical modeling studies.

ESTIMATES OF METABOLIC COST OF ANKLE, KNEE, AND HIP WORK

Using a simple relationship between metabolic and mechanical energy expenditure and our measurements from exoskeleton walking it is possible to estimate independent contributions of each of the lower limb joints to the overall metabolic energy expenditure of walking (Figure 6).

Figure 6. Schematic of joint level mechanics and energetics of human walking.

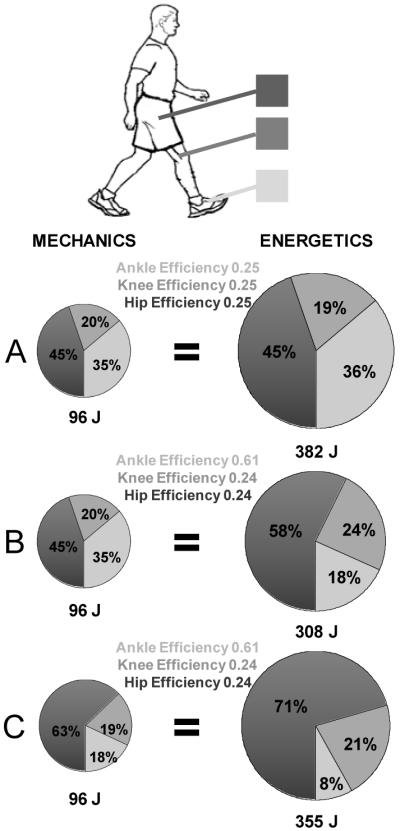
Pie charts indicate the relative amounts (%) of ankle (light gray), knee (medium gray) and hip (dark gray) positive mechanical work (left column) and metabolic energy (right column). The area of each pie chart reflects the magnitude of the total energy per stride that is also displayed numerically below each pie chart. The apparent efficiencies used to convert mechanical energy values to metabolic energy values are indicated in the center column. In panel A, we assumed that all the joints performed positive mechanical work with identical efficiencies set at 0.25 (16). This results in an overestimate of the measured metabolic cost. In panel B, we set the efficiencies so that the ankle joint efficiency matches our measured value of 0.61 (23). The knee and hip were assumed to operate with equal efficiencies (0.24) such that the metabolic energy matched the measured total net metabolic cost per stride (308 J). In panel C, we computed values for a compensated gait where half of the ankle joint work was redistributed to the hip joint. This is meant to represent a hypothetical clinical patient with reduced ankle plantar flexor power at pushoff (e.g. amputee, stroke, or spinal cord injury). Reducing ankle plantar flexor work by 50% and compensating with extra hip work results in a 15% increase in metabolic cost.

The efficiency (η) of mechanical work can be defined as the ratio of mechanical energy output to the net metabolic energy input required to perform the work. Following this definition, and acknowledging that positive and negative work are performed with different efficiencies, we can write a general expression for the net metabolic power of walking (Eq. 1).

$${\mathrm{P}}_{\mathrm{net}\mathrm{met}}=\frac{{\stackrel{‒}{{\mathrm{P}}^{+}}}_{\mathrm{mech}\Sigma \text{joints}}}{{{\eta }^{+}}_{\Sigma \text{joints}}}+\frac{{\stackrel{‒}{{\mathrm{P}}^{-}}}_{\mathrm{mech}\Sigma \text{joints}}}{{{\eta }^{-}}_{\Sigma \text{joints}}}$$ (1)

Equation 1 indicates that the net rate of metabolic energy consumption (P _{net met}) equals the sum of the metabolic costs to perform both positive work and negative work across the lower limb joints. The contributions of mechanical work to metabolic cost are given as the average (indicated by horizontal bars) mechanical power of three joints (Σ = ankle + knee + hip) in both legs over a stride divided by the efficiency of mechanical work (η⁺ for positive work; η⁻ for negative work).

In our calculations, we assumed that the metabolic cost of negative work is negligible during walking. This assumption is reasonable given that (1) the lower limb muscles perform ~50-300% more positive than negative work during walking (5, 18, 26) because significant energy is dissipated in joint contacts and jiggling tissue, (2) the efficiency of negative muscle work (−120%) is much higher than the efficiency of positive muscle work (10%-25%) (16), and (3) tendons and ligaments likely perform some of the negative work during walking rather than being entirely performed by muscles. Based on data for summed joint positive (1.44 W/kg) and negative (0.74 W/kg) power (26), and using η⁺ = 25% and η⁻ = −120%, we estimated that positive work accounts for 90% and negative work only 10% of the total metabolic cost of walking. Given this result, we simplified our analysis by eliminating the negative work term in Equation 1.

We made a second assumption that the metabolic cost of walking can be separated into independent contributions from the ankle, knee and hip each generating positive mechanical work with different joint efficiencies (Eq. 2). This assumption is based on discussion above in NOT ALL JOINTS ARE CREATED EQUAL.

$${\mathrm{P}}_{\mathrm{net}\mathrm{met}}=\frac{{\stackrel{‒}{{\mathrm{P}}^{+}}}_{\mathrm{mech}\mathrm{ankle}}}{{{\eta }^{+}}_{\mathrm{ankle}}}+\frac{{\stackrel{‒}{{\mathrm{P}}^{+}}}_{\mathrm{mech}\mathrm{knee}}}{{{\eta }^{+}}_{\mathrm{knee}}}+\frac{{\stackrel{‒}{{\mathrm{P}}^{+}}}_{\mathrm{mech}\mathrm{hip}}}{{{\eta }^{+}}_{\mathrm{hip}}}$$ (2)

Our data from nine subjects (mass 77.8 kg) walking at 1.25 m/s (stride period 1.17 seconds) with unpowered exoskeletons indicated a net metabolic energy cost of 3.39 W/kg (308 J) (23). Inverse dynamics calculations yielded average positive mechanical power for ankle (0.38 W/kg / 35 J), knee (0.20 W/kg / 18 J) and hip (0.47 W/kg / 43 J). By comparing unpowered and powered walking mechanics and energetics, we computed an apparent efficiency of ankle joint positive work of 0.61. With these data, we estimated the apparent efficiency for positive mechanical work at the knee and hip joints during human walking (assuming they are equal). This was done by combining the second and third terms on the right hand side of Equation 2 and solving for the combined knee/hip apparent efficiency (Eq. 3). Solving Equation 3 yielded a knee/hip apparent efficiency of 0.24.

$${{\eta }^{+}}_{\mathrm{knee}∕\mathrm{hip}}=\frac{{\stackrel{‒}{{\mathrm{P}}^{+}}}_{\mathrm{mech}\mathrm{knee}∕\mathrm{hip}}}{\left({\mathrm{P}}_{\mathrm{net}\mathrm{met}}-\frac{{\stackrel{‒}{{\mathrm{P}}^{+}}}_{\mathrm{mech}\mathrm{ankle}}}{{{\eta }^{+}}_{\mathrm{ankle}}}\right)}$$ (3)

It was then possible to estimate the relative contributions (%) of each of the joints to the total metabolic cost (308 J/stride) based on their relative contributions (%) to the summed joint mechanical work (96 J) (Figure 6B).

Figure 6A shows the metabolic cost of positive work at each of the three joints assuming they all operate with efficiency of 0.25. Using a conservative estimate for muscle efficiency of 0.25 (16) with our measured values of mechanical work resulted in a calculated metabolic cost of 382 J per stride. This overestimated the actual measured metabolic cost (308 J per stride) by 24%. There are two possibilities for this discrepancy: (1) the joints all operate with a higher efficiency of 0.31 or (2) each joint performs work with different mechanical efficiencies. Our direct measurement of ankle joint efficiency of 0.61 and our back-calculation of 0.24 for knee and hip efficiencies supports the second possibility.

CLINICAL IMPLICATIONS

Several clinical populations have increased metabolic cost of walking. For some of these populations, a likely contributor to their high energetic cost of locomotion is an inability to exploit the ‘spring in their step’. This could be due to uncoordinated activation of plantar flexor muscles (e.g. individuals with stroke, spinal cord injury, or cerebral palsy), plantar flexor weakness (e.g. elderly), or simply the lack of muscles and tendons to effectively time and release of elastic energy storage (e.g. amputees). In these cases, the individuals may redistribute the work load from the ankle to less efficient proximal joints (i.e. knee and/or hip). Increased reliance on hip and knee musculature, however, comes at a higher metabolic cost. In Figure 6C, we show how redistributing half of the normal ankle joint work to the hip would impact metabolic cost. There would be an increase in metabolic cost of ~15% compared to the metabolic cost of walking with normal ankle joint work (Figure 6B).

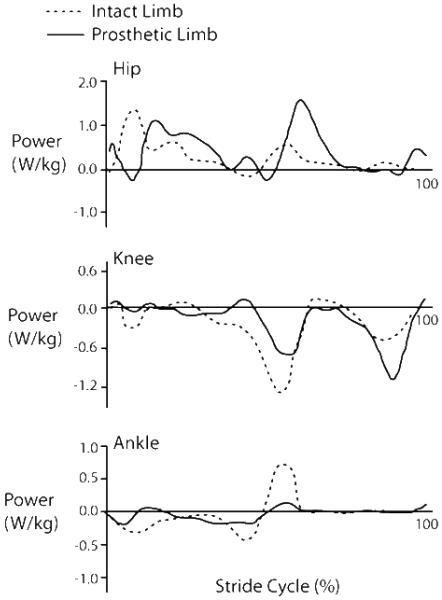
Transtibial amputees are a particularly interesting example of this redistribution of work. They have no Achilles tendon to store and return elastic energy. There are elastic prosthetic limbs which attempt to provide energy storage and return during walking. Yet, these prostheses produce little to no metabolic improvement for walking (13). This limited benefit may be because only a limited amount of the energy stored in the elastic prosthesis is recovered (~40%)(19) compared to the Achilles tendon which can recover up to 80-90% (2, 9). Furthermore, unlike the ‘catapult mechanism’ of the Achilles tendon which can store energy throughout stance and focus the release at push-off, only a small portion of the energy stored in the prosthesis is returned at the appropriate time (13, 19). Because of the decreased pushoff, transtibial amputees rely on the hip and knee joints to provide more mechanical power to their gait (21). Figure 7 shows the altered hip, knee and ankle powers for both the prosthetic limb and the intact limb of transtibial amputees during walking. The loss of active ankle plantar flexion is readily apparent when compared to the intact limb. The compensation of increased hip power is equally evident.

Figure 7. Joint mechanical powers at the hip, knee and ankle during gait in transtibial amputees.

Transtibial amputees walked at 1.27 m/s with a Solid Ankle Cushion Heel (SACH) prosthetic foot. The graph shows the joint powers for the intact (dashed) and prosthetic limbs (solid). The power generated by the prosthetic “ankle” at pushoff is significantly reduced compared to the intact ankle. Conversely, the corresponding hip power generation is markedly increased demonstrating the shift from ankle power to hip power. Figure was adapted from Sadeghi et al. (21).

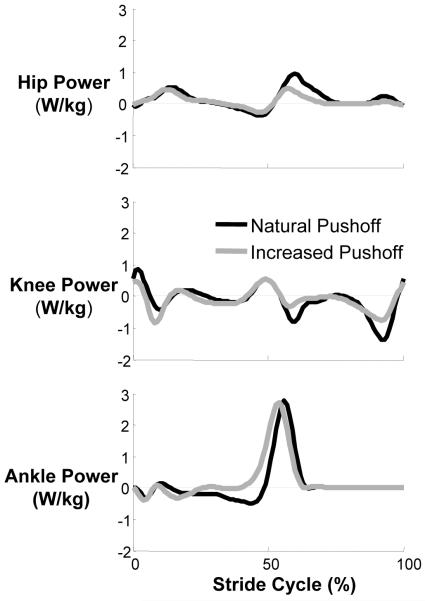
This shift from ankle to hip power is even more striking when comparing amputee to natural gait (Figure 7 vs. Figure 8). Young healthy subjects have a peak ankle power of approximately 3 W/kg when walking at 1.25 m/s (14), while amputees had less than 1 W/kg at the same speed even with the intact limb (21). Conversely, the hip flexor power peak following prosthetic limb push-off was nearly 150% of young healthy subjects. This abnormal distribution (or redistribution) of mechanical power to the hip and knee may help explain the high metabolic cost of walking even with an energy storing prosthetic foot. Similarly, when we asked the healthy subjects to simply “push more with your foot”, we found a significant reduction in hip flexion work accompanying the greater plantar flexor work at pushoff (Figure 7)(14). Taken together, all of these findings indicate a clear tradeoff of ankle and hip mechanical power during human walking that can influence metabolic energy expenditure.

Figure 8. Joint mechanical powers at the hip, knee and ankle during gait with natural and increased pushoff.

Healthy subjects walked at 1.25 m/s with natural gait (black) and consciously increasing plantar flexion pushoff (gray). The shift between ankle and hip joint powers is apparent as hip power generation at the end of stance is lower in the increased pushoff condition compared to natural pushoff. The figure is adapted from Lewis and Ferris (14).

SUMMARY

Due to a variety of factors, particularly differences in muscle-tendon architecture, joints of the lower limb perform mechanical work with different efficiencies during human walking. Plantar flexors at the ankle use elastic energy storage and return in the Achilles tendon to achieve an especially high efficiency of ~61%. There is an inherent tradeoff in power production at the hip and ankle such that deficiencies in one joint are compensated for by the other joint. Because of the contrasting joint efficiencies, reliance on hip work to compensate for decreased ankle work can substantially increase the metabolic cost of locomotion. This alteration in metabolic energy expenditure likely contributes to the high energetic cost of walking in a number of populations such as neurologically impaired individuals, the elderly, and amputees.