Quantitative prediction of protein–protein binding affinity with a potential of mean force considering volume correction

Abstract

Quantitative prediction of protein–protein binding affinity is essential for understanding protein–protein interactions. In this article, an atomic level potential of mean force (PMF) considering volume correction is presented for the prediction of protein–protein binding affinity. The potential is obtained by statistically analyzing X-ray structures of protein–protein complexes in the Protein Data Bank. This approach circumvents the complicated steps of the volume correction process and is very easy to implement in practice. It can obtain more reasonable pair potential compared with traditional PMF and shows a classic picture of nonbonded atom pair interaction as Lennard-Jones potential. To evaluate the prediction ability for protein–protein binding affinity, six test sets are examined. Sets 1–5 were used as test set in five published studies, respectively, and set 6 was the union set of sets 1–5, with a total of 86 protein–protein complexes. The correlation coefficient (R) and standard deviation (SD) of fitting predicted affinity to experimental data were calculated to compare the performance of ours with that in literature. Our predictions on sets 1–5 were as good as the best prediction reported in the published studies, and for union set 6, R = 0.76, SD = 2.24 kcal/mol. Furthermore, we found that the volume correction can significantly improve the prediction ability. This approach can also promote the research on docking and protein structure prediction.

Introduction

Protein–protein interactions participate in an extremely wide range of life processes, including cellular metabolism of matter and energy, signal transduction, and so on. Thus, understanding protein–protein interactions is a very important issue in biology. However, satisfactory solutions to many problems in this field have not been obtained yet, including predictions of protein–protein affinity and protein–protein structure. All of them require a precise energy function. Many efforts have been made to develop such functions but the achieved accuracy still need to be improved in practice.^1–3 In this article, we focus on structure-derived statistical potentials to predict protein–protein affinity.

Structure-derived statistical potentials have been widely applied not only in protein structure prediction and design but also in protein complexes studies, such as protein–ligand affinity prediction (the ligand can be protein, peptide, DNA, RNA, or other molecules), mutation-induced changes in protein stability, and rational drug design.^4–13 In those approaches, the potential is extracted by statistically analyzing known three-dimensional structure data of biomolecules. Therefore, they were also termed knowledge-based potentials. One kind of them, potential of mean force (PMF), is derived from the statistical mechanics of simple liquids,^14–16 which converts particle pair distribution of distance into distance-dependent potential function. PMF has been frequently used in affinity prediction and structure scoring, because its physical meaning and function curve are similar to those of the “true” energy potential, which in principle can be derived from fundamental analysis of the forces between particles,^10,17 such as quantum chemical calculations. Therefore, PMF was also called as energy-like potential or quantity.

Volume correction must be considered when PMF is applied in protein systems. It is one of the key factors that can improve the precision of prediction and the reasonableness of potential function. Since PMF was introduced into the studies of protein systems, the understanding and the application of volume correction (or frequency correction) have undergone a series of development.

Sippl¹⁸ observed the frequency of the alpha-C of a residue pairs and normalized it with the average frequency over all residue pairs. Then, the normalized frequency was transformed into potential directly without considerations of the frequency correction. This traditional PMF approach was the mainstream method in early researches.^19,20

Subsequently, some approaches to calculate PMF are based on the radial distribution function (RDF) in the statistical mechanics of simple liquids.^14–16 In those approaches, the frequency was normalized in the manner of dividing occurrence numbers in a sphere volume without any correction. However, the occupied volume in a more complex system, such as in a protein system, is not a whole sphere. Therefore, when normalizing the occurrence frequency of atom pairs, the whole sphere volume is not a good indicator of the actual occupied volume. For example, Bahar and Jernigan²¹ considered the theoretical basis of PMF as the RDF. They normalized the occurrence numbers with the numbers in a whole sphere volume (4πr²dr). They further analyzed in detail the distribution tendency of the occurrence numbers of residue pairs in protein systems with increasing distance and compared it with the occurrence numbers in a whole sphere (Fig. 2 in Ref. 21, the tangent in this figure corresponds to the distribution of numbers in a whole sphere). Form this figure, we can get the hint of correcting the distribution of the occurrence numbers in a whole sphere with a function to obtain the better approximation to the distribution in protein systems. Mitchell et al.²² found that the factor of a whole sphere (4πr²dr) gives an average potential that is weakly repulsive over the entire distance range with no attractive region at typical interaction distances. They thought that this abnormality is due to the occupied volume of atoms in protein complexes deviating significantly from r² proportionality.

Figure 2.

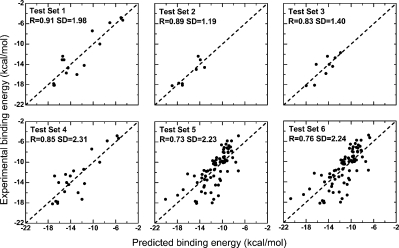
The predicted binding affinity by improved approach fitting with experimental data for six test sets. The linear correlation coefficient (R) and standard deviation (SD) were calculated. The results of the statistical analysis are given in Table I.

Imperfections in the aforementioned studies show that in systems as complicated as proteins, the occupied volume is not proportional to a whole sphere. In contrast to in simple liquids system, the normalized frequency of atom pairs (or residue pairs) can work well¹⁵ using f(r) = N(r)/volume(r), here occupied volume is a whole sphere: volume(r) = 4πr²dr.

Since then to obtain the real occupied volume in protein systems, the volume correction has been developed along two ways, one of which is based on correction functions and the other on structural statistics. The first way corrects occupied volume with a certain function to get the better approximation than a whole sphere volume 4πr²dr. Zhou and Zhou²³ established DFIRE approach, which corrected volume with r^α. The exponent α is a constant, whose empirical value was first found equal to 1.57²³ and refined to 1.61²⁴ subsequently. DFIRE was applied in the affinity prediction of protein complexes later.²⁵ In this article, we tested our approach on the test set from DFIRE. Shen and Sali²⁶ went a step further. They analytically derived a statistical potential termed DOPE for decoy discrimination of single protein structure. The DOPE corrects volume with a correction factor of r^α(r). The effective exponent α(r) is a function of interparticle distance r, which results in a more flexible application.

It should be noted that these approaches above corrected volume with a uniform factor to all atom types. In other words, they used the same correction factor for distinct atoms. But in fact, each of the atom types is different on occupied volume. Therefore, a distinct volume correction should be used for each of the atom types.

This problem is naturally solved by the second type approach of volume correction, which acquires the volume correction factors directly from statistics to structures. This type of approach, unlike the first one, is independent of a certain function form to correct occupied volume. Moreover, in contrast to the first way, it is able to distinguish different atom types surrounded by distinct environments, by generating a unique volume correction for each atom type. Therefore, a more accurate correction can be acquired. Muegge and Martin²⁷ corrected the volume based on structural statistics. In their approach, each atom type is treated with a different volume correction. Their approach performed well in the prediction of protein–ligand binding affinity. However, the implementation of their approach is very complicated in practice, which obstructed its popularity.

The approach presented in this article belongs to the second type of approach, but we circumvented the complicated step of volume correction process. The volume correction was achieved using a novel and very simple frequency correction. More reasonable potentials were obtained, and the prediction to protein–protein binding affinity on six test sets from five literatures also showed good performance of our approach.

Results and Discussions

Details of the pair potentials

Three pair potentials chosen as representative examples are shown in Figure 1. These potentials are backbone–backbone (B-B) potential 1-1, backbone-side chain (B-S) potential 7-4, and side chain–side chain (S-S) potential 8-6. The potentials calculated by Eq. (2), that is, our approach, are represented by the solid curve. For comparison, the potentials from Eq. (1), that is, the traditional approach, are represented by the dashed curve. The numbers 1-1, 7-4, and 8-6 are labels of atom pairs, whose atom types are defined in Table III.

Figure 1.

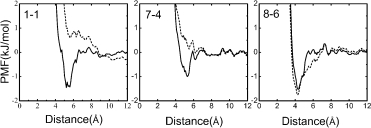
Examples of potential. 1-1 is backbone-backbone (B-B) potential, 7-4 is backbone-side chain (B-S) potential, and 8-6 is side chain-side chain (S-S) potential. The numbers in 1-1, 7-4, and 8-6 represent the atom types defined in Table II. The solid curves represent the potentials from improved approach, and the dashed curves represent the potentials from traditional approach.

Table III.

Atom Type Definition for Heavy Atoms of the Standard Amino Acids

Atom type	Type definition
1	Cα (all amino acids, except Gly)
2	Gly-Cα
3	N (all amino acids, except Pro)
4	C (all amino acids)
5	O (all amino acids)
6	Val-Cγ1, Val-Cγ2, Leu-Cδ1, Leu-Cδ2, Ile-Cγ2, Ile-Cδ, Thr-Cγ
7	Leu-Cγ, Ile-Cγ1, Gln-Cγ, Lys-Cγ, Lys-Cδ, Glu-Cγ, Arg-Cγ
8	Cβ (all amino acids, except Pro, Ser, Thr, Cys)
9	Met-Sδ
10	Pro-N
11	Phe-Cγ, Tyr-Cγ
12	Phe-Cδ1, Phe-Cδ2, Phe-Cɛ1, Phe-Cɛ2, Phe-Cζ, Tyr-Cδ1, Tyr-Cδ2, Tyr-Cɛ1, Tyr-Cɛ2
13	Trp-Cγ
14	Trp-Cɛ2
15	Ser-Cβ
16	Ser-Oγ, Thr-Oγ
17	Thr-Cβ
18	Asn-Nδ2, Gln-Nɛ2
19	Cys-Sγ
20	Lys-Nζ
21	Arg-Cζ
22	Arg-Nη1, Arg-Nη2
23	His-Cγ
24	His-Cδ2
25	His-Nɛ2
26	His-Cɛ1
27	Asp-Cγ, Glu-Cδ
28	Asp-Oδ1, Asp-Oδ2, Glu-Oɛ1, Glu-Oɛ2
29	Cys-Cβ
30	Met-Cɛ
31	Tyr-Cζ
32	Pro-Cδ
33	Asn-Cγ, Gln-Cδ
34	Asn-Oδ1, Gln-Oɛ1
35	Lys-Cɛ
36	Arg-Nɛ
37	Arg-Cδ
38	His-Nδ1
39	Trp-Nɛ1
40	Tyr-Oη
41	OXT (the extra oxygen at the carboxyl terminal)
42	Pro-Cβ
43	Pro-Cγ
44	Met-Cγ
45	Trp-Cɛ3, Trp-Cζ2, Trp-Cζ3, Trp-Cη2
46	Trp-Cδ1
47	Trp-Cδ2

For pair potentials 1-1 and 7-4 from traditional approach (dashed curves in Fig. 1), repulsion at all distances can be observed. Potential 8-6 from traditional approach is very similar to that from improved approach; the two curves share a normal shape without strong repulsion at all distances.

The solid curves in Figure 1 represent the potentials from our improved approach as previously mentioned, have classic picture of nonbonded atom pair interaction as Lennard-Jones potential. They exhibit strong repulsion at short distances, followed by one or several valleys with local minimums, representing the interaction preference at certain distances. When the distance between atom pairs is increased, the values of potentials trend zero, which means the atom pairs have very little interaction at such a long distance.

In short, strong repulsive interactions can be observed at all distances in B-B and B-S potentials from traditional approach (dashed curves in Fig. 1). Corresponding to our results, the potentials calculated from other traditional approaches in literatures also exhibit similar curves.^21,22 However, in potentials from improved approach, this strong repulsion is weakened (solid curves in Fig. 1). These potentials from improved approach are more reasonable and show a classical picture of nonbonded atom pair interaction as Lennard-Jones potential. This indicates better accordance of our approach with acknowledged theories.

In traditional approach, the abnormal repulsions at all distances of B-B and B-S potentials can be attributed to the shortage of observed frequency of atom pairs. The main reason for the shortage is the less exposure of the backbone atoms than the side chain atoms in protein–protein interface. As the space around backbone atom cannot be filled with atoms of the other chain, observed frequency of B-B and B-S atom pairs remains low.

Binding affinity prediction of protein–protein complexes for six test sets

To evaluate the prediction ability of our approach to the affinity prediction of protein–protein complexes, we collected as much test data as possible from the literature of binding affinity prediction and discarded none of them. Because there have not been an authoritative benchmark of test sets for binding affinity prediction of protein–protein complexes, we collected test data from published studies, which predicted protein–protein binding affinity using various approaches not just PMF. Then, we compared prediction ability of their methods with ours according to linear correlation between predicted affinity and experimental data. It should be noted that we discard none of the test data in the literature, because the correlation coefficient (R) could be significantly increased artificially by an additional restriction of included test data.

Finally, affinity predictions on six test sets (Table I) were done. The potentials for predictions were trained from 127 PDB entries (Table II). A total of 47 atom types for all the heavy atoms of the 20 amino acids were defined (Table III). Finally, 86 protein-protein complexes (Table IV) were predicted. Test sets 1–5 come from five published articles. Test set 6 is the union set of sets 1–5, which means it contains all nonrepeated data of the first five sets. For all the six test sets, we evaluated prediction ability using linear correlation coefficient (R) and standard deviation (SD) of fitting predicted affinity to experimental data, and then, we compared R and SD of our prediction with the linear correlation results reported in the literatures. The criterion of the better prediction should be larger R and smaller SD in absolute value contemporaneously. All of the literatures reported R, whereas only two of them reported SD yet. The results are presented in Table I and Figure 2.

Table I.

Linear Correlation Between Experimental Binding Affinity and Predicted Affinity for Six Test Sets

			R		SD
Test set	Ref. a	No. of complexes	Oursb	Literaturec	Oursb	Literaturec
1	a	15	0.91	0.96d	1.98	NAe
2	b	8	0.89	0.74	1.19	1.5
3	c	9	0.83	0.70	1.40	2.0
4	d	21	0.85	0.75	2.31	NAe
5	e	82	0.73	0.73	2.23	NAe
6	f	86	0.76	–	2.24	–

^aa, Ref. 28; b, Ref. 29; c, Ref. 30; d, Ref. 31; e, Ref. 25; f, union set of sets 1–5.

^bThe results from our approach.

^cThe results from literature.

^dIn the literature, for the polar and apolar components, the correlation coefficient is 0.63 and 0.77, respectively. When the two terms are added together and weighted by two free parameters α and β, the correlation extends to 0.96.

^eNA, no available standard deviation (SD) was reported in the literature.

Table II.

The 127 PDB Entries for Training Potentials

12gs	1a09	1a14	1a1n	1a2c	1a2k	1a2x	1a2y	1a3b	1a3r
1a46	1a4w	1a5g	1a5s	1a61	1a9e	1ab9	1abo	1abr	1abw
1agd	1ak4	1an1	1aqc	1aqd	1aqv	1avw	1axd	1axi	1bd2
1bhf	1bj1	1bnd	1brb	1brc	1bt6	1dkz	1dzb	1e4x	1e96
1eay	1eer	1efn	1efu	1exf	1fdl	1flt	1gbb	1gc1	1gg2
1gl1	1got	1gua	1gux	1gzs	1h0d	1h2s	1he1	1hwg	1ikf
1ir3	1itb	1jhg	1jhl	1kip	1lck	1ld9	1lfd	1mct	1mel
1mlc	1nmc	1oak	1oby	1obz	1oey	1oga	1ogt	1ohz	1okk
1okv	1ol5	1osp	1osz	1qew	1qja	1qls	1qo3	1rst	1rsu
1scn	1sfi	1shd	1sib	1slg	1slu	1sm3	1smf	1spp	1taf
1tbg	1tec	1tx4	1tze	1upt	1uzx	1vad	1wej	1www	1x11
1ycs	1zfp	2cbl	2fib	2h1p	2hrp	2jel	2prg	2seb	2tgp
2trc	2vaa	3cyh	3nse	3sgb	3sic	5csm

Table IV.

The PDB Interfaces and Experimental Affinities in Six Test Sets

PDB ID	Interface	Affinity (kcal/mol)	PDB ID	Interface	Affinity (kcal/mol)
2ptc	E/I	−18.1	1tpa	E/I	−17.8
2kai	AB/I	−12.4	4cpa	blank /I	−10.0
3cpa	blank/S	−5.3	3sgb	E/I	−12.7
2sec	E/I	−13.1	1cse	E/I	−13.1
1cho	E/I	−14.6	2tpi	Z/I	−18.1
2tpi	Z/S	−5.8	2tgp	Z/I	−18.2
2sni	E/I	−15.8	4tpi	Z/I	−17.7
1tec	E/I	−14.0	4sgb	E/I	−11.7
2sic	E/I	−12.7	2er6	E/I	−9.8
1acb	E/I	−16.1	1tbq	JK/S	−17.3
1atn	A/D	−11.8	3tpi	Z/S	−7.8
4htc	HL/I	−15.4	1bth	HL/P	−16.5
1dfj	E/I	−18.0	1avw	A/B	−12.3
1stf	E/I	−13.5	3hfl	LH/Y	−14.5
1vfb	AB/C	−11.4	1nsn	HL/S	−11.8
1igc	HL/A	−12.7	1ahw	AB/C	−11.5
1wej	HL/F	−9.5	1mel	M/B	−10.5
1nmb	HL/N	−10.0	1fdl	HL/Y	−11.4
2jel	HL/P	−11.5	1jhl	HL/A	−11.8
3hfm	HL/Y	−13.3	1mlc	AB/E	−9.7
1bql	HL/Y	−14.5	4ins	AB/CD	−7.4
1hbs	ABCD/EFGH	−4.8	1brs	B/E	−17.3
1tce	A/B	−5.8	1lck	A/B	−7.0
1lcj	A/B	−7.8	2pld	A/B	−9.0
1sps	A/D	−9.1	1b46	A/B	−7.2
1b3l	A/B	−8.0	1b9j	A/B	−8.1
1b58	A/B	−9.0	1jeu	A/B	−9.3
1jev	A/B	−9.4	1b5i	A/B	−9.6
1b32	A/B	−9.7	1b40	A/B	−9.9
1qkb	A/B	−10.0	1b4z	A/B	−7.1
2olb	A/B	−7.6	1qka	A/B	−8.1
1b3g	A/B	−9.2	1b3f	A/B	−9.4
1b05	A/B	−9.7	1b52	A/B	−9.7
1jet	A/B	−9.8	1b51	A/B	−10.0
1b5j	A/B	−10.1	1ola	A/B	−9.5
1dkz	A/B	−9.1	1dkg	AB/D	−10.3
2pcc	A/B	−10.0	1gua	A/B	−10.1
1ycs	A/B	−10.3	1efn	A/B	−16.6
1fss	A/B	−14.9	1mda	HL/A	−7.3
1ak4	A/D	−6.5	1ebp	A/C	−11.7
1hwg	C/A	−13.0	3hhr	B/A	−13.6
3ssi	Symmetry	−16.0	1avz	AB/C	−6.4
1a0o	A/B	−8.1	1gla	G/F	−6.7

Test set 1 (Table I) contains 15 protein–protein complexes from Ref. 28. In this literature, the affinity is described as the sum of solvation terms based on atomic solvation parameter (ASP) and an energy term to account for the loss of translational and rotational entropy. For the polar and apolar solvation components, the correlation coefficients (R) are 0.63 and 0.77, respectively. When they revised their function by adding the two terms together weighted by two newly introduced free parameters, α and β, the correlation extends to 0.96. And, no SD values were reported in the literature. In our prediction, R = 0.91 and SD = 1.98 kcal/mol (Fig. 2).

Test set 2 (Table I) contains eight protein–protein complexes from Ref. 29. In this literature, they used a method constructed from molecular surface preferences. For set 2, R = 0.74 and SD = 1.5 kcal/mol were reported. In our prediction, R = 0.89 and SD = 1.19 kcal/mol.

Test set 3 (Table I) contains nine protein–protein complexes from Ref. 30. In this literature, they used a method based on MJ potential. For set 3, R = 0.70 and SD = 2.0 kcal/mol were reported. In our prediction, R = 0.83 and SD = 1.40 kcal/mol (Fig. 2).

Test set 4 (Table I) contains 21 protein–protein complexes from Ref. 31, in which the method is based on ASP. R = 0.75 with no SD value was reported in the literature. In our prediction, R = 0.85 and SD = 2.31 kcal/mol (Fig. 2).

Test set 5 (Table I) contains 82 complexes from Ref. 25 predicted by DFIRE, which is the only test set predicted by PMF method. Our prediction performed equally well as the literature in term of correlation coefficients (R = 0.73).²⁵ The SD of our prediction is 2.23 kcal/mol. The literature did not report the SD.

Test set 6 contains all data in sets 1–5, adding up to 86 complexes. The R and the SD of our prediction are 0.76 and 2.24 kcal/mol, respectively. It is particularly worth noting that although set 6 contains more test data (86) than set 5 (82), but in our predictions R = 0.76 of set 6 is better than R = 0.73 of set 5. The reason is that these test sets were extracted from published articles directly and have not been refined. For example, test set 5 contains 20 OppA-peptide complexes, whose peptides have highly similar sequences, resulting in a biased prediction toward this type of complexes. Test set 6 contains more data, which partly balance out this effect.

A good test set served as a benchmark should be nonredundant or at least with restricted numbers of similar complexes. However, until now, there is no authoritative test set served as benchmark for binding affinity prediction of protein–protein complexes. We plan to build such a benchmark in our future studies.

Overall, test sets 1, 2, 3, and 4 contain less test data, so predictions can easily obtain good linear correlation (Table I) as in both our predictions and literature. Moreover, for all test sets except set 1, correlations of our prediction are better than report in the literature. Nevertheless, the meaning of the correlation for small test set should not be overestimated, as it is unstable. If one or a few test data in these small sets are changed, the correlation (R and SD) might be significantly changed. Therefore, performance on the four sets may not say much about prediction ability. For test set 5, a larger set, our prediction obtained as good correlation as literature (0.73). For set 6, which contains all data in sets 1–5, our prediction obtained even better R (0.76) than for set 5 (0.73).

The volume correction is very important for the prediction of binding affinity

We found that the introduction of volume correction makes the pair potentials more reasonable and results in great improvement on prediction ability for the binding affinity of protein–protein complexes.

Above in Figure 1, we have shown that B-B potential 1-1, B-S potential 7-4 from traditional approach without volume correction have strong repulsive interactions at all distances (dashed curves in Fig. 1). But, in potentials from our approach considering volume correction, this strong repulsion is weakened and the attractive valley appears (solid curves in Fig. 1). A classic picture of nonbonded atom pair interaction as Lennard-Jones potential was shown. It represents that volume correction can obtain more reasonable potential. In comparison, S-S potential 8-6 already has reasonable shape and has not large change after volume correction.

Correct understanding to the interactions of B-B and B-S atom pairs is very important for the binding affinity prediction, because B-B and B-S atom pair interactions make a large percentage contribution in protein–protein interactions. We analyzed the percentage contribution of B-B, B-S, and S-S pair based on 127 protein–protein complexes in the training set. The components of B-B, B-S, and S-S make up 23.5, 50.1, and 26.4% of the total interaction pairs, respectively. Therefore, if inaccurate estimates of B-B and B-S pair potentials are used to predict binding affinity, the results will be affected significantly. Figure 3 shows the prediction for 86 protein–protein complexes in test set 6. The traditional approach without volume correction obtained linear R = 0.07 and SD = 3.45 kcal/mol. Meanwhile, our approach considering volume correction obtained R = 0.76, SD = 2.24 kcal/mol. Above showed the introduction of volume correction is very important for the improvement of prediction ability.

Figure 3.

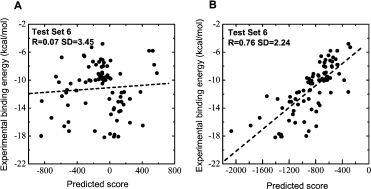
The binding affinity prediction to test set 6. The linear correlation coefficient (R) and standard deviation (SD) were calculated. (A) Prediction from traditional approach. (B) Prediction from improved approach considering volume correction.

A web server for the binding affinity prediction of protein–protein complexes

We developed a web server PPEPred (http://www.bioinfo.tsinghua.edu.cn/~suyu/ppepred/) for the binding affinity prediction of protein–protein (protein–peptide) complexes from three-dimensional structure data, based on the approach in this article. The parameters a and b for the prediction in Eq. (6) are 0.007850 and −4.491 kcal/mol from the linear fitting to test set 6. The inputs of PPEPred server are the structure name, two chains name, and user needs to upload the structure data of Protein Data Bank (PDB) file or user file in PDB format. The output is the affinity of this complex. The web server is free and open to everyone.

Materials and Methods

Potential of mean force

Traditional approaches of PMF were widely applied in the studies of protein structure and protein–protein interaction. Here, the traditional potential between two atoms of type i and type j with distance r can be described by the function:

(1)

where k_B is the Boltzmann constant and T is the absolute temperature. q_ij(r) is the normalized frequency between atom pairs of type i and type j, and q_xx(r) represents average normalized frequency covered all atom pairs, which are defined in Eq. (4). Other traditional approaches consider q_ij(r) and q_xx(r) as density in a whole sphere volume (4πr²dr). Both of them can obtain similar results in calculation.

However, there are some problems with traditional approaches mentioned earlier. q_ij(r) and q_xx(r) have distinct distribution, corresponding the average density in calculating the RDF in the theory of simple liquids. But, q_ij(r)/q_xx(r) ignored the distinct distribution between them. To get more reasonable potential, this deviation ought to be corrected in an improved approach.

Up till now, all the improved approaches corrected the deviation based on the average density on volume, named as volume correction. But, in comparison with the simple liquid systems, proteins are extremely complicated soft matter. In protein systems, these approaches were deduced in an extremely complicated manner, and the steps of implement also contain many details in practice, such as the approximation in acquiring the distributions of atom volume and adopting diverse width of bins at different distances in statistics.^25–27

On the contrary, in our approach, we directly correct the volume effect based on frequency, which can achieve the same goal of correction and largely simplify the process of implement in practice. The improved approach of PMF in our work is given by:

(2)

where k_B is the Boltzmann constant and T is the absolute temperature. q_ij(r) and q_xx(r) are the normalized frequency of atom pairs, which are defined in Eq. (4). f_cor is the correction factor, derived from smoothing q_xx(r)/q_ij(r) ranging from 0 to 12 Å, by a moving window of 3.5 Å width with bin of width 0.1 Å.

To obtain the stable potentials in statistics, we considered the potentials only when the total occurrence number of atom pairs was larger than 1000. If the total occurrence number of atom pairs of type i and type j was smaller than 1000, we set A_ij(r) = 0. That is, we ignored the contribution of a particular pair type if it had not sufficient data in statistics.

Later, we show how to obtain the normalized frequency q_ij(r) and q_xx(r) statistically.

First, according to statistics, we obtain N_ij(r), the occurrence numbers of atom pairs ij at a certain distance r, in a training database of protein–protein complexes, ranging from 0 to 12 Å at 0.1 Å intervals (but the occurrence numbers in which atom pairs distance is below 2.5 Å were set zero as unrealistically short for heavy atom pairs):

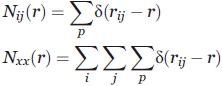(3)

where δ(x) is δ function, which is equal to 1 if its argument is zero, and zero otherwise. The subscript p designates that the summation cover all protein–protein complexes in the training database. The subscript i and j designate that the summation cover all atom pairs.

Then, we normalize the occurrence numbers to get the relative frequency:

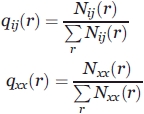(4)

where the summation is on atom pairs ranging from 0 to 12 Å.

Scoring and fitting experimental binding affinity

The scoring function to a protein–protein complex is defined as the summation over all atom pair interactions of the protein–protein complex:

(5)

where r_cutoff is the cutoff distance between atoms i and j. Here, 12 Å is used.

To relate the score above to an absolute binding affinity, we fit it to binding affinity in a linear manner:

(6)

The training set

The Brookhaven Protein Data Bank³² was used to get the training data set in deriving the potential. We included only X-ray structures of protein–protein and protein–peptide complexes with resolutions better than 2.5 Å. Based on these criteria, 438 entries were yielded. To eliminate the structure similarity, we further filtered these entries based on molecular information in PDB entry and the cited literature in REMARK, with the aid of the molecule graph software (RasMol). For the same structure, we only reserved the entry of the best resolution. Finally, the training set contained 178 interfaces (in Supporting Information) from 127 PDB entries (Table II).

Atom type definition for heavy atoms of the standard amino acids

We defined 47 atom types for all the heavy atoms of the 20 amino acids (Table III). The definition of atom type is based on its physicochemical property, connectivity, and environment, derived from 40 atom types in Ref. 33. To obtain more details of interactions, it would be better that we define as many atom types as possible. On the other hand, to obtain statistically sufficient data, we could not define too many atom types. Therefore, the number of atom types was a compromise between the two considerations.

Conclusions

We present a novel PMF considering volume correction. In the prediction of protein–protein binding affinity, six test sets were tested and good performance was shown. This approach circumvents the complicated step of volume correction process and is extremely easy to implement in practice.

In this article, our approach is used to predict protein–protein binding affinity. But in respect of methodology, the statistics and calculation of this approach do not specialize in protein–protein complexes. Therefore, it can be applied to other fields, in which traditional approaches of PMF have been widely applied, such as protein–ligand docking and protein threading in structure prediction. It is expected to have a good performance.