Abstract
Transmural electrophysiological heterogeneities have been shown to contribute to arrhythmia induction in the heart; however, their role in defibrillation failure has never been examined. The goal of this study is to investigate how transmural heterogeneities in ionic currents and gap-junctional coupling contribute to arrhythmia generation following defibrillation strength shocks. This study used a 3D anatomically realistic bidomain model of the rabbit ventricles. Transmural heterogeneity in ionic currents and reduced sub-epicardial intercellular coupling were incorporated based on experimental data. The ventricles were paced apically, and truncated-exponential monophasic shocks of varying strength and timing were applied via large external electrodes. Simulations demonstrate that inclusion of transmural heterogeneity in ionic currents results in an increase in vulnerability to shocks, reflected in the increased upper limit of vulnerability, ULV, and the enlarged vulnerable window, VW. These changes in vulnerability stem from increased post-shock dispersion in repolarisation as it increases the likelihood of establishment of re-entrant circuits. In contrast, reduced sub-epicardial coupling results in decrease in both ULV and VW. This decrease is caused by altered virtual electrode polarisation around the region of sub-epicardal uncoupling, and specifically, by the increase in (1) the amount of positively polarised myocardium at shock-end and (2) the spatial extent of post-shock wavefronts.
Keywords: Transmural electrophysiological heterogeneities, Vulnerability to electric shocks, Bidomain simulations
1. Introduction
Electrical defibrillation by the timely application of a strong electric shock to the heart is the only effective therapy against lethal arrhythmias. However, the mechanisms behind defibrillation failure still remain incompletely understood. A large body of experimental research has demonstrated that defibrillation and vulnerability to electric shocks are strongly linked as they are driven by the same underlying factors (Chen et al., 1986, 1991; Malkin et al., 1995). As a result, the upper limit of vulnerability (ULV), which is defined as the highest shock strength (SS) above which no arrhythmia is induced, can be used to approximate the defibrillation threshold as part of the clinical procedure of programming the implantable cardioverter/defibrillators.
Recently, the use of an anatomically based computational model of stimulation/defibrillation has provided significant insight into the mechanisms of cardiac vulnerability to electric shocks and defibrillation in normal (Trayanova et al., 2002; Aguel et al., 2003; Rodriguez et al., 2005), and diseased hearts (Rodriguez et al., 2004). These simulations have supplied information with high spatial and temporal resolution regarding the shock-induced electrical events within the depth of the myocardial wall, not accessible by current experimental techniques. However, one of the main limitations of these computational studies has been the fact that they considered cardiac tissue to be both electrophysiologically and structurally homogeneous.
Experimental studies of isolated ventricular tissue (Antzelevitch et al., 1999a, b; Idriss and Wolf, 2004), and of single myocytes isolated from various locations across the ventricular wall (McIntosh et al., 2000) have demonstrated that ionic properties change in the depth of the ventricular wall. In particular, three layers of functionally different cell types have been identified, namely the epicardial, endocardial, and midmyocardial layers (Ueda et al., 2004). Transmural dispersion in action potential duration (APD), which results from variations in cellular ionic properties, is known to modulate the arrhythmogenic substrate (Kuo et al., 1983; Laurita et al., 1998; Antzelevitch and Fish, 2001) and could thus play a role in the outcome of anti-arrhythmia therapy.
Furthermore, experimental studies (Drouin et al., 1995; Yan et al., 1998a; Poelzing et al., 2004; Yamada et al., 2004) have documented heterogeneity in intercellular gap-junctional coupling within the sub-epicardium of human, canine, and rodent ventricles. Reduced gap-junctional coupling causes slow conduction and unidirectional block leading to the establishment of re-entry (Peters et al., 1997). However, other studies (Huelsing et al., 2000) have suggested that reduced intercellular communication may be cardioprotective by preventing impulse propagation between midmyocardium and epicardium. The role of gap-junctional coupling heterogeneity in arrhythmogenesis remains unclear; so does its contribution to the success or failure of a defibrillation shock.
The goal of this study is to provide insight into the contribution of transmural heterogeneities in ionic currents and in gap-junctional coupling to the mechanisms of defibrillation failure. This is achieved by investigating the mechanisms of cardiac vulnerability to electric shocks using an anatomically accurate three-dimensional (3D) rabbit ventricular model (Vetter and McCulloch, 1998; Trayanova et al., 2002), which for the first time incorporates transmural heterogeneities in electrophysiological properties and gap-junctional coupling.
In understanding the mechanisms of defibrillation failure in the heterogeneous heart, of particular importance is knowledge of how the transmural heterogeneity in ionic currents and the reduced sub-epicardial coupling interact with the electrophysiological heterogeneity imposed by the application of a defibrillation shock, modulating virtual electrode polarisation (VEP) within the depths of the ventricular wall as well as the characteristics of the ensuing post-shock wavefronts. We hypothesise that transmural heterogeneities in both ionic properties and intercellular coupling alter the outcome of the shock by affecting the spatial extent of positive VEP and the characteristics of post-shock wavefronts. This, in turn, alters the global vulnerability parameters, such as the duration of the vulnerable window (VW) and the value of the ULV.
2. Methods
2.1. Computational model
This study used a 3D geometrically accurate rabbit ventricular model (Vetter and McCulloch, 1998) that incorporated realistic fibre architecture and representation of the blood within the ventricular cavities and the perfusing bath (Trayanova et al., 2002). The finite element mesh consisted of 829 021 tetrahedral elements, with a spatial resolution of 500 μm. The bidomain approach was used to simulate electrical activity in the myocardium, where a semi-implicit finite element approach was used to solve for the potentials, as previously described (Eason and Malkin, 2000). The time step was 5 μs during the application of external shocks, and 10 μs during propagation before and after shock application. The bidomain conductivities used in the rabbit ventricular model are based on data measured by Clerc (Clerc, 1976), as described previously (Eason and Malkin, 2000, Trayanova et al., 2002).
Membrane kinetics were represented by the Luo–Rudy dynamic model (Luo and Rudy, 1994) augmented for defibrillation (Ashihara and Trayanova, 2004). Transmural ventricular heterogeneities in the transient outward potassium current (Ito), in the slow and rapid delayed rectifier potassium currents (IKs, IKr), and in the sodium (INa) current were incorporated in the model based on experimental data (McIntosh et al., 1998, 2000; Dumaine et al., 1999; Xu et al., 2001), as done previously (Saucerman et al., 2004). The above are the main currents responsible for transmural heterogeneities in action potential shape and duration. The spatial distribution of transmural heterogeneity in ionic currents was incorporated using endocardial, epicardial and midmyocardial layers with relative thickness of 3:3:2 (Saucerman et al., 2004). Each myocardial node was assigned endocardial, midmyocardial or epicardial membrane kinetics, depending on its position within the ventricular wall. The maximum conductances for Ito, IKs, IKr and INa in each layer were multiplied by scaling factors SFto, SFKs, SFKr and SFNa, as listed in Table 1. A five-fold decrease in intercellular coupling was introduced within the sub-epicardium, i.e. at the border between the midmyocardial and epicardial layers, consistent with experimental data (Drouin et al., 1995; Yan et al., 1998a; Poelzing et al., 2004; Yamada et al., 2004).
Table 1.
Scaling factors (SF) used to multiply the maximum conductances of Ito, IKs, IKr and INa in the homogeneous model, and in the epicardial, midmyocardial and endocardial layers of the heterogeneous models
| Homogeneous | Epicardium | Midmyocardium | Endocardium | |
|---|---|---|---|---|
| SFto | 0 | 1 | 0.425 | 0 |
| SFKs | 1 | 1.154 | 0.384 | 0.462 |
| SFKr | 1 | 1.530 | 0.574 | 1.147 |
| SFNa | 1 | 0.375 | 0.5 | 0.438 |
2.2. Protocol for determining the vulnerability area
The protocol used for determining the vulnerability area (VA), i.e. the area on a 2D grid that encompasses episodes of re-entrant arrhythmia induction by the shock, was described in a previous paper (Rodriguez et al., 2004). In brief, the rabbit ventricular model was paced at the apex at a basic cycle length of 250 ms, to ensure that the ULV approximated the defibrillation threshold (Malkin et al., 1995). After seven paced beats, 8 ms truncated-exponential monophasic shocks of strength 3.81–38.09 V/cm were applied over a range of coupling intervals, CIs (100–200 ms) via large planar electrodes located at the vertical boundaries of the perfusing bath (Fig. 1). The electrode near the right ventricle (RV) was the cathode, and the one near the left ventricle (LV) was the grounding electrode. CI was defined as the time interval between the onset of the last pacing stimulus and the onset of the shock. SS referred to the leading-edge value of the electric field between electrodes. The VA was constructed for three cases: (1) homogeneous ventricular model, i.e. the same membrane kinetics and thus the same action potential shape and duration was considered at every node in the ventricular mesh; (2) heterogeneous ventricular model, i.e. epicardial–endocardial heterogeneity in ionic currents was implemented and (3) heterogeneous ventricular model that also incorporated sub-epicardial uncoupling.
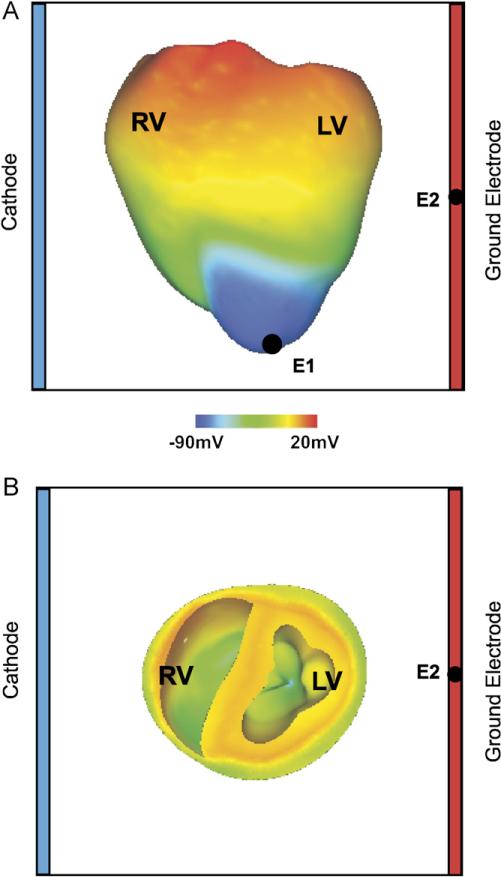
Fig. 1.
(A) Anterior epicardial and (B) basal transmural views of the rabbit ventricular model with the shock electrodes at the boundaries of the perfusing chamber, the pacing electrode at the apex (E1), and the ECG electrode (E2). Pre-shock epicardial transmembrane potential distribution corresponds to a coupling interval of 140 ms in the heterogeneous ventricles.
An arrhythmia was considered sustained if two or more beats were induced after the application of the shock. The VW was defined as the range of CIs for which a sustained arrhythmia ensued following the shock. The ULV was the highest SS above which no arrhythmia was induced.
2.3. Data analysis
To analyse the effect of incorporating heterogeneities in ionic currents and sub-epicardial coupling in ventricular electrical behaviour, activation and repolarisation times were quantified at each ventricular node. At each node, local activation time was calculated following the 7th pacing stimulus as the interval between the stimulus onset and the time of maximum action potential upstroke velocity. Local repolarisation time was calculated as the interval between the onset of the seventh stimulus and the time at which the node was 70% repolarised. APD was the difference between activation and repolarisation times. Local activation and repolarisation times and APD were measured during the 7th paced beat, at a basic cycle length of 250 ms. In addition, to better study arrhythmogenesis in the rabbit ventricles, the dynamics of the scroll-wave filaments, the organising centres of re-entrant activity, was analysed using an algorithm published previously (Trayanova et al., 2002; Larson et al., 2003). Pseudo-electrocardiograms (ECG) (Plonsey and Barr, 2000), were computed at a node marked E2 in Fig. 1, in a manner previously described by Gima and Rudy (2002), and using a three-point Gauss quadrature scheme for numerical integration over the finite element tetrahedral mesh.
3. Results
3.1. Electrical activity following apical stimulation
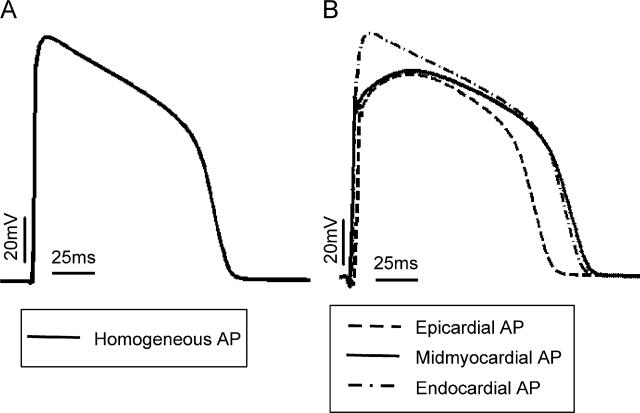
Fig. 2A presents the time course of an action potential computed using the ionic model implemented in the homogeneous ventricular model, while Fig. 2B presents the time course of action potentials computed using single cell models of epicardial (dashed line), midmyocardial (solid line) and endocardial (dot-dashed line) cells, with properties described in the Methods section. For the basic cycle length of 250 ms used in our study, APD is 110 ms in the homogeneous model, while it is 108, 140 and 131 ms in the epicardial, midmyocardial and endocardial cells, respectively. The epicardial cell has the shortest APD and the midmyocardial the longest, which is consistent with previous observations (Viswanathan et al., 1999; McIntosh et al., 2000; Gima and Rudy, 2002; Aslanidi et al., 2005; Sampson and Henriquez, 2005). Note also that the midmyocardial and epicardial action potentials are characterised with a notch that follows the upstroke; it is due to Ito (McIntosh et al., 2000).
Fig. 2.
Time course of an action potential computed using (A) a single cell model with membrane kinetics as used in the homogeneous model and (B) models of epicardial (solid), midmyocardial (dotted) and endocardial (dashed) single cells as implemented in the heterogeneous models. Basic cycle length is 250 ms.
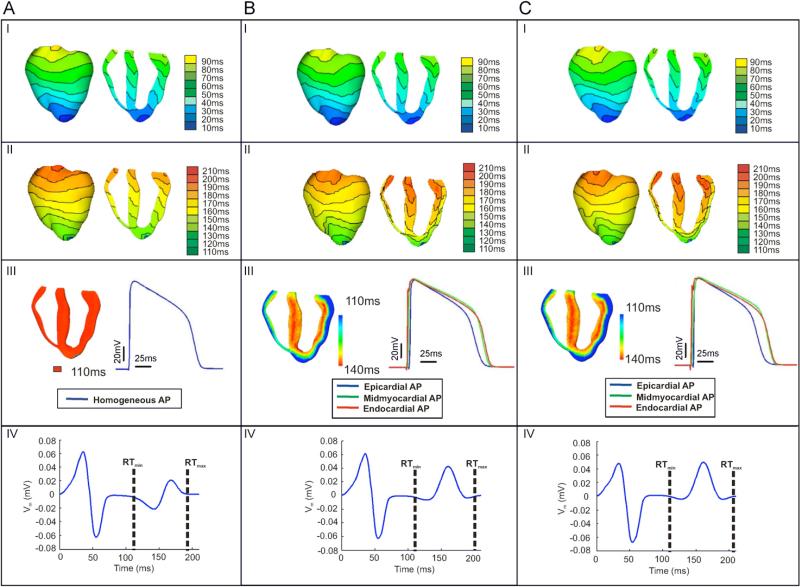
Fig. 3 presents activation and repolarisation maps (rows I and II), APD maps and action potential traces (row III), and pseudo-ECGs (row IV) following the application of an apical pacing stimulus to the homogeneous ventricles (A), the heterogeneous ventricles (B), and the heterogeneous ventricles with sub-epicardial uncoupling (C). In all three models, activation proceeds from apex to base with the longest local activation time being 85 ms in the homogeneous model, 81 ms in the heterogeneous model, and 83 ms in the heterogeneous model with sub-epicardial uncoupling. This represents a 4.7% and 2.4% increase in average conduction velocity, with respect to the homogeneous model, in the heterogeneous model and in the heterogeneous model with sub-epicardial uncoupling, respectively. The increase in average conduction velocity might be due to differences in INa.
Fig. 3.
Electrical activity following the application of the 7th apical pacing stimulus to the homogeneous ventricles (panel A), the heterogeneous ventricles (panel B), and the heterogeneous ventricles with sub-epicardial uncoupling (panel C), I). Activation maps; (II) repolarisation maps; (III) APD maps (left) and time course of the action potentials (right) from an LV node in the homogeneous model (panel A), and from LV nodes located in the mid-section of the epicardial (blue), the midmyocardial (green), and the endocardial (red) layers of the heterogeneous model (panel B) and the heterogeneous model with sub-epicardial uncoupling (panel C) IV) time course of the pseudo-ECGs recorded at the E2 electrode as shown in Fig. 1. RTmin and RTmax indicate the earliest and latest local repolarisation times (RT) within the ventricles.
The activation maps presented in Fig. 3, panel I, reveal that, in the three models, local activation times are affected by fibre orientation, and that transmural dispersion in activation times is present in the ventricles even in the homogeneous model, in which membrane kinetics are the same at every node (Fig. 3A, I). Fig. 3B and C, panel I, show that in the two heterogeneous models activation proceeds slower in the midmyocardial region than in the endocardial or epicardial regions (Fig. 3B and C, panel I, transmural views).
As shown in Fig. 3A, in the homogeneous model, the repolarisation sequence follows the activation (Fig. 3A I and II), with the earliest (RTmin) and latest (RTmax) local repolarisation times being 110 and 195 ms, respectively. In contrast, in both heterogeneous models, the presence of transmural heterogeneity in ionic currents results in a complex repolarisation pattern, particularly within the LV wall (Fig. 3B and C, II panels). In both cases, the epicardial layer repolarises faster than either the midmyocardial or endocardial layers, and as a result, the repolarisation sequence does not follow the activation sequence in the heterogeneous models. Shortest and longest local repolarisation times are 110 and 201 ms in the heterogeneous model and 110 and 206 ms in the heterogeneous model with sub-epicardial uncoupling. Thus, while the shortest local repolarisation time is similar in all three models, the longest local repolarisation time is larger in the heterogeneous models than in the homogeneous model, due to the longer APD in the midmyocardial layer. The maximum transmural dispersion in repolarisation times (calculated as the maximum difference in repolarisation times across the ventricular wall) is 10 ms in the homogeneous model and 30 ms in both heterogeneous models.
Differences between activation and repolarisation patterns in the heterogeneous models stem from transmural differences in APD, as illustrated in Fig. 3, panel III. The left image in each panel III of Fig. 3 shows APD maps, while the right image presents the time course of action potentials recorded in the middle of the LV free wall of the homogeneous ventricles (Fig. 3A, panels III), and in the middle of the epicardial (blue), midmyocardial (green) and endocardial (red) layers of the LV free wall in the heterogeneous model (Fig. 3B, panels III) and in the heterogeneous model with sub-epicardial uncoupling (Fig. 3C, panels III). As shown in previous studies (Yan et al., 1998a; Idriss and Wolf, 2004; Sampson and Henriquez, 2005), the shape and duration of action potentials obtained from cells within the intact ventricles (Fig. 3A–C, panel III) differs from the single cell action potentials (Fig. 2). In both heterogeneous models, the action potential amplitude and shape is similar in the three cell layers, and APD increases monotonically across the ventricular wall, from 110 ms in the epicardium to 140 ms in the endocardium, representing a transmural dispersion in APD of 30 ms. Note that the distribution of APD is similar in both heterogeneous models (Fig. 3B and C, III).
Fig. 3A–C, panel IV, illustrate the pseudo-ECGs recorded in the homogeneous model, the heterogeneous model and the heterogeneous model with sub-epicardial uncoupling, respectively. The QRS complex is similar in the three models, consistent with the similar activation sequences, as shown in Fig. 3A–C, panel I. However, the differences in repolarisation sequence between the three models result in differences in amplitude and shape of the T-wave. In the homogeneous model, the T-wave is biphasic with phases of similar amplitude; the negative phase is of amplitude –0.022 mV and occurs at 142 ms following the pacing stimulus, while the positive phase reaches 0.021 mV and occurs at 168 ms. In contrast, in both heterogeneous models, the T-wave is nearly monophasic with a small negative peak of amplitude –0.007 mV occurring at 128 ms, followed by a positive wave with a maximum at 161 ms and of amplitude 0.043 and 0.050 mV without and with sub-epicardial uncoupling, respectively. Therefore, the T-wave shows a larger deviation from the baseline in the two heterogeneous models than in the homogeneous model. In all three models, the beginning and end of the T-wave roughly occur at RTmin and RTmax respectively, as illustrated in Fig. 3, panel IV.
3.2. Area of vulnerability
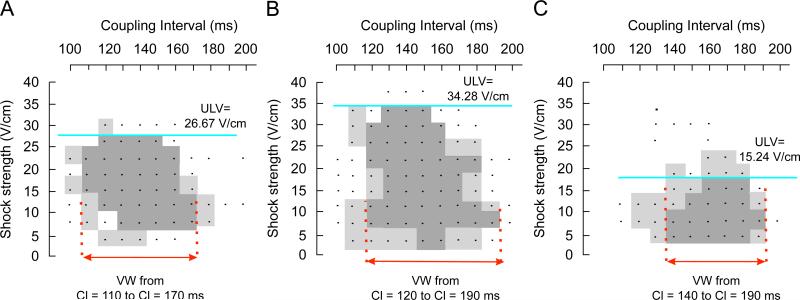
Fig. 4 presents VAs for the three models with each dot representing an episode of shock delivery. Dark grey areas encompass episodes of induction of sustained arrhythmias, while light grey areas refer to episodes of unsustained arrhythmias. Our simulations demonstrate that the presence of transmural heterogeneity in ionic currents results in an increase in vulnerability to electric shocks (Fig. 4B). In the homogeneous model (Fig. 4A), the ULV is 26.67 V/cm and the VW extends from CIs of 110–170 ms, whereas in the heterogeneous model, the ULV increases to 34.28 V/cm and VW shifts to CIs of 120–190 ms. In contrast, sub-epicardial uncoupling in the heterogeneous model results in a significant decrease in the ULV, namely to 15.24 V/cm (Fig. 4C). In this case, the duration of the VW is reduced, spanning CIs from 140 to 190 ms. In order to elucidate the mechanisms underlying the changes in vulnerability caused by transmural heterogeneity in ionic currents and by decreased gap-junctional coupling within the sub-epicardium, we analysed the pre-shock state of the tissue, the shock-induced VEP, and the post-shock electrical activity in the three models for various SSs and CIs.
Fig. 4.
Vulnerability areas for (A) the homogeneous model, (B) the heterogeneous model and (C) the heterogeneous model with sub-epicardial uncoupling. Dots represent episodes of shock delivery. Dark and light grey areas encompass episodes of sustained and unsustained re-entry, respectively.
3.3. VEP and post-shock activity for shocks within the VA
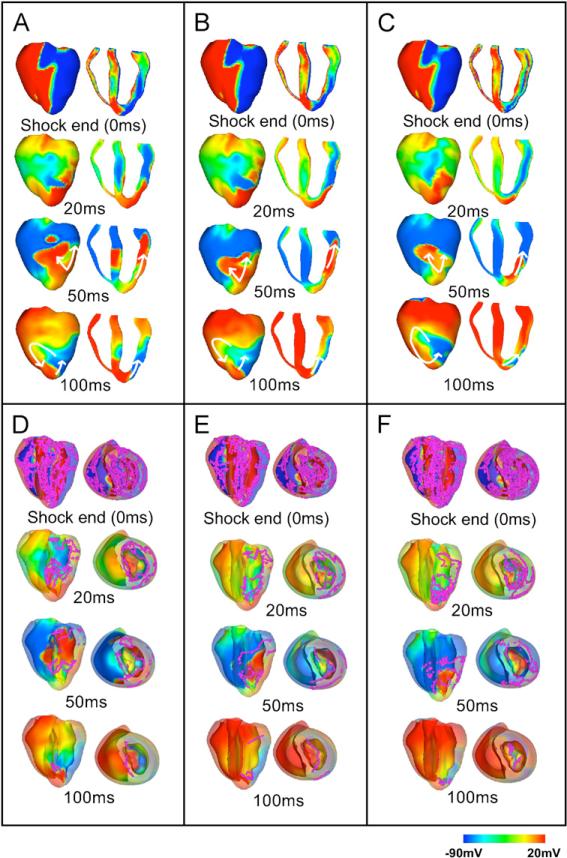
To identify differences in the mechanisms of shock-induced arrhythmogenesis introduced by transmural electrophysiological heterogeneity, we analysed the distribution of transmembrane potential at shock-end and its post-shock evolution in the three models. Fig. 5 illustrates this analysis for an episode where the shock was applied at a CI of 140 ms; the SS was 11.43 V/cm for the homogeneous and the heterogeneous models (panels A and B), and 7.62 V/cm for the heterogeneous model with sub-epicardial uncoupling (panel C). The chosen episodes are within the VA in each respective model. The distributions of scroll-wave filaments in the 3D volume of the ventricles are also shown in Fig. 5D–F, where the myocardium has been rendered semitransparent and both anterior epicardial and apical views are shown.
Fig. 5.
Transmembrane potential distributions and distributions of filaments at shock-end (0 ms panels) and at 20, 50 and 100 ms following a shock applied at CI = 140 ms of strength 11.43 V/cm in the homogeneous (panels A and D) and in the heterogeneous (panels B and E) model, and of strength 7.62 V/cm in the heterogeneous model with sub-epicardial uncoupling (panels C and F). Panels A–C show anterior epicardial and transmural views. In panels D–F, the epicardial surface has been rendered semi-transparent to allow visualisation, in pink, of scroll-wave filaments. Colour scale is saturated, i.e. transmembrane potential above 20 mV and below –90 mV appear red and blue, respectively. Arrows indicate the direction of wave propagation.
In all models, the shock induces two main areas of opposite-in-sign VEP on the epicardial surface (Fig. 5A–C, shock-end panels), with the LV epicardial surface negatively polarised and the RV epicardium positively polarised, consistent with previous theoretical and experimental studies (Efimov et al, 2000; Rodriguez et al., 2005). In contrast, in the depth of the ventricular wall, the shock induces a complex distribution of VEP, which results in a dense congregation of filaments throughout the ventricular volume (Fig. 5D–F). The overall pattern of transmural VEP is similar in the homogeneous and the heterogeneous models; however, important differences in the transmural VEP can be identified when comparing these models to the heterogeneous model with sub-epicardial uncoupling. The discontinuity in intracellular conductivity introduced by the sub-epicardial uncoupling results in strong VEP induced by the shock alongside the boundary between the LV epicardial and midmyocardial layers (Fig. 5C, 0 ms panel, transmural view). This also leads to a larger density of filaments within the LV free wall in the heterogeneous model with sub-epicardial uncoupling compared to the other two models (compare Fig. 5C–F, 0 ms panels).
In all three models, following shocks within the VA, propagation proceeds from apex to base through the LV shock-induced excitable area (Fig. 5A–C, 20 and 50 ms panels), and then continues towards the septum and RV (Fig. 5A–C, 50 ms panels), once tissue there has recovered from shock-induced positive polarisation. Eventually, propagation re-enters through the apex towards the LV, completing the first cycle of re-entry (Fig. 5A–C, 100 ms panels), and proceeds to establish a sustained arrhythmia in all three models. The same type of re-entry is induced in all three models, which, for this particular combination of SS and CI, is a figure-of-eight re-entry where two rotors are induced, one counterclockwise on the anterior side and one clockwise on the posterior side of the ventricles, with a common pathway in the apex. (Fig. 5A–C, 100 ms panels).
As shown in Fig. 5D–F, the number of filaments in the ventricles decreases very rapidly following the end of the shock, which is consistent with previous studies (Trayanova et al., 2004); the post-shock evolution of filament dynamics is similar in the three models. Surviving filaments are predominantly concentrated in the LV wall in all three cases (Fig. 5D–F, 20 and 50 ms panels). At 100 ms post-shock (Fig. 5D–F, 100 ms panels) only two filaments remain, located in the septum in the homogeneous model, and within the LV free wall in both heterogeneous models.
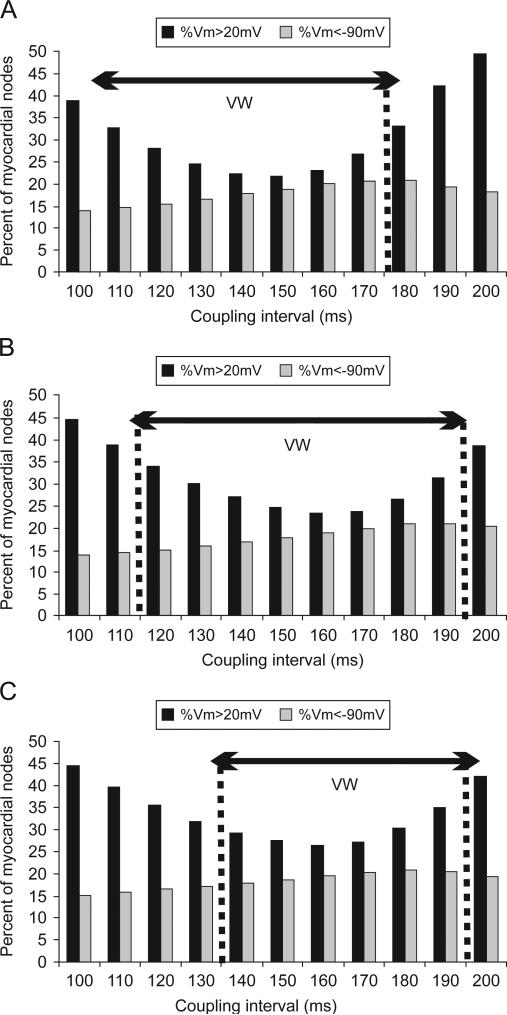
Consistent with our previous study (Arevalo et al., 2007), varying shock timing (i.e. CI), results in a significant change in shock-end VEP and specifically, in the amount of myocardial areas of shock-induced positive and negative polarisation. This is quantified in Fig. 6, which shows the amount of myocardial tissue experiencing shock-end potentials above 20 mV (black bars) and below –90 mV (grey bars) at the end of a 11.43-V/cm strength shock, calculated as a percentage of all nodes in the ventricular volume, and plotted as a function of CI. As shown in Fig. 5 as well as in previous publications (Efimov et al., 2000; Rodriguez et al., 2005), the amount of tissue experiencing shock-induced positive and negative polarisation plays a key role in the outcome of the shock. Indeed, areas of shock-induced negative polarisation represent excitable areas through which post-shock activations could propagate, while areas of positive polarisation provide the stimulus for the onset of post-shock propagation and also represent strongly depolarised tissue that remains refractory for a significant period of time following shock-end, blocking any further propagation. Therefore, changes in the amount of myocardial tissue experiencing positive and negative polarisation with varying CI ultimately determine the outcome of shocks applied at different CIs and thus are responsible for the existence of the VW.
Fig. 6.
Percentage of myocardial nodes that are of transmembrane potential above +20 mV (black bars) and below –90 mV (grey bars) at the end of a 11.43 V/cm shock applied at CIs in the range of 100–200 ms in the homogeneous model (panel A), the heterogeneous model (panel B), and the heterogeneous model with sub-epicardial uncoupling (panel C).
From Fig. 6, it is evident that the effect of varying CI on the amount of myocardial tissue of shock-end positive and negative polarisation is similar in the three models. In all cases, the amount of negatively polarised tissue increases with increasing CI and then decreases slightly for long CIs. In all three models, the amount of tissue negatively polarised is below 20% for all CIs. Importantly, Fig. 6 shows that the extent of the areas of positive polarisation is smaller for shocks applied within the VW than for shocks applied outside the VW in all three models. For CIs outside the VW, the large amount of strongly depolarised tissue leads to propagation block following shock-end, and therefore results in failure to induce arrhythmia (Arevalo et al., 2007). In contrast, for CIs within the VW, in all models, positively polarised tissue represents less than 36% of total myocardial mass. The large amount of tissue that is excitable (even if it is mildly depolarised) at shock-end for CIs within the VW indicates that, in all three models, large excitable areas are present in the ventricles shortly after shock-end, allowing for propagation of post-shock activations and eventually, re-entry induction. The histograms presented in Fig. 6 show that the range of CIs with an amount of positively polarised tissue smaller than 36% shifts from 110–170 ms in the homogeneous model to 120–190 ms in the heterogeneous model. The same shift is observed in the VW.
However, in the heterogeneous model with sub-epicardial uncoupling, short CIs, i.e, less than 140 ms, are outside the VW despite the fact that they result in an amount of tissue positively polarised at shock-end that is smaller than 36% of total ventricular volume. As shown in Fig. 5, 0 ms panels, VEP in the depth of the LV wall exhibits a more complex pattern in the heterogeneous ventricles with sub-epicardial uncoupling than in the homogeneous and the heterogeneous ventricles, due to VEP present alongside the border between epicardial and midmyocardial layers.
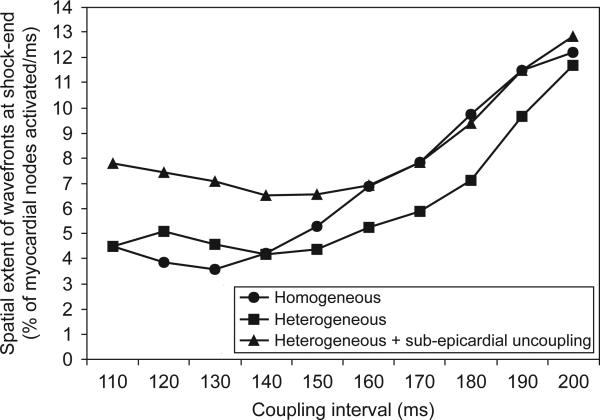
Differences in amount and distribution of areas of shock-induced positive and negative polarisation also result in variations in the characteristics of the post-shock wavefronts. Fig. 7 presents quantification of the spatial extent of post-shock wavefronts (calculated as the number of nodes in the computational mesh activated at shock-end as a percentage of all ventricular nodes) for each model as a function of CI in the 11.43-V/cm shock episode. Note that for CIs<140 ms, the spatial extent of wavefronts is up to 98% larger in the heterogeneous model with sub-epicardial uncoupling, as compared to either the homogeneous or the heterogeneous model. This large extent of shock-end wavefronts in the heterogeneous model with sub-epicardial uncoupling results in a fast consumption of the excitable areas following the end of the shock. Thus, for CIs<140 ms, shortly after shock-end, propagation is blocked surrounded by refractory tissue and no re-entry is induced. This explains the rightward shift of the minimum CI limit of the VW when sub-epicardial uncoupling is incorporated.
Fig. 7.
Spatial extent of post-shock wavefronts (calculated as a percentage of all myocardial nodes activated during the first two milliseconds following shock-end) as a function of coupling interval at the end of a 11.43-V/cm shock in all three models.
3.4. VEP and post-shock activity for high strength shocks close to the ULV
The presence of transmural heterogeneity in ionic currents in the ventricles is associated with an increase in the ULV from 26.67 V/cm in the homogeneous model to 34.28 V/cm in the heterogeneous model (Fig. 4). In order to elucidate the mechanisms underlying this increase, Fig. 8A and B examine the evolution of electrical activity for a shock of strength 30.46 V/cm applied at a CI of 140 ms in the homogeneous and the heterogeneous ventricles. The chosen CI is the one at which the ULV is attained in both the homogeneous and the heterogeneous models, while SS of 30.46 V/cm is below the ULV for the heterogeneous model and above the ULV for homogeneous model. Therefore, by examining the differences in shock-end VEP and post-shock electrical activity in each case, it is possible to pinpoint the mechanisms underlying the increase in ULV caused by heterogeneity in ionic currents.
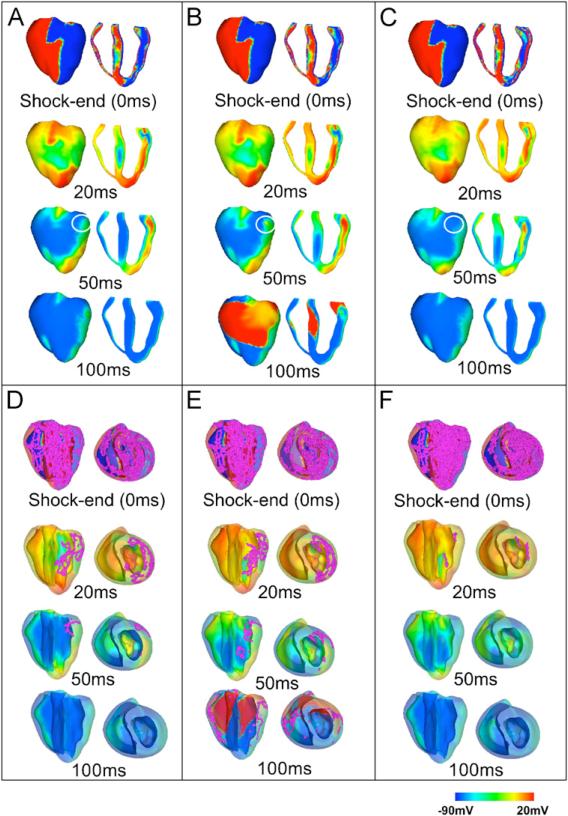
Fig. 8.
Transmembrane potential and filament distributions at shock-end (0 ms panels) and at 20, 50 and 100 ms following a 30.5-V/cm shock applied at a CI of 140 ms to the homogeneous ventricles (panels A and D), to the heterogeneous ventricles (panels B and E), and to the heterogeneous ventricles with sub-epicardial uncoupling (panels C and F). Panels A–C show anterior epicardial and transmural views. In panels D–F, the epicardial surface has been rendered semi-transparent to allow visualisation, in pink, of scroll-wave filaments. Colour scale is saturated, i.e. transmembrane potential above 20 mV and below –90 mV appear red and blue, respectively. Arrows indicate the direction of propagation, and circles denote the presence or lack thereof of a local wavefront on the epicardial surface at 50 ms post-shock.
VEP and the distribution of shock-end filaments are similar in both the homogeneous and the heterogeneous models (Fig. 8A–E, 0 ms panels). As in previous studies (Efimov et al., 2000; Rodriguez et al., 2005), Fig. 8, 0 ms panels, shows that shocks of high strength, close to the ULV, result in strong VEP, with the majority of the ventricular tissue experiencing potentials above +20 mV or below –90 mV. The amount of tissue polarised to intermediate potentials between these two values is 37.07% and 36.54% of total myocardial mass in the homogeneous and in the heterogeneous ventricles, respectively. The main post-shock excitable area is located within the LV free wall, while the majority of RV and septal tissue is positively polarised by the shock (Fig. 8A and B, 0 ms panels). At 20 ms post-shock (Fig. 8A and B, 20 ms panels), wavefronts propagate through the LV post-shock excitable area in both models, and filaments are concentrated within the LV wall (Fig. 8D and E, 20 ms panels). Note that propagation through the midmyocardium is slightly slower in the heterogeneous model than in the homogeneous model, due to a lower maximum conductance for INa in the heterogeneous model (compare Fig. 8A and B, 20 ms post-shock).
The main difference in post-shock activity between the homogeneous and the heterogeneous models occurs at 50 ms post-shock in Fig. 8A and B, and ultimately determines the outcome of the shock. In the homogeneous ventricles the excitable area within the LV free wall (Fig. 8A, 50 ms post-shock, encircled area) is consumed and thereafter the wave is blocked, surrounded by refractory tissue. Filaments are annihilated at 100 ms post-shock, signifying that no arrhythmia is induced (Fig. 8A and D, 50 ms and 100 ms panels). However, in the model with heterogeneity in ionic currents, tissue in the epicardium exhibits a shorter APD (Fig. 3B, panel III), and consequently recovers excitability faster than midmyocardial or endocardial tissue. This allows for the wavefront at 50 ms post-shock to break through onto the epicardial surface (Fig. 8B, 50 ms panels, encircled area). The wave then continues through the septum and the RV, which have already recovered from shock-induced positive polarisation. The existence of a pathway for propagation leads to the establishment of an intramural re-entrant circuit (Fig. 8B and E, 100 ms panels), with filaments still present at 100 ms post-shock (Fig. 8E, 100 ms panel). Thus, the inclusion of transmural heterogeneity in ionic currents results in increased post-shock dispersion in repolarisation, which leads to increased likelihood of establishment of an intramural re-entrant circuit within the LV wall for high SSs. This explains the increase in the ULV caused by transmural heterogeneity in ionic currents (Fig. 4).
As shown in Fig. 4, the ULV is lowered from 34.28 V/cm in the heterogeneous model to 15.24 V/cm in the heterogeneous model with sub-epicardial uncoupling. To elucidate the mechanisms underlying this decrease, we examined, in Fig. 8B and C, the shock-end VEP and post-shock electrical activity for SS of 30.46 V/cm and CI of 140 ms, for which shock parameters an arrhythmia is induced in one case (heterogeneous model) and not in the other (heterogeneous model with sub-epicardial uncoupling).
As can be seen in Fig. 8B and C, shock-end panels, sub-epicardial uncoupling in the heterogeneous model results in altered VEP with an increase in the spatial extent of areas of shock-induced positive polarisation, particularly within the LV free wall (Fig. 8B and C, 0 ms panels). The amount of positively polarised tissue is 38.2% of the total myocardial volume in the heterogeneous model with sub-epicardial uncoupling, as compared to 35% in the heterogeneous model. Fig. 8F, 0 ms panels, shows that altered VEP introduced by sub-epicardial uncoupling is accompanied by a larger density of scroll-wave filaments. Furthermore, our simulation results show that changes in VEP due to sub-epicardial uncoupling result in altered characteristics of the post-shock wavefronts and in particular, in an increase in the spatial extent of post-shock wavefronts (as defined previously) from 10.44% in the heterogeneous model to 12.95% in the heterogeneous model with sub-epicardial uncoupling.
Both the increase in the amount of shock-end positively polarised myocardium and in the spatial extent of post-shock wavefronts contribute to the decrease in the ULV, since lower SSs are required to cause post-shock activations to traverse the post-shock excitable areas before the surrounding tissue, positively polarised at shock-end, recovers excitability. Fig. 8C, 20 ms panel, presents the distribution of transmembrane potential after the post-shock excitable area is consumed and shows that propagation is terminated in the heterogeneous model with sub-epicardial uncoupling. Accordingly, the density of filaments decreases rapidly after shock-end (Fig. 8F, 20 ms panel) and filaments are completely annihilated at 50 ms post-shock, signifying that no re-entry is induced in this model (Fig. 8C and F, 50 ms and 100 ms panels). In contrast, in the heterogeneous model, as mentioned previously, propagation proceeds through the LV wall and breaks through onto the epicardial surface at 50 ms post-shock, establishing a re-entrant circuit.
Thus, Fig. 8B and C demonstrate that the decrease in the ULV associated with sub-epicardial uncoupling in the heterogeneous ventricles results from differences in VEP and in the characteristics of the post-shock wavefronts. Specifically, the larger amount of the positively polarised myocardium and the increase in the spatial extent of post-shock wavefronts prevent the establishment of re-entrant circuits following shocks of high strength, and ultimately lead to a decrease in the ULV.
4. Discussion
This study used an anatomically realistic model of the rabbit ventricles to investigate the role of transmural heterogeneities in ionic currents and of gap-junctional coupling in modulating cardiac vulnerability to electric shocks. Our bidomain simulations demonstrate that transmural heterogeneities in ionic currents in the ventricles result in an increase in vulnerability to electric shocks, manifested as increased ULV and extended VW. These changes in vulnerability stem from increased post-shock dispersion in repolarisation caused by the transmural heterogeneity in ionic currents, which leads to an increased likelihood of establishment of re-entrant circuits. In contrast, sub-epicardial gap-junctional uncoupling in the heterogeneous ventricular model results in a significant decrease in vulnerability to electric shocks, with significantly lower ULV and narrower VW compared to both the heterogeneous and the homogeneous models. Our simulations show that reduced vulnerability to shocks in the presence of sub-epicardial uncoupling is due to alterations in VEP and in the characteristics of post-shock wavefronts. The study dissects the mechanisms underlying the changes in cardiac vulnerability to electric shocks due to both heterogeneities in ionic currents and gap-junctional coupling.
4.1. Transmural electrophysiological heterogeneities in the ventricles
A large body of research has shown that the ventricular myocardium exhibits heterogeneous electrophysiological properties caused by regional differences in ionic currents. Experimental studies using isolated endocardial, midmyocardial and epicardial myocytes report transmural differences in Ito in canine, rabbit, guinea pig and human (Li et al., 1998; McIntosh et al., 1998; Antzelevitch et al., 1999a, b), in INa in canine (Antzelevitch et al., 1999a, b), in IKs in canine and rabbit (Liu and Antzelevitch, 1995; Xu et al., 2001; Yan et al., 2001), and to a smaller extent, in IKr in rabbit (Xu et al., 2001). In our study, transmural heterogeneities in ionic currents have been incorporated based on rabbit experimental data (McIntosh et al., 1998, 2000; Xu et al., 2001), as done in a previous simulation study (Saucerman et al., 2004). Consistent with previous research (McIntosh et al., 1998, 2000; Viswanathan et al., 1999; Xu et al., 2001; Gima and Rudy, 2002; Idriss and Wolf, 2004; Saucerman et al., 2004; Sampson and Henriquez, 2005), our study shows that the transmural differences in ionic currents result in differences in the shape and duration of the action potential in epicardial, midmyocardial and endocardial cells. In isolated single cells, the presence of a prominent Ito current in epicardial and midmycardial myocytes gives rise to a notch following the upstroke of the action potential, which is absent in endocardial action potentials (Fig. 2). In addition, smaller IKr and IKs in midmyocardial and endocardial myocytes as shown in Table 1 result in APDs that are 32 and 23 ms longer in midmyocardial and endocardial myocytes, respectively, than in epicardial cells (Fig. 2), for the basic cycle length of 250 ms used in our study.
As in previous studies (Yan et al., 1998a; Sampson and Henriquez, 2005), when transmural differences in ionic currents are incorporated in our rabbit ventricular model, electrotonic interactions alter the shape and duration of the action potentials in the three cell layers compared to those of the single cell (action potentials in Figs. 2 and 3, panel III). Firstly, the notch present in the action potentials of isolated epicardial and midmyocardial cells is not observed in action potentials recorded in the heterogeneous ventricular model, and, secondly, the LV transmural APD profile in the rabbit model is characterised by a gradual APD increase to 30 ms from epi- to endocardium, with cells in the midmyocardial layer exhibiting intermediate APD (Fig. 3). These results are consistent with experimental recordings in adult rabbit LV wedge preparations (Yan et al., 2001; Idriss and Wolf, 2004). Increasing basic cycle length results in increased transmural dispersion in APD in the rabbit ventricles. However, rapid pacing rates prior to shock application have been shown to result in a better agreement between ULV and defibrillation threshold (Malkin et al., 1995) since the activation sequence is very rapid during fibrillation. Therefore, in this study, the ventricles were paced at a basic cycle length of 250 ms before shock application.
Transmural differences in APD caused by transmural heterogeneity in ionic currents also mean increased transmural dispersion in repolarisation (Fig. 3, panel II). This results in a significant change in the shape of the T-wave, as shown in Fig. 3, panel IV, as well as in previous studies (Yan et al., 1998b; Gima and Rudy, 2002; Idriss and Wolf, 2004; Ritsema van Eck et al., 2005). It should be noted however, that, while there is a large body of evidence supporting the existence of transmural heterogeneities in ionic currents and electrophysiological properties of ventricular tissue, some experimental studies have documented little or no transmural differences in APD in vivo (Anyukhovsky et al., 1996, 1999; Taggart et al., 2001; Conrath et al.; 2004).
In addition to transmural differences in ionic currents, recent experimental studies have reported an increase in tissue resistivity in the subepicardium in dog (Yan et al., 1998a), rodent (Yamada et al., 2004) and human (Drouin et al., 1995), which might be attributable to a reduced expression of connexin43 (Yamada et al., 2004). Our results demonstrate that sub-epicardial uncoupling does not lead to significant changes in the electrical activity following apical stimulation (Fig. 3). However, it leads to differences in shock-end VEP and post-shock behaviour that alter the shock outcome and lead to changes in vulnerability to shocks, as addressed in the following sections.
4.2. Mechanisms underlying the changes in vulnerability to shocks caused by transmural electrophysiological heterogeneities
Our simulation results show that incorporating transmural heterogeneity in ionic currents does not alter the overall pattern of shock-end VEP in the ventricles. However, in the heterogeneous model, local repolarisation times in the midmyocardial and the endocardial layers are longer than in the homogeneous model (Fig. 3). Therefore, a similar level of post-shock recovery is established later in the heterogeneous model than in the homogeneous model. This explains the overall rightward shift of the VW in the heterogeneous model as compared to the homogeneous model.
Since it arises from the VEP pattern, early post-shock activity is also similar in the homogeneous and the heterogeneous ventricles (Figs. 5 and 8, 20 ms panels). Propagation proceeds through the post-shock excitable area located within the LV free wall, while tissue rendered refractory at shock-end recovers. However, in the heterogeneous ventricles post-shock dispersion in repolarisation within the LV free wall is enhanced by the transmural APD dispersion; this increases the likelihood of establishment of shock-induced re-entrant circuits within the LV free wall, and explains the increase in ULV.
While decreased gap-junctional coupling between the midmyocardial and epicardial layers does not alter ventricular electrical activity following pacing (Fig. 2), it leads to a significant change in VEP and thus plays a key role in vulnerability to shocks. Sub-epicardial gap-junctional uncoupling within the LV free wall represents a discontinuity in the bidomain intracellular conductivities, which leads to the formation of shock-induced VEP (Entcheva et al., 1999). Areas of positive and negative polarisation are induced alongside the boundary between epicardial and midmyocardial layers, as shown in Figs. 5 and 8, 0 ms panels. This results in an increase in the amount of positively polarised tissue at shock-end, and in the spatial extent of the post-shock wavefronts. Both factors contribute to (i) a decrease in the ULV in the presence of sub-epicardial uncoupling, since lower SSs are required to cause post-shock activations to traverse the post-shock excitable areas before refractory tissue recovers; and (ii) a rightward shift of the minimum CI limit in the VW, with no arrhythmia induced for CIs<140 ms.
Therefore, this study proves that transmural heterogeneities in ionic currents and gap-junctional uncoupling modulate cardiac vulnerability to electric shocks by altering shock-induced VEP, the characteristics of post-shock propagation, and the post-shock dispersion of refractoriness. Experimental studies have shown that transmural dispersion in refractoriness resulting from transmural electrophysiological heterogeneity is dependent on factors such as age (Idriss and Wolf, 2004) and, importantly, is determined by the pacing rate, due to the different restitution properties of epicardial, midmyocardial and endocardial cells (Drouin et al., 1995; Yan et al., 1998a, 2001; Li et al., 1998; Antzelevitch et al., 1999a, b; Idriss and Wolf, 2004). Our results suggest that dispersion in post-shock refractoriness affects vulnerability to electric shocks. Thus, factors that enhance transmural dispersion in repolarisation, such as age and pacing protocol, are also expected to affect changes in vulnerability to electric shocks through mechanisms that are similar to those described in the sections above.
In the present study, a uniform field and a monophasic shock waveform were applied to the homogeneous, the heterogeneous, and the heterogeneous ventricles with sub-epicardial uncoupling to reveal the contribution of transmural heterogeneities in ionic currents and sub-epicardial gap-junctional uncoupling to the mechanisms of cardiac vulnerability to electric shocks. By using this protocol, this contribution was not masked by applied field nonuniformity and additional nonlinear effects associated with biphasic waveform shocks. The findings of this study have a direct application to external defibrillation with monophasic shocks. The relevancy of these results can be further extended to biphasic defibrillation waveforms, as transmural heterogeneities in ionic currents and intercellular coupling will still be present in the ventricles, and thus shock-induced effects and 3D post-shock activity will still be partially determined by transmural electrophysiological heterogeneities.
4.3. Limitations
The limitations of the ventricular rabbit model used in this study have been described elsewhere (Trayanova et al., 2002). Here we overcome some of the limitations of previous models by incorporating a realistic representation of transmural heterogeneity in ionic currents and sub-epicardial uncoupling based on experimental data. However, model limitations include the lack of additional heterogeneities in ionic currents such as apico-basal and interventricular gradients (Brahmajothi et al., 1997; Volders et al., 1999; Cheng and Kodama, 2004), and accurate representation of heterogeneities in late INa (Antzelevitch et al., 1999a, b).
Despite these limitations, this study provides a detailed understanding of the role of transmural electrophysiological heterogeneity in ionic currents and gap-junctional uncoupling in cardiac vulnerability to electric shocks. It should be noted that differences in size, electrophysiological properties and geometry between human and rabbit hearts, and the heterogeneities in the electrophysiological properties in diseased hearts might limit the applicability of our results to the human heart.
Acknowledgements
This work was supported by Rhodes Scholarship (T.M.), EPSRC-funded Integrative Biology e-Science pilot project (D.G.), the UK National Grid Service, and NIH Grant HL063195 (N.T). A portion of this work was published in abstract form (Maharaj et al., 2006).
References
- Aguel F, Eason J, Trayanova N. Advances in modeling cardiac defibrillation. Int. J. Bifurcations Chaos. 2003;13:3791–3805. [Google Scholar]
- Antzelevitch C, Fish J. Electrical heterogeneity within the ventricular wall. Basic Res. Cardiol. 2001;96:517–527. doi: 10.1007/s003950170002. [DOI] [PubMed] [Google Scholar]
- Antzelevitch C, Shimizu W, Yan GX, Sicouri S, Weissenburger J, Nesterenko VV, Burashnikov A, di Diego J, Saffitz J, Thomas GP. The M cell: its contribution to the ECG and to normal and abnormal electrical function of the heart. J. Cardiovasc. Electrophysiol. 1999a;10(8):1124–1152. doi: 10.1111/j.1540-8167.1999.tb00287.x. [DOI] [PubMed] [Google Scholar]
- Antzelevitch C, Yan GX, Shimizu W, Burashnikov A. Electrical heterogeneity, the ECG, and cardiac arrhythmias. In: Zipes DP, Jalife J, editors. Cardiac Electrophysiology: From Cell to Bedside. W.B. Saunders Co.; Philadelphia: 1999b. pp. 222–228. [Google Scholar]
- Anyukhovsky EP, Sosunov EA, Rosen MR. Regional differences in electrophysiological properties of epicardium, midmyocardium, and endocardium, in vitro and in vivo correlations. Circulation. 1996;94:1981–1988. doi: 10.1161/01.cir.94.8.1981. [DOI] [PubMed] [Google Scholar]
- Anyukhovsky EP, Sosunov EA, Gainullin RZ, Rosen MR. The controversial M cell. J. Cardiovasc. Electrophysiol. 1999;10:244–260. doi: 10.1111/j.1540-8167.1999.tb00667.x. [DOI] [PubMed] [Google Scholar]
- Arevalo H, Rodriguez B, Trayanova N. Arrhythmogenesis in the heart: insights from multiscale modelling studies. Chaos. 2007;17(1–13):015103. doi: 10.1063/1.2430637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashihara T, Trayanova N. Asymmetry in membrane responses to electric shocks: Insights from bidomain simulations. Biophys. J. 2004;87:2271–2282. doi: 10.1529/biophysj.104.043091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aslanidi OV, Clayton RH, Lambert JL, Holden AV. Dynamical and cellular electrophysiological mechanisms of ECG changes during ischaemia. J. Theor. Biol. 2005;237(4):369–381. doi: 10.1016/j.jtbi.2005.04.022. [DOI] [PubMed] [Google Scholar]
- Brahmajothi MV, Morales MJ, Reimer KA, Strauss HC. Regional localization of ERG, the channel protein responsible for the rapid component of the delayed rectifier, K+ current in the ferret heart. Circ. Res. 1997;81:128–135. doi: 10.1161/01.res.81.1.128. [DOI] [PubMed] [Google Scholar]
- Chen PS, Shibata N, Dixon EG, Wolf PD, Danieley ND, Sweeney MB, Smith WM, Ideker RE. Activation during ventricular defibrillation in open-chest dogs. J. Clin. Invest. 1986;77(3):810–823. doi: 10.1172/JCI112378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen PS, Feld GK, Mower MM, Peters BB. Effects of pacing rate and timing of defibrillation shock on the relation between the defibrillation threshold and the upper limit of vulnerability in open chest dogs. J. Am. Coll. Cardiol. 1991;18:1555–1563. doi: 10.1016/0735-1097(91)90690-b. [DOI] [PubMed] [Google Scholar]
- Cheng JH, Kodama I. Two components of delayed rectifier K+ current in heart: molecular basis, functional diversity, and contribution to repolarization. Acta Pharmacol. Sin. 2004;25:137–145. [PubMed] [Google Scholar]
- Clerc L. Directional differences of impulse spread in trabecular muscle from mammalian heart. J. Physiol. (London) 1976;225:335–346. doi: 10.1113/jphysiol.1976.sp011283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conrath CE, Wilders R, Coronel R, de Bakkerd JMT, Taggart P, de Grootd JR, Opthof T. Intercellular coupling through gap junctions masks M cells in the human heart. Cardiovasc. Res. 2004;62(2):407–414. doi: 10.1016/j.cardiores.2004.02.016. [DOI] [PubMed] [Google Scholar]
- Drouin E, Charpentier F, Gauthier C, Laurent K, Le Marec H. Electrophysiologic characteristics of cells spanning the left ventricular wall of human heart: evidence for presence of M cells. J. Am. Coll. Cardiol. 1995;26:185–192. doi: 10.1016/0735-1097(95)00167-x. [DOI] [PubMed] [Google Scholar]
- Dumaine R, Towbin JA, Brugada P, Vatta M, Nesterenko DV, Nesterenko VV, Brugada J, Brugada R, Antzelevitch C. Ionic mechanisms responsible for the electrocardiographic phenotype of the Brugada syndrome are temperature dependent. Circ. Res. 1999;85:803–809. doi: 10.1161/01.res.85.9.803. [DOI] [PubMed] [Google Scholar]
- Eason J, Malkin RA. A simulation study evaluating the performance of high density electrode arrays on myocardial tissue. IEEE Trans. Biomed. Eng. 2000;47:893–901. doi: 10.1109/10.846683. [DOI] [PubMed] [Google Scholar]
- Efimov IR, Aguel F, Cheng Y, Wollenzier B, Trayanova N. Virtual electrode polarization in the far field: implications for external defibrillation. Am. J. Physiol. Heart Circ Physiol. 2000;279:1055–1070. doi: 10.1152/ajpheart.2000.279.3.H1055. [DOI] [PubMed] [Google Scholar]
- Entcheva E, Trayanova N, Claydon FJ. Patterns of and mechanisms for shock-induced polarization in the heart: a bidomain analysis. IEEE Trans. Biomed. Eng. 1999;46:260–270. doi: 10.1109/10.748979. [DOI] [PubMed] [Google Scholar]
- Gima K, Rudy Y. Ionic current basis of electrocardiographic waveforms: a model study. Circ. Res. 2002;90:889–896. doi: 10.1161/01.res.0000016960.61087.86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huelsing DJ, Spitzer KW, Pollard AE. Electrotonic suppression of early afterdepolarizations in isolated rabbit Purkinje myocytes. Am. J. Physiol. Heart Circ. Physiol. 2000;279:H250–H259. doi: 10.1152/ajpheart.2000.279.1.H250. [DOI] [PubMed] [Google Scholar]
- Idriss SF, Wolf PD. Transmural action potential repolarisation heterogeneity develops postnatally in the rabbit. J. Cardiovas. Electrophysiol. 2004;15:795–801. doi: 10.1046/j.1540-8167.2004.03622.x. [DOI] [PubMed] [Google Scholar]
- Kuo CS, Munakata K, Reddy CP, Surawicz B. Characteristics and possible mechanism of ventricular arrhythmia dependent on the dispersion of action potential durations. Circulation. 1983;67:1356–1367. doi: 10.1161/01.cir.67.6.1356. [DOI] [PubMed] [Google Scholar]
- Larson C, Dragnev L, Trayanova N. Analysis of electrically-induced reentrant circuits in a sheet of myocardium. Ann. Biomed. Eng. 2003;31:768–780. doi: 10.1114/1.1581289. [DOI] [PubMed] [Google Scholar]
- Laurita KR, Girouard SD, Akar FD, Rosenbaum DS. Modulated dispersion explains changes in arrhythmia vulnerability during premature stimulation of the heart. Circulation. 1998;98:2774–2780. doi: 10.1161/01.cir.98.24.2774. [DOI] [PubMed] [Google Scholar]
- Li G, Feng J, Lixia Y, Carrier M. Transmural heterogeneity of action potentials and Ito 1 in myocytes isolated from the human right ventricle. Am. J. Physiol. Heart Circ. Physiol. 1998;44:H369–H377. doi: 10.1152/ajpheart.1998.275.2.H369. [DOI] [PubMed] [Google Scholar]
- Liu DW, Antzelevitch C. Characteristics of the Delayed Rectifier Current (IKr and IKs) in canine ventricular epicardial, midmyocardial, and endocardial myocytes: a weaker IKs contributes to the longer action potential of the M cell. Circ. Res. 1995;76:351–365. doi: 10.1161/01.res.76.3.351. [DOI] [PubMed] [Google Scholar]
- Luo CH, Rudy Y. A dynamic model of the cardiac ventricular action potential: I. Simulations of ionic currents and concentration changes. Circ. Res. 1994;74:1071–1097. doi: 10.1161/01.res.74.6.1071. [DOI] [PubMed] [Google Scholar]
- Maharaj T, Rodriguez B, Blake R, III, Trayanova N, Gavaghan D. Role of transmural heterogeneities in vulnerability to electric shocks. Heart Rhythm. 2006;3(5):S225–S225. doi: 10.1016/j.pbiomolbio.2007.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malkin RA, Idriss SF, Walker RG, Ideker RE. Effect of rapid pacing and T-wave scanning on the relation between the defibrillation and upper-limit-of-vulnerability dose–response curves. Circulation. 1995;92:1291–1299. doi: 10.1161/01.cir.92.5.1291. [DOI] [PubMed] [Google Scholar]
- McIntosh MA, Cobbe SM, Kane KA, Rankin AC. Action potential prolongation and potassium currents in left-ventricular myocytes isolated from hypertrophied rabbit hearts. J. Mol. Cell. Cardiol. 1998;30:43–53. doi: 10.1006/jmcc.1997.0570. [DOI] [PubMed] [Google Scholar]
- McIntosh MA, Cobbe SM, Smith GL. Heterogeneous changes in action potential and intracellular Ca2+ in left ventricular myocyte sub-types from rabbits with heart failure. Cardiovasc. Res. 2000;45(2):397–409. doi: 10.1016/s0008-6363(99)00360-0. [DOI] [PubMed] [Google Scholar]
- Peters NS, Coromilas J, Severs NJ, Wit AL. Disturbed connexin43 gap junction distribution correlates with the location of reentrant circuits in the epicardial border zone of healing canine infarcts that cause ventricular tachycardia. Circulation. 1997;95:988–996. doi: 10.1161/01.cir.95.4.988. [DOI] [PubMed] [Google Scholar]
- Plonsey R, Barr RC. second ed. Kluwer Academic, Plenum Press; New York, NY: 2000. Bioelectricity: A Quantitative Approach; p. 1490163. [Google Scholar]
- Poelzing S, Akar FD, Baron E, Rosenbaum DS. Heterogeneous connexin43 expression produces electrophysiological heterogeneities across ventricular wall. Am. J. Physiol. Heart Circ. Physiol. 2004;286:H2001–H2009. doi: 10.1152/ajpheart.00987.2003. [DOI] [PubMed] [Google Scholar]
- Ritsema van Eck HJ, Kors JA, van Herpen G. The U wave in the electrocardiogram: a solution for a 100-year old riddle. Cardiovasc. Res. 2005;67:256–262. doi: 10.1016/j.cardiores.2005.04.010. [DOI] [PubMed] [Google Scholar]
- Rodríguez B, Tice B, Eason J, Aguel F, Trayanova N. Cardiac vulnerability to electric shocks during phase 1A of acute global ischemia. Heart Rhythm. 2004;1(6):695–703. doi: 10.1016/j.hrthm.2004.08.018. [DOI] [PubMed] [Google Scholar]
- Rodríguez B, Li L, Eason JC, Efimov IR, Trayanova N. Differences between left and right ventricular chamber geometry affect cardiac vulnerability to electric shocks. Circ. Res. 2005;97:168–175. doi: 10.1161/01.RES.0000174429.00987.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sampson KJ, Henriquez CS. Electrotonic influences on action potential duration dispersion in small hearts: a simulation study. Am. J. Physiol. Heart Circ. Physiol. 2005;289:H350–H360. doi: 10.1152/ajpheart.00507.2004. [DOI] [PubMed] [Google Scholar]
- Saucerman JJ, Healy SN, Belik ME, Puglisi JL, McCulloch AD. Proarrhythmic consequences of a KCNQ1 AKAP-binding domain mutation computational models of whole cells and heterogeneous tissue. Circ. Res. 2004;95:1216–1224. doi: 10.1161/01.RES.0000150055.06226.4e. [DOI] [PubMed] [Google Scholar]
- Taggart P, Sutton PM, Opthof T, Coronel R, Trimlett R, Pugsley W, Kallis P. Transmural repolarisation in the left ventricle in humans during normoxia and ischaemia. Cardiovasc. Res. 2001;50(3):454–462. doi: 10.1016/s0008-6363(01)00223-1. [DOI] [PubMed] [Google Scholar]
- Trayanova N, Eason J, Aguel F. Computer simulations of cardiac defibrillation: a look inside the heart. Comput. Visual Sci. 2002;4:259–270. [Google Scholar]
- Trayanova N, Aguel F, Larson HC. Modelling cardiac defibrillation: an inquiry into post-shock dynamics. In: Zipes DP, Jalife J, editors. Cardiac Electrophysiology: From Cell to Bedside. fourth ed. 2004. pp. 282–290. [Google Scholar]
- Ueda N, Zipes DP, Wu J. Functional and transmural modulation of M cell behavior in canine ventricular wall. Am. J. Physiol. 2004;287:H2569–H2575. doi: 10.1152/ajpheart.00526.2004. [DOI] [PubMed] [Google Scholar]
- Vetter FJ, McCulloch AD. Three-dimensional analysis of regional cardiac function: a model of rabbit ventricular anatomy. Prog. Biophys. Mol. Biol. 1998;69:157–183. doi: 10.1016/s0079-6107(98)00006-6. [DOI] [PubMed] [Google Scholar]
- Viswanathan PC, Shaw RM, Rudy Y. Effects of IKr and IKs heterogeneity on action potential duration and its rate dependence a simulation study. Circulation. 1999;99:2466–2474. doi: 10.1161/01.cir.99.18.2466. [DOI] [PubMed] [Google Scholar]
- Volders PGA, Sipido KR, Carmeliet E, Spätjens RLHMG, Wellens HJJ, Vos MA. Repolarizing K+ currents Ito1 and IKs are larger in right than left canine ventricular midmyocardium. Circulation. 1999;99:206–210. doi: 10.1161/01.cir.99.2.206. [DOI] [PubMed] [Google Scholar]
- Xu X, Rials SJ, Wu Y, Salata JS, Liu T, Bharucha DB, Marinchak RA, Kowey PR. Left ventricular hypertrophy decreases slowly but not rapidly activating delayed rectifier potassium currents of epicardial and endocardial myocytes in rabbits. Circulation. 2001;103:1585–1590. doi: 10.1161/01.cir.103.11.1585. [DOI] [PubMed] [Google Scholar]
- Yamada K, Kanter EM, Green KG, Saffitz JE. Transmural distribution of connexins in rodent hearts. J. Cardiovasc. Electrophysiol. 2004;15:1–6. doi: 10.1046/j.1540-8167.2004.03514.x. [DOI] [PubMed] [Google Scholar]
- Yan GX, Shimizu W, Antzelevitch C. Characteristics and distribution of M cells in arterially perfused canine left ventricular wedge preparations. Circulation. 1998a;98:1921–1927. doi: 10.1161/01.cir.98.18.1921. [DOI] [PubMed] [Google Scholar]
- Yan GX, Shimizu W, Antzelevitch C. Cellular basis for the normal T-wave and the electrocardiographic manifestations of the long-QT syndrome. Circulation. 1998b;98:1928–1936. doi: 10.1161/01.cir.98.18.1928. [DOI] [PubMed] [Google Scholar]
- Yan GX, Rials SJ, Wu Y, Liu T, Xu X, Marinchak RA, Kowey PR. Ventricular hypertrophy amplifies transmural repolarization dispersion and induces early afterdepolarization. Am. J. Physiol. Heart Circ. Physiol. 2001;281:H1968–H1975. doi: 10.1152/ajpheart.2001.281.5.H1968. [DOI] [PubMed] [Google Scholar]