Abstract
Climatically driven Moran effects have often been invoked as the most likely cause of regionally synchronized outbreaks of insect herbivores without identifying the exact mechanism. However, the degree of match between host plant and larval phenology is crucial for the growth and survival of many spring-feeding pest insects, suggesting that a phenological match/mismatch-driven Moran effect may act as a synchronizing agent.
We analyse the phase-dependent spatial dynamics of defoliation caused by cyclically outbreaking geometrid moths in northern boreal birch forest in Fennoscandia through the most recent massive outbreak (2000–2008). We use satellite-derived time series of the prevalence of moth defoliation and the onset of the growing season for the entire region to investigate the link between the patterns of defoliation and outbreak spread. In addition, we examine whether a phase-dependent coherence in the pattern of spatial synchrony exists between defoliation and onset of the growing season, in order to evaluate if the degree of matching phenology between the moth and their host plant could be the mechanism behind a Moran effect.
The strength of regional spatial synchrony in defoliation and the pattern of defoliation spread were both highly phase-dependent. The incipient phase of the outbreak was characterized by high regional synchrony in defoliation and long spread distances, compared with the epidemic and crash phase. Defoliation spread was best described using a two-scale stratified spread model, suggesting that defoliation spread is governed by two processes operating at different spatial scale. The pattern of phase-dependent spatial synchrony was coherent in both defoliation and onset of the growing season. This suggests that the timing of spring phenology plays a role in the large-scale synchronization of birch forest moth outbreaks.
Keywords: population synchrony, forest insects, spread distance distributions, spring phenology, defoliation, MODIS-NDVI
1. Introduction
Herbivore populations with cyclic population dynamics sometimes exhibit high-density outbreaks that have devastating impacts on their food plants. Understanding the circumstances that permit such outbreaks has been a long-standing issue in ecology. In particular, some species of forest insects have become renowned for exhibiting population outbreaks (Myers 1988; Berryman 1996). Forest insect outbreaks are often regional in the sense that large tracts of forest are defoliated simultaneously, although the spatial outbreak extent may show substantial variation in both time and space for a given species (Liebhold & Kamata 2000). Analyses of spatio-temporally pattered outbreak dynamics may yield important insights into the underlying population dynamical processes (Liebhold et al. 2004).
Generally there are two approaches that may be adopted for analysing spatio-temporal data on herbivore outbreaks. One approach focuses on the concept of population synchrony, defined as the correlation in population rate of change between sites within a population's distribution range (Bjørnstad et al. 1999; Liebhold et al. 2004). Central to this approach is to assess how synchrony depends on distance. Of interest is also whether such synchrony–distance relations (often estimated in terms of spatial autocorrelograms) is anisotropic (i.e. directionally dependent) in the sense that they change in space or time (Bjørnstad et al. 1999). Spatial changes may imply environmental gradients (Hagen et al. 2008) or nonlinear endogenous dynamics giving rise to complex spatio-temporal patterns (Sherratt & Smith 2008). Temporal changes may take the form of phase-dependent synchrony (Haydon et al. 2003), meaning that the degree of synchrony differs between the increase, peak and crash phase of the outbreak cycle. Such phase-dependency can be indicative of which processes promotes outbreaks.
The other approach focuses on the analysis of the rate of spread of outbreaks. This is the natural approach in the studies of outbreaking invasive species (e.g. Tobin et al. 2007). In that case the rate of spread, as quantified by the distribution of spread distances, is likely to be directly related to the dispersal distance distribution of the invasive species. Although the ‘rate of spread approach’ also may be applied to species exhibiting spatially extensive outbreak dynamics within their native range, the underlying processes are more elusive since various population and community processes (other than dispersal) may be involved. Nevertheless, modelling the distribution of spread distances may give clues to what are the most likely underlying processes, in particular, when conducted in combination with the more conventional analysis of population synchrony.
In this study we apply both approaches to a severe outbreak of birch forest geometrids in northern Fennoscandia. The two geometrid moth species in question, Epirrita autumnata and Operophtera brumata, exhibit cyclic outbreak dynamics, which sometimes leads to spatially extensive defoliation of the mountain birch forest in this region (Tenow 1972; Ruohomäki et al. 2000; Tanhuanpää et al. 2002). The outbreak cycles have often been assumed to be on a sufficiently large scale to be explained by a regionalized Moran effect (Berryman 1996; Ruohomäki et al. 2000). Among several possible mechanisms that may underlie Moran effects, variable spring temperatures causing a varying degree of matching in the phenologies of moth and their host plant (i.e. birch) have recently been highlighted for the insect–host plant system in question (Stenseth & Mysterud 2002; van Asch & Visser 2007; Hagen et al. 2008). As phenological patterns are observed to be structured according to latitudinal and altitudinal gradients (Karlsen et al. 2008), as well as topographical features, such a phenological mismatch-driven Moran effect could also be responsible for the more complex spatial dynamics recently reported for birch forest moths (Klemola et al. 2006; Tenow et al. 2007). Yet, other studies have hinted that dispersal (either in the moths or their enemies) may be important, at least under some circumstances (Ims et al. 2004). Previous studies of spatio-temporal dynamics of birch forest geometrids have been analysed according to the population synchrony approach (Klemola et al. 2006; Tenow et al. 2007; Hagen et al. 2008).
Here we present, to our knowledge, the first analysis of spatio-temporal herbivore outbreak dynamics with a particular reference to food plant phenology as a putative Moran effect. Our analyses are facilitated by regional satellite-derived time series of forest defoliation caused by the moth as well as phenology of their host plant covering all phases of an outbreak cycle. Owing to their extensive spatial coverage, such time series provides better opportunities for comprehensive analyses than the spatially restricted and scattered ground-based population count data which so far has formed the basis for such analyses.
The goal of our study is threefold. First, we use both the analytical approaches outlined above to establish to what extent patterns of population synchrony and patterns of outbreak (i.e. defoliation) spread are linked. We use the term ‘spread’ in the widest possible sense, knowing well that the mechanism(s) operating behind the observed spatial dynamics does not necessarily include actual dispersal of individual moths. By spread we refer to any between-year change in the spatial distribution of outbreaks. Second, we evaluate whether these spatial processes are dependent on the phase of the outbreak cycle. Finally, we examine whether there is any spatial phase-dependent coherence between the moth outbreaks and birch phenology, expressed as the timing of onset of the growing season; i.e. thus evaluating if the degree of matching between the phenology of the moth and their host plant could act as a Moran effect.
2. Material and methods
(a). Study system
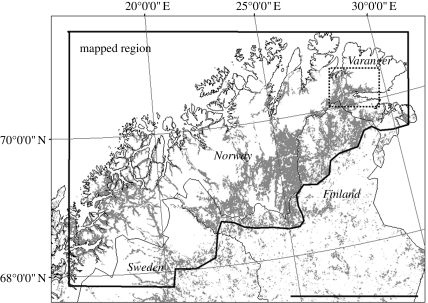
In the present study we consider Fennoscandia north of 68° N (figure 1). We delineate the study region to the east by the approximate birch/mixed birch-coniferous forest limit, a total area of about 106700 km2 of which roughly 30 per cent is forested. Northern Fennoscandia lies in the arctic/alpine-boreal transition zone and includes the northern parts of Norway, Sweden and Finland. The Scandinavian mountain chain (the Scandes) divides the area into a humid oceanic region along the western coast, and a dry continental region to the southeast. Birch (Betula pubescens, Ehrh.) forests dominate the lowland, except in the southeast where dominance gradually shifts to conifers. In the western region, wind-protected areas are characterized by tall birch forest types where herbs and ferns dominate the ground cover. By contrast, the continental east is characterized by low-growing and open, multi-stemmed birch forest types where lichen and crowberry dominate the ground cover. Throughout the whole region, intermediate bilberry birch forest types cover large areas (Hämet-Ahti 1963; Väre 2001; Johansen & Karlsen 2005).
Figure 1.
A map showing the extent of the mapped region in northern Fennoscandia. Grey shaded areas show the distribution of birch dominated forest in the region. The hatched square delineates the sub-region of Varanger for which a detailed depiction of the geometrid outbreak was made (see figure 6). Scale bar, 200 km.
In the northern boreal birch forests of Fennoscandia, winter moth and autumnal moth are the most important cause of disturbance. Both species exhibit cyclic population outbreaks at approximately 10 year intervals in this region (Tenow 1972; Haukioja et al. 1988; Bylund 1999). The two species, when occurring in sympatry within their outbreak range, exhibit largely synchronous dynamics, with winter moth dominating at termination of the outbreaks (Tenow et al. 2007; Klemola et al. 2008). The cyclicity of the outbreaks is documented in qualitative historical records as far back as the 1860s (Tenow 1972; Nilssen et al. 2007). Individual outbreaks vary greatly in amplitude, duration and spatial extent (Tenow 1972; Ruohomäki et al. 2000; Klemola et al. 2006; Tenow et al. 2007). The outbreaks can be massive and have dramatic effects, with severe defoliation over vast areas and occasionally death of the forest (Tenow 1972; Kallio & Lehtonen 1973; Lehtonen & Heikkinen 1995; Tenow & Bylund 2000). Defoliation of birch by geometrids in this region is of a seasonal character. The larvae hatch in approximate synchrony with budburst (late May—early June in northern Fennoscandia). The feeding periods last for four to eight weeks depending on the temperature and forage quality (Ruohomäki et al. 2000) after which the larvae drop to the ground and pupate in the soil. At high larval densities a large proportion of birch leaves are consumed at the bud stage and never unfold. After severe defoliation there is little or no refoliation during the same growing season.
(b). Estimates of annual defoliation
Historically, no systematic monitoring of the extent and distribution of forest damage caused by geometrids in northern Fennoscandia has ever been in place. Recently however, Moderate Resolution Imaging Spectroradiometer (MODIS) satellite imagery (the MOD13Q1 product; Huete et al. 2002) has been successfully used to map the annual distribution of defoliation in northern Fennoscandia covering the last 9 years (2000–2008) and a full outbreak cycle by geometrids in the region (Jepsen et al. 2009). Defoliation scores based on changes in summer normalized difference vegetation index (NDVI) were shown to be both a good proxy for local larval densities measured on the ground and an accurate predictor for the prevalence of defoliation when evaluated against independent data from other areas in the region (Jepsen et al. 2009).
The basic data for our analysis were time series of defoliation scores binned to produce annual maps of the presence/absence of severe defoliation using a threshold defoliation score. A threshold defoliation score of 14 per cent was shown to produce the most accurate discrimination between areas with and without visible defoliation (Jepsen et al. 2009). The spatial grain of the original data is 250 × 250 m determined by the grain of the satellite imagery used for the classification. In order to analyse patterns of spatial dynamics in defoliation we aggregated the 250 m presence/absence data into grid cells of increasing size from 6.25 × 6.25 km to 100 × 100 km containing the proportion of forested area in each grid cell predicted to be defoliated. We did this to assess whether our results were sensitive to the grain used in the analysis (sensu Wiens 1989).
(c). Estimates of annual onset of the growing season
Several studies have been devoted to developing and evaluating satellite-based approaches for mapping the onset and duration of the growing season in northern Fennoscandia in recent years (Karlsen et al. 2006, 2008; Beck et al. 2007). In the most recent approach (Karlsen et al. 2008), annual maps of the mean date for onset and end of the growing season for the years 2000–2006 were developed for the entire northern Fennoscandia based on the same MODIS-NDVI data used for mapping moth defoliation (Jepsen et al. 2009). The satellite-based time series of the onset of the growing season were shown to have a moderate-high correlation with the onset of leafing of birch from phenological stations distributed across northern Fennoscandia (Karlsen et al. 2008). This time series have since been extended to include 2007 (Karlsen et al. 2009). The spatial extent and grain was identical to the annual defoliation maps yielding a unique opportunity for comparative analysis of the spatial dynamics of defoliation and spring phenology across an entire region. In order to do so at varying spatial scales, we aggregated the original 250 m time series for the onset of the growing season into grid cells of increasing size from 6.25 × 6.25 km to 100 × 100 km containing the mean date for onset of the growing season in each grid cell.
(d). Analysis of spatial synchrony and defoliation spread
The presence and geographical scale of spatial synchrony between time series of defoliation as well as between time series of onset of the growing season were examined separately for each spatial grain (6.25–100 km) in R using non-parametric covariance functions (function ‘Sncf’ in library ‘ncf’, Bjørnstad et al. 1999; Bjørnstad & Falck 2001). We calculated spatial covariance functions of the entire time period (2000–2008 for defoliation, 2000–2007 for the onset of growing season) and for each of three phases of the outbreak cycle.
To characterize the distribution of spread distances through the outbreak cycle we calculated the straight-line distance from each defoliated pixel in year t to the nearest defoliated area in year t − 1 using the original 250 × 250 m pixels. To avoid noise from scattered single pixels we only considered distances to neighbours with a minimum area of 5 pixels (corresponding to an area of approx. 0.3 km2). We compared the frequency distribution of observed spread distances to the distribution of distances between a random sample of forested pixels and the nearest defoliated area in a given year. Spread events with distance zero (e.g. recurring outbreaks in a pixel for two or more consecutive years) were excluded from the analysis.
Nonlinear models were fitted to the observed spread data and the least-square estimates of the model parameters estimated in R (the ‘nls’ function in library ‘stats’; Bates & Watts 1988). We compared the performance of four standard spread models: a simple diffusion model (termed ‘Diffusion’) in which the spread probability decrease with distance following a normal curve, a fat-tailed leptokurtic spread model (termed ‘Leptokurtic’), in which the probability for both very short and long distance spread is higher than in a diffusion model, and finally two fat-tailed stratified models which assumes a two-scale spread probability. The first is a diffusion–diffusion model (termed ‘StratifiedDD’), in which spread probability is described using two diffusion models operating at different scales, and the second a diffusion-leptokurtic model (termed ‘StratifiedDL’), which uses a short-range diffusion and a long-range leptokurtic model. The diffusion model describes the hypothetical situation where new defoliation spread out from existing defoliated areas at a constant spread rate. However, natural spread data are frequently characterized by fat-tailed distributions (Kot et al. 1996) owing to the presence of long-distance spread events, and leptokurtic and stratified dispersal kernels have repeatedly been shown to provide better estimates of the dispersal and spread of both native and invasive organisms (Kot et al. 1996; Chesson & Lee 2005; Johnson et al. 2006; Liebhold & Tobin 2008). Specifically, a stratified spread model is a likely candidate if the observed spread is determined by two independent mechanisms, for instance short-range dispersal (by flight or wind) coupled with long-range wind- or human-mediated dispersal (Liebhold et al. 1992; Sharov & Liebhold 1998; Gilbert et al. 2004), or a regionally synchronizing factor in the environment (a Moran effect).
3. Results
(a). General characteristics of the outbreak
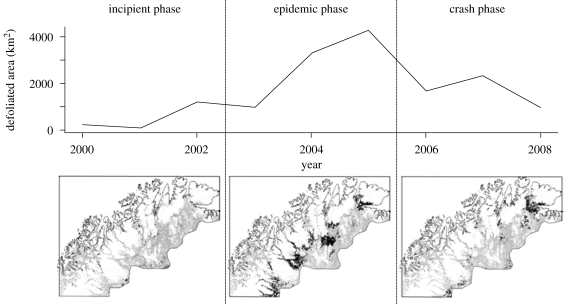
The total area estimated to be severely defoliated annually (figure 2, upper panel) show that a full outbreak cycle was completed during the years 2000–2008. The outbreak did not have a clearly defined epicentre, but rather began more or less simultaneously in multiple locations across the region (figure 2, incipient phase). Defoliation peaked in 2004–2005 during which 3–4000 km2 of the birch forest belt in the study region was affected by severe defoliation annually (10–15% of total birch forest area: figure 2, epidemic phase). The Varanger region in northeast Norway (outlined in figure 1) was most severely affected, with local defoliation lasting for 3–5 years in some places (as opposed to 1–3 years in most other regions). In the course of the outbreak cycle, a total area of just above 10 000 km2 was affected by severe defoliation at least once, corresponding to one-third of the birch forest in the region.
Figure 2.
The total area of birch forest in the mapped region affected by severe defoliation annually for the years 2000–2008 (upper panel). The outbreak cycle was divided into three phases: the incipient, the epidemic and the crash phase. The lower panel shows the areas affected by severe defoliation during the three phases in black. The distribution of birch-dominated forest is shown in grey.
Based on the regional evolution of the outbreak (figure 2) we defined the following three phases for the purpose of the analysis of synchrony and spread: (figure 2); the incipient phase (2000–2002) characterized by low, slowly increasing, prevalence of defoliation; the epidemic phase (2003–2005) during which the prevalence of defoliation increased dramatically and eventually peaked in the entire region and the crash phase (2006–2008 for defoliation, 2006–2007 for the onset of growing season) where the prevalence of defoliation diminished almost to pre-epidemic levels.
(b). Synchrony in outbreak and spring phenology
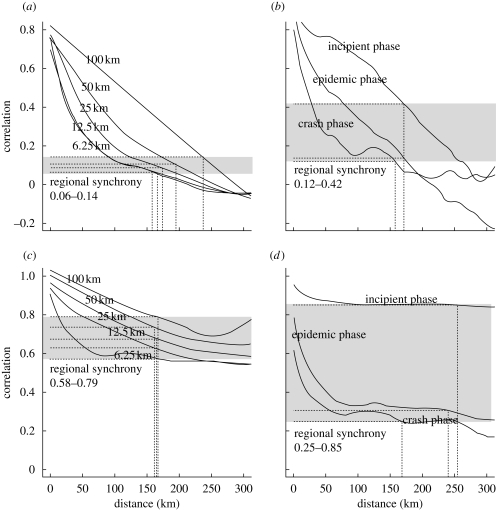
Spatial synchrony in the prevalence of defoliation was evident up to a distance of approximately 200 km (155–230 km depending on the grain; figure 3a). The regional synchrony (i.e. the average synchrony across the entire region) was generally low when considering the time series covering the whole outbreak period (figure 3a). A separate analysis of synchrony for each outbreak phase revealed a markedly higher regional synchrony in the incipient phase compared with later phases of the outbreak (figure 3b). This was owing to a steeper decay in synchrony with distance in the epidemic and crash phases than in the incipient phase. The pattern of spatial synchrony in the mean onset of growing season had some striking similarities to the patterns of moth defoliation. A strong local spatial synchrony was evident up to a distance of approximately 170 km (figure 3c). As for defoliation, the incipient phase of the outbreak (2000–2002) was characterized by a markedly higher regional synchrony in the onset of the growing season than the later phases of the outbreak (figure 3d). Generally however, a higher level of regional synchrony was present in the onset of the growing season than in defoliation, independent of spatial grain and outbreak phase.
Figure 3.
Non-parametric covariance functions (Bjørnstad & Falck 2001) showing synchrony-distance relations for both geometrid outbreaks and spring phenology. (a) Spatial synchrony of outbreaks over all outbreak phases for grid cells (grain) of increasing size (6.25 × 6.25 km–100 × 100 km); (b) outbreak synchrony for the incipient, epidemic and crash phase of the outbreak calculated for the smallest grid cell size (6.25 km). The range of the regional average synchrony is shown as grey shaded bars. The geographical scale of synchrony (where the curve covariance function crosses the average regional synchrony) is shown by dashed lines; (c,d) corresponding figures for spatial synchrony in the mean onset of the growing season.
(c). Spread of outbreaks
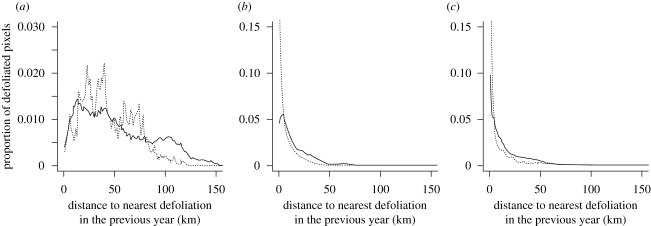
The distribution of distances between defoliated pixels and the closest defoliated area in the previous year was highly phase-dependent (figure 4). It decreased markedly as the outbreak progressed (spread distance in kilometres, median (interquartile range): incipient = 39.1 (39.1); epidemic = 4.5 (9.9); crash = 3.25 (13.3)). During the incipient phase (figure 4), intermediate spread distances (in the range 20–80 km) were over-represented when compared with a chance occurrence, while very long spread distances (100–150 km) were clearly under-represented. In the epidemic and crash phase, shorter spread distances (0–15 km) were strongly over-represented when compared with a chance occurrence.
Figure 4.
Frequency distribution of observed distances from defoliated pixels (dashed line) and a random sample of forested pixels (solid line, n = 25 000 yr−1) to the nearest defoliated area in the previous year during the (a) incipient (n = 16 509, nrandom = 50 000), (b) epidemic (n = 117 690, nrandom = 75 000) and (c) crash phase (n = 54 590, nrandom = 75 000) of the outbreak.
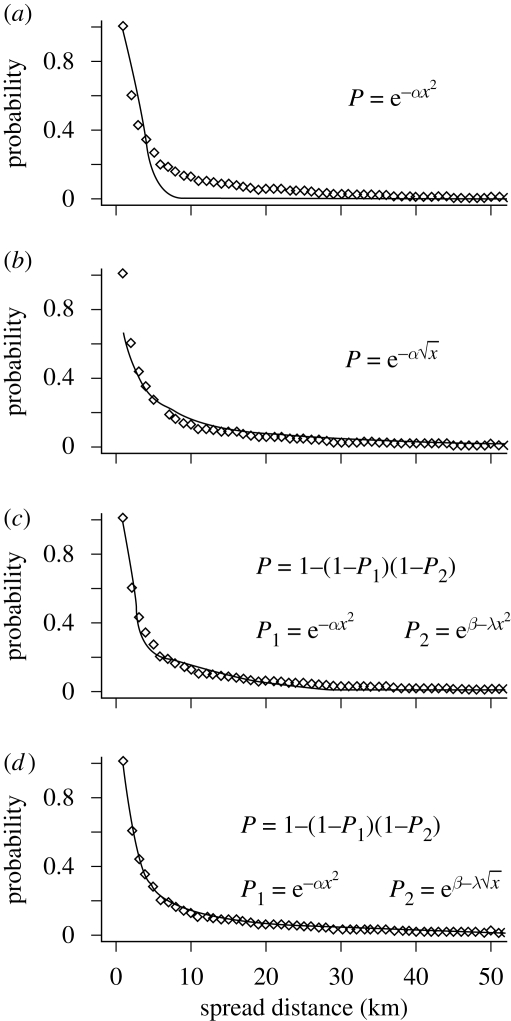
The observed pattern of defoliation spread was best described as a two-scale stratified process, as the stratified spread models provided the best fit both to the data as a whole and to the epidemic/crash phase of the outbreak separately (table 1 and figure 5). The best fit was obtained using a stratified diffusion–leptokurtic model (StratifiedDL). This suggests that the spread of defoliation in this system is determined by two independent processes, a very short-range diffusion-like process and a fat-tailed long-range process.
Table 1.
Parameters (see formulae in figure 5), 95 per cent confidence limits (CI) and fit statistics (Akaike Information criteria, AIC and log-likelihood, LL) for models fitted to the pooled data over all years (2000–2008) and separately to the incipient, epidemic and crash phase of the outbreak. (None of the standard spread models fitted well during the incipient phase of the outbreak. The stratified model based on a short-range diffusion and a long-range leptokurtic distribution (StratifiedDL) provided by far the best fit (lowest AIC/highest LL) to the observed defoliation spread distances during the epidemic and crash phase, as well as for the dataset as a whole.)
| model | α | CI | β | CI | γ | CI | AIC | LL | d.f. |
|---|---|---|---|---|---|---|---|---|---|
| all data | |||||||||
| diffusion | 0.09 | [0.078;0.102] | −1241 | 623 | 2 | ||||
| leptokurtic | 0.59 | [0.58;0.61] | −1425 | 715 | 2 | ||||
| stratifiedDD | 0.23 | [0.20;0.25] | −1.5 | [−1.58;−1.42] | 0.004 | [0.003;0.005] | −1844 | 926 | 4 |
| stratifiedDL | 0.73 | [0.67;0.81] | 0.25 | [0.21;0.29] | 0.73 | [0.71;0.75] | −2397 | 1203 | 4 |
| incipient | |||||||||
| diffusion | 0.00024 | [0.00021;0.00027] | −211 | 107 | 2 | ||||
| leptokurtic | 0.17 | [0.16;0.19] | −190 | 97 | 2 | ||||
| stratifiedDD | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| stratifiedDL | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| epidemic | |||||||||
| diffusion | 0.048 | [0.043;0.054] | −1217 | 611 | 2 | ||||
| leptokurtic | 0.54 | [0.53;0.56] | −1354 | 679 | 2 | ||||
| stratifiedDD | 0.16 | [0.14;0.17] | −1.226 | [−1.299;−1.155] | 0.0046 | [0.0041;0.0052] | −1864 | 936 | 4 |
| stratifiedDL | 1.80 | [1.45;2.44] | 0.58 | [0.56;0.59] | 0.767 | [0.760;0.774] | −2527 | 1268 | 4 |
| crash | |||||||||
| diffusion | 0.22 | [0.20;0.24] | −1505 | 755 | 2 | ||||
| leptokurtic | 0.74 | [0.71;0.77] | −1336 | 670 | 2 | ||||
| stratifiedDD | 0.33 | [0.31;0.35] | −2.09 | [−2.18;−1.99] | 0.0042 | [0.003;0.005] | −1995 | 1002 | 4 |
| stratifiedDL | 0.50 | [0.46;0.55] | −0.40 | [−0.54;−0.26] | 0.72 | [0.67;0.78] | −2199 | 1104 | 4 |
Figure 5.
The four spread models (solid lines): (a) diffusion; (b) leptokurtic; (c) stratifiedDD; and (d) stratifiedDL, fitted to observed defoliation spread distances (diamonds) for pooled data over all years (2000–2008).
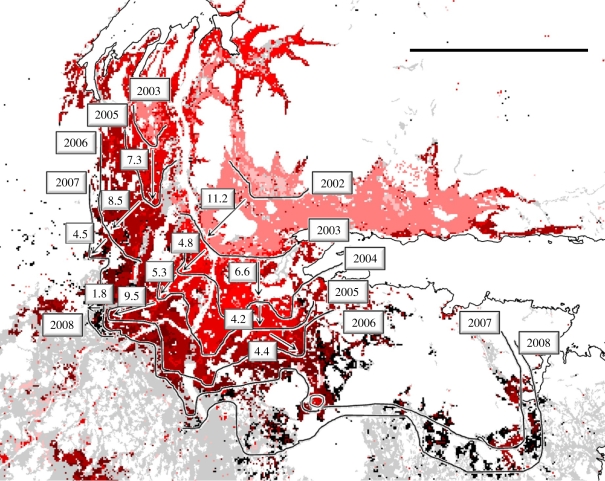
Figure 6 shows a visual representation of the gradual spread of defoliation in the Varanger area in northeast Norway from 2002 to 2008 through the epidemic and crash phases of the outbreak. Defoliation in this region was particularly severe and long-lasting and hence provides a unique illustration of the short-range pattern of defoliation spread in the system. Spread distances ranged from 1–12 km between years and were larger during the early years of the outbreak (2002–2003). As the outbreak entered the crash phase, the advancing front of the spread became increasingly fuzzy and no good distinction can be made between 2007 and 2008.
Figure 6.
Observed pattern of annual spread of defoliation in the Varanger region (70°15′ N, 29°0′ E) in northeast Norway for the years 2002 (lightest red) to 2008 (darkest red). Black lines show the approximate ‘front’ of the spread in a southeasterly direction. Numbers in boxes indicate the year and examples of between-year spread distances (in kilometres). Scale bar, 30 km.
4. Discussion
(a). Phase-dependent and scale-specific outbreak spread and synchronization
Few studies on cyclic species have yet been dedicated to assess variation in spatial dynamics at different phases of the population cycle (Haydon et al. 2003; Aukema et al. 2006). Our investigation of defoliation patterns caused by cyclic geometrid moths in northern boreal birch forest provided evidence of highly phase-dependent spatial dynamics. The incipient phase of the outbreak was characterized by high regional synchrony, and long defoliation spread distances (up to approx. 80 km) between years. Later phases of the outbreak were characterized by much lower regional synchrony and defoliation spread over much shorter distances (a few kilometres). Thus our results may suggest that the observed defoliation spread (and synchronization) was the result of two processes operating at different spatial scales and phases of cycle according to the following scenario: the outbreak was initiated in multiple locations simultaneously, possibly by a favourable environmental condition, which permits high local population growth rates over reasonably large areas. This gave rise to the long defoliation ‘spread’ distances, which cannot reasonably be attributed to moth dispersal per se. Thus the scale of population synchrony in this initial phase of the population cycle is determined by the scale of the synchronizing factor in the environment. As the population cycle progresses, new outbreaks, and consequently, defoliation happens increasingly as a result of a gradual spread out from the existing defoliated areas. At this stage dispersal could have contributed more to the spread. This causes much shorter defoliation spread distances and lower regional synchrony during the epidemic and crash phase of the population cycle when compared with the incipient phase. However, even within the realm of the generally short-tailed spread distance distributions of the epidemic and crash phase, the best spread models suggested that two processes were operating, perhaps owing to a persistent effect of the processes that dominated in the incipient phase. Alternatively, the scale of synchrony could simply be set by the configuration of outbreaks during the incipient phase of the population cycle, which subsequently functions as ‘sources’ for new defoliation in the later phases of the cycle. In this manner a single favourable year could be influential to the spatial evolution of the entire outbreak.
Like most other studies addressing the spatial dimensions of cyclic outbreak dynamics, previous analyses of birch forest moths have focused solely on the issue of regional synchrony across the temporal extent of the study (Klemola et al. 2006; Tenow et al. 2007), thus without attempting to partition out phase- or scale-dependent patterns and processes as we have done here. Nevertheless, the previous studies have concluded that although dispersal could not be ruled out as a contributing synchronizing mechanism (Ims et al. 2004), a regionalized climatic Moran effect is more likely. Our results comply with and extend on this conclusion. Mass-dispersal of larvae over long distances (as would be required to initiate new outbreaks) is probably limited, although the process is little studied under field conditions (Bell et al. 2005). Experimental studies of ballooning winter and autumnal moth larvae (Edland 1971; Tammaru et al. 1995) as well as the closely related Bruce spanworm, Operophtera bruceata (Brown 1962) show that ballooning rates drop quickly with distance beyond a few hundred metres.
(b). Host plant phenology as a putative Moran effect
So far the most direct evidence for a Moran effect on the spatio-temporal dynamics of forest insects has been derived from the analyses of spatial meteorological data (e.g. temperature), which has shown that synchrony in climatic variables can exhibit similar spatial profiles (i.e. auto-covariance functions) to population synchrony in some species of forest insects (Peltonen et al. 2002). In northern Fennoscandia, metrological stations are too few and too poorly interspersed over climate gradients within the outbreak range of birch forest moth to allow a similar comparison. Instead, we used MODIS-NDVI data in order to determine the onset of plant growth in the spring, which provided a full spatial coverage of the focal region. Onset of plant growth also represents a more biologically explicit variable for spring feeding insects than some arbitrarily selected climatic variable. That the temporal match between larvae hatching and budburst is an important determinant for the survival and growth of larvae has long been recognized (Stenseth & Mysterud 2002; Van Asch & Visser 2007). Larvae that hatch too early compared with budburst will suffer starvation and increased mortality (Wint 1983; Tikkanen & Julkunen-Tiitto 2003), while late-hatching larvae will experience food of lower quality and suffer reduced growth and fecundity (Van Dongen et al. 1997; Haukioja et al. 2002). We found that the onset of plant growth in spring has a phase-dependent pattern of spatial synchrony that was similar to that present in the prevalence of defoliation. This suggests that the timing of spring phenology plays a decisive role in the synchrony moth outbreaks on a regional scale in northern Fennoscandia, probably by initiating local population outbreaks simultaneously over a large spatial scale.
The spatio-temporal pattern of birch phenology in northern Fennoscandia is primarily determined by strong geographical (north–south, oceanic-continental) and altitudinal gradients. However, locally within these phenological gradients, onset of the growing season may vary as much as three to five weeks between years with larger variation in oceanic than continental regions (Karlsen et al. 2007). In addition, geographical gradients appear to exist in the effect of temperature on the advance of spring phenology. In the continental part of Fennoscandia, a 1°C increase in temperature has been found to correspond to 3–8 days earlier onset of the growing season (Karlsson et al. 2003; Shutova et al. 2006; Pudas et al. 2008), while the same temperature increase translates to a 7–10 days earlier onset of the growing season in oceanic northwest Norway (Karlsen et al. 2007, 2008). Assuming that larval hatching depends more directly on temperature than does budburst (Topp & Kirsten 1991; Van Asch & Visser 2007), there is a large potential for local and regional differences in the degree of match between larval hatching and birch budburst in individual years. Thus for the observed massive large-scale outbreak to develop, meteorological conditions providing a good phenological match must have occurred simultaneously at a large scale. While we accordingly found evidence for large-scale synchronization of spring phenology during the incipient phase of the cycle, still more research is needed. In particular, aspects of the spring phenology of the moths (egg-hatching time distributions under various temperature regimes) need to be established as to elucidate the exact conditions that provide the necessary phenological matching for outbreaks to take place.
5. Conclusion
We have made progress on three aspects of the issue of spatial dynamics of cyclically outbreaking herbivores. First, we have demonstrated a striking phase-dependence in the synchronization of outbreaks of northern birch forest moths, with evidence for most extensive synchronization and spread taking place in the incipient phase of the outbreak cycle. Second, by modelling outbreak spread distance distributions, we gained more detailed information about the scale of the underlying processes than by only focusing on outbreak synchrony. In particular, we found that the relative importance of long-distance and short-distance spread events shifted among the different phase of the cycles. Third, by analysing satellite-derived data on both forest defoliation and spring phenology, we show that they have matching synchrony-distance profiles. This provides support for the hypothesis that a climate event in the spring influential to phenology of moths and their host plant is likely to act as a Moran effect.
Acknowledgements
This work was funded by the Department of Biology, University of Tromsø and the Research Council of Norway.
References
- Aukema B. H., Carroll A. L., Zhu J., Raffa K. F., Sickley T. A., Taylor S. W.2006Landscape level analysis of mountain pine beetle in British Columbia, Canada: spatiotemporal development and spatial synchrony within the present outbreak. Ecography 29, 427–441 (doi:10.1111/j.2006.0906-7590.04445.x) [Google Scholar]
- Bates D. M., Watts D. G.1988Nonlinear regression analysis and its applications New York, NY: Wiley [Google Scholar]
- Beck P. S. A., Jonsson P., Hogda K. A., Karlsen S. R., Eklundh L., Skidmoree A. K.2007A ground-validated NDVI dataset for monitoring vegetation dynamics and mapping phenology in Fennoscandia and the Kola peninsula. Int. J. Remote Sens. 28, 4311–4330 (doi:10.1080/01431160701241936) [Google Scholar]
- Bell J. R., Bohan D. A., Shaw E. M., Weyman G. S.2005Ballooning dispersal using silk: world fauna, phylogenies, genetics and models. Bull. Entomol. Res. 95, 69–114 [DOI] [PubMed] [Google Scholar]
- Berryman A. A.1996What causes population cycles of forest Lepidoptera? Trends Ecol. Evol. 11, 28–32 (doi:10.1016/0169-5347(96)81066-4) [DOI] [PubMed] [Google Scholar]
- Bjørnstad O. N., Falck W.2001Nonparametric spatial covariance functions: estimation and testing. Environ. Ecol. Stat. 8, 53–70 [Google Scholar]
- Bjørnstad O. N., Ims R. A., Lambin X.1999Spatial population dynamics: analyzing patterns and processes of population synchrony. Trends Ecol. Evol. 14, 427–432 (doi:10.1016/S0169-5347(99)01677-8) [DOI] [PubMed] [Google Scholar]
- Brown C. E.1962The life history and dispersal of the Bruce spanworm, Operophtera bruceata (Lep.: Geometridae). Can. Entomol. 94, 1103–1107 [Google Scholar]
- Bylund H.1999Climate and the population dynamics of two insect outbreak species in the North. Ecol. Bull. 47, 54–62 [Google Scholar]
- Chesson P., Lee C. T.2005Families of discrete kernels for modeling dispersal. Theoret. Popul. Biol. 67, 241–256 (doi:10.1016/j.tpb.2004.12.002) [DOI] [PubMed] [Google Scholar]
- Edland T.1971Wind dispersal of the winter moth, Operophtera brumata (L.) (Lep. Geometridae) and its relevance to control measures. Norsk Entomol. Tidsskrift 18, 103–105 [Google Scholar]
- Gilbert M., Gregoire J. C., Freise J. F., Heitland W.2004Long-distance dispersal and human population density allow the prediction of invasive patterns in the horse chestnut leafminer Cameraria ohridella. J. Anim. Ecol. 73, 459–468 (doi:10.1111/j.0021-8790.2004.00820.x) [Google Scholar]
- Hagen S. B., Jepsen J. U., Yoccoz N. G., Ims R. A.2008Anisotropic patterned population synchrony in climatic gradients indicates nonlinear climatic forcing. Proc. R. Soc. B 275, 1509–1515 (doi:10.1098/rspb.2008.0122) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hämet-Ahti L.1963Zonation of the mountain birch forests in northernmost Fennoscandia. Ann. Bot. Soc. Zool. Bot. Fennica 34, 1–127 [Google Scholar]
- Haukioja E., Neuvonen S., Hanhimäki S., Niemelä P.1988The autumnal moth in Fennoscandia. In Dynamics of forest insect populations: patterns, causes and management strategies (ed. Berryman A. A.), pp. 163–177 New York, NY: Academic Press [Google Scholar]
- Haukioja E., Ossipov V., Lempa K.2002Interactive effects of leaf maturation and phenolics on consumption and growth of a geometrid moth. Entomol. Experimental Appl. 104, 125–136 (doi:10.1023/A:1021280106023) [Google Scholar]
- Haydon D. T., Greenwood P. E., Stenseth N. C., Saitoh T.2003Spatio-temporal dynamics of the grey-sided vole in Hokkaido: identifying coupling using state-based Markov-chain modelling. Proc. R. Soc. Lond. B 270, 435–445 (doi:10.1098/rspb.2002.2230) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huete A., Didan K., Miura T., Rodriguez E. P., Gao X., Ferreira L. G.2002Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 83, 195–213 (doi:10.1016/S0034-4257(02)00096-2) [Google Scholar]
- Ims R. A., Yoccoz N. G., Hagen S. B.2004Do sub-Arctic winter moth populations in coastal birch forest exhibit spatially synchronous dynamics? J. Anim. Ecol. 73, 1129–1136 (doi:10.1111/j.0021-8790.2004.00882.x) [Google Scholar]
- Jepsen J. U., Hagen S. B., Høgda K. A., Ims R. A., Karlsen S. R., Tømmervik H., Yoccoz N. G.2009Monitoring the spatio-temporal dynamics of geometrid moth outbreaks in birch forest using MODIS-NDVI data. Remote Sens. Environ. 13, 1939–1947 [Google Scholar]
- Johansen B., Karlsen S. R.2005Monitoring vegetation changes on Finnmarksvidda, Northern Norway, using Landsat MSS and Landsat TM/ETM+ satellite images. Phytocoenologia 35, 969–984 (doi:10.1127/0340-269X/2005/0035-0969) [Google Scholar]
- Johnson D. M., Liebhold A. M., Tobin P. C., Bjornstad O. N.2006Allele effects and pulsed invasion by the gypsy moth. Nature 444, 361–363 (doi:10.1038/nature05242) [DOI] [PubMed] [Google Scholar]
- Kallio P., Lehtonen J.1973Birch forest damage caused by Oporina autumnata (Bkh.) in 1966–99 in Utsjoki. Reports from Kevo Subarctic Research Station, vol. 10, pp. 55–69 [Google Scholar]
- Karlsen S. R., Elvebakk A., Hogda K. A., Johansen B.2006Satellite-based mapping of the growing season and bioclimatic zones in Fennoscandia. Global Ecol. Biogeogr. 15, 416–430 (doi:10.1111/j.1466-822X.2006.00234.x) [Google Scholar]
- Karlsen S. R., Solheim I., Beck P. S. A., Hogda K. A., Wielgolaski F. E., Tommervik H.2007Variability of the start of the growing season in Fennoscandia, 1982–2002. Int. J. Biometeorol. 51, 513–524 (doi:10.1007/s00484-007-0091-x) [DOI] [PubMed] [Google Scholar]
- Karlsen S. R., et al. 2008MODIS-NDVI-based mapping of the length of the growing season in northern Fennoscandia. Int. J. Appl. Earth Obs. Geoinform. 10, 253–266 (doi:10.1016/j.jag.2007.10.005) [Google Scholar]
- Karlsen S. R., Ramfjord H., Hogda K. A., Johansen B., Danks F. S., Brobakk T. E.2009A satellite-based map of onset of birch (Betula) flowering in Norway. Aerobiologia 25, 15–25 (doi:10.1007/s10453-008-9105-3) [Google Scholar]
- Karlsson P. S., Bylund H., Neuvonen S., Heino S., Tjus M.2003Climatic response of budburst in the mountain birch at two areas in northern Fennoscandia and possible responses to global change. Ecography 26, 617–625 (doi:10.1034/j.1600-0587.2003.03607.x) [Google Scholar]
- Klemola T., Huitu O., Ruohomäki K.2006Geographically partitioned spatial synchrony among cyclic moth populations. Oikos 114, 349–359 (doi:10.1111/j.2006.0030-1299.14850.x) [Google Scholar]
- Klemola T., Andersson T., Ruohomaki K.2008Fecundity of the autumnal moth depends on pooled geometrid abundance without a time lag: implications for cyclic population dynamics. J. Anim. Ecol. 77, 597–604 (doi:10.1111/j.1365-2656.2008.01369.x) [DOI] [PubMed] [Google Scholar]
- Kot M., Lewis M. A., Van den Driessche P.1996Dispersal data and the spread of invading organisms. Ecology 77, 2027–2042 (doi:10.2307/2265698) [Google Scholar]
- Lehtonen J., Heikkinen R. K.1995On the recovery of mountain birch after Epirrita damage in Finnish Lapland, with a particular emphasis on reindeer grazing. Ecoscience 2, 349–356 [Google Scholar]
- Liebhold A., Kamata N.2000Introduction: are population cycles and spatial synchrony a universal characteristic of forest insect populations? Popul. Ecol. 42, 205–209 (doi:10.1007/PL00011999) [Google Scholar]
- Liebhold A. M., Tobin P. C.2008Population ecology of insect invasions and their management. Ann. Rev. Entomol. 53, 387–408 (doi:10.1146/annurev.ento.52.110405.091401) [DOI] [PubMed] [Google Scholar]
- Liebhold A. M., Halverson J. A., Elmes G. A.1992Gypsy moth invasion in North America: a quantitative analysis. J. Biogeogr. 19, 513–520 (doi:10.2307/2845770) [Google Scholar]
- Liebhold A., Koenig W. D., Bjørnstad O. N.2004Spatial synchrony in population dynamics. Ann. Rev. Ecol. Evol. Syst. 35, 467–490 (doi:10.1146/annurev.ecolsys.34.011802.132516) [Google Scholar]
- Myers J. H.1988Can a general hypothesis explain population-cycles of forest Lepidoptera? Adv. Ecol. Res. 18, 179–242 (doi:10.1016/S0065-2504(08)60181-6) [Google Scholar]
- Nilssen A. C., Tenow O., Bylund H.2007Waves and synchrony in Epirrita autumnata/Operopthera brumata outbreaks. II. Sunspot activity cannot explain cyclic outbreaks. J. Anim. Ecol. 76, 269–275 (doi:10.1111/j.1365-2656.2006.01205.x) [DOI] [PubMed] [Google Scholar]
- Peltonen M., Liebhold A. M., Bjørnstad O. N., Williams D. W.2002Spatial synchrony in forest insect outbreaks: roles of regional stochasticity and dispersal. Ecology 83, 3120–3129 [Google Scholar]
- Pudas E., Tolvanen A., Poikolainen J., Sukuvaara T., Kubin E.2008Timing of plant phenophases in Finnish Lapland in 1997–2006. Boreal Environ. Res. 13, 31–43 [Google Scholar]
- Ruohomäki K., Tanhuanpää M., Ayres M. P., Kaitaniemi P., Tammaru T., Haukioja E.2000Causes of cyclicity of Epirrita autumnata (Lepidoptera, Geometridae): grandiose theory and tedious practice. Popul. Ecol. 42, 211–223 (doi:10.1007/PL00012000) [Google Scholar]
- Sharov A. A., Liebhold A. M.1998Model of slowing the spread of gypsy moth (Lepidoptera: Lymantriidae) with a barrier zone. Ecol. Appl. 8, 1170–1179 (doi:10.1890/1051-0761(1998)008[1170:MOSTSO]2.0.CO;2) [Google Scholar]
- Sherratt J. A., Smith M. J.2008Periodic travelling waves in cyclic populations: field studies and reaction-diffusion models. J. R. Soc. Interface 5, 483–505 (doi:10.1098/rsif.2007.1327) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shutova E., et al. 2006Growing seasons of Nordic mountain birch in northernmost Europe as indicated by long-term field studies and analyses of satellite images. Int. J. Biometeorol. 51, 155–166 (doi:10.1007/s00484-006-0042-y) [DOI] [PubMed] [Google Scholar]
- Stenseth N. C., Mysterud A.2002Climate, changing phenology, and other life history and traits: nonlinearity and match-mismatch to the environment. Proc. Natl Acad. Sci. USA 99, 13379–13381 (doi:10.1073/pnas.212519399) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tammaru T., Kaitaniemi P., Ruohomäki K.1995Oviposition choices of Epirrita autumnata (Lepidoptera: Geometridae) in relation to its eruptive population dynamics. Oikos 74, 296–304 (doi:10.2307/3545659) [Google Scholar]
- Tanhuanpää M., Ruohomaki K., Turchin P., Ayres M. P., Bylund H., Kaitaniemi P., Tammaru T., Haukioja E.2002Population cycles of the autumnal moth in Fennoscandia. In Population cycles: the case for trophic interactions (ed. Berryman A. A.), pp. 142–154 Oxford, UK: Oxford University Press [Google Scholar]
- Tenow O.1972The outbreaks of Oporinia autumnata Bkh. and Operopthera spp. (Lep., Geometridae) in the Scandinavian mountain chain and Northern Finland 1862–1968. Zool. Bidrag från Uppsala (Suppl. 2), 1–107 [Google Scholar]
- Tenow O., Bylund H.2000Recovery of a Betula pubescens forest in northern Sweden after severe defoliation by Epirrita autumnata. J. Veg. Sci. 11, 855–862 (doi:10.2307/3236555) [Google Scholar]
- Tenow O., Nilssen A. C., Bylund H., Hogstad O.2007Waves and synchrony in Epirrita autumnata/Operopthera brumata outbreaks. I. Lagged synchrony: regionally, locally and among species. J. Anim. Ecol. 76, 258–268 (doi:10.1111/j.1365-2656.2006.01204.x) [DOI] [PubMed] [Google Scholar]
- Tikkanen O. P., Julkunen-Tiitto R.2003Phenological variation as protection against defoliating insects: the case of Quercus robur and Operophtera brumata. Oecologia 136, 244–251 (doi:10.1007/s00442-003-1267-7) [DOI] [PubMed] [Google Scholar]
- Tobin P. C., Liebhold A. M., Roberts E. A.2007Comparison of methods for estimating the spread of a non-indigenous species. J. Biogeogr. 34, 305–312 (doi:10.1111/j.1365-2699.2006.01600.x) [Google Scholar]
- Topp W., Kirsten K.1991Synchronization of preimaginal development and reproductive success in the winter moth, Operophtera brumata L. J. Appl. Entomol.-Zeitschrift Fur Angewandte Entomologie 111, 137–146 [Google Scholar]
- Van Asch M., Visser M. E.2007Phenology of forest caterpillars and their host trees: the importance of synchrony. Ann. Rev. Entomol. 52, 37–55 (doi:10.1146/annurev.ento.52.110405.091418) [DOI] [PubMed] [Google Scholar]
- Van Dongen S., Backeljau T., Matthysen E., Dhondt A. A.1997Synchronization of hatching date with budburst of individual host trees (Quercus robur) in the winter moth (Operophtera brumata) and its fitness consequences. J. Anim. Ecol. 66, 113–121 [Google Scholar]
- Väre H.2001Mountain birch taxonomy and floristics of mountain birch woodlands. In Mountain birch forest ecosystems, vol. 27 (ed. Wielgolaski F. E.), pp. 35–46 Paris, France: UNESCO [Google Scholar]
- Wiens J. A.1989Spatial scaling in ecology. Func. Ecol. 3, 385–397 (doi:10.2307/2389612) [Google Scholar]
- Wint W.1983The role of alternative host-plant species in the life of a polyphagous moth, Operophtera brumata (Lepidoptera, Geometridae). J. Anim. Ecol. 52, 439–450 [Google Scholar]