The effect of viscoelasticity on the stability of a pulmonary airway liquid layer

Abstract

The lungs consist of a network of bifurcating airways that are lined with a thin liquid film. This film is a bilayer consisting of a mucus layer on top of a periciliary fluid layer. Mucus is a non-Newtonian fluid possessing viscoelastic characteristics. Surface tension induces flows within the layer, which may cause the lung’s airways to close due to liquid plug formation if the liquid film is sufficiently thick. The stability of the liquid layer is also influenced by the viscoelastic nature of the liquid, which is modeled using the Oldroyd-B constitutive equation or as a Jeffreys fluid. To examine the role of mucus alone, a single layer of a viscoelastic fluid is considered. A system of nonlinear evolution equations is derived using lubrication theory for the film thickness and the film flow rate. A uniform film is initially perturbed and a normal mode analysis is carried out that shows that the growth rate g for a viscoelastic layer is larger than for a Newtonian fluid with the same viscosity. Closure occurs if the minimum core radius, R_min(t), reaches zero within one breath. Solutions of the nonlinear evolution equations reveal that R_min normally decreases to zero faster with increasing relaxation time parameter, the Weissenberg number We. For small values of the dimensionless film thickness parameter ε, the closure time, t_c, increases slightly with We, while for moderate values of ε, ranging from 14% to 18% of the tube radius, t_c decreases rapidly with We provided the solvent viscosity is sufficiently small. Viscoelasticity was found to have little effect for ε>0.18, indicating the strong influence of surface tension. The film thickness parameter ε and the Weissenberg number We also have a significant effect on the maximum shear stress on tube wall, max(τ_w), and thus, potentially, an impact on cell damage. Max(τ_w) increases with ε for fixed We, and it decreases with increasing We for small We provided the solvent viscosity parameter is sufficiently small. For large ε≈0.2, there is no significant difference between the Newtonian flow case and the large We cases.

INTRODUCTION

The lung consists of a branching network of airways, which are responsible for conducting air to and from the small (300 μm in diameter) respiratory sacs called alveoli. These airways and alveoli are coated on the inside with a thin liquid layer whose thickness is 2%–4% of the airway diameter under normal conditions,^{1, 2} but may be as much as 20% in disease.³ In the first 15–16 airway generations, this film is a bilayer consisting of a mucus layer on top of a serous, or periciliary, fluid layer.⁴ The mucus is a non-Newtonian fluid⁵ that exhibits viscoelastic and shear thinning characteristics, and possesses a yield stress.^{6, 7} In the terminal bronchioles, beyond generation 17, there is essentially a single fluid layer whose viscous properties are similar to those of water.

It is well recognized that the liquid lining of the lung can cause the closing off of a small airway.^{8, 9} This can happen as the result of a liquid plug (lens) forming due to a capillary (surface tension) instability known as the Rayleigh instability. In addition, this surface tension instability may provoke the collapse of the compliant airway wall, resulting in a capillary-elastic instability. Investigation of plug formation from a liquid coating the inside of a small tube was performed by Everett and Haynes,¹⁰ who found that a critical volume of liquid is required, above which a plug forms and below which the liquid only coats the wall but does not form a plug. The critical volume V_c is approximately 5.47a³, where a is the tube radius. A similar value was also found in a subsequent study specifically related to airway closure.¹¹

Airway closure can occur in healthy adult subjects, children born prematurely, and aging adults.^{12, 13} An airway may close near the end of expiration when its diameter is small. The critical lung volume at which closure occurs is called the closing volume. The single-breath nitrogen washout test, one component of a standard pulmonary function test, is often used to measure the occurrence of airway closure. When this test shows the early stages of airway closure, it is often interpreted that the ventilation distribution is inhomogeneous within the lung, which may be caused by a number of normal and pathological conditions.^{14, 15} It is known that naturally occurring surfactants in the lung are found in the airway fluid and reduce the surface tension to approximately 20 dynes∕cm,¹⁶ much lower than the normal air-water value of about 70 dynes∕cm. The experimental studies in Liu et al.¹⁷ of a model airway showed that adding surfactant prevented liquid plug formation and allowed air flow to pass.

A plugged airway at the end of expiration can be reopened during inspiration as incoming air flow pushes the liquid plug downstream and the airway diameter increases. Once the plug ruptures, air flow is re-established and gas exchange may continue. However, there are clinical situations such as asthma, emphysema, and cystic fibrosis where the liquid contains large amounts of abnormal mucus whose non-Newtonian properties, such as shear-dependent viscosity, yield stress and viscoelasticity can prevent the closed airway from reopening. This can lead to serious and sometimes fatal results.¹⁸

There have been many fluid mechanical models of the statics and dynamics of airway closure.^{11, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29} Hammond³⁰ was one of the first to formulate a model to study the stability of an annular thin liquid film coating a rigid tube with circular cross section assuming a passive air-core phase. He found that waves initially amplified but eventually saturated into almost disconnected liquid collars. By including a more accurate approximation for the interfacial curvature in Hammond’s model, Gauglitz and Radke³¹ established that if the ratio of film thickness to tube radius, ε, exceeds a certain threshold, ε_c≈0.12, liquid plug formation can occur. This value is related to the critical liquid volume¹⁰ mentioned above. More recently Halpern and Grotberg²⁷ showed that the stress generated by an oscillatory core flow could have a stabilizing effect and increase ε_c.

In this paper we focus our attention on the role of mucus alone, and examine the stability of a single viscoelastic fluid layer coating the inner surface of a rigid tube with circular cross section. We use the Oldroyd-B model to describe the viscoelastic properties of the fluid occupying the annular region. Shear thinning will not be included in the current model. We also consider simpler constitutive equations such as the Maxwell and Jeffreys models. The air-core phase is assumed to be passive. The governing equations are given in Sec. 2 of the paper. In Sec. 3, lubrication theory is used to approximate the governing equations. We first consider the weakly viscoelastic limit and carry out a regular perturbation analysis similar to that employed in Ref. 32 for small Weissenberg numbers We. At leading order, the Newtonian case, which has been previously studied, is obtained. We also investigate the evolution of the air-liquid interface for larger values of We but use the Jeffreys model instead of the Oldroyd-B model. An algebraic-differential equation is derived for the position of the interface using an approach that is similar to that used to investigate the rupture of a viscoelastic liquid layer on a solid substrate.^{33, 34} The main difference between the Oldroyd-B and the Jeffreys models is that the Jeffreys model does not include nonlinear upper convective terms representing the advection and rotation of the stress tensor. A linear stability analysis, described in Sec. 4, is used to determine the initial growth rate of the air-liquid interface when it is perturbed by a small amplitude wave. Numerical results obtained by solving the nonlinear evolution equations are given in Sec. 5 for the Oldroyd-B and linear viscoelastic models. Application of the current model to airway closure is discussed in Sec. 6, and some conclusions appear in Sec. 7.

GOVERNING EQUATIONS

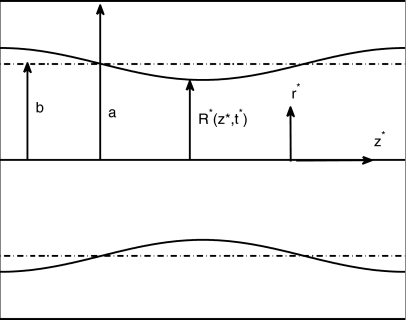
In this section, we provide the basic equations of motion and the boundary conditions for a model of airway closure in which the film consists of a single layer. We consider an axisymmetric configuration in a tube of radius a containing two immiscible fluids, the core fluid being air and occupying the region 0≤r^*≤b and the other being an annular layerb≤r^*≤a of non-Newtonian fluid coating the inner surface of the tube, as shown in Fig. 1. The air-core phase is assumed to be passive. The interface is perturbed from its equilibrium position, r^*=b, so that it is located at r^*=R^*(z^*,t^*), where (r^*,θ,z^*) are the usual cylindrical coordinates and t^* is time. The velocity in the film layer is defined by u^*=(u^*,0,w^*), where u^* and w^* are the radial and axial components of velocity, the stress tensor is given by T^*=−p^*I+τ^* where p^* is the fluid pressure, and τ^* is the deviatoric component of the stress tensor, which is defined below.

Figure 1.

Variables describing geometry of the air-liquid interface: r^*=a is the tube radius, r^*=b is the unperturbed location of the air-liquid interface, and r^*=R^*(z^*,t^*) denotes the perturbed position of the interface at time t^*.

The liquid film continuity and momentum equations are

$${\nabla }^{\ast }\cdot {\mathbf{u}}^{\ast }=0,\rho \left(\frac{\partial {\mathbf{u}}^{\ast }}{\partial t^{\ast }}+\left({\mathbf{u}}^{\ast }\cdot {\nabla }^{\ast }\right){\mathbf{u}}^{\ast }\right)=-{\nabla }^{\ast }{p}^{\ast }+{\nabla }^{\ast }\cdot {\mathbf{\tau }}^{\ast }.$$ (1)

The Oldroyd-B model is used to describe the viscoelastic character of the liquid film. It assumes a diluted concentration of a polymer in a Newtonian solvent. A typical polymer chain is modeled as a linear elastic dumbbell, and with the aid of kinetic theory a constitutive equation can be derived to describe polymeric stresses.³⁵ The stress tensor τ^* is written as the sum of a Newtonian contribution connected with the solvent and a contribution S^* due to the polymer,

$${\mathbf{\tau }}^{\ast }={\mu }_s^{\ast }\left({\nabla }^{\ast }{\mathbf{u}}^{\ast }+{\left({\nabla }^{\ast }{\mathbf{u}}^{\ast }\right)}^T\right)+{\mathbf{S}}^{\ast },$$ (2)

where ${\mu }_s^{*}$ is the solvent viscosity. The tensor S^* satisfies the following equation:

$$\Lambda \left(\frac{\partial {\mathbf{S}}^{\ast }}{\partial t}+\left({\mathbf{u}}^{\ast }\cdot {\nabla }^{\ast }\right){\mathbf{S}}^{\ast }-\left({\nabla }^{\ast }{\mathbf{u}}^{\ast }\right)\cdot {\mathbf{S}}^{\ast }-{\mathbf{S}}^{\ast }\cdot {\left({\nabla }^{\ast }{\mathbf{u}}^{\ast }\right)}^T\right)+{\mathbf{S}}^{\ast }={\mu }_p^{\ast }\left[\left({\nabla }^{\ast }{\mathbf{u}}^{\ast }\right)+{\left({\nabla }^{\ast }{\mathbf{u}}^{\ast }\right)}^T\right],$$ (3)

where Λ is a characteristic relaxation time and ${\mu }_p^{*}$ is the viscosity of the polymer. The above equations are solved subject to the boundary conditions described below. At the tube wall no-slip and penetration conditions are applied, so that

$${\mathbf{u}}^{\ast }{|}_{r^{\ast }=a}=\mathbf{0}.$$ (4)

The stress and kinematic boundary conditions at the air-liquid interface are given by

$$-p^{\ast }\mathbf{n}+{\mathbf{\tau }}^{\ast }\cdot \mathbf{n}=-p_{\text{air}}^{\ast }\mathbf{n}+\sigma {\kappa }^{\ast }\mathbf{n},$$ (5)

$$\left({\mathbf{u}}^{\ast }-{\dot{\mathbf{X}}}^{\ast }\right)\cdot \mathbf{n}=0,$$

where $p_{\text{air}}^{*}$ is the pressure of the air phase, which is assumed to be constant, $\mathbf{n}={\left(1+R_{z^{*}}^{*2}\right)}^{-1∕2}\left(1,0,-R_{z^{*}}^{*}\right)$ is the unit normal vector pointing into the liquid film, κ^*=∇^*⋅n is the curvature of the interface, σ is the surface tension, which is assumed to be constant, and X^*=⟨R^*(z^*,t^*),θ,z^*⟩ is a position vector defining the location of the air-liquid interface. Periodic boundary conditions are imposed at z^*=0,L^*, the tube ends,

$${\mathbf{u}}^{\ast }{|}_{z^{\ast }=0}={\mathbf{u}}^{\ast }{|}_{z^{\ast }=L^{\ast }},{\nabla }^{\ast }{p}^{\ast }{|}_{z^{\ast }=0}={\nabla }^{\ast }{p}^{\ast }{|}_{z^{\ast }=L^{\ast }},$$ (6)

$$R^{\ast }{|}_{z^{\ast }=0}=R^{\ast }{|}_{z^{\ast }=L^{\ast }}.$$

LUBRICATION THEORY

In this section, lubrication theory is used to derive a system of simplified differential equations that describe the evolution of the air-liquid interface by assuming that the film thickness parameter ε=(a−b)∕a is small. Previous Newtonian models that predict plug formation^{20, 36} introduced a local radial coordinate y=(a−r^*)∕ε and retained the leading order terms in ε in the momentum and continuity equations and boundary conditions but with two important exceptions. The curvature κ^* was not expanded in powers of ε in the normal stress condition. In particular, the 1∕R^* dependency in the transverse component of curvature was kept in the evolution equation. Also, the axisymmetric form of the kinematic boundary condition was used as opposed to the planar form, which is obtained at leading order in ε. In this paper, we do not replace the terms containing r^* with the local coordinate y that appear in the governing equations and boundary conditions. The justification for doing this will be briefly discussed later in the validation Sec. 5A.

The governing equations and boundary conditions are nondimensionalized as follows:

$$r=\frac{r^{\ast }}{a},z=\frac{z^{\ast }}{a},R=\frac{R^{\ast }}{a},p=\frac{p^{\ast }}{\epsilon \sigma ∕a},$$ (7)

$$w=\frac{w^{\ast }}{U_{\text{cap}}},u=\frac{u^{\ast }}{\epsilon U_{\text{cap}}},t=\frac{t^{\ast }}{a∕U_{\text{cap}}},$$

$${\tau }_{zr}=\frac{{\tau }_{zr}^{\ast }}{{\epsilon }^2\sigma ∕a},{\tau }_{zz}=\frac{{\tau }_{zz}^{\ast }}{\epsilon \sigma ∕a},{\tau }_{rr}=\frac{{\tau }_{rr}^{\ast }}{{\epsilon }^3\sigma ∕a},{\tau }_{\theta \theta }=\frac{{\tau }_{\theta \theta }^{\ast }}{{\epsilon }^3\sigma ∕a},$$

$$S_{zr}=\frac{S_{zr}^{\ast }}{{\epsilon }^2\sigma ∕a},S_{zz}=\frac{S_{zz}^{\ast }}{\epsilon \sigma ∕a},S_{rr}=\frac{S_{rr}^{\ast }}{{\epsilon }^3\sigma ∕a},S_{\theta \theta }=\frac{S_{\theta \theta }^{\ast }}{{\epsilon }^3\sigma ∕a},$$

where U_cap=ε³σ∕μ^* is a capillary velocity scale and${\mu }^{*}={\mu }_p^{*}+{\mu }_s^{*}$ is the total viscosity. To leading order in ε, the momentum and continuity equations are given by

$$\frac{\partial p}{\partial z}=\frac{1}{r}\frac{\partial }{\partial r}\left[r\left(\epsilon S_{rz}+{\epsilon }^2{\mu }_r\frac{\partial w}{\partial r}\right)\right]+\frac{\partial S_{zz}}{\partial z},\frac{\partial p}{\partial r}=0,$$ (8)

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r\epsilon u\right)+\frac{\partial w}{\partial z}=0,$$

where ${\mu }_s={\mu }_s^{*}∕{\mu }^{*}$. The constitutive Eq. 3 become

$$We\left(\frac{\partial S_{zr}}{\partial t}+w\frac{\partial S_{zr}}{\partial z}+\epsilon u\frac{\partial S_{zr}}{\partial r}-\epsilon \frac{\partial w}{\partial r}{S}_{rr}-\frac{\partial w}{\partial z}{S}_{zr}-\epsilon \frac{\partial u}{\partial r}{S}_{zr}-\frac{\partial u}{\partial z}{S}_{zz}\right)+S_{zr}=\epsilon {\mu }_p\frac{\partial w}{\partial r},$$ (9)

$$We\left(\frac{\partial S_{zz}}{\partial t}+w\frac{\partial S_{zz}}{\partial z}+\epsilon u\frac{\partial S_{zz}}{\partial r}-2\epsilon \frac{\partial w}{\partial r}{S}_{zr}-2\frac{\partial w}{\partial z}{S}_{zz}\right)+S_{zz}=0,$$

$$We\left(\frac{\partial S_{rr}}{\partial t}+w\frac{\partial S_{rr}}{\partial z}+\epsilon u\frac{\partial S_{rr}}{\partial r}-2\epsilon \frac{\partial u}{\partial r}{S}_{rr}-2\frac{\partial u}{\partial z}{S}_{zr}\right)+S_{rr}=2\epsilon {\mu }_p\frac{\partial u}{\partial r},$$

where We=ΛU_cap∕a is the Weissenberg number and${\mu }_p={\mu }_p^{*}∕{\mu }^{*}$. The equation for S_θθ is not given since it is not required for the models considered in Secs. 3A, 3B. The tangential and normal stress boundary conditions 5 are given by the following expressions:

$$\left(1-{\left(\frac{\partial R}{\partial z}\right)}^2\right)\left(\epsilon S_{zr}+{\epsilon }^2{\mu }_s\frac{\partial w}{\partial r}\right)=\frac{\partial R}{\partial z}{S}_{zz},$$ (10)

$$\epsilon p=\frac{\frac{{\partial }^{2}R}{\partial z^2}}{{\left(1+{\left(\frac{\partial R}{\partial z}\right)}^2\right)}^{3∕2}}-\frac{1}{R{\left(1+{\left(\frac{\partial R}{\partial z}\right)}^2\right)}^{1∕2}}+\frac{1}{\left(1-\epsilon \right)}.$$

The kinematic boundary condition 5 can be written as

$$\frac{\partial R}{\partial t}=\frac{1}{R}\frac{\partial Q}{\partial z},$$ (11)

where $Q={\int }_R^{1}wrdr$ is the axial flow rate in the film layer.

Small Weissenberg limit

In this section, we consider a weakly viscoelastic fluid, and assume that We⪡1. A regular perturbation scheme is used where all the dependent variables are expanded in power series in We in a manner similar to Ref. 32. The leading order problem corresponds to a Newtonian film coating the tube wall. The constitutive equations yield

$$S_{zr}^{\left(0\right)}=\epsilon {\mu }_p\frac{\partial w^{\left(0\right)}}{\partial r},$$ (12)

$$S_{zz}^{\left(0\right)}=0,$$

$$S_{rr}^{\left(0\right)}=2\epsilon {\mu }_p\frac{\partial u^{\left(0\right)}}{\partial r}.$$

The first two equations of Eq. 12 are substituted into the axial momentum Eq. 8 to yield

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r{\epsilon }^2\frac{\partial w^{\left(0\right)}}{\partial r}\right)=\frac{\partial p^{\left(0\right)}}{\partial z}.$$ (13)

This is then integrated twice to yield the axial component of velocity,

$$w^{\left(0\right)}=-\frac{1}{4{\epsilon }^2}\frac{\partial p^{\left(0\right)}}{\partial z}\left(1-r^2+2R^{\left(0\right)2}\text{\hspace{0.17em}log}r\right),$$ (14)

where the stress free condition ∂w⁽⁰⁾∕∂r=0 has been applied at r=R⁽⁰⁾. The radial component of velocity is determined from the continuity equation and is given by

$$u^{\left(0\right)}=-\frac{1}{16{\epsilon }^{3}r}\frac{{\partial }^2{p}^{\left(0\right)}}{\partial z^2}\left\{1-2R^{\left(0\right)2}+r^2\left[r^2-2+2R^{\left(0\right)2}-4R^{\left(0\right)2}\text{\hspace{0.17em}log}r\right]\right\}+\frac{1}{4{\epsilon }^{3}r}\frac{\partial p^{\left(0\right)}}{\partial z}\frac{\partial R^{\left(0\right)}}{\partial z}{R}^{\left(0\right)}\left(1-r^2+2r^2\text{\hspace{0.17em}log}r\right).$$ (15)

The stress component $S_{rr}^{\left(0\right)}=2\epsilon {\mu }_p\partial u^{\left(0\right)}∕\partial r$ is thus

$$S_{rr}^{\left(0\right)}=\frac{{\mu }_p}{8{\epsilon }^2{r}^2}\frac{{\partial }^2{p}^{\left(0\right)}}{\partial z^2}\left\{1-2R^{\left(0\right)2}-r^2\left[3r^2-2-2R^{\left(0\right)2}-4R^{\left(0\right)2}\text{\hspace{0.17em}log}r\right]\right\}-\frac{{\mu }_p}{2{\epsilon }^2{r}^2}\frac{\partial p^{\left(0\right)}}{\partial z}\frac{\partial R^{\left(0\right)}}{\partial z}{R}^{\left(0\right)}\left(1-r^2-2r^2\text{\hspace{0.17em}log}r\right).$$ (16)

The leading order evolution equation for R⁽⁰⁾ is obtained by substituting w⁽⁰⁾ into the kinematic boundary condition 11, and is given by

$$\frac{\partial R^{\left(0\right)}}{\partial t}=\frac{1}{R^{\left(0\right)}}\frac{\partial Q^{\left(0\right)}}{\partial z}=-\frac{1}{16{\epsilon }^2{R}^{\left(0\right)}}\frac{\partial }{\partial z}\left\{\left[\left(1-R^{\left(0\right)2}\right)\left(1-3R^{\left(0\right)2}\right)-4R^{\left(0\right)4}\text{\hspace{0.17em}log}R\right]\frac{\partial p^{\left(0\right)}}{\partial z}\right\}.$$ (17)

The order We momentum and continuity equations are of the same form as the leading order equations. The constitutive equations at this order can be written as

$$\epsilon {\mu }_p\frac{\partial w^{\left(1\right)}}{\partial r}-S_{zr}^{\left(1\right)}=\frac{\partial S_{zr}^{\left(0\right)}}{\partial t}+w^{\left(0\right)}\frac{\partial S_{zr}^{\left(0\right)}}{\partial z}+\epsilon u^{\left(0\right)}\frac{\partial S_{zr}^{\left(0\right)}}{\partial r}-\epsilon \frac{\partial w^{\left(0\right)}}{\partial r}{S}_{rr}^{\left(0\right)}-\frac{\partial w^{\left(0\right)}}{\partial z}{S}_{zr}^{\left(0\right)}-\epsilon \frac{\partial u^{\left(0\right)}}{\partial r}{S}_{zr}^{\left(0\right)}-\frac{\partial u^{\left(0\right)}}{\partial z}{S}_{zz}^{\left(0\right)},$$ (18)

$$S_{zz}^{\left(1\right)}=2\epsilon \frac{\partial w^{\left(0\right)}}{\partial r}{S}_{zr}^{\left(0\right)},$$

$$2\epsilon {\mu }_p\frac{\partial u^{\left(1\right)}}{\partial r}-S_{rr}^{\left(1\right)}=\frac{\partial S_{rr}^{\left(0\right)}}{\partial t}+w^{\left(0\right)}\frac{\partial S_{rr}^{\left(0\right)}}{\partial z}+\epsilon u^{\left(0\right)}\frac{\partial S_{rr}^{\left(0\right)}}{\partial r}-2\epsilon \frac{\partial u^{\left(0\right)}}{\partial r}{S}_{rr}^{\left(0\right)}-2\frac{\partial u^{\left(0\right)}}{\partial z}{S}_{zr}^{\left(0\right)}.$$

The interfacial boundary conditions 10 become

$$\epsilon S_{zr}^{\left(1\right)}+{\epsilon }^2{\mu }_s\frac{\partial w^{\left(1\right)}}{\partial r}-\frac{\frac{\partial R^{\left(0\right)}}{\partial z}}{1-{\left(\frac{\partial R^{\left(0\right)}}{\partial z}\right)}^2}{S}_{zz}^{\left(1\right)}=0,$$ (19)

$$\epsilon p^{\left(1\right)}=\frac{\frac{{\partial }^2{R}^{\left(1\right)}}{\partial z^2}}{{\left(1+{\left(\frac{\partial R^{\left(0\right)}}{\partial z}\right)}^2\right)}^{3∕2}}-\frac{3\frac{{\partial }^2{R}^{\left(0\right)}}{\partial z^2}\frac{\partial R^{\left(0\right)}}{\partial z}\frac{\partial R^{\left(1\right)}}{\partial z}}{{\left(1+{\left(\frac{\partial R^{\left(0\right)}}{\partial z}\right)}^2\right)}^{5∕2}}+\frac{R^{\left(1\right)}}{R^{\left(0\right)2}{\left(1+{\left(\frac{\partial R^{\left(0\right)}}{\partial z}\right)}^2\right)}^{1∕2}}+\frac{\frac{\partial R^{\left(0\right)}}{\partial z}\frac{\partial R^{\left(1\right)}}{\partial z}}{R^{\left(0\right)}{\left(1+{\left(\frac{\partial R^{\left(0\right)}}{\partial z}\right)}^2\right)}^{3∕2}},$$

$$\frac{\partial R^{\left(1\right)}}{\partial t}=\frac{1}{R^{\left(0\right)}}\left(\frac{\partial Q^{\left(1\right)}}{\partial z}-\frac{\partial }{\partial z}\left(w_s^{\left(0\right)}{R}^{\left(0\right)}{R}^{\left(1\right)}\right)-\frac{R^{\left(1\right)}}{R^{\left(0\right)}}\frac{\partial Q^{\left(0\right)}}{\partial z}\right),$$

where $Q^{\left(1\right)}={\int }_{R^{\left(0\right)}}^1{w}^{\left(1\right)}rdr$ is the axial flow rate correction and $w_s^{\left(0\right)}$ is the surface axial component of velocity. The stress component $S_{zz}^{\left(1\right)}$ is determined from the constitutive Eq. 18,

$$S_{zz}^{\left(1\right)}=2\epsilon S_{zr}^{\left(0\right)}\frac{\partial w^{\left(0\right)}}{\partial r}=\frac{{\mu }_p}{2{\epsilon }^2}{\left(\frac{\partial p^{\left(0\right)}}{\partial z}\right)}^2{\left(r-\frac{R^{\left(0\right)2}}{r}\right)}^2.$$ (20)

$S_{zr}^{\left(1\right)}+\epsilon {\mu }_s\partial w^{\left(1\right)}∕\partial r$ is then obtained by substituting Eq. 20 into the axial momentum equation, integrating the resulting equation and applying the tangential stress condition atr=R⁽⁰⁾,

$$S_{zr}^{\left(1\right)}+\epsilon {\mu }_s\frac{\partial w^{\left(1\right)}}{\partial r}=\frac{1}{2\epsilon }\frac{\partial p^{\left(1\right)}}{\partial z}\left(r-\frac{R^{\left(0\right)2}}{r}\right)-\frac{{\mu }_p}{4{\epsilon }^3}\frac{\partial p^{\left(0\right)}}{\partial z}\frac{{\partial }^2{p}^{\left(0\right)}}{\partial z^2}\left(r^3-4R^{\left(0\right)2}r+3\frac{R^{\left(0\right)4}}{r}+4\frac{R^{\left(0\right)4}}{r}\text{log}\frac{r}{R^{\left(0\right)}}\right)+\frac{{\mu }_p}{{\epsilon }^3}{\left(\frac{\partial p^{\left(0\right)}}{\partial z}\right)}^2\frac{\partial R^{\left(0\right)}}{\partial z}{R}^{\left(0\right)}\left(r-\frac{R^{\left(0\right)2}}{r}-2\frac{R^{\left(0\right)2}}{r}\text{log}\frac{r}{R^{\left(0\right)}}\right).$$ (21)

The axial component of velocity w⁽¹⁾ is determined by integrating the constitutive equation for $S_{zr}^{\left(1\right)}$ Eq. 18,

$$w^{\left(1\right)}\left(z,r,t\right)=-\frac{1}{4{\epsilon }^2}\left[\frac{\partial p^{\left(1\right)}}{\partial z}+{\mu }_p\frac{{\partial }^2{p}^{\left(0\right)}}{\partial zdt}\right]\left[1-r^2+2R^{\left(0\right)2}\text{\hspace{0.17em}log}r\right]+\frac{{\mu }_p}{8{\epsilon }^4{r}^2}{\left[\frac{\partial p^{\left(0\right)}}{\partial z}\right]}^2\frac{\partial R^{\left(0\right)}}{\partial z}{R}^{\left(0\right)}\left\{\left(r^2-1\right)\left[r^2-R^{\left(0\right)2}\right]+6r^2\left[1-R^{\left(0\right)2}\right]\text{log}r+4R^{\left(0\right)2}{r}^2\left[4\text{\hspace{0.17em}log}{R}^{\left(0\right)}-\text{log}r\right]\text{log}r\right\}-\frac{{\mu }_p}{32{\epsilon }^4{r}^2}\frac{{\partial }^2{p}^{\left(0\right)}}{\partial z^2}\frac{\partial p^{\left(0\right)}}{\partial z}\left\{\left[R^{\left(0\right)2}-1\right]\left[2r^2-R^{\left(0\right)2}-9r^2{R}^{\left(0\right)2}+2R^{\left(0\right)4}\right]+4r^2\left[1-4R^{\left(0\right)2}+R^{\left(0\right)2}{r}^2+2R^{\left(0\right)4}\text{\hspace{0.17em}log}r+5R^{\left(0\right)4}-8R^{\left(0\right)4}\text{\hspace{0.17em}log}{R}^{\left(0\right)}\right]\text{log}r\right\}-\frac{{\mu }_p}{{\epsilon }^2}\frac{\partial p^{\left(0\right)}}{\partial z}\frac{\partial R^{\left(0\right)}}{\partial t}\text{log}r.$$ (22)

The axial flow rate $Q^{\left(1\right)}={\int }_0^Y{w}^{\left(1\right)}rdr$ is given by

$$Q^{\left(1\right)}=-\frac{1}{16{\epsilon }^2}\left[{\mu }_p\frac{{\partial }^2{p}^{\left(0\right)}}{\partial z\partial t}+\frac{\partial p^{\left(1\right)}}{\partial z}\right]\left\{\left[1-R^{\left(0\right)2}\right]\left[1-3R^{\left(0\right)2}\right]-4R^{\left(0\right)4}\text{\hspace{0.17em}log}{R}^{\left(0\right)}\right\}-\frac{{\mu }_p}{32{\epsilon }^4}{\left[\frac{\partial p^{\left(0\right)}}{\partial z}\right]}^2\frac{\partial R^{\left(0\right)}}{\partial z}{R}^{\left(0\right)}\left\{\left[R^{\left(0\right)2}-1\right]\left[R^{\left(0\right)2}-7\right]+4R^{\left(0\right)2}\left[8-5R^{\left(0\right)2}+6R^{\left(0\right)2}\text{\hspace{0.17em}log}{R}^{\left(0\right)}\right]\text{log}{R}^{\left(0\right)}\right\}+\frac{3{\mu }_p}{64{\epsilon }^4}\frac{\partial p^{\left(0\right)}}{\partial z}\frac{{\partial }^2{p}^{\left(0\right)}}{\partial z^2}\left\{\left[1-R^{\left(0\right)2}\right]\left[1-3R^{\left(0\right)2}\right]-4R^{\left(0\right)4}\text{\hspace{0.17em}log}{R}^{\left(0\right)}\right\}\left[1-R^{\left(0\right)2}+2R^{\left(0\right)2}\text{\hspace{0.17em}log}{R}^{\left(0\right)}\right]+\frac{{\mu }_p}{4{\epsilon }^2}\frac{\partial p^{\left(0\right)}}{\partial z}\frac{\partial R^{\left(0\right)}}{\partial t}\left[1-R^{\left(0\right)2}+2R^{\left(0\right)2}\text{\hspace{0.17em}log}{R}^{\left(0\right)}\right],$$ (23)

which can then be substituted into the kinematic boundary condition 19 to yield an evolution equation for R⁽¹⁾. In the results section, the Oldroyd-B model derived above will be compared with the Jeffreys based model derived in the next section for arbitrary We.

Evolution equations for arbitrary We

In this section we relax the restriction that the Weissenberg number is small, and we follow the same approach taken by Refs. ^{33, 34} by assuming that τ_zr is the dominant component of the stress tensor and neglecting the other components and by neglecting the upper convective terms of the Oldroyd-B model. The first assumption about the shear stress is based on the scalings introduced in Eq. 7, which imply that ${\tau }_{zr}^{*}⪢{\tau }_{rr}^{*}$ and ${\tau }_{zz}^{*}⪢{\tau }_{rr}^{*}$ since ε⪡1. These inequalities suggest that the streamwise normal stress and the shear stress are the most dominant components of stress. In addition, the small We analysis performed in the previous section showed that there was no contribution to S_zz at leading order. However, this does not fully justify the assumption of dropping S_zz and neglecting the upper convective terms for arbitrary We. In the case where τ_zr is assumed to be dominant, the approximate axial and radial momentum equations and the continuity equation in the film region are

$$\frac{\partial p}{\partial z}=\frac{\epsilon }{r}\frac{\partial }{\partial r}\left(r{\tau }_{zr}\right),\frac{\partial p}{\partial r}=0,\frac{\partial w}{\partial z}+\frac{\epsilon }{r}\frac{\partial }{\partial r}\left(ru\right)=0.$$ (24)

The linearized form of the constitutive Eq. 3 without the nonlinear upper convective terms is known as the Jeffreys model. For the shear component, S_zr, it is given by

$$\left(1+We\frac{\partial }{\partial t}\right)S_{zr}=\epsilon {\mu }_p\frac{\partial w}{\partial r}.$$ (25)

A constitutive equation for τ_zr can be obtained by applying the operator (1+We∂∕∂t) to τ_zr=εμ_s∂w∕∂r+S_zr and by using Eq. 25,

$$\left(1+We\frac{\partial }{\partial t}\right){\tau }_{zr}=\epsilon \left(1+{\lambda }_2\frac{\partial }{\partial t}\right)\frac{\partial w}{\partial r},$$ (26)

where λ₂=Weμ_s is known as the retardation parameter. Note that the Newtonian relationship between stress and rate of strain is recovered by setting We=0 (⇒λ₂=0) in Eq. 26. The tangential and normal stress boundary conditions are given by the following expressions:

$${\tau }_{zr}=0,$$ (27)

$$\epsilon p=\frac{\frac{{\partial }^{2}R}{\partial z^2}}{{\left(1+{\left(\frac{\partial R}{\partial z}\right)}^2\right)}^{3∕2}}-\frac{1}{R{\left(1+{\left(\frac{\partial R}{\partial z}\right)}^2\right)}^{1∕2}}+\frac{1}{\left(1-\epsilon \right)}.$$

Since the pressure is independent of r, the axial momentum Eq. 24 can be integrated to obtain the following expression for τ_zr:

$${\tau }_{zr}=\frac{1}{2\epsilon }\frac{\partial p}{\partial z}\left(r-\frac{R^2}{r}\right).$$ (28)

Note that a stress free boundary condition τ_zr=0 has been applied at r=R. An equation for the axial component of velocity is then obtained by substituting the latter into the constitutive Eq. 26 and integrating it,

$$\left(1+{\lambda }_2\frac{\partial }{\partial t}\right)w=-\frac{1}{4{\epsilon }^2}\left(1+We\frac{\partial }{\partial t}\right)\left(\frac{\partial p}{\partial z}\left(1-r^2+2R^2\text{\hspace{0.17em}log}r\right)\right).$$ (29)

The kinematic boundary condition can also be written as

$$\frac{\partial R}{\partial t}=\frac{1}{R}\frac{\partial Q}{\partial z},$$ (30)

where $Q={\int }_R^{1}wrdr$ satisfies

$$Q+{\lambda }_2\left(\frac{\partial Q}{\partial t}+R\frac{\partial R}{\partial t}{w}_s\right)=-\frac{1}{16{\epsilon }^2}\left(\frac{\partial p}{\partial z}+We\frac{{\partial }^{2}p}{\partial z\partial t}\right)\left[\left(1-R^2\right)\left(1-3R^2\right)-4R^4\text{\hspace{0.17em}log}R\right]+\frac{We}{4{\epsilon }^2}R\frac{\partial R}{\partial t}\frac{\partial p}{\partial z}\left(1-R^2+2R^2\text{\hspace{0.17em}log}R\right),$$ (31)

and w_s is the axial component of velocity evaluated at the interface r=R. We follow the approach taken in Ref. 33 to obtain an expression for w_s. {There seems to be an error in the derivation of the evolution equation for the film thickness that is used to describe the rupture of a thin liquid layer found in Appendix B of Ref. 34. They derive an equation for the surface velocity by directly substituting the surface location [equivalent to r=R(z,t) in the current paper] into Eq. 29 without taking into account that (∂w∕∂z)|_r=R(z,t)≠∂w|_r=R(z,t)∕∂z} Equation 29 is integrated with respect to t,

$$w=\frac{1}{{\lambda }_2}{\int }_{-\infty }^t{e}^{-\left(t-\widehat{t}\right)∕{\lambda }_2}\left(1+We\frac{\partial }{\partial \widehat{t}}\right)Fd\widehat{t},$$ (32)

where

$$F=-\frac{1}{4{\epsilon }^2}\frac{\partial p}{\partial z}\left(1-r^2+2R^2\text{\hspace{0.17em}log}r\right).$$

Next, Eq. 32 is integrated by parts and then evaluated at r=R,

$$w_s=-\frac{1}{4{\mu }_s{\epsilon }^2}\frac{\partial p}{\partial z}\left(1-R^2+2R^2\text{\hspace{0.17em}log}R\right)-\frac{1}{4}\left(1-\frac{1}{{\mu }_s}\right)\left(\left(1-R^2\right)\widehat{F}+2\text{\hspace{0.17em}log}R\widehat{G}\right),$$ (33)

where $\widehat{F}$ and $\widehat{G}$ satisfy

$$\widehat{F}+{\lambda }_2\frac{\partial \widehat{F}}{\partial t}=\frac{1}{{\epsilon }^2}\frac{\partial p}{\partial z},\widehat{G}+{\lambda }_2\frac{\partial \widehat{G}}{\partial t}=\frac{1}{{\epsilon }^2}{R}^2\frac{\partial p}{\partial z}.$$ (34)

In order to determine R(z,t), Eq. 30 is solved numerically subject to Eqs. 31, 33, 34.

LINEAR STABILITY ANALYSIS

A standard normal mode analysis can be used to investigate the effects of viscoelasticity using the Jeffreys model described in Sec. 3. Note that the Oldroyd-B model reduces to the Jeffreys model since the nonlinear upper-convective terms play no role since they are negligibly small when the base state is quiescent. We let

$$R=1+\epsilon \left(A{e}^{gt+ikz}-1\right),$$ (35)

where k is the wave number of a disturbance wave on the air-liquid interface, g is the growth rate, and A is a small amplitude. Equation 35 is substituted into Eqs. 30, 31, 33, 34, which are then linearized in the limit ε→0. The growth rate satisfies the following quadratic equation:

$$3{\lambda }_2{g}^2+\left(3-k^2\left(1-k^2\right)We\right)g-k^2\left(1-k^2\right)=0.$$ (36)

Solving the above equation for the unstable root yields

$$g=\frac{1}{6{\lambda }_2}\left(-\left(3-k^2\left(1-k^2\right)We\right)+\sqrt{{\left(3-k^2\left(1-k^2\right)We\right)}^2+12{\lambda }_2{k}^2\left(1-k^2\right)}\right)$$ (37)

for λ₂≠0. Figure 2 shows a plot of the growth rate versus the wave number for several values of We with the solvent viscosity μ_s=0.5. Instability occurs when g>0, that is for k in the range 0<k<1 for any We. The maximum growth rate occurs at $k=1∕\sqrt{2}$, independent of We, and increases with We, indicating that viscoelastic effects are initially destabilizing. If λ₂=0, corresponding to the simple Maxwell model, Eq. 36 only has one solution, and g is given by

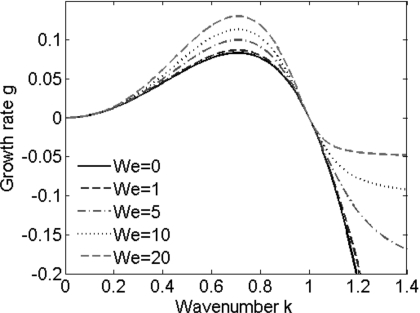
$$g=\frac{k^2\left(1-k^2\right)}{3-We{k}^2\left(1-k^2\right)}.$$ (38)

As for λ₂≠0, instability occurs if 0<k<1, but only for small We. The maximum growth rate has a value of 1∕(12−We), which becomes unbounded at We=12. Similar results have been found by Ref. 34 who investigated the instability of a thin viscoelastic film, which ruptures due to van der Waals forces. This blow up corresponding to a nonphysical singularity at finite wave number can be removed by either including inertia or by considering the retarding effect of a solvent fluid (λ₂>0).

Figure 2.

Results from normal mode analysis using the Jeffreys model with μ_s=0.5 showing how the growth rate g varies with wave number k for different values of We.

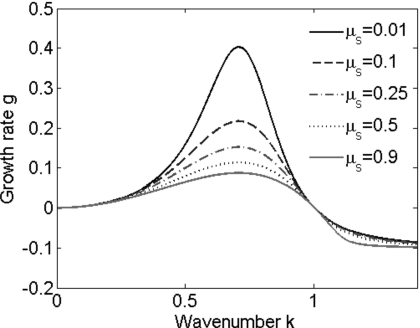
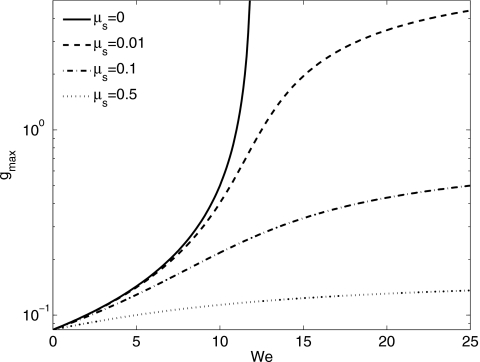
Figure 3 shows the effect of μ_r on g. For all μ_s>0,g≥0 in 0≤k≤1. As μ_s increases, the maximum growth rate, which occurs at $k=1∕\sqrt{2}$, decreases. The variation of the maximum growth with respect to We is shown in Fig. 4 for different values of μ_s.

Figure 3.

The effect of the solvent viscosity μ_s=μ₂∕We on the growth rate using the Jeffreys model, with We=15. Note that in the limit as μ_s→0 (λ₂→0), the linear Maxwell model is recovered, and for this choice of We, the growth rate is singular at k=0.526 and k=0.851.

Figure 4.

The effect of the Weissenberg number We and the ratio of solvent viscosity to total viscosity μ_s on the maximum growth rate, g_max. Note that the linear Maxwell is obtained in the limit μ_s→0, and in this case g_max is singular at We=12. For μ_s>0 and any We the maximum growth rate remains finite.

NONLINEAR STABILITY RESULTS

The linear stability analysis described in Sec. 4 is only valid at early times when the disturbances are infinitesimally small. Nonlinear terms in the evolution equations derived in Sec. 3A for the small We Oldroyd-B model and in Sec. 3B for the arbitrary We Jeffreys model equation become important once the disturbances are not so small. These equations are solved numerically on a uniform grid covering the domain 0≤z≤L. In both cases, systems of algebraic and differential equations are obtained by replacing the spatial derivatives with fourth order finite differences. These systems are then solved numerically using DASPK,^{37, 38} a large scale differential algebraic system solver, in the domain 0≤z≤L subject to periodic boundary conditions. The initially flat interface is perturbed such that the initial condition for R takes the form

$$R\left(z,0\right)=1-\epsilon \left(A\text{\hspace{0.17em}cos}\frac{2\pi z}{L}+1\right).$$ (39)

In all the computations A=0.01 and L=2^3∕2π is the most dangerous wavelength based on the linear stability theory presented in Sec. 4 for a Newtonian layer.

Validation

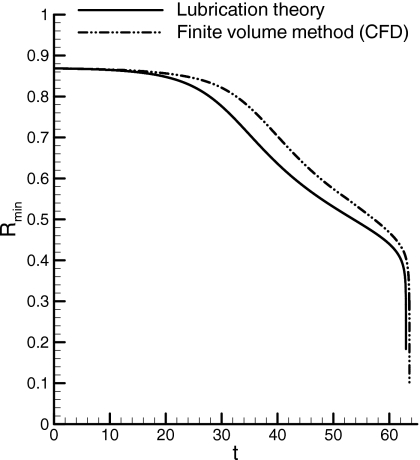
Gauglitz and Rakde³¹ showed numerically using a lubrication theory model that for the evolution of a Newtonian liquid layer, there is a critical value of ε, ε_c≈0.12, above which the liquid film breaks up, resulting in the formation of liquid plugs. We have confirmed this critical value by (i) using the lubrication theory model described in Sec. 3 and by (ii) solving numerically the Navier–Stokes and continuity equations together with the interfacial and boundary conditions 4, 5, 6 using the finite volume method. In Fig. 5 the minimum core radius R_min=R(0,t) is plotted as a function of time t for a Newtonian liquid layer with ε=0.13. As can be seen, the lubrication theory model agrees very well with the direct numerical simulation, which was obtained by solving the Navier–Stokes equations and boundary conditions using a finite volume method.³⁹ All the parameters in the finite volume simulation were the same as in the lubrication theory model except that unsteady effects were retained. The Ohnesorge number, $Oh={\mu }_s∕\sqrt{\rho \sigma a}$, the ratio of viscous forces to inertial and surface tension forces was large, equal to 10. Also, this figure shows that evolution toward liquid plug formation (R_min=0) is very fast once R_min reaches approximately 0.4 so that the closure time can be fairly accurately predicted by solving the lubrication theory model.

Figure 5.

Minimum core radius vs time for a Newtonian liquid layer with ε=0.13. Comparison between lubrication theory model and numerical solution of the Navier–Stokes equations using a finite volume method.

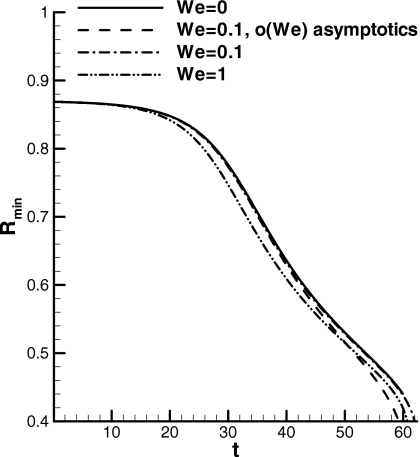
In order to validate the evolution equation based on the Jeffreys model derived in Sec. 3B, comparisons were made with the Oldroyd-B fluid model developed in Sec. 3A for small Weissenberg number. The solvent viscosity was chosen to be μ_s=0.5, based on rheological properties of biological fluids.³² As shown in Fig. 6, agreement is very good for small values of We. It is perhaps not too surprising that the two models agree when disturbances are initially small since this is when the upper-convective terms that appear in the Oldroyd-B model are negligible. Also at later times, for small We, the two models do not deviate too much from the Newtonian case. This figure also shows that R_min decreases more rapidly for We≠0, which is consistent with the linear stability results presented in the previous section.

Figure 6.

The minimum core radius R_min vs time t for a Newtonian fluid (solid line), an Oldroyd-B fluid with We=0.1 (dashed line) using the small We asymptotics of Sec. 3A, a Jeffreys fluid with We=0.1 (dash-dot line), and a Jeffreys fluid with We=1 (dash-dot-dot line). For the viscoelastic cases μ_s=0.5.

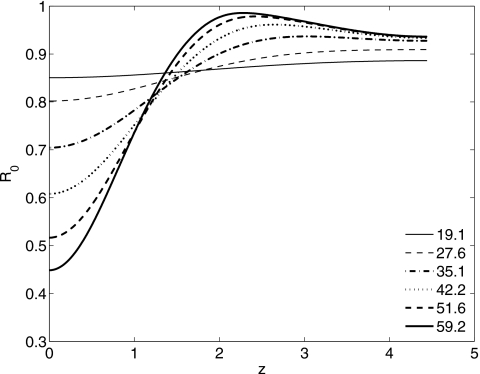
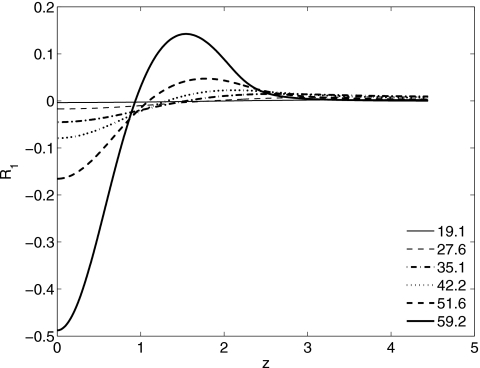
In Fig. 7, the evolution of a Newtonian liquid layer is shown, with ε=0.13, A=0.01, and L=2^3∕2π. As a result of the jump in normal stress due to surface tension, a pressure gradient is established in the liquid layer that drives flow into a growing bulge near z=0. The O(We) correction to the location of the interface R₁ is plotted in Fig. 8 at the same times as the leading order profiles shown in Fig. 7. Near the growing bulge R₁(z,t)<0, implying that the instability is more severe for a viscoelastic layer (with We≠0). By mass conservation, R₁ has to be positive in parts of the domain, implying that the viscoelastic layer thins more rapidly in places than a Newtonian layer.

Figure 7.

Evolution of a Newtonian liquid layer. The location of the air-liquid interface R(z,t) is plotted as a function of z, for 0≤z≤L∕2 at the times indicated in the figure legend. Here ε=0.13, A=0.01, L=2^3∕2π.

Figure 8.

The order We correction to the location of the air-liquid interface as a function of z at the same times as in the previous figure and for the same ε using the small We Oldroyd-B model. Here μ_s=0.5.

Nonlinear stability results for arbitrary We

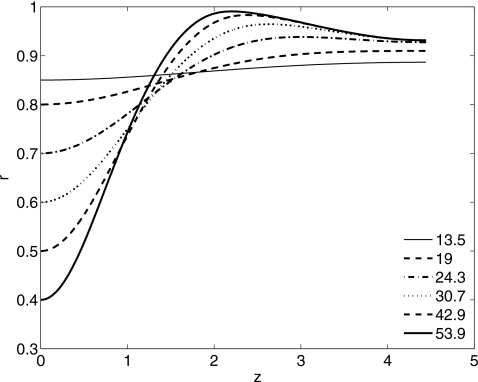
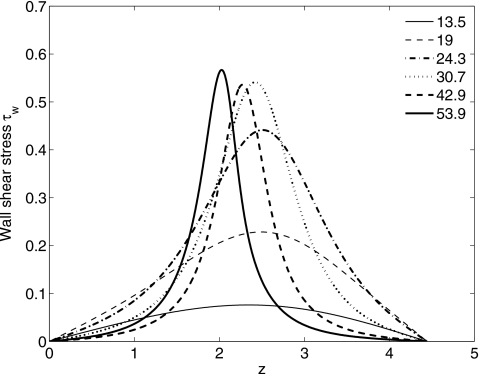
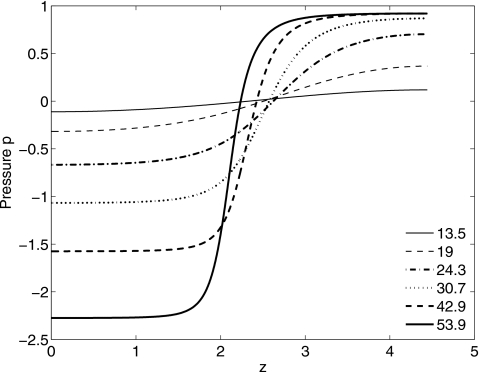
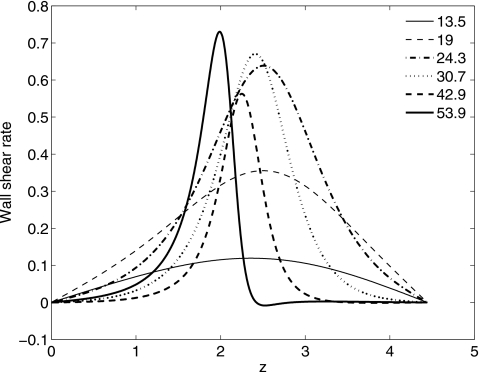
In this section, we present results for arbitrary We using the Jeffreys (λ₂≠0) models. Figure 9 shows a typical evolution of the interface for a non-Newtonian layer with ε=0.13, We=10, and μ_s=0.5. As with the small We Oldroyd-B model, a growing lobe forms near z=0 as fluid drains into it. At early times, this flow is strongly dependent on We and μ_s, and is quite slow for quite small We and∕or large μ_s (see Fig. 13 later). It is also slow once the film layer becomes very thin (but before closure occurs). The wall shear stress τ_w=τ_zr|_r=1 Eq. 28, the pressure p given by Eq. 27, and the wall shear rate ε∂w∕∂r|_r=1 are shown in Figs. 101112, respectively. The maximum τ_w and pressure gradient increase with time and occur where the film layer is thinnest. There are two constant pressure regions corresponding to two growing lobes, where the velocity must be quite small. The larger lobe eventually blocks the air-core phase. It can be inferred from Figs. 1012 that the apparent viscosity, the ratio of shear stress to shear rate, can be less than one in the bulge region, suggesting that the rate of filling of the bulge for a viscoelastic layer is faster than that of a Newtonian layer.

Figure 9.

Air liquid interface R(z,t) plotted as a function of z at different times (shown in the figure) during evolution toward closure for a Jeffreys fluid. Here ε=0.13, We=10, μ_s=0.5.

Figure 13.

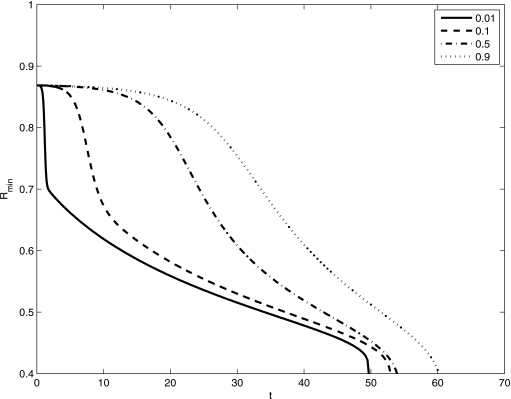
The effect of the Weissenberg number We on the minimum core radius R_min=R(0,t), for two different solvent viscosities (a) μ_s=0.5 and (b) μ_s=0.01. The film thickness parameter is ε=0.13.

Figure 10.

The wall shear stress τ_w as a function of z at different times (indicated in the figure). The parameters are the same as Fig. 9.

Figure 11.

The film pressure p vs z for the same parameter values as in the previous figure.

Figure 12.

Wall shear rate vs z for the same parameters as in Fig. 9.

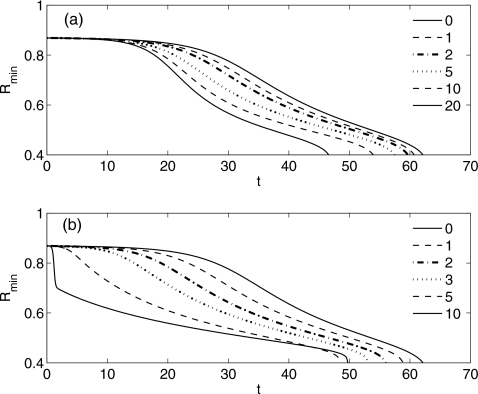
Closure, or tube occlusion, occurs if R_min=R(0,t)→0 in finite time, and this is provided there is sufficient fluid in the film layer. In Figs. 13a, 13b, R_min is plotted as a function of time for different values of We using the Jeffreys model with (a) μ_s=0.5 and (b) μ_s=0.01. The film thickness parameter is ε=0.13. (Note that the We=0 case corresponds to a Newtonian liquid layer.) These figures show that the initial growth rate increases with We, which is consistent with the linear stability results of the previous section and that R_min→0 faster as We increases. This indicates that a more viscoelastic fluid drains more quickly into the dominant growing bulge at z=0 and reaches the critical volume required for closure more quickly. The influence of μ_s on R_min is particularly noticeable for large We and small μ_s at early times as displayed in Fig. 14 for We=10 and ε=0.13. As μ_s decreases the initial growth rate increases. This is because the film reacts like a solid as opposed to a viscous fluid. At larger times, this behavior changes, and the film behaves more like a viscous fluid.

Figure 14.

The effect of solvent viscosity μ_s on R_min using the Jeffreys model derived in Sec. 3B. Here ε=0.13, We=10.

In order to examine the effect of the film thickness parameter ε on the closure time it is convenient to introduce new parameters and variables that do not depend on ε. We define a time scale T_s=aμ∕σ so that the original time scale T_cap=T_s∕ε³. The Weissenberg number We(ε)=λ∕T_cap is also dependent on ε. Therefore, when varying ε, the Weissenberg number changes in the following way:

$$We\left(\epsilon \right)=\frac{\lambda }{T_{\text{cap}}}={\left(\frac{\epsilon }{{\epsilon }_{\text{ref}}}\right)}^{3}W{e}_{\text{ref}},$$

where $W{e}_{\mathrm{ref}}=\lambda {\epsilon }_{\mathrm{ref}}^3∕T_s$. We chose ε_ref=0.12 in the results shown below.

Airway closure normally occurs toward the end of expiration since this is when ε reaches its maximum value (i.e., when the airway radius attains its minimum). Therefore, it seems reasonable to stipulate that airway closure must happen within one breath. The closure time T_c is defined to be the time taken for R_min(T_c)=0. Also, due to the periodic nature of the breathing cycle, T_c≤T_b, where T_b is the time taken for one breath. It is not possible to compute T_c exactly and the lubrication theory model breaks down once R_min becomes small. Instead we choose the following definition:

$$R_{\text{min}}\left(T_c\right)\le 0.4\text{and}{T}_c\le T_b.$$

For the time being we relax this definition and do not apply the second inequality, which specifically applies to pulmonary airway closure, and discuss its consequences in the next section.

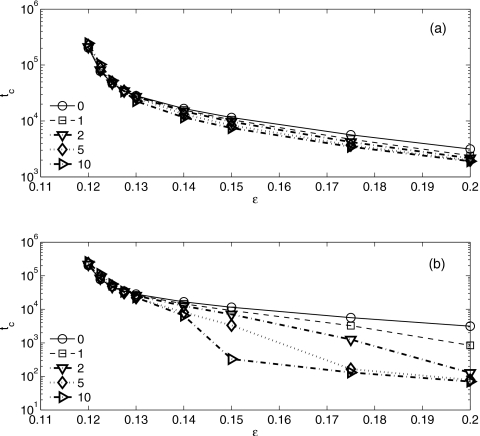
As shown earlier, direct numerical simulations of the Newtonian case reveal that the evolution toward closure is very fast once R_min reaches 0.4 for small values of ε, such as ε=0.13. This suggests that the closure time can be accurately extrapolated once R_min reaches 0.4. In Figs. 15a, 15b the closure time t_c=T_c∕ε³ is plotted as function of the film thickness parameter ε for different We_ref and μ_s. For fixed We_ref, t_c decreases with increasing ε. For small ε, t_c increases slightly with increasing We_ref, but for larger ε t_c decreases with increasing We_ref, which is consistent with the results shown in Fig. 9. For moderate ε there is a significant drop in t_c at large We_ref provided μ_s is fairly small [see Fig. 15b]. At larger ε≈0.2, even for small μ_s, t_c is not strongly dependent on We_ref, indicating the strong influence of surface tension.

Figure 15.

The influence of We and ε on the closure time t_c for two different solvent viscosities (a) μ_s=0.5 and (b) μ_s=0.01.

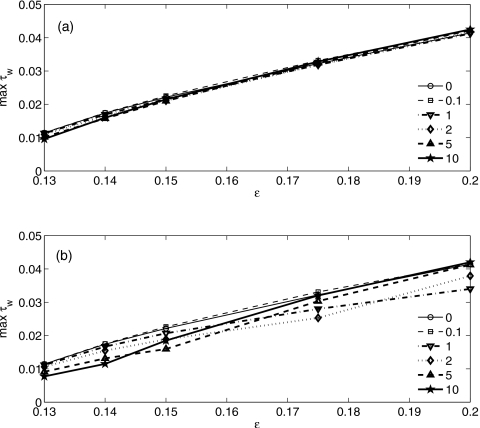
In Fig. 16 the maximum wall shear stress ${\tau }_w={\tau }_w^{*}∕\left(\sigma ∕a\right)$ evaluated when R_min reaches 0.4 is shown to increase with increasing ε. For large μ_s, We_ref has no significant effect on τ_w, as indicated by Fig. 16a. However, as shown in Fig. 16b, for small ε and μ_s τ_w decreases with increasing We_ref, but for large ε≈0.2, there is no significant difference between the Newtonian case and large We_ref≥5.

Figure 16.

Influence of the film thickness parameter ε and the Weissenberg number We_ref on the maximum wall shear stress τ_w, for two different solvent viscosities (a) μ_s=0.5 and (b) μ_s=0.01.

APPLICATION TO PULMONARY AIRWAY CLOSURE

In the results section we defined the closure time T_c such that R_min(T_c)≤0.4 and T_c≤T_b without applying the second inequality. Here we discuss its significance as it relates to airway closure. The value of T_b can vary significantly between adults and neonates. Adults typically breathe 12–16 breaths per minute while neonates breathe between 40 and 70 breaths per minute.⁴⁰ Therefore, the dimensional breath cycle ranges from 0.86 to 5 s. In order to estimate dimensional values for closure time from the values of t_c shown in Fig. 15, we also need to specify the viscosity of the liquid layer μ^*, the tube radius a, and the surface tension σ. The viscosity of mucus ranges from 100 Poise to 10 000 Poise. So it is reasonable to expect that the effective viscosity of the airway liquid is somewhat smaller due to the presence of the periciliary liquid. In a study of surfactant spreading on a viscoelastic liquid layer,³²${\mu }_s^{*}$ was chosen to be approximately 0.01 Poise and $0.01\text{Poise}\le {\mu }_p^{*}\le 100\text{Poise}$.⁴¹ The airway radius, $a_n^{*}$, which decreases with airway generation number n, can be approximated using the following formula:⁴²

$$a_n^{\ast }=a_0^{\ast }{2}^{-n∕3},$$

where $a_0^{\ast }\approx 0.45\mathrm{cm}$ is the radius of an adult trachea. We choose the surface tension to be σ=20 dynes∕cm. If we set ${\mu }_p^{*}=1\text{Poise}$ and consider airway generation 12 with $a_{12}^{*}=0.028\mathrm{cm}$, the time scale $T_s=a_{12}^{*}{\mu }^{*}∕\sigma =0.0014\mathrm{s}$. Therefore, T_b=3520 for a typical breath that lasts 5 s. According to the results presented in Fig. 15b, closure can occur for any value of We_ref provided ε≥0.18, and does not occur within 5 s if ε<0.14 for the values of We_ref that were considered. For intermediate values of ε, 0.14<ε<0.18, closure can occur provided We_ref is sufficiently large. At the other extreme, for a much less viscous polymer, say${\mu }_p^{*}=0.01\text{Poise}$, T_s≈2.8×10⁻⁵ s and T_b≈1.8×10⁵. Consequently closure can occur for most of the chosen values of ε displayed in Fig. 15a. These conclusions about closure depend on the value of T_b, which critically depends on the time for one breath, the airways radius (generation), the film viscosity, and the surface tension. A decrease in T_b has a “stabilizing” effect. This occurs if either the airway radius or the film viscosity increases, or the surface tension decreases.

The maximum wall shear stress during the closure event can also be estimated. The capillary pressure scale is $\sigma ∕a_{12}^{*}\approx 714\text{dynes}∕{\mathrm{cm}}^2$, and based on the results shown in Fig. 16, $7\text{dynes}∕{\mathrm{cm}}^2<{\tau }_w^{*}<32\text{dynes}∕{\mathrm{cm}}^2$. These levels are somewhat smaller than those that cause epithelial cell damage^{43, 44} because the computed stresses shown in Fig. 16 were evaluated when R_min=0.4. However, stress levels of this magnitude are thought to stimulate physiologic responses. For example, the major cytoskeletal components of alveolar epithelial cells can be disassembled by shear stresses of the order of 30 dynes∕cm².⁴⁵ It is also well known that biochemical and electrical signals can be induced by fluid stresses on endothelial cells. This phenomenon is known as mechanotransduction.⁴⁶

CONCLUSIONS

In this paper we investigated the stability of a viscoelastic liquid layer coating the inner surface of a rigid cylindrical tube as a simplified model of airway closure, focusing on the viscoelastic character of the liquid layer. Several different constitutive equations were used to model the viscoelastic fluid. One model used the Oldroyd-B equation, which includes upper convective terms. Combined with lubrication theory, a regular perturbation analysis for small We was carried out, from which a set of evolution equations for the film thickness were obtained. The other model that was considered used the Jeffreys constitutive equation, and did not include the nonlinear upper-convective terms. For the linear constitutive model, a system of four coupled partial differential equations was derived using lubrication theory that describes the evolution of the air-liquid interface and the axial flow rate of the film layer for arbitrary We.

A linear stability analysis was performed to investigate the initial temporal growth of a sinusoidal small amplitude perturbation. In the very early stages of growth, the Oldroyd-B and Jeffreys models behave in a similar fashion since the nonlinear upper convective terms are negligibly small. For the Jeffreys model, the system is unstable for the same range of wave numbers as a Newtonian fluid and the maximum growth rate increases with We implying that viscoelasticity is initially destabilizing. As the solvent viscosity parameter μ_s decreases the maximum growth rate increases. The linear Maxwell model is obtained in the limit as μ_s→0. For μ_s=0 and We≥12, a singularity appears, and the growth rate can become unbounded at some finite wavelength. When We⪢1, the relaxation time scale is much larger than the capillary-viscous time scale, and the response of the polymeric fluid in the film layer to an interfacial perturbation can be instantaneous like that of an elastic material (see also Ref. 34). A similar singularity was obtained by Halpern and Grotberg²⁰ who investigated the stability of a liquid-lined elastic tube with and without wall damping. The singularity disappears when the Jeffreys model is used instead of the linear Maxwell model since the effect of a solvent is included, which provides viscous damping.

The nonlinear simulations yielded several interesting results. For sufficiently small values of ε<0.119, closure does not occur within a breathing cycle $T_b^{*}$. This result seems to be unaffected by viscoelasticity, and is due to the fact that the film layer becomes exceedingly thin with time and the draining flow into larger growing bulge is very slow. For intermediate values of ε, closure time can be significantly affected by viscoelasticity. For example, from the results shown in Fig. 15b, t_c∼2×10² for We_ref=10, but t_c∼10⁴ for We_ref≈1. We also examined the influence of the film thickness parameter ε and the Weissenberg number We on the maximum shear stress evaluated at the tube wall, max(τ_w), because of its potential impact on cell damage. We found that max(τ_w) increases with ε for fixed We due to the greater destabilizing effect of surface tension and larger flows within the layer, and that it decreases with increasing We for small ε provided μ_s is sufficiently small. For large ε≈0.2, there was no significant difference between the Newtonian flow case and the large We case.

Finally, we would like to make a few concluding remarks about some of the underlying assumptions. The lubrication theory models presented in this paper will ultimately break down. This is true for a Newtonian liquid layer as well as a viscoelastic one. Once the layer becomes sufficiently thick and the flow layer sufficiently large, some of the neglected viscous, unsteady, and convective terms become important. In addition, for a viscoelastic liquid layer described by the Oldroyd-B constitutive relation, the upper convective terms will ultimately become important and have to be incorporated in order to fully understand the complete dynamics of airway closure.