Abstract
In order to maintain stable functionality in the face of continually changing input, neurones in the CNS must dynamically modulate their electrical characteristics. It has been hypothesized that in order to retain stable network function, neurones possess homeostatic mechanisms which integrate activity levels and alter network and cellular properties in such a way as to counter long-term perturbations. Here we describe a simple model system where we investigate the effects of sustained neuronal depolarization, lasting up to several days, by exposing cultures of primary hippocampal pyramidal neurones to elevated concentrations (10–30 mm) of KCl. Following exposure to KCl, neurones exhibit lower input resistances and resting potentials, and require more current to be injected to evoke action potentials. This results in a rightward shift in the frequency-input current (FI) curve which is explained by a simple linear model of the subthreshold I–V relationship. No changes are observed in action potential profiles, nor in the membrane potential at which action potentials are evoked. Furthermore, following depolarization, an increase in subthreshold potassium conductance is observed which is accounted for within a biophysical model of the subthreshold I–V characteristics of neuronal membranes. The FI curve shift was blocked by the presence of the L-type Ca2+ channel blocker nifedipine, whilst antagonism of NMDA receptors did not interfere with the effect. Finally, changes in the intrinsic properties of neurones are reversible following removal of the depolarizing stimulus. We suggest that this experimental system provides a convenient model of homeostatic regulation of intrinsic excitability, and permits the study of temporal characteristics of homeostasis and its dependence on stimulus magnitude.
The intrinsic electrical properties of neurones are fundamental to their function in the nervous system. These properties determine a cell's characteristic firing patterns and the manner in which they integrate synaptic input. As pointed out by Marder & Goaillard (2006), a typical neurone in the mammalian central nervous system (CNS) lives for a significant proportion of the animal's lifetime. During this time, numerous perturbations in electrogenic input will be imposed as a result of the normal function of the nervous system: synapses form, are eliminated and alter in strength, and afferent input and endogenous activity vary constantly as a result of external stimuli. The changes in a given cell's physiological environment are particularly pronounced during development, as its surrounding neuronal network develops and as sensory input initiates (Spitzer, 1991; Turrigiano & Nelson, 2004). Consequently, individual cells will be exposed to periods of quiescence and periods of very high activity, yet they establish and maintain stable and stereotyped behaviour. It has long been hypothesized that in order to retain stable function in a network of many cells, neurones and other excitable cells possess homeostatic mechanisms which integrate activity levels and alter network and cellular properties in such a way as to counter long-term perturbations (Turrigiano, 1999; Davis & Bezprozvanny, 2001).
Homeostatic control of mean network activity occurs via multiple mechanisms. One example results in distributed changes in synaptic strength, a phenomenon termed ‘synaptic scaling’ (Turrigiano, 1999). Synaptic scaling involves up-regulation of excitatory synaptic strength and down-regulation of inhibitory synaptic strength in response to activity deprivation (Turrigiano et al. 1998; Kilman et al. 2002). In response to elevated activity, or sustained depolarization, opposite synaptic modifications occur (Leslie et al. 2001). An alternative, non-synaptic mode of controlling mean activity on the single-cell level involves the dynamic modulation of intrinsic neuronal excitability. The host of ionic conductances expressed in neuronal membranes, including voltage-gated ion channels and passive ‘leak’ channels, together determine the integrative and excitable properties of neurones, and several studies have documented evidence for homeostatic regulation of the expression of the associated membrane conductances (Franklin et al. 1992; Turrigiano et al. 1994; Desai et al. 1999; Brickley et al. 2001; van Welie et al. 2004).
Despite existing work on activity homeostasis via modulation of intrinsic excitability, a comprehensive understanding of the phenomena and mechanisms involved is currently lacking due to the diversity of experimental preparations and modes of induction. In the present study we characterize a simple and particularly robust model of homeostatic regulation of intrinsic excitability (HRIE) using hippocampal neurones by examining the effect of chronic depolarization on the intrinsic properties of the cells over time scales of hours to weeks. In addition, we examine the degree to which the homeostatic response is proportional to the magnitude of the imposed perturbation and find that the effect is reversible once the perturbation is removed. Reversibility indicates that the effect is genuinely homeostatic in nature and not, for example, the result of accelerating a pre-determined developmental change, or of inducing a more stable LTD-like form of intrinsic plasticity. Finally, we explore a potential mechanism by which activity levels are integrated to control the homeostatic response and in doing so provide evidence that sustained calcium influx through L-type voltage-gated calcium channels provides the necessary ‘depolarization signal’ for such integration. Calcium influx-dependent HRIE has been assumed in theoretical models of homeostasis (LeMasson et al. 1993; Liu et al. 1994; Golowasch et al. 1999b) and calcium influx is known to interfere with HRIE in preparations such as the crustacean stomatogastric ganglion (Turrigiano et al. 1994; Golowasch et al. 1999a). However, neither the type of HRIE examined in this paper, nor its dependence on calcium influx through voltage-gated channels has been described in mammalian CNS neurones to date.
Methods
Cell culture
We confirm that animals were killed in accordance with current UK Home Office legislation as specified in The Animals (Scientific Procedures) Act 1986 and that our experiments comply with the policies and regulations of The Journal of Physiology as discussed by Drummond (2009). Briefly, pregnant Sprague–Dawley rats were terminally anaesthetized by exposure to halothane and then decapitated; primary hippocampal cultures were prepared from E18 embryos. Hippocampi were dissected and treated in 0.03% trypsin/EDTA for 15 min at 37°C, then gently triturated with fire-polished Pasteur pipettes. Viable cells were counted and plated at a density of 55–120 cells mm−2 on poly d-lysine/collagen-coated glass coverslips, then maintained in Neurobasal+B27 supplemented with l-glutamine, penicillin/streptomycin and 1% fetal bovine serum. Twenty-four hours after plating the medium was changed and supplemented with fresh medium. Cells were fed by replacing half of the medium with fresh medium on day(s) in vitro (DIV) 4, at which point cytosine arabinoside (5 μm) was added to prevent excessive glial cell proliferation. Cultures were maintained at 37°C, 5% CO2 in a humidified incubator.
Under our culture conditions, which employed the use of optimized Neurobasal/B27 media (Brewer et al. 1993), no difference in cell viability was evident when KCl was omitted.
Electrophysiology
Whole-cell recordings were obtained from pyramidal-like neurones using thick-walled borosillicate glass electrodes with a tip resistance of 5–8 MΩ. The internal solution contained (in mm): potassium gluconate 130, KCl 10, Hepes 10, EGTA 0.1, glucose 10, Mg-ATP 4, Na-GTP 0.5, sodium phosphocreatine 10, with pH adjusted to 7.3 with KOH. Experiments were conducted at room temperature (20–22°C) in external solution containing (in mm): NaCl 150, KCl 3, Hepes 10, MgCl2 2, CaCl2 3, glucose 10 (pH 7.3). Current-clamp recordings were performed in the presence of blockers of fast synaptic transmission: 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; 5 μm), D-2-amino-5-phosphonopentanoic (D-AP5; 50 μm) and picrotoxin (50 μm). Access resistances were <30 MΩ and only cells with stable resting membrane potentials and input resistances were included in the analysis. During experiments where accurate measurements of spike shape and voltage threshold were analysed, recordings were performed using a Multiclamp 700B amplifier (Molecular Devices, Sunnyvale, CA, USA) in bridge-balance mode with pipette capacitance fully neutralized. In other experiments, where only spike counts, resting potential and input resistance were measured, recordings were made using an Axopatch 2D or Axoclamp 200B (Molecular Devices). The liquid junction potential was measured directly and found to be +14 mV. The membrane potentials are reported without subtracting this value unless otherwise stated.
To measure frequency-input current (FI) curves, pulses of current (500 ms) in the range +5 to +300 pA were delivered in a random order at 4 s intervals and an average taken over three trials. A −10 pA pulse lasting 500 ms was included every 30 s to monitor input resistance. Recordings were digitized and analysed using custom software written in LabView (National Instruments, Austin, TX, USA).
Analysis
Rheobasic current threshold was estimated from FI curve data as the average magnitude of current injection required to elicit spikes over three trials for each cell. Voltage threshold was defined as the point of maximum curvature of the voltage waveform between the onset of stimulation and the spike maximum (Sekerli et al. 2004). Curvature for the voltage waveform as a function of time is given by:
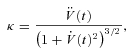 |
where dots indicate time derivatives and V is membrane potential. Statistical analyses were performed using R (http://www.r-project.org), implementing unpaired, two-way heteroscedastic t tests (with Bonferroni's correction for multiple comparisons, where appropriate) and ANOVA.
The GHK (Goldman–Hodgkin–Katz) surface plot in Fig. 5 was constructed in the following way. The GHK I–V equation was used:
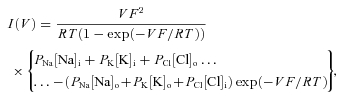 |
where I is membrane current, V is membrane potential, R is the gas constant, F is Faraday's constant, T is temperature in Kelvin, Px is the permeability of ion X, [X]o is the concentration of ion X in the external recording solution and [X]i is its intracellular concentration. Internal and external concentrations of the ionic species are assumed to be equal to the corresponding recording solutions.
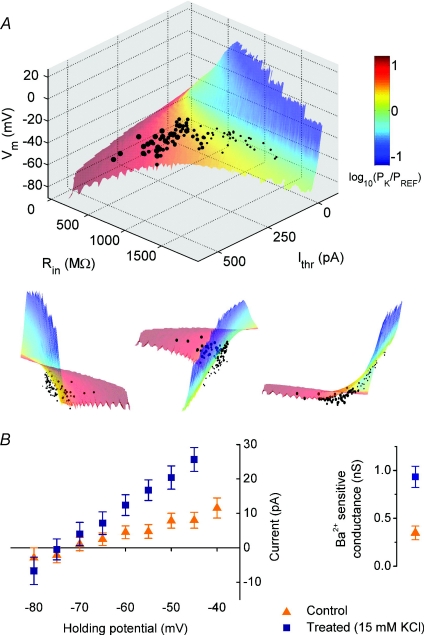
Figure 5. GHK parameter surface for Ohmic model of subthreshold membrane I–V relation.
A, an orthographic surface plot of the theoretical relation between resting membrane potential (Vm), input resistance (Rin) and rheobase (Ithr) assuming a fixed rheobasic voltage threshold of −50 mV and a linear subthreshold I–V relation determined by the Goldman–Hodgkin–Katz equation. The free parameters in the surface are the relative permeabilities of Na+, K+ and Cl− ions and the surface is colour-coded according to relative K+ permeability PK/PREF (log units) where PREF is a normalizing reference permeability. Experimental data, corrected for the liquid junction potential, are plotted with the diameter of each point corresponding to the magnitude of depolarization (i.e. KCl concentration used). Included in the plot are all data for cells grown in control medium (5 mm KCl (small circles)) and medium with final concentrations of 10 (small circles), 15 (medium circles) and 30 mm KCl (large circles) for at least 7 days. Alternative projections of the data are presented beneath the plot. B, barium sensitive leak current in control (n= 13) and treated cells (n= 12, 15 mm KCl, 8–11 days). The residual steady current at the holding potentials shown was obtained by subtracting holding currents recorded in the presence of BaCl2 (1 mm) from control currents. Slope conductance for each group was calculated by linear regression.
Each point on the surface was determined by fixing an empirically measured voltage threshold for spike initiation (Vthr) and then defining the rheobase (Ithr), resting potential (Vm) and input resistance (Rin) according to the following relationships for the GHK I–V equation:
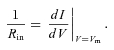 |
The surface is the result of varying each of the permeability terms (Px) in the GHK equation over a range that generates (Ithr, Rin, Vm) tuples in the region of the experimental data.
Results
Chronic depolarization causes a compensatory shift in the intrinsic excitability of cultured hippocampal neurones
In order to examine the impact of sustained depolarization on intrinsic membrane properties, an initial experiment was conducted in which hippocampal neurones were grown in media supplemented with KCl (final concentration 15 mm) from 1 day after plating onwards.
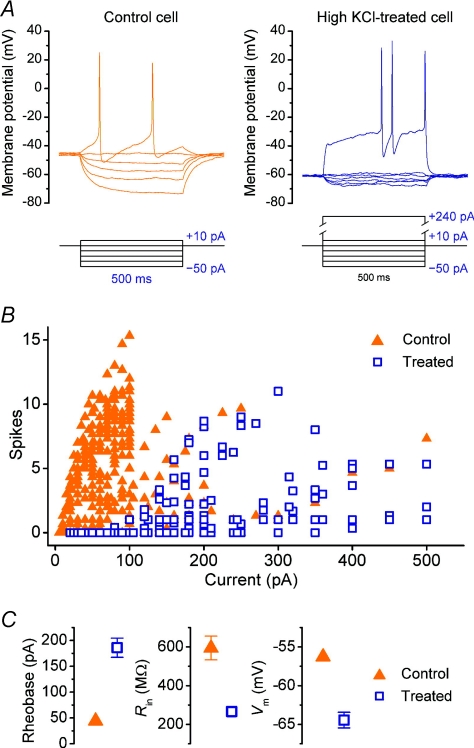
After 7–13 DIV, cells grown in high KCl medium exhibited marked differences in their intrinsic properties when compared to ‘sister’ control cells from the same culture that were grown in normal culture medium. Both groups of cells were recorded under identical conditions with external solution containing a nominally physiological extracellular potassium concentration (3 mm). As can be seen in Fig. 1, significantly more steady current was required to elicit action potentials in the chronically depolarized cells compared to control cells, exhibited by a rightward shift in the FI curve (spike rate vs. current) in the treated case, relative to control (Fig. 1B). The rheobasic current threshold (the amount of steady current required to induce spiking) was estimated to be +44.3 ± 8.4 pA for control cells and +186.0 ± 18.6 pA for treated cells (n= 38 and 20 respectively; P < 0.001, t test). This difference was accompanied by a hyperpolarizing shift in the resting membrane potential (control: −56.3 ± 0.7 mV; treated: −64.4 ± 1.0 mV; P < 0.001, t test) and a decrease in input resistance (control: 590 ± 60 MΩ; treated: 270 ± 20 MΩ; P < 0.001, t test) (Fig. 1C).
Figure 1. Chronic depolarization diminishes intrinsic excitability of hippocampal neurones.
A, current-clamp traces from a cultured hippocampal neurone grown in normal medium (left) and depolarizing medium supplemented with KCl (15 mm), recorded at 12 DIV. Current injections are delivered in 500 ms-long pulses with magnitudes as indicated underneath each trace; the maximum current injection in each plot is that required to elicit action potentials. B, the number of action potentials (spikes) elicited per 500 ms current pulse as a function of pulse amplitude for (n= 38) control cells and (n= 20) high KCl-treated cells. C, comparison of mean rheobase (or ‘current threshold’), input resistance (Rin) and resting membrane potential (Vm) of cells in panel B; error bars denote s.e.m.
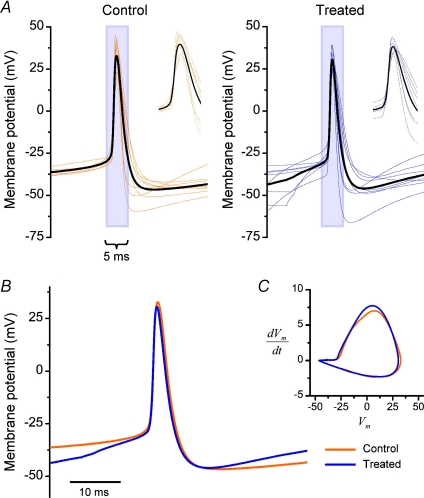
To examine whether the change in rheobasic current threshold is accompanied by changes in voltage threshold or spike shape, a subset of recordings were performed on cells with low access resistance (<10 MΩ) and with pipette capacitance compensation and bridge balance carefully adjusted to minimize errors in the voltage waveform introduced by current injection. Once again, the rheobasic current threshold was elevated in treated cells (+135 ± 30 pA, n= 8) compared to control (+28 ± 8 pA; n= 8; P < 0.05, t test) (data not shown). However, no difference in the action potential profile was exhibited between groups (Fig. 2), as quantified by the rheobasic voltage threshold (control: −25.5 ± 0.7 mV; treated: −26.7 ± 1.9 mV; P= 0.6, t test), spike width (control: 3.1 ± 0.3 ms; treated: 2.8 ± 0.3 ms; P= 0.4, t test), spike amplitude (control +34.2 ± 3.6 mV; treated: +31.4 ± 2.1 mV; P= 0.5; t test) and spike after-hyperpolarization (AHP) (control: −48.2 ± 1.9 mV; treated: −47.4 ± 3.0 mV; P= 0.8, t test).
Figure 2. Action potential waveforms: control vs. chronically depolarized cells.
A, spike-triggered averages of action potentials in control (n= 8, left) and chronically depolarized cells (n= 8, right). Each plot is the average of three action potentials evoked by minimal steady depolarization and aligned to the 0 mV-crossing times, with the bold, black trace representing the group mean for each condition. B–C, group means from A compared by aligning to the 0 mV-crossing times (B) and by plotting in phase-space (C).
An immediate question follows from these observations: how does the resting membrane potential of treated cells respond when cells are returned to a high-KCl external medium? The homeostatic principle predicts that they should depolarize to a lesser extent than naive control cells. To address this question, treated cells and age-matched sister control cells were recorded in normal ACSF before bath-applying ACSF containing 15 mm KCl acutely (see online Supplemental Fig. S1). The mean resting potential for cells in each group before application was found to be −51.5 ± 1.3 mV (control, n= 6) and −56.7 ± 1.5 mV (treated, n= 6; P < 0.05). Following KCl application the membrane potentials stabilized at −24.7 ± 1.6 mV (control) and −32.7 ± 1.4 mV (treated). Furthermore, treated cells remained capable of firing action potentials in elevated KCl, whilst control cells were placed in depolarization block. These data indicate that treated cells compensate for the depolarizing conditions, though we should stress that the conditions in which the cells are grown are somewhat different from recording conditions, so it is not possible to infer the behaviour of the membrane potential of cells undergoing prolonged depolarization whilst being incubated.
It is evident in the example membrane potential traces in both Fig. 1 and Fig. 3 that chronically depolarized cells fire action potentials at irregular intervals, in contrast to control cells which showed relatively evenly spaced action potentials during the stimulating current pulses. This distinction was commonly observed, so we quantified the degree of spiking regularity in each condition. The latency to first spike (Supplemental Fig. S2) exhibited a higher coefficient of variation among treated cells (2.02) compared to control cells (0.75). This indicates a greater degree of ‘jitter’ in the timing of the first spike at threshold in treated cells. We also quantified spike timing regularity by calculating the maximum coefficient of variation of inter-spike interval, ρ:= Max(COV(ISI)), over all stimulus intensities used in FI curve construction for each cell in each condition. When pooled, treated cells again displayed a greater degree of irregularity in their spiking, having mean ρ= 0.3 ± 0.05 (n= 9) whilst for control cells, ρ= 0.2 ± 0.02 (n= 10; P= 0.02, t test).
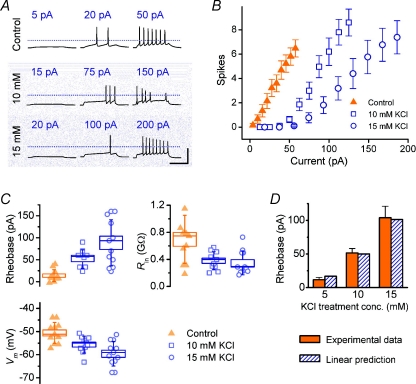
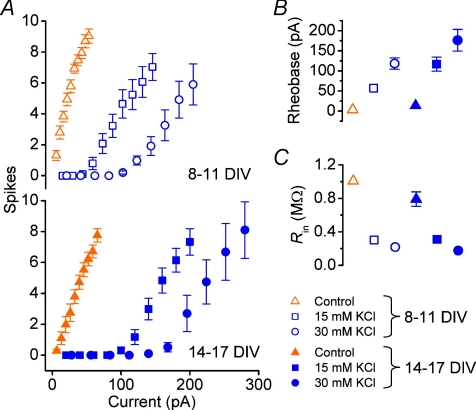
Figure 3. Concentration/depolarization magnitude dependence of KCl-induced homeostasis of intrinsic properties.
A, example current-clamp traces from cells grown in control medium and in ‘sister’ cultures grown in medium supplemented with KCl, and obtained on the same day (11 DIV) by injecting steady current at magnitudes indicated into a cell grown in control medium and cells from sister cultures grown in medium supplemented with KCl, at concentrations indicated. Scale bar = 100 mV, 250 ms; dotted lines indicate 0 mV reference. B, averaged FI curves for cells grown in KCl at two different concentrations (10 mm, n= 10; 15 mm, n= 9) with data from sister control cultures included for comparison (n= 10 cells). All recordings were performed at 8–11 DIV. C, intrinsic properties of cells in B. D, linear estimate of mean rheobase for each condition obtained by calculating the current required to reach threshold from mean resting potential using mean input resistance estimates and Ohm's law. Experimental values from C are included for comparison.
The current rheobase shift is dose dependent and accurately predicted by a change in the linear subthreshold electrical properties of the cells
A homeostatic response that acts to stabilize mean membrane potential should scale excitability in proportion to the degree of depolarization. We therefore examined whether the magnitude of the change in intrinsic properties exhibited any dose dependence with respect to the concentration of KCl used in the treatment. Three different concentrations of KCl (control = 5 mm, 10 mm and 15 mm) were used to chronically depolarize cells for 7–10 days, after which the intrinsic properties and FI curves were measured for each group (Fig. 3).
As in the previous experiment, a rightward shift in the FI curve was induced by 10 mm KCl compared to control; this shift is nearly double for 15 mm KCl, as can be seen by comparing the mean rheobase values (control: +11.7 ± 3.5 pA; 10 mm KCl: +51.5 ± 6.6 pA; 15 mm KCl: +104 ± 17 pA; Fig. 3C). Input resistance was lower in treated cells compared to control (control: 760 ± 100 MΩ; 10 mm KCl: 380 ± 40 MΩ; 15 mm KCl: 270 ± 30 MΩ) and the resting membrane potential became more hyperpolarized as KCl treatment concentration was increased (control: −50.6 ± 1.4 mV; 10 mm KCl: −55.6 ± 1.1 mV; 15 mm KCl: −59.7 ± 2.0 mV). All of the trends in these parameters were statistically significant (P < 0.01, one-way ANOVA).
To what extent do the changes in subthreshold intrinsic properties explain the accompanying changes in rheobase? A simple linear model of the subthreshold current–voltage relation gives a prediction of the rheobase as a function of input resistance and the voltage difference in resting and spike-threshold membrane potential. Using Ohm's law to relate these quantities leads to the following estimate:
where Ithr is the rheobasic current threshold, Vthr the voltage threshold, Vm the resting membrane potential and Rin the input resistance. Figure 3D compares this estimate with the experimental value for each group and demonstrates excellent agreement with the experimental values. This simple relationship suggests that the phenomenon is largely accounted for by changes in subthreshold, linear electrical properties of the cells.
The homeostatic response is co-dependent on duration and level of depolarization
The magnitude of the rheobase shift varies in proportion to the level of sustained depolarization, and may be taken as a measure of the homeostatic response. So far, this response has only been measured at a single time point. This raises the question whether, at the point of measuring the response, it has stabilized, or whether the magnitude of the response, as quantified by the rheobasic current threshold, continues to shift with prolonged depolarization. Indeed, numerous possibilities exist for the temporal characteristics of the phenomenon: it may be a discrete, step change which remains stable in spite of continuous depolarization; it may continue to exacerbate over time; or it may plateau and even diminish.
To ascertain which profile applies, we varied the duration as well as the magnitude of chronic depolarization. Cells were grown in 15 and 30 mm KCl alongside control cells and recorded at two time points, 8–11 DIV and at 14–17 DIV (Fig. 4). The higher value of 30 mm KCl was used in this experiment to ensure a large effect size, based on the assumption that the effect remains proportional to concentration over this range.
Figure 4. Co-dependence of intrinsic homeostasis on duration and magnitude KCl-induced depolarization.
A, top, pooled FI curves for cells grown for 8–11 days in control media (control, n= 11), and KCl-supplemented depolarizing medium (15 mm, n= 11 and 30 mmn= 11). Bottom, pooled FI curves for cells grown for 14–17 days in sister cultures using the same KCl concentrations (control, n= 11; 15 mm, n= 11; 30 mm, n= 10). B–C, mean rheobase current (B) and input resistance (C) of cells in A.
As anticipated, the 30 mm KCl group shows a more pronounced shift in the current threshold than the 15 mm cells. This shift grows with time: at 14–17 DIV it is approximately double the effect size at 8–11 DIV at both concentrations (+57 ± 6 pA vs.+117 ± 18 pA for 15 mm cells; +118 ± 14 pA vs.+176 ± 27 pA for 30 mm cells). Two-way ANOVA showed the dependence of rheobase on duration of depolarization and KCl concentration to be significant (P= 2.5 × 10−13 for age, P= 6.0 × 10−4 for KCl concentration). Interestingly, there was no significant interaction between the factors (P= 0.13), indicating a degree of independence between the effects of duration and magnitude of depolarization on the homeostatic response. Such independence would be anticipated for a model of homeostasis in which the magnitude of perturbation (depolarization) from a set-point (physiological resting membrane potential) is substantially larger than the capacity of the cells to compensate for the perturbation.
Evidence for altered potassium ‘leak’ conductance
Can the combined changes in the intrinsic properties, as characterized by the rheobase, resting potential and input resistance, be captured in a simple biophysical model of the linear subthreshold I–V characteristics of the membrane? Given that all cells are recorded from under the same conditions, notably the same external and internal recording solutions, and assuming that cells are effectively dialysed by the internal solution, the only way to account for the observed differences in resting membrane potential is through changes in the permeabilities of the important ionic species either side of the cell membrane, namely K+, Na+ and Cl−. When the fluxes of all ions are combined, the relative permeabilities of these ions, their intracellular and extracellular concentrations, and the resulting relationship between membrane potential and net current are related according to the Goldman–Hodgkin–Katz (GHK) equation (see Methods).
Figure 5A shows a surface plot of the theoretical relation between resting membrane potential (Vm), input resistance (Rin) and rheobase current (Ithr) assuming a fixed rheobasic voltage threshold and a linear subthreshold I–V relation determined by the GHK equation (see Methods). The voltage threshold is set to the mean of the voltage thresholds measured empirically as the mean of the maximum subthreshold voltage deflection, taking account of the liquid junction potential. This value was found to be −49.4 ± 3.0 mV (n= 94 cells, across all treatments). The surface is constructed by varying permeability terms for K+, Na+ and Cl− (see Methods). Experimental data from the preceding figures are plotted along with the surface. We must emphasize that the surface has not been ‘fitted’ to the data except for specifying the rheobasic voltage threshold, which is the sole free parameter of the model.
By shading the surface according to potassium permeability (PK), it becomes clear that the cells that have been chronically depolarized using the highest concentrations of KCl (30 mm) sit toward the region of highest relative PK values. This suggests that a shift in potassium permeability can explain the effect of depolarization on intrinsic properties. It is also evident that the experimental data points sit somewhat beneath the surface, which is to be expected because points on the surface correspond to neurones with an approximately linear (GHK) I–V relation, whereas in reality active conductances will break this linearity.
Is potassium permeability, in fact, altered in cells that have been chronically depolarized? To address this question we performed voltage-clamp recordings on treated cells (15 mm KCl, 7–10 days) in the presence and absence of BaCl2 (1 mm), which blocks a broad range of potassium channels, including several subtypes associated with ‘leak’ conductances (Coetzee et al. 1999; Patel & Honore, 2001). As can be seen in Fig. 5B, the barium-sensitive component of leak current is larger in treated cells compared to control, with the corresponding mean slope conductance for treated cells (930 ± 110 pS, n= 12) markedly greater than control (350 ± 70 pS, n= 13, P < 0.001, t test).
Temporal profile and reversibility of homeostasis
One week is a long time relative to the developmental period of the rodent brain and presumably a long time relative to sustained elevations of neural activity that may occur in the brain normally, or even during pathological states. If neurones modulate their intrinsic properties to achieve homeostasis in a physiological context, they should exhibit modulation on shorter time scales as well. The changes in excitability documented in this study so far are dramatic and the result of many days of continuous depolarization. We therefore characterized the effect of chronic depolarization over briefer periods.
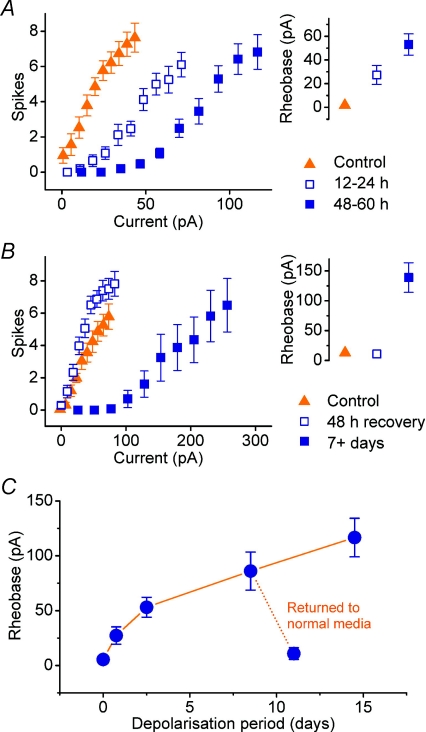
Figure 6A shows the result of depolarizing cells for shorter periods, 12–24 and 48–60 h, using 15 mm KCl in both cases. Though smaller than in previous experiments, there is again a rightward shift in the FI curve of the treated relative to the control group and in proportion to the duration of treatment. This is quantified by a difference in the current threshold between the groups: +1.8 ± 1.3 pA (control) compared with +28.9 ± 8.5 pA (12–24 h) and +52.4 ± 9.8 pA (48–60 h; P= 0.0004, one-way ANOVA). Two-tailed, Bonferroni-corrected t tests revealed statistical significance between the treated groups and control (P < 0.05 in both cases).
Figure 6. Temporal profile and reversibility of homeostatic shift in excitability.
A, pooled FI curves and mean rheobase of cells depolarized for periods over a time scale of 5 days (control, n= 10; 12–24 h bin, n= 11; 48–60 h bin, n= 11). B, pooled FI curves and mean rheobase estimates of cells that have been depolarized for 7 days then returned to control conditions for 48 h (n= 16; control, n= 13). Data from cells grown in sister cultures that were kept in depolarizing medium (KCl, 15 mm, n= 13) are plotted using filled rectangles for comparison. C, summary for all experiments of the temporal profile of the mean rheobase as a function of depolarization duration using KCl (15 mm).
In addition, the control cells in this experiment were found to be hyper-excitable, and often fired spontaneously in the absence of depolarizing current, even though fast synaptic transmission is blocked in all recordings. In these cases, a small (<10 pA), constant hyperpolarizing current was applied whilst measuring the FI curve. The amplitude of this hyperpolarizing current is subtracted from the injected current values in the FI curve assay, thus correcting the measured current threshold. This hyper-excitability is evident in the low mean current threshold in the control group for this experiment as compared to previous experiments. Such hyper-excitability was not observed in previous experiments, and might be a result of recording from the cells soon after the medium was completely replaced – a measure implemented to ensure a proper control condition for the 12–24 h-depolarized group.
By definition, a homeostatic phenomenon must exhibit reversibility in order to keep the relevant target variables within a target range; therefore, the system should revert to its original state once the perturbing stimulus is removed. Here, we would expect the intrinsic excitability of the chronically depolarized cells to return toward control levels once the depolarizing medium is replaced with normal medium.
Figure 6B shows FI curves for cells from the same cultures grown in three different conditions. The ‘recovery’ group was grown in medium containing 15 mm KCl for 7 days from 1 DIV. The medium was then completely replaced with normal culture medium for a further 60 h before recording. As a negative control, cells were grown at the same time in normal medium, which was replaced at the same time prior to recording. The positive control was provided by a group grown in 15 mm KCl-containing medium from 1 DIV, which was replenished at the same time as the other two groups.
A reversal of the effect was observed in the recovery group (n= 16), whose FI curve closely approximates the negative control (n= 13). Both the current threshold (negative control group: 13 ± 6 pA; recovery group: 11 ± 5 pA; P= 0.59, t test) and FI slope (negative control group: 0.10 ± 0.01 spikes pA−1; recovery group: 0.11 ± 0.01 spikes pA−1; P= 0.36, t test) are indistinguishable between these groups, whilst the positive control group (n= 13) exhibits the expected shift in current threshold (140 ± 20 pA; P < 0.01, Bonferroni-corrected t test).
The homeostatic response is dependent on calcium influx through nifedipine-sensitive voltage-gated calcium channels, but not NMDA receptors
Calcium influx has been identified as a likely candidate for the ‘depolarization signal’ or ‘activity signal’ in neurones (Turrigiano et al. 1994; Barish, 1998; Golowasch et al. 1999a). Moreover, depolarization-induced calcium influx is known to be involved in the regulation of ion channel expression through trafficking, translation and transcription (Barish, 1998). Voltage-gated calcium channels, especially the nifedipine-sensitive ‘L-type’ family, are a natural target for this experiment because calcium influx through these channels in particular is known to regulate gene expression via activation of CREB (cAMP response element binding protein) (Ghosh et al. 1994; Deisseroth et al. 1998; Mermelstein et al. 2000; West et al. 2001), a transcription factor that has been directly linked to the regulation of intrinsic excitability in a recent study (Dong et al. 2006).
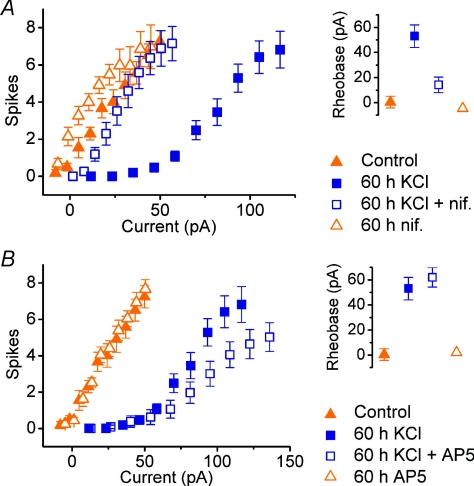
To examine the possible involvement of L-type calcium channels in HRIE, the L-type blocker nifedipine (Tsien et al. 1988) was co-applied (final concentration, 5 μm) during depolarization (KCl, 15 mm) over a period of 60 h to cells that had been grown in control conditions until 7 DIV. Figure 7A shows the resulting FI curves measured in control cells (n= 11) compared to cells grown in 15 mm KCl (n= 12), and cells grown in both 15 mm KCl and nifedipine (n= 9) for the 60 h period before recording. As part of the same experiment, a further control group was recorded from that consisted of cells that were grown in medium containing nifedipine, but no additional KCl, over the same period (n= 11).
Figure 7. Depolarization-induced intrinsic homeostasis is dependent on the activity of nifedipine-sensitive (L-type) calcium channels, but not NMDA receptors.
A, pooled FI curves and mean rheobase estimates for cells grown for 7–8 days in normal medium, then 60 h in fresh medium (control, n= 11) or medium containing 15 mm KCl (n= 12), 5 μm nifedipine (‘nif’, n= 11) or both (n= 9). B, effect of NMDA receptor antagonism. Pooled FI curves and mean rheobase estimates for cells grown for 7–8 days in normal medium, then 60 h in fresh medium (control, n= 11) or medium containing 15 mm KCl (n= 12), 50 μm D-AP5 (n= 11) or both (n= 9).
The cells that were subjected to depolarization alone exhibit a rightward shift in their FI curve. Current thresholds were +0.5 ± 4.7 pA (control), +53 ± 9 pA (15 mm KCl), +14 ± 6 pA (KCl + nifedipine) and −4.6 ± 1.6 (nifedipine). As observed in the experiments using short depolarization periods, the control cells were hyper-excitable in some cases, and for the cells treated with nifedipine this was observed in almost all cases. Again, this could be put down to the effect of changing the medium completely and recording from the cells before they have time to recover.
In addition, the cells treated with nifedipine during depolarization exhibited a much smaller shift in current threshold. Comparison with treated cells reveals a statistically significant difference in this threshold (P < 0.01, Bonferroni-corrected t test), indicating that nifedipine does indeed interfere with the expression of the homeostatic response. The difference in current threshold between control cells and cells treated with nifedipine alone was not significant (P= 0.46, t test), nor was the difference in threshold between control cells and depolarized cells that were treated with nifedipine (P= 0.06, t test).
If calcium influx does indeed provide a signal for modulating intrinsic properties within a cell, then sources other than L-type calcium channels may also be capable of initiating this response. In neurones, N-methyl-D-aspartate (NMDA) receptors are important conduits of calcium influx during synaptic activity (Mayer & Westbrook, 1987). Moreover, NMDA-dependent calcium influx is enhanced by membrane depolarization due to the relief of voltage-dependent block of the channels by magnesium (Jahr & Stevens, 1990). To see whether NMDA receptor activity influences the modulation of intrinsic excitability, an experiment similar to the previous experiment was conducted, this time using the antagonist D-AP5 (50 μm) to prevent NMDA receptor activation. In contrast to nifedipine, D-AP5 was found to have no effect on the shift in current threshold caused by depolarization (15 mm KCl for 60 h). Moreover, no alteration in intrinsic excitability was observed in cells that were incubated with D-AP5 for the same period in the absence of KCl-induced depolarization.
Figure 7B shows pooled FI curves for cells subjected to 60 h of depolarization and control cells in the presence and absence of D-AP5 (50 μM). The mean current threshold in each group was measured to be +1.0 ± 4.7 pA (control, n= 11), +53 ± 9 pA (15 mm KCl, n= 12), +62 ± 8 pA (15 mm KCl + D-AP5, n= 15) and +2.1 ± 3.6 pA (D-AP5 only). These values were not significantly different for depolarized groups (P= 0.4, t test), nor were the values for non-depolarized groups (P= 0.9).
Discussion
In this study we have presented a simple model of HRIE using primary hippocampal cultures. The use of elevated concentrations of extracellular KCl to chronically depolarize cells is a straightforward way to impose an electrochemical activity-like stimulus in neurones. Moreover, neuronal cultures offer a convenient and well-characterized model system for studying the physiological effects of this kind of manipulation. Accordingly, studies of phenomena such as synaptic scaling (Leslie et al. 2001) and the regulation of voltage-gated calcium currents (Franklin et al. 1992) and channel expression (Moulder et al. 2003) have indeed employed KCl-induced depolarization toward this end. Despite the simplicity of this manipulation, the effects of such chronic depolarization on intrinsic neuronal properties and the FI relationship have not been characterized to date. Such a characterization is important for at least two reasons: the effect constitutes a remarkably robust and versatile model for HRIE that permits the study of temporal characteristics of homeostasis and its dependence on stimulus magnitude; secondly, in a more technical vein, the work in this study highlights important side-effects that arise from using depolarizing media to promote neuronal survival in cell culture models, a practice that is common for low-density hippocampal cultures (Collins et al. 1991; Fitzsimonds et al. 1997; Moulder et al. 2003).
Biophysically, the homeostatic effect we have characterized may be relatively simple. A linear estimate of the rheobase derived from measurements of input resistance and relative voltage threshold in treated cells predicts the observed shift in rheobase accurately (Fig. 3), suggesting that a change in the passive characteristics largely accounts for the effect.
Indeed, a more detailed (GHK) model of the physical relationship between input resistance, resting potential and rheobase explains the homeostatic shift in intrinsic properties as a function of ionic permeability remarkably well. It is important to emphasize that the GHK model does not take into account active conductances such as voltage-gated sodium conductances necessary for action potential generation. In other words, the model is equivalent to an integrate-and-fire neurone with a fixed threshold, but with a subthreshold I–V relation described by the GHK relation. Despite its simplicity, the theoretical relation described by the surface in Fig. 5 provides a useful tool for interpreting the experimental data. In particular, as subthreshold potassium permeability increases, the shift in intrinsic properties predicted by the model follows that observed in cells that are exposed to increasing levels of depolarization. This purely theoretical account of the underlying change in passive membrane properties is substantiated by the observation that the Ba2+-sensitive leak conductance, which is mediated by potassium channels, is significantly greater in treated cells. Both channel density modifications and alteration of the unitary channel conductance by post-translational modification could yield such permeability changes.
Other experimental studies suggest that leak conductance is regulated in a functionally relevant way, such as to counter imbalances in inhibitory drive (Brickley et al. 2001) and to shape integrative properties of cells thought to be involved in specific information processing circuits (Garden et al. 2008). The diversity of channels responsible for mediating leak conductance and the lack of specific pharmacological agents makes a precise characterization difficult. Here we have focused our attention on leak conductance, and on a subset of (barium-sensitive) potassium conductances responsible for leak. We did, however, examine the possibility that calcium permeability might be involved (Supplemental Fig. S3), but found that broad-spectrum calcium channel blockade had no observable effect on intrinsic properties. We also examined TTX-sensitive inward currents in control and treated cells and found a reduced magnitude in the peak amplitude in treated cells (Supplemental Fig. S4). While voltage-gated sodium channels are clearly important in neuronal excitability, their inactivity in the subthreshold membrane potential range means that alterations in their expression cannot account for the coordinated shift in rheobase, resting potential and input resistance observed here. Their reduced expression may underlie the irregularity observed in repetitive spiking in treated cells, however.
Chronic depolarization was induced in cells over several different time periods from 12 h to 2 weeks. By characterizing the intrinsic excitability in terms of current threshold, we were able to map the temporal profile of the effect, shown in Fig. 6. Interestingly, the profile of the effect has a high initial rate of change which reduces to a slower, steady rate after 2 days. Two explanations may account for this. First, suppose the cells have a pre-determined ‘target’ membrane potential that they achieve by modulating their intrinsic properties, and that the rate at which these properties are altered at any given time is proportional to the discrepancy between their current membrane potential and the target membrane potential. In more quantitative terms, this process might correspond to a first order proportional controller with potassium permeability, or ‘channel density’ as the control variable and mean membrane potential as the response variable:
where PK denotes potassium permeability, V is membrane potential, Vt is some target membrane potential and α is a rate constant for the process. The angle brackets around V indicate time-averaging. In this model, a sustained KCl-induced depolarization in V would lead to a proportional increase in potassium permeability. This would, in turn, bring about a gradual repolarizaton of the membrane potential as treatment continues, leading to a reduced rate of change in potassium permeability, and a slowing in the rate of increase in rheobase. A second explanation for the slowing of the shift in rheobase over time is that the decrease in rate may be a consequence of metabolic load. The cellular resources available for homeostasis might begin to saturate after 2 days of continuous depolarization, resulting in a slowing of the change in magnitude of the effect. This might, for example, be due to limits in the number of ion channels the cells can express, or due to additional demand placed on trafficking and regulatory mechanisms involved in ion channel expression.
Such inferences must remain hypothetical until we know more about the precise composition of ionic conductances in the cells and how they are regulated. Indeed, the model presented above can only partially account for our observations. In particular, it predicts a levelling-off of the changes in intrinsic properties with time, provided the target membrane potential can be achieved in depolarizing conditions. However, two features in the experimental data suggest that this target is not achieved over the time periods and KCl concentrations investigated here. Firstly, although the plot in Fig. 6C exhibits a slowing in the rate of change of rheobase with time, a plateau is not evident (although it may be present within the error bounds). Secondly, 15 mm KCl-treated cells, when recorded in the presence of 15 mm KCl, do not have a resting membrane potential comparable to that of control cells recorded in control conditions (Supplemental Fig. S1). However, a much higher KCl concentration (30 mm) produced greater shifts in the FI curve than 15 mm KCl over the same duration (Fig. 4). Thus, while it appears that the cells do not achieve full homeostatic compensation when exposed to 15 mm KCl, this is not due to a saturation in their capacity to alter their intrinsic properties.
The changes in intrinsic properties proved to be reversible, which is a key property of homeostasis that distinguishes it from phenomena that might be better termed plastic. Plastic changes may be interpreted as those that remain relatively stable over time, a property that is important for any model of learning and memory – especially in the case of synaptic plasticity (Bliss & Collingridge, 1993; Martin et al. 2000). Homeostatic processes, by contrast, are those that continually modify the properties of a system in the face of external perturbations. In this study we found that the intrinsic excitability of chronically depolarized cells does indeed return to control levels over a period of days.
The results presented in this work prompt wider questions, for example what biochemical signalling pathways are responsible for activity-dependent ion channel expression? Theoretical and experimental work has provided some insights. Intracellular calcium is often posited as the ‘activity sensor’ in neurones which triggers the homeostatic response, and has been shown to produce realistic behaviour in computer models of homeostasis which use intracellular calcium as the state variable that governs ion channel regulation (LeMasson et al. 1993; Siegel et al. 1994; Liu et al. 1998). This hypothesis is attractive for two reasons. Firstly, intracellular calcium concentration is dependent on membrane depolarization through the action of voltage-gated calcium channels. Secondly, calcium is a ubiquitous intracellular second messenger, on which numerous enzymatic pathways depend, including ion channel gene expression (reviewed in Barish, 1998).
The shift in excitability was almost entirely blocked over the 60 h depolarization period when nifedipine was included in the culture medium, suggesting that calcium influx through L-type calcium channels is an essential component of the signalling pathway. In fact, the inclusion of nifedipine alone was capable of enhancing neuronal excitability over this time course. This may be due to the fact that basal L-type calcium influx is present in control conditions, so a further reduction in L-type activity induces the same type of changes in excitability, relative to control values.
Other work has uncovered several distinct regulatory mechanisms involved in controlling ion channel expression in an activity-dependent way, using similar models. Prolonged seizure-like excitation in organotypic hippocampal slices is known to induce compensatory changes in synaptic strength and intrinsic properties. In one study (Seeburg & Sheng, 2008) this was found to depend on the activity of a polo-like kinase. Interestingly, these kinases are important in regulating the cell cycle and are implicated in pathological states such as tumour growth in non-neuronal cells. This suggests that ion channel regulation involves fundamental biochemical pathways that are common to many cell types.
In similar experimental models, direct phosphorylation of Kv2.1 channels is observed in response to elevated, seizure-like activity in systematic studies in the hippocampi of rats in vivo and in vitro (Misonou et al. 2004, 2006). This initial response is accompanied by corresponding changes in membrane conductance density and in the surface expression pattern of subunits, revealed by whole-cell recordings and immunocytochemistry. In Drosophila, direct regulation of sodium channel subunit mRNA translation via the action of a translational repressor, pumillo, has been demonstrated to both enhance and reduce excitability when excitatory synaptic transmission is, respectively, blocked and facilitated (Mee et al. 2004).
Although the techniques employed in this study are purely electrophysiological, the model system we have chosen should be particularly attractive to investigators who are interested in profiling genes and proteins involved in homeostasis, and HRIE in particular. We hold this view for several reasons: the effect is highly reproducible and easy to manipulate; the cell culture system is well-characterized; and, most importantly, the constituent cells are readily accessible to biochemical techniques such as protein level quantification, immunocytochemistry and gene expression analysis.
The importance of understanding activity homeostasis reaches beyond fundamental cellular physiology. Owing to its role in shaping neural activity, deficits in the underlying mechanisms responsible for this kind of homeostasis may contribute to pathological conditions associated with hyper-excitability (such as epilepsy), or its converse (such as cortical spreading depression). Conversely, homeostatic responses to perturbations in the physiological environment brought about by acute trauma or disruption of normal metabolism may contribute to the aetiology of lasting damage to the affected system (Galvan et al. 2000; Howard et al. 2007; Beck & Yaari, 2008, review). Outside of the context of pathology, the presence of a homeostatic control of network activity has been shown to enhance the stability of network behaviour and interact with synaptic plasticity mechanisms to facilitate information processing in neural circuits, both theoretically (Triesch, 2007) and experimentally (Aizenman et al. 2003).
In conclusion, the system and the phenomena presented in this study constitute a previously uncharacterized and exceptionally robust and simple model of HRIE. Using the model, we have dissected important features of the homeostatic response, namely its temporal characteristics, proportionality, reversibility and dependence on calcium channel activity. Future work will be able to exploit this model to investigate further the ion channels and signalling pathways that participate in this kind of homeostasis.
Acknowledgments
This work was supported by the EPSRC and MRC funded Doctoral Training Centre in Neuroinformatics and Computational Neuroscience at the University of Edinburgh. We thank Matthew Nolan for constructive criticisms on an earlier draft of this manuscript.
Glossary
Abbreviations
- ACSF
artificial cerebrospinal fluid
- AHP
afterhyperpolarization
- DIV
days in vitro
- FI
frequency-input current
- GHK
Goldman–Hodgkin–Katz
- HRIE
homeostatic regulation of intrinsic excitability
- ISI
interspike interval
- LTD
long-term depression
Author contributions
T.O’L. conceived the project, designed, carried out and analysed the experiments, and wrote the manuscript. M.C.W.vR. and D.J.A.W. designed experiments, provided advice and suggestions for experiments and analysis and revised the manuscript. All authors read and approved the final version of the manuscript. All experiments were carried out in D.J.A.W.'s laboratory in the Centre for Integrative Physiology at The University of Edinburgh.
Supplemental material
Figure S1. Bath-applied KCl: control and treated cells.
(Top) example recordings of cells in current-clamp showing the effect of acute bath application of 15 mM KCl after a baseline period in external solution containing 5.4 mM KCl. These KCl concentrations are chosen to match those in the culture media during incubation. Both cells are recorded at 11 DIV. (Bottom) quantification of the average membrane potential of 6 cells (8-11 DIV) in each condition, averaged at 5-second intervals. The final membrane potential for each group is -24.7 ± 1.6 mV (control) and -32.3 ± 1.7 mV (15 mM KCl treated cells, p < 0.01).
Figure S2. First spike latency and mean inter-spike-interval (ISI) measures in control and treated cells
(Top) inverse spike latency, defined as the reciprocal of the time delay (in ms) to first spike from the onset of stimulation, or zero if the cell does not spike. All recordings were performed at 8-11 DIV. (Bottom) reciprocal mean inter-spike-interval for spike trains comprising two or more action potentials, set to zero otherwise.
Figure S3. Effect of calcium conductance blockade on intrinsic properties of control cells
Pooled FI curves for control cells (n = 11) recorded in the absence and presence of 200 μM CdCl2, with mean rheobase current threshold (right) and input resistance estimates (far right).
Figure S4. TTX-sensitive inward currents in treated and control cells
(Top) Example inward current traces for a treated and control cell step-depolarized in voltage-clamp from a holding potential of -80 mV to -30 mV in the presence and absence of TTX (1 μM). The traces shown are the result of subtracting membrane current recorded in the presence of TTX from that recorded in its absence in the same cell. (Bottom left) mean of the peak inward TTX-sensitive current in control (n = 15) and treated (n = 17) cells recorded at 8-11 DIV. Maximum values (at a step potential of -30 mV) are significantly different between conditions: -3777 ± 321 pA for control and -1537 ± 190 pA for treated cells, (p = 2×10−5, t-test). (Bottom right) current amplitude normalised to cell capacitance. Peak density amplitudes are also significantly different between groups (p = 3.5×10−3, t-test). Mean access resistance values for both groups were not statistically significantly different (control: 21.5 ± 1.4 MΩ, treated: 21.7 ± 1.6 MΩ; p = 0.9, t-test).
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors
References
- Aizenman CD, Akerman CJ, Jensen KR, Cline HT. Visually driven regulation of intrinsic neuronal excitability improves stimulus detection in vivo. Neuron. 2003;39:831–842. doi: 10.1016/s0896-6273(03)00527-0. [DOI] [PubMed] [Google Scholar]
- Barish ME. Intracellular calcium regulation of channel and receptor expression in the plasmalemma: potential sites of sensitivity along the pathways linking transcription, translation, and insertion. J Neurobiol. 1998;37:146–157. [PubMed] [Google Scholar]
- Beck H, Yaari Y. Plasticity of intrinsic neuronal properties in CNS disorders. Nat Rev. 2008;9:357–369. doi: 10.1038/nrn2371. [DOI] [PubMed] [Google Scholar]
- Bliss TV, Collingridge GL. A synaptic model of memory: long-term potentiation in the hippocampus. Nature. 1993;361:31–39. doi: 10.1038/361031a0. [DOI] [PubMed] [Google Scholar]
- Brewer GJ, Torricelli JR, Evege EK, Price PJ. Optimized survival of hippocampal neurons in B27-supplemented Neurobasal, a new serum-free medium combination. J Neurosci Res. 1993;35:567–576. doi: 10.1002/jnr.490350513. [DOI] [PubMed] [Google Scholar]
- Brickley SG, Revilla V, Cull-Candy SG, Wisden W, Farrant M. Adaptive regulation of neuronal excitability by a voltage-independent potassium conductance. Nature. 2001;409:88–92. doi: 10.1038/35051086. [DOI] [PubMed] [Google Scholar]
- Coetzee WA, Amarillo Y, Chiu J, Chow A, Lau D, McCormack T, Moreno H, Nadal MS, Ozaita A, Pountney D, Saganich M, Vega-Saenz de Miera E, Rudy B. Molecular diversity of K+ channels. Ann N Y Acad Sci. 1999;868:233–285. doi: 10.1111/j.1749-6632.1999.tb11293.x. [DOI] [PubMed] [Google Scholar]
- Collins F, Schmidt MF, Guthrie PB, Kater SB. Sustained increase in intracellular calcium promotes neuronal survival. J Neurosci. 1991;11:2582–2587. doi: 10.1523/JNEUROSCI.11-08-02582.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis GW, Bezprozvanny I. Maintaining the stability of neural function: a homeostatic hypothesis. Annu Rev Physiol. 2001;63:847–869. doi: 10.1146/annurev.physiol.63.1.847. [DOI] [PubMed] [Google Scholar]
- Deisseroth K, Heist EK, Tsien RW. Translocation of calmodulin to the nucleus supports CREB phosphorylation in hippocampal neurons. Nature. 1998;392:198–202. doi: 10.1038/32448. [DOI] [PubMed] [Google Scholar]
- Desai NS, Rutherford LC, Turrigiano GG. Plasticity in the intrinsic excitability of cortical pyramidal neurons. Nat Neurosci. 1999;2:515–520. doi: 10.1038/9165. [DOI] [PubMed] [Google Scholar]
- Dong Y, Green T, Saal D, Marie H, Neve R, Nestler EJ, Malenka RC. CREB modulates excitability of nucleus accumbens neurons. Nat Neurosci. 2006;9:475–477. doi: 10.1038/nn1661. [DOI] [PubMed] [Google Scholar]
- Drummond GB. Reporting ethical matters in The Journal of Physiology: standards and advice. J Physiol. 2009;587:713–719. doi: 10.1113/jphysiol.2008.167387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzsimonds RM, Song HJ, Poo MM. Propagation of activity-dependent synaptic depression in simple neural networks. Nature. 1997;388:439–448. doi: 10.1038/41267. [DOI] [PubMed] [Google Scholar]
- Franklin JL, Fickbohm DJ, Willard AL. Long-term regulation of neuronal calcium currents by prolonged changes of membrane potential. J Neurosci. 1992;12:1726–1735. doi: 10.1523/JNEUROSCI.12-05-01726.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galvan CD, Hrachovy RA, Smith KL, Swann JW. Blockade of neuronal activity during hippocampal development produces a chronic focal epilepsy in the rat. J Neurosci. 2000;20:2904–2916. doi: 10.1523/JNEUROSCI.20-08-02904.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garden DL, Dodson PD, O’Donnell C, White MD, Nolan MF. Tuning of synaptic integration in the medial entorhinal cortex to the organization of grid cell firing fields. Neuron. 2008;60:875–889. doi: 10.1016/j.neuron.2008.10.044. [DOI] [PubMed] [Google Scholar]
- Ghosh A, Ginty DD, Bading H, Greenberg ME. Calcium regulation of gene expression in neuronal cells. J Neurobiol. 1994;25:294–303. doi: 10.1002/neu.480250309. [DOI] [PubMed] [Google Scholar]
- Golowasch J, Abbott LF, Marder E. Activity-dependent regulation of potassium currents in an identified neuron of the stomatogastric ganglion of the crab Cancer borealis. J Neurosci. 1999a;19:RC33. doi: 10.1523/JNEUROSCI.19-20-j0004.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Casey M, Abbott LF, Marder E. Network stability from activity-dependent regulation of neuronal conductances. Neural Comput. 1999b;11:1079–1096. doi: 10.1162/089976699300016359. [DOI] [PubMed] [Google Scholar]
- Howard AL, Neu A, Morgan RJ, Echegoyen JC, Soltesz I. Opposing modifications in intrinsic currents and synaptic inputs in post-traumatic mossy cells: evidence for single-cell homeostasis in a hyperexcitable network. J Neurophysiol. 2007;97:2394–2409. doi: 10.1152/jn.00509.2006. [DOI] [PubMed] [Google Scholar]
- Jahr CE, Stevens CF. Voltage dependence of NMDA-activated macroscopic conductances predicted by single-channel kinetics. J Neurosci. 1990;10:3178–3182. doi: 10.1523/JNEUROSCI.10-09-03178.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilman V, van Rossum MC, Turrigiano GG. Activity deprivation reduces miniature IPSC amplitude by decreasing the number of postsynaptic GABAA receptors clustered at neocortical synapses. J Neurosci. 2002;22:1328–1337. doi: 10.1523/JNEUROSCI.22-04-01328.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeMasson G, Marder E, Abbott LF. Activity-dependent regulation of conductances in model neurons. Science. 1993;259:1915–1917. doi: 10.1126/science.8456317. [DOI] [PubMed] [Google Scholar]
- Leslie KR, Nelson SB, Turrigiano GG. Postsynaptic depolarization scales quantal amplitude in cortical pyramidal neurons. J Neurosci. 2001;21:RC170. doi: 10.1523/JNEUROSCI.21-19-j0005.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Bangalore R, Rutledge A, Triggle DJ. Modulation of L-type Ca2+ channels in clonal rat pituitary cells by membrane depolarization. Mol Pharmacol. 1994;45:1198–1206. [PubMed] [Google Scholar]
- Liu Z, Golowasch J, Marder E, Abbott LF. A model neuron with activity-dependent conductances regulated by multiple calcium sensors. J Neurosci. 1998;18:2309–2320. doi: 10.1523/JNEUROSCI.18-07-02309.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Goaillard JM. Variability, compensation and homeostasis in neuron and network function. Nat Rev. 2006;7:563–574. doi: 10.1038/nrn1949. [DOI] [PubMed] [Google Scholar]
- Martin SJ, Grimwood PD, Morris RG. Synaptic plasticity and memory: an evaluation of the hypothesis. Annu Rev Neurosci. 2000;23:649–711. doi: 10.1146/annurev.neuro.23.1.649. [DOI] [PubMed] [Google Scholar]
- Mayer ML, Westbrook GL. Permeation and block of N-methyl-D-aspartic acid receptor channels by divalent cations in mouse cultured central neurones. J Physiol. 1987;394:501–527. doi: 10.1113/jphysiol.1987.sp016883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mee CJ, Pym EC, Moffat KG, Baines RA. Regulation of neuronal excitability through pumilio-dependent control of a sodium channel gene. J Neurosci. 2004;24:8695–8703. doi: 10.1523/JNEUROSCI.2282-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mermelstein PG, Bito H, Deisseroth K, Tsien RW. Critical dependence of cAMP response element-binding protein phosphorylation on L-type calcium channels supports a selective response to EPSPs in preference to action potentials. J Neurosci. 2000;20:266–273. doi: 10.1523/JNEUROSCI.20-01-00266.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misonou H, Menegola M, Mohapatra DP, Guy LK, Park KS, Trimmer JS. Bidirectional activity-dependent regulation of neuronal ion channel phosphorylation. J Neurosci. 2006;26:13505–13514. doi: 10.1523/JNEUROSCI.3970-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misonou H, Mohapatra DP, Park EW, Leung V, Zhen D, Misonou K, Anderson AE, Trimmer JS. Regulation of ion channel localization and phosphorylation by neuronal activity. Nat Neurosci. 2004;7:711–718. doi: 10.1038/nn1260. [DOI] [PubMed] [Google Scholar]
- Moulder KL, Cormier RJ, Shute AA, Zorumski CF, Mennerick S. Homeostatic effects of depolarization on Ca2+ influx, synaptic signalling, and survival. J Neurosci. 2003;23:1825–1831. doi: 10.1523/JNEUROSCI.23-05-01825.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel AJ, Honore E. Properties and modulation of mammalian 2P domain K+ channels. Trends Neurosci. 2001;24:339–346. doi: 10.1016/s0166-2236(00)01810-5. [DOI] [PubMed] [Google Scholar]
- Seeburg DP, Sheng M. Activity-induced Polo-like kinase 2 is required for homeostatic plasticity of hippocampal neurons during epileptiform activity. J Neurosci. 2008;28:6583–6591. doi: 10.1523/JNEUROSCI.1853-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekerli M, Del Negro CA, Lee RH, Butera RJ. Estimating action potential thresholds from neuronal time-series: New metrics and evaluation of methodologies. IEEE Trans Biomed Eng. 2004;51:1665–1672. doi: 10.1109/TBME.2004.827531. [DOI] [PubMed] [Google Scholar]
- Siegel M, Marder E, Abbott LF. Activity-dependent current distributions in model neurons. Proc Natl Acad Sci U S A. 1994;91:11308–11312. doi: 10.1073/pnas.91.24.11308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spitzer NC. A developmental handshake: neuronal control of ionic currents and their control of neuronal differentiation. J Neurobiol. 1991;22:659–673. doi: 10.1002/neu.480220702. [DOI] [PubMed] [Google Scholar]
- Triesch J. Synergies between intrinsic and synaptic plasticity mechanisms. Neural Comput. 2007;19:885–909. doi: 10.1162/neco.2007.19.4.885. [DOI] [PubMed] [Google Scholar]
- Tsien RW, Lipscombe D, Madison DV, Bley KR, Fox AP. Multiple types of neuronal calcium channels and their selective modulation. Trends Neurosci. 1988;11:431–438. doi: 10.1016/0166-2236(88)90194-4. [DOI] [PubMed] [Google Scholar]
- Turrigiano G, Abbott LF, Marder E. Activity-dependent changes in the intrinsic properties of cultured neurons. Science. 1994;264:974–977. doi: 10.1126/science.8178157. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG. Homeostatic plasticity in neuronal networks: the more things change, the more they stay the same. Trends Neurosci. 1999;22:221–227. doi: 10.1016/s0166-2236(98)01341-1. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG, Leslie KR, Desai NS, Rutherford LC, Nelson SB. Activity-dependent scaling of quantal amplitude in neocortical neurons. Nature. 1998;391:892–896. doi: 10.1038/36103. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG, Nelson SB. Homeostatic plasticity in the developing nervous system. Nat Rev. 2004;5:97–107. doi: 10.1038/nrn1327. [DOI] [PubMed] [Google Scholar]
- van Welie I, van Hooft JA, Wadman WJ. Homeostatic scaling of neuronal excitability by synaptic modulation of somatic hyperpolarization-activated Ih channels. Proc Natl Acad Sci U S A. 2004;101:5123–5128. doi: 10.1073/pnas.0307711101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West AE, Chen WG, Dalva MB, Dolmetsch RE, Kornhauser JM, Shaywitz AJ, Takasu MA, Tao X, Greenberg ME. Calcium regulation of neuronal gene expression. Proc Natl Acad Sci U S A. 2001;98:11024–11031. doi: 10.1073/pnas.191352298. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.