Geodesic Based Registration of Sensor Data and Anatomical Surface Image Data

Abstract

This paper presents two related methods for registering an image of an anatomical object with data from sensors arranged on the object. One method is described with reference to a test case involving a rectangular electrode plaque disposed on a heart surface, which is imaged with MRI. Data from the electrodes is fused with the MRI image at the appropriate locations. The registration scheme involves four parts. First, selected landmarks on a data surface (e.g., electrode plaque) are registered to known locations on a target anatomical surface image. Second, the anatomical surface is represented numerically with a spherical harmonic expansion. Third, given the registration of the select data surface landmarks, the location of the outer four corners of the rectangular electrode plaque are located on the anatomical surface. Fourth, a quasi-evenly spaced grid within these four corners is formed on the anatomical surface. The third and fourth steps involve calculating geodesics on the anatomical surface, preferably by utilizing the spherical harmonic expansion. According to the second registration method, spherical harmonics and geodesics are used to extract a mesh from the anatomical surface. Laplace’s equation is solved on this mesh to generate a mapping from the anatomical surface to the data surface (electrode plaque).

INTRODUCTION

One type of registration problem that can arise in medical imaging involves the fusion of an anatomical surface image with data that corresponds to selected locations on the image. For example, in experiments that involve both the imaging of a heart and the recording of electrical signals from an electrode sock surrounding the heart,¹ it may be desirable to fuse the electrical information with the anatomical information in a single image. Similarly, high-density electrode plaques have been used to provide detailed maps of the spread of activation across the surface of an infarcted heart.² Accurate registration of such plaques to the heart surface may help to show how the large-scale structure of the infarcted region affects the spread of activation. In this work, we set forth a landmark based registration scheme that is suitable for this type of registration.

We assume that the data to be fused with the anatomical surface is derived from sensors arranged in a known manner on some sort of surface (“data surface”), an example of which is an electrode plaque on a circuit board. The data surface is then affixed to an anatomical subject that is imaged. According to the present scheme, the entire data surface is registered to the anatomical surface by directly registering only a few points on the data surface (e.g., electrode plaque) with the anatomical surface. From these few points, a mapping is derived that allows the entire data surface to be registered to the anatomical surface.

There are a number of landmark registration schemes that enable source and target points to be registered to one another through the use of rigid⁵ and non-rigid transformations.⁷ Most pertinent to the present work, there are techniques that involve the warping of a source surface onto a target surface in such a manner that landmarks on the two surfaces are brought into alignment. ⁷ These techniques tend to involve a large number of landmarks and tend to be highly sophisticated because they are often applied tocomplex problems such as comparing different brains.⁶

The schemes described in this paper take advantage of the relatively simpler nature of the registration problem at hand. These schemes are easy to implement and capable of generating mappings based on relatively few landmarks (e.g., 2–16) by imposing constraints on the form of the mapping. According to one scheme, the mapping is constrained to be quasi-affine, so that the Euclidean dimensions of the data surface, which may be a rectangle, are mostly preserved. For example, if the data surface is a rectangle, the side lengths of the mapped rectangle (i.e., the rectangle projected on to the anatomical surface) are constrained to have similar magnitudes to the corresponding side lengths of the 2-D rectangle. The constraints are imposed by calculating geodesics on the anatomical surface, which is defined by spherical harmonics.

Spherical harmonics and geodesics also underpin another scheme described in this paper, according to which the mapping between source and target is not constrained to be quasi-affine. This scheme utilizes the well known method of applying Laplace’s equation to perform surface mapping in general and in the context of medical imaging.¹⁰ The application of spherical harmonics and geodesics enables the extraction of a relatively fine mesh, on which the Laplace equation is solved, from a relatively sparse set of boundary points (e.g., around 8 or 15 points).

METHODS

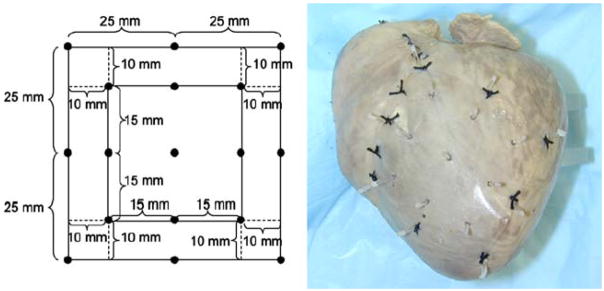
The first registration technique will be described with reference to a particular test registration problem. Specifically, a plastic rectangle, analogous to an electrode plaque, was registered to a canine heart. The test was performed only once, i.e., only a single canine heart was used. Various points were marked off on a piece of plastic, as shown in Fig. 1. The nine interior points were the data surface/rectangle to be registered. The eight outer points served as landmarks, as will be further apparent from the discussion below. For this test problem, the data surface and the landmarks existed on the same (plastic) surface but it was only the inner (30 × 30 mm²) rectangle that was mapped to the heart surface.

FIGURE 1.

Test registration problem. A plastic rectangle with dimensions shown in the left panel was sutured to the epicardium of a canine heart (right panel). The perimeter points served as landmarks for the registration method, while the interior points comprise the grid to be registered. The heart (and plastic) was then impaled with gadolinium infused needles at each of the eight perimeter landmark points and nine interior grid points, resulting in the configuration shown in the right hand panel.

The piece of plastic was then sutured to the epicardium of the canine heart. The heart (and plastic) was then impaled with marker needles containing a contrast agent (Gd-DPTA) at each of the eight landmark points and each of the nine data surface points. The heart was then scanned in a 1.5 T magnetic resonance imaging scanner (Siemens Sonata) by a 3-D gradient echo sequence with a spatial resolution of 0.4 × 0.4 × 0.4 mm³. The location of the markers was determined by visual inspection of the resulting image. The location of the landmark points was used in the registration scheme, as will be further described below. The location of the data surface points served as the standard against which to test the registration scheme.

The first registration scheme involved four parts. First, selected landmarks on the source image were registered to known locations on the target anatomical surface image. Second, the anatomical surface image was represented numerically with a spherical harmonic expansion. Third, given the registration of the select points, the outer four corners of the actual data rectangle were located on the anatomical surface image. Fourth, a quasi-evenly spaced grid within this rectangle was formed on the image surface. The third and fourth steps involved calculating geodesics on the anatomical surface image by utilizing spherical harmonic expansions.

In effect, registration is performed by locating the outer four corners of the data surface rectangle on the anatomical surface image, and then creating a mapping by uniform division of geodesics between the points. The method is a variant of a scheme described by Wang et al. in which brain surfaces are registered by matching selected points and generating a mapping based on the equally spaced division of geodesics between the selected points on each of two brain surfaces to be registered.⁹

The second registration scheme will be described after the first one.

Landmark Registration

Convenient landmark points on the anatomical surface image were selected. For the test case, as mentioned, magnetic resonance imaging was used to scan a heart and an attached plastic sheet, and gadolinium infused markers served as the landmark points. The coordinates (in the MRI reference frame) of the gadolium markers were then obtained by inspection of the 3-D imaging volume. The distances, as measured along the anatomical surface, between these landmark points and corresponding corners of the data surface were then determined. In the test problem, these surface distances were assumed to be equal to the Euclidean distances between various landmarks and data surface corners (see Fig. 1).

Spherical Harmonic Expansion

The anatomical surface image consisted of a point cloud embedded in a 3-D MRI voxel based coordinate system. The desired (outer heart) point cloud was then extracted from the MRI volume image.

Spherical harmonics have been used to characterize the heart,^3,4 and are generally suitable for spheroid type objects. The relation between the coordinates of a surface (the point cloud) and its spherical harmonic expansion was set as follows:

$$X({\psi }_x,{\theta }_x)=X_{\text{o}}+r_x({\psi }_x,{\theta }_x)\left(\begin{array}{c}cos{\theta }_{x}sin{\psi }_x\\ sin{\theta }_{x}sin{\psi }_x\\ cos{\psi }_x\end{array}\right)$$ (1)

where X are the coordinates of the raw data points on the surface in the imaging coordinate system, X_o is a chosen origin in this coordinate system, r_x are the radial coordinates, relative to the origin X_o, corresponding to X, θ_x are the azimuthal angles corresponding to X with respect to the origin X_o, and ψ_x are the polar angles corresponding to X with respect to X_o.

In turn, the radial coordinates r_x (ψ_x,θ_x) defined a surface represented by a spherical harmonic expansion:

$$\begin{array}{l}{R}_b=\sum _{i=0}^N\{a_i{P}_i(cos{\varphi }_b)+\sum _{m=1}^i(a_{im}cos(m{\theta }_b)\\ +b_{im}sin(m{\theta }_b))P_i^m(cos{\varphi }_b)\}\\ {\mathbf{R}}_{\text{b}}=\mathbf{P}\ast \mathbf{C}\end{array}$$ (2)

where R_b is the radius of each point on the surface, N is the number of terms in the spherical harmonic expansion, P_i is the Legendre function of degree i of the first kind, $P_i^m$ is the associated Legendre function of degree i and order m, a_i, a_im, b_im are coefficients (to be determined), P and C are matrix and vector representations of the Legendre function values and coefficients, respectively, and R_b is a vector representation of the radii R_b. The coefficients C were found by setting R_b equal to the raw radii r_x, computing P at the raw data angles (ψ_x,θ_x), and then solving the least squares equation (C=P\R_b in Matlab notation) for C.

The appropriate number of terms (N) in the expansion was found by experimentation. In the problem at hand, N = 8 was used. The origin X_o was then be selected with an optimization routine in such a manner to decrease the relative error, as defined in Eq. (3) below, to an acceptable value, which was chosen as 2%.

$$\text{Relative}\text{error}={\left|\right|r_x({\psi }_x,{\theta }_x)-(X-X_{\text{o}})\left|\right|}_2/{\left|\right|(X-X_{\text{o}})\left|\right|}_2.$$ (3)

The spherical harmonic expansion provides a representation of the anatomical surface image in terms of radii R_b that are a function of the two angular parameters, ψ_x and θ_x. This representation, and not the raw data, was used for the remaining steps of the registration scheme. The MRI coordinates of the gadolinium markers were transformed to the surface coordinate system by calculating the angles (ψ,θ) of the MRI coordinates with respect to the origin X_o.

Computing Geodesics

It was assumed that the data surface conformed to the anatomical surface without stretching or compressing. More formally, the 2-D Euclidean distance between any two points measured on the data surface was assumed to be equal to the distance between those points when the data surface was attached to the anatomical surface. According to this assumption, straight lines in the 2-D data surface coordinate system map to geodesics on the anatomical surface. Consequently, the minimum length surface path (geodesic) between any two points on the anatomical surface, within the data surface region, mapped to a straight line in the data surface 2-D space. Thus, when the geodesic between two points on the anatomical surface was found, the corresponding straight line in the data surface space was registered to the anatomical surface.

Geodesics were found by searching through paths defined in the spherical harmonic coordinate system to locate a path with a locally minimum path length. The search was performed by representing each path with splines, and adjusting the characteristics of the splines until a locally minimum distance was found.

In particular, the distance D between two points (a,b) on the anatomical surface image surface was represented as a path through the (θ,ψ) spherical harmonic coordinates, parameterized by a parameter t: (θ(t),ψ(t)), where t was arbitrarily chosen to range between 0 and 1 (t ε [0,1]) such that (θ(0), ψ(0)) = (θ_a, ψ_a) and (θ(1), ψ(1)) = (θ_b, ψ_b), where the subscripts on (θ,ψ) indicate the value of these coordinates at points a and b, respectively.

ψ(t) and θ(t) were each represented by respective interpolating quadratic splines with three knot points, two of which were the spline’s end points (t = 0,1) and the third of which was at t = 0.5: $\psi (t)={\sum }_{i=0}^2{c}_i\ast x^i$, with the coefficients c_i chosen such that ψ(0) = ψ_a, ψ(1) = ψ_b, and ψ(0.5) = ψ_x, where ψ_x was varied to locate the minimum distance path. The spline formulation for θ(t) was analogous.

The initial guess for the optimization routine was that the geodesic was a straight line through parameter space. For example, for the search through the ψ parameter space, the initial value of ψ_x (the value of ψ at t = 0.5), was the average of the values at the end-points, 0.5 * (ψ_a + ψ_b).

For the test heart surface, two types of splines were tested: quadratic splines with a single intermediate knot point, as described above, and cubic splines (with not-a-knot end conditions using Matlab’s csapi function) with five knot points at t = [0, 0.25, 0.5, 0.75, 1]. These two types of splines yielded essentially identical results.

An optimization routine (Matlab’s fminsearch function) was used to determine the values (θ(0.5), ψ(0.5)) at the intermediate control point (t = 0.5) such that the path distance D was minimized. For each path (θ(t),ψ(t)), the path distance D was computed by dividing the path into a large number of segments, computing the Euclidean distance for each segment, and summing these segment distances.

Locating Rectangle Corners

As mentioned, the four corners that defined the perimeter of the data surface were registered with respect to landmarks on the anatomical surface image surface that had a known spatial relationship to the four corners.

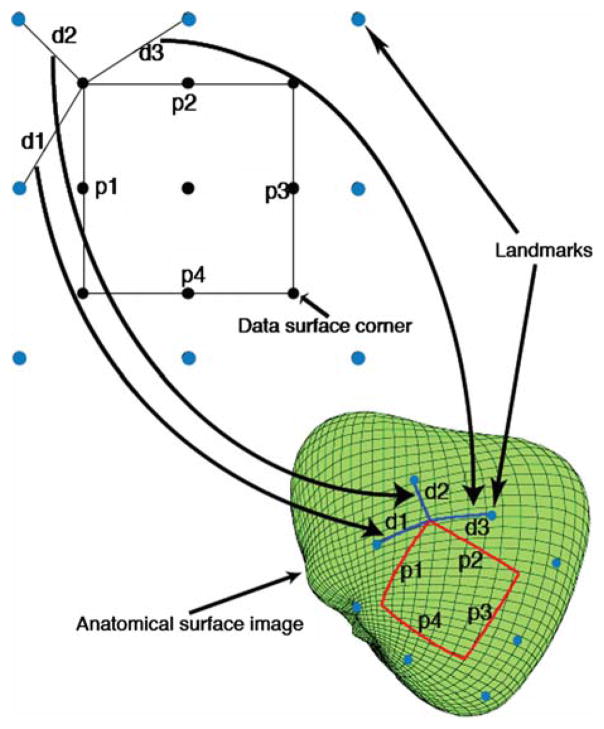
Two sets of constraints, the distances from the landmarks to the four corners and the dimensions of the data surface, were used to register the four corners on the anatomical surface image. The two sets of constraints were applied by solving an optimization problem that involved finding the rectangle that best matched the corners’ locations with respect to their corresponding landmarks, while yielding geodesic distances along the perimeter of the rectangle that were close to the corresponding Euclidean distances. The corresponding landmark for any corner was the closest landmark to that corner. For example, with reference to Fig. 2, the landmark corresponding to the upper left corner of the data surface corner (in black) is the upper left landmark corner (in blue), which is separated from the upper left data surface corner by a distance d2.

FIGURE 2.

Euclidean 2-D distances d1, d2, and d3 map to surface geodesics with identical distances. Landmarks on the 2-D data surface and the heart (anatomical image) surface are shown in light blue. The intersection of heart surface geodesics, having distances d1, d2, and d3, from the upper left three landmarks defines the data surface corner point to be registered. This is akin to a triangulation type registration technique. Similarly, the Euclidean perimeter distances p1, p2, p3, and p4 map to geodesics with approximately these lengths. The four data surface corner points were registered by solving an optimization problem that minimized both the error of both the distances between corner points and corresponding landmarks, and the error between the actual geodesic distances along the perimeter, and the Euclidean distances p1, p2, p3, and p4. See text for details.

More formally, to register multiple corners simultaneously while including perimeter dimensions as a constraint, the points x_c, c ε [1,4] on the surface were found by searching over possible corner point locations (x) such that the following quantity was minimized:

$${\Vert \sum _{i=1}^4{(d_i(x)-m_i)}^2+\sum _{k=1}^4{(d_k(x_k,x_{k+1})-p_{k,k+1})}^2\Vert }_2$$ (4)

where d_i(x) is the geodesic distance from the point x to the landmark associated with the ith data surface corner point, m_i is the actual measured distance between the ith data surface corner point and its associated landmark (e.g., m_i = d2 for the upper left corner Fig. 2), d_k(x_k, x_k+1) is the geodesic distance between successive possible corner point locations x_k and x_k+1 (which are taken cyclically with x₅ = x₁), and p_k,k+1 is the actual measured distance between successive data surface corner points, i.e., the length of a side of the black rectangle (square) shown in Fig. 2. With reference to Figs. 1 and 2, the actual measured distance m_i between any corner point and its associated landmark (i.e., the distance d2 in the upper left schematic in Fig. 2) was equal to 10*(2)^0.5. Referring to Fig. 1, the distance along each side of the black square shown in Fig. 2 was 30 mm, so that p_k,k+1 was always equal to 30 mm.

An alternative method was also implemented. According to this alternative method, a subset of the corner points were registered separately by triangulation. More particularly, these points were registered by minimizing the following quantity:

$${\Vert \sum _{j=1}^3{(d_j(x)-m_j)}^2\Vert }_2,$$ (5)

where d_j(x) is the geodesic distance from the point x to the landmark j and m_j is the actual measured distance between the corner point being registered and landmark j. Since the landmarks were arranged convexly, three landmarks uniquely defined a corner location according to the above least squares formulation. For example, to register the upper left data surface corner point (in black) shown in Fig. 2, Eq. (5) is applied with the distances m_j to the three closest landmarks (in blue) shown as d1, d2, and d3, respectively. These distances were equal to (10² + 15²)^0.5, 10 * (2)^0.5 and (10² + 15²)^0.5, respectively, based on the dimensions shown in Fig. 1.

The locations of the subset of corner points thus registered according to Eq. (5) were then considered fixed, and the remaining corner points were registered by minimizing a modified form of Eq. (4), in which the left-hand side was essentially replaced with Eq. (5), so that both triangulation and the distances around the data surface perimeter (i.e., 30 mm) were used to register the remaining corner points:

$${\Vert \sum _{i=1}^q\sum _{j=1}^3{(d_{ij}(x)-m_{ij})}^2+\sum _{k=1}^{q+1}{(d_k(x_k,x_{k+1})-p_{k,k+1})}^2\Vert }_2$$ (6)

where q ≥ 1 is the number of corner points remaining to be registered, m_ij is the actual measured distance between the ith corner point and landmark j, d_k(x_k, x_{k+ 1}) is the geodesic distance between successive possible corner points (which are taken cyclically with x₅ = x₁), and x_k, k > q, are the fixed data surface corner points that were previously registered through triangulation (Eq. 5). For example, if x₃ and x₄ were previously registered through triangulation, they are fixed, and Eq. (6) is minimized by searching for x₁ and x₂ by triangulation (left hand sum of Eq. 6) and by searching over all of the sides of the rectangle except the side connecting x₃ and x₄, i.e., the second sum in Eq. (6) includes the distances d(x₁, x₂), d(x₁, x₂), and d(x₄, x₁). For each corner point i remaining to be registered, the distances m_ij for j = 1,2,3 were equal to (10² + 15²)^0.5, 10 * (2)^0.5 and (10² + 15²)^0.5, respectively. The term p_k,k+1 was always equal to 30 mm.

This alternative scheme (applying Eqs. 5 and 6) may be desirable if there is a high degree of confidence in the location of some of the corners but not others. In the problem at hand, it was not known a priori which of the four corner locations (see Fig. 2) were known with a relatively higher degree of confidence (“fiducial corners”) compared to the other corner locations. After some experimentation to determine a set of fiducial corners that yielded the lowest value of Eq. (6), the two basal (top most) corners were chosen as the fiducial corners and were separately registered with triangulation (Eq. 5). The remaining two corners were registered with the mixed scheme (Eq. 6), using the corresponding closest corner landmarks in the left side of Eq. (6) and three perimeter side lengths (30 mm) in the right side of Eq. (6). (The three sides were those that included at least one of the two points to be registered with Eq. (6); the fourth side, between the two fiducial points, was not used in Eq. (6) because its length was fixed by the locations of the two fiducial points.)

Generating a Grid

Given the location of the outer four corners of the rectangular data surface on the anatomical surface image, an evenly spaced grid was generated on the anatomical surface image within these four corners by dividing each rectangle side into equal length segments, thereby defining a number of points on the rectangle’s perimeter, and connecting opposite pairs of these points with geodesics. The (θ,ψ) coordinates of the grid points were calculated by determining the approximate location of the intersection of two orthogonal geodesics.

Warping Scheme

The assumption of a Euclidean mapping is not valid where the anatomical surface is highly curved, which is especially likely when the data surface/electrode plaque is disposed over a relatively large portion of a spheroid. In this case, the Laplace equation provides an efficient means for performing the mapping, based on the assumption that the stretching/warping of the of the data surface/electrode plaque is essentially uniform.

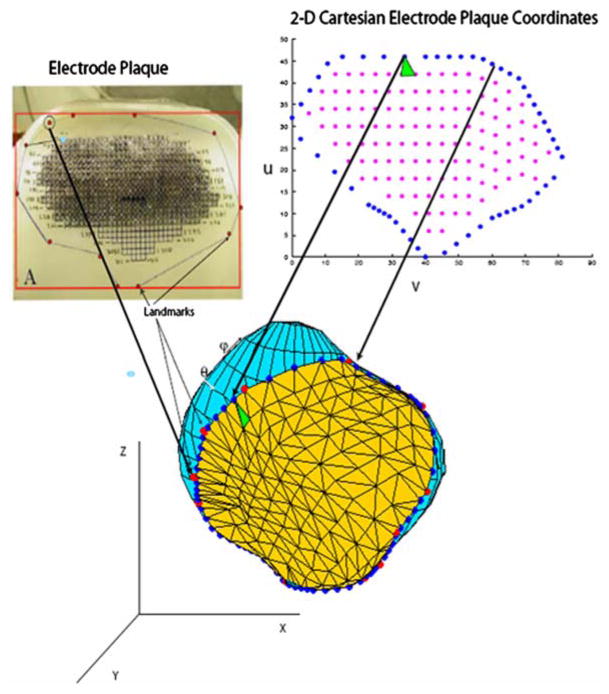
This method will be described with reference to Fig. 3, which shows a heart surface, represented with a spherical harmonic derived mesh, along with a number of landmarks (red circles) obtained in the manner previously described. The landmarks correspond to points along the outer boundary of an electrode plaque created by Ciaccio et al.,² as shown in the upper left panel. To solve the Laplace equation on that portion of the heart surface over which the plaque is disposed, a triangular mesh of this portion (shown in the Figure) was extracted as follows.

FIGURE 3.

Generation of the triangular surface mesh. An electrode plaque (see Ciaccio et al.²) with landmark points is shown in the upper left panel. Geodesics between the landmarks were computed and points along these geodesics (filled blue circles) determined the boundary of the grid on the heart surface. The correspondence between two boundary points in the 2-D cartesian (u,v) electrode plaque coordinate system and the 3-D heart surface is indicated by two arrows. The interior mesh points (magenta) were generated by sampling in the (u,v) coordinate system. Delauany triangulation was performed in the (u,v) coordinate system; one of the resulting triangles is shown in green in the (u,v) coordinate system and its corresponding triangle is shown on the heart surface. The (x,y,z) coordinates in the 3-D heart coordinate system of the interior (magenta) points were generated by interpolating the (θ,ψ) coordinates (shown on the heart surface) of the boundary points, and the resulting (θ,ψ) coordinates were translated into (x,y,z) coordinates to create the triangular 2-D mesh (embedded in 3-D space).

First, geodesics were computed between adjacent landmarks. The geodesics were divided into equal length segments, and the original 2-D plaque coordinates (u,v), which were known at the landmark points, were interpolated along the geodesics. For example, if the (u,v) coordinates of two landmarks are (0,0) and (0,1) respectively, and the (θ,ψ) coordinates of those landmarks are (0,0) and (0,π/2) respectively, the interpolated (u,v) and (θ,ψ) coordinates of a point midway (along a geodesic) between these landmark points are (0,0.5) and (0,π/4), respectively. The result of the above mentioned interpolation of geodesics between landmark points was a set of boundary points (shown as blue filled circles on the heart surface in Fig. 3) that determined the mapping of the boundary between the original (u,v) coordinates and the target( θ,ψ) coordinates.

When applied to the problem shown in Fig. 1, the above described mapping of the boundary (u,v) coordinates to the target (θ,ψ) coordinates resulted in significant errors due to distortion of the plastic sheet. In an attempt to overcome this problem, a modified version of the warping scheme, which will be referred to as the “proportional boundary distance” scheme, was applied to the Fig. 1 test problem.

The modification involved employing an alternative type of mapping scheme according to which some of the original 2-D plaque coordinates (landmark points) were not used because the inclusion of these points would have caused some distortion. More particularly, when geodesics were computed with these points included as landmarks, the computed geodesic distances were less accurate than when these points were excluded. Accuracy here means relative difference of the computed geodesic distance between two adjacent landmark points compared to the known Euclidean distance of 25 mm (see Fig. 1). The excluded landmarks were the mid-point boundary markers that are labeled as lm2, lm4, lm6, and lm8 in Fig. 7, which shows the eight original landmark points labeled as lm1–lm8. (Thus, the corner landmarks lm1, lm3, lm5, and lm7 were used as landmarks for calculating the geodesics that define the boundary of the plaque.)

FIGURE 7.

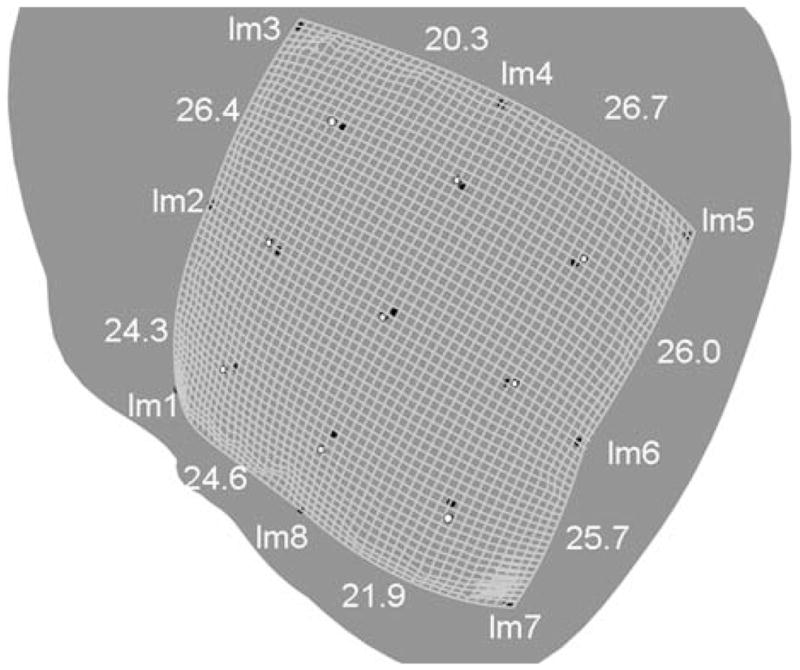
Laplacian scheme applied to the test problem shown in Fig. 1. The grid is 50 × 50 divisions, so that each square is approximately 1 × 1 mm². The actual (MRI image determined) eight boundary landmark points (lm1–lm8), and the nine interior points, are shown as black circles. The computed interior points are shown as white filled circles. The computed geodesic distances between landmarks are also shown. To allow for all of boundary and interior points to be seen in the figure, the heart had to be rotated; the resulting view, as shown, resulted in some parallax, such that the computed boundary appears to be outside all of the actual boundary points, which was not the case. The computed boundary aligned almost exactly with the four corner landmark points.

As will be described in the Results section, even with the exclusion of the four middle landmarks lm2, lm4, lm6, and lm8, when the warping registration method was applied to the Fig. 1 test problem, the computed geodesic distances between landmark boundary markers varied substantially from the Euclidean distances (25 mm) in the (u,v) plane representing the undistorted plastic sheet. This variance may have caused at least part of the error between the computed and actual coordinates of the nine interior test points.

In an attempt to compensate for this discrepancy between computed geodesic distances and assumed distances between boundary landmarks, instead of using the (u,v) coordinates at the mid-point boundary markers (lm2, lm4, lm6, and lm8 in Fig. 7), the boundary (u,v) coordinates were divided proportionately according to geodesic distances. For example, for the upper left line (between lm1 and lm3 in Fig. 7), in the unmodified warping scheme discussed above, the (u,v) coordinates of the three top boundary markers (lm1, lm2, and lm3 respectively) were (0,0), (25,0), and (50,0). For the adjusted scheme, since the geodesic distance between lm1 and lm2 was 24.3 mm and the geodesic distance between lm2 and lm3 was 26.4 mm, the adjusted (u,v) coordinates (hereinafter referred to as (u′, v′)), were assigned as (0,0), (24.3,0), and (50,0).

After the mapping of boundary coordinates in either the original warping scheme or the proportional boundary distance scheme, the boundary points formed the perimeter of a mesh on the target heart surface. The interior of the mesh may be filled in any number of ways. In the approach that was adopted, a set of points was sampled from the (u,v) coordinates, shown for the Fig. 3 problem in magenta in the upper right panel of Fig. 3, and Delaunay triangulation was carried out on this set of points along with the boundary points. (For the proportional boundary scheme applied to Fig. 1, this set of points was sampled from the adjusted coordinates (u′, v′)). One of the resulting triangles is shown in green in the upper right panel of the figure, and the corresponding mesh triangle is shown in the center panel. The (x,y,z) coordinates of the interior points were generated by interpolation of the mapping of the boundary coordinates.

Specifically, each boundary point has both surface coordinates (θ,ψ) and original (u,v) coordinates since the mapping for these points is known. Linear interpolation of the (θ,ψ) values as a function of the (u,v) coordinates resulted in an selection of (θ,ψ) values for the interior grid points. For example, assume that Delaunay triangulation carried out in the (u,v) plane resulted in an interior point triangle vertex with (u,v) coordinates of (0.5,0.5). It is necessary to find a (θ,ψ) point for this vertex, which is done by interpolating the (u,v) boundary coordinates. Specifically, if the (u,v) coordinates of two boundary points are (0.5,0) and (0.5,1) respectively, and the (θ,ψ) coordinates of those landmarks are (0,0) and (0,π/2) respectively, the interpolated (u,v) and (θ,ψ) coordinates of an interior point midway (in the (u,v) coordinate system) between these boundary points are (0.5,0.5) and (0, π/4), respectively. Thus, the (u,v) interior triangle vertex at (0.5,0.5) in the (u,v) coordinate system is assigned a (θ,ψ) coordinate of (0, π/4). This linear mapping of (u,v) to(θ,ψ) coordinates was done solely for convenience to select a reasonable set of (θ,ψ) points to correspond to the triangle vertices defined in the (u,v) coordinate system, thereby defining a mesh in the (θ,ψ) and (x,y,z) coordinate systems.

The values of u(x,y,z) and v(x,y,z) were computed by solving Laplace’s equation on this mesh separately for u and v, e.g., ∂²u(x, y, z)/∂x² + ∂²u(x, y, z)/∂y² + ∂²u(x, y, z)/∂z² = 0, subject to the (Dirichlet) boundary conditions that u and v (or u′ and v′ in the case of the proportional boundary distance scheme) were equal to the known values of the boundary points (blue filled circles). Laplace’s equation was solved with the finite element method.

Given the computed values of u and v at the mesh points, the reverse mapping from (u,v) to (x,y,z) coordinates was found by interpolation.

No error metrics were available for the registration problem associated with Fig. 3. Therefore, the above described warping scheme was tested on the registration problem associated with Fig. 1; the resulting errors (i.e., the distance between computed and actual data surface point locations) will be described in the Results section.

Multiquadric Spline Scheme

For purposes of comparison with the Euclidean/geodesic scheme and the warping scheme, multiquadric splines were applied to the test problem associated with Fig. 1. Multiquadric splines have been used to warp a source heart to a target heart, with a total of 81 landmarks on the epicardium and endocardium.⁸ In contrast, in the test case, there were only eight landmarks. The landmarks in the (u,v) coordinate system p_s were rotated, translated, and scaled by a uniform factor to produce a set of points p_rot (lying on a plane) that minimized the least squares error between p_rot and the landmarks on the heart surface p_lm: Min (Σ_i||α(Rp_s(i) + T) − p_lm(i)||²), where R is a 3 × 3 rotation matrix, T is a 3 × 1 translation matrix, α is a scaling factor, p_s(i) is a 3 × 1 vector containing the coordinates of the ith landmark on the data surface with coordinates (x,y,z) = (u,v,0), and p_lm(i) is the ith landmark on the heart surface. Thus, p_rot(i) = α(Rp_s(i) + T). The p_rot coordinates were then fit to the p_lm coordinates with splines⁸:

$$f(p)=\sum _{i=1}^N{a}_i{F}_i(p)+b_0+b_{1}x+b_{2}y+b_{3}z$$ (7)

where $F_i(p)=\sqrt{{\left|\right|p-p_{lm}(i)\left|\right|}^2+S^2}$ and b₀, b₁, b₂, and b₃, are coefficients to be determined.

The source points p_rot were fit separately to the x, y, and z coordinates of the target points (p_lm), yielding three different transformation functions f(p), one for x, y, and z respectively. See Wang et al.⁸ for additional details. The optimal value of S, 88, was found by experimentation.

RESULTS

First, the Euclidean/geodesic scheme was tested on both a sphere and a rotated ellipsoid. Geodesics for a sphere are represented analytically (by great circles) while geodesics for an ellipsoid may be calculated by numerical integration. For both the sphere and ellipsoid, the scheme converged to the proper geodesics.

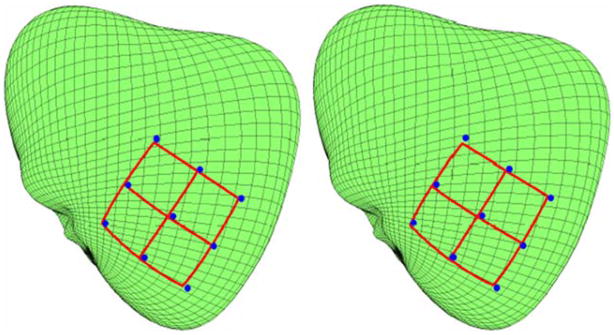
Figure 4 shows the grids generated with two different rectangle corner registration schemes. In the left panel, the basal (top most) two corners were separately registered with triangulation (Eq. 5), and the remaining two corners were registered with the Eq. (6), using the corresponding three closest landmarks and three perimeter side lengths as constraints, as described in the Methods section. In the right panel, all corners were simultaneously registered using the corresponding closest corner landmarks and all four perimeter lengths as constraints (Eq. 4).

FIGURE 4.

Generated grids for the mixed Euclidean scheme (Eqs. 5 and 6) and all corner registration (Eq. 4) scheme, respectively.

Error was defined as the Euclidean distance between the computed (x,y,z) coordinates and the true (x,y,z) coordinates of the nine points (in blue in Fig. 4). The true (x,y,z) coordinates were determined by locating the voxels in the MRI image where the nine Gd-DPTA markers intersected in the outer heart surface. Again, only one dataset, corresponding to the particular arrangement shown in Fig. 1, was used to test the above described registration schemes against a gold standard.

For the mixed scheme (Eqs. 5 and 6), the maximum absolute error for any grid point was 1.68 mm, the average absolute error was 0.88 mm, and the error for the center grid point was 0.94 mm. For the simultaneous corner registration scheme (Eq. 4), the maximum absolute error for any grid point was 1.66 mm, the average absolute error was 1.02 mm, and the error for the center grid point was 1.05 mm.

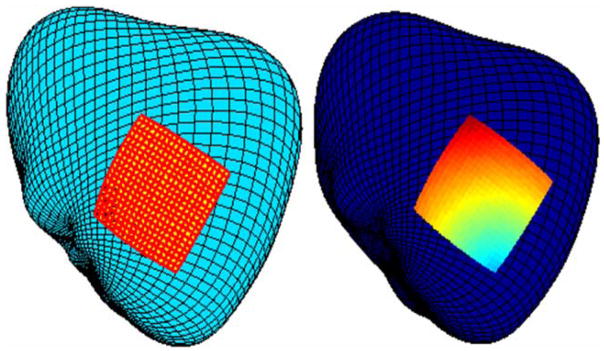
The left panel in Fig. 5 shows a high resolution grid computed with the mixed Euclidean/geodesic scheme. The right panel in Fig. 5 shows synthetic data displayed on the registered anatomical surface image.

FIGURE 5.

Generated high resolution grid (left) with synthetic data (right) for the Euclidean/geodesic scheme.

On a MacIntosh PowerBook G4 (1.5 GHz CPU) running Matlab, geodesics were computed in between 2 and 11 s.

Figure 6 shows a grid computed with the Laplace equation scheme that was applied to the registration problem shown in Fig. 3. The solution of the Laplace equation was very fast, on the order of a few seconds for the triangular mesh shown in Fig. 3. The exact locations of the actual interior electrode plaque points (Fig. 3) were not known so it was not possible to determine the difference between computed and actual electrode plaque point locations. Qualitatively, the computed grid appears to be reasonably uniform.

FIGURE 6.

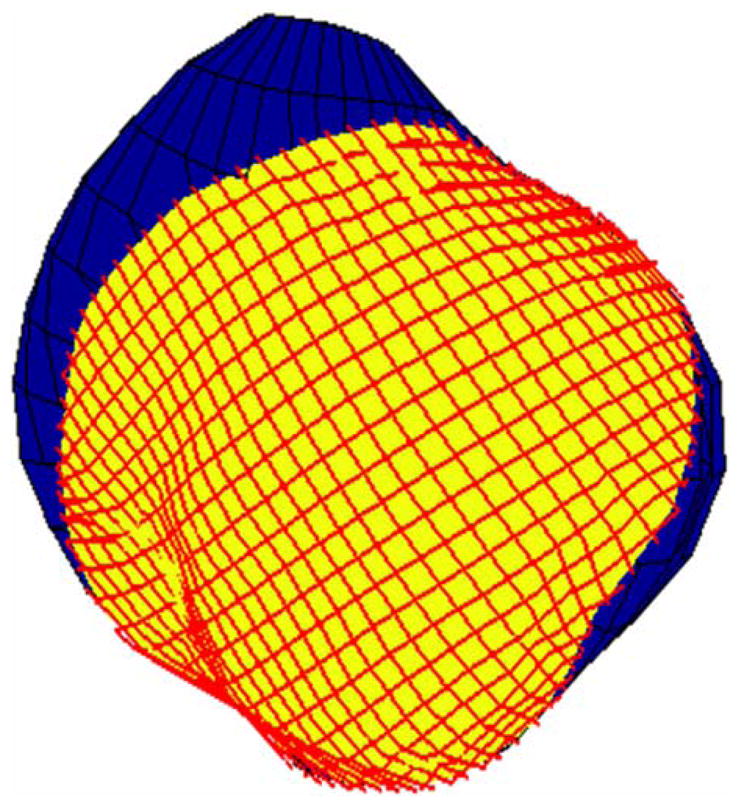
Generated high resolution grid for the Laplacian/warping scheme.

Figure 7 shows the grid generated by the warping/Laplace equation scheme applied to the test problem shown in Fig. 1. The grid divides the data surface into 50 × 50 divisions, so that each small square is approximately 1 × 1 mm². Actual landmark and test marker locations are shown in black. Computed locations for the test markers are shown as white filled dots. The maximum error was 2.7 mm, the minimum error was 0.79 mm, the error in the center was 1.4 mm, and the average error was 1.6 mm.

Figure 7 also shows the computed geodesic distances between the original boundary markers. These distances are 24.3, 26.4, 20.3, 26.7, 26.0, 25.7, 21.9, and 24.6 mm. The distance between the landmarks/boundary markers as measured along the undistorted plastic surface (see Fig. 1) was 25 mm. Thus, some of the computed geodesic distances were substantially different than the undistorted Euclidean distances. As alluded to in the Methods section, the non-uniformity of the difference between the computed and undistorted distances suggests that some parts of the plastic may have distorted more than others when the plastic was attached to the heart.

The alternative Laplacian scheme involving proportional boundary distances achieved relatively better results than the regular Laplacian scheme. In particular, the alternative scheme yielded a maximum error of 2.16 mm, a minimum error of 0.66 mm, an error in the center of 0.86 mm, and an average error of 1.38 mm.

For the multiquadric spline scheme, the mean error was 2.2 mm, with a maximum error of 4.8 mm and an error at the mid-point of 1.6 mm. The computed points did not lie on the outer heart surface.

Table 1 summarizes the results of the various schemes applied to the test problem shown in Fig. 1.

TABLE 1.

Errors associated with the different registration schemes.

	Mean error (mm)	Maximum error (mm)	Error at mid-point (mm)
Euclidean geodesic scheme—all corner scheme	1.02	1.66	1.05
Euclidean geodesic scheme—mixed scheme	0.88	1.68	0.94
Laplacian scheme—regular	1.6	2.7	1.4
Laplacian scheme—proportional boundary distance	1.38	2.16	0.86
Multiquadric splines	2.2	4.8	1.6

DISCUSSION

The results suggest that the Euclidean/geodesic scheme may be useful in cases when it is desirable to preserve the characteristics of a 2-D source image that is mapped to a 3-D anatomical surface image. The underlying assumption is that the 2-D image is mapped in such a way that distances are preserved, i.e., the source surface is not substantially stretched or compressed when it is disposed on the target source. In this case, the uniform geometry of the data source is reasonably well represented by the transformed source image. The regularity of the grid shown in Fig. 5 is an example of the preservation of a uniform source geometry (left panel) and synthetic data superimposed on this geometry (right panel).

With regard to the test registration problem associated with Fig. 1, the discrepancies between the computed grid point locations and corresponding gadolinium marker location arose from many error sources. First, it was difficult to discern the exact location of the gadolinium markers from the MRI image, and there is an inherent imprecision of 0.4 mm given the MRI voxel size. Second, there was an error in representing the target surface with spherical harmonics. In the present case, the difference between the spherical harmonic coordinates and actual MRI coordinates was approximately 2.3%. Third, the plastic sheet buckled in places when it was sutured to the heart (because the heart surface has spheroid characteristics), so that the Euclidean source distances (e.g., d1, d2, and d3 in Fig. 2) varied from the corresponding actual distances along the heart surface, as indicated by the non-uniform distances between landmarks shown in Fig. 7. This distortion caused an error in both the location of the corner grid points, and the location of the generated uniform grid points within these corners. Fourth, there was discretization error associated with the calculation of the geodesics. This was not likely a significant source of error since geodesic distances in both a sphere and a rotated ellipsoid showed that a grid resolution similar to the one adopted for the heart surface was sufficient to very accurately compute geodesic distances, with relative errors less than 1%.

The distortion due to the buckling of the plastic sheet appeared to be the most significant source of error, as suggested by the substantial variance between the assumed distance between landmarks (25 mm) and the computed distances shown in Fig. 7. The largest absolute error between landmarks (lm3 and lm4) was 4.7 mm (25–20.3 mm), which is a relative error of 18.8%.

There are at least three possibilities when an array of sensors, such as a plaque, is applied to a surface, such as the heart. First, the plaque could be stiff relative to the tissue and deform the heart surface when it is applied, potentially leaving gaps where the heart surface dimples or abruptly changes angles (like the septal valley formed around the left anterior descending artery). Second, the plaque could be extremely flexible, like tissue paper, and conform to the contours of the heart perfectly without distorting the tissue but becomes distorted itself (folds and wrinkles). Third, the stiffness of the array could be somewhere between these two.

The warping/Laplace scheme appears to produce a reasonably uniform grid, as shown in Figs. 6 and 7. Somewhat more precisely, application of the Laplace equation results in a coordinate system (u,v) in which ∂u/∂s|_v=const.= const, where s is the distance along the surface. This mapping is consistent with the assumption that the electrode plaque is uniformly stretched/compressed.

The Euclidean/geodesic scheme performed better than the Laplacian scheme in the solution of the test problem shown in scheme Fig. 1. This was expected since the Euclidean/geodesic utilizes more information than the Laplacian scheme in constructing a grid that matches the characteristics of the electrode plaque. Both schemes performed better than multiquadric splines. Again, the relative superiority of the Euclidean/geodesic and Laplacian schemes was expected, since these schemes, unlike multiquadric splines, necessarily generate points that lie on the outer heart surface.

As presently implemented, the Euclidean geodesic scheme, the best registration scheme in terms of accuracy, resulted in errors on the order of 1 mm. The warping/Laplacian scheme resulted in errors on the order of 1–2 mm. It may be possible to somewhat improve the accuracy by more carefully applying a conforming electrode plaque (instead of a plastic sheet), and by taking measurements with a string or the like of actual distances between landmark points. Nonetheless, the present schemes appear to be best suited for macroscopic registration problems, and may not be appropriate in cases where it is desired to register electrical signals with microscopic histologic structure, such as the geometry of an infarcted region within heart muscle.

As mentioned, the Euclidean/geodesic scheme is not suitable in cases where the subject anatomical surface (e.g., the outer heart surface) is curved in such a way that geodesics will not result in an evenly spaced grid. The outer heart surface could be tested for this property by computing geodesics in the manner described herein and then calculating the Euclidean distances along the grid to determine whether it is evenly spaced. However, since only a single dog heart was tested in connection with the present work, it is currently difficult to enumerate the types of shapes that the Euclidean/geodesic scheme may prove suitable.

The Laplacian/warping scheme is applicable when the assumption of uniform stretching/compression is reasonable. Again, since this scheme was tested only for a single dog heart, the extent to which it is appropriate for other hearts or objects is not known.

CONCLUSION

Two different schemes were described for registering surface sensor data with an anatomical surface that can be accurately represented by spherical harmonics. The schemes appeared to produce good results, at least in the context of the selected test cases, are very easy to implement, and do not require extensive computation time.