Tone Sequences With Conflicting Fundamental Pitch and Timbre Changes Are Heard Differently by Musicians and Nonmusicians

Abstract

An Auditory Ambiguity Test (AAT) was taken twice by nonmusicians, musical amateurs, and professional musicians. The AAT comprised different tone pairs, presented in both within-pair orders, in which overtone spectra rising in pitch were associated with missing fundamental frequencies (F0) falling in pitch, and vice versa. The F0 interval ranged from 2 to 9 semitones. The participants were instructed to decide whether the perceived pitch went up or down; no information was provided on the ambiguity of the stimuli. The majority of professionals classified the pitch changes according to F0, even at the smallest interval. By contrast, most nonmusicians classified according to the overtone spectra, except in the case of the largest interval. Amateurs ranged in between. A plausible explanation for the systematic group differences is that musical practice systematically shifted the perceptual focus from spectral toward missing-F0 pitch, although alternative explanations such as different genetic dispositions of musicians and nonmusicians cannot be ruled out.

The sounds of voiced speech and of many musical instruments are composed of a series of harmonics that are multiples of a low fundamental frequency (F0). Perceptually, such sounds may be classified along two major dimensions: (a) the fundamental pitch, which corresponds to F0 and reflects the temporal periodicity of the sound and (b) the spectrum, which may be perceived holistically as a specific timbre (brightness, sharpness) or analytically in terms of prominent frequency components (spectral pitch). Under natural conditions, fundamental and spectral pitch typically change in parallel. For example, the sharpness of a voice or an instrument becomes more intense for higher notes.

Fundamental pitch sensations occur even when the F0 is missing from the spectrum. This phenomenon has fascinated both auditory scientists and musicians since its initial description in 1841 (Seebeck). The perception of the missing F0 plays an important role in the reconstruction of animate and artificial signals and their segregation from the acoustic background. It enables the tracking of melodic contours in music and prosodic contours in speech, even when parts of the spectra are masked by environmental noise or are simply not transmitted, as in the case of the telephone, in which the F0 of the voice is commonly not conveyed. In early theories, researchers argued that the sensation had a mechanical origin in the auditory periphery (Fletcher, 1940; Schouten, 1940). However, recent neuroimaging studies from different groups, including our lab, suggest that pitch processing involves both the subcortical level (Griffiths, Uppenkamp, Johnsrude, Josephs, & Patterson, 2001) and the cortical level (Bendor & Wang, 2005; Griffiths, Buchel, Frackowiak, & Patterson, 1998; Krumbholz, Patterson, Seither-Preisler, Lammertmann, & Lütkenhöner, 2003; Patterson, Uppenkamp, Johnsrude, & Griffiths, 2002; Penagos, Melcher, & Oxenham, 2004; Seither-Preisler, Krumbholz, Patterson, Seither, & Lütkenhöner, 2004, 2006a, 2006b; Warren, Uppenkamp, Patterson, & Griffiths, 2003). The strong contribution of auditory cortex suggests that fundamental pitch sensations might be subject to learning-induced neural plasticity. Indirect evidence for this assumption comes from psychoacoustic studies, which show that the perceived salience of the F0 does not depend only on the stimulus spectrum but also on the individual listener (Houtsma & Fleuren, 1991; Renken, Wiersinga-Post, Tomaskovic, & Duifhuis, 2004; Singh & Hirsh, 1992; Smoorenburg, 1970). Surprisingly, the authors of these studies did not address the reasons for the observed interindividual variations. In the present investigation, we took up this interesting aspect and focused on the role of musical competence. It might be expected that musical training has an influence in that it involves the analysis of harmonic relations at different levels of complexity, such as single-tone spectra, chords, and musical keys. Moreover, it involves the simultaneous tracking of different melodies played by the instruments of an orchestra.

The findings presented here confirm the above hypothesis and demonstrate, for the first time, that the ability to hear the missing F0 increases considerably with musical competence. This finding suggests that even elementary auditory skills undergo plastic changes throughout life. However, differences in musical aptitude, constituting a genetic factor, might have had an influence on the present observations, as well.

Experiment

Method

Participants

Participants who had not played a musical instrument after the age of 10 years were considered nonmusicians. Participants with limited musical education who regularly (minimum of 1 hr per week during the past year) practiced one or more instruments were classified as musical amateurs. Participants with a classical musical education at a music conservatory and regular practice were considered professional musicians. All in all, we tested 30 nonmusicians (M = 30.9 years of age; 23 women, 7 men); 31 amateurs (M = 28.6 years of age, M = 12 years of musical practice; 24 women, 7 men); and 18 professionals (M = 31.2 years of age; M = 23.8 years of musical practice; 11 women, 7 men). The inhomogeneous group sizes reflect the fact that we had to exclude a considerable proportion of nonmusicians and amateurs from our final statistical analysis, in which only those participants with low guessing probability were accounted for (see Simulation-Based Correction for Guessing and Data Reanalysis section). Table 1 lists the instruments (voice included) played by the amateurs and professionals at the onset of musical activity (first instrument) and at the time of the investigation (actual major instrument).

Table 1. Number of Participants Who Played the Indicated Instruments at Onset of Musical Activity (First Instrument) and Who Play the Indicated Instruments Presently (Actual Major Instrument).

	First instrument		Actual major instrument
Instrument	Amateurs	Professionals	Amateurs	Professionals
Piano	6	10	6	6
Keyboard	—	—	1	—
Guitar	4	—	6	—
Violin	2	2	3	2
Viola	—	—	1	—
Cello	1	1	1	1
Recorder	15	2	1	1
Transverse flute	—	—	3	—
Clarinet	—	—	1	—
Bassoon	—	—	—	1
Oboe	—	1	—	3
Trumpet	—	1	1	1
Percussion	—	—	1	—
Xylophone	1	—	—	—
Voice	2	1	6	3

Auditory Ambiguity Test (AAT)

The AAT consisted of 100 ambiguous tone sequences (50 different tone pairs presented in both within-pair orders) in which a rise in the spectrum was associated with a missing F0 falling in pitch and vice versa (see Figure 1). Each tone had a linearly ascending and descending ramp of 10 ms and a plateau of 480 ms. The time interval between two tones of a pair was 500 ms, and the time interval between two successive tone pairs was 4,000 ms. The sequences were presented in a prerandomized order in 10 blocks, each of which comprised 10 trials. The participants had to assess, in a two-alternative forced-choice paradigm, whether the pitch of a tone sequence went up or down. The score that could be achieved in the AAT varied from 0 (100 spectrally based responses) to 100 (100 F0-based responses). The stimuli were generated by additive synthesis through use of a freeware programming language (C-sound, Cambridge, MA). They were normalized so that they had the same root-mean-square amplitude value.

Figure 1.

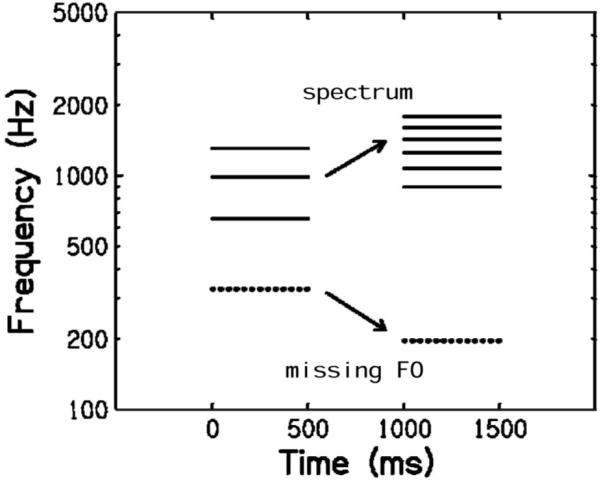
Example of an ambiguous tone sequence. The spectral components of the first tone represent low-ranked harmonics (2nd to 4th) of a high missing F0, whereas for the second tone, they represent high-ranked harmonics (5th to 10th) of a low missing F0. In the case of spectral listening, a sequence rising in pitch would be heard, whereas pitch would fall in the case of F0-based listening.

The tones of a pair had one of the following spectral profiles: (a) low-spectrum tone: 2nd–4th harmonic, high-spectrum tone: 5th–10th harmonic, N = 17 tone pairs; (b) low-spectrum tone: 3rd–6th harmonic, high-spectrum tone: 7th–14th harmonic, N = 17 tone pairs; and (c) low-spectrum tone: 4th–8th harmonic, high-spectrum tone: 9th–18th harmonic, N = 16 tone pairs. Note that the frequency ratio between the lowest and highest frequency component of a tone was always 1:2, corresponding to one octave. To achieve a smooth, natural timbre, we decreased the amplitudes of the harmonics by 6 dB per octave relative to F0. The frequency of the missing F0 was restricted to a range of 100–400 Hz. Five different frequency separations of the missing F0s of a tone pair were considered: (a) ±204 cents (musical interval of a major second; two semitones; frequency ratio of 9:8); (b) ±386 cents (musical interval of a major third; four semitones; frequency ratio of 5:4); (c) ±498 cents (musical interval of a fourth; five semitones; frequency ratio of 4:3); (d) ±702 cents (musical interval of a fifth; seven semitones; frequency ratio of 3:2); (e) ±884 cents (musical interval of a major sixth; nine semitones; frequency ratio of 5:3). For each of these five interval conditions, the type of spectral profile was matched as far as possible (each type occurring either six or seven times). Because of the ambiguity of the stimuli (cf. Figure 1), an increasing F0 interval was associated with a decreasing frequency separation of the overtone spectra. As the spectrum of each tone comprised exactly one octave, corresponding to a constant range on a logarithmic scale, the spectral shift between the two tones of a pair can be expressed in terms of a specific frequency ratio, and it does not matter whether the lowest or the highest frequency is considered. The magnitudes of spectral- and F0-based pitch shifts were roughly balanced at the F0 interval of the fifth (frequency ratio for missing F0: 1.5; frequency ratio for spectral profile type a: 1.666; frequency ratio for spectral profile type b: 1.555; frequency ratio for spectral profile type c: 1.5). For smaller F0 intervals, the shift was relatively larger for the spectral components, whereas for wider F0 intervals, the shift was relatively larger for the missing F0.

Procedure

A computer monitor informed the participants that they were about to hear 100 tone sequences (50 tone pairs presented in both within-pair orders). Participants were instructed to decide, for each pair, whether they had heard a rising or falling pitch sequence and to note their decision on an answer sheet. No information was provided on the ambiguous nature of the stimuli, and the participants were kept in the belief that there was always a correct and an incorrect response alternative. We encouraged the participants to rely on their first intuitive impression before making a decision, but we allowed them to imagine singing the tone sequences or to hum them. In the case of indecision, the test block with the respective trial could be presented again (10 trials, each with a duration of 40.5 s). But, to keep the testing time short, the participants rarely used this option.

The test was presented via headphones (AKG K240) in a silent room at a sound pressure level of 60 dB. To familiarize the participants with the AAT, we presented the first test block twice but considered only the categorizations for the second presentation. The test was run without feedback. The AAT was performed twice, with a short pause in between, so that four responses were obtained for each tone pair.

Data Analysis

The AAT scores (proportion of trials categorized in terms of the missing F0s) from the two test presentations were averaged. As the average scores were not normally distributed, nonparametric statistics, which were based on the ranking of test values (Friedman test, Mann-Whitney U test, Kruskal-Wallis test, Spearman rank correlation, Wilcoxon signed-rank test), were used.

Results

Effect of Musical Competence

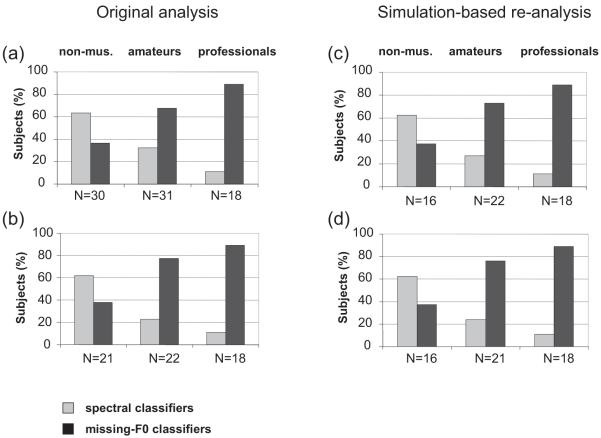
The mean AAT scores were 45.9 in nonmusicians, 61.6 in amateurs, and 81.6 in professional musicians. A Mann–Whitney U test on the ranking of the achieved scores indicated that all differences between groups were highly significant (nonmusicians vs. amateurs, U = 275, Z = −2.7, p = .0061; nonmusicians vs. professionals, U = 76, Z = −4.1, p < .0001; amateurs vs. professionals, U = 137, Z = −2.9, p = .0032). When all participants were dichotomously categorized as either “spectral” or “missing-F0 classifiers,” the proportion of missing-F0 classifiers increased significantly with growing musical competence: A liberal categorization criterion (AAT score either up to or above 50) resulted in χ²(2, N = 79) = 11.6, p = .0031 (see more details in Figure 2a); a stricter categorization criterion (AAT score either below 25 or above 75) resulted in χ²(2, N = 61) = 12.9, p = .0016 (see more details in Figure 2b).

Figure 2.

Percentage of spectral classifiers and missing-F0 classifiers among the three musical competence groups. In Panels a and b, assignment is based on the Auditory Ambiguity Test (AAT) score. In Panels c and d, assignment is based on the guessing-corrected F0-prevalence value. The criteria for group assignment were, for Panels a and c, AAT score or F0-prevalence value either up to or above 50 (liberal criterion) and, for Panels b and d, AAT score or F0-prevalence value either below 25 or above 75 (stricter criterion). non-mus. = nonmusicians.

Effect of Interval Width

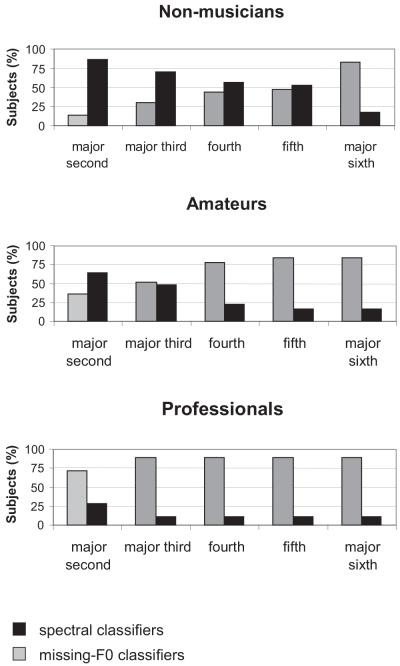
The likelihood of F0-based judgments systematically increased with interval width, χ²(4, N = 79) = 197.4, p < .0001; Friedman ranks: 1.3 (major second), 2.3 (major third), 3.0 (fourth), 3.9 (fifth), 4.5 (major sixth). The mean proportions of F0-based decisions were 43% for the major second, 55% for the major third, 60% for the fourth, 68% for the fifth, and 75% for the major sixth. The effect was significant for all three musical competence groups: nonmusicians, χ²(4, N = 30) = 100.5, p < .0001; amateurs, χ²(4, N = 31) = 85.4, p < .0001; professionals, χ²(4, N = 18) = 20.8, p < .0003. More detailed results are shown in Figure 3. We again categorized participants as “spectral classifiers” (up to 50% of F0-based classifications) and “missing-F0 classifiers” (otherwise), but now this categorization was done separately for each interval condition so that a subject could belong to different categories, depending on the interval. Figure 4 shows the results for the three musical competence groups. For nonmusicians and amateurs, the proportion of missing-F0 classifiers increased gradually with F0-interval width. The equilibrium point, at which spectral and missing-F0 classifiers were equally frequent, was around the fifth in the sample of nonmusicians and around the major third in the sample of amateurs. For the professionals, there was a clear preponderance of F0 classifiers at all intervals, although less pronounced at the major second. An equilibrium point would possibly be reached at an interval smaller than two semitones.

Figure 3.

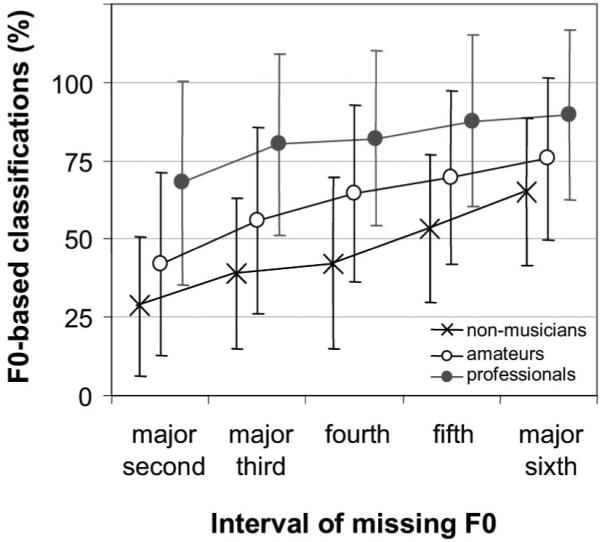
Interval-specific response patterns for the three musical competence groups (error bars represent standard deviations).

Figure 4.

Percentage of participants who predominantly classified the tasks of a respective interval condition in terms of spectral or missing-F0 cues (spectral classifier: Auditory Ambiguity Test [AAT] score ≤ 50%, missing-F0 classifier: AAT score > 50%).

Spectral Profile Type

The type of spectral profile had a significant effect on the classifications, Friedman test: χ²(2, N = 79) = 21.3, p < .0001. The mean proportion of F0-based responses was 60.8% for tone pairs of type a, 63.8% for tone pairs of type b, and 55.7% for tone pairs of type c. As each trial of the AAT consisted of two tones with different spectral characteristics, the effects cannot be tied down to specific parameters. Therefore, we refrain from interpreting the effect in the Discussion.

Ordering of Tone Sequences

It did not matter whether the missing F0s of the tone pairs were falling and the spectra were rising (60.1% F0-based responses) or whether the missing F0s of the tone pairs were rising and the spectra were falling (60.3% F0-based responses; Wilcoxon signed rank test: Z = −0.2, p = .84).

Simulation-Based Correction for Guessing and Data Reanalysis

Before drawing definite conclusions, we had to take into account that only a minority of participants responded in a perfectly consistent way. Thus, the assumption is that, with a certain probability, our participants made a random decision or, in other words, they were guessing. To check for inconsistencies in the responses, we derived two additional parameters. By relating these parameters to the results of extensive model simulations, we estimated not only a probability of guessing but also a parameter that may be considered a guessing-corrected AAT score. After applying this correction, we will present a statistical reanalysis.

Method

Reanalysis of the Participants’ Responses

To assess the probability of guessing, we exploited the fact that tone pairs had to be judged four times (50 tone pairs presented in both orders; AAT test performed twice). The four judgments should be identical for a perfectly performing subject, but inconsistencies are expected for an occasionally guessing subject (one deviating judgment or two judgments of either type). To characterize a subject on that score, we determined the percentage of inconsistently categorized tone pairs, p_inconsistent. It can be expected that this parameter will monotonically increase with the probability of guessing. The second parameter, called the percentage of inhomogeneous judgments, p_{inhomogeneous}, seeks to characterize a subject’s commitment to one of the two perceptual modes. This parameter is defined as the percentage of judgments deviating from the subject’s typical response behavior (indicated by the AAT score). For spectral classifiers, this is the percentage of F0-based judgments, whereas for missing-F0 classifiers, it is the percentage of spectral judgments. For reduction of the effect of guessing, the calculation of this parameter ignored equivocally categorized tone pairs (two judgments of either type) and, in the case of only three identical judgments, the deviating judgment. While p_inconsistent ranges between 0% and 100%, p_{inhomogeneous} is evidently limited to 50%, which is the expected value for a subject guessing all of the time or for a perfectly performing subject without a preferred perceptual mode.

Model

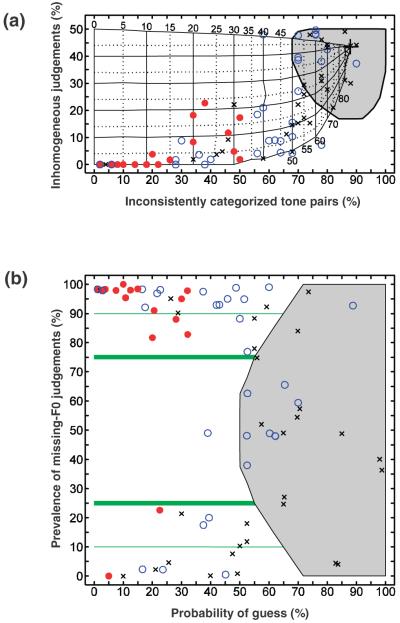
Although the associations of the above parameters with the probability of guessing and the determination for one or the other perceptual mode, respectively, is evident, the method for interpreting them in a more quantitative sense is not obvious. To solve this problem, we performed extensive Monte Carlo simulations. We assumed that participants made a random choice with probability p_guess and a deliberate decision with probability 1 – p_guess. The proportion of deliberate decisions in favor of F0 was specified by the parameter p_F0, called the missing-F0 prevalence value. For the sake of simplicity, we assumed that p_F0 was the same for all tone pairs. For given parameter combinations (p_guess, p_F0), the investigation of 100,000 participants was simulated, and each virtual subject was evaluated in exactly the same way as a real subject. This means that for each virtual subject, we finally obtained a parameter pair (p_inconsistent, p_{inhomogeneous}). Note that the prevalence values p_F0 and 100%-p_F0 yield identical results in this model so that simulations can be restricted to values 0 ≤ p_F0 ≤ 50%. An example of the simulated results (four specific groups of participants; AAT with 50 tone pairs) is shown in Figure 5. The two axes represent the percentages of inconsistent and inhomogeneous categorizations, respectively. Each symbol corresponds to 1 virtual subject. Four clusters of symbols, each representing a specific group of participants, can be recognized. The center of a cluster is marked by a cross; it represents the two-dimensional (2D) median derived by convex hull peeling (Barnett, 1976). Because the percentage of inconsistent classifications is between 0 and 100, corresponding to twice the number of tone pairs in the test, the clusters are organized in columns at regular intervals of 2%. The cluster at the upper right corresponds to participants guessing all of the time (p_guess of 100%), whereas the cluster at the lower left corresponds to a population of almost perfectly performing participants (p_guess of 10%) with a missing-F0 prevalence p_F0 of 0% (or 100%). As long as p_guess is relatively small, the value derived for p_{inhomogeneous} is typically distributed around p_F0 or 100% – p_F0. The other two clusters in Figure 5 were obtained for a missing-F0 prevalence of 20% (or 80%) and 5% (or 95%), respectively; the probability p_guess was 20% and 40%, respectively. Note that a perfectly performing subject (p_guess of 0%) would be characterized by p_inconsistent = 0; moreover, p_{inhomogeneous} would correspond to either p_F0 or 100% p_F0, with p_F0 being the AAT score.

Figure 5.

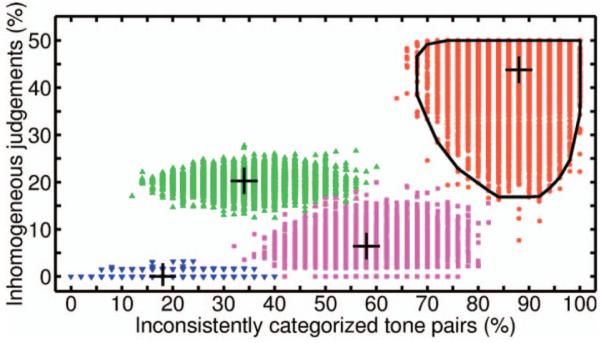
Simulation results for four specific groups of participants. Each of the four clusters (in which the center is marked by a cross) represents one group, specified by the parameters p_guess and p_F0. From right to left: participants guessing all of the time (p_guess = 100%, p_F0 = undefined); participants with an intermediate guessing probability (p_guess = 40%, p_F0 = 5% or 95%); participants with a low guessing probability (p_guess = 20%, p_F0 = 20% or 80%); participants with almost perfect performance (p_guess = 10%, p_F0 = 0% or 100%). For further details, see the in-text discussion of this figure.

Maximum Likelihood Estimation of the Unknown Model Parameters

The model parameters considered in Figure 5 were chosen such that the resulting clusters were largely separated. It is clear that a higher similarity of the parameters would have resulted in a considerable overlap. Thus, in practice, unequivocally assigning a subject characterized by (p_inconsistent, p_{inhomogeneous}) to a certain group of virtual participants characterized by p_guess, p_F0 is impossible. Nevertheless, supposing that p_inconsistent, p_{inhomogeneous} corresponds to a point close to the center of a specific cluster (e.g., one of those in Figure 5), the conclusion can be made that the subject’s performance is more likely described by the model parameters associated with that cluster than by other parameter constellations. Thus, model parameters (p_guess, p_F0) could be determined so that the center of the resulting cluster corresponds to the observed data point (p_inconsistent, p_{inhomogeneous}). This idea basically corresponds to maximum-likelihood parameter estimation. Simulations also provide a basis for discarding participants with high guessing probability. The contour line in the upper right cluster in Figure 5 represents the 99.9% percentile for participants with p_guess = 100%; it is based on the simulation of 100,000 virtual participants. Supposing that an observed data point (p_inconsistent, p_{inhomogeneous}) is located outside the area enclosed by that curve, it is highly unlikely that the respective subject was guessing all the time.

Results

Figure 6a shows the same parameter space as that of Figure 5, which means that the abscissa is the percentage of inconsistent classifications, p_inconsistent, and the ordinate is the percentage of inhomogeneous classifications, p_{inhomogeneous}. Each of the 79 participants is represented by exactly one data point. The 99.9% percentile for participants guessing all of the time (displayed in Figure 5 as a contour line) now corresponds to the boundary of the gray area. Participants with data points inside this area (“forbidden region”) were excluded from further analysis because they could not be sufficiently distinguished from participants guessing all the time. All in all, 56 participants met the inclusion criterion (16 nonmusicians, 22 amateurs, 18 professionals). This meant that we had to exclude almost half of the nonmusicians and about one third of the amateurs but none of the professionals. The dependence of the exclusion rate on musical competence was statistically significant, χ²(2, N = 79) = 11.9, p = .0026.

Figure 6.

Simulation-based correction for guessing. (a) Outer axes represent experimental parameters and inner grid represents model parameters; for further details, see in-text discussion of this figure. (b) Mapping of experimental parameters onto the model parameters. Response characteristics of individual participants are visualized in a two-dimensional parameter space, with the probability of guess as the abscissa and the prevalence of missing F0 judgments as the ordinate. Participants guessing all the time would be mapped, with probability 99.9%, into the gray area, signifying the “forbidden region.” Data points falling into this region were excluded from further statistical analysis. The prevalence of nonmusicians (×) above the 75% line and of amateurs (open circles) and professionals (filled circles) below the 25% line shows that musical expertise is associated with a significant shift from spectral hearing toward F0-based hearing.

The inner grid in Figure 6a is based on extensive model simulations. The model parameters p_guess and p_F0 were systematically varied in steps of 5%, and simulations as exemplified in Figure 5 were performed. In this way, we obtained 100,000 estimates of p_inconsistent, p_{inhomogeneous} for each combination of p_guess, p_F0, which provided the basis for the estimation of a 2D median,¹ which corresponds to a grid point in Figure 6a. The small numbers on the vertical grid lines indicate the associated model parameter p_guess, whereas the model parameter p_F0 may be read on the scale for p_{inhomogeneous} (remember that for p_guess = 0 and p_F0 < 50%, p_{inhomogeneous} and p_F0 are identical).²

By associating each data point with the closest grid point, mapping the experimental parameters (p_inconsistent, p_{inhomogeneous}) onto the model parameters (p_guess, p_F0) is now possible, thereby characterizing each subject in terms of a model. Because our grid is relatively coarse, we refined this mapping by interpolation and extrapolation techniques. Figure 6b shows the result. The abscissa is the subject’s guessing probability, p_guess, and the ordinate is the prevalence of F0-based categorizations, p_F0. The gray area represents the counterpart of the forbidden region in Figure 6a. In contrast to the simulations, in which it was sufficient to consider p_F0 values between 0% and 50%, we now consider the full range, that is, 0%–100% (by accounting for the AAT score, distinguishing between p_F0 and 100% – p_F0 is easy). The prevalence value p_F0, that is, the estimated predominance of missing-F0 hearing, may be interpreted as a guessing-corrected AAT score. The distribution of the prevalence value p_F0 was clearly bimodal: Except for one amateur musician, the value was either below 25% or above 75% (indicated by thick horizontal lines in Figure 6b). For the majority of participants (73.2%), the value was even below 10% or was above 90% (indicated by thin horizontal lines in Figure 6b).

Musical Competence

A comparison of the three musical competence groups confirmed the conclusions derived from the original data. Only 37.5% of the nonmusicians but 73% of the amateur musicians and 89% of the professional musicians based their judgments predominantly on F0-pitch cues. A nonparametric Mann–Whitney U test on the ranking of the individual missing-F0 prevalence values indicated that the effect was due mainly to the difference between nonmusicians and musically experienced participants (nonmusicians vs. amateurs: U = 84.5, Z = −2.7, p = .0068; nonmusicians vs. professionals, U = 43, Z = −3.5, p = .0005; amateurs vs. professionals, U = 161.5, Z = −1.0, p = .32). When the participants were categorized as either “spectral” or “missing-F0 classifiers,” a significant increase again was observed in the proportion of missing-F0 classifiers with growing musical competence: With a liberal criterion for group assignment (missing-F0 prevalence value either up to or above 50%), the p value was .0049, χ²(2, N = 56) = 10.6; with a stricter criterion for group assignment (missing-F0 prevalence value either below 25% or above 75%), the p value was .0036, χ²(2, N = 55) = 11.3. A comparison between the original analysis (see Figure 2, Panels a and b) and the simulation-based reanalysis (see Figure 2, Panels c and d) shows no obvious difference.

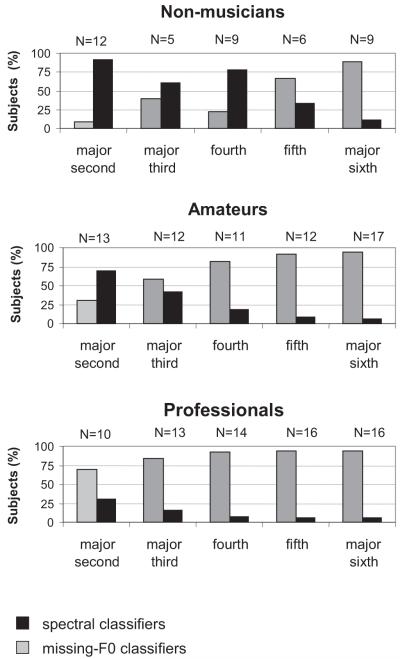
Figure 7 shows the relative proportions of spectral and missing-F0 classifiers (up to or more than 50% of missing-F0 categorizations; N = the number of participants accounted for). The distribution pattern is very similar to the one obtained for the original data (see Figure 4). The apparent irregularity around the fourth in nonmusicians most likely results from the reduced sample size. In summary, the reanalyses corroborated our hypothesis that the effects seen in the original data were, first and foremost, due to true perceptual differences.

Figure 7.

Percentage of spectral classifiers and missing-F0 classifiers (up to or more than 50% of interval-specific tasks categorized in terms of the missing F0) among the participants meeting the inclusion criterion. N = number of participants included in the respective comparison. The distribution pattern is similar to the one obtained for the original data (see Figure 4).

Specific Factors Associated With Musical Competence

In the following section, we address the question of whether the two factors of (a) age when musical training started and (b) instrument that was initially and actually played were related to the observed perceptual group differences. As the categorization of participants according to specific criteria led to relatively small subgroups, all participants were included in the following analyses, irrespective of their guessing probabilities. Comparisons were made between amateur and professional musicians only. The parameter was the guessing-corrected AAT prevalence value.

Onset of musical activity

We calculated a Spearman rank order correlation for all musically experienced participants (amateurs and professionals) to test whether the age when training started critically affected the AAT prevalence value. This was not the case (ρ= −0.079, p = .5). In addition, two parallel samples of amateurs and professionals were built, which were matched for the onset of musical practice. Each of these samples contained 15 participants, all of whom had started to practice at the following ages: 3 years (n = 2), 4 years (n = 3), 5 years (n = 2), 6 years (n = 2), 7 years (n = 1), 8 years (n = 2), 9 years (n = 1), 10 years (n = 1), and 15 years (n = 1). The AAT prevalence values were still significantly different for the two groups (mean value for amateurs: 69.7; mean value for professionals: 89.1; U = 51, Z = −2.5, p = .01). These results indicate that the onset of musical practice is not critical for the prevalent hearing mode, as measured by the AAT.

First instrument

As evident from Table 1, the probability of having played a certain instrument at the onset of musical activity (first instrument) and in advanced musical practice (actual major instrument) differed between amateurs and professionals. Although about half of the amateurs had started with the recorder (48.4%), this was the case for only a minority of professionals (11.1%). Most professionals (55.5%) but relatively few amateurs (19.3%) indicated that their first instrument had been the piano. The recorder produces almost no overtones, whereas the spectra of piano tones are richer, with a prominent F0 and lower harmonics that decrease in amplitude with harmonic order (Roederer, 1975). It may, therefore, be speculated that playing the piano as the first instrument sensitizes participants to harmonic sounds and facilitates the extraction of F0, whereas playing the recorder might have no effect or a different effect. To test this hypothesis, we performed two selective statistical comparisons in which we excluded all participants who had started with one of these instruments. The significant difference in the AAT prevalence values of amateur and professional musicians was changed neither by the exclusion of the recorder players (U = 74, Z = −2, p = .04) nor by the exclusion of the piano players (U = 43.5, Z = −2.4, p = .018). Consistently, when all of the indicated first instruments were considered, it was found that they had no systematic influence on the AAT prevalence values (Kruskal–Wallis test: H = 11, df = 8, p = .2). It may be argued that it makes a difference whether the first musical exercises were done with string, keyboard, or wind instruments or with the vocal cords and whether this action required active intonation (bow instruments, trombone, singing) or not (plucked instruments, keyboard, percussion, most wind instruments). Separate analyses, in which we considered these aspects, were insignificant, as well (category of instrument: H = 3.4, df = 4, p = .49; intonated vs. nonintonated playing: U = 144, Z= −0.9, p = .35). These results allow rejection of the hypothesis that the first instrument determines the prevalent hearing mode.

Actual major instrument

The spectrum of actually played instruments was slightly broader and more balanced between the two musical competence groups than for the first instrument (see Table 1). A comparison considering all indicated major instruments revealed no systematic influence on the AAT prevalence values (Kruskal–Wallis test: H = 12.4, df = 13, p = .5). Neither the instrument category (H = 2, df = 4, p = .73), nor the necessity of controlling pitch during playing (U = 266, Z = −0.1, p = .9) had an effect, thus arguing against the hypothesis that the major instrument determines the prevalent hearing mode.

Discussion

The reanalyzed data support the hypothesis that the observed differences in the AAT prevalence values of nonmusicians, musical amateurs, and professional musicians are due to true perceptual differences. In the following, three different hypotheses are formulated to explain this effect.

Hypothesis 1: The observed interindividual differences are due to learning-induced changes in the neural representation of the pitch of complex tones.

According to our initial hypothesis, the most plausible explanation would be that playing an instrument enhances the neural representation of the fundamental pitch of complex tones. Support for this interpretation comes from the previous finding that musicians are superior to nonmusicians when the task involves tuning a sinusoid to the missing F0 of a single complex tone (Preisler, 1993). A high learning-induced plasticity would be consistent with recent neuroimaging studies, underlining the importance of cortical pitch processing (Bendor & Wang, 2005; Griffiths, Buchel, Frackowiak, & Patterson, 1998; Krumbholz, Patterson, Seither-Preisler, Lammertmann, & Lütkenhöner, 2003; Patterson, Uppenkamp, Johnsrude, & Griffiths, 2002; Penagos, Melcher, & Oxenham, 2004; Seither-Preisler, Krumbholz, Patterson, Seither, & Lütkenhöner, 2004, 2006a, 2006b; Warren, Uppenkamp, Patterson, & Griffiths, 2003). Moreover, the plasticity hypothesis would be in line with two influential auditory models on pitch processing.

Terhardt, Stoll, and Seewann (1982) formulated a pattern-recognition model, which starts from the assumption that individuals acquire harmonic templates in early infancy by listening to voiced speech sounds. According to the model, in the case of the missing F0, the individual would use the learned templates to complete the missing information. From this point of view, a higher prevalence of F0-pitch classifications in musicians could indicate that extensive exposure to instrumental sounds further consolidates the internal representation of the harmonic series based on F0.

The auditory image model of Patterson et al. (1992) postulates a hierarchical analysis, which ends in a stage that combines the spectral profile (spectral pitches and timbre) and the temporal profile (fundamental pitch) of the auditory image—a physiologically motivated representation of sound (Bleeck & Patterson, 2002). A change in the relative weight of the two profiles in favor of the temporal profile could account for learning-induced shifts from spectral sensations toward missing-F0 sensations.

Hypothesis 2: The observed interindividual differences are due to genetic factors and/or early formative influences.

It may also be the case that the observed perceptual differences reflect congenital differences in musical aptitude and that highly gifted participants are more sensitive to the fundamental pitch of complex tones. In its extreme form, this assumption is not tenable because musical aptitude is not necessarily related to the social facilities required for learning an instrument and eventually becoming a musician. The present data do not allow us to exclude congenital influences. To quantify the relative contributions of learning-related and genetic factors, we would need to perform a time-consuming longitudinal study from early childhood to adulthood that investigates how musical practice influences the individual AAT score over time.

The situation is more clear-cut with regard to the hypothesis that our observations are a function of early formative influences. To this end, the onset of musical activity and the type of the first instrument played could be critical in establishing the prevalent hearing mode. Our results clearly argue against this view because none of these aspects had a systematic effect on the AAT prevalence value.

Hypothesis 3: The observed interindividual differences are due to variations in focused attention on melodic pitch contours.

In Western tonal music, melodic intervals are normally drawn from the chromatic scale, dividing the octave into 12 semitones. In our study, all F0-intervals were drawn from this scale, whereas the spectral intervals were irregular. It may be speculated that the professionals focused their attention on the musically relevant F0-intervals, even if these intervals were small relative to the concomitant spectral changes. Amateurs and nonmusicians may have been less influenced by this criterion so that their perceptual focus was more strongly directed toward the changes of the immediate physical sound attributes. It is unlikely, however, that melodic processing was the only influential factor because musicians are already superior when they have to tune a sinusoid to the missing F0 of a single complex tone (Preisler, 1993).