A Multiple-plane Approach to Measure the Structural Properties of Functionally Active Regions in the Human Cortex

Abstract

Advanced magnetic resonance imaging (MRI) techniques provide the means of studying both the structural and the functional properties of various brain regions, allowing us to address the relationship between the structural changes in human brain regions and the activity of these regions. However, analytical approaches combining functional (fMRI) and structural (sMRI) information are still far from optimal. In order to improve the accuracy of measurement of structural properties in active regions, the current study tested a new analytical approach that repeated a surface-based analysis at multiple planes crossing different depths of cortex. Twelve subjects underwent a fear conditioning study. During these tasks, fMRI and sMRI scans were acquired. The fMRI images were carefully registered to the sMRI images with an additional correction for cortical borders. The fMRI images were then analyzed with the new multiple-plane surface-based approach as compared to the volume-based approach, and the cortical thickness and volume of an active region were measured. The results suggested (1) using an additional correction for cortical borders and an intermediate template image produced an acceptable registration of fMRI and sMRI images; (2) surface-based analysis at multiple depths of cortex revealed more activity than the same analysis at any single depth; (3) projection of active surface vertices in a ribbon fashion improved active volume estimates; and (4) correction with gray matter segmentation removed non-cortical regions from the volumetric measurement of active regions. In conclusion, the new multiple-plane surface-based analysis approaches produce improved measurement of cortical thickness and volume of active brain regions. These results support the use of novel approaches for combined analysis of functional and structural neuroimaging.

Introduction

One of the fundamental questions in neuroscience is the relationship between neural activity and structural properties of different brain regions. Investigation of this relationship will enrich our understanding of neuro-substrates involved in biological or pathological brain function. During decades of research, many invasive procedures have been used to study this question in animals. None of these techniques, however, can be applied to humans, leading to a knowledge gap regarding the relationship between human brain activity and its substrates. The development of non–invasive magnetic resonance imaging (MRI) techniques provides the opportunity to study the relationship of brain activity with structural substrates in humans in vivo. Structural MRI (sMRI) images of the brain allow the study of volume, voxel-based morphometry (VBM), cortical thickness, and cortical surface shape and folding of brain regions (Ashburner and Friston, 2000; Caviness et al., 1999; Fischl et al., 1999; Good et al., 2001; Karl et al., 2006; Kasai et al., 2008; Lerch and Evans, 2005; Pienaar et al., 2008; Sallet et al., 2003). Correlating sMRI with functional MRI (fMRI), magnetoencephalography (MEG), positron emission tomography (PET), or event-related potentials (ERP) advances knowledge of the structure - activity relationship (Araki et al., 2005; Bremner et al., 2003; Schneider et al., 2002; Schuff et al., 2001). Functional MRI is more often combined with sMRI because its superior spatial and temporal resolutions improve detection of brain activity as compared to other functional neuroimaging techniques. Combining functional and structural MRI scanning is also an efficient use of laboratory resources. However, the few pioneering studies to employ this promising technique have used different analytical approaches in relating the fMRI and sMRI data. (DaSilva et al., 2008; Hadjikhani et al., 2007; Milad et al., 2007a; Rasser et al., 2005; Remy et al., 2005; Schaechter et al., 2006; Siegle et al., 2003; Siok et al., 2008). As summarized below, these approaches could clearly benefit from further development.

Numerous studies have approached this question by measuring the volume or mean cortical thickness of anatomically defined brain regions where activity was detected with the fMRI (Remy et al., 2005; Siegle et al., 2003; Siok et al., 2008). However, the activity only occurred in part of the anatomical region, therefore, the volume or the mean cortical thickness of the anatomical region may not reflect the subtle differences in active regions. Other studies selected theoretically more sensitive approach by examining differences in cortical thickness or volume of the functionally active regions, and a correlation between thickness and the regional activity (DaSilva et al., 2008; Hadjikhani et al., 2007; Rasser et al., 2005; Schaechter et al., 2006). However, these studies employed a range of analytical approaches to define the activity, differing in the normalization, smoothing, and definition of active regions. These differences may affect localization of fMRI activity, as well as the statistical power of the analysis (Hagler et al., 2006; Hayasaka et al., 2004).

Some studies used volume-based group analysis that is characterized by three-dimensional (3-D) smoothing in Euclidean space and 3-D cross-subject normalization according to a standard space (DaSilva et al., 2008; Milad et al., 2007a; VanEssen, 1997). Volume-based analyses encompass the whole brain at once, but have a number of intrinsic problems. For example, the 3-D smoothing may dilute the activity in gray matter with adjacent white matter or CSF. It may also extend active regions beyond the cortex since the 3-D smoothing of fMRI images is not restricted within the cortical boundary (e.g., Fig-1A). Furthermore, the 3-D smoothing may extend the activity in a gyrus onto a part of an adjacent gyrus in Euclidean spaces that are not biologically connected (e.g., Fig-1B). 3-D normalization in volume-based group analysis does not intend to match the gyri and sulci as surface-based normalization does (see below) (VanEssen and Drury, 1997). However, a number of studies ignore the differences in two normalization approaches by using 3-D normalization in defining group activity in the standard space, but then using surface-based normalization parameters created by programs of cortical thickness measurement to convert these active regions from the standard space back to individual spaces for cortical thickness or volume measures (DaSilva et al., 2008; Milad et al., 2007a). These inconsistencies between two types of normalizations could contribute to observed differences. In short, the 3-D normalization method is less than ideal for defining active regions, and measuring their structural properties.

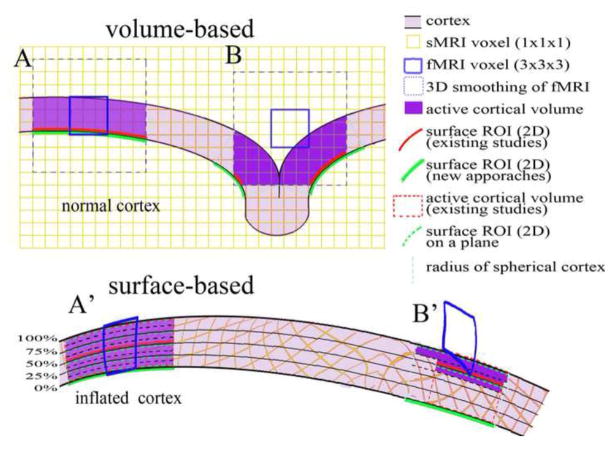
Figure 1.

Illustration of analytical approaches. A part of normal cortex with curvature is at the top and the same part of the cortex on the spherical model of cortex (spherical cortex) is at the bottom. The small yellow squares are sMRI voxels and the large blue boxes are fMRI voxels. Note that the voxels are transformed in the spherical cortex during the inflation of cortex to sphere. In the Volume-based analysis, A: a fMRI voxel (blue line box) was smoothed to 1 voxel length in 3-D in Euclidean space (blue dash line box), and occupies the active cortical volume (purple shaded). The intersection of the smoothed voxel and a cortical surface is defined as a surface ROI in existing studies (red line) or in the volume-based analysis of the current study (green line). Two surface ROIs are similar if the smoothed voxel occupies the entire cortical depth. B: A fMRI voxel is registered in part of cortical depth, and 3-D smoothing expends the active volume to an adjacent gyrus. The surface ROI is split on both gryi. The current study defined a larger surface ROI (green line) than existing studies (red line). A′: The A is transformed in the spherical cortical model. Previous studies defined active vertices on one depth at surface ROI (red line) and projected the surface ROI to the entire cortex as active volume (red dash box). The new multiple-plane approach defined the active vertices on five planes at 0, 25, 50, 75, and 100% of cortical thickness from white matter border (black lines), and projected the active vertices of each plane to sMRI voxels (yellow) in a ribbon of 12.5% of cortical thickness above and below the plane within cortex (black dash line). Active vertices on all planes are summed on one surface as a surface ROI (green line) for thickness measurement, and hit voxels in all ribbons are assembled together as a volume ROI to estimate the active volume (purple). B′: The B is transformed in the spherical cortical model. The multiple-plane approach defines a larger surface-ROI (green line) than existing studies (red line) because it summed activity on two planes. In contrast, this approach estimates a smaller active volume (purple) than existing studies (red dash line box).

Surface-based analysis is a recently developed method to overcome the shortcomings of volume-based analysis. Surface-based analysis is characterized by two-dimensional (2-D) smoothing along the cortical surface and cross-subject normalization according to the gyri and sulci. In surface-based analysis, the activity of individual subjects is identified in non-smoothed fMRI images, and the coefficient image of a contrast is registered on the sMRI image of this subject (Anticevic et al., 2008; Desai et al., 2005; Greve and Fischl, 2009; Spiridon et al., 2006). The cortical surface is reconstructed from the sMRI images. The coefficient image is smoothed along the cortical surface to restrain the smoothing in the cortex and to avoid expanding the activity onto unconnected gyri (e.g., Fig-1A′, B′). The cortical surface of each subject is registered using gyri and sulci as landmarks to reduce the mismatch of gyri (Desai et al., 2005; Fischl et al., 1999; Jo et al., 2007). The active vertices on the surface of standard space are individualized according to the same parameters as surface-based normalization to avoid any inconsistence in normalization and individualization (Anticevic et al., 2008; Schaechter et al., 2006). This approach theoretically allows to overcome some of the shortcomings of a volume-based analysis. However, the initial implementation of a surface-based analysis has not been error free. First, a majority of studies only analyzed the activity on one depth of cortex in a surface-based analysis. This results in overlooking the activity at other depths of the cortex, if the active fMRI voxels are not registered at the selected cortical depth (e.g., Fig-1B′) (Burton et al., 2008; Hagler et al., 2006; Schaechter et al., 2006). Additional smoothing or extensive interpolation may recruit more activity at other depths, but these approaches sacrifice resolution (Anticevic et al., 2008; Cohen et al., 2008; Operto et al., 2008). Other studies registered mean or maximal activity across the entire thickness of each cortical column onto a single surface of cortex, which also can theoretically lead to false positive findings after 2-D smoothing along the cortical surface (Desai et al., 2005; Napadow et al., 2006). Furthermore, some studies simply calculate the volume of active cortical region by multiplying the area of active vertices on the surface with the cortical thickness, based on the assumption that activity on one surface represents activity in the entire depth of cortex (Anticevic et al., 2008). This assumption is questionable given the fact that activity at different depths of cortex is not always the same if an active fMRI voxel does not cover the entire depth of cortex (Desai et al., 2005). This may lead to misestimating the volume of active cortical regions (e.g., Fig-1B′). Thus, while the surface-based analysis is preferable for the studies that link function and structure of brain regions, existing procedures are not error-free if the active fMRI voxels do not cover entire depth of the cortex.

Further development of analytic approaches is needed for accurate investigation of the structural properties of active regions. To overcome the shortcomings of the existing surface-based analysis in identifying the active cortical regions for measurement of structural properties, we designed a new surface-based approach (e.g., Fig-1A′, B′). In this new approach, the same surface-based analysis is performed independently on multiple planes at different depth of the cortex. The supra-threshold activity on each plane in the individual space is then summarized onto a surface to create a surface region of interest (surface ROI) for measuring cortical thickness of the active cortical region. To measure the cortical volume of the active region, the activity on each plane is projected to a ribbon of cortex that covers a portion of thickness, instead of the entire thickness, and then assembles the hit voxels from all ribbons into a 3-D volume region of interest (volume ROI); the volume ROI is finally corrected with segmentation of gray matter to remove the non-cortical voxels. Theoretically, this multiple-plane approach should be less likely to result in miscalculating either the number of active vertices measuring the cortical thickness of active regions or the number of cortical voxels measuring the volume of active cortical regions. In the present manuscript we describe the application of this novel method for identifying active regions for the measurement of cortical thickness and cortical volumes of functionally active regions. The analysis is performed using Freesurfer, a validated surface-based analytical software package (http://www.surfer.nmr.mgh.harvard.edu/fswiki). Freesurfer is able to perform analyses at any depth of cortex.

Materials and methods

Participants

For the current study we scanned twelve subjects including recently returning veterans with PTSD diagnosis (n=6), and age and gender-matched non-veteran healthy controls (n=6). PTSD diagnosis was established using the Structured Clinical Interview for DSM-IV and Clinician Administered PTSD Scale. All subjects were right-handed males between 21 and 29 years old. The two groups (PTSD, control) did not differ in age, gender, education, or other demographics. After a complete description of the study was provided to the participants, written informed consent was obtained. The study was approved by the University of Michigan and the Ann Arbor Veterans Affairs Healthcare System.

Fear conditioning paradigm

Over a two-day period, subjects underwent functional (fMRI) and structural (sMRI) scanning. The experimental paradigm was designed to study fear conditioning, fear extinction, and extinction retention. We utilized a modified human conditioned fear paradigm, originally described by Milad et al. (Milad et al., 2007b). Different colored lights (blue, yellow, pink) – conditioned stimuli (CS) were shown in a ‘context’ of office or conference room. Context was manipulated so that one context indicated danger (i.e. context where shocks are presented during acquisition) and one represented safety (i.e. context where no shocks were received). Context type and stimuli order were counterbalanced. On Day 1, subjects engaged in three tasks: habituation, acquisition, and extinction. In each task, context alone occurred for 2–7sec, before the light came on for a total of 2–7sec. Each epoch was 9 sec in length. Inter-stimulus intervals were marked by a fixation cross, and these were jittered (12–18sec). During the habituation phase, no shocks were administered. During the acquisition phase, fear responses to stimuli were conditioned by pairing two of the colors with mild electric shocks (CS+) to the forearm. The third color was never paired with shock (CS−). The two CS+ (8 of each) were blocked, and each were interleaved with presentations of the CS− (16 presentations in total). The CS+s were reinforced with shock 60% of the time during acquisition only. During the extinction phase, fear responses to one of the CS+ were extinguished via repeated presentation (N = 16) of the CS+ without shock (CS+E), interleaved with presentations of the CS− (N = 16). The other CS+ was not presented during extinction and thus remained un-extinguished (CS+U). On Day 2, subjects underwent extinction recall, which tested the retention of extinction memory and involved presentation of the CS+E (N = 8), CS+U (N = 8) and CS− (N = 16) within the safety context. During extinction recall stimuli (CS+E) were presented in the absence of shock.

The paradigms were created with E-Prime (PST, Inc., Pittsburgh, PA), and run on a Dell workstation during the scan. Stimuli were presented by a BrainLogics (PST, Inc., Pittsburgh, PA) digital MR projector, which provides high resolution video (1024 × 768) by back projection. The time series of conditions were logged in E-Prime. The stimulus-presentation system was tested to insure that no artifacts are introduced and that there is no increase in the image-level noise. Lenses were available to correct vision for subjects with glasses.

Data acquisition

Subjects were positioned in the MR scanner and their heads comfortably restrained to reduce head movement. Heart rate and respiration measurements were acquired for removal of physiological noise in the imaging process.

Scans were collected on a 3.0 Tesla General Electric Signa^® Excite^™ scanner (Milwaukee, WI) in the fMRI Center at the University of Michigan. After subjects were positioned in the scanner on both days, a T1-weighted low resolution structural image (mediator) was prescribed approximately parallel to the AC-PC line [gradient recall echo sequence (GRE), repetition time (TR) = 250msec, echo time (TE) = 5.7msec, flip angle (FA) = 90°, 2 excitations, field of view (FOV) = 22cm, matrix = 256 × 256, slice thickness = 3mm, 40 axial slices to cover the whole brain], which was similar to the prescription of the functional acquisitions. Functional images were acquired with a T2*-weighted, reverse spiral acquisition sequence (gradient recall echo, TR = 2000 msec, TE =30 msec, FA = 90°, FOV = 22 cm, matrix = 64 × 64, slice thickness = 3 mm with no gap, 40 axial slices to cover the whole brain). The intermediate template and fMRI images were acquired using a GE Quadrature sending and receiving head coil. On day 1, subjects participated in a separate imaging study of emotion reported elsewhere, and then underwent one run for each phase described above: habituation (around 5 min), fear acquisition (around 14 min) and extinction (around 14 min). On day 2, approximately 24 hours after the acquisition phase, subjects underwent one run for extinction recall (around 14 min). The 4 initial volumes were discarded from each run to allow for equilibration of the scanner signal. The recall run consists of 410 volumes. On day 2, prior to acquisition of the intermediate template and functional scans, a high-quality T1-weighted structural image (sMRI) was obtained using a 3D Volume Inversion Recovery Fast Spoiled Gradient Recall Echo (IR-FSPGR) protocol (TR = 12.3 msec, TE= 5.2 msec, FA = 9°, TI=650 msec, FOV = 26 cm, matrix = 256 × 256 for in-plane resolution of 1 mm; slice thickness = 1 mm with no gap, 160 contiguous axial slices to cover the whole brain). We have used a similar protocol in previous cortical thickness studies (Wang et al., 2008). The sMRI images were acquired with an 8-channel GE Phase Array receiving head coil. Multiple MRI specific markers (Beekly Ltc.) were attached on the forehead of some subjects throughout the experiment on day 2 for the evaluation of the accuracy of registration between fMRI and sMRI images. The markers were about 8 mm diameter and 15 mm long and were visible as dots outside the skull in an axial view when attached perpendicular to the axial plane.

Data analyses

Cortical thickness measurement

Cortical thickness measurements were made on sMRI images with FreeSurfer programs (http://www.surfer.nmr.mgh.harvard.edu/fswiki) on a Linux workstation (Dale et al., 1999; Fischl et al., 1999). These programs use automated methods to measure cortical thickness with submillimeter resolution (Fischl and Dale, 2000). The programs have been shown to be valid (Fischl and Dale, 2000; Rosas et al., 2002; Salat et al., 2004) and reliable (Han et al., 2006; Wang et al., 2008), and have been used to study cortical thickness for a range of conditions (Kuperberg et al., 2003; Sailer et al., 2003; Salat et al., 2004). Thickness analyses involved preprocessing T1-weighted MRI data (including motion correction, transformation to Talairach space, intensity normalization, and skull stripping), segmentation, tessellation, and smoothing of the cortical gray/white border performed to construct a cortical surface model. All individual MRI slices were visually inspected and inaccuracies in borders were manually corrected if necessary. The cortex was cut at middle line and inflated to create a spherical model of each hemisphere. Tessellation patterns of sulci were opened to generate an inflated hemisphere model which exposed hidden sulcal cortical areas. Thickness measures were generated from spatial intensity gradients of the white, gray, and cerebrospinal fluid and thus were not restricted to original voxel dimensions (Fischl and Dale, 2000). Cortical thickness measures were derived from determination of the average of the shortest distances from the gray/white border to pial surface and from the pial surface to gray/white border for each vertex (1 by 1 mm² area on the surface). Iteration of this process provided a continuous grid of vertex thickness measures covering each hemisphere (approximately 150,000 vertices/hemisphere). Thickness was then mapped onto an inflated hemisphere model that allowed for visualization of thicknesses of gyri and sulci.

fMRI analysis

Pre-processing

The sMRI, mediator, and fMRI images were reconstructed and pre-processed with in-house scripts. In this stage, the skull was striped from all images using BET from FSL (FMRIB’s Software Library, www.fmrib.ox.ac.uk/fsl). The fMRI images underwent removal of physiological artifacts from the time course using the RETROICOR algorithm (Hu et al., 1995; Pfeuffer et al., 2002), and slice timing correction and head motion correction using FSL. The additional steps of pre-processing, including spatial smoothing and high-pass temporal filtering (200s), were applied to the motion corrected data using FSL 4.1.2 (Geha et al., 2008).

The registration of fMRI images of a subject onto his sMRI image is a critical step for localization of functionally active regions. The existing studies on structure and activity used the registration procedures in widely accepted imaging processing software, such as FLIRT in FSL (FMRIB’s Linear Image Registration Tool, http://www.fmrib.ox.ac.uk/fsl/FLIRT/index.html). FLIRT routinely uses linear transformation to register the fMRI image onto sMRI image according to a cost function of correlation ratio (Jenkinson et al., 2002; Jenkinson and Smith, 2001). Although FLIRT, as well as other registration tools, produces a reasonable registration of fMRI and sMRI images, several approaches have been developed to improve the registration. The Freesurfer group improved FLIRT registration using boundary-based registration, which uses the borders of white matter (WM)/grey matter (GM) and pial/GM created by Freesurfer analysis as a cost function in the registration (Greve and Fischl, 2009). In addition, we have achieved good registration in previous studies by using a low resolution T1-weighted structural image with the same prescription as our fMRI images as an intermediate template (mediator) for the registration (Fitzgerald et al., 2008). Therefore, we tested whether the additional boundary-based correction and an intermediate template mediator can improve the FLIRT registration. We compared our registration procedure with FLIRT in FSL, and procedures without either boundary-based correction or the intermediate template. In FSL, one volume of the functional image of each run was used as a template, and all volumes in the run were realigned to this template. The template image, a T2*-weighted image of whole brain, was registered to the sMRI image, either directly or via a mediator (a low resolution T1-weighted template image of whole brain). FSL/FLIRT was used to produce the registration, and then Freesurfer/boundary-based registration was performed to improve the registration according to the borders of grey matter determined by Freesurfer. Four combinations of algorithms and images were tested.

1. FLIRT_T2*: the fMRI template was directly registered to the sMRI image using FSL/FEAT/registration;

2. (FLIRT_mediator)+(FLIRT_T2*): the fMRI template was registered to the mediator, and the mediator was registered to the high resolution sMRI image; finally the fMRI template was registered to high resolution sMRI image using the parameter from the two intermediate steps. This was done using FLIRT in FSL/FEAT/registration;

3. FLIRT+B_T2*: the fMRI template was directly registered to the T1 image using FLIRT and boundary-based correction (B) in Freesurfer.

4. (FLIRT+B_mediator)+(FLIRT+B_T2*): The mediator was registered to the T1 image using FLIRT and boundary-based correction to create intermediate registration parameters. The fMRI template was registered to the T1 image using these intermediate registration parameters, and then corrected for tissue boundaries.

The FLIRT registration is constrained to be an affine transformation with 9 degrees of freedom (DOF). The skull-removed mediator and sMRI images were used in these procedures. The outcomes of these procedures were visually evaluated according to (1) the alignment of the midline in axial and coronal views and the corpus callosum in the sagittal view; (2) the alignment of the cortex to the Freesurfer surfaces of WM and GM. These procedures were also tested on structural images with skull in order to further evaluate the accuracy of registrations based on the Beekly markers attached on forehead. The registrations that most closely align the anatomical landmarks in skull-removed images and that accurately match the Beekly markers in the axial view of brain with skull images are considered good registrations.

volume-based analysis

Individual fMRI analysis

The fMRI images were spatially smoothed using a Gaussian kernel of full width at half maximum (FWHM) 4 mm for volume-based analysis. The limited smoothing is useful to preserve the spatial information of fMRI activity (Hagler et al., 2006). The activity of individuals was calculated with FILM general linear model in FSL (Woolrich et al., 2004). The current technique note used only the recall run for demonstration since a previous study using a similar behavioral paradigm in normal subjects reported significant activity in the recall phase (Milad et al., 2007b).

Group mean activity

In the recall run, the time series of CS+E, CS+U, and CS− conditions, as well as fixation and contexts, were modeled in a general linear model (GLM). In this technique development, we only report the greater activity in CS+ (both E and U) than fixation [(CS+)-fixation] during recall phase for the demonstration of methodology.

The registration procedure recommended by FSL was used in volume-based analysis to register the subject’s fMRI image on his sMRI images. Registration included following steps: (1) fMRI image to intermediate template (FLIRT DOF 9); (2) intermediate template to sMRI image (FLIRT DOF 12); (3) fMRI to sMRI image. Subsequently, the individual sMRI images were registered to a standard template (avg152_T1_ brain) using FLIRT (DOF 12), and the parameters of this registration were used to normalize the individual fMRI data to the standard space for volume-based group analysis. After normalization of individual fMRI data, the mean activity of [(CS+)-fixation] was calculated using a one sample T-test in FSL/FEAT.

Thickness of ROI

An ROI is defined as a cluster of contiguous voxels that reach p<0.002 in the contrast of [(CS+)-fixation]. Such clusters were converted back to the individual spaces according to the normalization parameters of each subject using FSL/Featquery. The individualized cluster was registered and re-sampled to high-resolution sMRI space using the same registration parameters as surface-based analysis for the comparison. The minimal interpolation, nearest neighbor, was applied in re-sampling. The entire thickness of each surface vertex (1 by 1 mm²) was searched in a stepwise fashion for any overlap with the individualized cluster. The increment factor (alpha) of steps was small (=0.001) to avoid missing voxels in the cluster. The vertices that had voxels activated in the cluster at any depth were selected to create a 2-D surface ROI. The cortical thickness of each vertex included in the surface ROI was extracted from the cortical thickness map.

Volume of ROI

The cortical voxels of the individualized cluster are determined using the segmentation map of gray matter created by Freesurfer. The volume of these cortical voxels equals to the number of voxels times the size of each voxel (1×1×1 mm³ in sMRI space).

surface-based analysis

pre-processing

The fMRI images are first registered on the sMRI with registration procedure 4. Other steps are the same as volume-based analysis except the exclusion of smoothing of fMRI images.

Individual fMRI analysis

The activity in the non-smoothed fMRI images was identified in FSL using same GLM as the volume-based analysis. The non-smoothed images provide good spatial accuracy of activity for surface rendering.

Group mean activity

The surface-based fMRI analysis was performed in Freesurfer following the procedure on http://surfer.nmr.mgh.harvard.edu/fswiki/FsTutorial/MultiModal/. The individual spherical models of hemispheres were normalized to a spherical atlas of Freesurfer based on alignment of the cortical folding patterns (Makris et al., 2006). An average subject was created for analysis. The parameters of this anatomical normalization were used to normalize the individual non-smoothed contrast images of [(CS+)-fixation] that had been registered to the individual sMRI image. The surface-based analysis was independently performed on five planes along the thickness of cortex determined by Freesurfer. The WM surface was set as 0%, and pial surface was set as 100%. Three more planes were set at 25, 50 and 75% of cortical thickness from WM surface (Figure-1A′, B′; black lines). The physical distances between planes varied depending on the thickness at each vertex, but the planes would not intersect with each other unless the thickness was zero at a vertex. The individual activity located on a plane of each subject was normalized to the corresponding plane in average subject’s space. The normalized individual activity was then spatially smoothed along the surface using a 2-dimensional Gaussian filter with FWHM kernel of 4 mm. The mean activity of [(CS+)-fixation] was calculated using a one sample T-test. The significant vertices in all five planes were summed on the WM surface of average subject to create a surface ROI of mean activity of [(CS+)-fixation] in the average space.

Thickness of ROI

The significant vertices (P<0.002) of [(CS+)-fixation] on each of the 5 planes were individualized to the individual spaces. The individualized supra-threshold vertices on any plane were summed to create a surface ROI for the individual. The thickness of vertices in the individual surface ROI was extracted from his thickness map.

Volume of ROI

To determine the voxels in the surface-based ROIs, we projected the individualized supra-threshold vertices on each plane to a ribbon around the plane (Figure 1-A′, B′; black dash lines). The planes of the pial surface and of the WM surface were inwardly projected to 12.5% of cortical thickness, respectively. The other three planes were projected to 25% of cortical thickness centered at the plane. Each surface vertex was projected to 1mm³ space in the ribbon, and any 3-D 1mm³ voxel in the ribbon was included if it was hit by the projection of any surface vertices. The hit voxels from all ribbons were merged to create a 3-D volume ROI. The 3-D volume ROI was registered on a segmentation map of GM to remove the non-cortical voxels. The volume of the final 3-D ROI was equal to the number of voxels times the size of each voxel (1×1×1 mm in sMRI space).

Statistical analysis

The mean thickness, number of vertices, and volume of individualized ROIs of the surface-based group analysis were compared with those of ROIs of the volume-based group analysis in the same cortical areas with paired T-tests in SPSS. The data are reported as Mean±SD.

Results

Registration of activity onto T1 image at individual level

All four registration procedures produce a good alignment between the fMRI and sMRI images of the midline and internal capsule in axial and coronal views and corpus callosum in the sagittal view under visual inspection (e.g., Figure 2). The WM surface and pial surface defined by Freesurfer fit in the contour of tissue boundaries on the fMRI image, and this fitness of surfaces is better in the superior than inferior portion of the brain across all procedures. Procedure 1 and 4 consistently produced good registration in all 12 subjects, but procedures 2 and 3 produced less than good registration in 1 subject.

Figure 2.

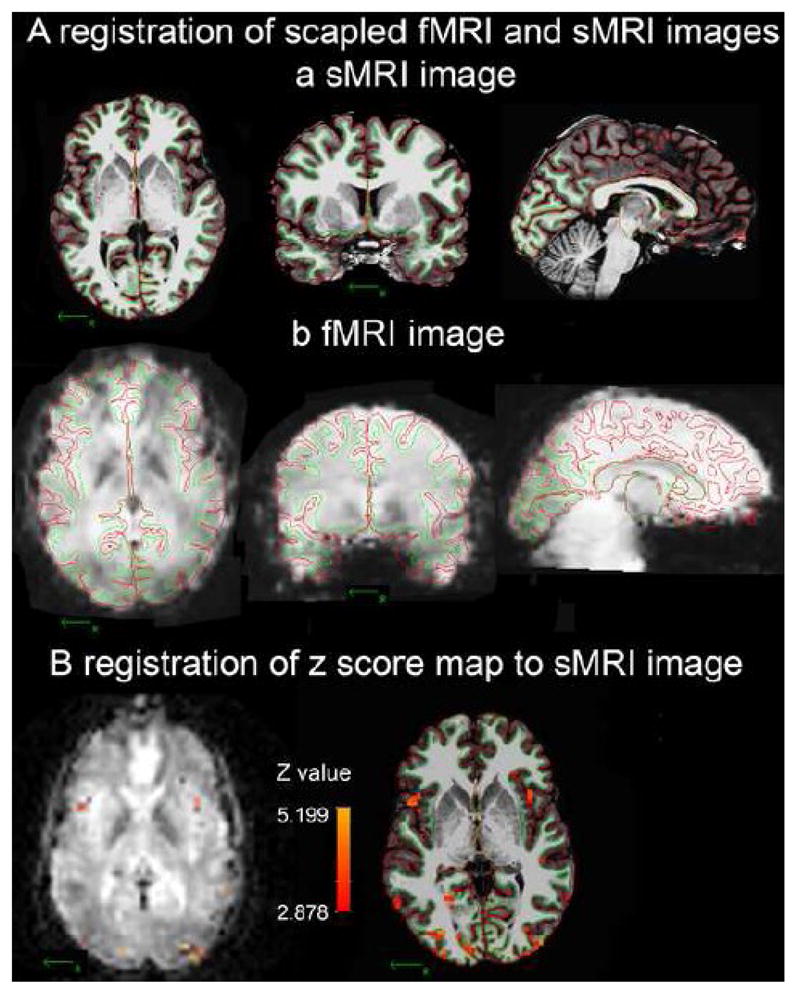
Example of registration of fMRI activity onto a high quality sMRI image at the individual level. The WM/GM border (green line) and GM/pial border (red line) were created by Freesurfer in the skull-removed sMRI image. A: the borders of one subject derived from his sMRI image (a: coronal, axial and sagittal views) were registered on his fMRI template (b: coronal, axial and sagittal views). B: Registering the significant voxels of [(CS+)-fixation] from the fMRI template onto the sMRI image using final registration parameters created by procedure 4.

The accuracy of these procedures was further evaluated in the axial view of images with skull with Beekly MRI markers attached on the foreheads of three subjects. The markers were visible on the sMRI images of all 3 subjects, but they were only visible on the fMRI templates of two subjects. The registration procedures 1 and 4 failed to register the images with skull in one of these two subjects. All four procedures only succeeded in the registration of fMRI template to sMRI image in one subject; and the outcome in this subject is shown in Figure 3. The center of a marker on the sMRI image was registered onto the marker on fMRI template after procedure 4, but not after procedures 1, 2, and 3. In the opposite direction, the center of the marker on the fMRI template fell onto the marker on T1 image after procedures 4 and 2, but fell outside the marker after procedures 1 and 3. This result suggests that using a mediator improved the registration. The distance from the center of marker on the fMRI template to the center of the marker on the sMRI image was shorter in Procedure 4 than Procedure 2, indicating that boundary-based correction improved registration. Given that the diameter of Beekly markers on the axial view is less than 8 mm, the spatial error of procedure 2 and 4 was less than the radius (4 mm) of the marker in the axial view.

Figure 3.

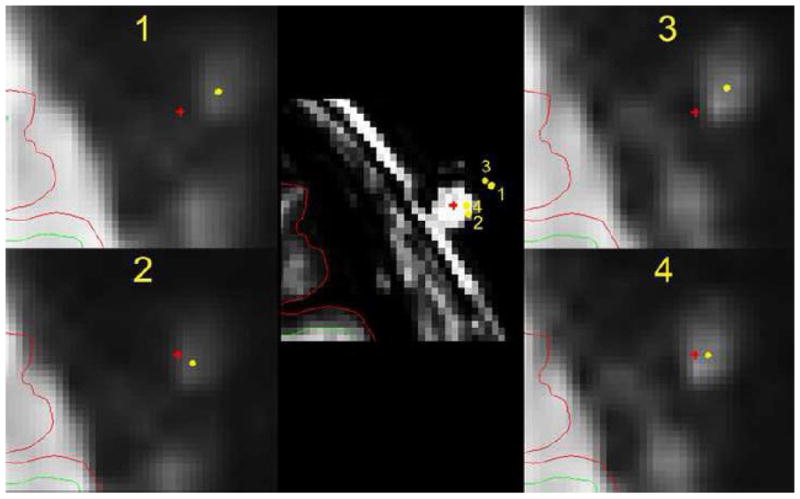
Estimation of accuracy of registration procedures with an extracanonical marker. The fMRI template was registered and resampled to the sMRI with skull image using procedure 1, 2, 3, and 4 (see method). The center of the marker (the bright dot outside the brain) on this slice of the resampled fMRI template is labeled with a yellow dot. The center of the marker (the bright dot on the skull) on the same slice of sMRI image (middle) is labeled with a red cross. Procedure 1, 2, 3, and 4 produced different registration of marker center of sMRI onto fMRI slice as illustrated in each figure at periphery. The marker center of the fMRI template is registered on the sMRI slice (middle) at four locations using procedure 1, 2, 3, and 4. The diameter of the marker is about 8 mm. All other conventions are the same as in the figure 2.

Volume-based group analysis

The volume-based analyses using FSL/FEAT revealed activity associated with [(CS+)-fixation] in bilateral insular, orbitofrontal, parietal, caudal anterior cingulate, dorsal medial frontal, supra-marginal, and visual cortices, in addition to left inferior parietal, right middle frontal cortices (e.g., Figure 4-A).

Figure 4.

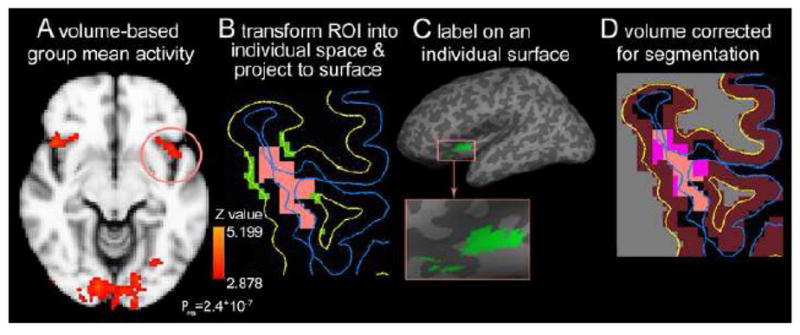
Extraction of ROI derived from volume-based analysis. A: A cluster spreading across the left insula, orbitofrontal and parietal cortex (circled) was selected as a ROI from volume-based group analysis of significant (P<0.002) mean activity of [(CS+)-fixation].. B: individualized ROI (orange area) is registered on an axial sMRI slice, and then the portion of the cluster between pial surface (blue line) and white matter surface (yellow line) is projected to the white matter surface to create a surface label (green) for thickness measure. C: the surface label of the individualized cluster extends in the insula cortex, and crosses a sulcus (dark gray area in the enlarged view) to the orbitofrontal cortex. D: The individualized cluster is corrected with segmentation of gray matter (violet) in Freesurfer. The overlap regions (pink) are the cortical voxels of the individualized cluster of this contrast.

A cluster in left insular, orbitofrontal and parietal regions was individualized using FSL/Featquery. The individualized cluster was re-sampled and registered at similar regions of individual brain as in the average subject’s space (e.g., Figure 4-B). The individualized cluster was then rendered on the individual cortical surface as a 2D surface ROI (e.g., Figure 4-B). The surface ROIs of all subjects spread on their left insula, orbitofrontal, and parietal cortices (e.g., Figure 4-C). The cortical thickness of vertices within the 2D surface ROIs were extracted and mean thickness of this ROI in all subjects was 3.06±0.29 mm. The 3D cluster was also registered on the gray matter map created by Freesurfer in the segmentation step in order to identify the cortical voxels in the cluster (e.g., Figure 4-D). The cortical voxels of the cluster were defined as a 3D volume ROI that contains 565.4±124.4 voxels. The volume of cortical tissue in the cluster was estimated as 565.4±124.4 mm³ given that the voxels were 1×1×1 mm.

Surface-based group analysis

The surface-based group mean activity of [(CS+)-fixation] was identified on each plane at 0%, 25%, 50%, 75%, and 100% of cortical thickness from the WM surface to the pial surface in the average subject’s space. The activity was not identical on all planes (e.g., Figure 5-A). Overall, the activities across all planes are located in the bilateral insular, orbitofrontal, triangular, supra-marginal, caudal anterior cingulate, posterior cingulate, dorsal medial frontal, middle frontal, supra-marginal and visual cortices, in addition to the left inferior parietal, pre-central, post-central, and right middle temporal cortices (e.g., Figure 5-A). This distribution is similar to the volume-based group mean activity, but apparently more than volume-based mean activity.

Figure 5.

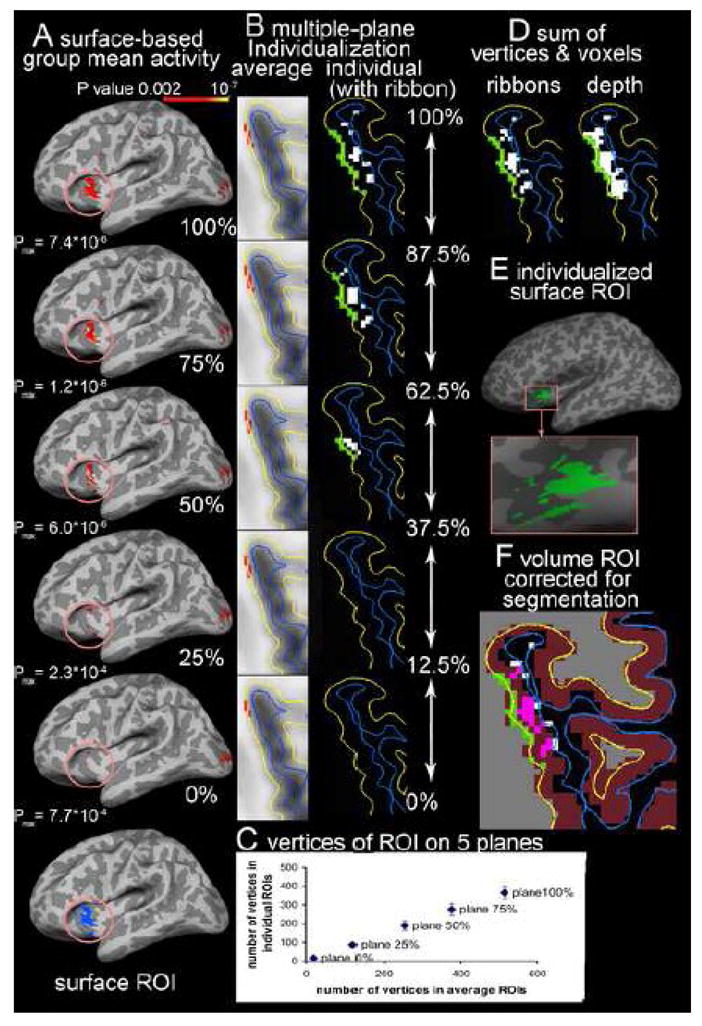
Extractions of ROIs derived from multiple-plane surface-based analysis. The activity was associated with [(CS+)-fixation]. A: In the average space, the significant vertices (P<0.002) associated with [(CS+)-fixation] are identified on the planes at 100%, 75%, 50% 25% and 0% of cortical thickness from white matter (WM) surface, and the activity on 5 planes is not identical (only lateral side of left hemisphere showed). Activity in the similar insula and orbitofrontal cortex as in Figure 4 is selected (circled) as a ROI. B: the surface label (red) of significant activity on each plane is converted from average surface (average) to the individual surface (individual) of the same subject in Figure 4 to create the individualized surface label (green). The individualized label is projected to voxels (white) in the ribbons covering 12.5% of cortical thickness above and below the plane. C: the labels on 5 planes are summed to create a 2D surface ROI of this subject for cortical thickness measure. D: The hit voxels in all ribbons were summed (ribbons) to create a 3D volume ROI that contains less voxels than the 2D surface projection ROI to the entire depth of cortex (depth). E: the surface ROI occupies a similar region as the volume-based ROI, but has less discontinuation at sulcus (dark gray area) than the volume-based ROI in figure 4-C. F: The volume ROI was corrected with segmentation of gray matter (violet) in Freesurfer to identify the cortical voxels (pink) of volume ROI.

We focused on the similar region of the left insula, and the orbitofrontal and parietal cortices as the demonstration of volume-based group analysis for comparison. The supra-threshold vertices (P<0.002) in this region (circled in the figure) are selected on each plane (figure 5-A). The supra-threshold vertices were not identical across 5 planes. The pial surface had 515 supra-threshold vertices spreading in the insula and orbitofrontal cortex (OFC) with a peak P value of 7.4×10⁻⁶; in contrast, the WM surface only had 21 supra-threshold vertices with a peak P value of 7.7×10⁻⁴ and limited in OFC. The supra-threshold vertices on the 5 planes were merged on the WM surface to create a surface ROI. This surface ROI contained 638 vertices, which is more than supra-threshold vertices on any single plane.

Our previously created surface-based normalization parameters were used to convert the labels to the individual subjects (e.g., Figure 5-B). The individualization preserved the difference in the number of significant vertices along the cortical depth (WM surface: 16.4±1.9; 25% thickness: 86.3±10.5; 50% thickness: 188.3±23.4; 75% thickness: 275.3±21.4; pial surface: 366.7±35.5) (Figure 5-C). As illustrated in the axial slice of one subject in Figure 5-B, the individualized label is larger in the pial surface, but disappeared on the WM surface, which is consistent with the trend in the average subject’s space. The individualized label from each plane was then merged to create a surface ROI for each subject (e.g., Figure 5-D green vertices on WM surface (yellow line) and figure 5-E)). The individual surface ROIs were located at similar region as the surface ROI on the average subject’s surface (Figure 5-A), suggesting the individualization preserved the location of significant vertices. The cortical thickness of vertices within the surface ROI is extracted from thickness map of each subject; and the mean thickness of the surface ROI in all subjects was 2.87±0.22 mm.

Projection of significant vertices on each plane to the voxels within the ribbon of 12.5% of cortical thickness above or below the plane created an estimated 3-D volume for the significant vertices on the plane (e.g., figure 5-B). The number of hit voxels in each ribbon of 12.5 ~ 25% cortical thickness is consistent with the number of vertices on the original plane, which results in a decrease in the number of hit voxels from the pial to the WM surfaces. The voxels hit by the projection of the surface vertices on any plane are merged to create a 3D volume ROI (Figure 5-D ribbons). The sum of voxels from all ribbons was less than the number of voxels hit by projection of the same surface ROI to the entire depth of cortex, because few voxels were hit in the ribbon close to the WM surface (ribbons: 698.4± 94.8 vs. entire depth: 1289.0±169.6; e.g., figure 5-D ribbons vs. depth). Further correction of the volume ROI with Freesurfer segmentation of gray matter removed some voxels at the edge of cortex (e.g., figure 5-F). The mean number of cortical voxels in volume ROIs of all subjects was 367.7±64.7. The mean volume of cortical tissue in the volume ROIs was estimated as 367.7±64.7mm³.

Surface ROI derived from surface-based analysis contained a similar number of vertices as the surface ROI derived from volume-based analysis (paired T test: P>0.95), but had more significant vertices in the insula, and fewer vertices in the orbitofrontal and parietal cortices as compared to the surface ROI of volume-based analysis. As indicated in the selected slice in Figure 4 and 5, two types of analyses identified similar vertices in the insular cortex, but unlike volume-based cluster, the surface-based ROI did not spread cross sulcus onto the adjacent OFC. We also obtained statistically significant differences in the values for mean cortical thickness of the ROI between findings derived from surface-based analysis versus volume-based analysis (paired T test: P<0.05). The volume of cortical tissue involved in the two volume ROIs was also significantly different (paired T test; P<0.0001). These differences may result from the different distributions of vertices.

Discussion

It is of a growing interest to study the structural properties of functionally active cortical regions using MRI techniques; however, the available approaches to investigate this issue are far from optimal. In this technique note, we tested a new approach of surface-based analysis to measure the mean thickness and volume of active cortical regions. We found that (1) registration of fMRI and sMRI images with additional boundary based correction and an intermediate low-resolution structural template (mediator) produced a good alignment of brain structures and shortened the distance between the centers of an extra-cranial marker on fMRI and sMRI images after FLIRT registration, indicating that these two additional steps improved FLIRT registration; (2) the multiple-plane surface-based group analysis identified more supra-threshold vertices than the surface-based analysis at any single depth (638 vertices vs. 515 or less); (3) the multiple ribbon projection of supra-threshold vertices estimates a smaller volume of active cortical regions than the entire-depth projection of the same supra-threshold vertices, suggesting the new approach overcame the miscalculation of volume of active brain regions in previous surface-based analysis; and (4) correction of a volume ROI using segmentation of gray matter after either volume-based or surface-based analysis removed a significant number of non-grey-matter voxels, which theoretically improved the accuracy of measure of cortical grey matter volume. These findings provide new ideas for the optimization of measurement of structural properties of functionally active regions.

Multiple-plane surface-based group analysis

Our finding that the functional activity on the planes at different depths of cortex was not identical raises question regarding the use of any one plane to represent activity of the entire cortical thickness. Although the voxel size in an fMRI image is comparable to the average thickness of cortex, a fMRI voxel may be registered in a part of cortex on the sMRI image, regardless of the size of voxels. Therefore, it is possible that significant activity only occupies a portion of cortical depth. This problem has raised concerns with respect to surface-based analysis. While existing solutions are acceptable for surface illustration of activity, they are problematic for surface-based analysis (Anticevic et al., 2008; Desai et al., 2005; Napadow et al., 2006). For example, using large size interpolation to recruit the adjacent supra-threshold voxels, or registering the mean or maximal P value across the depth of cortex onto one surface, omits the distance along the depth of cortex. Therefore, these approaches will produce false results after 2-D smoothing along the surface.

The new multiple-plane approach offers a possible solution for this problem by multiple sampling of activity along the depth of cortex. Increased sampling along the cortical depth logically reduces the chance of missing voxels that are partially registered in the cortex. We designed 5 planes in this initial test because the range of cortical thickness is 0 ~ 5 mm in Freesurfer, and the re-sampled fMRI voxels are 1 mm thick. Five planes are likely to include every voxel within the entire depth of cortex. Increasing the number of planes lead to recruitment of more supra-threshold voxels, especially in the thicker cortical regions. However, reasonable selections of depths to be tested may reduce the number of planes that are needed. In the current results, the 2-D surface ROIs after surface-based analysis are defined as a sum of supra-threshold vertices at multiple depths of cortex, which is obviously larger than activity at any single cortex depth. These results demonstrate that the multiple-plane approach is likely more accurate than the routine single-depth approach in the definition of 2-D surface ROIs. Similarly, the multiple-sampling concept also helps in the projection of supra-threshold voxels to the cortical surface after volume-based analysis. We used a very small increment factor (alpha = 0.001) in the searching of supra-threshold voxels along the thickness at each of the surface vertices after volume-based analysis. This over-sampling approach projects more activity onto the surface than the default setting (alpha = 0.1; data not shown).

The distribution of activity in the selected ROI along the cortical depth in the current results is similar to the laminar profiles of fMRI activity reported in previous studies using unique imaging techniques to achieve sub-millimeter voxel size (Ress et al., 2007; Yang et al., 1998). However, the multiple-plane approach is distinct from the previous studies as it does not require extremely high-resolution fMRI images to differentiate cortical laminae. Thus we believe our new approach only maximizes the representation of activity in the cortex, and should not be perceived as representing to cortical layers.

The new multiple-plane surface-based analysis preserves the advantage of surface-based analysis over volume-based analysis. A major disadvantage of volume-based analysis is the 3-D smoothing in Euclidean space. This type of smoothing can smooth the cortical activity into white matter or CSF, and smooth over sulci and onto the adjacent gyri. These types of smoothing errors both dilute the real significance of activation, and could also shift the peak of activity topographically (Jo et al., 2008). The surface-based analysis is less susceptible to these limitations (Anticevic et al., 2008; Schaechter et al., 2006; Van Essen and Dierker, 2007). In our results, the 2-D surface ROIs derived from multiple-plane surface-based analysis, have less discontinuation at sulci than the surface ROIs created by volume-based analysis. Furthermore the 3-D volume ROI of present surface-based analysis also remains within insular cortex, unlike the volume ROI of our volume-based analysis. This suggests that the new approach of surface-based analysis does not sacrifice the advantage of surface-based analysis over volume-based analysis. Unexpectedly, the peak activity in the selected region was higher in volume-based than in surface-based analysis. Limited sampling could have potentially contributed to these results.

Estimation of active cortical volume

On one hand, the volume-based analysis may overestimate the volume of cortical tissues that have supra-threshold activity, when the 3-D smoothing expends the activity to biologically unconnected gyri (e.g., Fig-1B). Since our findings show that activity is not the same at every depth of cortex, it follows that the single-depth approach might not provide an accurate estimation of active cortical volume either. In the new multiple-plane surface-based analysis, the supra-threshold activity at each of 5 planes is projected to the voxels in a ribbon of 12.5% of cortical thickness above and below the plane. This approach increases the number of sampling planes to 5, but restrains the distance of projection of each plane to 25% (12.5% near the cortical borders) of cortical thickness, improved resolution along the cortical depth. The new approach apparently limits the chance of missing activity due to the selection of plane (e.g., Fig-1B′). The current results suggest that the new approach also avoids overestimation of active volume caused by “blind” projection of single-plane activity to inactive portions of cortex below or above the plane. Therefore, summary of the hit voxels in all ribbons around 5 planes at different depths provides a theoretically more accurate estimation of volume of active brain tissue than existing volume-based and surface-based analyses.

Removal of non-cortical tissue from the active cortical volume is another step to increase the accuracy of estimation. In the volume-based analysis, part of a large smoothed supra-threshold fMRI voxel may be re-sampled to some small sMRI voxels outside cortex, so that including these voxels apparently overestimates the active cortical volume. In the surface-based analysis, although the analysis has been restrained within cortex determined by thickness measure programs, these programs use interpolation to define the cortical borders which could lead to inclusion of voxels with a mixture of gray matter and other tissue (Fischl et al., 1999). Inclusion of these mixed voxels may result in overestimation of the active volume, too. Therefore, correcting the functionally defined ROIs for the gray matter segmentation gives a conservative estimation of cortical volume of the activated region. In combination with the multiple-plane surface-based analysis, this correction theoretically avoids the shortcomings in the existing approaches for volumetric measure of active cortical volume.

Registration of fMRI and sMRI images

The registration of T2*-weighed image to the T1-weighted images is critical for all fMRI analysis, and this step is particularly important for studying the structural properties of active brain regions since inaccurate registration will result in measuring inactive regions. Therefore, it is necessary to use the best registration possible for this line of research. FLIRT, as well as other registration tools used in most existing studies, has been well validated (Gholipour et al., 2007; Jenkinson et al., 2002; Jenkinson and Smith, 2001; Roche et al., 1998; Smith et al., 2004). Several procedures have been developed to improve the registration of these tools. Intermediate templates have been used to improve the registration in these tools (Jo et al., 2009), and current results support using an intermediate template for better registration of fMRI and sMRI images. A recently reported cortical boundary-based correction of FLIRT is an important technical advance because a good alignment of cortex is essential for accurate measurement of cortical thickness and volume of functionally active regions (Greve and Fischl, 2009). Saad et al. (2009) have found that correction for registration based on the outline of the brain improves the inter-modal registration. The boundary-based correction in Freesurfer matches both borders of cortex, which represents a theoretical advance from matching one border of cortex as in the Saad et al. report (Saad et al., 2009). In the current results, we tested this new procedure with both visual inspection of brain registration, and external markers, a classic technique to evaluate the registrations (Maurer et al., 1996). Although visual inspection of the results of this correction is equivalent to FLIRT registration, this step produces a noticeable improvement in accuracy of registration as indicated by the shorter distance between centers of the extracranial marker on T1 and T2* weighted images. If this distance truly represents the error of registration, the error of less than 4 mm is comparable to the voxel size (3 mm³) in the fMRI images. Our results are consistent with other validations of this new approach (Greve and Fischl, 2009), however caution should be exercised while considering these results because the external cranial markers may be distorted differentially from brain tissues (Maurer et al., 1996). Thus, the final procedure with the two additional steps described in the current report produced robust and accurate registration that provides sound basis for localization of functional activity in the individual brain.

Prospective

We have discussed a new approach to improve the accuracy of measurement of structural properties of functionally defined ROIs in order to better relate structural and functional information. Understanding the neuro-substrates of brain activity associated with normal psychological functions or mental disorders, such as PTSD, will significantly advance our understanding of brain functions and pathogeneses of various mental diseases. Furthermore, predicting the functional consequences of structural changes in the brain is a necessary step for the development of treatments and preventive strategies. In addition, the new multiple-plane surface-based analysis of fMRI data outperformed existing volume-based and surface-based analyses, so that it may lead to additional progress in this line of research.

The new approach tested in this study is by no means optimal, but this approach tested a few concepts that are critical for measuring structural properties of active regions. Further verification of these concepts in other cortical regions will improve and extend the application of this new approach. Extending the generalizibility of our premises by the analysis of other functional neuroimaging data, such as other types of activation, will also be important in future studies. We hope these concepts, integrated with other developments of functional and structural neuroimaging analyses, promote further discussion on converging functional and structural neuroimaging research.