SYNOPSIS
Objective
We determined which children should be tested for elevated blood lead levels (BLLs) in the face of financial and practical barriers to universal screening efforts and within 2009 Centers for Disease Control and Prevention recommendations allowing health departments to develop BLL screening strategies.
Methods
We used the Michigan database of BLL tests from 1998 through 2005, which contains address, Medicaid eligibility, and race data. Linking addresses to U.S. Census 2000 data by block group provided neighborhood sociodemographic and housing characteristics. To derive an equation predicting BLL, we treated BLL as a continuous variable and used Hierarchical Linear Modeling to estimate the prediction equation.
Results
Census block groups explained more variance in BLL than tracts and much more than dichotomized zip code risk (which is current pediatric practice). Housing built before 1940, socioeconomic status and racial/ethnic characteristics of the block group, child characteristics, and empirical Bayesian residuals explained more than 41% of the variance in BLL during 1998–2001. By contrast, zip code risk and Medicaid status only explained 15% of the BLL variance. An equation using 1998–2001 BLL data predicted well for BLL tests performed in 2002–2005. While those who received BLL tests had above-average risk, this method produced minimal bias in using the prediction equation for all children.
Conclusions
Our equation offers better specificity and sensitivity than using dichotomized zip codes and Medicaid status, thereby identifying more high-risk children while also offering substantial cost savings. Our prediction equation can be used with a simple Internet-based program that allows health-care providers to enter minimal information and determine whether a BLL test is recommended.
Lead has long been known to be a potent neurotoxin with deleterious outcomes. Starting in the 1980s, blood lead levels (BLLs) as low as 10 micrograms per deciliter (μg/dL) were found to be associated with adverse effects on cognitive development, growth, and behavior among children.1–6 Thus, the identification and treatment of children with elevated BLLs (EBLLs) is critical. Recent research has revealed evidence of effects on intelligence quotient (IQ) score at BLLs <10 μg/dL, and no study has been able to identify a safe level.7
Our analysis of the Michigan database of BLL tests showed that the number of cases with a BLL ≥10 μg/dL has decreased during the past decade, even as the number of BLL tests has increased. However, in 2002–2005, there were still approximately 10,000 cases of such EBLLs that were confirmed with a venous test, and more than 1,000 additional EBLL cases in which no venous test was performed.
To minimize the effects of lead poisoning, one must identify those with the highest risk as soon as possible to begin environmental intervention and, where necessary, chelation therapy. This is a procedure in which lead ions in the bloodstream are bonded to an organic molecule, thereby preventing the lead from entering into unwanted chemical reactions in the body of an affected individual. While the cost of a single BLL test is not high, universal testing of children would be very costly. Therefore, the Centers for Disease Control and Prevention (CDC) developed guidelines to target BLL testing toward children at highest risk.8 CDC determined that the greatest risk factor for EBLL is old, poorly maintained housing.9–11 Furthermore, in 1997, CDC recommended using the following information to identify children at high risk: housing age and percent of population with incomes below the federal poverty level (FPL) in the zip code in which the child lives, and self-report questions about exposure to lead and peeling paint.8 In 1998, the Centers for Medicare and Medicaid Services mandated that all Medicaid-enrolled children receive a BLL test at 12 and 24 months of age.
However, actual testing of Medicaid children was far below the mandated goal. Eight states that compared Medicaid data with surveillance data from 1997 through 2001 reported that 17.9% to 52.9% of Medicaid enrollees younger than 72 months of age had been tested for BLL.12 Michigan, for its part, enacted Public Act 55 of 2004,13 which required Medicaid providers to increase testing of Medicaid children to 80%. By September 2008, the rate of testing those on Medicaid had improved so that approximately 64% of Medicaid children had been tested by age 2, and the rate of testing has remained at this level through the year ending September 2009.14,15 Clearly, testing every child on Medicaid is still a very difficult goal to achieve.
Meanwhile, public health officials have realized that better risk assessment methods are necessary. Many public health departments, including Michigan's, have used zip codes (along with Medicaid eligibility) to assess risk of EBLLs and have typically dichotomized zip codes as high or low risk based on the proportion of old housing and the proportion in poverty. The Michigan Department of Community Health (MDCH) has classified half of all zip codes as “high BLL risk,”16 and many of these zip codes have a great deal of socioeconomic heterogeneity. Thus, better methods are clearly needed. In 2009, CDC recommended that universal testing of children on Medicaid not be required and that states may target children who are considered high risk, based on updated state and local surveillance and evaluation strategies.17
We used statistical analysis of all BLL test data in Michigan for 1998–2005 to optimize the prediction of BLL from readily available data and to compare the predictive validity of several lead poisoning risk assessment methods. While the data that we analyzed were from Michigan, this approach can be implemented in other states and nations.
This study made several significant advances in targeting children at high risk. Some studies,18 rather than dichotomizing zip code risk, treat zip code characteristics as continuous variables with which to predict the proportion with EBLL. However, Krieger et al.19,20 have compared the predictive validity of various levels of geographic units (zip codes, census tracts, and census block groups) and found census tracts to be most predictive for several health outcomes. In addition, Curtis et al.21 pointed out that zip codes are unreliable for longitudinal data because their boundaries are periodically changed to accommodate new zip codes or better align with municipal borders. Hence, we evaluated the utility of zip codes as a predictor and compared the degree to which various geographic levels predict BLL.
While we join others who have assessed risk based on census block groups instead of zip codes,10,19,20,22–24 this study is an improvement in several respects. Previous studies have treated BLL as a dichotomous variable (elevated or not) when it is, in fact, continuous and resembles a dose-response relationship in which the higher the BLL, the lower the child's IQ.25 The Board on Population Health and Public Health Practice26 stated that any model of prevention should recognize degrees of risk rather than just risk vs. no risk. In this study, we predicted BLL as a continuous variable. Moreover, unlike previous studies, our prediction equation took into account both the sociodemographic and housing characteristics of the child's neighborhood, and the following individual characteristics of each child: Medicaid status,27,28 race (African American),29 age, and year of test.
Public health professionals have generally assumed that the neighborhood housing characteristic that best predicts BLL is the proportion of housing built before 1950.30 However, starting in 1940, the paint industry gradually reduced the sale of lead paint, and in 1955, the paint industry adopted a voluntary standard limiting interior paints to no more than 1% lead.31 In 1978, the Consumer Product Safety Commission banned the sale of residential paint containing more than 0.06% lead.32,33 Hence, we investigated various possible housing ages as predictors of BLL. Most importantly, we investigated whether the proportion of housing built before 1940 is an even better predictor. We did not examine the predictive validity of the proportion of houses built in each decade before 1940, because U.S. Census data do not contain this information.
Krieger et al.20 found that the percentage of the population below the FPL is one of the best predictors of geographic health disparities. However, they did not investigate the predictive validity of other neighborhood income levels; therefore, we cannot know which level is most predictive of BLL. Is it the proportion below the FPL, the proportion below 50% of the FPL, or some other income level?
We also aimed to show that knowing a child's prior residential address in addition to the current one can further improve our model's ability to predict BLL. We analyzed the predictive validity of our equation in two ways. First, we assessed the ability of our equation, based on U.S. Census data, to predict BLL several years after the Census. Second, we performed a statistical sensitivity analysis to estimate the extent to which our prediction equations may have been biased from BLL tests being given primarily to high-risk children instead of a general-population random sample.
Finally, we computed sensitivity and specificity to measure how well our prediction equation identified which children have EBLLs. In the process, we showed that our method could result in substantial cost savings as compared with older methods, while still identifying more children with EBLL. This analysis permitted us to compare the costs and benefits of using our equation to determine which children should be tested with the current policy of testing all children on Medicaid, regardless of other risk factors.
METHODS
Data
MDCH maintains a database of all BLL tests that contains child's birth date, BLL test outcome, address at test time, Medicaid status, and racial identification. Each address is geocoded by MDCH with the latitude, longitude, and U.S. Census 2000 census block group. We then linked each case to Census data about the racial/ethnic breakdown, housing characteristics, income, and education of residents of the block group.
Prior research has shown that BLL peaks between 18 and 36 months of age, and slowly declines during the next few years.6,34 In addition, the database clearly shows that BLLs have decreased in recent years. These facts suggest that the child's age and the year of testing are also important factors in predicting BLL.
We restricted our analysis to children who had not reached their sixth birthday when tested. For 1998–2001, we used data from 221,721 unique children, of whom 72.4% were enrolled in Medicaid. The 2002–2005 data contained 340,188 unique children, of whom 69.8% were Medicaid enrolled.
Race was missing in 22.9% of cases in 1998–2001 and 36.1% of cases in 2002–2005. Although black/white segregation has declined in most metropolitan areas and cities in the U.S., black people still generally live in primarily black neighborhoods in three Michigan cities: Detroit, Flint, and Benton Harbor.35 This fact enabled us to substantially reduce the loss of cases from missing data by assuming that the child was not black if the block group was less than 10.0% African American and assuming the child to be black if the block group was more than 90.0% African American.
This assumption reduced the percentage of missing cases to only 6.6% in 1998–2001 and 9.7% in 2002–2005. It had only a slight effect on the computed correlation between whether the child was black and the percent black in the block group (increasing it from 0.823 to 0.852).
We used venous test results when they were available. While Michigan policy is to request a venous retest whenever a capillary test indicates a BLL >10 μg/dL, no venous follow-up was performed on 28.8% of 33,659 such tests. In such cases, we used the capillary results for analysis.
Data analysis strategy
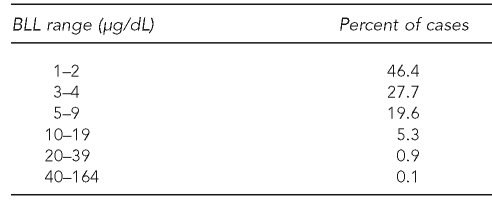
The MDCH database contains BLLs ranging from 1 to 164 μg/dL (Table 1). Dichotomizing BLL as elevated or not, as many guidelines do, has serious limitations because the range of BLL is so large and its effects resemble a dose-response relationship.6,7,25 Therefore, we treated BLL as a continuous variable.
Table 1.
Distribution of BLL results in the Michigan Department of Community Health database, 1998–2005 (n=533,647)
BLL = blood lead level
μg/dL = micrograms per deciliter
Regression analysis assumes that residuals are normal and have homogeneity of variance.36 Consistent with previous findings,37 BLL was normally distributed after logarithmic transformation. The transformation that minimizes both skew and heteroscedasticity of variances is Ln(BLL−0.5), where Ln is the logarithm to base e (≈ 2.718). This logarithmic function of BLL was the dependent variable in all regressions. Because the minimum BLL recorded in the MDCH database is 1.0, it is likely that many BLL results recorded as 1.0 would actually be closer to 0.5 if the measurement was more precise.
We grouped data into two time periods (1998–2001 and 2002–2005) to see how well the equation developed from one time period predicted BLL several years later. Except when measuring the effect of residential mobility, the analyses only used the highest BLL result for each child in each four-year period. Because of data management issues, a small proportion (8.1%) of the more than 500,000 cases appear in the data for both four-year periods.
We balanced maximizing the proportion of variance explained with parsimony, and so did not report coefficients <0.10—except for coefficients of dummy variables—even if they were statistically significant. (With more than 200,000 cases per four-year period, very small coefficients can be highly significant.)
We used ordinary least squares (OLS) multiple regression for exploratory regression analysis and R-squared. However, the final prediction equations used Hierarchical Linear Modeling (HLM)38 for two reasons. First, when data are grouped (in this case by block groups), the coefficients and the standard errors are more accurate with HLM. Second, HLM permitted us to make BLL estimates for each block group that took into account the departures of block group sample data from the overall prediction equation, but avoided confusing random variation with systematic effects.
RESULTS
Zip codes, census tracts, and block groups as predictors of BLL
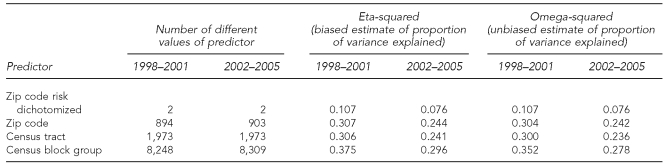
We first compared the proportion of variance in BLL explained by block group, census tract, zip code (each as a nominal variable), and dichotomized zip code risk (high vs. low). We focused on omega-squared, the unbiased estimate of variance explained, as this corrects for any increase in the explained variance that results from an increase in the number of values of the independent variable.
Table 2 shows that census block group explains the greatest proportion of variance in BLL (omega-squared is 0.352 for 1998–2001 and 0.278 for 2002–2005) and dichotomized zip code risk explains the least proportion of variance in BLL (omega-squared is 0.107 for 1998–2001 and 0.076 for 2002–2005). Further, individual zip code has an omega-squared of 0.304 for 1998–2001 and 0.242 for 2002–2005, which is not only much greater than the dichotomized zip codes, but is slightly greater than that for census tracts (0.300 for 1998–2001 and 0.236 for 2001–2005).
Table 2.
Proportion of variance in Ln(BLL–0.5) from the Michigan Department of Community Health database, explained by dichotomized zip code risk, zip code, census tract, and block group by four-year perioda
aFor the years 1998–2001, all analyses are based on approximately 220,000 cases. For the years 2002–2005, all analyses are based on approximately 340,000 cases. In each analysis, the geographic unit was the sole predictor.
Ln = logarithm
BLL = blood lead level
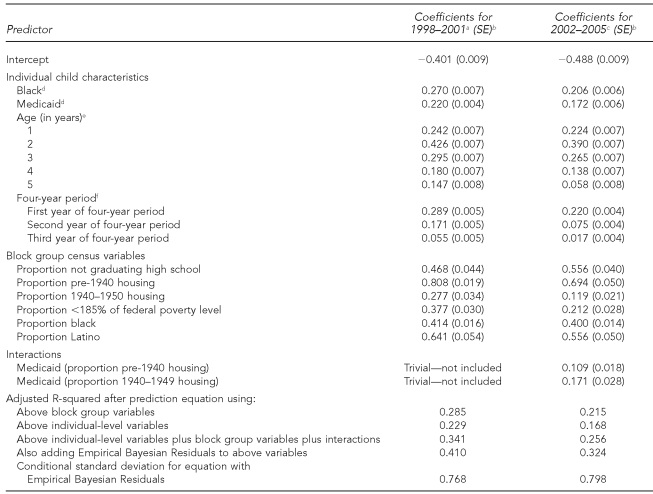
Second, we compared the variance explained by the old method (emphasizing dichotomized zip code and Medicaid status) with our prediction equation. Together, zip code and Medicaid produced an adjusted R-squared of 0.152 for 1998–2001 and 0.109 for 2002–2005 (data not shown). In contrast, as shown in the bottom rows of Table 3, substituting block group characteristics for zip code substantially increases R-squared, and adding other individual characteristics does so even more.
Table 3.
Predicting Ln(BLL–0.5) in the Michigan Department of Community Health database, from race, Medicaid status, age, and block group census variables in the years 1998–2001 and 2002–2005 using Hierarchical Linear Modeling
aFor 1998–2001, n=206,991; year 1 = 1998.
bAll coefficients are p<0.001.
cFor 2002–2005, n=307,204; year 1 = 2002.
dBlack and Medicaid are each coded 0 if that characteristic is absent and 1 if it is present.
eThe reference group for dummy variables was age = 0 (i.e., <1 year of age).
fThe reference group for dummy variables for year tested was the last year of each four-year period.
Ln = logarithm
BLL = blood lead level
SE = standard error
Predicting BLL from block group, child's race, and Medicaid status
While the U.S. Census provides a large number of potentially relevant variables, we sought a parsimonious prediction equation by only including those variables that added a nontrivial increment to our ability to predict BLL.
Socioeconomic status and BLL.
For each block group, we computed the proportion of the population with income below various percentages of the FPL: <50% FPL, <100% FPL, <150% FPL, and <185% FPL. (Children younger than age 2 are eligible for Medicaid if the family income is <185% FPL.) We found that the block group proportion with incomes <185% FPL had the highest bivariate correlation with BLL among all of the aforementioned income levels. Furthermore, adding the proportion of households at each of the three other income levels into the regression added <0.01% to R-squared. Hence, the proportion with income <185% FPL is the only indicator of neighborhood income that we use. The proportion of individuals who have not graduated from high school has a larger association with BLL than any other education level.39
Table 3 presents the unstandardized regression coefficients from an HLM in which we predict Ln(BLL–0.5) from all of the variables. The second column of Table 3 contains coefficients for the period 1998–2001, and the third column contains the coefficients for 2002–2005. Each coefficient represents the predicted change in the Ln(BLL–0.5) if a predictor had the value 1 rather than 0. Thus, a coefficient of 0.20 indicates that the BLL of a child with a value of 1 on that variable is predicted to be 22.14% higher, controlling for other variables in the model (e0.20=1.2214), than the BLL of a child with a value of 0 on that same variable.
Age of housing and rental status.
Although the CDC BLL risk assessment questionnaire8 assumes that risk from house paint did not decrease until after 1950, we analyzed the effect of the proportion of housing built in various decades, starting with all pre-1940 housing. Table 3 shows that the coefficients for the effect of proportion of housing built prior to 1940 on Ln(BLL–0.5) (0.808 for 1998–2001 and 0.694 for 2002–2005) are much larger than the corresponding coefficients for housing built in the next decade, 1940–1949 (0.277 for 1998–2001 and 0.119 for 2002–2005). Surprisingly, the proportion of housing built between 1950 and 1980 had no perceptible effect on BLL, even though lead paint was not entirely banned until 1978.
Some have suspected that rental housing is more poorly maintained and, therefore, is especially conducive to high BLLs. However, in both four-year periods, the proportion of housing that is rental had a coefficient of only 0.05, and even adding its interactions with other variables adds less than 0.1% to R-squared.
Race/ethnicity.
The MDCH database identifies six different racial groups. However, if we created dummy variables for groups other than African American, we would add <0.01% to R-squared. As such, we combined all non-black people and used this as the reference category. Table 3 shows that when controlling for Medicaid status and neighborhood characteristics, a black child had a Ln(BLL–0.5) that was 0.270 greater than other children in 1998–2001 and 0.206 greater in 2002–2005.
Because all predictors have a minimum of 0 and a maximum of 1 (100%), we were able to compare the size of the unstandardized coefficients to determine which variables had the greatest effect. However, note that the value of a multiple regression coefficient can be substantially reduced by the presence of other predictors with which it is highly correlated.36
The coefficients for the effect of percent African American in the block group on Ln(BLL–0.5) (0.414 in 1998–2001 and 0.400 in 2002–2005) were much smaller than the coefficients for corresponding coefficients for percent Latino (0.641 in 1998–2001 and 0.556 for 2002–2005), because the percent African American was accompanied in the equation by the variable indicating whether the child was black (the correlation between percent African American in the neighborhood and whether the child was black exceeded 0.8). By contrast, the variable indicating whether the child was Latino was not in the regression because this information was not available for most of the cases. Therefore, the coefficients for percent Latino were larger than for percent African American because they were not reduced by a similar redundancy in the equation.
Child's age.
We used child's age as a predictor via a set of dummy variables, with those younger than one year of age as the reference category. The results were consistent with prior findings,6,10,29 which indicated that 2-year-olds have substantially higher BLLs than other groups. The dummies for year tested indicated that when controlling for other variables, the predicted BLLs decreased each year.
Interaction effects.
We examined a large number of interaction terms: products of percent old housing, multiplied by black race, Medicaid status, and the age dummies, but found that only Medicaid status multiplied by proportions of pre-1940 housing and 1940–1949 housing had sufficient effects on our dependent variable to include in Table 3, and only in the second four-year period of 2002–2005 (0.109 for pre-1940 housing and 0.171 for 1940–1949 housing).
BLL results: 2002–2005 vs. 1998–2001
Table 3 permits us to see how patterns of BLL risk have changed and whether a prediction equation developed for one set of years is useful for future prediction. The intercept was more negative for 2002–2005 (−0.488) than for 1998–2001 (−0.401), indicating that a child with the same characteristics would be predicted to have a lower BLL in 2005 than in 2001. This is because the central tendency of BLL has decreased over time. The slope coefficients for 2002–2005 were smaller for all variables except the proportion not graduating from high school (0.468, 0.556) and the interaction terms. R-squared was also lower in the latter years.
However, the corresponding slope coefficients for the two time periods had almost exactly the same order. Moreover, by applying the Table 3 coefficients derived from the 2002–2005 data to the 1998–2001 data, the predicted values of Ln(BLL–0.5) from the coefficients for the latter years had an extremely high correlation (0.997) with the predicted values from the former years' equation. The 1998–2001 equation would, however, provide overestimates if applied to the 2002–2005 data, because the mean Ln(BLL–0.5) decreased.
When block group sample means differ from predicted means
The slope coefficients in Table 3, combined with the individual's score on each predictor, provided predicted values of our dependent variable for each child. The mean block group values of the dependent variable typically deviated from those predicted by the independent variables. We next considered whether such a deviation indicated that the block group's mean Ln(BLL–0.5) truly differed from the predicted value or was the result of sampling error.
HLM computed the best estimate for the population mean of our dependent variable for each block group by taking into account both the overall regression equation and the block group sample data. This Empirical Bayesian estimate of the intercept for each block group—not to be confused with the probability from typical Bayesian inference—weighted the block group sample mean more heavily when the sample size was larger in the block group. These estimates were combined with the characteristics of each child to produce the final predicted Ln(BLL–0.5) for the child. In the 1998–2001 data, these predicted values ranged from –0.72 to 2.66, corresponding to BLLs of 1.0 μg/dL to 14.8 μg/dL. In the 2002–2005 data, these predicted values ranged from –0.76 to 2.30, corresponding to BLLs of 1.0 μg/dL to 10.5 μg/dL.
The bottom row of Table 3 shows that for both time periods, substituting the Empirical Bayesian estimates for the predicted (fitted) values from the regression substantially increased the percent of variance explained.
Possible effects of a biased sample
BLL tests are disproportionately given to those considered to have above-average risk.40 Does the non-randomness of our sample substantially threaten our goal of a prediction equation that provides unbiased estimates of expected BLL of all children in Michigan?
We distinguished the effects of two kinds of selection bias. With exogenous selection, the sample is not representative of the population, but the probability of being selected is entirely determined by the predictors in the model; in this case, the coefficients of an OLS regression remain unbiased and consistent.41 Much of the selection bias in our data fits this criterion. Those who are black, Medicaid enrolled, and live in low-income neighborhoods with old housing are more likely to be tested, but these variables are in our model.
However, the probability of selection may also be correlated with the error of prediction.41 We performed a statistical sensitivity analysis to examine how much this would bias the prediction equation. We created a duplicate dataset for the 1998–2001 data and pretended that these new cases had never been tested. Thus, the correlations among all predictors were the same for both the tested and “untested” cases. We next assigned a BLL to each of these untested cases such that the assigned BLLs had a mean of 21% less than the test cases; however, this ratio had some random variation. The assigned scores had a 0.948 correlation with the matched tested cases.
In the regression equation based on the combined (tested plus untested) data, the intercept was 0.122 lower than the intercept from only the tested, while the slope coefficients were typically within 0.02 of each other. The predicted values of our dependent variable ranged between 0.116 and 0.125 less in the regression equation using all cases than in the equation using only those tested. Thus, this sampling bias produced a slight overestimate (12%) of a child's expected BLL. However, the correlation between the two sets of predicted values exceeded 0.9999, and we concluded that the predicted BLL estimated by our equation was quite robust with respect to plausible differences between our sample and the total population.
Residential mobility and BLL
We used the 2002–2005 data to explore the effects of changing residences. Of the approximately 340,000 children tested in those years, about 76,000 had two or more test results. Of these children, 46.2% moved before their second test and a large majority (88.3%) of those who moved relocated to a different block group. When predicting the result of the second BLL test, adding the predicted BLL risk from the block group for the first BLL test increased R-squared by 0.9% above that explained by the characteristics of the second block group alone. Thus, the prior address made only a small contribution to predicting BLL. However, if such information is readily available, it is worth using.
Among low-income people, frequent changes of residence may be indicators of financial and family crises that indicate greater poverty and/or fewer coping skills than among more residentially stable people in the same neighborhood.42–44 Further analysis showed that moving increased BLL, but only to the extent that each block group had houses that were built prior to 1950.
Estimating cost-effectiveness
We compared the cost-effectiveness of using our equation to determine which children need testing with that of existing risk assessments based on zip code and Medicaid status. To estimate the cost of a BLL test, we noted that while children covered by Medicaid are eligible for free testing, Medicaid reimburses health-care providers $3.06 for venipuncture and $8.00 for a capillary blood draw. In addition, the MDCH laboratory charges $16.91 to analyze the test. Private providers, laboratories, and Women, Infants, and Children clinics charge between $15.00 and $50.00 for the entire procedure. Taking all of this into account, we regarded $30.00 as a reasonable estimate of the full cost for each BLL test.
While research suggests that no amount of lead in the blood is completely safe, public health agencies use certain cutoff points to distinguish cases of greater concern (e.g., EBLL) from those of lesser concern (i.e., nonelevated BLL). MDCH uses two such cutoff points: 10 μg/dL and a newer, more conservative one of 5 μg/dL.14
To evaluate the potential cost of various methods and their effectiveness in identifying those with EBLL, we computed both sensitivity (the proportion of true positives that are correctly identified as such) and specificity (the proportion of true negatives that are correctly identified as such) under several testing criteria. However, doing so required that we not only dichotomize BLL into elevated vs. nonelevated, but also dichotomize our risk criterion to distinguish those who needed testing from those who did not. One possible testing criterion is to test those, and only those, who either live in a high-risk zip code or are on Medicaid.
Alternative criteria were based on using our prediction equation. To do so, we first computed a BLL risk score for each child, based on the regression coefficients in Table 3, and added an Empirical Bayesian Residual, which varied by block group. This risk score was the predicted value of Ln(BLL–0.5) for the child. However, as with any regression, the actual scores of Ln(BLL–0.5) varied around the predicted score.
Next, we set criterion values for our risk score, such that we recommended testing those and only those whose risk score exceeded the criterion. Our values of sensitivity and specificity depended on the chosen criterion. The Medicaid regulations and 1997 CDC guidelines,8 which require that all children on Medicaid or in high-risk areas must receive a BLL screening test at 12 and 24 months of age, clearly assume that high sensitivity is more important than high specificity. Hence, all the criteria that we examined provided a very high sensitivity.
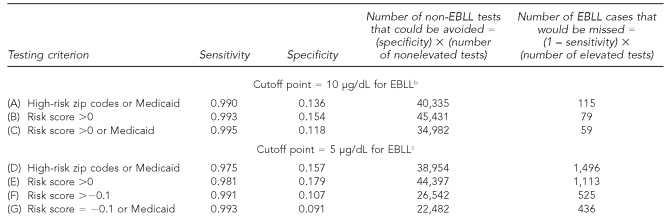
Table 4 contains the sensitivity and specificity results from the 2002–2005 data for several different testing criteria and two cutoff points for EBLL. In row A, we show the CDC/MDCH criterion of testing all who live in a high-risk zip code or are on Medicaid. Row B assesses testing of all who have a risk score >0 (i.e., all with predicted values of BLL>1.5 μg/dL). Row C assumes that we tested all those who either had a risk score >0 or were on Medicaid.
Table 4.
Sensitivity and specificity of BLL risk scoresa from prediction equation vs. Medicaid or high-risk zip codes, using 2002–2005 Michigan Department of Community Health data and two cutoff points for EBLL
aThe BLL risk score is the predicted value of Ln(BLL–0.5) from the regression coefficients predicting Ln(BLL–0.5) from race, Medicaid status, age, and block group census variables. All computations use the 307,204 cases that have no missing data on any of the variables.
bWhen EBLL is considered to be 10 μg/dL, the number of EBLL test results is 11,391.
cWhen EBLL is considered to be 5 μg/dL, the number of EBLL results is 59,611.
BLL = blood lead level
EBLL = elevated blood lead level
μg/dL = micrograms per deciliter
To understand the tradeoffs involved, the two right-hand columns show, for each criterion, how many tests of true negatives would be avoided and how many true positives would be missed. Comparing rows A and B, which use the EBLL cutoff point of 10 μg/dL, reveals that if we tested all with a risk score >0, we could achieve both higher sensitivity (0.993 vs. 0.990) and higher specificity (0.154 vs. 0.136) than if we used the 1997 CDC criterion of Medicaid and/or zip code. Our procedure would miss 36 (115 minus 79) fewer cases of EBLL, while avoiding 5,096 negative tests (45,431 minus 40,335) and, at $30.00 per test, would have saved approximately $152,880.
Using our prediction equation, which took Medicaid status into account and required that those with risk scores >0 be tested (as in row B of Table 4), would have resulted in testing 95.1% of those on Medicaid. But suppose we would have tested all with a risk score >0 but also tested all children on Medicaid, regardless of risk score. Comparing row C with row B shows that doing so would have slightly increased sensitivity from 0.993 to 0.995, but would have lowered specificity from 0.154 to 0.118. Our procedure would have failed to identify an additional 20 EBLL cases (79 minus 59) who would have been tested had we also tested all Medicaid children, while avoiding 10,449 more BLL tests (45,431 minus 34,982), thereby saving $313,470 in testing costs. Under the 2009 CDC guidelines, public health departments may decide if the extra cost is worth the benefits.17
Rows D and E of Table 4 show a similar pattern for the lower EBLL cutoff point of 5 μg/dL, as found in rows A and B. Comparing rows D and E, we see that testing all who have a risk score >0 again gave greater sensitivity (0.981 vs. 0.975) and greater specificity (0.179 vs. 0.157) than dichotomized zip code risk or Medicaid. If, however, we wanted as high a sensitivity as achieved in row B at this lower EBLL cutoff point, we would need to test at an even lower risk score: those with a risk score of at least –0.1 (equivalent to a predicted BLL of 1.404, see row F).
By comparing rows F and G, we assessed the cost and benefits of adding the requirement to test all on Medicaid, but at the lower cutoff point of 5 μg/dL. Our procedure would have missed 89 cases (525 minus 436) compared with testing all on Medicaid, but would have required 4,060 (26,542 minus 22,482) fewer tests, at a savings of more than $120,000.
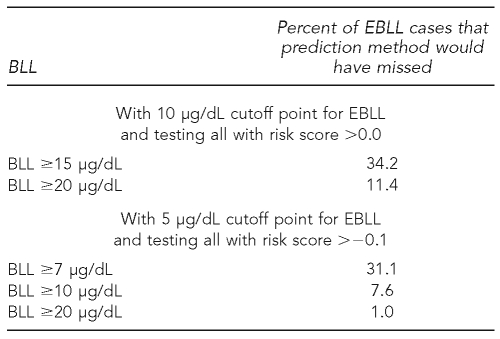
While our prediction method would have left a few EBLL cases untested, these accounted for less than 1% of all cases tested by the MDCH in our database. At the current cutoff point of 10 μg/dL, we would have missed 0.69% (79/11,391); at a cutoff point of 5 μg/dL, we would have missed 0.88% (525/59,611). Furthermore these “missed” cases were overwhelmingly cases that were just barely above the cutoff point for EBLL. As can be seen in Table 5, only about one-third of the missed cases had BLLs that were at least 50% above the cutoff point for EBLL, and only about 10% of them had BLLs that were at least twice as high as the cutoff point.
Table 5.
Distribution of BLLs in the Michigan Department of Community Health database of BLL tests, 2002–2005, for those elevated cases that would be missed, using BLL risk scoresa and cutoff points
aThe risk score is the predicted value of Ln(BLL–0.5) from the regression coefficients predicting Ln(BLL–0.5) from race, Medicaid status, age, and block group census variables.
BLL = blood lead level
EBLL = elevated blood lead level
μg/dL = micrograms per deciliter
DISCUSSION
Using census block groups explains much more of the variance in BLL than does dichotomizing zip codes into high and low risk. Contrary to other findings,19,20 block groups better predict BLL than do census tracts, and our study confirms the conjecture that one's BLL is more closely associated with characteristics of one's immediate environment than with characteristics of a larger area, such as a tract or zip code.45
The age of housing and the socioeconomic status of the block group can explain most of the variance in BLLs. However, the race of the child and racial/ethnic character of the neighborhood have nontrivial effects, even after controlling for the other variables.
The risk of lead poisoning does not decrease until a family's income is >185% FPL. Furthermore, housing built before 1940 poses far greater risk than housing built between 1940 and 1949.23 By contrast, the proportion of rental housing in a block group has only trivial effects.
Our model's predictions were improved by including Empirical Bayesian Residuals as predictors. The equations for 1998–2001 and 2002–2005 made very similar predictions, except that predicted BLL was lower in more recent years. Even if those who are tested have higher BLLs than others, our prediction equation can still be usefully applied to all children in the state, even five years after the 2000 Census.
Our prediction equation provides a noticeable improvement in predicting BLL compared with zip code risk and Medicaid status. As we have shown, our equation provides a cost savings and identifies more cases of EBLL. Knowing the child's previous residence can add to the accuracy of risk prediction.
Our sensitivity and specificity analysis required dichotomizing both actual BLL results and risk scores. However, our prediction equations and risk scores are undoubtedly more accurate than those in previous research studies10,18–20,22 because our equations were developed from treating both observed and predicted BLLs as continuous variables, rather than as dichotomies.
Limitations
Our study had several limitations. These data came from only one state and during an eight-year period. In addition, some of the elevated capillary tests were not followed up with a more accurate venous test, but data from these capillary tests were analyzed along with the venous tests.
CONCLUSIONS
While the Centers for Medicare and Medicaid Services mandates that all Medicaid children be tested,14,46 many states, including Michigan, do not meet this mandate. This article provides an empirical way for public health officials to answer the question of whether requiring testing of all children on Medicaid (rather than relying strictly on our prediction equation) is the best way to balance cost savings and public health concerns.
While Medicaid eligibility and dichotomized zip code risk have a much lower predictive validity than our equation, they present a very simple decision procedure to the staff at a public health clinic or medical office. By contrast, using our prediction equation seems, at first glance, quite daunting.
However, with the aid of Internet-based software, our prediction equation is able to efficiently identify neighborhoods and individuals with high risk of EBLLs. Our website (http://midata.msu.edu/bll) is very useful for determining if a child should be tested. In addition to the address, the program requests the Medicaid status, race, and age of the child. From the address, the census block group is determined and its characteristics are entered into the prediction equation. The program then indicates whether a BLL test is recommended, and this depends on whether the child's predicted value of Ln(BLL–0.5) exceeds the cutoff point chosen by MDCH. MDCH has authorized its use as one way to determine whether a BLL test is needed.
Similar prediction equations can be developed for other states from BLL test data, U.S. Census information, and address. This will improve decisions as to which children should be targeted for testing. In doing so, it will reduce costs while simultaneously identifying more cases of EBLL.
Acknowledgments
The authors thank Robert L. Scott for providing the Michigan Department of Community Health (MDCH) data; Christopher F. Ake, Elaine M. Allensworth, Yasmina Bouraoui, Kenneth Frank, Sharon Hudson, Joseph Messina, Warren A. Brown, and Jeffrey Wooldridge for valuable advice; and Sean Frost and Richard Miles for assistance with data management.
Footnotes
This study was supported by the Centers for Disease Control and Prevention (CDC) grant # PA00053 Supplemental Studies Part C. The views expressed in this article are those of the authors and do not necessarily represent the views of CDC or MDCH.
REFERENCES
- 1.Fulton M, Raab G, Thomson G, Laxen D, Hunter R, Hepburn W. Influence of blood lead on the ability and attainment of children in Edinburgh. Lancet. 1987;1:1221–6. doi: 10.1016/s0140-6736(87)92683-3. [DOI] [PubMed] [Google Scholar]
- 2.Bellinger D, Leviton A, Waternaux C, Needleman H, Rabinowitz M. Longitudinal analyses of prenatal and postnatal lead exposure and early cognitive development. N Engl J Med. 1987;316:1037–43. doi: 10.1056/NEJM198704233161701. [DOI] [PubMed] [Google Scholar]
- 3.Dietrich KN, Krafft KM, Bornschein RL, Hammond PB, Berger O, Succop PA, et al. Low-level fetal lead exposure effect on neurobehavioral development in early infancy. Pediatrics. 1987;80:721–30. [PubMed] [Google Scholar]
- 4.McMichael AJ, Baghurst PA, Wigg NR, Vimpani GV, Robertson EF, Roberts RJ. Port Pirie Cohort Study: environmental exposure to lead and children's abilities at the age of four years. N Engl J Med. 1988;319:468–75. doi: 10.1056/NEJM198808253190803. [DOI] [PubMed] [Google Scholar]
- 5.Commission on Life Sciences. Measuring lead exposure in infants, children, and other sensitive populations. Washington: National Academy Press; 1993. [PubMed] [Google Scholar]
- 6.Chen A, Dietrich KN, Ware JH, Radcliffe J, Rogan WJ. IQ and blood lead from 2 to 7 years of age: are the effects in older children the residual of high blood lead concentrations in 2-year-olds? Environ Health Perspect. 2005;113:597–601. doi: 10.1289/ehp.7625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lanphear BP, Hornung R, Khoury J, Yolton K, Baghurst P, Bellinger DC, et al. Low-level environmental lead exposure and children's intellectual function: an international pooled analysis. Environ Health Perspect. 2005;113:894–9. doi: 10.1289/ehp.7688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Centers for Disease Control and Prevention (US) Screening young children for lead poisoning. Guidance for state and local public health officials. Atlanta: Department of Health and Human Services, Public Health Service (US); 1997. [Google Scholar]
- 9.Centers for Disease Control and Prevention (US) Preventing lead poisoning in young children. Atlanta: CDC; 2005. [Google Scholar]
- 10.Lanphear BP, Byrd RS, Auinger P, Schaffer SJ. Community characteristics associated with elevated blood lead levels in children. Pediatrics. 1998;101:264–71. doi: 10.1542/peds.101.2.264. [DOI] [PubMed] [Google Scholar]
- 11.Jacobs DE, Clickner RP, Zhou JY, Viet SM, Marker DA, Rogers JW, et al. The prevalence of lead-based paint hazards in U.S. housing. Environ Health Perspect. 2002;110:A599–606. doi: 10.1289/ehp.021100599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Meyer PA, Pivetz T, Dignam TA, Homa DM, Schoonover J, Brody D. Surveillance for elevated blood lead levels among children—United States, 1997–2001. MMWR Surveill Summ. 2003;52(10):1–21. [PubMed] [Google Scholar]
- 13.Act No. 55 Public Acts of 2004. [cited 2009 Oct 8]. Available from: URL: https://legislature.mi.gov/documents/2003-2004/publicact/pdf/2004-PA-0055.pdf.
- 14.Michigan Childhood Lead Poisoning Prevention and Control Commission. Plan to eliminate childhood lead poisoning in Michigan. 2007. Jun 23, [cited 2009 Oct 9]. Available from: URL: http://www.bridges4kids.org/leadreport2007.pdf.
- 15.Michigan Department of Community Health. Medicaid blood lead testing. Lansing (MI): Michigan Department of Community Health; 2008. Dec, [Google Scholar]
- 16.Michigan Department of Community Health/Childhood Lead Poisoning Prevention Program. Statewide lead testing/lead screening plan. Revised 2009 Jul 10. [cited 2009 Oct 9]. Available from: URL: http://www.mnceh.org/Fact%20Sheets%20-%20MNCEH/MDCH%20Lead%20Testing%20Screening.pdf.
- 17.Wengrovitz AM, Brown MJ. Recommendations for blood lead screening of Medicaid-eligible children aged 1–5 years: an updated approach to targeting a group at high risk. MMWR Recomm Rep. 2009;58(RR09):1–11. [PubMed] [Google Scholar]
- 18.Haley VB, Talbot TO. Geographic analysis of blood lead levels in New York State children born 1994–1997. Environ Health Perspect. 2004;112:1577–82. doi: 10.1289/ehp.7053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Krieger N, Chen JT, Waterman PD, Soobader MJ, Subramanian SV, Carson R. Choosing area based socioeconomic measures to monitor social inequalities in low birth weight and childhood lead poisoning: the Public Health Disparities Geocoding Project (US) J Epidemiol Community Health. 2003;57:186–99. doi: 10.1136/jech.57.3.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Krieger N, Chen JT, Waterman PD, Rehkopf DH, Subramanian SV. Race/ethnicity, gender, and monitoring socioeconomic gradients in health: a comparison of area-based socioeconomic measures—the Public Health Disparities Geocoding Project. Am J Public Health. 2003;93:1655–71. doi: 10.2105/ajph.93.10.1655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Curtis GB, Braggio J, Fokum F, Roberts JR, Scott R, Staley F, et al. Using GIS to assess and direct childhood lead poisoning prevention: guidance for state and local childhood lead poisoning prevention programs. Atlanta: Department of Health and Human Services (US); 2004. [Google Scholar]
- 22.Reissman DB, Staley F, Curtis GB, Kaufmann RB. Use of geographic information system technology to aid health department decision making about childhood lead poisoning prevention activities. Environ Health Perspect. 2001;109:89–94. doi: 10.1289/ehp.0110989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Roberts JR, Hulsey TC, Curtis GB, Reigart JR. Using geographic information systems to assess risk for elevated blood lead levels in children. Public Health Rep. 2003;118:221–9. doi: 10.1093/phr/118.3.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sargent JD, Brown MJ, Freeman JL, Bailey A, Goodman D, Freeman DH., Jr. Childhood lead poisoning in Massachusetts communities: its association with sociodemographic and housing characteristics. Am J Public Health. 1995;85:528–34. doi: 10.2105/ajph.85.4.528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Canfield RL, Henderson CR, Jr, Cory-Slechta DA, Cox C, Jusko TA, Lanphear BP. Intellectual impairments in children with blood lead concentrations below 10 μg per deciliter. N Engl J Med. 2003;348:1517–26. doi: 10.1056/NEJMoa022848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Institute of Medicine. The future of the public's health in the 21st century. Washington: National Academies Press; 2002. [PubMed] [Google Scholar]
- 27.Update: blood lead levels—United States, 1991–1994. MMWR Morb Mortal Wkly Rep. 1997;46(7):141–6. [published erratum appears in MMWR Morb Mortal Wkly Rep 1997;46(26):607] [PubMed] [Google Scholar]
- 28.General Accountability Office (US) Medicaid: elevated blood lead levels in children. Washington: General Accountability Office; 1998. GAO publication no. GAO/HEHS-98-78. [Google Scholar]
- 29.Lanphear BP, Weitzman M, Eberly S. Racial differences in urban children's environmental exposures to lead. Am J Public Health. 1996;86:1460–3. doi: 10.2105/ajph.86.10.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kim DY, Staley F, Curtis G, Buchanan S. Relation between housing age, housing value, and childhood blood lead levels in children in Jefferson County, KY. Am J Public Health. 2002;92:769–72. doi: 10.2105/ajph.92.5.769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.American Standards Association. American Standards specifications to minimize hazards to children from residual surface coating materials. Standard Z66. 1955. pp. 1–1955. [Google Scholar]
- 32.Warren C. Little pamphlets and big lies: federal authorities respond to childhood lead poisoning, 1935–2003. Public Health Rep. 2005;120:322–9. doi: 10.1177/003335490512000318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Laraque D, Trasande L. Lead poisoning: successes and 21st century challenges. Pediatr Rev. 2005;26:435–43. [PubMed] [Google Scholar]
- 34.Dietrich KN, Ris MD, Succop PA, Berger OG, Bornschein RL. Early exposure to lead and juvenile delinquency. Neurotoxicol Teratol. 2001;23:511–8. doi: 10.1016/s0892-0362(01)00184-2. [DOI] [PubMed] [Google Scholar]
- 35.Frey WH, Myers D. Racial segregation in US metropolitan areas and cities, 1990–2000: patterns, trends, and explanations. Ann Arbor (MI): University of Michigan Population Studies Center; 2005. Apr, PSC Research Report No. 05-573. [Google Scholar]
- 36.McClendon MJ. Multiple regression and causal analysis. Itasca (IL): F.E. Peacock Publishers; 2002. [Google Scholar]
- 37.Brody DJ, Pirkle JL, Kramer RA, Flegal KM, Matte TD, Gunter EW, et al. Blood lead levels in the US population: phase I of the Third National Health and Nutrition Examination Survey (NHANES III, 1988 to 1991) JAMA. 1994;272:277–83. doi: 10.1001/jama.272.4.277. [published erratum appears in JAMA 1995;274:130] [DOI] [PubMed] [Google Scholar]
- 38.Raudenbush SW, Bryk AS. Hierarchical linear models: applications and data analysis methods. 2nd ed. Thousand Oaks (CA): Sage Publications; 2001. [Google Scholar]
- 39.Kaufmann RB, Clouse TL, Olson DR, Matte TD. Elevated blood lead levels and blood lead screening among US children aged one to five years: 1988–1994. Pediatrics. 2000;106:E79. doi: 10.1542/peds.106.6.e79. [DOI] [PubMed] [Google Scholar]
- 40.Kemper AR, Cohn LM, Fant KE, Dombkowski KJ. Blood lead testing among Medicaid-enrolled children in Michigan. Arch Pediatr Adolesc Med. 2005;159:646–50. doi: 10.1001/archpedi.159.7.646. [DOI] [PubMed] [Google Scholar]
- 41.Wooldridge JM. Introductory econometrics: a modern approach. 2nd ed. Mason (OH): South-Western College Publishing; 2002. [Google Scholar]
- 42.Furstenberg FF, Jr, Morgan SP, Allison PD. Paternal participation and child's well-being after marital dissolution. Am Sociol Rev. 1987;52:695–701. [Google Scholar]
- 43.Hagan J, MacMillan R, Wheaton B. New kid in town: social capital and the life course effects on family migration of children. Am Sociol Rev. 1996;61:368–85. [Google Scholar]
- 44.Van Vliet W. Children who move: relocation effects and their context. J Planning Literature. 1986;1:403–26. [Google Scholar]
- 45.Hipp JR. Block, tract, and levels of aggregation: neighborhood structure and crime and disorder as a case in point. Am Sociol Rev. 2007;72:659–80. [Google Scholar]
- 46.National Health Law Program. Children's health under Medicaid: a national review of early and periodic screening, diagnosis and treatment, 1999–2003. Los Angeles: National Health Law Program; 2005. May, [Google Scholar]