Three methods tested to model SF-6D health utilities for health states involving comorbidity/co-occurring conditions

Abstract

Objective

Compare three commonly used methods to combine the impacts of multiple health conditions on SF-6D health utility scores.

Study Design

We used data from the 1998–2004 Medicare Health Outcomes Survey to compare three commonly suggested models of multiple health conditions’ impacts on health-related quality of life: additive, minimum, and multiplicative. We modeled SF-6D scores using information about 15 health conditions, both unadjusted and adjusted for age, sex, education, and income. Model performance was assessed using mean squared error, mean predictive error by number of health conditions, and mean predictive error for groups with specific combinations of health conditions.

Results

95,195 observations were used for model estimation and 94,794 observations were used for model testing. The adjusted models always had better performance than the unadjusted models. The multiplicative model showed smaller mean predictive error than the other models in both those younger than age 65 and those aged 65 and older. Mean predictive error for the multiplicative model was generally within the minimally important difference of the SF-6D.

Conclusion

All tested models are imperfect in these Medicare data, but the multiplicative model performed best.

What is new?

1. This article is the first to empirically test three common methods to combine the impacts of single health conditions on health utility when multiple health conditions are present. Of the methods tested, the multiplicative method performed best in out-of-sample tests.

2. The additive method, which has been the most widely used method for the calculation of quality-adjusted life years, performed well for combinations of seven or less health conditions.

3. These findings have implications for the construction of catalogs of health conditions’ impact on health utility as well as combining the impact of multiple health conditions in cost-effectiveness analyses.

4. This article also provides a catalog of the impact of 15 different health conditions on the SF-6D health utility score using data from the Medicare Health Outcomes Study.

Introduction

Cost-effectiveness analysis (CEA) of interventions and regulations that impact health requires a method to quantify changes in health. Both the Panel on Cost-Effectiveness in Health and Medicine (PCEHM) and the Committee to Evaluate Measures of Health Benefits for Environmental, Health, and Safety Regulation (CEMHB) recommended using generic health-related quality of life instruments with preference-based scoring systems to quantify health. The resulting scores, referred to as “health utility,” are constructed so that full health is anchored at 1.0 and death is anchored at 0 [1,2].

CEA requires an estimate of the impact of delaying or removing a given health condition on health utility. CEA often incorporates previously published health utilities rather than perform primary data analysis [3]. Combining impact estimates from several smaller studies, however, can be complicated by variations in sampling, health utility measurement, and adjustment for important covariates. Large population surveys are an attractive option for generating “condition catalogs,” which report the average difference between health utilities of people with and without selected named health conditions. These surveys sample and represent the experience of large segments of the population and allow for consistent impact estimation across many different health conditions. While large surveys may include enough people who only report a single health condition to directly estimate the health utility for that condition, there are not enough people who report a combination of two or more conditions to report the observed health utility score for groups with a specific combination of conditions.

CEAs often must address the impacts of several health conditions at the same time because the population of interest has coexisting conditions or the intervention of interest affects several health conditions. In the absence of catalogs of utility impacts of multiple conditions, these impacts must be modeled using single condition catalogs. There is currently no standardized guidance regarding the combination of single condition impacts to model the impact of the combination of those health conditions. Determining the most appropriate method to combine health utility estimates for multiple health conditions is important for both analyses that use health utilities from the literature and analyses that collect primary data. Even when collecting primary data about health utilities, obtaining health utilities for every possible combination of health conditions may be prohibitively expensive or time consuming. It is more feasible to collect health utilities for individual health conditions and then to use a pre-specified algorithm to combine these single health utilities when the impact of multiple health conditions on health utility is needed for the analysis.

Both the PCEHM and CEMHB called for consistently estimated catalogs of health utilities that could be used as a source of values for CEA. The CEMHB also specified that “such research should give special attention to the documentation of co-morbid conditions and the development of health-related quality of life values for health states involving multiple impairments” [2]. Thus, condition catalogs could include the impact of health conditions conditioned on presence of other health conditions and demographic variables.

To estimate the impact of a health condition using a sample of persons with the health condition, the PCEHM and CEMBH have suggested comparing the sample’s average health utility scores and average health utilities in a national data set adjusted to the same age and sex distribution as the sample. A list of these estimates could then be used to make a condition catalog. These estimates would accurately reflect impact of single health conditions if all conditions are generally of low prevalence and independently distributed in the population. Low prevalence is necessary so that the age- and sex-adjusted normative scores do not include many individuals with the condition, otherwise the cataloged differences would underestimate the effect of very prevalent health condition on health utility. Without independence, the impact of a single health condition may be overestimated because it tends to cluster with other health conditions.

Neither the low prevalence nor independence assumption holds for many conditions in population-based datasets. Particularly at older ages, there are conditions with very high prevalence, e.g., 45% of those aged 65 and over report having been diagnosed with arthritis [4]. There are also several highly prevalent conditions of interest that cluster together, such as cardiovascular conditions (e.g., stroke, coronary artery disease, and myocardial infarction), immunologically mediated conditions (e.g. asthma, eczema, and allergy), and sexually transmitted infections. The prevalence of chronic conditions in the United States is increasing as life expectancy increases, our population ages, and many diseases that were once fatal have become manageable chronic conditions [5]. Currently, about 80% of US adults aged 65 years and older report at least one chronic condition, and 50% report at least two [6]. It has been estimated that half of all Americans will have a chronic health condition by 2020 and almost half of these individuals will have two or more such conditions [7].

Available condition catalogs of health utilities have used different methods to adjust for the presence of multiple health conditions when assessing impact of a given condition. The first catalogs ignored co-morbidities and simply reported the mean health utility score for those with a particular health condition [8–10]. The most recent catalogs control for many chronic health conditions in a single regression equation using an additive model that assumes the impact of any given health condition is the same regardless of the presence of other health conditions [11–14]. This model assumption has not been formally tested. Other research groups, particularly those working with the Health Utilities Index and Disability Adjusted Life Years, assume a multiplicative method is most appropriate for combining health utility impacts of multiple health conditions [15,16]. This method assumes the impact of any health condition is a constant proportion of underlying health utility. A recent formal test of additive, multiplicative, and minimum methods used directly elicited utilities and found that a minimum method performed best [17]. However, this test used directly elicited utilities from a patient sample and the results may vary for health utility scores from instruments that use community-based preferences. Previous simulation research has shown that disability adjusted life expectancy calculated using the additive and multiplicative methods is quite similar except in groups with several chronic health conditions, such as elderly populations [16]. This simulation research used disability adjusted life expectancy which is different from the quality adjusted life expectancy calculated using health utilities [18].

In this report, we test three mathematical methods that combine information about single health conditions to estimate health utilities for persons with more than one health condition: the additive, minimum, and multiplicative methods. We conduct this test using data from the Medicare Health Outcomes Survey. The sampling frame for this very large dataset is a large section of the US population where co-occurring chronic conditions are common, allowing us to evaluate the ability of these methods to predict health utility scores in groups where multiple health conditions are present. We test the three modeling methods using the SF-6D health utility score computed from the SF-36 version 1 questionnaire.

Data and Methods

Data

The Medicare Health Outcomes Survey (HOS) (formerly known as the Health of Seniors Survey) is used to measure outcomes in seniors enrolled in Medicare managed care plans. It is mailed and self-administered with baseline and 1-year follow-up surveys. If enrollees do not respond to two mailed questionnaires, the data collection agency attempts to reach them by telephone. Each year, beginning in 1998, 1,000 Medicare beneficiaries were randomly sampled from each Medicare Advantage (MA) managed care plan. There are many MA plans, so each cohort has over 99,000 completed baseline surveys [19]. We used the first baseline questionnaire completed by each of the unique individuals surveyed between 1998 and 2004. This project used items from baseline surveys that are consistent across all cohorts.

We excluded surveys completed by proxy respondents, surveys with less than 80% of the items answered, and surveys without information necessary for the models (SF-6D score, health conditions, age, sex, education, income). Of the surveys which fit these inclusion criteria and we randomly selected 95,195 baseline surveys for model estimation and used the remaining 94,794 for model evaluation.

Because the enrollment criteria for Medicare drastically change at the age of 65, we split the observations into two groups. US citizens and permanent residents over the age of 65 are eligible for Medicare if they or their spouse worked at least 10 years in Medicare-covered employment (referred to as the “65-and-older” group). US citizens younger than the age of 65 are eligible for Medicare if they have received social security disability benefits for 24 months or have been diagnosed with one of a set of specific health conditions, though enrollees with end-stage renal disease are excluded from this survey (referred to as the “under-65” group).

Dependent Variables

The SF-36 version 1 [20] was administered in the HOS survey from 1998 to 2004. This widely used health status instrument is often reported as 8 scales or 2 component scores. For use in CEA, a single health utility score named the SF-6D can be scored using 11 of the 36 questions from the SF-36. The SF-6D has 6 health domains: physical functioning, role limitations, social functioning, pain, mental health, and vitality. These domains have 4 to 6 levels. A household sample of adults from the United Kingdom (n=836) provided standard gamble valuations for several SF-6D health states – a health state is a specific combination of levels across the six domains. These valuations were used to create an algorithm that can be used to convert a combination of domain levels to an SF-6D score. The maximum SF-6D score is 1.0, the minimum score for a living person is 0.30, and the state “dead” is scored as 0.0 [21, 22].

Independent Variables

The HOS questionnaire also asked respondents to report presence or absence of several health conditions. We used 15 self-reported health conditions that were collected in each baseline survey between 1998 and 2004:

• vision impairment (from “Can you see well enough to read newspaper print (with your glasses or contacts if that’s how you see best)?”)

• hearing impairment (from “Can you hear most of the things people say (with a hearing aid if that’s how you hear best)?”)

• problems controlling urination (from “Do you have difficulty controlling urination?”)

• depression for most of the last year. (from “In the past year, have you felt depressed or sad much of the time?”)

There were also several questions formatted as “Has a doctor every told you that you have …

• angina pectoris or coronary artery disease

• congestive heart failure

• myocardial infarction or heart attack

• other heart conditions, such as problems with heart valves or the rhythm of your heartbeat

• a stroke

• emphysema or asthma or COPD

• Crohn’s disease or ulcerative colitis or inflammatory bowel disease

• arthritis of the hip or knee

• arthritis of the hand or wrist

• sciatica

• diabetes, high blood sugar, or sugar in the urine”

Although each of these labels represents a health condition with a spectrum of manifestations, for purposes of modeling utilities they are treated as unitary entities. We include on these 15 conditions because they are chronic in nature and should affect the respondent’s health when they completed the survey. The duration of reported health conditions is unknown, so the final estimates are the average impact on health and function for all severities and durations of a particular health condition. We should note that it is possible—even likely—that individuals have health conditions which are not on this list.

Our models adjusted for age, sex, education, and income, as do recent health condition catalogs [11–14]. We used CMS-reported age (measured in years) and sex, as well as education (less than high school, high school or GED, more than high school) and household income (less than $10,000/year, $10,000 to $20,000/year, and more than $20,000/year) based on self-reported categorical information in the HOS questionnaire.

Methods Tested

All models were estimated using WinBUGS 1.4.1 [23]. All models had 3 chains with a 10,000 iteration burn-in and a 5,000 iteration statistical sample. Model convergence was assessed using the Gelman-Rubin statistic.

Observed SF-6D health utility for each individual HOS respondent was modeled in two steps. First, a latent summary health scale, Health, was fit using each method described below. Scores on this scale were then censored in the models at the maximum (1.0) and minimum scores (0.30) of the SF-6D. These censored scores estimated the observed SF-6D scores.

Additive

In this method, each health condition has a constant impact on health utility regardless of other covariates (age, sex, other health conditions). For example, the impact of diabetes on health utility could be −0.04 and the impact of congestive heart failure could be −0.10. The combined impact on health utility in an individual with both of these health conditions would be calculated by adding the impacts: −0.04 + −0.10 = −0.14. Using this method for individuals with many health conditions can result in very low or negative health utility scores.

For observations i, i=1 … I:

$${\mathit{Health}}_i=\mathit{const}+{\beta }_1(\mathit{Cond}{1}_i)+{\beta }_2(\mathit{Cond}{2}_i)+\dots +{\beta }_{15}(\mathit{Cond}{15}_i)+{\epsilon }_i,$$

where const and β_n, n=1 … 15 are assigned non-informative normal priors, N(0,1000), Condn is an indicator for the n^th condition, and ε is a normally distributed error term with mean equal to zero and variance 1/τ, where τ is assigned a non-informative prior, gamma(.001, .001).

The adjusted form of this model also includes a continuous variable for age in years (age), an indicator variable for sex (sex), 2 indicator variables for education (edu1, edu2), and 2 indicator variables for income (inc1, inc2):

$$\begin{array}{l}{\mathit{Health}}_i=\mathit{const}+{\beta }_1(\mathit{Cond}{1}_i)+{\beta }_2(\mathit{Cond}{2}_i)+\dots +{\beta }_{15}(\mathit{Cond}{15}_i)+\\ {\beta }_{\mathit{age}}(\mathit{age})+{\beta }_{\mathit{sex}}(\mathit{sex})+{\beta }_{\mathit{inc}1}(\mathit{inc}1)+{\beta }_{\mathit{inc}2}(\mathit{inc}2)+{\beta }_{\mathit{edu}1}(\mathit{edu}1)+{\beta }_{\mathit{edu}2}(\mathit{edu}2)+{\epsilon }_i\end{array}$$

where β_age, β_sex, β_inc1, β_inc2, β_edu1, and β_edu2 are each assigned a non-informative prior, N(0,1000). Sex=1 if sex is male, Edu1=1 if education is high school or GED, Edu2=1 if education is beyond high school, Inc1=1 if income is less than $10,000 per year, Inc2=1 if income is $10,000 to $20,000 per year.

Minimum

In the minimum method an individual with multiple conditions is modeled by recognizing only the health condition with the minimum single condition utility score, i.e. the health condition with the greatest impact will “trump” the other health conditions and the aggregate score will reflect only the decrement associated with the minimum condition. . For example, the impact of diabetes on health utility could be −0.04 and the impact of congestive heart failure could be −0.10. The impact on health utility in an individual with both health conditions would be calculated by taking the impact which gives the minimum score (−0.10).

Minimum models used the same algebraic form for Health_i as the additive model. Instead of representing multiple health conditions in the equation, however, each individual’s aggregate health utility was modeled with only one health condition—that having most single condition impact. To implement this, conditions were rank ordered from 1 to 15, where 1 has the most effect on utility. Of the health conditions reported by each individual, the health condition with the rank closest to 1 had its indicator variable set to 1 and all other condition indicators, Condn_i, were set to 0 in the equation representing the individual’s combined state. The model was then estimated using these modified data. Since it was unknown a priori which rank order would perform best, the five models with the largest R-squared were selected using proc GLM in SAS 9.0. The best performing model of these five was selected using Deviance Information Criterion [24]. The rank order selected for the under-65 group was depression, sciatica, problems controlling urination, arthritis of the hip or knee, gastrointestinal diseases, arthritis of the hand or wrist, respiratory diseases, other heart problems, coronary artery disease, congestive heart failure, diabetes mellitus, problems hearing, stroke, problems reading, and acute myocardial infarction. The rank order selected for the 65-and-older group was depression, respiratory diseases, arthritis of the hip or knee, problems controlling urination, sciatica, congestive heart failure, stroke, gastrointestinal diseases, problems reading, problems hearing, arthritis of the hand or wrist, diabetes mellitus, other heart problems, coronary artery disease, and acute myocardial infarction.

Multiplicative

The multiplicative method assumes that each health condition has a constant proportional decrement on health utility, so the absolute impact of a health condition is dependent on other covariates. The multiplicative method implies that health utility decreases as the number of health conditions increases, but the overall score decreases slower than in the additive model at lower health utility scores. For example, the proportional impact of stroke could be 0.18, so the presence of stroke will decrease health utility by 18%. For an individual with characteristics such that their health utility is 0.90 before a stroke, their health utility would be 0.90*0.82 = 0.74 with a stroke for a change of −0.16 on the interval health utility scale. For an individual with characteristics such that their health utility is 0.60 before a stroke, their health utility would be 0.60*0.82 = 0.49 with a stroke for a change of −0.11 on the interval health utility scale.

$${\mathit{Health}}_i={\mathit{const}}^{\ast }{(1-{\beta }_1(\mathit{Cond}{1}_i))}^{\ast }{(1-{\beta }_2(\mathit{Cond}{2}_i))}^{\ast }{\dots }^{\ast }(1-{\beta }_{15}(\mathit{Cond}{15}_i))+{\epsilon }_i$$

For the adjusted form, a multiplicative fixed effect (δ_i) was calculated for each individual. This fixed effect was multiplied to the terms containing each of the health conditions

$$\begin{array}{l}{\mathit{Health}}_i={\delta }_i{(1-{\beta }_1(\mathit{Cond}{1}_i))}^{\ast }{(1-{\beta }_2(\mathit{Cond}{2}_i))}^{\ast }{\dots }^{\ast }(1-{\beta }_n(\mathit{Cond}{n}_i))+{\epsilon }_i\\ {\delta }_i=\mathit{const}+{\beta }_{\mathit{age}}(\mathit{age})+{\beta }_{\mathit{sex}}(\mathit{sex})+{\beta }_{\mathit{inc}1}(\mathit{inc}1)+{\beta }_{\mathit{inc}2}(\mathit{inc}2)+{\beta }_{\mathit{edu}1}(\mathit{edu}1)+{\beta }_{\mathit{edu}2}(\mathit{edu}2)\end{array}$$

Model Evaluation

The estimated SF-6D scores were calculated using the method described in the Appendix. The output from the Bayesian analyses is a posterior distribution for each parameter in a model. One random draw from each distribution jointly determines one possible regression solution for the model parameters. We sampled 5,000 such solutions, computed the mean squared error (MSE) for each solution, and then averaged the 5,000 MSEs as a measure of model fit.

We also calculated predicted SF-6D summary score for respondents using the means of the posterior distributions for the coefficients from each model to determine point estimates for the parameters. First, we calculated the average difference between the observed and predicted SF-6D scores for individuals, stratified by the total number of health conditions. Strata include 0, 1, 2, …, 11 health conditions as very few individuals reported 12, 13, 14, or 15 health conditions. Second, we calculated the mean of the average MSEs associated with each method with for individuals, stratified by number of health conditions. Third, we selected individuals with a specific combination of conditions to create groups (e.g., 70 individuals reported only vision problems and arthritis of the hip or knee, 151 individuals reported only arthritis of the hip or knee, arthritis of the hand or wrist, and angina). We compared the observed and predicted group means for these health condition combinations when the group had over 50 observations. All model performance evaluation used the reserved half of the sample.

Results

Table 1 includes demographic information about the Medicare HOS samples used for model estimation and model testing. Ages range from 22 to 102 years old. About a quarter of the sample has less than high school education. 80% of the sample reports at least one of the health conditions. The group younger than age 65, which includes individuals who receive social security disability benefits as well as individuals who have certain conditions, given Medicare entitlement by act of Congress, has more males and reports lower income than the 65-and-older group. The under-65 group also reports more of the 15 health conditions used in these analyses, with only 5.2% of respondents reporting none of these conditions. The under-65 group uniformly reports higher health condition prevalence than the 65-and-older group with over twice the prevalence of vision problems, gastrointestinal conditions, respiratory conditions, congestive heart failure, sciatica, and depression. The most prevalent reported conditions are problems controlling urination, arthritis of the hip or knee, arthritis of the hand or wrist, and sciatica with over 20% of the sample reporting these conditions. Over 43% of those in the under-65 group report depression. The least reported condition is vision problems with a prevalence of 7.3% in the under-65 group and 3.5% in the 65-and-older group. Within the sample used in this analyses, 88% completed mailed questionnaires and 12% completed the questionnaire by telephone.

Table 1.

Information and demographics about the samples used for model estimation and model testing

	Younger than 65		65 and Older
	Model Estimation	Model Testing	Model Estimation	Model Testing
Number	5969	5932	89226	88862
Minimum SF-6D	0.301	0.301	0.301	0.301
Maximum SF-6D	1.0	1.0	1.0	1.0
Average SF-6D	0.573	0.572	0.740	0.739
Minimum Age	22	23	65	65
Maximum Age	64	64	102	106
Average Age	55.2	55.0	73.4	73.4
Female	49.9%	49.9%	54.7%	54.6%
Education: less than High School	23.6%	24.6%	23.2%	23.2%
Education: High School or GED	37.1%	37.1%	36.5%	36.4%
Education: more than High School	39.3%	38.8%	40.3%	40.4%
Income: less than $10,000/year	25.1%	25.9%	14.1%	14.2%
Income: $10,000 –20,000/year	37.6%	36.2%	29.5%	29.4%
Income: more than $20,000/year	37.3%	37.9%	56.4%	56.4%
reporting no conditions	5.2%	4.8%	19.2%	19.0%
reporting 1 condition	11.2%	11.2%	22.0%	22.3%
reporting 2 conditions	15.4%	16.0%	19.9%	19.8%
reporting 3 conditions	16.3%	15.4%	15.2%	15.2%
reporting 4 conditions	15.3%	15.3%	10.2%	10.1%
reporting 5 condition	13.4%	13.2%	6.3%	6.1%
reporting 6 conditions	9.6%	9.1%	3.6%	3.5%
reporting 7 conditions	5.9%	6.6%	1.8%	1.8%
reporting 8 conditions	3.4%	3.4%	1.0%	1.0%
reporting 9 condition	2.4%	2.1%	0.5%	0.5%
reporting 10 conditions	1.2%	0.9%	0.2%	0.2%
reporting 11 conditions	0.5%	0.3%	0.1%	0.1%
reporting 12 or more conditions	0.3%	0.3%	0.1%	0.1%

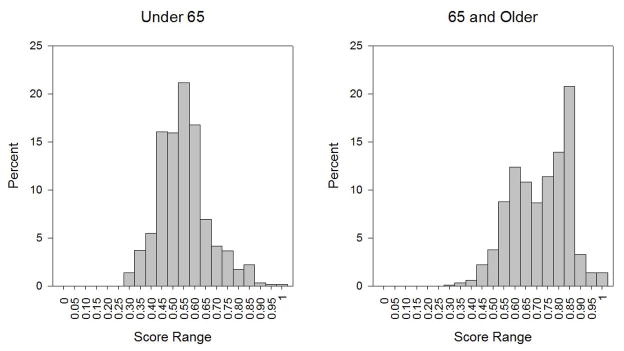
Figure 1 illustrates the distribution of SF-6D scores in the under-65 and 65-and-older groups used for model estimation. These distributions are nearly identical to the distributions of SF-6D scores in the groups used for model testing. As expected because the under-65 group is primary sampled from individuals with disabilities, they report lower SF-6D scores than the 65-and-older group. The 65-and-older group shows a slight ceiling effect, with 1.4% of respondents at the highest SF-6D score, 1.0. Only 0.5% of the under-65 group was at the lowest SF-6D score, 0.30.

Figure 1. Distribution of observed SF-6D health utility scores.

The theoretical maximum and minimum SF-6D scores are 1.0 and 0.30. The under-65 group, which primary includes individuals with disabilities, reports lower SF-6D scores than the 65-and-older group.

Table 2 includes the mean and 95% credible interval values for the health condition parameter estimates from the three age-, sex-, income-, and education-adjusted models for both the under-65 and 65-and-over groups. Table 2 also includes the mean squared error associated with each model from the testing sample. The multiplicative and additive models have similar overall mean squared error between actual and predicted SF-6D scores and these two models show improvement over the minimum model. The models without adjustment for age, sex, education, and income had a similar relationship across the three models (results not shown, available from the authors upon request). All models showed convergence by visual inspection of the Gelman-Rubin statistic.

Table 2.

Parameter estimates from the competing models from the models adjusted for age, sex, education, and income

	Under-65			65 and Older
Parameter	Additive Model, mean and 95% CI	Minimum Model, mean and 95% CI	Multiplicative Model, mean and 95% CI	Additive Model, mean and 95% CI	Minimum Model, mean and 95% CI	Multiplicative Model, mean and 95% CI
Constant	0.618 (0.603, 0.636)	0.673 (0.653, 0.693)	0.624 (0.603, 0.647)	0.968 (0.958, 0.975)	1.002 (0.989, 1.009)	0.986 (0.975, 0.996)
Age in years	0.0009 (0.0007, 0.0012)	0.0004 (0.0001, 0.0007)	0.0010 (0.0006, 0.0013)	−0.0021 (−0.0022, −0.0020)	−0.002 (−0.003, −0.002)	−0.0023 (−0.0025, −0.0022)
Male	−0.001 (−0.006, 0.003)	0.003 (−0.002, 0.008)	−0.002 (−0.008, 0.004)	0.003 (0.001, 0.004)	0.001 (−0.00005, 0.003)	0.003 (0.002, 0.005)
Education: High School or GED	0.0003 (−0.006, 0.007)	0.002 (−0.004, 0.008)	−0.0001 (−0.007, 0.007)	0.009 (0.007, 0.011)	0.013 (0.011, 0.015)	0.011 (0.009, 0.013)
Education: more than High School	0.006 (0.00007, 0.013	0.008 (0.001, 0.014)	0.007 (0.0002, 0.014)	0.016 (0.014, 0.017)	0.019 (0.017, 0.021)	0.017 (0.015, 0.019)
Income: less than $10,000/year	−0.001 (−0.008, 0.006)	−0.004 (−0.010, 0.002)	−0.002 (−0.009, 0.005)	−0.026 (−0.028, −0.024)	−0.031 (−0.033, −0.029)	−0.028 (−0.031, −0.026)
Income: $10,000 –20,000/year	−0.009 (−0.015, −0.003)	−0.010 (−0.016, −0.005)	−0.011 (−0.018, −0.005)	−0.018 (−0.020, −0.017)	−0.021 (−0.023, −0.019)	−0.020 (−0.021, −0.018)
Depression for most of the last year	−0.088 (−0.093, −0.083)	−0.182 (−0.193, −0.171)	0.145 (0.137, 0.153)	−0.118 (−0.120, −0.115)	−0.224 (−0.227, −0.221)	0.167 (0.163, 0.170)
Emphysema or asthma or chronic obstructive pulmonary disease	−0.013 (−0.018, −0.007)	−0.052 (−0.071, −0.033)	0.023 (0.014, 0.033)	−0.041 (−0.043, −0.039)	−0.122 (−0.125, −0.119)	0.058 (0.055, 0.061)
Arthritis of the hip or knee	−0.025(−0.031, −0.019)	−0.079 (−0.092, −0.066)	0.043 (0.034, 0.053)	−0.042 (−0.044, −0.041)	−0.108 (−0.110, −0.106)	0.057 (0.055, 0.059)
Problems controlling urination	−0.025 (−0.030, −0.019)	−0.089 (−0.102, −0.075)	0.045 (0.037, 0.054)	−0.038 (−0.039, −0.036)	−0.080 (−0.083, −0.077)	0.052 (0.050, 0.054)
Sciatica	−0.037 (−0.043, −0.032)	−0.117 (−0.129, −0.105)	0.065 (0.057, 0.073)	−0.034 (−0.036, −0.032)	−0.067 (−0.071, −0.064)	0.047 (0.045, 0.050)
Stroke	−0.002 (−0.009, 0.006)	0.024 (−0.006, 0.056)	0.002 (−0.011, 0.016)	−0.032 (−0.034, −0.029)	−0.065 (−0.071, −0.059)	0.046 (0.042, 0.050)
Congestive heart failure	−0.004 (−0.012, 0.005)	0.0003 (−0.050, 0.050)	0.008 (−0.007, 0.022)	−0.029 (−0.033, −0.026)	−0.090 (−0.097, −0.084)	0.045 (0.041, 0.050)
Crohn’s disease or ulcerative colitis or inflammatory bowel disease	−0.019 (−0.026, −0.011)	−0.068 (−0.097, −0.040)	0.034 (0.020, 0.049)	−0.029 (−0.032, −0.026)	−0.068 (−0.076, −0.059)	0.044 (0.039, 0.048)
Vision impairment	0.0002 (−0.009, 0.009)	0.023 (−0.010, 0.057)	−0.003 (−0.019, 0.013)	−0.023 (−0.027, −0.020)	−0.049 (−0.056, −0.041)	0.034 (0.029, 0.039)
Hearing impairment	−0.002 (−0.010, 0.005)	0.023 (−0.018, 0.061)	0.005 (−0.008, 0.017)	−0.023 (−0.025, −0.020)	−0.047 (−0.052, −0.042)	0.033 (0.030, 0.036)
Arthritis of the hand or wrist	−0.015 (−0.021, −0.008)	−0.056 (−0.075, −0.038)	0.026 (0.016, 0.035)	−0.022 (−0.024, −0.021)	−0.036 (−0.039, −0.032)	0.030 (0.028, 0.033)
Diabetes	−0.002 (−0.007, 0.004)	−0.044 (−0.062, −0.026)	0.005 (−0.005, 0.015)	−0.021 (−0.023, −0.019)	−0.024 (−0.029, −0.019)	0.029 (0.026, 0.031)
Other heart conditions (valve, murmur)	−0.012 (−0.018, −0.006)	−0.044 (−0.062, −0.026)	0.022 (0.012, 0.032)	−0.020 (−0.021, −0.018)	−0.040 (−0.044, −0.036)	0.027 (0.025, 0.030)
Angina pectoris or coronary artery disease	−0.010 (−0.017, −0.0023)	−0.002 (−0.030, 0.025)	0.016 (0.002, 0.029)	−0.017 (−0.020, −0.015)	−0.035 (−0.041, −0.029)	0.025 (0.022, 0.028)
Myocardial infarction	0.005 (−0.004, 0.013)	−0.015 (−0.101, 0.070)	−0.008 (−0.023, 0.008)	−0.006 (−0.009, −0.004)	−0.016 (−0.027, −0.004)	0.009 (0.006, 0.013)
Mean Squared Error	0.0088 (0.0087, 0.0088)	0.0092 (0.0092, 0.0093)	0.0087 (0.0087, 0.0088)	0.0104 (0.0104, 0.0104)	0.0113 (0.0113, 0.0113)	0.0103 (0.0103, 0.0103)

For both the under-65 and 65-and-older groups using the best-performing multiplicative model, the health condition with the largest impact on SF-6D scores of those studied here is depression with a proportional decrement of 0.167 in the 65-and-older group and a proportional decrement of 0.145 in the under-65 group. The health condition with the smallest proportional decrement in SF-6D score is myocardial infarction (0.009) for the 65-and-older group. There are two conditions in the under-65 group, myocardial infarction and vision impairment, with means below zero which would indicate health improvement with these health conditions. These condition impact estimates are very close to zero with credible intervals that cross zero and could be interpreted as not having and impact on health utility in this group. While no 95% credible interval for a parameter estimate in the 65-and-older group cross zero, 95% credible intervals for 6 of the 15 health conditions cross zero in the under-65 group. In general, credible intervals for parameter estimates for the under-65 group are much wider than credible intervals for the 65-and-older group because the 65-and-older group has substantially more observations.

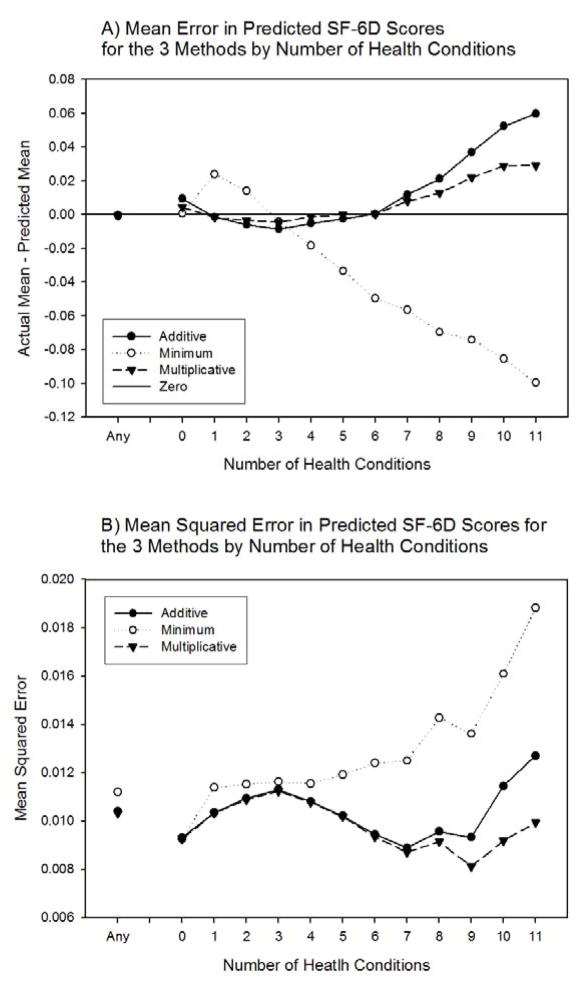
Figure 2 illustrates model tests by number of health conditions for the models with adjustment for age, sex, education, and income from the 65-and-older group. The multiplicative method has least mean predictive error for people reporting less than 7 of the health conditions (Figure 2A). The model using the minimum method has the most error except for groups with 0 and 3 conditions. No model does well for persons reporting more than 7 of the conditions. The three methods have similar mean squared error (Figure 2B) when mean squared error is calculated over all observations. The model using the multiplicative method achieves the smallest mean squared error across each subset of individuals reporting 0 to 11 of the health conditions. The model using the minimum method has the largest mean squared error across these groups.

Figure 2. Mean predictive error and mean squared error for each of the three methods in the 65-and-older group.

The model using the multiplicative method has the smallest mean predictive error as well as the smallest mean squared error by number of health conditions. The model using the minimum method has the most error.

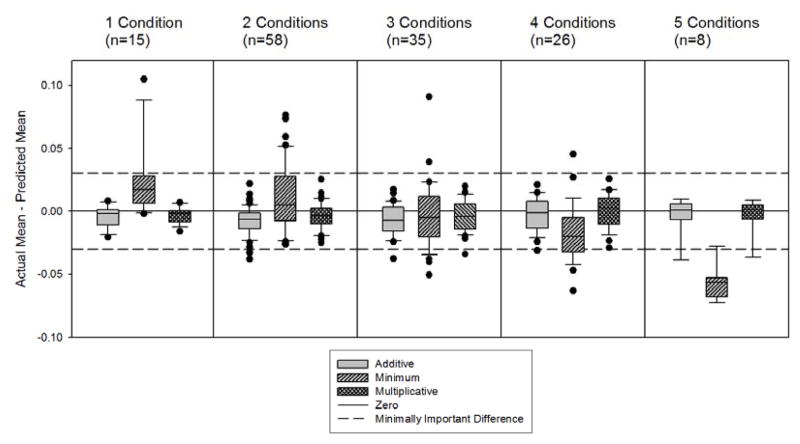
Analyses presented in Figure 2 are based on very large heterogeneous groups, e.g., all individuals who report n conditions of any combination. We also selected combinations of specific health conditions with more than 50 observations. In these groups, the predictive error associated with models using the additive and multiplicative methods is quite similar – estimates of predictive error from both models are centered around zero and have similar spread (Figure 3). The minimum model has a substantially larger spread when predicting SF-6D scores for groups with named combinations of health conditions.

Figure 3. Mean predictive error for specific combinations of conditions with 50 or more observations. Mean predictive error was calculated for each of the three methods in the 65-and-older group.

This figure represents the difference between the mean of actual SF-6D scores and the mean of predicted SF-6D scores for groups with a specific combination of 1 to 5 health conditions. For example, one of the points in the 2 Conditions panel represents those reporting arthritis of the hip or knee and problems hearing and no other conditions. “n” is the number of such groups within a panel. The lowest boundary of the box indicates the 25th percentile, a line within the box marks the median, and the highest boundary of the box indicates the 75th percentile. Whiskers (error bars) above and below the box indicate the 90th and 10th percentiles. Any outlying points are also illustrated. The error in mean estimates for the models using the additive and multiplicative methods is centered around zero and the spread is smaller than the model using the minimum method.

The models adjusted for age, sex, education, and income performed better for all methods than models without adjustments. These adjustment variables have the same relationship to SF-6D score in all three models for individuals who report no health conditions, but differ for individuals who report any health condition. Relationships between the three competing methods were similar in the unadjusted models when compared to the adjusted models presented in the tables and figures. This similarity suggests the differences in model performance are a result of the health condition models and not a result of the relationship between the adjustment variables and health conditions (results not shown, available from the authors upon request).

Discussion

This report presents comparisons of three commonly used or suggested methods [11–17] for combining the impacts from single health conditions to estimate the health utility associated with multiple conditions. For the SF-6D health utility score from the Medicare Health Outcomes Survey, the multiplicative method, where the impact of each condition is a constant proportional reduction of overall utility, showed better performance when compared to additive or minimum methods. The multiplicative method had the best performance as measured by overall mean squared error as well as mean squared error by total number of health conditions. Models using the multiplicative method also had the smallest mean predictive error for specific combinations of health conditions. These results inform the construction of condition catalogs and the inclusion of multiple health conditions in CEA modeling analyses.

The values of the coefficients presented in Table 2 can be used as a table of multiplicative impact factors for combinations of conditions for populations similar to those sampled in the Medicare Health Outcomes Survey (a file of samples from the posterior distributions of the parameters is available from the authors upon request). These values represent the average impact on health and function for all severities and durations of a particular health condition. The sample is limited to Medicare beneficiaries who were healthy enough to respond to this survey. The data are limited by response rates and the data collected by the survey. Researchers and analysts who need consistently estimated impacts of several common health conditions in Medicare populations will find this catalog useful. We encourage careful consideration of the source of health utility impact estimates as there are other catalogs available using other populations [8–14] and a registry of health utility estimates [25].

The analyses performed for this report should be replicated in other large datasets before making a strong recommendation concerning best method to combine single condition health utility impacts to represent impact of co-conditions. We have used the HOS data for the current study because this large sample has a high proportion of respondents with multiple identified conditions. Also, few HOS respondents score at the ceiling of the health utility score, so our analyses are largely un-influenced by skewed data and ceiling effects. However in general population data, such as the Medical Expenditure Panel Survey [26] or Canadian Community Health Survey [27], the utility scores are more skewed and have substantial ceiling effects, especially at younger ages. While the censoring used in models in this report was applied to under 1% of the sample, this censoring may be more important for model performance in other datasets where data are more skewed. Use of latent variable models such as Tobit and censored least absolute deviations is currently in vogue in catalog construction [12–14]. For any catalog constructed using an unobserved latent scale, appropriate use of the catalogs may require calculating the expected observed health utilities (as in the Appendix).

One limitation of our study, as well as all current condition catalogs, is that we used cross-sectional data to derive health condition impact factors that will be used as estimates of utility change when a condition is acquired or relieved. Such estimates would be made best using longitudinal data. However, the necessary longitudinal population data are not available.

Most of the health conditions considered in this report had an impact of −0.02 or −0.03 on SF-6D health utility scale. This is near the minimally important difference (MID) for the SF-6D of 0.03 to 0.04 [28, 29]. The MID for a health utility score is the smallest difference in scores that is perceived by patients as beneficial or harmful [30]. For the best performing models, combinations of 2, 3, or 4 conditions only showed an average bias of −0.004 in predicted mean score, well below the MID.

This report compares several simple methods by which the impact of co-occuring health conditions might be modeled using single condition impact factors. These three methods do not cover the entire space of possible methods, but provide a basis of comparison for future research. There are other methods that are currently untested, such as log-based transformations, as well as specific variants of thee methods studied here, such as the censored least absolute deviations variant of the additive method. The best performing method in our study, the multiplicative model, shows substantial mean predictive error in groups with more than 7 health conditions.

The Medicare Health Outcomes Survey dataset is exceptional for testing methods to model impact of multiple conditions because the majority of the sampled Medicare recipients report 2 or more health conditions. This dataset also contains two distinctly different populations that produced similar results in our analysis. Because most of these data were from respondents with multiple health conditions, overall model performance criteria agreed with explorations of model performance by number of health conditions. In other general population datasets, such as the Canadian Community Health Survey, the majority of respondents do not report any health conditions specifically asked about in the survey. In such datasets, overall model performance across all the dataset may not be the most appropriate criteria for determining the best method to model the smaller subset of individuals with multiple health conditions.

This report has illustrated the importance of explicitly testing several competing methods before constructing catalogs of the impact of individual health conditions on health utility from large datasets. For the SF-6D in the Medicare Health Outcomes Survey, a multiplicative method performs somewhat better than the additive method, and quite a bit better than the minimum method. Future work should test these methods against other methods and develop catalogs for use in cost-effectiveness analyses. Future evaluation of different methods should focus on the observations that report multiple health conditions and not only overall model performance.

Appendix

The models used in this report were estimated using a latent health construct that was censored at the maximum and minimum health utility scale scores. The distribution of scores over the latent construct was assumed to be normal.

For example, presume the latent health construct, Y*_i is follows:

$$Y_i^{\ast }={x^{\prime }}_i\beta +{\epsilon }_i,\text{where}{\epsilon }_i\sim N(0,\sigma )$$

If this variable is right censored at the maximum health utility score of 1.0 and left censored at the minimum health utility score of 0.30, the censored random variable, Y_i, that is the observed variable, is defined as:

$$\begin{array}{l}{Y}_i=Y_i^{\ast }\text{if}0.3<Y_i^{\ast }<1\\ Y_i=1\text{if}{Y}_i^{\ast }\ge 1\\ Y_i=0.3\text{if}{Y}_i^{\ast }\le 0.3\end{array}$$

Using x′_i β, it is simple to calculate the expected score for Y*_i, the latent health construct. The expected score for the latent health construct, however, is not as meaningful as the expected score for the observed random variable.

The expected score from the latent health construct is not the correct expectation for the observed variable, which should be calculated using the censored normal distribution. The appropriate formula for the expected observed value that has two bounds is:

$$\mathit{Expected}={(a_1-x^{\prime }\beta )}^{\ast }\mathrm{\Phi }(\frac{a_1-x^{\prime }\beta }{\sigma })+(a_2-{(a_2-x^{\prime }\beta )}^{\ast }\mathrm{\Phi }(\frac{a_2-x^{\prime }\beta }{\sigma })+{\sigma }^{\ast }(\phi (\frac{a_1-x^{\prime }\beta }{\sigma })-\phi (\frac{a_2-x^{\prime }\beta }{\sigma }))$$

a₁ = lower bound

a₂ = upper bound

σ = standard deviation of the latent variable error term

x′β = predicted value for latent variable

φ = normal probability density function, using the standard normal

Φ =normal cumulative distribution function, using the standard normal