Monte Carlo simulation of mechanical unfolding of proteins based on a simple two-state model

Abstract

Single molecule methods are becoming routine biophysical techniques for studying biological macromolecules. In mechanical unfolding of proteins, an externally applied force is used to induce the unfolding of individual protein molecules. Such experiments have revealed novel information that has significantly enhanced our understanding of the function and folding mechanisms of several types of proteins. To obtain information on the unfolding kinetics and the free energy landscape of the protein molecule from mechanical unfolding data, a Monte Carlo simulation based on a simple two-state kinetic model is often used. In this paper, we provide a detailed description of the procedure to perform such simulations and discuss the approximations and assumptions involved. We show that the appearance of the force versus extension curves from mechanical unfolding of proteins is affected by a variety of experimental parameters, such as the length of the protein polymer and the force constant of the cantilever. We also analyze the errors associated with different methods of data pooling and present a quantitative measure of how well the simulation results fit experimental data. These findings will be helpful in experimental design, artifact identification, and data analysis for single molecule studies of various proteins using the mechanical unfolding method.

1. Introduction

In biological systems the most important molecules, such as proteins, nucleic acids, and polysaccharides, are all polymers. Understanding the properties and functions of these polymeric molecules is crucial in elucidating the molecular mechanisms of the structures and processes in cells. The large sizes of these molecules impose certain limitations on the information attainable from bulk measurements, because the macromolecules in a population can have very diverse conformations and react differently to external stimuli. The individualized, and sometimes rare, behaviors of macromolecules can have important implications for their functions inside the cell. Recently developed single molecule techniques, in which these macromolecules are studied one at a time, have provided important and complementary information about the function mechanisms of several biological systems [1].

Single molecule techniques for the study of biological macromolecules include optical measurements, i.e., single molecule fluorescence microscopy and spectroscopy, and mechanical manipulations of individual macromolecules [2], i.e., force microscopy and spectroscopy using atomic force microscopes (AFM), laser tweezers [3], magnetic tweezers [4] or biomembrane force probes [5]. Of these mechanical manipulation methods, AFM is the most widely used due to the availability of user-friendly commercial instruments. AFM has been employed on several types of biological macromolecules, such as mechanically unfolding proteins [6] and forcing structural transitions in DNA [7] and polysaccharides [8]. An AFM uses a sharp tip integrated at the end of a cantilever to interact with the sample. Cantilever bending is measured by a laser reflected off the cantilever and incident on a position sensitive photodetector. When the bending force constant of the cantilever is known [9], the force applied to the sample can then be calculated. The forces that can be applied and measured with an AFM range from tens of piconewtons to hundreds of nanonewtons. The investigation of the unfolding and refolding processes of individual protein molecules by the AFM is feasible because many globular proteins can be unfolded by external forces in this range. Since elucidating the mechanism of protein folding is currently one of the most important problems in biological sciences, the potential of the AFM for revealing significant and unique information about protein folding has stimulated much effort in both experimental and theoretical research.

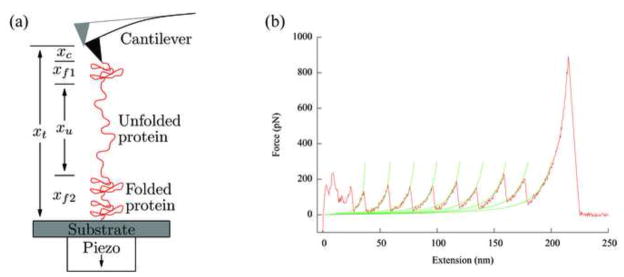
In a mechanical unfolding experiment, a protein polymer is tethered between two surfaces: a flat substrate and an AFM tip. The polymer is stretched by increasing the separation between the two surfaces (Fig. 1a). The most common mode is the constant speed experiment in which the substrate surface is moved away from the tip at a uniform rate. The tethering surfaces, i.e., the AFM tip and the substrate, have much larger radii of curvatures than the dimensions of single domain globular proteins that are normally used for folding studies. This causes difficulties in manipulating individual protein molecules because nonspecific interactions between the AFM tip and the substrate may be stronger than the forces required to unfold the protein when the surfaces are a few nanometers apart. To circumvent these difficulties, globular protein molecules are linked into polymers, which are then used in the AFM studies [6,10,11]. When such a polymer is pulled from its ends, each protein molecule feels the externally applied force, which increases the probability of unfolding by reducing the free energy barrier between the native and unfolded states. The unfolding of one molecule in the polymer causes a sudden lengthening of the polymer chain, which reduces the force on each protein molecule and prevents another unfolding event from occurring immediately. The force versus extension relationship, or force curve, shows a typical sawtooth pattern (Fig. 1b), where each peak corresponds to the unfolding of a single protein in the polymer. Therefore, the individual unfolding events are separated from each other in space and time, facilitating single molecule studies.

Fig. 1.

(a) Schematic of the experimental setup for mechanical unfolding of proteins using an AFM (not to scale). An experiment starts with the tip in contact with the substrate surface, which is then moved away from the tip at a constant speed. x_t is the distance traveled by the substrate, x_c is the cantilever deflection, x_u is the extension of the unfolded polymer, and x_f = x_f1+x_f2 is the extension of the folded polymer. (b) An experimental force curve from stretching a ubiquitin polymer with the rising parts of the peaks fitted to the WLC model. The pulling speed used was 1 μm/s. The irregular features at the beginning of the curves were due to nonspecific interactions between the tip and the substrate surface, and the last high force peak was caused by the detachment of the polymer from the tip. Note that the abscissa is the extension of the protein chain (x_t − x_c).

Much theoretical and computational work has been done in order to extract information about the structural, kinetic and energetic properties of the protein molecules from the experimental data of force-induced protein unfolding measurements. Steered molecular dynamics simulations [12], as well as calculations and simulations using lattice [13] and off-lattice models [14,15], have provided insights into structural and energetic changes during force-induced protein unfolding. However, these simulations often involve time scales that are orders of magnitude smaller than those of the experiments, and the parameters used in the calculations are often neither controllable nor measurable experimentally. As a result, a Monte Carlo simulation approach based on a simple two-state kinetic model for the protein is usually used to analyze data from mechanical unfolding experiments. A comparison of the force curves measured experimentally and those generated from simulation can yield the unfolding rate constant of the protein in the absence of force as well as the distance from the native state to the transition state along the pulling direction. The Monte Carlo simulation method has been used since the first report of mechanical unfolding experiment using AFM [16], however, a comprehensive description and discussion of the simulation procedures, as well as the intricacies involved, have not been reported. In this paper, we provide a detailed description of the simulation procedure, including theories, approximations, and assumptions involved. We also explain the procedure for the extraction of kinetic properties of the protein from experimental data, and introduce a quantitative measure of fit quality between simulation and experimental results. In addition, the effects of various experimental parameters on force curve appearance are demonstrated, and the errors associated with different methods of data pooling are discussed. We believe that these results will be useful in experimental design, artifact identification, and data analysis for single molecule mechanical unfolding experiments.

2. Methods

In simulating the mechanical unfolding process, a force curve is generated by calculating the amount of the cantilever bending as the substrate surface moves away from the tip. The cantilever bending is obtained by balancing the tension in the protein polymer and the Hookean force of the bent cantilever. The unfolding probability of the protein molecules in the polymer is then calculated for that tension, and whether an unfolding event occurs is determined according to a Monte Carlo method. The simulation was implemented in C¹.

2.1. Generating force curves

The fundamental abstraction of the simulation is the “domain”, which represents a discrete chunk of the flexible chain between the substrate and the cantilever holder. Each of these domains is assigned a particular state; for example, the domain representing the cantilever is assigned to the “cantilever” state, and the domains representing protein molecules are assigned to either the “folded” or the “unfolded” state. When balancing the tension along the chain, we assume that the spatial order of domains along the chain is irrelevant [17], and therefore, the domains can be rearranged and grouped by their states. To determine the tension in the chain and the amount of cantilever bending in balance when n states are populated, n +1 equations with n +1 unknowns need to be solved:

$$F_i(x_i)=F_t$$ (1)

$$\sum _i{x}_i=x_t$$ (2)

where F are tensions, x are extensions, and the subscripts i and t represent a particular state group and the total chain, respectively (Fig. 1a). From this F(x_t) may be computed using any multi-dimensional root-finding algorithm.

Inside this framework, we choose a particular model F_i(x_i) for each type of domain states. Cantilever elasticity is described by Hooke’s law, which gives:

$$F={\kappa }_c{x}_c$$ (3)

where κ_c is the bending spring constant and x_c is the deflection of the cantilever (Fig. 1a). Unfolded domains are modeled as a Worm-Like Chain (WLC) [16,18,19], in which the tension, F, is related to the extension (end-to-end distance), x_u, by:

$$F=\frac{k_{B}T}{p_u}(\frac{1}{4{(1-x_u/L_u)}^2}-\frac{1}{4}+\frac{x_u}{L_u})$$ (4)

where p_u is the persistence length and L_u is the contour length of the unfolded chain. The chain of N_f folded domains is modeled as a string free to assume any extension up to a fixed length L_f = N_fL_f1:

$$F(x_f)=\{\begin{array}{ll}0\hfill & \text{if}{x}_f<L_f\hfill \\ \infty \hfill & \text{if}{x}_f>L_f\hfill \end{array}$$ (5)

where L_f1 is the separation of the two linking points on a folded domain, and x_f is the end-to-end distance of the chain of folded domains. In this model, any non-zero tension will fully extend these folded domains. As discussed in section 3.3, the contribution of the folded domains to the elastic behaviors of the polymer-cantilever system is relatively insignificant.

In the simulation, the protein polymer is assumed to be stretched in the direction perpendicular to the surface, which is a good approximation in most experimental situations, because the unfolded length of a protein molecule is much larger than that of the folded form. Therefore, after one molecule is unfolded, the polymer becomes much longer and the angle between the polymer and the surface becomes close to 90 degrees [20]. The joints between domain groups are assumed to lie along a line between the surface tether point and the position of the tip (Eq. 2). The effects of this assumption are also minimized due to greater length of the unfolded domain. Finally, the interactions between different parts of the polymer and between the chain and the surface (except at the tethering points) are not considered. This is reasonable since these interactions should not make substantial contributions to the force curve at the force levels of interest, where the polymer is in a relatively extended conformation.

Consider an experiment of pulling a polymer with N identical protein molecules at a constant pulling speed. At the start of the experiment, the polymer is unstretched (x_t = 0), which means that all the domains are unstretched and the cantilever is undeflected, while the tip is in contact with the surface. There is one domain in the cantilever state, N in the folded state, and none in the unfolded state. As the surface is moved away from the tip at a constant speed v, the chain becomes more extended and the cantilever deflection increases (Fig. 1a), such that

$$x_t=\sum _i{x}_i=vt$$ (6)

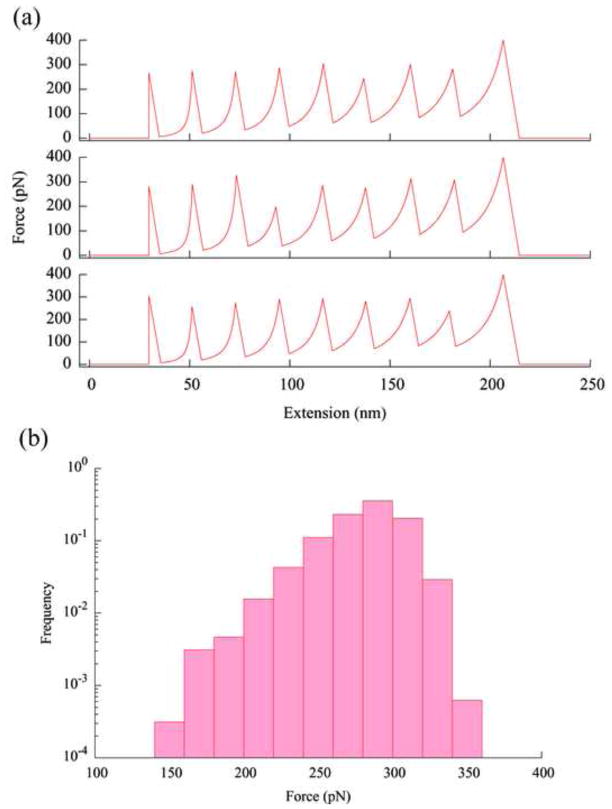
where x_i is the extension of a type of domains (Fig. 1a). The simulation assumes that the pulling takes discrete steps in space and treats x_t as constant over the duration of one time step Δt. Because of the use of adaptive time steps as discussed in Section 2.3, the space steps Δx_t = vΔt may have different sizes. At each step, the total extension is calculated using Eq. (6), and the tension F(x_t = vt) is determined by numerically solving the equations (1) and (2) using the models (3) to (5), for known values of the parameters in the various states (κ, N_f, N_u, L_f, L_u, p_u, v). When one of the molecules in the polymer unfolds (Section 2.2), there is now one in the unfolded state and N − 1 in the folded state. In the next step, a newly balanced tension between the cantilever and the polymer is determined by solving for F(x_t) as discussed above, with the total extension x_t incremented by vΔt and a new unfolded contour length L_u. The sudden lengthening of the polymer chain results in a corresponding abrupt drop in the force, leading to the formation of one sawtooth in the force curve. As the pulling continues and more molecules unfold, force curves with a series of sawteeth are generated (Fig. 2a).

Fig. 2.

(a) Three simulated force curves from pulling a polymer of eight identical protein molecules. Simulation was carried out using these parameters: pulling speed v = 1 μm/s, cantilever spring constant κ = 50 pN/nm, temperature T = 300 K, persistence length of unfolded proteins p_u = 0.40 nm, Δx_u = 0.225 nm, and k_u0 = 5×10⁻⁵ s⁻¹. The contour length between the two linking point is L_u=28.1 nm in an unfolded protein and the distance between these two points in a folded protein is L_f =3.7 nm. These parameters are those used in the experiments of pulling ubiquitin molecules connected through the N-C termini [10,11]. Detachment from the tip is assumed to occur at a force of 400 pN. In experiments, detachments have been observed to occur at a variety of forces. (b) The distribution of the unfolding forces from 400 simulated force curves (3200 data points) as those shown in (a). The frequency is normalized by the total number of points, i.e., the height of each bin is equal to the number of data points in that bin divided by the total number of data points (3200, for this histogram).

The tension calculation assumes an equilibrated chain, therefore consideration must be given to the chain’s relaxation time, which should be short compared to the force loading time scale. The relaxation time for a WLC is given by [21]:

$$\tau (p,L,T,\eta )\approx \eta \frac{k_{B}Tp}{F^2}$$ (7)

where η is the dynamic viscosity, F is the tension, and p is the persistence length. For force greater than 1 pN, with η_water/k_BT = 2.45 × 10⁻¹⁰ s/nm³, τ < 2 ns for the protein polymer used in the simulation. Therefore, the polymer chain is equilibrated almost instantaneously within a time step, which is in the order to tens of μs. The relaxation time of the cantilever can be determined by measuring the cantilever deflection induced by liquid motion, and fitting the time dependence of the deflection to an exponential function [22]. For a 200 μm rectangular cantilever with a bending spring constant of 20 pN/nm, the measured relaxation time in water is ~50 μs (data not shown). This relative large relaxation time constant makes the cantilever acts as a low-pass filter and also causes a lag in the force measurement.

2.2. Unfolding protein molecules by force

According to the theory developed by Bell [23] and extended by Evans and Ritchie [21], an external stretching force F increases the unfolding rate constant of a protein molecule:

$$k_u=k_{u0}{e}^{F\mathrm{\Delta }{x}_u/k_{B}T}$$ (8)

where k_u0 is the unfolding rate in the absence of an external force, and Δx_u is the distance between the native state and the transition state along the pulling direction. The probability for a protein molecule to unfold under an applied force is:

$$P_1=\mathrm{\Delta }t·k_u$$ (9)

where Δt is the time duration for each pulling step, over which F is a constant. This expression is accurate for P₁≪1. From the binomial distribution, the probability of at least one of a group of N_f identical domains to unfold in a given time step is

$$P=1-{(1-P_1)}^{N_f}=N_f{P}_1$$ (10)

where the approximation is valid when N_fP₁ ≪ 1. To determine if an unfolding event occurs at a particular point of time during pulling, the probability calculated using Eq. (10) is compared with a randomly generated number uniformly distributed between 0 and 1. If P is bigger than the random number, a domain unfolds, changing the population of each domain state, and a new balance in force and extension between the polymer and the cantilever is determined. If no unfolding event occurs the pulling continues and the unfolding probability is calculated again in the next step at a higher force. When all the molecules in the polymer have unfolded, the pulling continues until a pre-determined force level is reached, where the polymer is assumed to detach from one of the tethering surfaces. The cantilever deflection becomes zero after this point.

Although the Bell model (Eq. (8)) is the most widely used approach to analyze data from mechanical stretching experiments due to its simplicity and its applicability to various biopolymers [24], other theoretical models have been proposed to interpret mechanical unfolding data. For example, Schlierf and Rief [25] used the mechanical unfolding data of the protein ddFLN4 to demonstrate that Kramers’ diffusion model fit the measured unfolding force data better than the Bell model for proteins with broad free energy barriers. For proteins with relatively narrow unfolding transition states, the Bell model provides a good approximation.

2.3. Choosing the simulation time steps

The demands on the time step vary throughout a simulated pulling process due to the non-linear elasticity of the polymer. Within a specified time duration (or a specified pulling distance), the force change is small at low force levels and large at high force levels. To be efficient, the simulation algorithm adapts the time step in such a way that keeping the time steps large where the step size has little effect, while shrinking the time step size when smaller step size is necessary. Within each time step, the total chain extension x_t is treated as a constant and a force balance is assumed to reach very quickly among the various domains. This balanced force is used to determine the unfolding probability (Eqs. (9) and (10)), which dictates the domain state populations in the next time step. The time step is chosen to be short enough such that the approximations made in Eq. (9) and (10) are valid, and the probability of multiple unfolding events in a single step is low (P < 10⁻³). The size of the time step used is recalculated for each step to make sure that both of these criteria are satisfied.

3. Results and Discussion

3.1. Force curves generated by simulation

Figure 2a shows three simulated force curves from pulling a polymer composed of eight identical protein molecules, using parameters from typical experimental settings. The order of the peaks in the force curves reflects the temporal sequence of the unfolding events instead of the positions of the protein molecules in the polymer [17]. As observed experimentally (Fig. 1a), the forces at which identical protein molecules unfold fluctuate, revealing the stochastic nature of protein unfolding since no instrumental noise is included in the simulation. Figure 2b shows the distribution of the unfolding forces, i.e., the highest force in each peak (except the last peak in a force curve), from a total of 400 force curves (3200 force values). The unfolding forces have an average of 281 pN with a standard deviation of 25 pN.

3.2. Dependence of the unfolding force on the unfolding order and polymer length

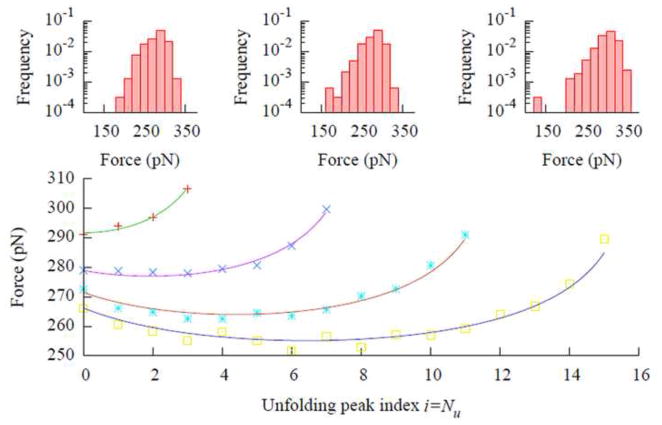
Analysis of the mechanical unfolding data is complicated by the dependence of the average unfolding force on the unfolding order, due to the serial linkage of the molecules. Under an external stretching force F, the probability of some domain unfolding in polymer with N_f folded domains is N_fP₁ (Eq. (10)), which is higher than the unfolding probability for a single molecule, P₁. Consequently, the average unfolding force is lower for the earlier unfolding events when N_f is larger, and the unfolding force should increase as more and more molecules become unfolded. However, there is a competing factor that opposes this trend. As the protein molecules unfold, the chain becomes softer and the force loading rate becomes lower when the pulling speed is constant, leading to a decrease in the unfolding force. The dependence of the average unfolding force on the unfolding order is the result of these two opposing effects. Figure 3 shows the dependence of the average unfolding forces on the unfolding force peak order (the temporal order of unfolding events) for four polymers with 4, 8, 12, and 16 identical protein molecules, respectively. The effect of polymer chain softening dominates the initial unfolding events, and the average unfolding force decreases as more molecules unfold. After several molecules have unfolded, the softening for each additional unfolding event becomes less significant, the change in unfolding probability becomes dominant, and the unfolding force increases upon each subsequent unfolding event [26].

Fig. 3.

The dependence of the unfolding force on the (temporal) unfolding order for 4 polymers with 4, 8, 12, and 16 molecules of identical proteins. Each point in the plot is the average of 400 data points. The first point in each curve represents the average of only the first peak in each of the 400 simulated force curves, the second point represents the average of only the second peak, and so on. The solid lines are fits of Eq. (13) to the simulated data, with best fit κ_WLC = 203, 207, 161, and 157 pN/nm, respectively, for lengths 4 through 16. The insets show the force distributions of the first, fourth, and eighth peaks, left to right, for the polymer with eight protein molecules. The parameters used for generating the data were the same as those used for Fig. 2a, except the polymer length, and the histograms in the insets were normalized in the same way as in Fig. 2b.

The validity of this explanation by demonstrated by calculating the average unfolding force using probability distribution resulting from the two competing factors. The rate of unfolding events with respect to force is

$$r_{uF}=-\frac{{dN}_f}{dF}=-\frac{{dN}_f/dt}{dF/dt}=\frac{N_f{k}_u}{\kappa v}=\frac{N_f{k}_{u0}}{\kappa v}exp\left(\frac{F\mathrm{\Delta }{x}_u}{k_{B}T}\right)=\frac{1}{\rho }exp\left(\frac{F-\alpha }{\rho }\right)$$ (11)

where N_f is the number of folded domains, κ =(1/κ_c + N_u/κ_WLC)⁻¹, is the spring constant of the cantilever-polymer system, κ_WLC is the effective spring constant of one unfolded domain (κ_WLC is a nonlinear function of F. It is assumed to be constant over the range of unfolding forces), κv is the force loading rate, and k_u is the unfolding rate constant (Eq. (8)). In the last expression, ρ ≡ k_BT/Δx_u, and α≡ρln(κv/N_fk_u0ρ). The event probability density for events with an exponentially increasing likelihood follows the Gumbel (minimum) probability density [27], with ρ and α being the scale and location parameters, respectively:

$$P(F)=\frac{1}{\rho }exp\left[\frac{F-\alpha }{\rho }-exp\left(\frac{F-\alpha }{\rho }\right)\right]$$ (12)

Such a distribution has a mean of <F>= α − γ_eρ and a variance of σ²=π²ρ²/6, where γ_e = 0.577… is the Euler-Mascheroni constant. Therefore, the unfolding force distribution has a variance σ²=(πk_BT/Δx_u) ²/6 and an average of

$$\langle F(i)\rangle =\frac{k_{B}T}{\mathrm{\Delta }{x}_u}\left(ln\frac{\kappa v\mathrm{\Delta }{x}_u}{N_f{k}_{u0}{k}_{B}T}-{\gamma }_e\right)$$ (13)

where N_f and κ depend on the domain index i=N_u, (N_u+N_f =N, the total number of protein domains in the polymer). Curves based on this formula fit the simulated data remarkably well considering the effective WLC stiffness is the only fitted parameter.

From Fig. 3, it can be seen that the proper way to process data from mechanical unfolding experiments is to group the curves according to the length of the polymer and to perform statistical analysis separately for peaks with the same unfolding order. However, in most experiments, the tethering of the polymer to the AFM tip is by nonspecific adsorption; as a result, the polymers being stretched between the tip and the substrate have various lengths. In addition, the interactions between the tip and the surface often cause irregular features in the beginning of the force curve (Fig. 1b), making the identification of the first peak uncertain. Furthermore, it is often difficult to acquire a large amount of data in single molecules experiments. These difficulties make the aforementioned data analysis approach unfeasible for many mechanical unfolding experiments. As a result, the values of all force peaks from polymers of different lengths are often pooled together for statistical analysis. To assess the errors caused by such pooling, simulation data was analyzed using different pooling methods and the results were compared. Figure 2b shows that, for a polymer with eight protein molecules, the average unfolding force is 281 pN with a standard deviation of 25 pN when all data is pooled. If only the first peaks in the force curves are analyzed, the average force is 279 pN with a standard deviation of 22 pN. While for the fourth and eighth peaks, the average forces are 275 pN and 300 pN, respectively, and the standard deviations are 23 pN and 25 pN, respectively. As expected from the Gumbel distribution, the width of the unfolding force distribution (insets in Fig. 3) is only weakly unfolding order, but the average unfolding forces can be quite different for the same protein because of the differences in unfolding order and polymer length.

3.3. The effect of polymer inhomogeneity

The unfolded polypeptide chain has been shown to follow the WLC model quite well, though other polymer models, such as the freely-jointed chain (FJC) model [28], can also be used to fit the force-extension relationship [29]. A chain of folded proteins, however, cannot be described well by polymer models. Several studies have used WLC and FJC to fit the elastic properties of molecules of the modular protein titin [30,31], but the native titin contains hundreds of folded and unfolded domains. For the short protein polymers commonly used in mechanical unfolding studies, the cantilever dominates the elasticity of the polymer-cantilever system before any protein molecules unfold. After the first unfolding event occurs, the unfolded portion of the chain is already longer and softer than the sum of all the remaining folded domains, and dominates the elastic property of the whole chain. Force curves generated using different models to describe the folded domains yielded almost identical unfolding force distributions (data not shown). Therefore, the details of the model chosen for the folded domains has negligible effect on the unfolding forces, which was also suggested by Staple et al. [32].

3.4. The effect of cantilever force constant

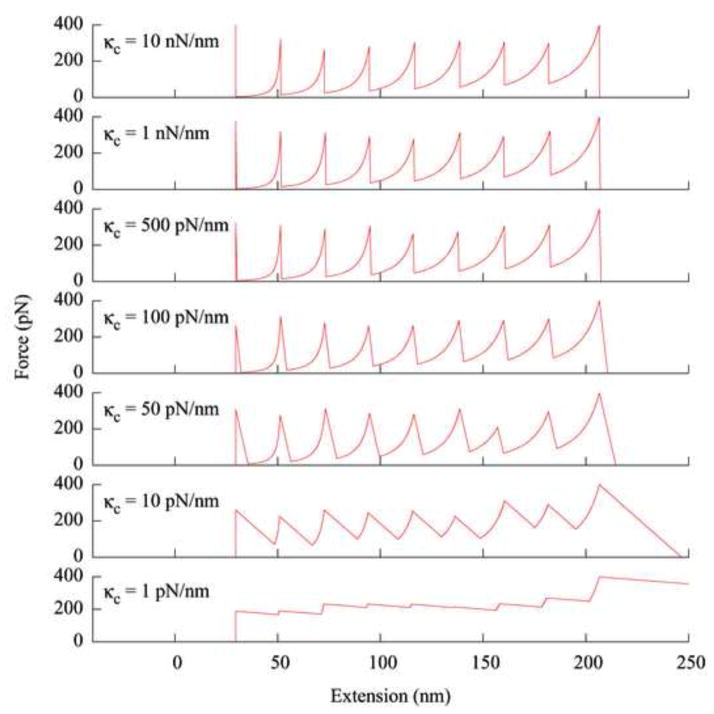
In mechanical unfolding experiments, the ability to observe the unfolding of a single protein molecule depends on the tension drop after an unfolding event such that another molecule does not unfold immediately after. The magnitude of this drop in tension is determined by many factors, including the magnitude of the unfolding force, the contour and persistence lengths of the protein polymer, the contour length increase from unfolding, and the stiffness (force constant) of the cantilever. Among these, the effect of the cantilever force constant is particularly interesting because cantilevers with a wide range of force constants are available. In addition, different single molecule manipulation techniques, such as the AFM and laser tweezers, differ mainly in the range of the spring constants of their force transducers. Figure 4 shows the simulated force curves from pulling an octomer of protein molecules using cantilevers with different force constants, while other parameters are identical. For this model protein, the appearance of the force curve does not change appreciably until the force constant of the cantilever reaches a certain value (κ_c~50 pN/nm). When κ_c is lower than this value, the individual unfolding events become less identifiable. In order to observe individual unfolding events, the cantilever needs to have a force constant high enough so that the bending at the maximum force is small in comparison with the contour length increment from the unfolding of a single molecule. Figure 4 also shows that the back side of the force peaks becomes more tilted as the cantilever becomes softer. This is due to the fact that the extension (end-to-end distance) of the protein polymer has a large sudden increase as the tension rebalances after an unfolding event.

Fig. 4.

The Simulated force curves obtained from pulling a polymer of eight protein molecules using cantilevers with different force constants. Parameters used in generating these curves are the same as those used in Fig. 2, except the cantilever force constant.

It should also be mentioned that the contour length increment from each unfolding event is not equal to the distance between adjacent peaks in the force curve because the chain is never fully stretched. This contour length increment can only be obtained by fitting the curve to WLC or other polymer models (Fig. 1b).

3.5. Determination of Δx_u and k_u0

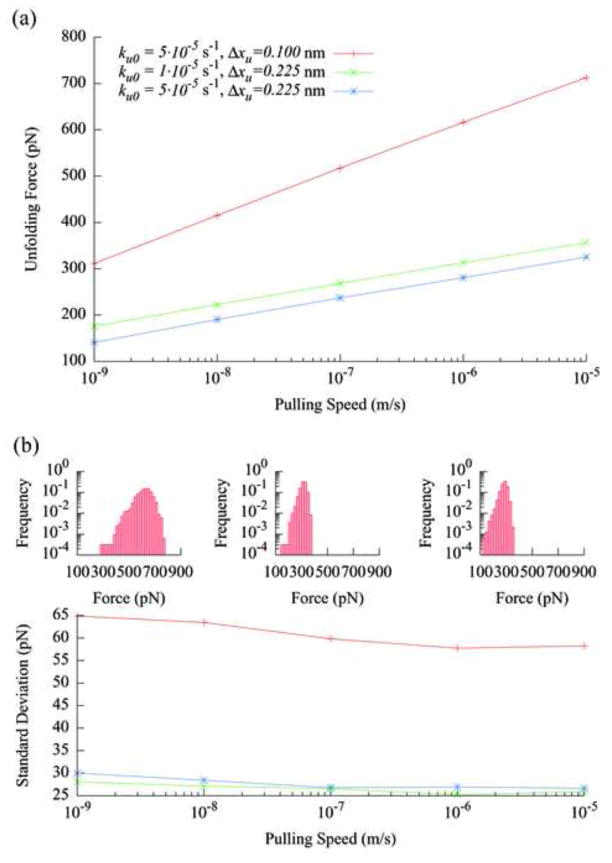
The zero-force unfolding rate, k_u0, and the distance from the native state to the transition state, Δx_u, are the two kinetic parameters obtainable for mechanical unfolding experiments by matching the simulated data with measured results. Figure 5a shows the dependence of the unfolding force on the pulling speed for different values of k_u0 and Δx_u. As expected, the unfolding force increases linearly with the pulling speed in the linear-log plot [21]. While the magnitude of the unfolding forces is affected by both k_u0 and Δx_u,, the slope of the speed dependence is primarily determined by Δx_u. Figure 5b shows that the width of the unfolding force distribution is very sensitive to changes in Δx_u, as expected from the Gumbel distribution discussed in Section 3.2. To obtain the values of k_u0 and Δx_u for the protein, the pulling speed dependence and the distribution of the unfolding forces from simulation, such as those shown in Fig. 5a and the insets of Fig. 5b, are compared with the experimentally measured results. The values of k_u0 and Δx_u that provide the best match are designated as the parameters describing the protein under study. Since k_u0 and Δx_u affect the unfolding forces differently, the values of both parameters can be determined simultaneously. The data used in plotting Fig. 5 includes all force peaks from the simulated force curves because most experimental data is analyzed that way.

Fig. 5.

(a) The dependence of the unfolding forces on the pulling speed for three different model protein molecules as characterized by the parameters k_u0 and Δx_u. The polymer length is eight molecules, and each symbol is the average of 3200 data points. (b) The pulling speed dependence of the standard deviations of the unfolding force data shown in (a), using the same symbols. The insets show the force distribution histograms for the three proteins at the pulling speed of 1 μm/s. The left, middle and right histograms are for the proteins represented by the top, middle and bottom lines in (a), respectively.

In the published literature, the comparison of the force distributions from simulation and experiments was mostly done by carrying out simulations using a handful of possible unfolding parameters and selecting the best fit by eye. This approach does not allow estimation of uncertainties in the fitting parameters, as pointed out by Best et al. [33]. A more rigorous approach involves quantifying the “goodness" of fit between the experimental and simulated force distributions, allowing the use of a numerical minimization algorithm to pick the best fit parameters. We used the Jensen-Shannon divergence [34,35], a measure of the similarity between two probability distributions:

$$D_{JS}(p_e,p_s)=D_{KL}(p_e,p_m)+D_{KL}(p_s,p_m)$$ (14)

with D_KL being the Kullback-Leibler divergence:

$$D_{KL}(p_p,p_d)=\sum _i{p}_p(i){log}_2\left(\frac{p_p(i)}{p_q(i)}\right)$$ (15)

and

$$p_m(i)\equiv [p_e(i)+p_s(i)]/2$$ (16)

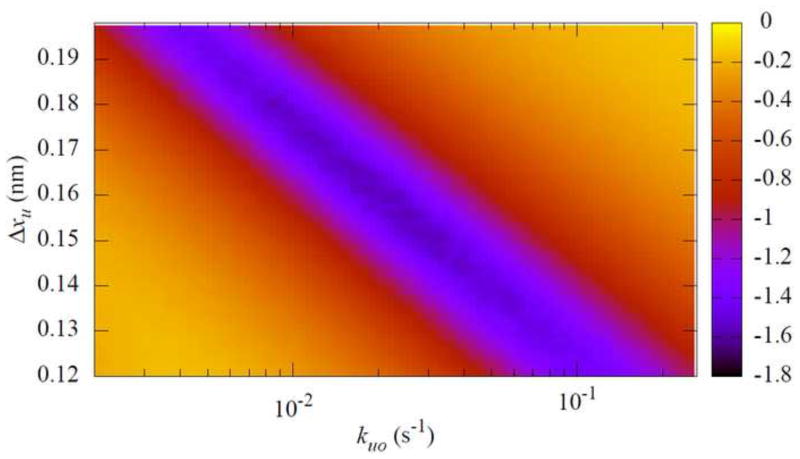
where the sum is over all bins in the unfolding force histograms, p_e(i) and p_s(i) are the values of the ith bin in the experimental and simulated unfolding force histograms, respectively. Figure 6 shows the Jensen-Shannon divergence calculated using Eq. (14) between an experimental data set and simulation results obtaining using a range of values of k_u0 and Δx_u. There is an order of magnitude range of k_u0 that can produce a reasonable fit, which is consistent with the results that Best et al. [33] obtained using a chi square test on the data of unfolding force dependence on the loading rate. By using both the pulling speed dependent and the unfolding force distribution data, the values of k_u0 and Δx_u can be determined to a modestly narrower range. When reliable information about the parameters is known from other sources, their values can then be determined to a much better precision. For example, in our earlier study of mechanical unfolding of ubiquitin [10], the previously reported k_u0 value from thermodynamic measurements [36] was used as a guide to obtain the values of the two parameters. In another example, it was shown that if Δx_u did not change for mutants of a protein, then the values of k_u0 for these mutants could be determined from the mechanical unfolding data with much reduced uncertainties [33].

Fig. 6.

Fit quality between an experimental data set and simulation data sets obtained using various values of k_u0 and Δx_u. The experimental data are from octameric ubiquitin pulled at 1 μm/s[10], and the simulation parameters are the same as those in Fig. 2. The best fit parameters are Δx_u = 0.18 nm and k_u0 = 8.1×10⁻³ s⁻¹. The simulation histograms were built from 400 force curves for each parameter pair. The color scale shown on right is log₁₀(D_JS).

4. Conclusions

We have described the method of performing Monte Carlo simulations based on a simple two-state model, for the mechanical unfolding of protein molecules and discussed the complications involved in the simulation procedure. In addition to the extraction of kinetic properties of the protein from mechanical unfolding data, such simulations can help to elucidate the effects of various experimental parameters on the appearance of force curves, and to estimate the errors associated with data pooling. To date, the force-induced unfolding approach has been used to investigate only several different types of proteins. As the technique is used to study a wider range of proteins, this simple simulation method will be useful for data analysis, experimental design and artifact identification.