Abstract
The growing dataset of K+ channel x-ray structures provides an excellent opportunity to begin a detailed molecular understanding of voltage-dependent gating. These structures, while differing in sequence, represent either a stable open or closed state. However, an understanding of the molecular details of gating will require models for the transitions and experimentally testable predictions for the gating transition. To explore these ideas, we apply Dynamic Importance Sampling (DIMS) to a set of homology models for the molecular conformations of K+ channels for four different sets of sequences and eight different states. In our results, we highlight the importance of particular residues upstream from the PVP region to the gating transition. This supports growing evidence that the PVP region is important for influencing the flexibility of the S6 helix and thus the opening of the gating domain. The results further suggest how gating on the molecular level depends on intra-subunit motions to influence the cooperative behavior of all four subunits of the K+ channel. We hypothesize that the gating process occurs in steps: first sidechain movement, then inter- S5-S6 subunit motions, and lastly the large-scale domain rearrangements.
Keywords: ion-channels, conformational change, transition path sampling, membrane proteins
INTRODUCTION
An important breakthrough in our understanding of the nerve impulse was provided by the Hodgkin-Huxley equations and their description of time and voltage dependent conductance changes.1–2 Since that time our understanding of the molecular details of these voltage dependent channels has grown markedly. In particular, the recent x-ray structures of K+ channels have created the opportunity to begin understanding voltage gating on a molecular level.3–7 A true molecular understanding of the K+ channel will require that the connections from these x-ray structures be understood at the molecular level. For example, using the structures as starting points we can begin to understand how a set of possible transitions connect the open and closed conformations. A complete molecular understanding of gating would produce a molecular picture of the nerve impulse propagation studied by Hodgkin and Huxley1; it would provide a detailed picture of cell-physiology that establishes a firm foundation for understanding other membrane protein channels and transporters.2 Thus, this type of molecular understanding is well worth pursuing, even though the experimental details to verify particular candidate transition paths are not yet in place.
The set of x-ray crystallographically defined structures and their architecture provide a beginning point to approach an understanding of the K+ channel gating transitions. Several different K+ channel ion-conduction pore domain structures have been solved3–13, including more recent structures of KcsA found in the closed and open states14–15. These structures provide a family of open and closed states available to study the molecular details of the transition process called gating. The structures consist of a voltage-sensor domain and/or a pore domain. The pore domain contains the S5-P-S6 region which is responsible for the conductance of ions across the membrane. The exact sequence of the pore domain varies among K+ channels. However, there is a signature sequence, TTVGYG, common to all K+ channels that creates a narrow region within the channel responsible for the selectivity and passage of K+ ions across the membrane. While the sequences of these channels differ, the secondary structures are similar comprising two helices that surround the selectivity filter region and have a backbone root means square difference (RMSD) values ranging from 1.1 Å to 6.9 Å in reference to the high resolution KcsA structure (PDB ID: 1k4c).3–7,14
It is currently not possible to experimentally observe the molecular details of the gating transition or the factors that contribute to large-scale channel motions; however, we may be getting closer to experimentally determining possible intermediate structures.15 The crystallographic structures provide us with three closed (PDB ID: 1k4c, 3eff,1p7b) and three open (PDB: 2a79, 1lnq, 1orq) confirmations of the pore domain3–7,14; no intermediate structures have been solved. The differences between the open and closed conformations suggest that K+ channels undergo large-scale motions upon gating near the intercellular region. Moreover, the differences between these structures imply a high-energy barrier present to transition between these states.
Several computational studies have used the available X-ray structures as a reference or starting point to explore motions involved in the transition.16–20 These studies provide the foundation for examining many functional aspects of permeation and selectivity by complementing and reinforcing experimental data relating to the stability and hydration of the channels. They also bring new awareness to concepts concerning the sampling of intermediate events, the relative free-energy landscape, energy barriers surrounding ion channels, and the timescale required to simulate the full gating transition. One study by Biggin and Sansom predicted open channel state models for KcsA, Kv, and Kir channels by placing each of the closed channels in their own membrane environment and growing a van der Waals sphere centered at the intracellular gate region to open the gate.21 Further studies used a similar approach by placing a cylinder at the pore axis and iteratively inflating and deflating it during Monte Carlo simulations to explore terminal behavior of the inner helices for the KscA channel.22
Recent studies have developed methods that may enhance sampling over the millisecond to second timescale needed for K+ channel gating transitions: Normal Mode Analysis23–26, Gaussian Elastic Network models27–28, Kinetic Monte Carlo Reaction Path Following (kMCRPF) 29–32, and Targeted-Molecular Dynamics33–38. Normal Mode Analysis (NMA) was applied to the KcsA revealing the hinge points during the gating process.23–26 This method calculates the degrees of freedom of the motion at discrete times within a harmonic approximation. The calculations show directions in conformational space where the sampling of the protein’s energy landscape can be improved. The use of Gaussian elastic network models (GNM) has shown a shared gating mechanism with two dominant modes between the KcsA, KirBac, MthK, KvAP, and Shaker channels. 27–28 The first dominant modes showed a rotation that widens the pore and the other mode showed a deformation of the cylindrical symmetry of the pore. 27–28 GNM uses a network of springs to represent interactions between selected atoms and analyzes the normal modes of the network. The kMCRPF method directs the protein along large-scale conformational transitions using a reaction coordinate.29–31 When the end-point conformations are known, normal-modes analysis can be combined with kMCRPF to predict directions for conformational changes along the transition path.31 Another transition method which moves along large-scale conformational transitions is rapidly exploring random trees (RRTs) which is a variant of probabilistic roadmap methods and Monte Carlo in that it generates conformations along a path at random.32 This method has been applied understand merging pathways between KcsA and KvAP channel conformations.32
Popular methods for generating transitions have been targeted or steered MD simulations.33–38 These methods guide the protein to the target conformation by imposing external forces onto the usual deterministic MD forces. The transition side-steps the long transition times by forcing a system from the start to the end state while computing dynamics. In one type of TMD, the applied forces are a function of the distances between the current and target positions of the atoms, a harmonic potential function is frequently used.33–34 TMD was applied to demonstrate how the opening of the KcsA channel would occur.33,35 Steered Molecular Dynamics (SMD) was applied to the KvAP channel to study pore conductance.36 For SMD, the simulation is accelerated along a reaction coordinate by applying forces in a specified time-dependent manner.37–38 These types of simulations are capable of finding multiple transition paths by repeating simulations from differing starting conditions.
In this study, we utilized Dynamic Importance Sampling (DIMS) to generate a variety of transitions for KcsA, KvAP, Kv1.2 and MthK sequences between known open and closed conformations.3–6,14 These structures provide us with two closed (PDB ID: 1k4c, 3eff) and two open (PDB ID: 1lnq, 2a79) confirmations of the pore domain necessary for generating our transitions; the open state of KvAP (PDB ID: 1orq) was not used for this study as it is believed to be distorted.19 One advantage of using DIMS compared to previous methods is that we are able to use the same starting and ending configurations to generate families of diverse transitions.
Our study provides new insights into possible mechanisms for gating transitions in K+ channels. The calculations show that independent of sequence the various pore domains have a common gating mechanism. Our calculations provide molecular insights into how intra-subunit motions influence the cooperativity of subunits during the transition. This has led us to hypothesize that the gating process occurs in several sequential steps: sidechain movement, inter-S5-S6 subunit motions, and then large conformational rearrangements. Furthermore, we see differences as well as common features between MthK, Kv1.2, KvAP, and KcsA. These results could be important in the evaluation of future structural information to determine key intermediate structures along the transition path.
METHODS
Protein Sequence and Structure
The structures of five different pore domains have been determined by crystallography (PDB IDs: 2a79, 1orq, 1k4c, 1lnq, 3eff).3–6,14 The crystallographic structures were abstracted to include only the pore region, S5-S6, for each channel. The KcsA, KvAP, Kv1.2 and MthK sequences for the pore domains were aligned using ClustalW.39 To generate starting structures for the transitions, all K+ channel sequences were then mapped onto two template structures using Modeller9v2 40: the open MthK x-ray structure (PDB ID: 1lnq) and closed high-resolution KcsA x-ray structure (PDB ID: 1k4c) [SI Table 1]. Each end-point structure was minimized using the steepest-decent algorithm for 200 steps and then a family of transitions was generated for each sequence.
An additional set of transitions was generated for the Kv1.2 channel using a different open state. For these simulations, the open template structure was the native open Kv1.2 x-ray structure (PDB ID: 2a79) and the closed template structure was the pervious KcsA structure (PDB ID: 1k4c) [SI Table 1]. As performed above, each template structure was minimized using the steepest-decent algorithm for 200 steps and then a family of transitions was generated for each sequence. These structures were considered to examine the differences between open state structures and how they would modify the transitions between open and closed states. The KvAP structure (PDB ID: 1orq) was not used as a template structure in this study as the protein structure is believed to be distorted.19
Generating Transitions
We investigated the pore gating-transition mechanism of the K+ channel using a variant of importance sampling, Dynamic Importance Sampling (DIMS).41–43 The approach of importance sampling can be understood by considering the computation of an average of a quantity g over a phase space x. With unbiased sampling the computed average is determined by the relative probability of visiting each location Q(x) and the values at those locations g(x). A biased sampling, with correction, will lead to an increased efficiency of sampling. A new distribution D(x) is created and samples collected under D(x) are corrected relative to Q(x) producing an unbiased estimate of the average.
| [1] |
This enables improved efficiency at the expense of requiring the design of the biasing distribution.
Based on Wagner’s stochastic formulation of importance sampling, DIMS was developed by Zuckerman and Woolf as a way to dynamically improve sampling in situations with defined beginning and ending points and no obvious reaction coordinate.41–43 The current implementation requires a relative progress variable, such as RMSD, to assess the progress towards the target as the transition occurs. This choice of progress variable provides a preliminary scheme for our biasing distribution. The DIMS method has been released in the latest version, c35b2, of the CHARMM program.44
To generate transitions, DIMS with our soft-ratcheting implementation was used.42 The soft-ratcheting algorithm generates transitions based on a score of the relative move towards or away from the target. The bias is applied to movement away from the target with an increasing likelihood based on the predicted, unbiased step away from the target. The value of Δϕ reflects this computed movement, with a negative Δϕ meaning movement towards the target and therefore no biasing needed.
| [2] |
In the above equation, Δϕ0 is a parameter controlling the width of the (backwards) decay. This “soft-ratcheting” accepts all steps proceeding towards the desired final state and a fraction of steps away from the target. An optimal DIMS-Cartesian value of 10−6 was used to maintain a higher diversity of states being sampled along our trajectories. This value has been found to give a good distribution in other DIMS calculations.44 This bias was applied to a subset of atoms, the Cα and Cβ carbons. The open and closed conformations used to generate the DIMS transitions for each channel were based on the closed KcsA (PDB ID: 1k4c) and the open MthK (PDB ID: 1lnq). Fifty-five trajectories were generated for each K+ channel sequence in the open → closed and closed → open transition pathways (see Figure 1]. A single soft-ratcheting transition typically completed within 18–20 h of CPU time on a modest Intel Xeon processor and took on the order of about 130 ps simulated time which is approximately 10,000 times faster than it would take a typical unbiased MD simulation to complete the transition.
Figure 1.
Sequences and structure of the pore domain. (A) An alignment of the four different K+ channel pore-domain sequences. (B) Cartoon of two different configurations of the K+ pore domain representing the closed state transition to the open state. Black and yellow lines outline representations of the implicit bilayer (hydrophobic core and interface regions).
All simulations used CHARMM, version c35b2, with the CHARMM22 with CMAP corrections force field.45,46 The molecular dynamics (MD) calculations were performed with Langevin dynamics using a timestep of 1 fs, a friction coefficient of 25.0 ps−1 on heavy atoms and a bath temperature of 300K for each simulation. An implicit solvent for the membrane was represented using the GBSW model.47–50 The GBSW parameters chosen were a thickness of 28 Å for the membrane hydrophobic core, 6 Å for each membrane interface, and a surface tension coefficient of 0.04 kcal/(mol* Å2) to represent the nonpolar solvation energy. These parameters were chosen to model a dipalmitoylphosphatidylcholine bilayer.
Analysis
To assess trajectory diversity, the cumulative Onsager-Machlup (OM) score was computed for each trajectory using the CORREL facility in CHARMM. The Onsager-Machlup score can be derived from stochastic considerations and suggests that an optimal path will minimize differences between the atomic forces and velocities on each atom51:
| [3] |
where F̍i is the vector of the force for atom i take from the force field, mi is the mass of atom i, η is friction coefficient, x̍i is vector of the spatial coordinates, t represents a particular time step, and Δt is integration step. The cumulative OM score, S(t), is computed and normalized
| [4] |
The OM score of a trajectory of length ttraj is the cumulative score provided by the last frame.
| [5] |
The OM score reflects the balance between kinetics and force along the conformational transition defined in the trajectory. It is derived from analysis of the least-action path between states and relates to the relative probability of a particular path being close to an optimal least-action determined path. These OM scores can be used to give an idea of the relative likelihood of a particular conformation since it is impossible to sample on all paths and thus the normalization and comparison to a determined set of least-action defined paths is not possible.
To determine whether the motions with the conformational fluctuations are encoded within other K+ channel structures principal component analysis (PCA) was used. The method is similar to that used to reveal key fluctuations of the NikR protein by Bradley et. al.52 The PCA for α carbons of the channel pore domain was performed using the quasiharmonic vibran module in CHARMM. The vector (Δx) described the displacement of α carbon atoms from the minimized starting open to a final closed structure determined by X-ray crystallography. The open and closed structures were created through homology modeling using Modeller and threading each sequence through the K+ channel pore x-ray structures.3–4,6,14,40 The open and closed conformations used in the transitions were KcsA (1k4c) and MthK (1lnq). Four different displacement vectors were calculated: 1) the closed KcsA structure (1k4c) and the open MthK (1lnq) conformation, 2) the closed KcsA structure (1k4c) and the open Kv1.2 (2a79) conformation, 3) the closed KcsA structure (3eff) and the open MthK (1lnq) conformation, 4) the open Kv1.2 (2a79) and the KcsA (1k4c) for DIMS transitions using the Kv1.2 as the open state reference point. The question of whether the displacement vectors from the X-ray structures, Δx, represented in the vector space described by subsets of PCA modes changed were determined by calculating the weight factor (α(i)) for each PCA mode as follows:
| [6] |
A subset S of modes was used to calculate a reconstructed vector (υ̃) as follows:
| [7] |
The similarity between Δx and each PCA mode (vi orυ̃) was assessed by their overlap as measured by the angle between the two vectors:
| [8] |
The relative correspondence of the reconstructed vectors was computed:
| [9] |
This relative correspondence provides a measure of how well the displacement due to the reconstructed vector agrees with the observed crystallographic displacement vector. This calculation will assess the conformational fluctuations among the different K+ channel structures.
To calculate the hinge degrees of freedom for each monomeric unit of the channel we used Swink developed by Cordes et. al.53 The calculations for the pore surface of the channel used HOLE.54 Chi angle, S5/S6 correlation, and S6 angle analysis was performed using the analysis library scripts MDAnalysis.55 The sidechains conformational changes were monitored based on their rotation about the chi angle. The chi angle, also called the rotamer angle, is the calculated dihedral angle based on the atom types N, CA, CB, and CG:
| [10] |
θ is the dihedral angle, a⃗ is the normal vector (a cross product of the coordinates of (Natom − CAatom) and (CBatom − CAatom)) and b⃗ is the normal vector (a cross product of the coordinates of (CAatom − CBatom) and (CGatom − CBatom)).
RESULTS
The DIMS algorithm was used to examine forward and reverse transition pathways for four K+ channels. To apply the method to the different pore domain sequences [Figure 1A] they were mapped onto the open and closed conformations. Figure 1B shows the two conformations used for the closed and open states (the closed KcsA structure and the MthK open structure) and how these configurations are positioned within the bilayer. Fifty-five different trajectories were simulated for each sequence and in each transition direction. These families of K+ channel transitions were used to determine if the average transition pathway of these channels share common motions.
Individual Trajectory Independence
A single trajectory of a transition cannot provide enough information to determine the average pathway and fluctuations. Therefore, assessing the diversity of a family of transition-paths is important to evaluate the intermediate states along the pathways. As an initial assessment, a set of rank-ordered OM scores shows the diverse nature and extent of sampling for our family of trajectories [SI Figure 1]. The OM scores provided an initial estimate for the amount of motion present within each individual trajectory. The scores differ depending on total number of atoms within the system and the direction of the transition simulated. Since the OM score can be related to the time length of the transition, we observed that the open → closed transition simulations were shorter than the closed → open transition for all channels. This type analysis only provided an initial indication of transition time length and thus to understand the structural diversity within the transition further analysis was performed.
In order to further evaluate the aspects of independence and diversity among trajectories, the large-scale channel motions were tracked through structural determinants as the progress variable moves toward the target. Previous computational studies such as those performed by Shrivastava et. al. have suggested that there are specific regions of the K+ channel that are more mobile while others are more rigid.27 These studies have also suggested that more mobile regions of the channel are located close to the gate region (the beginning of the S5 domain and the end of the S6 domain).27,35,56–59 Our results also show high mobility in these regions based on an atomic density profile taken for each sequence over the full length of their transitions [SI Figure 2]. The KcsA, KvAP, Kv1.2, and MthK sequences exhibit low mobility (highest atomic density) appear around the region surrounding the selectivity filter, while regions downstream from the glycine hinge located near the gate have a higher mobility (lowest atomic density) [SI Figure 2].
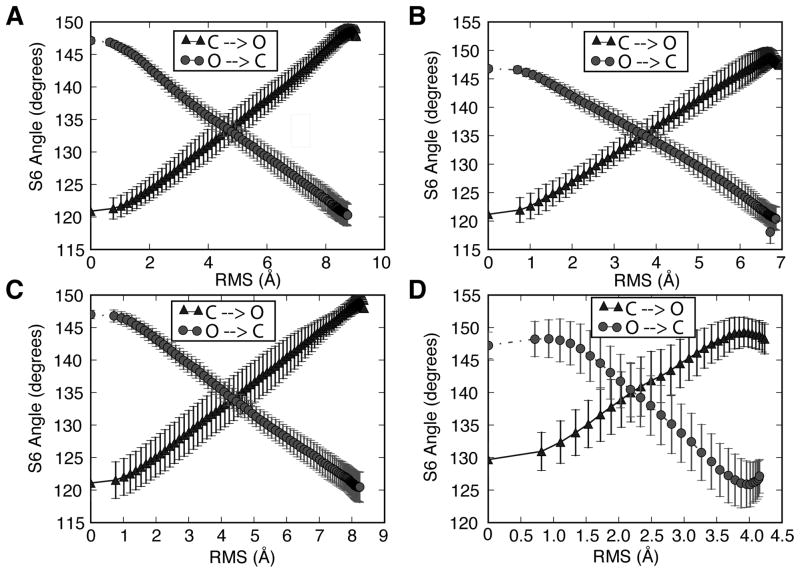
The mobile S5-S6 regions of the channel can provide an initial metric for measuring the diversity of our intermediates as the transition progresses. Figure 2 shows this with the S6 helix angle, where the angle exhibits a range of intermediate states while the transition progresses within the RMS-space. The calculation of the S6 angle is relative to the z-axis. The amount of deviation of the average S6 orientation varies as the set of trajectories progress [Figure 2]. The deviation of the S6 helix angle near the starting and ending configurations of the transitions is approximately ±1°. The point where the range of the S6 angle values varies significantly is near the transition mid-point for each of the sequences. A deviation of ±5° from the average S6 angle can be seen at these RMS ranges. It is interesting to note that the midpoint S6 value is slightly larger for the open to closed transitions than for the closed to open transitions [Figure 2]. It is also interesting that the MthK structure profile is noticeably different from the other channels. We suggest that this may be due to the small size of the channel as it is significantly shorter in sequence length and thus it may be able to sample more conformations compared to the other three channels [Figure 1 and 2]. This may suggest a higher diversity of intermediate states was sampled when transitioning from the open to closed states. The fluctuation levels at various RMS values along the transition give an indication of the diversity of paths sampled along the progress variable. These results suggest good sampling of intermediate conformations during the transitions generated by DIMS.
Figure 2.
The average angle of the S6 domain relative to the z-axis as a function of RMS, the DIMS progress variable. The errorbars indicate the standard deviation at a particular RMS value. Both transition path directions are shown. (A) KcsA (B) KvAP (C) Kv1.2 (D) MthK.
Hinge Region Changes
With the diverse nature of the family of transitions, we can begin assess S6 helix motions and understand how these large-scale motions relate to other experimental and computational studies. Experimental studies have shown that the highly conserved glycine acts as a molecular “hinge” 56 in the middle of the inner helix. Site-directed mutagenesis studies have been used to examine the mutation of glycine to alanine. These results show through the presence of no activity the critical role this residue plays in channel function.57 Mashl and Jakobsson used endpoint TMD to demonstrate that the fluctuations for the glycine hinge are smaller than the larger fluctuations found near residues upstream from the Pro-Val-Pro (PVP) region.35 The observation of reduced fluctuations suggests that the glycine hinge must follow a specific pathway during the transition and this specificity makes this glycine position important to the ability of the channel to function.
Our results show similar mobility to that found by Mashl and Jakobsson based on a selection of the “hinge” residue along the S6 helix. The glycine hinge region had ±2.5° of fluctuation for all K+ channel sequences [SI Figure 3] which was small in comparison to the fluctuations observed upstream of the PVP region discussed later. This small deviation in kink angle at such a highly conserved residue suggests this residue is crucial to the ability of the channels to transition. This concept further supports similar findings from experimental mutational and computational studies. This suggests that our results are consistent with both experiment and previous computational work in highlighting the importance of the glycine region as a local hinge point.35
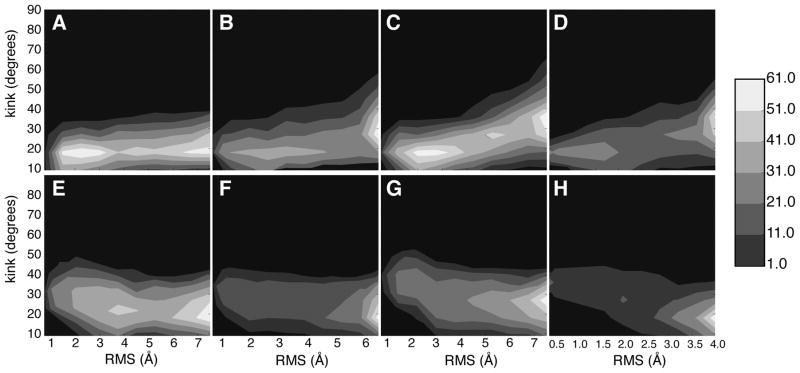
We also observed changes in the hinge by calculating the kink angle near the conserved PVP region. The kink angle of S6 over time for the regions upstream of the PVP region is shown in Figure 3. The degree of kink for the starting and ending states was the same for all of the sequences as is expected based on the nature of the algorithmic design of DIMS. As the transition progresses, the contours show that large regions of kink space were sampled during the simulations for each sequence in both the forward and reverse pathways. This further emphasizes diverse sampling from the DIMS algorithm and that the family of computed transitions are self-consistent. Our kink results illustrate that the forward and reverse large conformational changes share a common pathway for these channels [Figure 3]. The dense regions of the contours show the average path for the transition kink angle. The transitions from the closed to open states shift the kink angle from 18° to 30° [Figure 3A–D]. For the open to closed transitions, the kink angle changes from 18° to 25° however the observed nature of the contour and the angle pathway appears different from the previous set of transitions [Figure 3E–H]. The shape of these paths remains consistent for all of the channels along a specific direction. This consistency suggests that the channels share a common path in terms of large-scale domain motions.
Figure 3.
The S6 kink angle located near the PVP region as a function of RMS (A) KcsA sequence closed to open transitions (B) KvAP sequence closed to open transitions (C) Kv1.2 sequence closed to open transitions (D) MthK sequence closed to open transitions (E) KcsA sequence open to closed transitions (F) KvAP sequence open to closed transitions (G) Kv1.2 sequence open to closed transitions (H) MthK sequence open to closed transitions
Cooperativity during the Transition
As described above, the DIMS results show regions of different mobility for the individual subunits and that these regions are common among the different K+ channels. This section addresses the question of how these individual subunits move in relation to one another. In particular, we are curious if the collective motions of the subunits are similar between the different channels and whether these individual subunit movements are cooperative.
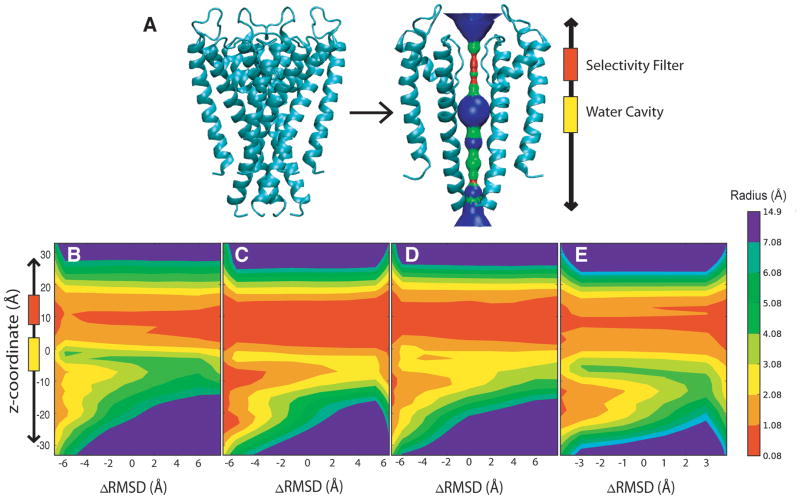
Perozo and co-workers experimentally showed, through EPR studies, that as the S6 and S5 helices would swing out away from the central permeation cavity.60,61 Based a top-down view of the pore domain, the S5 helices rotate counterclockwise while the S6 helices rotate in a counterclockwise direction. This large-scale domain rearrangement as the channel opens leads to an increase in the diameter of the pore cavity near the gate region of the channel. These EPR experiments also illustrated the innate rigidity of the selectivity filter as compared to the flexibility of the S6 helices. We observe similar rigidity within the selectivity filter and water cavity regions and large-scale domain rearrangement of the S6 and S5 helices near the gate region during our DIMS transitions [Figure 4].
Figure 4.
The pore domain radius value as function of ΔRMSD (in the closed → open direction) and z-position for the trajectories. The contour color-bar indicates the pore radius value in Ångstroms. (A) Sideview of pore domain depicting basic HOLE profile (B) KcsA transitions (C) KvAP transitions (D) Kv1.2 transitions (E) MthK transitions
Initial evidence that a collective motion between subunits occurs in our DIMS trajectories is observed in pore radius profiles generated using the HOLE program. The resulting K+ channel profiles show the average pore radius value for z-coordinates as the transition progresses [Figure 4]. The ΔRMSD used is the difference in RMSD of conformation from the references A and B, ΔRMSD = RMSDA − RMSDB. As the transition proceeds, the increase of the ΔRMSD value denotes the movement toward the target structure along the average pathway. These profiles of the pore radius initially show that during the transitions the motion is predominantly near the gate region of the channel. The profile may also suggest that the gate region motions change in a manner that is more consistent with subunits moving collectively rather than independently.
An intriguing result from the set of DIMS calculations is the observation that each of the different structural variants saw a similar set of changes along the transition. For example, in Figure 4, the set of K+ channel profiles show a set of similar closed to open transitions. The open to closed transitions also show a similar profile [SI Figure 4]. Note that the radius for particular regions of the channel such as the selectivity filter and water cavity regions remains constant. For example, the average radius value of 1 Å for the selectivity filter is located around ~ 5 Å to 10 Å. In addition, all the sequences have an internal water cavity radius value of 2 Å to 4 Å positioned at an approximate z-coordinate of 0 to +5 Å that remains constant in relation to ΔRMSD. The pore radius for the rest of the channel changes as the transition progresses from a closed to open state. These computed results indicate both a common transition pathway and the beginnings of collective motions of the subunits between the different K+ channel profiles.
To understand the source from which these collection motions stem, we assess the cooperativity of subunits by calculating the coupling between S5 and S6 motions for each subunit. Figure 5 shows the median correlation between subunits S5 and S6. The size of each square reflects the frequency or number of times the median correlation value occurs as the transition progresses. The ensemble of transitions for each channel was assessed in a closed (−ΔRMSD) to open (+ΔRMSD) direction for each possible subunit combination of S5 and S6 movements. In the closed state large correlations are present between the S5 and S6 units independent of subunit. As the transition progresses toward the open state, the correlation motions of S5 and S6 within the same subunit show that S5 influences the S6 gate regions thus opening the channel. One or two subunits are shown to influence other subunit movements. In other words, the transition progressing from closed to open begins with correlations between intra-subunit S5 and S6 within the closed state, then inter-subunit correlations couple motions leading to the opening of the channel gate region and allow ions to pass.
Figure 5.
Correlations between S5 and S6 movement for all subunits as the pore domain changes conformation observed within the same subunit and with adjacent subunits. Left to right: closed state (−ΔRMSD) to open state (+ΔRMSD). (A) Top down view indicating the location of subunit numbers (B) KcsA transitions (C) KvAP transitions (D) Kv1.2 transitions (E) MthK transitions
Subtle Sidechain Motions
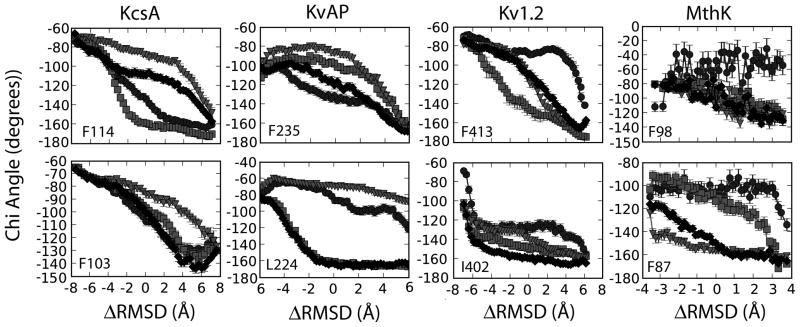
To identify aspects that facilitate cooperative interactions among subunits, we revisit and further explore regions near the glycine hinge and the PVP sequence by looking at the behavior of individual sidechains during the transition. Several residues have been shown experimentally to influence S5 and S6 movement and thus contributing to channel function and the transition.35,62,63 Here we present chi-angle changes for several different residues as the transition progresses [Figure 6, SI Figure 5, SI Figure 15, and Table 1]. The residue types differ among K+ channels and throughout the rest of the paper we will use the KcsA residue number and type when referring to these residues [Table 1]. These residues found to contribute to the channel function are spatially located near the selectivity filter or upstream from the PVP region in sequence space where larger fluctuations in the backbone hinge region occur.
Figure 6.
Characterization of behavior for hydrophobic residues important to the gating process. Each shape represents a different segment number of the channel (square = segment 1, diamond = segment 2, triangle = segment 3, circle = segment 4).
Table 1.
The residue number and type associated the chi angle calculations for the different K+ channels [Figure 1, Figure 6, and SI Figure 15].
| Shaker | KcsA | KvAP | Kv1.2 | MthK |
|---|---|---|---|---|
| F484 | R117 | K238 | F416 | -- |
| F481 | F114 | F235 | F413 | F98 |
| S479 | T112 | N233 | S411 | E96 |
| L472 | L105 | L226 | L404 | V89 |
| I470 | F103 | L224 | I402 | F87 |
| V467 | I100 | I221 | V399 | I84 |
| A463 | M96 | M217 | A395 | I80 |
| T442 | T75 | T196 | T374 | T59 |
| V438 | E71 | V192 | V370 | V55 |
Previous research suggests that F114 directly affects the channel’s ability to gate (in KcsA).63 We suggest that this residue’s rotamer configurations allow the S5 and S6 domains to move past each other leading to the beginning stages of channel gating. These movements and direct correlation with the cooperativity of subunits may explain why this particular residue type is conserved across the different K+ channel sequences. We also hypothesize that F103 influences the cooperativity among subunits. The F103 residue on four separate subunits begins to change rotamer conformations at different points during the transition. For instance, the chi value for subunit #1 is approximately −40 ° near the closed state but shifts to ~ −179° half-way along the transition [Figure 6]. This behavior is clearly seen for the rest of the subunits when the average chi value is plotted along the transition. Figure 6 also shows how the F103 and F114 chi angles for each subunit change at different times along the transition. The changes for these residues correspond to the inter-subunit correlation [Figure 5–6]. We hypothesize that these residues influence the large-scale domain rearrangement and possibly the overall function of the channel.
Mutational effects on transitions
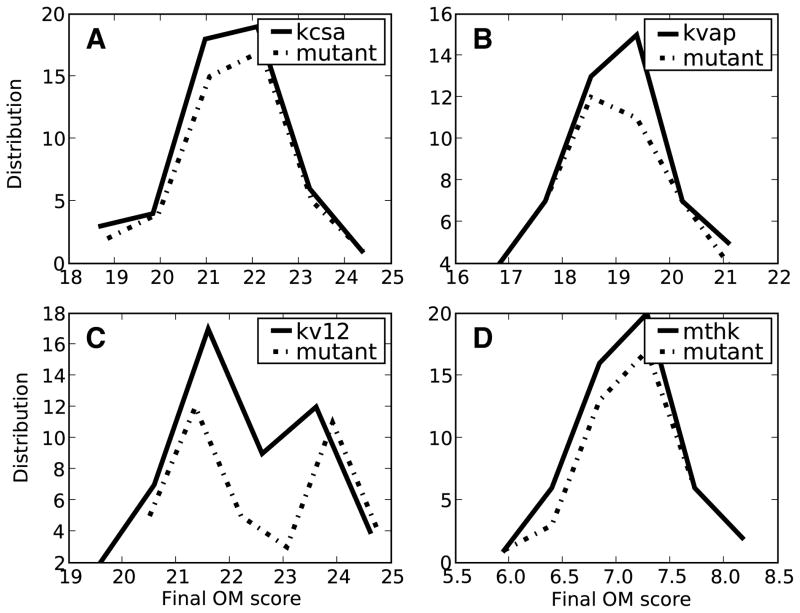
Previous research has shown that several different mutations within the water cavity and gate regions of the K+ channel affect the channel function.63 To determine if sidechain F103 affects the KcsA channel’s ability to change conformations, we looked at the average time of transition completion. While this residue is not conserved throughout all K+ channel sequences the residue located within the same sequence space characterizes a residue at this position as similar; large and hydrophobic. We compared the rate of an ensemble of transitions with the rate of the wild-type channels using the OM score. Figure 7 shows a histogram of the OM scores for both the wild-type and the F103A mutant. The assumption is that if the median OM score for the mutant shifted from the wild-type then the mutation would shift the kinetic rate of the ensemble transition. No shift in the median OM score was present for the mutant [Figure 7]. This result provides an initial indication that a population shift may occur for the transition when the F103A mutation is present.
Figure 7.
WT and F103A mutant cumulative Onsager-Machlup (OM) scores. The rank ordering of the trajectories shows the diversity of the transitions for each sequence in the closed → open direction. The solid line represents the WT transition and the dashed-line represent the mutant transition. (A) KcsA transitions, (B) KvAP transitions, (C) Kv12 transitions, (D) MthK transitions.
Evaluating Encoded Motions
Currently, there are 2 closed state crystal structures3,14 but two different open state crystal structures.4,6 One question is -- are the motions for the transition from the closed to open state encoded within the various open state structures? Or phrased differently, along the transition pathways do we observe motions that would favor these two structures as intermediates? To further understand the context of the structural transition of the pore domain for KcsA and Kv1.2 structures, Principal Component Analysis (PCA) was used. For this section, we focus only on the KcsA and Kv1.2 ensemble of transitions as the question of encoded motions involve X-ray structures for these K+ channels only. PCA was used as an additional avenue to quantitatively determine if the fluctuations during the transition carried the low frequency modes necessary to reach specific points during the conformational change.
Figure 8 shows the relative overlap for a particular subset of modes with the open to closed displacement vector for each voltage drop. Low relative correspondence values indicate a higher percentage of the modes contributing to the motions opening the channel. As the total number of modes increases, the amount of relevant motion closing the channel increases [Figure 8]. Along the transition from the closed to the open direction, a subset of the first 130 modes captured the motions of the transition if any of the motions were present. The relative correspondence changes linearly as the number of modes included within the subset increases.
Figure 8.
Motions encoded within different structures using the percent overlap of the displacement vector for the pore domain as a function of mode. Each line represents a different displacement vector (KcsaA → Kv1.2, KcsaA (1k4c) → MthK, KcsA (3eff) → MthK, and Kv1.2 → KcsA). Note: the KcsA → X (X = MthK, Kv1.2) displacement vectors were analyzing transitions generated between the KcsA (1k4c) and MthK (1lnq) endpoints and the Kv1.2 → KcsA displacement vector was analyzing for transitions generated between the KcsA (1k4c) and Kv1.2 (2a79) endpoints.
The PCA analysis determines if motions along the transition are encoded within the structures and if two of the three structures (3eff and 2a79) are possible intermediates during the transition. To put the structures into perspective, the backbone RMSD between the two DIMS endpoint structures is ~6.9 Å ± 0.5 Å; the open Kv1.2 structure has a backbone RMSD of ~ 3.4 Å in relation to the closed state and a more fully closed KcsA configuration (3eff) has a backbone RMSD of ~1.1 Å from the closed structure. The PCA results show that the KcsA (3eff) structure would be sampled along the transition between the 2 DIMS endpoints, while the Kv1.2 structure would not be an intermediate for this transition [Figure 8]. A separate Kv1.2 transition using the closed and the open Kv1.2 structure revealed that only a transition using these two configurations would best capture both motions for the open Kv1.2 and closed KcsA configurations [Figure 8].
DISCUSSION
Previous studies of K+ channels have focused primarily on the secondary structure and mobility of various regions of the protein.26–28,33,35–36,56–65 We show a complete set of closed ↔ open transitions for different K+ channels and how these transitions are relevant for understanding the gating mechanism. Our transition results show similar mobile domains and secondary structure aspects, however we provide new insights into sidechain behavior and intra-and inter- correlations of the S5 and S6 helices. The DIMS transition results indicate that the gating process occurs in steps: F103 and F114 sidechain movement, then inter- S5-S6 subunit motions, and lastly the large-scale domain rearrangements.
The residues upstream from the PVP region have a direct impact on the gating transition and channel function.35,63–64 We show that the F103 and F114 residues in KcsA, subsequent positions within other K+ channels [Table 1], are fundamental for gating due to changes in rotamer conformations during the transition. These residues may influence channel function and the overall transition due to their bulky size, hydrophobic nature, and proximity to the S5 helix. By systematically mutating these individual residues which are upstream from the PVP gate region or near the selectivity filter of these channels to small residues, the kinetic rate may shift or a loss of channel function may occur.63,64 Similar findings have been shown by Hackos et. al.,63 Labros et. al.,64 and Mashl and Jakobsson35 where they suggest that mutations led to differences in the kinetic rate. However, based on our F103 mutation analysis using the OM scores, we hypothesize that some mutations do not necessarily affect the kinetic rate of the transition but shift the population of well-defined energy states. In other words, some mutations may lead to changes in the relative free energy surface thus altering the least cost energy pathway.
When replacing these bulky sidechains with smaller ones, such as alanine, it impacts on channel dynamics or disrupts the local structure enough to prevent normal gate function and thus the large-scale rearrangement. During the transition, the N-terminal region of the S5 and the C-terminal region of the S6 domains undergo large conformational rearrangements.58–60,63 The hinge bending of the S6 helix can result in a stable open state of the channel similar to other studies.59 Further studies suggest that mutating the sequence near the PVP region on the S6 helix alters the S6 hinge motion while mutation to an AVPP sequence renders the K+ channel reluctant to open or to gate.64 We suggest that sidechain behavior influences cooperativity between the S5 and S6 helices between K+ channel subunits. While the large-scale motions of the S5 and S6 helices allow for the passage of ions, the subtle motions of the sidechains upstream from the PVP region and near the selectivity filter influence subunit behavior. The subtle differences in terms of sidechain rotamer conformations may influence the large-scale domain motions sampled. Previous data suggested that sidechains on the S6 helix and near the selectivity filter occlude the pore during the closed state of the channel.62–63
The individual S6 domain rearrangement influences the pore radius of the K+ channels as they gate. As the F103 and F114 residues on the individual subunits change rotameric states, the S5 and S6 helices large-scale motions increase and correspond to inter-subunit correlations. The correlations of inter- and intra- S5-S6 subunit motions drive the transition between open ↔ closed conformations. Based on our results, we hypothesize that the gating mechanism can begin with a single subunit or combination of two subunits thus influencing the collective motions of all four subunits [Figure 5]. While the S5-S6 correlations directly indicate cooperativity between subunits, this cooperativity may only point towards a possible allosteric mechanism common among all K+ channels. This hypothesis also allows for the possibility of directional dependence for the transition path being influenced by the cooperative mechanisms between subunits.
The pore radius profiles for the ensemble of closed → open transitions and open → closed transitions for the K+ channels initially suggests a directional pathway dependence. Interestingly, this observation was true independent of sequence or size of the channel and serves as an initial indication of directional dependence. Previous computational studies have elucidated a pathway dependence based on the direction of the biased simulation.35,66 In the absence of intermediate structural data, it is difficult to assess whether the directional dependence occurs biologically or relates to the choice of progress variable, RMSD. Despite indications of a directional dependence of paths, these K+ channel pathways undergo similar conformational trends and behaviors and our results indicate that DIMS is sampling on possible K+ channel transition paths. Experimental studies using x-ray scattering, similar to those performed by Shimizu et. al., may provide insights into structural characteristics exhibiting directional dependence during the transition path.65
In previous DIMS studies, this method sampled various biological intermediate structures during the transitions.67 In the absence of intermediate structural data, we begin to examine if the K+ channel motions encoded in two other channel configurations (2a79 and 3eff) are observed during the motions of our transitions through the use of PCA analysis. The new closed KcsA structure’s motions are encoded within the transitions and may be due to the similarity between the two KcsA structures. The motions required to transition between the closed and open Kv1.2 state may be following different free-energy surfaces. Further experimental structures will need to be determined to show if these results are similar to the real physiological mechanisms. Studies performed by Shimizu et. al. might provide useful information for uncovering structural information along the transition paths necessary thus leading to direct comparisons between computational transitions and experiment.65
Taken together, our results suggest potassium channels experience two types of motion: large-scale backbone domain motion and subtle sidechain motions. We hypothesize that both types of motions mentioned above occur in steps. The sidechain motion precedes the S5-S6 domain rearrangement and this order of events may be necessary for the channel to function. A recent study has also suggested that subtle differences in terms of rotamer conformations influence the large-scale domain motions.68 The necessity of these two types of motion, which occur as the channel gates, may provide indications along the lines of a two-gate model proposed by Liu and Joho.69
CONCLUSIONS
The results presented here are important for understanding K+ channel gating. We use the DIMS method to sample along diverse transition pathways while maintaining the integrity of key structural elements. This is seen in the parts of the structure related to ion selection and the analysis of the cavity radius. Our results are in agreement with previous studies that the sequence of the K+ channel does not dictate the transition pathway. In addition, we show that cooperativity between S5 and S6 domains helps to stabilize K+ channels during the transition. This supports our hypothesis that the structural transitions behind gating start with local perturbations in the sidechain rotamer population, spreads to the S5-S6 region and then involves a cooperative transition between all four subunits.
Supplementary Material
Acknowledgments
The authors thank Oliver Beckstein for valuable discussion, Juan Perilla for further DIMS code development, and Naveen Michaud-Agrawal for the development of MDAnalysis. The research was partially funded by a grant from the NIH (#GM064746).
Contributor Information
Elizabeth J. Denning, Department of Biophysics and Biophysical Chemistry, Johns Hopkins School of Medicine, Baltimore, Maryland 21205
Thomas B. Woolf, Departments of Physiology and of Biophysics and Biophysical Chemistry, Johns Hopkins School of Medicine, Baltimore, Maryland 21205.
References
- 1.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hille B. Ion Channels of Excitable Membranes. 3. Sinauer; Sunderland, MA: 2001. [Google Scholar]
- 3.Zhou Y, Morais-Cabral JH, Kaufman A, MacKinnon R. Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 Å resolution. Nature. 2001;414:43–48. doi: 10.1038/35102009. [DOI] [PubMed] [Google Scholar]
- 4.Jiang Y Lee A, Chen J, Cadene M, Chait BT, MacKinnon R. Crystal Structure and Mechanism of a Calcium-Gated Potassium Channel. Nature. 2002;417:515–522. doi: 10.1038/417515a. [DOI] [PubMed] [Google Scholar]
- 5.Jiang Y, Lee A, Chen J, Ruta V, Cadene M, Chait BT, MacKinnon R. X-ray structure of a voltage-dependent K+ channel. Nature. 2003;423:33–41. doi: 10.1038/nature01580. [DOI] [PubMed] [Google Scholar]
- 6.Long SB, Campbell EB, McKinnon R. Crystal Structure of a Mammalian Voltage-Dependent Shaker Family K+ Channel. Science. 2005;309:897–903. doi: 10.1126/science.1116269. [DOI] [PubMed] [Google Scholar]
- 7.Kuo A, Gulbis JM, Antcliff JF, Rahman T, Lowe ED, Zimmer J, Cuthbertson J, Ashcroft FM, Ezaki T, Doyle D. Crystal structure of the potassium channel KirBac1.1 in the closed state. Science. 2003;300:1922–1926. doi: 10.1126/science.1085028. [DOI] [PubMed] [Google Scholar]
- 8.Zhou M, MacKinnon R. A mutant KcsA K(+) channel with altered conduction properties and selectivity filter ion distribution. J Mol Bio. 2004;338:839–846. doi: 10.1016/j.jmb.2004.03.020. [DOI] [PubMed] [Google Scholar]
- 9.Lockless SW, Zhou M, MacKinnon R. Structural and thermodynamic properties of selective ion binding in a K channel. PLoS Biol. 2007;5:e121. doi: 10.1371/journal.pbio.0050121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yohannan S, Hu Y, Zhou Y. Crystallographic study of the tetrabutylammonium block to the KcsA K+ channel. J Mol Bio. 2007;366:806–814. doi: 10.1016/j.jmb.2006.11.081. [DOI] [PubMed] [Google Scholar]
- 11.Lenaeus MJ, Vamvouka M, Focia PJ, Gross A. Structural basis of TEA blockade in a model potassium channel. Nat Struct Mol Biol. 2005;12:454–459. doi: 10.1038/nsmb929. [DOI] [PubMed] [Google Scholar]
- 12.Faraldo-Gómez JD, Kutluay E, Jogini V, Zhao Y, Heginbotham L, Roux B. Mechanism of intracellular block of the KcsA K+ channel by tetrabutylammonium: insights from X-ray crystallography, electrophysiology and replica-exchange molecular dynamics simulations. J Mol Bio. 2007;365:649–662. doi: 10.1016/j.jmb.2006.09.069. [DOI] [PubMed] [Google Scholar]
- 13.Zhou Y, MacKinnon R. The occupancy of ions in the K+ selectivity filter: charge balance and coupling of ion binding to a protein conformational change underlie high conduction rates. J Mol Bio. 2003;333:965–975. doi: 10.1016/j.jmb.2003.09.022. [DOI] [PubMed] [Google Scholar]
- 14.Uysal S, Vásquez V, Tereshko V, Easki K, Fellouse FA, Sidhu SS, Koide S, Perozo E, Kossiakoff A. Crystal structure of full-length KcsA in its closed conformation. Proc Natl Acad Sci USA. 2009;106:6644–6649. doi: 10.1073/pnas.0810663106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chakrapani S, Jogini V, Cuello LG, Cortes M, Perozo E. On the Structure-Function correlates of Ion Occupancy and modulation of C-type Inactivation. Biophysical Society Meeting. 2009 March; 2009. [Google Scholar]
- 16.Capener CE, Shrivastava IH, Ranatunga KM, Forrest LR, Smith GR, Sansom MSP. Homology modeling and molecular dynamics simulation studies of an inward rectifier potassium channel. Biophys J. 2000;78:2929–2942. doi: 10.1016/S0006-3495(00)76833-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Domene C, Grottesi A, Sansom MSP. Filter flexibility and distortion in a bacterial inward rectifier K+ channel: simulation studies of KirBac1.1. Biophys J. 2004;87:256–267. doi: 10.1529/biophysj.104.039917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Roux B, Allen T, Berneche S, Im W. Theoretical and Computational models of Biological Ion Channels. O Rev Biophys. 2004;37:15–103. doi: 10.1017/s0033583504003968. [DOI] [PubMed] [Google Scholar]
- 19.Roux B, Schulten K. Computational Studies of Membrane Channels. Structure. 2004;12:1343–1351. doi: 10.1016/j.str.2004.06.013. [DOI] [PubMed] [Google Scholar]
- 20.Shrivastava IH, Capener CE, Forrest LR, Sansom MSP. Structure and dynamics of K channel pore-lining helices: a comparative simulation study. Biophys J. 2000;78:79–92. doi: 10.1016/S0006-3495(00)76574-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Biggin PC, Sansom MSP. Open-state models of a potassium channel. Biophys J. 2002;83:1867–1876. doi: 10.1016/S0006-3495(02)73951-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tikhonov DB, Zhorov BS. In silico activation of KcsA K+ channel by lateral forces applied to the C-termini of inner helices. Biophys J. 2004;87:1526–1536. doi: 10.1529/biophysj.103.037770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brooks BR, Karplus M. Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc Natl Acad Sci USA. 1983;80:6571–6575. doi: 10.1073/pnas.80.21.6571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Go N, Noguti T, Nisikawa T. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc Natl Acad Sci USA. 1983;80:3696–3700. doi: 10.1073/pnas.80.12.3696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Levitt M, Sander C, Stern PS. Normal-mode dynamics of a protein: bovine pancreatic trypsin inhibitor. Int J Quant Chem: Quant Biol Symp. 1983;10:181–199. [Google Scholar]
- 26.Shen Y, Kong Y, Ma J. Intrinsic flexibility and gating mechanism of the potassium channel KcsA. Proc Natl Acad Sci USA. 2002;99:1949–1953. doi: 10.1073/pnas.042650399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Shrivastava IH, Bahar I. Common mechanism of pore opening shared by five different potassium channels. Biophys J. 2006;90:3929–3940. doi: 10.1529/biophysj.105.080093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Haliloglu T, Ben-Tal N. Cooperative transition between open and closed conformations in potassium channels. PLoS Computational Biology. 2008;4:e1000164. doi: 10.1371/journal.pcbi.1000164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Miloshevsky GV, Jordan PC. Permeation and gating in proteins: kinetic Monte Carlo reaction path following. J Chem Phys. 2005;122:214901. doi: 10.1063/1.1924501. [DOI] [PubMed] [Google Scholar]
- 30.Miloshevsky GV, Jordan PC. The open state gating mechanism of gramicidin A requires relative opposed monomer rotation and simultaneous lateral displacement. Structure. 2006;14:1241–1249. doi: 10.1016/j.str.2006.06.007. [DOI] [PubMed] [Google Scholar]
- 31.Jordan PC. Monte Carlo normal mode following: a new way to study ion channel gating. Biophysical Society Meeting. 2007 March; 2007. [Google Scholar]
- 32.Enosh A, Raveh B, Furman-Schueler O, Halperin D, Ben-Tal N. Generation, comparison, and merging of pathways between protein conformations: gating in K-channels. Biophys J. 2008;95:3850–3860. doi: 10.1529/biophysj.108.135285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Compoint M, Picaud F, Ramseyer C, Girardet C. Targeted molecular dynamics of an open-state KcsA channel. J Chem Phys. 2005;122:134707. doi: 10.1063/1.1869413. [DOI] [PubMed] [Google Scholar]
- 34.Cheng X, Wang H, Grant B, Sine SM, McCammon JA. Targeted molecular dynamics study of C-loop closure and channel gating in nicotinic receptors. PLoS Comp Biol. 2006;2:1173–1184. doi: 10.1371/journal.pcbi.0020134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mashl RJ, Jakobsson E. End-Point Targeted Molecular Dynamics: Large-Scale Conformational Changes in Potassium Channels. Biophys J. 2008;94:4307–4319. doi: 10.1529/biophysj.107.118778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Monticelli L, Robertson KM, MacCallum JL, Tieleman DP. Computer simulation of the KvAP voltage-gated potassium channel: steered molecular dynamics of the voltage sensor. FEBS Lett. 2004;564:325–332. doi: 10.1016/S0014-5793(04)00271-6. [DOI] [PubMed] [Google Scholar]
- 37.Park S, Schulten K. Calculating potentials of mean force from steered molecular dynamics simulations. J Chem Phys. 2004;120:5946–5961. doi: 10.1063/1.1651473. [DOI] [PubMed] [Google Scholar]
- 38.Gullingsrud J, Schulten K. Gating of MscL studied by steered molecular dynamics. Biophys J. 2003;85:2087–2099. doi: 10.1016/s0006-3495(03)74637-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Larkin MA, Blackshields G, Brown NP, Chenna R, McGettigan PA, McWilliam H, Valentin F, Wallace IM, Wilm A, Lopez R, Thompson JD, Gibson TJ, Higgins DG. ClustalW and ClustalX version 2. Bioinformatics. 2007;23:2947–2948. doi: 10.1093/bioinformatics/btm404. http://www.ebi.ac.uk/Tools/clustalw2/index.html. [DOI] [PubMed]
- 40.Marti-Renom MA, Stuart A, Fiser A, Sánchez R, Melo F, Sali A. Comparative protein structure modeling of genes and genomes. Annu Rev Biophys Biomol Struct. 2000;29:291–325. doi: 10.1146/annurev.biophys.29.1.291. [DOI] [PubMed] [Google Scholar]
- 41.Zuckerman DM, Woolf TB. Dynamic reaction paths and rates through importance-sampled stochastic dynamics. J Chem Phys. 1999;111:9475–9484. [Google Scholar]
- 42.Zuckerman DM, Woolf TB. Rapid Determination of Multiple Reaction Pathways in Molecular Systems: The Soft-Ratcheting Algorithm. 2002:1–13. [Google Scholar]
- 43.Woolf TB, Zuckerman DM, Lu N, Jang H. Tools for channels: moving towards molecular calculations of gating and permeation in ion channel biophysics. J Mol Graph Model. 2004;22:359–68. doi: 10.1016/j.jmgm.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 44.Perilla JR, Denning EJ, Beckstein O, Woolf TB. Computing ensembles of transitions from stable states: Dynamic Importance Sampling. doi: 10.1002/jcc.21564. in submission. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J Comp Chem. 1983;4:187–217. [Google Scholar]
- 46.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 47.Feig M, Im W, Brooks CL., III Implicit solvation based on generalized Born theory in different dielectric environments. J Chem Phys. 2004;120:903–911. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- 48.Feig M, Onufriev A, Lee MS, Im W, Case DA, Brooks CL., III Performance comparison of generalized born and Poisson methods in the calculation of electrostatic solvation energies for protein structures. J Comp Chem. 2004;25:265–284. doi: 10.1002/jcc.10378. [DOI] [PubMed] [Google Scholar]
- 49.Im W, Feig M, Brooks CL., III An implicit membrane generalized Born theory for the study of structure, stability, and interactions of membrane proteins. Biophys J. 2003;85:2900–2918. doi: 10.1016/S0006-3495(03)74712-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Im W, Lee MS, Brooks CL., III Generalized Born model with a simple smoothing function. J Comp Chem. 2003;24:1691–702. doi: 10.1002/jcc.10321. [DOI] [PubMed] [Google Scholar]
- 51.Onsager L, Machlup S. Fluctuations and Irreversible Processes. Phys Rev. 1953;91:1505–1512. [Google Scholar]
- 52.Bradley MJ, Chivers PT, Baker NA. Molecular dynamics simulation of the Escherichia coli NikR protein: equilibrium conformational fluctuations reveal interdomain allosteric communication pathways. J Molecular Bio. 2008;378:1155–1173. doi: 10.1016/j.jmb.2008.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cordes FS, Bright JN, Sansom MSP. Proline-induced distortions of transmembrane helices. J Mol Biol. 2002;323:951–60. doi: 10.1016/s0022-2836(02)01006-9. [DOI] [PubMed] [Google Scholar]
- 54.Smart OS, Goodfellow JM, Wallace BA. The Pore Dimensions of Gramicidin A. Biophys J. 1993;65:2455–2460. doi: 10.1016/S0006-3495(93)81293-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Michaud-Agrawal N. http://code.google.com/p/mdanalysis.
- 56.Ding S, Ingleby L, Ahern CA, Horn R. Investigating the putative glycine hinge in Shaker potassium channel. J Gen Physiol. 2005;126:213–226. doi: 10.1085/jgp.200509287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Yifrach O, MacKinnon R. Energetics of pore opening in a voltage-gated K+ channel. Cell. 2002;111:231–239. doi: 10.1016/s0092-8674(02)01013-9. [DOI] [PubMed] [Google Scholar]
- 58.Holyoake J, Domene C, Bright JN, Sansom MSP. KcsA closed and open: modelling and simulation studies. Eur Biophys J. 2004;33:238–246. doi: 10.1007/s00249-003-0355-2. [DOI] [PubMed] [Google Scholar]
- 59.Bright JN, Sansom MSP. Kv channel S6 helix as a molecular switch: simulation studies. IEE Proc Nanobiotechnol. 2004;151:17–27. doi: 10.1049/ip-nbt:20040101. [DOI] [PubMed] [Google Scholar]
- 60.Perozo E, Cortes DM, Cuello LG. Structural rearrangements underlying K+-channel activation gating. Science. 1999;285:73–78. doi: 10.1126/science.285.5424.73. [DOI] [PubMed] [Google Scholar]
- 61.Espinosa F, Fleischhauer R, McMahon A, Joho RH. Dynamic interaction of S5 and S6 during voltage-controlled gating in a potassium channel. J Gen Physiol. 2001;118:157–170. doi: 10.1085/jgp.118.2.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Labro AJ, Raes AL, Grottesi G, Hoorick D, Sansom MSP, Snyders DJ. Kv channel gating requires a compatible S4-S5 linker and bottom part of S6, constrained by non-interacting residues. J Gen Physiol. 2008;132:667–680. doi: 10.1085/jgp.200810048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hackos D, Chang T, Swartz K. Scanning the intracellular S6 activation gate in the shaker K+ channel. J Gen Physiol. 2002;119:521–531. doi: 10.1085/jgp.20028569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Labro AJ, Grottesi A, Sansom MSP, Raes AL, Snyders DJ. A Kv channel with an altered activation gate sequence displays both “fast” and “slow” activation kinetics. AJP: Cell Physiol. 2008;294:C1476–C1484. doi: 10.1152/ajpcell.00479.2007. [DOI] [PubMed] [Google Scholar]
- 65.Shimizu H, Iwamoto M, Konno T, Nihei A, Sasaki YC, Oik S. Global Twisting Motion of Single Molecular KcsA Potassium Channel upon Gating. Cell. 2008;132:67–78. doi: 10.1016/j.cell.2007.11.040. [DOI] [PubMed] [Google Scholar]
- 66.Huang H, Ozkirimli E, Post CB. Comparison of Three Perturbation Molecular Dynamics Methods for Modeling Conformational Transitions. J Chem Theory and Comp. 2009;5:1304–1314. doi: 10.1021/ct9000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Beckstein O, Denning EJ, Perilla JR, Woolf TB. Zipping and Unzipping of Adenylate Kinase: Atomistic Insights into the Ensemble of Open ↔ Closed Transitions. J Mol Bio. 2009 doi: 10.1016/j.jmb.2009.09.009. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Ho BK, Agard DA. Probing the Flexibility of Large Conformational Changes in Protein Structures through Local Perturbations. PLoS Comp Bio. 2009;5:1–13. doi: 10.1371/journal.pcbi.1000343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Liu Y, Joho RH. A side chain in S6 influences both open-state stability and ion permeation in a voltage-gated K+ channel. Eur J Physiol. 1998;435:654–661. doi: 10.1007/s004240050566. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.