Abstract
Purpose
Small field-of-view (FOV) dedicated cardiac SPECT systems suffer from truncated projection data. This results in (1) neglect of liver activity that otherwise could be used to estimate (and subsequently correct) the amount of scatter in the myocardium by model-based scatter correction, and (2) distorted attenuation maps. In this study, we investigated to what extent truncation impacts attenuation correction and model-based scatter correction in the cases of 99mTc, 201Tl, and simultaneous 99mTc/201Tl studies. In addition, we evaluated a simple correction method to mitigate the effects of truncation.
Methods
Digital thorax phantoms of different sizes were used to simulate the full FOV SPECT projections for 99mTc, 201Tl, and simultaneous 99mTc/201Tl studies. Small FOV projections were obtained by artificially truncating the full FOV projections. Deviations from ideal heart positioning were simulated by axially shifting projections resulting in more severe liver truncation. Effects of truncation on SPECT images were tested for ordered subset (OS) expectation maximization reconstruction with (1) attenuation correction and detector response modelling (OS-AD), and (2) with additional Monte-Carlo-based scatter correction (OS-ADS). To correct truncation-induced artefacts, we axially extended truncated projections on both sides by duplicating pixel values on the projection edge.
Results
For both 99mTc and 201Tl, differences in the reconstructed myocardium between full FOV and small FOV projections were negligible. In the nine myocardial segments, the maximum deviations of the average pixel values were 1.3% for OS-AD and 3.5% for OS-ADS. For the simultaneous 99mTc/201Tl studies, reconstructed 201Tl SPECT images from full FOV and small FOV projections showed clearly different image profiles due to truncation. The maximum deviation in defected segments was found to be 49% in the worst-case scenario. However, artificially extending projections reduced deviations in defected segments to a few percent.
Conclusion
Our results indicate that, for single isotope studies, using small FOV systems has little impact on attenuation correction and model-based scatter correction. For simultaneous 99mTc/201Tl studies, artificial projection extension almost fully eliminates the adverse effects of projection truncation.
Keywords: Cardiac SPECT, Truncation, Attenuation correction, Scatter correction, Small field-of-view
Introduction
Myocardial SPECT imaging plays a central role in diagnosing coronary heart diseases [1]. In the United States alone, nine million cardiac SPECT studies are performed every year [2]. Currently, many small field-of-view (FOV) dedicated cardiac SPECT systems (SF-SPECT) are being used worldwide. Specifically optimized for the workflow of cardiac studies, the compact SF-SPECT systems can be more cost effective and time efficient than general purpose systems.
Truncated projections are frequently found while using SF-SPECT due to the smaller FOV (about lateral 36 cm and axial 20 cm) compared with the full FOV systems (about lateral 50 cm and axial 38 cm). In general, truncation led to deterioration of the reconstructed images in two ways: (1) lateral projection truncation of transmission data may generate artefacts and distortions in attenuation maps, thus compromising the accuracy of attenuation correction, and (2) the smaller axial dimension of the FOV causes liver truncation since the liver is projected onto the edges of the camera. Missing liver tissue projection can negatively affect model-based scatter correction methods [3–9] because these methods rely on full projections that include the surrounding activity of the heart, especially the liver, in order to accurately estimate the amount of scatter compensation needed in the myocardium.
Several studies [10–13] have shown that truncation of the attenuation map may have little impact on accurate attenuation correction for the heart. One study has shown that the impact of truncation only becomes noticeable when the lateral dimension of the detector is smaller than 60% of the lateral width of the patient’s thorax [10], which rarely happens for the available small FOV systems. The magnitude of the effect of the axial truncation of the liver on the accuracy of scatter correction still needs to be determined. Several studies have shown that scatter has to be corrected to achieve optimal clinical SPECT images [14–17]. For 99mTc and 201Tl studies, model-based scatter correction has beneficial properties compared to the more widely applied window-based correction, e.g. in terms of lesion contrast, quantitative accuracy and noise control [8, 18–20]. Model-based scatter correction calculates the scatter projections by modelling the physics of photon transport during iterative image reconstruction. It employs the actual iteration of reconstructed activity and the attenuation map for scatter calculation. Therefore, if liver tissue that contributes to scatter in the myocardium is truncated in the projection data, the accuracy of model-based scatter correction is compromised.
In addition to single-isotope SPECT, model-based scatter correction has shown promise for accurately correcting down-scatter in simultaneous 99mTc/201Tl cardiac SPECT [3, 4, 21]. Substantial clinical advantages may be realized by simultaneous 99mTc/201Tl SPECT as compared with separated stress and rest cardiac SPECT, e.g. perfect registration between stress and rest studies, increased patient comfort and doubled patient throughput. However, in simultaneous 99mTc/201Tl dual isotope imaging, model-based scatter correction is even more prone to projection truncation than in single isotope imaging, since down-scatter photons from the liver may severely affect the estimation of 201Tl distribution in the myocardium.
The aim of the present study was to investigate the effects of projection truncation on attenuation correction and model-based scatter correction for 99mTc, 201Tl, and simultaneous 99mTc/201Tl cardiac SPECT, as well as the effectiveness of a simple truncation correction method.
Materials and methods
Phantoms and projection simulation
The dynamic NCAT phantom [22–24] was used for this study. It provides a realistic and flexible model of the human anatomy and physiology, including cardiac motion. The severity of truncation is influenced by thorax size, heart size, and the axial heart position on the projection. In a survey conducted by Chang et al. [25], an average lateral thorax width of 36 cm with a standard deviation of 3 cm was found. To evaluate the effect of truncation for normal sized and large patient thoraxes, two thorax phantoms were generated by scaling the NCAT phantom to lateral widths of 36 cm and 42 cm [26] (see Table 1). Since many patients with myocardial infarction have severe left ventricle (LV) dilatation [27], the effect of heart size on truncation was also investigated in this study. To obtain a realistic estimate of heart size, we investigated a group of 64 consecutive patients who came to the St. Antonius Hospital in Nieuwegein for myocardial SPECT imaging. We measured the number of transverse slices containing the LV in their reconstructed SPECT images. The average heart dimension between the top-most and bottom-most transverse slices was found to be 9.1 cm with a standard deviation of 0.8 cm. Based on these results, two heart phantoms of different sizes were generated: one normal sized heart of 9.1 cm, and one large heart of 10.7 cm (mean+2SD). In total, four combinations of different sized thorax and heart phantoms were used to represent different patient anatomies (see Table 1).
Table 1.
Variations used to generate different patient anatomies and to axially shift projections. The combination of a large thorax and off-centre projection results in the worst truncation scenario
| Thorax size (cm) | Heart dimension (cm) | Axial heart shift (cm) | |
|---|---|---|---|
| Variation 1 (normal) | 36 (mean) | 9.1 (mean) | 0 |
| Variation 2 (large) | 42 (mean+2SD) | 10.7 (mean+2SD) | 1.9 (mean+2SD) |
In clinical practice, the heart contour is sometimes difficult to be determined at the persistence screen, due to relatively low counts in SPECT projections. Therefore, it may be hard to position the heart exactly at the centre of the projection. This mispositioning can be important for the accuracy of model-based scatter correction if the heart is projected below the projection centre so that a substantial area of liver is missing. To examine this effect, we measured the axial shift between the centre of the LV and the centre of the SPECT projection for the same group of 64 patients. An average axial shift of −0.9 cm (+ shift towards the patient’s head, more severe liver truncation; − shift towards the patient’s feet, less liver truncation) with a standard deviation of 1.4, cm was found. To study the effect of mispositioning, we shifted the simulated projections towards the patient’s head by 1.9 cm (mean+2SD; see Table 1).
Among all the phantom configurations investigated, those with a large thorax and off-centre projection had a larger area of active liver tissue missing in the truncated projections. Therefore, scatter from active liver tissue into the myocardium will be more severely underestimated by model-based scatter correction. Moreover, a larger thorax induces a more severe attenuation effect. Thus, the myocardium in the large-thorax phantom and with shifted projection would be expected to suffer the most from projection truncation and could be regarded as the worst-case scenario.
The selected heart:liver:lung:background relative activity concentration ratios were 75:75:4:2 for 99mTc and 43:19:1:2 for 201Tl. These reflect typical distributions encountered in clinical studies [21, 28]. The activities in the myocardium were set based on 1.1% uptake for 925 MBq 99mTc and 3% uptake for 148 MBq 201Tl [29, 30]. Because the basal part of the inferior and septal wall is known to be most likely affected by the artefacts of attenuation and scatter, a perfusion defect (6 ml) was placed in the basal part of the inferior and septal wall to study the effect of truncation.
We simulated a noncircular camera orbit in which the detectors rotate along an elliptical orbit. Most SF-SPECT systems use this type of orbit in order to align the camera heads closer to the patient contour than is possible with a circular orbit. As a result, the image resolution and uniformity are improved [31]. An elliptical orbit also reduces lateral projection truncation since a larger portion of the thorax can be included in the FOV than with a circular orbit for the relative 90° dual-headed systems.
Projection data were computed using a Monte Carlo simulator that rapidly and realistically models the effects of attenuation, collimator-detector response, and scatter [5]. This simulator has been carefully validated for 99mTc, 201Tl, and simultaneous 99mTc/201Tl studies [4, 18, 28]. With this simulator, 107 photon paths were generated which included a maximum of ten orders of Compton scatter. The simulation modelled data acquisition for a dual-head SPECT camera with a FOV of 50.8×38.1 cm and low-energy high-resolution collimators (hole length 30 mm, and diameter 1.4 mm). A 180° noncircular study for simultaneous transmission and emission scans was simulated with 64 projections for 99mTc, 201Tl, and simultaneous 99mTc/201Tl studies. In this way, the transmission scans and emission data can be assumed to be acquired simultaneously. The acquisition matrix was 128×128 pixels with a pixel size of 3.26 mm. For 99mTc a photopeak window of 140 keV ±10% was used. For 201Tl the lower and higher 201Tl photopeak window (72 keV +10% and 167 keV +10%) were used. Downs-scatter contaminated projections mimicking simultaneous 99mTc/201Tl studies were obtained by adding the down-scattered 99mTc projections in the lower 201Tl energy window (72 keV ±10%) to the simulated 201Tl projections. For all three studies, transmission projection data were simulated in a 20% wide energy window centred at 100 keV. The amount of 99mTc uptake in the myocardium is 2.3 times that of 201Tl, and the abundance of the 167 keV 201Tl peak is only 10%. Thus, the down-scatter of the 201Tl photons in the 99mTc image is less than a few percent and its impact was neglected.
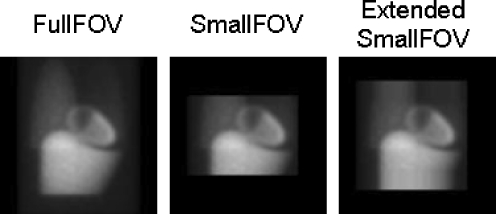
The small FOV projection data were simulated from the data of the full FOV SPECT by setting the pixels outside the small FOV to zero. With the use of the noncircular orbit information to track the corner of the two full FOV camera heads, the emission and transmission projections were truncated from the side opposite the corner (Fig. 1) to exactly model the acquisition of the widely used small FOV Philips CardioMD system (36.0×20.4 cm). This detector size is very similar to that of the other widely used small FOV systems, e.g. Siemens c.cam (36.0×20.4 cm) and GE Ventri (37.0×19.0 cm).
Fig. 1.
Projection of full FOV system, truncated projection of small FOV system, and axially extended small FOV projection
Image reconstruction and assessment
For the 99mTc and 201Tl studies, ordered subset expectation maximization (OS-EM) [32] image reconstruction algorithms with two different types of photon transport modelling were compared. For both methods, we used precalculated point spread function tables that describe the gaussian distance-dependent detector response of a point source in air. The full-width at half-maximum (FWHM) of the gaussian kernels was calculated on the basis of geometric collimator resolution and intrinsic detector resolution [5]. In the OS-AD method, nonuniform attenuation correction (A) and detector response modelling (D) were incorporated into the OS-EM method. Attenuation maps were used to perform nonuniform attenuation correction. The OS-ADS method, fully 3-D Monte Carlo-based reconstruction, was performed using dual matrix OS-EM [6]. Attenuation and detector blurring were modelled in both forward and backward projections. Monte Carlo simulation was, however, used only during the calculation of the forward projection [7]. The Monte Carlo simulator was accelerated using convolution-based forced detection [5], with which 105 photon paths per subset were found to be sufficient for reconstructions of cardiac perfusion studies [33]. Seven orders of Compton scatter were generated.
For the simultaneous 99mTc/201Tl studies, the 99mTc study was reconstructed with the OS-ADS method in the same way as the separated 99mTc studies. Then, down-scatter projections were calculated based on the reconstructed 99mTc image and the attenuation map. The simulation of down-scatter was based on 107 photon paths calculated including ten orders of Compton scatter [4]. The 201Tl images were reconstructed with the OS-ADS method in the same way as the separated 201Tl studies but with the addition of the simulated down-scatter projections to the denominator of the dual matrix OS-EM algorithm.
Previous studies have shown that the use of over-iteration followed by postfiltering can lead to better results than early stopping of the iteration process [34, 35]. Therefore, for the OS-AD and OS-ADS algorithms, a relatively high number of iterations (30) with eight subsets were performed. This procedure was followed by 3-D postfiltering with a gaussian filter kernel (FWHM, three pixels).
Attenuation maps were reconstructed using the ordered-subset convex algorithm [36] with eight subsets and 30 iterations. To reduce noise, the attenuation maps were filtered using a 3-D gaussian kernel (FWHM, 2.5 pixels). Then, median filtering was applied twice using a 3-D cubic kernel of 5×5×5 pixels. The accuracy of this transmission reconstruction algorithm has been carefully validated [36].
Effects of lead X-ray contamination were neglected during simulation of down-scatter projections and in modelling during reconstruction. Dual-isotope studies by de Jong et al. [4] have shown that image profiles are only marginally different (a couple of percent) between those including and those not including the lead X-ray in the simulation. Another study by de Jong et al. [9] also confirms that lead X-ray contamination is an order of magnitude less in intensity than down-scatter of 99mTc in the 72 keV window. We therefore ignored this effect during simulation.
We compared image profiles through the inferior perfusion defect in the short-axis view images between the full FOV and small FOV data. For a more global and quantitative analysis, bull’s-eyes (polar maps) were constructed from short-axis images by sampling the maximum counts in the myocardial wall. The anterior, lateral, inferior and septal walls of the myocardium were sampled cylindrically, and the apex was sampled spherically [1, 37]. The bull’s-eye was divided into nine segments: apex, anterior mid, anterior basal, lateral mid, lateral basal, inferior mid, inferior basal, septal mid, and septal basal. For each segment, the average pixel value in the bull’s eye image was calculated. To investigate the effect of truncation, the deviation in percentage between the full FOV and small FOV data was calculated for each segment. The deviation in percentage was defined as:
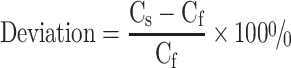 |
1 |
where Cs is the average pixel value of a certain segment in the small FOV data and Cf is the average pixel value of a certain segment in the full FOV data.
Truncation compensation
For simultaneous 99mTc/201Tl studies, the down-scatter of 99mTc has a wide extent. A study with a 99mTc point source in the centre of a water-filled cylinder phantom with radius of 11.1 cm has shown that the FWHM of the down-scatter response is 8 cm [9]. The radius represents an average depth of the heart in the human thorax. The liver truncation usually is only a couple of centimetres away from the inferior wall of the myocardium. Therefore, this truncation can have an adverse influence on down-scatter modelling of the myocardium.
Given the distance between the missing liver tissue and the myocardium, the down-scatter response has a very smooth profile. A coarse correction method for the truncated liver could be sufficient to remedy the down-scatter estimate. This method may not need to recover the exact contour of the missing part of liver but only provide a rough estimate of the amount of scatter from the missing liver tissue. Therefore, we propose a simple correction method that axially extends the small FOV projections by several centimetres on both sides by simply duplicating the boundary projection pixels, as shown in Fig. 1. To investigate how large the axial extension should be, the small FOV was extended by 4, 8 and 12 cm, which were respectively 0.5, 1 and 1.5 times FWHM of the down-scatter response. We calculated the deviation in each segment between the full FOV data and the extended small FOV data using Eq. 1, with Cs as the average pixel value of a certain segment in the extended small FOV data.
Results
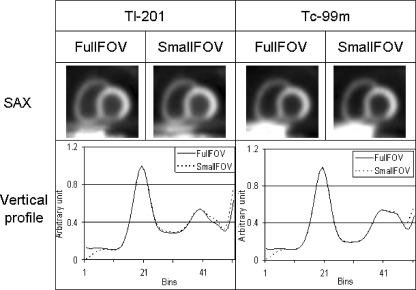
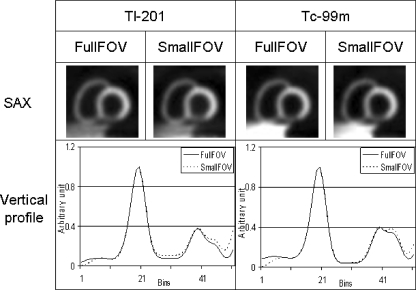
For OS-AD, Fig. 2 shows short-axis views of a large myocardium in the worst-case scenario. Vertical profiles through the perfusion defect in the inferior wall show little difference in the reconstructed myocardium between the full FOV and small FOV data, both for 99mTc and 201Tl. As shown in Table 2, within the nine myocardial segments, the greatest deviations were 1.3% for 201Tl and 0.95% for 99mTc. Less-severe deviations were found for the smaller phantom and with a centrally positioned heart. The deviations caused by projection truncation can be regarded as marginal and should not affect diagnosis. For OS-ADS, little difference was also shown between the full FOV and small FOV data (Fig. 3). The greatest deviations (Table 2) were 3.5% for 201Tl and 2.9% for 99mTc. Only very small deviations were found for smaller thorax phantoms. In all cases, the deviations seemed to be too limited to influence the outcome of clinical diagnosis. Therefore, we can conclude that the missing liver tissue has little impact on the accuracy of both OS-AD and OS-ADS, both for 99mTc and 201Tl. As shown in Table 2, deviations in the myocardium were marginally larger with OS-ADS than with OS-AD. In this study, the truncation was only present on the reverse side of the thorax and it was far from the heart even for the worst-case scenario. The cupping artefact due to truncation in the emission data therefore has minimal impact on the myocardium.
Fig. 2.
OS-AD method. Top: Short-axis (SAX) views based on full FOV and small FOV projections for the worst-case scenario. Bottom: Vertical profiles through the inferior defect
Table 2.
Deviations between full FOV data and small FOV data in each of the nine myocardial segments calculated for the worst-case scenario, for the OS-AD and OS-ADS methods
| Segment | Deviation (%) | |||
|---|---|---|---|---|
| OS-AD | OS-ADS | |||
| 201Tl | 99mTc | 201Tl | 99mTc | |
| Total | 0.18 | 0.098 | 0.016 | −1.1 |
| Apex | 0.10 | 0.024 | 0.23 | −2.4 |
| Anterior mid | −0.48 | −0.015 | 0.20 | −1.1 |
| Anterior basal | 0.53 | 0.20 | 0.022 | 2.4 |
| Lateral mid | 0.46 | −0.011 | −2.3 | −1.9 |
| Lateral basal | 0.81 | 0.88 | 0.63 | 2.8 |
| Inferior mid | 0.17 | 0.030 | −0.65 | 0.87 |
| Inferior basala | 1.3 | 0.89 | 3.3 | 2.9 |
| Septal mid | −0.68 | −0.95 | −0.23 | −2.0 |
| Septal basala | 0.92 | 0.025 | 3.5 | −1.4 |
aSegments containing perfusion defect.
Fig. 3.
OS-ADS method. Top: Short-axis (SAX) views based on full FOV and small FOV projections for the worst-case scenario. Bottom: Vertical profiles through the inferior defect
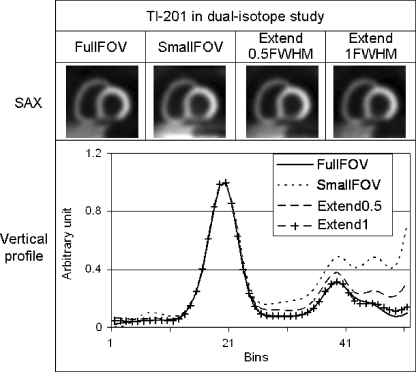
For simultaneous 99mTc/201Tl imaging, vertical profiles in the short-axis views in Fig. 4, reconstructed with the OS-ADS method, clearly show that truncation of the liver tissue with the small FOV systems led to deterioration of the lesion contrast in the worst-case scenario. Axial extension of the small FOV by half FWHM led to partial recovery of lesion contrast and extension by one FWHM resulted in almost the same lesion contrast as provided by the full FOV data. A quantitative comparison for each myocardial segment is shown in Table 3. Extending the small FOV by one FWHM decreased the deviations in the basal part of the inferior and septal walls containing the defect from 49% to 1.8% and from 23% to 1.4%, respectively. The deviations were also calculated for the normal sized NCAT phantom with a normal sized heart and nonshifted projection. Extension by one FWHM was a good correction in this case too. Table 4 shows activity deviations in the myocardial segments containing a perfusion defect and illustrates the effect of truncation and the effectiveness of axial projection extension in correcting the deviations in all the scenarios. As shown in Table 4, artificial projection extension almost fully eliminated the adverse effects of projection truncation.
Fig. 4.
201Tl images in a simultaneous 99mTc/201Tl study, reconstructed with the OS-ADS method. Top: Short-axis (SAX) views based on full FOV, small FOV, and extended small FOV projections for the worst-case scenario. Bottom: Vertical profiles through the inferior defect
Table 3.
OS-ADS method. Deviations among the full FOV, small FOV, and extended small FOV data in each of the nine myocardial segments calculated for the worst-case scenario of simultaneous 99mTc/201Tl SPECT
| Segment | Deviation (%) | |||
|---|---|---|---|---|
| Small FOV | Extended by 0.5 FWHM | Extended by 1 FWHM | Extended by 1.5 FWHM | |
| Total | 7.8 | 3.0 | 0.75 | −0.43 |
| Apex | 6.8 | 2.5 | 0.68 | 0.10 |
| Anterior mid | 2.0 | −0.40 | −1.2 | −1.3 |
| Anterior basal | 10 | 3.8 | 2.6 | 2.9 |
| Lateral mid | 6.2 | 3.0 | 1.4 | 0.023 |
| Lateral basal | 7.8 | 4.1 | 2.2 | −0.65 |
| Inferior mid | 7.9 | 2.2 | −0.68 | −1.2 |
| Inferior basala | 49 | 15 | 1.8 | −1.4 |
| Septal mid | 4.0 | 0.72 | −1.7 | −2.1 |
| Septal basala | 23 | 5.5 | 1.4 | −1.0 |
aSegments containing perfusion defect.
Table 4.
OS-ADS method. Deviations in segments containing the perfusion defect for all eight scenarios
| Scenario | Deviation (%) | |||
|---|---|---|---|---|
| Inferior basal | Septal basal | |||
| Small FOV | Extended by 1 FWHM | Small FOV | Extended by 1 FWHM | |
| Normal | 22 | 1.3 | 15 | 0.91 |
| Large thorax | 45 | 2.5 | 21 | −0.52 |
| Large heart | 18 | −2.1 | 9.6 | −0.28 |
| Axial heart shift | 34 | −0.78 | 18 | 1.1 |
| Large thorax and large heart | 42 | 1.5 | 24 | −1.9 |
| Large thorax and axial heart shift | 47 | 2.2 | 25 | 0.87 |
| Large heart and axial heart shift | 36 | 1.4 | 22 | 1.6 |
| Large thorax and large heart and axial heart shift | 49 | 1.8 | 23 | 1.4 |
Discussion
In this study, the impact of truncation on SF-SPECT was investigated by comparing full FOV and small FOV data for 99mTc, 201Tl, and simultaneous 99mTc/201Tl studies. For 99mTc and 201Tl single-isotope studies, little difference between the full FOV and small FOV data was found in the reconstructed myocardium. For simultaneous 99mTc/201Tl studies, truncation of the liver tissue had a strong impact on the tracer distribution in the reconstructed myocardium and led to significant deterioration of lesion contrast. After axially extending the small FOV by one FWHM of the down-scatter response, this truncation artefact was almost completely eliminated.
The projection extension method tested is a simple but adequate method to estimate down-scatter of the 99mTc photons originating from the liver. In the eight scenarios studied, extension by one FWHM almost completely eliminated the truncation effect and therefore can be called a robust correction method. Our simulation study indicated that the amount of axial projection extension required may not be necessarily specific to each individual scenario. Given the distance between the missing liver tissue and the myocardium, the down-scatter response had a very smooth profile. Therefore, a coarse correction method of axially extending the small FOV by one FWHM was sufficient to estimate the amount of scatter from the missing liver tissue reliably.
To correct for down-scatter from the liver in dual isotope studies, the model-based correction method proposed in this paper needs some liver activity to be included in the FOV. We checked all the projections for the 64 patients and shifted the projections to simulate the worst off-centre positioning scenario investigated in this study, i.e. axially shifting the liver towards outside the FOV by 1.9 cm (mean+2SD, see Table 1). For all these cases, there is still a considerable amount of liver included in the FOV. Therefore, the liver might be missed only in very rare cases. Nevertheless, requiring liver activity in the FOV remains a potential weakness of this method.
This simple truncation correction method was designed for a 3-D model-based approach and not for a less-advanced approach, e.g. no scatter correction or a triple-energy window method. Our results indicate that truncation correction induced by SF-SPECT is only necessary for simultaneous 99mTc/201Tl studies. For such studies, 3-D model-based scatter correction is very much preferred over a less-advanced approach due to down-scatter from the liver. This simple correction method may be useful in such cases. For single isotope studies, SF-SPECT does not need our correction method for either 3-D or 2-D reconstruction approaches.
The literature is somewhat mixed as to the effect of attenuation map truncation on myocardial SPECT images. Several studies [10–13] have found that truncation of the attenuation map may have little impact on accurate attenuation correction for the heart. However, the impact of truncation may become noticeable when the lateral dimension of the detector is smaller than 60% of the lateral width of the patient’s thorax [10]. Chen et al. [38] also found that truncation can only have a sizeable impact when it is so severe that it affects the left side of the patient. The study by Celler et al. [39] showed two types of truncation may produce false-positive defects in the myocardium, namely incomplete rotation in an asymmetric fan-beam system and suboptimal positioning of the patient in a Profile transmission system. Most small FOV systems use parallel beams and therefore they are not subject to the incomplete rotation problem. Most small FOV systems, including the CardioMD system which we studied here, have a scanning line transmission system and do not have the mispositioning problem of the Profile system. Nevertheless we fully agree with Celler et al. that strict quality control and an appropriate testing protocol is needed for both Profile and scanning line systems.
Conclusion
Our results indicate that, for 201Tl and 99mTc studies, projection truncation associated with SF-SPECT has no serious impact on attenuation correction and model-based scatter correction. Although truncation has an effect in simultaneous 99mTc/201Tl studies, a simple digital extension of projection images almost fully eliminates the degrading effects of truncation. This study indicated that SF-SPECT may achieve image quality similar to that achieved by full field-of-view SPECT, even for simultaneous 99mTc/201Tl imaging.
Acknowledgments
This research was supported by research grants from Philips Medical Systems and the Medical Council of the Dutch Organization for Scientific Research (grant 917.36.335).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- 1.de Puey EG, Garcia EV, Berman DS. Cardiac SPECT imaging. 2. Philadelphia: Lippincott Williams and Wilkins; 2001. [Google Scholar]
- 2.Ballok ZE. Nuclear cardiology. Heart Lung Circ. 2005;14(Suppl 2):S27–S30. doi: 10.1016/j.hlc.2005.08.012. [DOI] [PubMed] [Google Scholar]
- 3.Kadrmas DJ, Frey EC, Tsui BMW. Simultaneous technetium-99m/thallium-201 SPECT imaging with model-based compensation for cross-contaminating effects. Phys Med Biol. 1999;44:1843–1860. doi: 10.1088/0031-9155/44/7/319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.de Jong HW, Beekman FJ, Viergever MA, van Rijk PP. Simultaneous Tc-99m/Tl-201 dual-isotopeTc-99m/Tl-201 SPET with Monte Carlo-based down-scatter correction. Eur J Nucl Med. 2002;29:1063–1071. doi: 10.1007/s00259-002-0834-1. [DOI] [PubMed] [Google Scholar]
- 5.De Jong HW, Slijpen ET, Beekman FJ. Acceleration of Monte Carlo SPECT simulation using convolution-based forced detection. IEEE Trans Nucl Sci. 2001;48:58–64. doi: 10.1109/23.910833. [DOI] [Google Scholar]
- 6.Kadrmas DJ, Frey EC, Karimi SS, Tsui BM. Fast implementations of reconstruction-based scatter compensation in fully 3D SPECT image reconstruction. Phys Med Biol. 1998;43:857–873. doi: 10.1088/0031-9155/43/4/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Beekman FJ, De Jong HW, van Geloven S. Efficient fully 3-D iterative SPECT reconstruction with Monte Carlo-based scatter compensation. IEEE Trans Med Imaging. 2002;21:867–877. doi: 10.1109/TMI.2002.803130. [DOI] [PubMed] [Google Scholar]
- 8.Kadrmas DJ, Frey EC, Tsui BM. Application of reconstruction-based scatter compensation to thallium-201 SPECT: implementations for reduced reconstructed image noise. IEEE Trans Med Imaging. 1998;17:325–333. doi: 10.1109/42.712122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.de Jong HW, Wang WT, Frey EC, Viergever MA, Beekman FJ. Efficient simulation of SPECT down-scatter including photon interactions with crystal and lead. Med Phys. 2002;29:550–560. doi: 10.1118/1.1462638. [DOI] [PubMed] [Google Scholar]
- 10.Gregoriou GK, Tsui BM, Gullberg GT. Effect of truncated projections on defect detection in attenuation-compensated fanbeam cardiac SPECT. J Nucl Med. 1998;39:166–175. [PubMed] [Google Scholar]
- 11.Gullberg GT, Morgan HT, Zeng GL, Christian PE, Di Bella EV, Tung CH, et al. The design and performance of a simultaneous transmission and emission tomography system. IEEE Trans Nucl Sci. 1998;45:1676–1698. doi: 10.1109/23.685291. [DOI] [Google Scholar]
- 12.Tung CH, Gullberg GT, Zeng GL, Christian PE, Datz FL, Morgan HT. Nonuniform attenuation correction using simultaneous transmission and emission converging tomography. IEEE Trans Nucl Sci. 1992;39:1134–1143. doi: 10.1109/23.159773. [DOI] [Google Scholar]
- 13.Manglos SH, Gagne GM, Bassano DA. Quantitative analysis of image truncation in focal-beam CT. Phys Med Biol. 1993;38:1443–1457. doi: 10.1088/0031-9155/38/10/006. [DOI] [Google Scholar]
- 14.Hendel RC, Berman DS, Cullom SJ, Follansbee W, Heller GV, Kiat H, et al. Multicenter clinical trial to evaluate the efficacy of correction for photon attenuation and scatter in SPECT myocardial perfusion imaging. Circulation. 1999;99:2742–2749. doi: 10.1161/01.cir.99.21.2742. [DOI] [PubMed] [Google Scholar]
- 15.Tsui BM, Frey EC, LaCroix KJ, Lalush DS, McCartney WH, King MA, et al. Quantitative myocardial perfusion SPECT. J Nucl Cardiol. 1998;5:507–522. doi: 10.1016/S1071-3581(98)90182-9. [DOI] [PubMed] [Google Scholar]
- 16.Iida H, Shoji Y, Sugawara S, Kinoshita T, Tamura Y, Narita Y, et al. Design and experimental validation of a quantitative myocardial Tl-201 SPECT system. IEEE Trans Nucl Sci. 1999;46:720–726. doi: 10.1109/23.775605. [DOI] [Google Scholar]
- 17.Narayanan MV, King MA, Pretorius PH, Dahlberg ST, Spencer F, Simon E, et al. Human-observer receiver-operating-characteristic evaluation of attenuation, scatter, and resolution compensation strategies for (99m)Tc myocardial perfusion imaging. J Nucl Med. 2003;44:1725–1734. [PubMed] [Google Scholar]
- 18.Xiao J, de Wit TC, Staelens S, Beekman FJ. Evaluation of 3D Monte-Carlo based scatter correction for Tc-99m cardiac perfusion SPECT. J Nucl Med. 2006;47:1662–1669. [PubMed] [Google Scholar]
- 19.Gur YS, Farncombe TH, Pretorius PH, Gifford HC, Narayanan MV, Frey EC, et al. Comparison of scatter compensation strategies for myocardial perfusion imaging using Tc-99m labeled sestamibi. IEEE Trans Nucl Sci. 2002;49:2309–2314. doi: 10.1109/TNS.2002.803859. [DOI] [Google Scholar]
- 20.Beekman FJ, Kamphuis C, Frey EC. Scatter compensation methods in 3D iterative SPECT reconstruction: a simulation study. Phys Med Biol. 1997;42:1619–1632. doi: 10.1088/0031-9155/42/8/011. [DOI] [PubMed] [Google Scholar]
- 21.Song X, Frey EC, Wang WT, Du Y, Tsui BM. Validation and evaluation of model-based crosstalk compensation method in simultaneous Tc-99m stress and Tl-201 rest myocardial perfusion SPECT. IEEE Trans Nucl Sci. 2004;51:72–79. doi: 10.1109/TNS.2003.823017. [DOI] [Google Scholar]
- 22.Segars WP, Lalush DS, Tsui BM. A realistic spline-based dynamic heart phantom. IEEE Trans Nucl Sci. 1999;46:503–506. doi: 10.1109/23.775570. [DOI] [Google Scholar]
- 23.Segars WP, Lalush DS, Tsui BMW. Modeling respiratory mechanics in the MCAT and spline-based MCAT phantoms. IEEE Trans Nucl Sci. 2001;48:89–97. doi: 10.1109/23.910837. [DOI] [Google Scholar]
- 24.Segars WP. Development of a new dynamic NURBS-based cardiac-torso (NCAT) phantom. PhD dissertation, The University of North Carolina, May 2001.
- 25.Chang W, Loncaric S, Huang G, Sanpitak P. Asymmetric fan transmission CT on SPECT systems. Phys Med Biol. 1995;40:913–28. doi: 10.1088/0031-9155/40/5/013. [DOI] [PubMed] [Google Scholar]
- 26.Lalush DS, Tsui BM. Performance of ordered-subset reconstruction algorithms under conditions of extreme attenuation and truncation in myocardial SPECT. J Nucl Med. 2000;41:737–744. [PubMed] [Google Scholar]
- 27.Cohn JN, Ferrari R, Sharpe N. Cardiac remodeling – concepts and clinical implications: a consensus paper from an international forum on cardiac remodeling. Behalf of an International Forum on Cardiac Remodeling. J Am Coll Cardiol. 2000;35:569–582. doi: 10.1016/S0735-1097(99)00630-0. [DOI] [PubMed] [Google Scholar]
- 28.Xiao J, de Wit TC, Zbijewski W, Staelens S, Beekman FJ. Evaluation of 3D Monte Carlo-based scatter correction for Tl-201 cardiac perfusion SPECT. J Nucl Med. 2007;48:637–644. doi: 10.2967/jnumed.106.037259. [DOI] [PubMed] [Google Scholar]
- 29.Berman DS, Kiat H, Train KV, Friedman JD, Wang FP, Germano G. Dual-isotope Tc-99m/Tl-201 myocardial perfusion SPECT with rest thallium-201 and stress Tc-99m sestamibi. Nucl Cardiol. 1994;12:261–270. [PubMed] [Google Scholar]
- 30.Lowe VJ, Greer KL, Hanson MW, Jaszczak RJ, Coleman RE. Cardiac phantom evaluation of simultaneously acquired dual isotope rest thallium-201/stress technetium-99m SPECT. J Nucl Med. 1993;34:1998–2006. [PubMed] [Google Scholar]
- 31.Gottschalk SC, Salem D, Lim CB, Wake RH. SPECT resolution and uniformity improvements by noncircular orbit. J Nucl Med. 1983;24:822–828. [PubMed] [Google Scholar]
- 32.Hudson HM, Larkin RS. Accelerated image-reconstruction using ordered subsets of projection data. IEEE Trans Med Imaging. 1994;13:601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
- 33.De Wit TC, Xiao J, Beekman FJ. Monte Carlo-based statistical SPECT reconstruction: influence of number of photon tracks. IEEE Trans Nucl Sci. 2005;52:1365–1369. doi: 10.1109/TNS.2005.858220. [DOI] [Google Scholar]
- 34.Miller TR, Wallis JW. Clinically important characteristics of maximum-likelihood reconstruction. J Nucl Med. 1992;33:1678–1684. [PubMed] [Google Scholar]
- 35.Beekman FJ, Slijpen ET, Niessen WJ. Selection of task-dependent diffusion filters for the post-processing of SPECT images. Phys Med Biol. 1998;43:1713–1730. doi: 10.1088/0031-9155/43/6/024. [DOI] [PubMed] [Google Scholar]
- 36.Kamphuis C, Beekman FJ. Accelerated iterative transmission CT reconstruction using an ordered subsets convex algorithm. IEEE Trans Med Imaging. 1998;17:1101–1105. doi: 10.1109/42.746730. [DOI] [PubMed] [Google Scholar]
- 37.Germano G, Kavanagh PB, Waechter P, Areeda J, Van Kriekinge S, Sharir T, et al. A new algorithm for the quantitation of myocardial perfusion SPECT. I: technical principles and reproducibility. J Nucl Med. 2000;41:712–719. [PubMed] [Google Scholar]
- 38.Chen J, Galt JR, et al. Transmission scan truncation with small-field-of-view dedicated cardiac SPECT systems: impact and automated quality control. J Nucl Cardiol. 2005;12:567–573. doi: 10.1016/j.nuclcard.2005.04.013. [DOI] [PubMed] [Google Scholar]
- 39.Celler A, Dixon KL, Chang Z, Blinder S, Powe J, Harrop R. A new algorithm for the quantitation of myocardial perfusion SPECT. I: technical principles and reproducibility. J Nucl Med. 2000;46:335–343. [Google Scholar]