MIClique: An Algorithm to Identify Differentially Coexpressed Disease Gene Subset from Microarray Data

Abstract

Computational analysis of microarray data has provided an effective way to identify disease-related genes. Traditional disease gene selection methods from microarray data such as statistical test always focus on differentially expressed genes in different samples by individual gene prioritization. These traditional methods might miss differentially coexpressed (DCE) gene subsets because they ignore the interaction between genes. In this paper, MIClique algorithm is proposed to identify DEC gene subsets based on mutual information and clique analysis. Mutual information is used to measure the coexpression relationship between each pair of genes in two different kinds of samples. Clique analysis is a commonly used method in biological network, which generally represents biological module of similar function. By applying the MIClique algorithm to real gene expression data, some DEC gene subsets which correlated under one experimental condition but uncorrelated under another condition are detected from the graph of colon dataset and leukemia dataset.

1. Introduction

Microarray data may provide much useful information for disease gene identification and medical diagnosis because microarray has the ability to measure the expression levels of thousands of genes simultaneously [1]. Among the huge number of genes, only a small fraction of them show strong correlation with a certain phenotype. Many statistical and supervised methods such as t-test, neural network are utilized to mine genes that are differentially expressed under different conditions [2, 3]. However, these gene selection techniques are often based on individual gene prioritization by measuring the correlation of each gene with particular disease types. The individual gene prioritization list does not indicate interaction relationships among genes. So these traditional techniques might ignore the differentially coexpressed (DCE) gene subsets which are defined to be highly correlated under one experimental condition but uncorrelated under another condition [4]. Disease-related differentially coexpressed genes are those which exhibit similar expression patterns in normal samples but share no similarity in disease samples. Figure 1 depicts the simulated differentially coexpressed disease genes between normal samples (samples1–20) and disease samples (samples 21–40). The coexpression pattern in normal samples disappears in disease samples.

Figure 1.

Illustration of differentially coexpressed (DEC) disease gene subset between normal samples and disease samples. The left 20 samples are normal samples and the right 20 samples are disease samples.

Identification of disease specific DEC gene subsets is very helpful for disease diagnosis and clinical treatment. The DEC genes should be analyzed by gene subsets instead of individual genes. Clustering algorithms are often used to find gene groups which display similar expression profiles [5, 6]. However, the DEC genes only show highly correlated expression patterns in one biological state, not across the entire dataset. Biclustering is a method to identify gene subsets exhibiting consistent patterns over a subset of experimental conditions, but this method is still not proper for identification of DEC gene groups because the experimental conditions may not be in the same biological state [7, 8].

Kostka and Spang proposed the first method to investigate DEC gene subsets by using an additive model and a stochastic search algorithm [9]. AlteredExpression was an improved algorithm based on additive model to detect optimal DEC gene subsets with best RRV (ratio of residual variance between two different samples) and minimal F-score [10]. Varadan and Anastassiou proposed an approach called Entropy Minimization and Boolean Parsimony (EMBP) to identify gene subsets whose joint expression state predicts the presence or absence of a particular disease with minimum uncertainty [4]. The coXpress was developed to identify groups of gene that are differentially coexpressed in different biological states by using a resampling method to calculate t-value for each clustered group [11]. These methods took into account all possible gene subsets by searching the whole dataset; it was a huge computational burden as the number of genes increases.

In this paper, the MIClique algorithm is proposed to explore DEC gene subsets in an intuitive way based on mutual information (MI) and clique analysis. Mutual information is used to measure the coexpression relationship between each pair of genes in two different kinds of samples, and then the symmetric mutual information matrices are binarized by selecting two threshold values. The adjacency matrix of graph is obtained by logical operation with vertices corresponding to genes and edges corresponding to relationships between genes. Gene cliques detected by MIClique represent DEC gene subsets, which are highly correlated under one experimental condition but uncorrelated under another condition.

2. Materials and Methods

2.1. Mutual Information (MI)

The interaction relationships of genes are very complex, including linear and nonlinear. Compared with linear similarity measures such as Euclidean distance and Pearson correlation [12, 13], the mutual information is a general measure of statistical dependence between variables and capable of detecting any type of functional relationship, which is widely used in gene expression analysis [14]. For the application of MI on gene expression data, the continuous experimental data need to be partitioned into discrete intervals or bins [15]. Entropy and MI are two central concepts of Shannon's theory of information [16]. Table 1 describes the related concepts of MI.

Table 1.

Concepts of entropy and MI defined by Shannon's theory of information.

Concepts of Shannon's theory of information	Descriptions
$H(X)=-{\displaystyle \sum }_x^{}p(x){\log \hspace{0.17em}}_2\hspace{0.17em}p(x)$	The uncertainty of a random variable X is measured by its entropy H(X); p(x) is the probability density of X
$H(X\mid Y)=-{\displaystyle \sum }_x^{}p(x\mid y){\log \hspace{0.17em}}_2\hspace{0.17em}p(x\mid y)$	The uncertainty of a random variably X given knowledge of another random variable Y is measured by the conditional entropy H(X ∣ Y)
$H(X,Y)=-{\displaystyle \sum }_x^{}{\displaystyle \sum }_y^{}p(x,y)\text{lo}{\text{g}}_{2}p(x,y)$	The uncertainty of a pair of random variables X, Y is measured by the entropy H(X ∣ Y)
H(X, Y) = H(X) + H(Y ∣ X) = H(Y) + H(X ∣ Y)
$\text{MI}(X;Y)={\displaystyle \sum }_x^{}{\displaystyle \sum }_y^{}p(x,y)\text{lo}{\text{g}}_2\frac{p(x,y)}{p(x)p(y)}$	Given two random variables X and Y, the amount of information that each one of them provides about the other is the mutual information MI(X; Y)
MI(X; Y) = H(X) + H(Y) − H(X, Y)

The physical meaning of MI(X; Y) is the reduction of the uncertainty of X due to knowledge of Y (or vice versa). Note that H(X) = I(X; X), and so entropy is the self-information. The nonnegative MI(X; Y) equals zero if and only if X and Y are statistically independent, meaning that the variables X and Ydo not follow any kind of dependence.

2.2. Clique Enumeration of Graph Theory

Graph theoretical concepts are useful for the description and analysis of relationships in biological systems. Clique analysis is a core component of graph in many biological applications such as gene expression networks analysis, cis regulatory motif finding, and matching three-dimensional molecular structures [17]. Generally clique represents biological module of similar function and biological annotations.

For a simple undirected graph G with the set of vertices and edges, two vertices are called adjacent if they are joined by an edge. The degree of a vertex is the number of connected edges; thus the degree of an isolated vertex is zero. Weight of each edge is a value between the pair connection, which might represent costs, lengths, or correlation, and so forth. A complete graph is a graph with every pair of nodes joined by an edge. Clique is complete subgraph and all pairs of vertices in the clique are connected. A maximal clique is a clique not contained in any other complete subgraph. The adjacency matrix of an undirected graph is a symmetric matrix B = (b_ij) in which the entry b_ij = 1 if the node i and node j are connected by an edge and 0 otherwise. If the graph is a clique, then B is a matrix with 1 off the diagonal and 0 on the diagonal. If the graph contains a clique, the adjacency matrix of that clique is a submatrix of B. Identification of all maximal cliques in a graph is a problem of clique enumeration [18]. Bioconductor, the open project for the analysis and comprehension of genomic data, provides a large collection of software for working with graphs and cliques [19]. Some social network analysis tools are also efficient in clique analysis [20].

But for imperfect systems or experimental data, the requirement of complete connectivity for maximal cliques is stringent; so more general notions of cohesive subgroups should be considered including n-cliques, k-plexes, and k-core [21]. For undirected and unweighted graph, a commonly used measure of network cohesion is density, which simply refers to the ratio of the number of edges that is actually present in the graph to maximum possible number of edges. A large density indicates high interconnectedness and cohesion in the network. The density of clique is 1.

2.3. The Main Process of MIClique

For each set of microarray data E = (e_ij)_NXS involving N genes from S samples, e_ij is the expression value of the ith gene in jth sample. The sample set is divided into two subsets: S₁ (normal samples) and S₂ (disease samples); so E_NXS is also divided into (E₁)_NXS1 and (E₂)_NXS2. Differentially coexpressed disease genes are those of high mutual information values in normal samples but of low MI values in disease samples.

The detailed process of MIClique is as follows.

Step 1 —

Calculating the mutual information of each pair of genes in E₁ and E₂, then two square symmetric mutual information matrices (MI₁)_NXN and (MI₂)_NXN are obtained. A big value of mutual information MI₁(i, j) means that the gene i and gene j are strongly coexpressed in normal samples, while a low value represents weak coexpression.

Step 2 —

Binarizing the mutual information matrices by selecting two threshold values T₁ and T₂ (T₁ > T₂), respectively, for MI₁ and MI₂, one has the following.

1. If MI₁(i, j) ≥ T₁, then M₁(i, j) = 1, else M₁(i, j) = 0.

2. If MI₂(i, j) ≤ T₂, then M₂(i, j) = 1, else M₂(i, j) = 0.

3. M(i, j) = M₁(i, j)  &  M₂(i, j).

4. If i = j then M(i, j) = 0.

The matrices M₁and M₂ are binarized mutual information matrices for MI₁ and MI₂. M is a logical symmetric matrix obtained by “AND” operation on M₁ and M₂. If M(i, j) is 1, it means that gene i and gene j are coexpressed in normal samples while suffer an alteration in disease groups.

Step 3 —

The M matrix can be transformed to the adjacency matrix of a graph G with vertices corresponding to genes and edges corresponding to biological interactions. There is an edge between vertices i and j in G if M(i, j) = 1. The DEC disease genes, which present a similar expression pattern in normal samples but suffer a distinct alteration in disease samples, are represented as a completely connected subgraph. So the problem of identifying DEC disease gene subsets is converted into clique detection based on adjacency matrix.

2.4. Threshold Selection

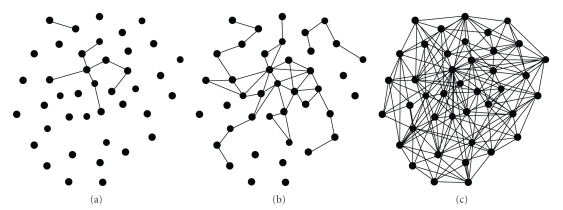
How to select the threshold values of T₁ and T₂ is very important for biological experimental interpretation. Different threshold values lead to different results. If the T₁ is high and T₂ is low, the graph has few edges and many isolated vertices. As T₁ decreases and T₂ increases, more edges are added to the graph, until it is completely connected. A graph with a large number of isolated vertices generally will fail to fall into a clique, but too many edges will cause a lot of overlapped cliques, which also are not very informative for data analysis. Proper thresholds will lead to a proper percentage of isolated vertices and reasonable experimental results. The threshold values are related with data sources and data types, and so forth, and they can be selected by graph density and percentage of isolated vertex. Figure 2 gives the gene networks for normalized simulated gene data by MIClique algorithm. The percentage of isolated vertices decreases and the number of edges increases as T₁ decreases and T₂ increases.

Figure 2.

Gene networks for simulated gene data with different thresholds. (a) T₁ = 2.2;  T₂ = 0.8; (b) T₁ = 2.0;  T₂ = 1.0; (c) T₁ = 1.8;  T₂ = 1.2.

3. Results and Discussion

Real gene expression data including colon dataset and Leukemia dataset are selected to illustrate the application of the proposed MIClique algorithm [22, 23]. The colon dataset contains expression levels of 2000 genes with the highest minimal intensity selected from 6500 genes across 62 samples, 40 tumor samples, and 22 normal samples. The dataset was normalized before further data analysis. The leukemia dataset contains gene expression profiles of acute leukemias measured using Affymetrix high-density oligonucleotide arrays: acute lymphoblastic leukemia (ALL) and acute myeloid leukemia (AML). The dataset contains 7129 human genes, 47 cases of ALL (38 B-cell ALL and 9 T-cell ALL), and 25 cases of AML. Only 3374 genes remained after data preprocessing.

3.1. Results of Colon Dataset

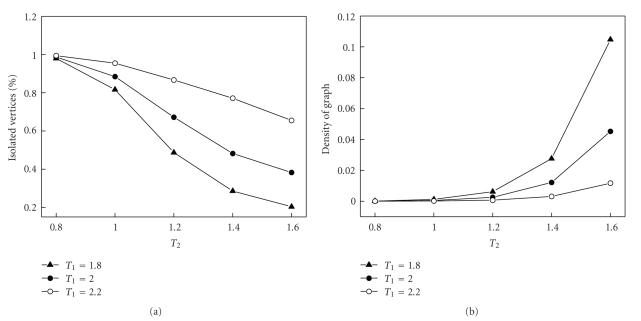
Different threshold values are selected for colon dataset. Figure 3 gives the percentage of isolated vertices and the density of the graph (number of edges present in graph divided by maximum possible number of edges, which is C₂₀₀₀²). The final thresholds for colon data are selected as T₁ = 2.2 and T₂ = 1.0. Then the data are transformed into gene network by MIClique algorithm.

Figure 3.

Different threshold values lead to different results for colon dataset. (a) Percentage of isolated vertices. (b) Density of the graph (number of edges divided by maximum possible number of edges, which is C₂₀₀₀²).

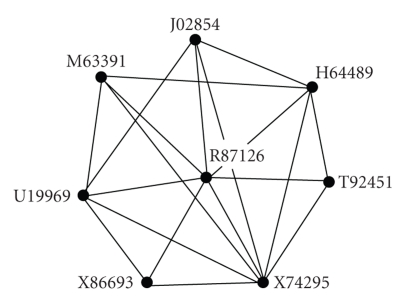
The maximal cliques are detected from this gene network, with the minimum size of clique as four. An overlapped clique group with six cliques and eight genes is found. Table 2 lists the gene accession numbers in each clique and Figure 4 displays the overlapped clique group graphically. These tightly overlapped cliques form a cohesive subgroup. There are eight vertices and 19 edges in the cohesive subgroups with the density of 0.68 (the maximum possible number of edges is C₈²).

Table 2.

Genes accession numbers in each clique identified by MIClique from colon dataset.

Clique number	Genes in each clique
1	M63391 H64489 R87126 X74295
2	H64489 R87126 T92451 X74295
3	H64489 R87126 X74295 J02854
4	R87126 X74295 X86693 U19969
5	R87126 X74295 J02854 U19969
6	M63391 R87126 X74295 U19969

Figure 4.

The cohesive subgroup identified from colon dataset; the overlapped clique group with six cliques and eight genes.

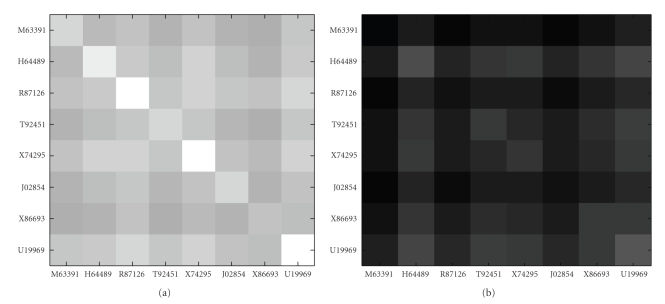
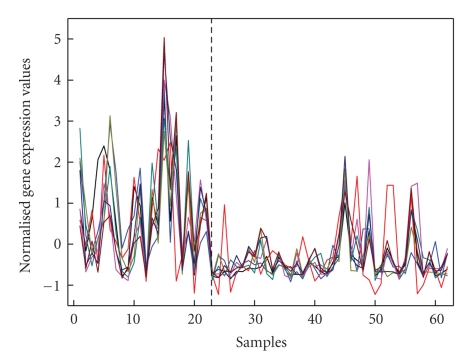
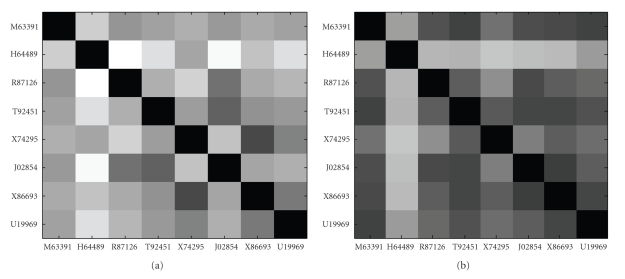
Figure 5 shows MI values of the eight genes, where each plot is a representation of the MI matrix in either the normal samples or disease samples. Each MI value in the matrix is represented as a square, with the color of the square representing the amount of value. The color scale used is black to white, with black representing the smallest value of MI and white representing largest value of MI. The MI values range from 2.072 to 2.477 in normal samples and from 0.508 to 1.095 in disease samples. This view shows all the MI values in an intuitive way. These eight genes form a differentially coexpressed gene subset, which is disease-related gene module identified by MIClique algorithm. Table 3 lists the Genbank accession number, the gene symbols, accession number in UniProtKB (UniProt Knowledgebase), and gene descriptions given by colon data. The UniProtKB is the central hub for the collection of information on proteins such as amino acid sequence, protein name or description, taxonomic data, and biological ontology [24]. Figure 6 depicts gene expression profiles of the eight genes in normal and disease samples. As shown in Figure 6, the profiles of these genes are highly coexpressed in normal samples (samples 1–22) while the coexpression pattern disappears in disease samples (samples 23–62).

Figure 5.

Images of the MI matrices for the eight genes in colon dataset. (a) Normal samples. (b) Disease samples.

Table 3.

Eight differentially coexpressed genes in cohesive subgroup identified from colon dataset.

Accession number	Gene symbol	UniProtKB ID	Gene descriptions
M63391	DESMIN (DES)	P17661	Human desmin gene, complete cds
H64489	CD37	P11049	Leukoyte antigen CD37 (Homo sapiens)
R87126	MYH9_HUMAN	P14105	Myosin heavy chain, nonmuscle (Gallus gallus)
T92451	TPM2	P07951	Tropomyosin, Fibroblast and epithelial muscle-type (Human)
X74295	ITGA7	Q13683	H.sapiens mRNA for alpha 7B integrin
J02854	MYL2	P10916	Myosin regulatory light chain 2, smooth muscle isoform (Human)
X86693	SPARCL1(Hevin)	Q14515	H.sapiens mRNA for hevin like protein
U19969	ZEB1(ZEB)	Q13088	Human two-handed zinc finger protein ZEB mRNA

Figure 6.

Differentially coexpressed profiles of the eight genes in two kinds of samples; samples 1–22 represent normal samples and samples 23–62 are disease samples.

Table 4 lists gene annotations of the eight genes from Gene Ontology (GO) obtained by AmiGO searching tool. GO is a database to support biologically meaningful annotation for the description of the molecular function, biological process, and cellular component of gene products [25]. As observed in Table 4, some of the genes are of the common biological functions and involved in the same biological processes such as muscle development, calcium ion binding, and regulation of striated muscle contraction. The results of Aigner et al. showed that ZEB1 is associated with human colorectal cancer, and ZEB1 is a key player in pathologic epithelial to mesenchymal transition (EMT) associated with tumour progression [26]. Claeskens et al. have proved that Hevin is downregulated in many cancers and Hevin may be a potential target for cancer diagnosis and therapy [27]. Meanwhile the results of colon dataset by MIClique coincide with those of other researchers. For example, all these eight genes are included in the differentially expressed genes for colon dataset selected by unified framework [28]; some of these genes are consistent with the results of other researchers [29–31].

Table 4.

GO annotations of eight DEC genes identified from colon dataset by MIClique.

Gene Symbol	Ontology	GO Terms
DESMIN	Biological process	Cytoskeleton organization; muscle contraction; regulation of heart contraction
	Cellular component	Z disc
	Molecular function	Protein binding; structural constituent of cytoskeleton
CD37	Biological process	Protein amino acid N-linked glycosylation
	Cellular component	Plasma membrane; integral to plasma membrane
MYH9	Biological process	Actin cytoskeleton reorganization; actin filament-based movement; angiogenesis; blood vessel endothelial cell migration; cytokinesis; membrane protein ectodomain proteolysis; monocyte differentiation; platelet formation; protein transport; regulation of cell shape
	Cellular component	Cleavage furrow; contractile ring; cytoplasm; cytosol; integrin complex; nucleus; plasma membrane; ruffle; stress fiber
	Molecular function	Actin filament binding; ATPase activity; microfilament motor activity; protein anchor; protein homodimerization activity
TPM2	Biological process	Regulation of ATPase activity
	Cellular component	Muscle thin filament tropomyosin
	Molecular function	Actin binding; structural constituent of muscle
ITGA7	Biological process	Cell-matrix adhesion; muscle organ development; integrin-mediated signaling pathway
	Molecular function	Calcium ion binding; protein binding; receptor activity
MYL2	Biological process	Cardiac myofibril assembly; heart contraction; negative regulation of cell growth; regulation of striated muscle contraction; ventricular cardiac muscle morphogenesis
	Cellular component	Sarcomere
	Molecular function	Actin monomer binding; calcium ion binding; myosin heavy chain binding; protein binding; structural constituent of muscle
SPARCL1	Biological process	Signal transduction
	Molecular function	Calcium ion binding
ZEB1	Biological process	Cell proliferation; immune response; negative regulation of transcription from RNA polymerase II promoter; regulation of transcription, DNA-dependent
	Molecular function	Transcription coactivator activity; transcription corepressor activity; transcription factor activity; zinc ion binding

3.2. Comparisons with Other Similarity Measures

The definition of the similarity measures is very important for identification of the relationships among genes. Euclidean distance and correlation coefficient are traditional similarity measures commonly used in gene expression analysis. But both of them are unsuitable for nonlinear relationships that might exist between the patterns. Euclidean distance fails to detect the simultaneous upregulated or downregulated expression levels with large amplitude absolute changes. Compared with Euclidean distance and Pearson correlation coefficient, the usage of the MI measure yields a more significant performance [32].

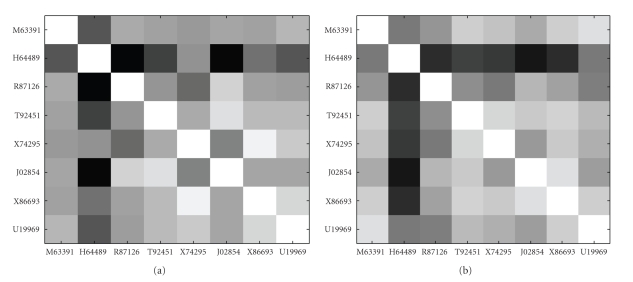
Figures 7 and 8 show Euclidean distance values matrices and Pearson correlation coefficient values matrices of the eight genes identified by MIClique from colon dataset respectively. The Euclidean distance values range from 2.025 to 7.073 in normal samples and range from 1.676 to 5.497 in disease samples. The Pearson correlation coefficient values range from 0.151 to 0.946 in normal samples and range from 0.242 to 0.891 in disease samples. Both of the figures display no indication of differentially coexpression patterns among the eight genes.

Figure 7.

Images of the Euclidean distance matrices for the eight genes from colon dataset. (a) Normal samples. (b) Disease samples.

Figure 8.

Images of the Pearson correlation coefficient matrices for the eight genes from colon dataset. (a) Normal samples. (b) Disease samples.

3.3. Leukemia Data

The samples of leukemia dataset are divided into two subclasses of disease samples: acute lymphoblastic leukemia (ALL) and acute myeloid leukemia (AML). The MIClique algorithm is applied to the preprocessed and normalized leukemia dataset with T₁ = 2.2 and T₂ = 0.9. A group of DEC genes is identified, which are coexpressed in ALL samples but not in AML samples. The MI values of these eight genes in DEC group range from 1.944 to 3.348 in ALL samples and range from 0.764 to 1.225 in AML samples with the average MI values 2.550 in ALL samples and 0.934 in AML samples, respectively. Table 5 lists the Genbank accession numbers, gene symbols, and gene descriptions given by leukemia dataset. Besides the MIClique can identify DEC genes correlated in AML but not in ALL. All these DEC genes are helpful for understanding disease pathogenesis of leukemia and biological function of gene modules.

Table 5.

Differentially coexpressed genes correlated in ALL but not in AML in Leukemia dataset.

Accession numbers	Gene symbols	UniProt	Gene descriptions
HG4074-HT4344	FEN1(RAD2)	P39748	Rad2
L41870	RB1	P06400	Retinoblastoma 1 (including osteosarcoma)
U18062	TAF7(TAFII55)	Q15545	Human TFIID subunit TAFII55 mRNA
M92287	CCND3	P30281	Cyclin D3
U28833	RCAN1(DSCR1)	Q9UF15	Down syndrome critical region protein (DSCR1) mRNA
X56468	YWHAQ	P27348	14-3-3 protein tau
X84373	NRIP1(RIP140)	P48552	Nuclear factor RIP140
Z23064	RBMX	P38159	Heterogeneous nuclear ribonucleoprotein G

4. Conclusions

The difference between the MIClique and supervised gene selection methods is that MIClique algorithm evaluates the contributions of genes to phenotype by gene subets, rather than individual genes. Although the aim of MIClique is not to select discriminative genes between normal and disease tissues, or between different types of disease samples, the identified genes are still very informative for samples classification. For example, most of the genes identified by MIClique from colon dataset are also differentially expressed genes, which are consistent with the results of other researches.

It is clear that the MIClique algorithm is very efficient in identifying DEC genes. The DEC genes focus on the interaction among gene pairs and disease-related gene network, which is very important for understanding disease pathogenesis and biological function of gene modules. The MIClique algorithm has provided a new and intuitive way to biological and clinical cancer research.