DNA Breathing Dynamics in the Presence of a Terahertz Field

Abstract

We consider the influence of a terahertz field on the breathing dynamics of double-stranded DNA. We model the spontaneous formation of spatially localized openings of a damped and driven DNA chain, and find that linear instabilities lead to dynamic dimerization, while true local strand separations require a threshold amplitude mechanism. Based on our results we argue that a specific terahertz radiation exposure may significantly affect the natural dynamics of DNA, and thereby influence intricate molecular processes involved in gene expression and DNA replication.

Spectroscopic techniques in the terahertz range are currently emerging as new tools for the investigation of biological macromolecules (1). In spite of the experimental difficulties (caused by the water's giant Debye dipole moment, which leads to a substantial dielectric relaxational loss in the THz range) a notable amount of research effort is being devoted to the development of sophisticated THz bio-imaging (2). Nevertheless, very little is known about THz-radiation's influence on biological systems, and the mechanisms that govern this influence. The possibility that low frequency electromagnetic radiation may affect genetic material, enzymatic reactions, etc. was introduced long ago (3), and since then has been a subject of constant debate. The energy of such radiation is too low to directly disrupt any chemical bonds or cause electronic transitions. Only a resonance-type interaction might lead to an appreciable, biological effect. In biomolecules such interactions are possible through the ubiquitous hydrogen bonds that have energies in the THz range. Numerous in vivo and in vitro experiments have been conducted to clarify low frequency radiation's ability to cause biological effects, such as chromosomal aberration, genetic damage etc. The experimental studies have been conducted under a variety of conditions, but mostly at frequencies below 0.01 THz, power below 1 mW/cm², and short exposure times. The data collected in these conditions led to mixed conclusions: some studies reported significant genetic damages while others, although similar, showed none (4). The major international research project, ”THz-bridge” (5), which was specifically concerned with THz radiation genotoxicity concluded that: under some specific conditions of exposure, change in membrane permeability of liposomes was detected and an induction of genotoxicity was observed to occur in lymphocytes. Hence, this project confirmed the existence of THz genotoxicity, but it remains unclear under which specific conditions such effects occur.

Recent measurements confirm that only extended (6 hours) exposure to a weak THz field can cause genomic instability in human lymphocytes (6). Independently, it was reported that neurons exposed in vitro to powerful THz radiation (over 30 mW/cm² ) cause infringement of the morphology of the cellular membranes and intracellular structures (7). The same work also showed that at decreasing power and/or at different frequencies the morphological changes do not occur. Recently, it was further pointed out that exposure to a low level THz radiation can interfere with the protein-recognition processes (8). It was also shown that exposure of mice to 3.6 THz high power (15 mW/cm²) radiation, for 30 min caused behavioral changes (9), while under short (5 min) exposure the changes could not be detected. Thus the available experimental data strongly suggest that THz-radiation can affect biological function, but only under specific conditions, viz. high power, or/and extended exposure, or/and specific THz frequency.

The present work is devoted to developing a qualitative description of the existence of such THz effects. We argue that the appropriate conditions correspond to irradiation parameters that assure the existence of linear and nonlinear resonances between DNA conformational dynamics and THz field Fig.1.

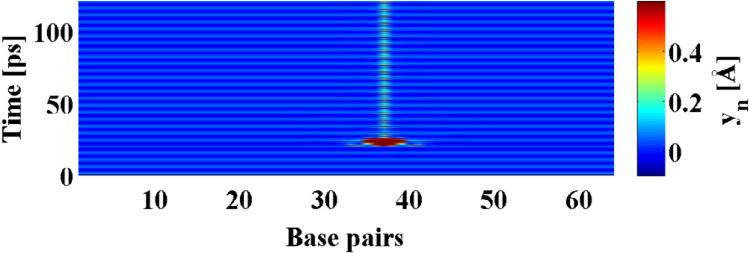
Fig. 1.

Spontaneous formation of a localized permanent opening in dsDNA in the presence of a THz field with amplitude A = 144 pN, and Ω = 2 and a spatial fluctuation with high amplitude (see text).

We will base our analysis on the Peyrard-Bishop-Dauxois (PBD) model of dsDNA (10), which is arguably the most successful available model for describing the local DNA pairing/unpairing (breathing) dynamics (11). Of particular importance for the THz effect is our previous demonstration of strong correlations between regulatory activity, such as protein-DNA binding and transcription, and the equilibrium propensity of dsDNA for local strand separation (13; 12; 14; 15). With this background it is natural to consider the influence of THz radiation on dsDNA dynamics within the PBD modeling framework. One complication is that the specific physical nature of the interactions between DNA and the THz electromagnetic field is not known in detail. However, given the sensitivity of THz radiation to the strand pairing state of DNA (16), we will here simply augment the PBD to include a drive in the THz frequency range, without specifying the precise nature of the underlying physical coupling. Since the wavelength of the THz field is larger than 100 μm and the characteristic size the investigated dsDNA sequences is less than 20 nm it is reasonable to consider an uniform THz field. In this fashion the breathing dynamics (represented by the normalized separation y_n of complementary bases) of the n'th base pair in the presence of a monochromatic spatially homogeneous external field is described by

$$\begin{array}{cc}\hfill m{\ddot{y}}_n=-& U\prime \left(y_n\right)-W\prime (y_{n+1},y_n)-W\prime (y_n,y_{n-1})\hfill \\ \hfill -& m\gamma {\stackrel{.}{y}}_n+A\cos \left(\Omega t\right),\hfill \end{array}$$ (1)

where, the Morse potential U(y_n)= D_n(exp (−a_ny_n) −1)² represents the hydrogen bonding of the complementary bases. The parameters D_n and a_n depend on the type of the base pair (A-T or G-C). Similarly, $W(y_n,y_{n-1})=\frac{1}{2}\chi [y_n,y_{n-1}]{(y_n-y_{n-1})}^2$ with χ[y_n, y_n−1] = k(1 + ρexp (−β(y_n − y_n−1))) represents the stacking energy between consecutive base pairs. The term mγỵ_n is the drag caused by the solvent while A cos (Ωt) is the (THz) drive. For simplicity, we consider here a homogeneous poly(A) (17) DNA molecule with 64 base pairs. Our numerical simulations of this set of nonlinear coupled equations (using periodic boundary conditions) showed that the primary response of the system is spatially homogeneous (Fig.1 the first 40 ps). However, we observed that a presence of fluctuations may lead to the creation of persistent spatially localized openings of the double-stranded molecule, Fig.1. Because, such openings (bubbles) are known to functionally affect dsDNA we focus here on characterizing the conditions under which these states appear.

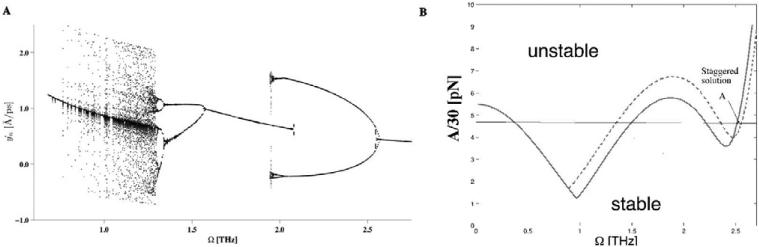
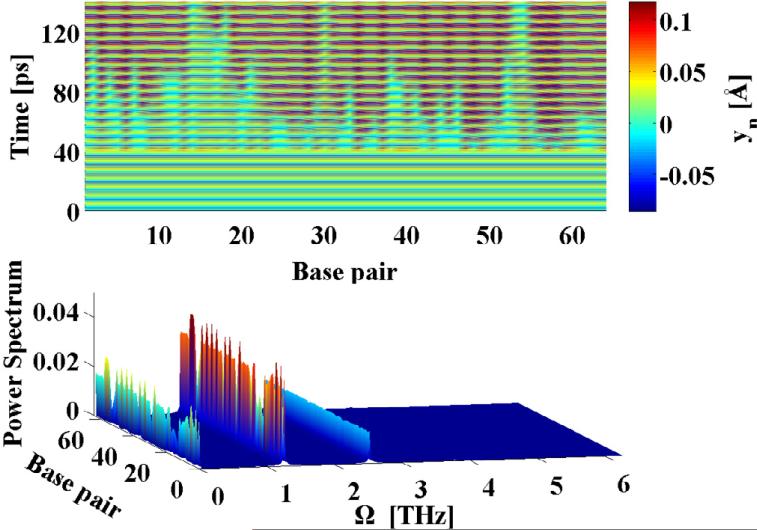
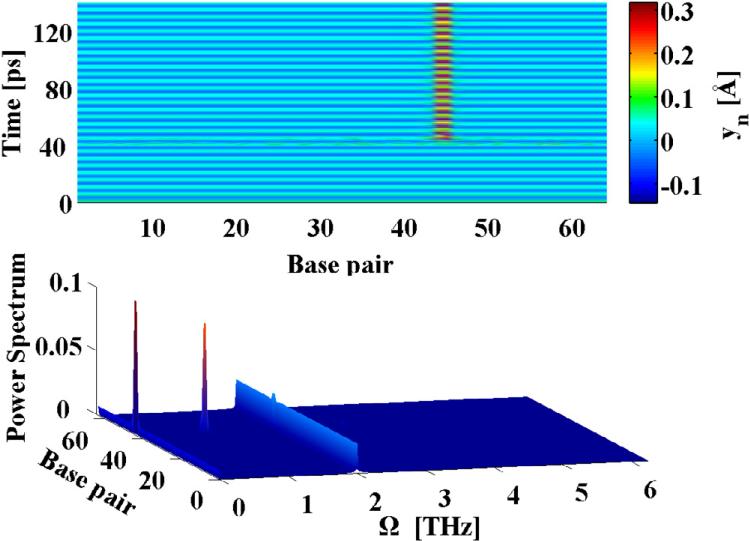
Since, the primary response of of the driven system is spatially uniform it can be understood in terms of a single classical damped and driven Morse oscillator. Such systems have been studied quite extensively in many other contexts (18), and are known to display rich dynamical behavior including limit cycles, period-doubling bifurcations etc. An illustration of this is shown in Fig.2, A, for our system parameters, in terms of the Poincaré section ỵ_n(t = mT), where T =2π/Ω, versus the driving frequency Ω for several integer values of m. Feigenbaum's period-doubling route to chaos is clearly seen in this figure, which demonstrates that this system's main instability mechanism is through period-doubling. As described earlier, our interest is to investigate whether the presences of a THz field can lead to the creation of spatially localized unbinding of the DNA double-strand. Such states are most easily created in connection with the period-doubling events, as a result of a spatially inhomogeneous perturbation. In order to investigate this phenomenon we adopt a method developed in Ref. (19). In this work the linear stability analysis (based on the Floquet theorem) of a single Morse oscillator was performed, and it was shown that in a rotating-wave approximation (20) the dynamics ensuing from a given perturbation is governed by the extended Hill equation. The stability analysis of the Hill equation has been developed by Ince (21) based on his extension of the Whittaker's method of solving Mathieu's equation (22). Since, our system is spatially extended, a perturbation may be spatially inhomogeneous. In this case the response of the system is characterized by y_n(t)= y⁰(t)+ z_n(t), where y⁰(t) is the spatially homogeneous and temporally periodic solution described above (see Fig. 2), A, and z_n(t) represents the perturbations in whose dynamics we are interested. In the most general form the perturbation is given in terms of Fourier modes: $z_n\left(t\right)={\sum }_k\exp \left[ikn\right]{\xi }_k\left(t\right)$ with wavenumber, k, and amplitude ξ_k(t). As with the single oscillator, the dynamics of the Fourier amplitudes ξ_k(t) of the perturbation are governed by set of uncoupled extended Hill equations. However, the coefficients of these equations depend on the wave-number k. The Ince stability analysis allows us to analytically determine (23) the Floquet exponents (i.e. the stability criteria) as functions of the spatial profile as given by k. For more technical details on the method see Ref. (24). The result of our analysis are the stability curves dividing the parameter space (A/m, Ω, k) into stability and instability zones. Figure 2, panel B shows the stability boundaries of a spatially homogeneous perturbation (k = 0, solid curve) and of a staggered (k = π, dashed curve) perturbation. Perturbations represented by other wave-numbers have stability boundaries in-between those shown in Fig. 2, B. Below these curves the spatially homogeneous states perform stable temporal oscillations at the frequency of the external drive and its higher harmonics, while above the curve the perturbation leads to period-doubled oscillations. It is clearly seen that for driving frequencies below Ω ~ 2.5 THz spatially homogeneous (k = 0) perturbations lead to the strongest instability (occurring at the lowest value of the driving amplitude). However, above Ω ~ 2.5 THz the staggered (k = π) perturbation becomes the primary instability mode. In the region above the stability boundary the period-doubled state will therefore tend to adopt the spatial profile of the most unstable Fourier-mode (homogeneous or staggered). The presence and location of the obtained instability curves (Fig. 2, B) were verified by exploring the parameter-space (A/m, Ω, k) by direct simulations of Eq. (1). The dynamics of small spatially random (uniformly distributed in the interval [−ε, ε] and thus containing all wave-numbers) perturbation z_n introduced on top of the spatially homogeneous and temporally periodic solution y⁰(t) was followed numerically. As this perturbation injects energy into all wave-numbers, the ensuing dynamics will emphasize the mode with the strongest instability. For point A (Fig. 2, B), the results are shown in Figure 3. The upper panel shows that after the introduction of the perturbation (at 40 ps) a spatially staggered structure forms. The power spectrum of this dynamics (lower panel in Fig. 3), shows that the frequency of the vibrations is mainly Ω/2, i.e. a period-doubling transition has occurred as expected from the above analysis. The power spectrum (lower panel) shows that the signature of the drive persists at Ω, in addition to a component at zero frequency, which results from the asymmetry of the base-pair potential U(y_n). A similar scenario is observed for driving frequencies below Ω ~ 2.5 THz, but in these cases the solutions remain spatially homogeneous after the introduction of the perturbation. The fact that the instability curves for 0 < k < π lie between the two curves in Fig. 2, B shows that it is, in general, impossible for any spatially localized feature with a finite (2 base pairs < λ < ∞) length scale λ to emerge as a result of a linear instability. This is in contrast with many other nonlinear condensed matter models, where spatially localized and temporally periodic modes (intrinsic localized modes or breathers) commonly arise through linear modulational instabilities. For our model of dsDNA a perturbation of finite amplitude ε is required to create localized unbindings of the DNA double strand through nonlinear mechanisms. An illustration of this is given in Fig. 4 for Ω = 2.0 THz, where the dynamics caused by a random perturbation with ε > 0.14 is shown to result in a localized opening of the DNA double strand. Again the power spectrum, given in the lower panel of Fig. 4 shows, as expected, that the localized state vibrates at the frequency Ω/2 in contrast to the uniform background, which remains synchronized to the external drive at Ω. A more detailed study of the nonlinear mechanisms underlying the creation of such localized unbinding states reveals that a localized injection of a certain amount of energy is required. Due to the asymmetry of the base pair potential, an effective way to achieve this is a localized compression of the double strand. Using this insight we found the perturbation $z_n=0.42\cos \left(\frac{\pi }{4}(n-n_0)\right)$, for −4 ≤ n − n_o ≤ 4 (z_n = 0 otherwise) to be an perturbation for the creation of a localized unbinding state at n₀, Fig.1. The phase portrait (not shown) of the base pair n₀, at the transient time period just before the breather is established, reveals the breather formation mechanism. First, the locally injected energy from the compression must be sufficient for a few consecutive base pairs to undergo a temporary local melting transition, i.e. reach the plateau of the Morse potential. Subsequently, the stacking interactions and friction dissipate the energy to gradually reach a steady state. At given driving amplitude and frequency, the dsDNA molecule has two steady conformational states with different average energies and amplitudes. Only in these states is the externally pumped energy exactly compensated by the energy dissipated by the friction. The first state is vibrating predominantly at the driving frequency Ω, while the second mainly oscillates at Ω/2. Hence, the breather formation proceeds in three stages: 1) all the base pairs are in the first state then; 2) a few of them undergo a temporary melting transition as a result of the perturbational energy injection. Finally, 3) the perturbed base pairs reach the second steady conformational state, after dissipating their additional energy.

Fig. 2.

A) Bifurcation diagram for a poly(A) molecule in an external THz field with amplitude A = 144 pN. B) The instability curves for wave vector k = 0 (solid curve) and k = π (dashed curve) are plotted. On the vertical axis is the amplitude of the external field, and on the horizontal axis is the frequency Ω of the THz field.

Fig. 3.

The k = π spatial pattern, at Ω = 2.52 THz, is presented. The upper panel shows evolution of the system. The lower panel shows the power spectrum of the breather motion.

Fig. 4.

Breather formation at Ω = 2.00 THz. The upper panel shows the evolution of the breather. The lower panel shows the power spectrum of the breather motion.

In summary, we have found that a THz field may cause dynamical separations of the DNA double-strand. In the presence of weak perturbations e.g. thermal fluctuations, small amplitude response occurs (at half the driving frequency) either in a spatially uniform manner or, at higher-frequencies, in an unusual spatially dimerized form. In the latter case, neighboring base pairs oscillate in an out-of-phase fashion. However, large localized openings (bubbles) in the DNA double strand can only occur via a nonlinear mechanism requiring a spatial perturbation above a certain amplitude threshold that is determined by the intensity and the frequency of the THz field.

We previously showed experimentally that the introduction of an artificial permanent bubble in dsDNA, via a short mismatched segment, is in fact sufficient for transcription even in the absence of any auxiliary factors (15). Our present finding of large localized openings resulting from an external THz field therefore underscores the importance of including the interactions of genomic DNA with the surrounding environment in DNA models. The amplitudes of the resulting openings observed in the presence of a THz field are significant compared to the dynamic signatures of protein binding sites and transcription start sites (14). This suggests that THz radiation may significantly interfere with the naturally occurring local strand separation dynamics of double-stranded DNA, and consequently, with DNA function.

Based on the model results present here, we believe that the main effect of THz radiation is to resonantly influence the dynamical stability of the dsDNA system. Hence, our instability curves define the parameters space (i.e. the amplitude of the field (or the power), and frequency) in which THz radiation can have an immediate effect. In contrast, nonlinear instability may occur at any point of the instability diagram but it requires fluctuations with significant amplitudes. In biological systems, such fluctuations are generated thermally. Hence, the occurrence of a fluctuation with sufficiently large amplitude is very rare, and therefore extended exposure is required for the THz effect to take place, via nonlinear instabilities, especially if the power is small. In this framework, it is than natural that the character of THz genotoxic effects are probabilistic rather than deterministic.