Estimates of the Effect of Natural Selection on Protein-Coding Content

Abstract

Analysis of natural selection is key to understanding many core biological processes, including the emergence of competition, cooperation, and complexity, and has important applications in the targeted development of vaccines. Selection is hard to observe directly but can be inferred from molecular sequence variation. For protein-coding nucleotide sequences, the ratio of nonsynonymous to synonymous substitutions (ω) distinguishes neutrally evolving sequences (ω = 1) from those subjected to purifying (ω < 1) or positive Darwinian (ω > 1) selection. We show that current models used to estimate ω are substantially biased by naturally occurring sequence compositions. We present a novel model that weights substitutions by conditional nucleotide frequencies and which escapes these artifacts. Applying it to the genomes of pathogens causing malaria, leprosy, tuberculosis, and Lyme disease gave significant discrepancies in estimates with ∼10–30% of genes affected. Our work has substantial implications for how vaccine targets are chosen and for studying the molecular basis of adaptive evolution.

Introduction

Application of ω to identify balancing natural selection acting on Major Histocompatibility Complex genes (Hughes and Nei 1988) stimulated the widespread use of this statistic to identify genes involved in the evolution of new function (Messier and Stewart 1997); protection against pathogens including Plasmodium (Hall et al. 2005), HIV (Iversen et al. 2006), and influenza (Mes and van Putten 2007); evolution of drug resistance in pathogens (Seoighe et al. 2007); and to provide decision support in vaccine design (Mes and van Putten 2007). Its estimation is an integral part of most published genome projects, and estimates are included in routine reports generated from genome portals (Hubbard et al. 2009).

In the most popular approaches to estimating ω, continuous-time Markov processes are used to model substitutions between codons. Substitutions are specified by an instantaneous rate matrix (Q) with parameters representing the frequencies of different nucleotides or codons in the end state sequence being changed to (π) and rate parameters that represent the relative rate of different kinds of codon change (e.g., ω and κ—the ratio of transition to transversion substitutions). In these models, when ω = 1, Q purportedly represents the neutral process. The complete specification of Q is used to compute the probabilities of substitution from any one codon to any other codon (for review, see Liò and Goldman 1998).

Codon models used to estimate ω must be correctly calibrated, that is, ω should equal 1 for neutrally evolving sequences, and ω should not be confounded by base composition or other properties of the sequences being compared. Two types of model are currently used to estimate ω, which differ in their definition of π; one defines π from nucleotide frequencies (NF; Muse and Gaut 1994) and the other from codon frequencies (CF; Goldman and Yang 1994). Thus, for example, Q(AGC,AAC), the element of Q corresponding to the codon change AGC → AAC, is defined as π(A)κω in NF models and π(AAC)κω in CF models, where π(A) and π(AAC) are the frequencies of A and AAC, respectively. The NF model therefore has 57 fewer parameters than the CF model. These model forms are defined more thoroughly in Theory and Methods.

In NF models, equilibrium codon frequencies are the product of nucleotide frequencies (adjusted to account for stop codons). However, nucleotides, even in noncoding regions, are subject to context effects of neighboring nucleotides and do not evolve independently (Blake et al. 1992; Karlin et al. 1998). In coding regions, nonmultiplicative codon frequencies may originate from context-dependent substitution processes, selection on synonymous sites (Chimpanzee Sequencing and Analysis Consortium 2005), or both. The influence of natural selection on codon usage is most pronounced in microbial genomes (Sharp et al. 2005, dos Reis and Wernisch 2009). Because codons never occur at frequencies that can be derived multiplicatively from their composite nucleotide frequencies, NF models will typically exhibit poorer fit to data than CF models (Lindsay et al. 2008) and may give biased estimates of ω.

Although the codon frequencies under CF models will better match the observed frequencies, the estimate of ω is confounded by components of π (Lindsay et al. 2008). For example, for the codon change AGA → AGT, in the case that the three sites evolve independently, the end state weighting under the NF model is just π(T). For the CF model applied in this context, the additional product π(A) ×π(G) is included because π(AGT) = π(A) ×π(G) ×π(T). So because the CF instantaneous rate matrix is defined for single nucleotide events, multiplying ω by the frequency of the entire neighborhood, rather than just the ending state, causes ω estimates to behave in a counterintuitive way. Critically, the CF model can indicate context effects that do not exist (Lindsay et al. 2008), which may cause CF to generate estimates of ω ≠ 1 even for neutrally evolving DNA sequences.

Here we demonstrate that ω estimated from both existing codon model forms are strongly affected by sequence composition, and we present a novel model form that avoids this flaw. We confirm the predicted sensitivities of the existing model forms using simulated data. We further demonstrate that the properties that cause these models to err are common in nature, particularly so in pathogen genomes. By an analysis of real biological sequences, we establish that the new model form is the most robust to the complexity of naturally occurring neutral evolutionary processes, confirming it as the most reliable choice for inferring the mode of natural selection.

Theory and Methods

A New Codon Model Form

We propose overcoming the drawbacks of the CF and NF models with an alternative model where substitution rates are weighted by the frequency of a nucleotide at one codon position, conditional on the nucleotides at the other two codon positions. For example, the change TAC → TAT is weighted by the frequency of T at the third codon position, conditional on TA at codon positions 1 and 2. This conditional nucleotide frequency (CNF) model has the same number of π parameters as the CF model and shares its property of readily achieving the observed codon frequencies, but because, like the NF model, it weights substitutions by nucleotide frequencies, it avoids the confounding effect of sequence composition on ω.

We only consider reversible Markov substitution processes on trinucleotides where every event involves exactly one nucleotide. The rate of substituting a = i₁i₂i₃ by a distinct b = j₁j₂j₃ has the form

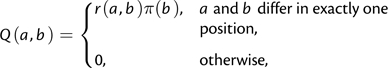(1)

where π is the equilibrium frequency vector and r is a symmetric matrix. This parameterization is called tuple frequency (TF) in Lindsay et al. (2008), but because our chief interest is in codons, we call it CF_tri. We propose an alternative parameterization of the models, called CNF_tri (conditional nucleotide frequency):

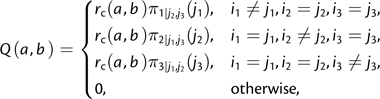(2)

where r_c is symmetric and π_1|j2,j3(·) is the conditional frequency of the first position given that the second and third nucleotides are j₂ and j₃, etc., computed from the equilibrium frequency vector π.

Using the definition of conditional probability, for example, π_1|j2,j3(j₁) = π(j₁j₂j₃)/π_2,3(j₂,j₃), it can be readily seen that equations (1) and (2) define the same models and that a given CNF_tri model can be specified as a CF_tri by

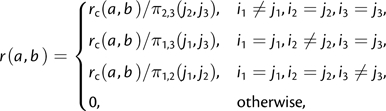(3)

and vice versa.

In equation (2), replace the conditional frequencies π_1|j2,j3(j₁), π_2|j1,j3(j₂), and π_3|j1,j2(j₃) by π_nu(j₁), π_nu(j₂), and π_nu(j₃), respectively, where π_nu is a set of nucleotide frequencies. This defines a restricted set of models, called NF_tri (nucleotide frequency). If we have a CNF_tri form with a homogeneous multiplicative π, that is, π(a) = π_nu(i₁)π_nu(i₂)π_nu(i₃) for some π_nu, then it is in NF_tri because conditional frequencies reduce to π_nu terms. Thus, NF_tri is a “simple” special case of the parameterization CNF_tri but not CF_tri.

The symmetric part r or r_c in the models, with 96 free parameters, makes it challenging to fit even large genomic data sets. An obvious solution is to make r or r_c “nucleotide like”, that is, the terms are determined only by the nucleotide changes, so that there are only six parameters in r or r_c. We call these submodels CF_tri,GTR, CNF_tri,GTR, and NF_tri,GTR, respectively. The reason for using the subscript GTR (general time reversible model; Lanave et al. 1984) is as follows. The reversible nucleotide process GTR has rates

(4)

where r_nu is symmetric and π_nu is the nucleotide equilibrium frequency vector. By a simple extension of the argument in Lindsay et al. (2008), three independent nucleotides evolve with

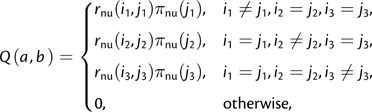(5)

which is in NF_tri,GTR. Conversely, every NF_tri,GTR is a nucleotide GTR process. The parameterizations and models are summarized in table 1.

Table 1.

Trinucleotide Model Notation

Frequency	General r	Nucleotide r	With Selection
Trinucleotide	CFtri	CFtri,GTR	CFtri,GTR,s
Conditional nucleotide	CNFtri	CNFtri, GTR	CNFtri,GTR,s
Nucleotide	NFtri	NFtri,GTR	NFtri,GTR, s

NOTE.—Frequency: state frequencies used to weight exchanges; General r: r is constrained only to be symmetric (eq. 3); Nucleotide r: r is specified by nucleotide terms only; With Selection: introduces an analog of ω into the model. CF_tri and CNF_tri are different parameterizations of the same models. CF_tri,GTR and CNF_{tri, GTR} are different models: nucleotide GTR processes (NF_tri,GTR) are simple special cases of CNF_tri,GTR but are not contained in CF_tri,GTR.

CNF_tri,GTR specializes very easily to give the nucleotide GTR processes, NF_tri,GTR: just let π be homogeneous multiplicative. However, NF_tri,GTR is not even in CF_tri,GTR unless π is quite special, for example, uniform. If we try to represent equation (5) in CF_tri,GTR, π must be homogeneous multiplicative, so that

which is inconsistent unless π_nu(A) = π_nu(C). The nucleotide GTR processes are in general not in CF_tri,GTR; rather, they appear in CF_tri as cumbersome special cases.

We now describe a fundamental flaw in the CF models by introducing “selection” to trinucleotide substitution processes. Let CF_tri,GTR,s denote the extension of CF_tri,GTR to encompass the influence of selection, multiplying “nonsynonymous” rates with a constant positive ω. Thus, CF_tri,GTR is a subset corresponding to ω = 1. Define CNF_tri,GTR,s and NF_tri,GTR,s similarly. Suppose the true process is GTR (with nonuniform π_nu). This is a neutral process in CNF_tri,GTR and NF_tri,GTR but not in CF_tri,GTR as shown in the previous paragraph. Thus, the standard theory does not conclude that the likelihood ratio test (LRT) statistic for CF_tri,GTR within CF_tri,GTR,s has an asymptotic χ₁² distribution. In contrast, the null distribution of the LRT statistic for CNF is asymptotically χ₁². In addition, we expect the estimation of ω = 1 to be consistent with CNF but not with CF.

Codon models are derived from trinucleotide models by dropping the stop codons. The abbreviations for codon models are consistent with the trinucleotide models, by dropping the subscript `tri'. The CF_GTR model is defined by equation (1) with a sense codon frequencies π consisting of 61 entries; this is the family pioneered by Goldman and Yang (1994). CNF_GTR is defined by equation (2) with conditional probabilities computed from a sense codon frequencies. Lastly, NF_GTR, specified with some nucleotide frequencies π_nu, is a generalization of the family pioneered by Muse and Gaut (1994). The subscript HKY after Hasegawa et al. (1985) is used instead of GTR in the special case where the r or r_c terms take only two possible values, depending on whether the substitution is a transition or a transversion. The codon parameterizations and models are summarized in table 2.

Table 2.

Codon Model Notation

Frequency	General r	Nucleotide r
Codon	CF	CFGTR
Conditional nucleotide	CNF	CNFGTR
Nucleotide	NF	NFGTR

NOTE.—Column headers are as per table 1. CF and CNF are different parameterizations of the same models. CF_GTR and CNF_GTR are different models. The special case of CNF_GTR when π is homogeneous multiplicative is CNF _×. NF_GTR is not CNF _× because of the stop codons.

For trinucleotides, NF_tri is a special case of CNF_tri when π is homogeneous multiplicative. This is not the case for codons, that is, when the sense codon frequencies π is proportional to a homogeneous multiplicative trinucleotide frequency, the special case, denoted by CNF_×, is close to, but not the same as, NF. Call four trinucleotides that agree in exactly two positions a close quartet. If a close quartet consists of only sense codons, the exchanges among them have the same rates under CNF_× and NF because the codon frequencies in the former are exactly π_nu. However, this breaks down if a close quartet contains less than four sense codons. For example, under NF_GTR, Q(TAT,TAC) = r_c(T,C)π_nu(C), but under CNF_×,GTR, it is

because of the stop codons TAA and TAG.

The selection parameter ω in the codon models plays a similar role as the context terms featured in dinucleotide models investigated by Lindsay et al. (2008). Hence, it is not surprising that pitfalls associated with CF/TF carry over to the trinucleotide case. Because the stop codons prevent a complete theoretical argument as presented in Lindsay et al., here is an approximate approach. A codon model should conclude that ω is 1 if the underlying substitution process is the nucleotide GTR. Because the codon model CF_GTR is similar to the trinucleotide model CF_tri,GTR, we expect estimates of ω from CF_GTR to be biased, concluding positive or negative selection when there is none. Analogously, the good properties of the codon version of CNF_GTR should hold by virtue of its similarity to the trinucleotide version. We test these predictions by analyses of simulated data and real intron sequences.

Model Implementation

The CNF substitution model was implemented in PyCogent (Knight et al. 2007) version 1.4.0.dev, and these modifications will be added to the PyCogent Sourceforge repository on acceptance of this article. The implementation was checked for accuracy using theoretical relationships among the models (see Lindsay et al. 2008). HKY, GTR (formally defined in Theory and Methods), and site class heterogeneity variants were all implemented using standard features of PyCogent. All models applied to an alignment were maximized numerically using the PyCogent built-in Powell numerical optimizer with a maximum of five restarts and exit condition (tolerance) set to 10 ^{− 8}. The equilibrium motif probabilities (probabilities of nucleotide, codon, or trinucleotide) were also numerically optimized. This treatment departs from the convention of estimating these probabilities as counts from the observed sequences. For comparison, we also employed the counts approach. The results between the two approaches were highly consistent. Unless otherwise stated, reported results are from the numerical optimization approach. We fit the null model (ω = 1) first and then the alternate model (ω ≠ 1). This procedure ensures that the log-likelihood for the alternate was always greater or equal to that of the null. Trinucleotide variants of the codon models were required for analysis of the intron data as introns contain trinucleotides corresponding to stop codons. The nucleotide HKY/GTR parameters were defined as before. Assuming the standard genetic code, we included an analog of the parameter ω in the trinucleotide model rate matrix when the trinucleotides exchanged correspond to different hypothetical amino acids and neither was a hypothetical stop codon.

Alignment of Protein-Coding Genes

Aside from the functionally unclassified Plasmodium genes (Carlton et al. 2008), all protein-coding sequences were aligned using the built-in PyCogent codon aligner (Knight et al. 2007) using the NF_HKY model. Aligned codon columns that contained a non-nucleotide character were removed and only resulting alignments ≥ 600 nt long were retained.

Sampling Protein-Coding Sequences

Genes in the Ensembl release 50 human, chimpanzee, and macaque genomes annotated as nuclear-encoded one-to-one orthologs were used. After the codon alignment and filtering step, 12,708 alignments remained. We used the Kyoto Encyclopedia of Genes and Genomes ortholog lists to identify one-to-one orthologs between Borrelia burgdorferi, Borrelia afzelli, and Borrelia garinii. After the codon alignment and filtering, 265 alignments remained. The same procedure was used to obtain 796 alignments from Mycobacterium tuberculosis and Mycobacterium leprae. The large sample of Plasmodium vivax and Plasmodium knowlesi genes was already classified with regard to orthology (Carlton et al. 2008). Using the same protein-coding sequence alignment filtering process, there were 2,840 alignments. The orthologs functionally classified as ligand or not originating from taxonomically independent, AT-rich Plasmodium species pairs (Plasmodium falciparum and Plasmodium reichenowi; Plasmodium yoelii and Plasmodium berghei) were from Weedall et al. (2008).

Sampling Intron Sequences

Aligned introns from the human, chimpanzee, and macaque genomes were obtained from Ensembl release 50 using human gene coordinates. A maximum of 100 alignments from each of five blocks of human autosomes (1–3, 3–6, 6–10, 10–15, and 15–22) were sampled to ensure representation across the human genome. Any sequence that may have evolved by a non–point mutation process (gaps in the alignment and simple tandem repeat sequences) was removed in a manner that preserved true trinucleotides (Lindsay et al. 2008). Alignments ≥ 50 kbp long were retained and divided into exactly 50 kbp (truncated to 16,666 trinucleotides) aligned blocks, resulting in 470 alignments.

Simulation of Neutrally Evolving Genes

Simulation of neutrally evolving sequences was done with different nucleotide and codon compositions using the following arbitrarily sampled protein-coding genes: primate orthologs to human gene ENSG00000143520 (∼50% GC); genes belonging to ortholog group K01873 from B. afzelli, B. burgdorferi, and B. garinii (∼30% GC); and an ortholog pair from M. leprae (ML0101) and M. tuberculosis (Rv3800c) (∼65% GC). To simulate sequences with multiplicative codon frequencies, an NF model with the constraint ω = 1 was fit to the selected real biological alignments and PyCogent's built-in alignment simulation function used to simulate 250, 90 kbp long alignments. Simulation of alignments with the observed codon frequencies was performed using the same procedure but employing the CNF_GTR(ω = 1) model. For the rate heterogeneity tests, alignments simulated with CNF_GTR(ω = 1) from the ENSG00000143520 alignment were used.

Statistics

For the standard test of neutrality, the null model was constrained so ω = 1 and lnL_null is the maximized log-likelihood for an alignment. The constraint was removed from the alternate (ω ≠ 1) resulting in the maximized log-likelihood lnL_alt. The likelihood ratio (LR) statistic is then LR = 2[lnL_alt − lnL_null]. For sufficiently long alignments, this LR statistic will be χ₁². For the rate heterogeneity test, the null model allowed ω ≠ 1, whereas the alternate hypothesis specified two site classes (0 ≤ ω ≤ 1 and ω > 1). Although these models differ by two free parameters, the χ₂² quantiles are conservative due to a boundary effect.

We measured the extent to which codon frequencies were nonmultiplicative as the χ² goodness of fit, computed in the standard way from observed codon frequencies counts and counts expected from the normalized product of nucleotide frequencies. The impact of assuming multiplicative codon frequencies was measured using the model form CNF_× (the CNF form with multiplicative codon π) which nests within CNF. The maximum likelihood estimates of ω () were estimated using the GTR variants of these models and denoted _CNF× and _CNF, respectively. The difference between these estimates was measured using an LR. For an individual alignment, _CNF× was determined from fitting CNF_×,GTR and _CNF from fitting CNF_GTR. We then defined a null CNF model, constraining ω_CNF = _CNF×, and maximized the log-likelihood. The difference was measured under the CNF model as .

We measured the extent to which estimates from the three model forms were significantly different using a modification of the LR metric described above. The primary difference for this analysis was replacing CNF_× and _CNF× with NF and _NF or with CF and _CF. We defined an estimate from NF ()/CF () as different from CNF (_CNF) when the LR > 3.84, which corresponds to a probability of 0.05 from χ₁².

Alignment GC% was computed as the mean G+C nucleotide percentage of all sequences.

All scripts and data used in this study are available on request.

Results and Discussion

Simulated Data Demonstrate Method Sensitivity to Composition

When the frequencies of trinucleotides (nucleotides grouped in triplets but not constrained by the genetic code) are multiplicative, the trinucleotide variants of NF and CNF models (NF_tri and CNF_tri) are identical, irrespective of what r terms are included but different from CF_tri (see Theory and Methods). However, because of how NF treats stop codons, the codon variants of the NF and CNF models are not identical even with multiplicative π, and thus their estimates of ω are expected to be slightly different (see Theory and Methods).

For the more realistic condition in which codon frequencies are nonmultiplicative, ω estimates obtained using NF and CNF will differ because NF enforces multiplicative π, whereas CNF does not. The effect of nonmultiplicative π on estimates of ω based on CF is difficult to predict because of the additional sensitivity to composition.

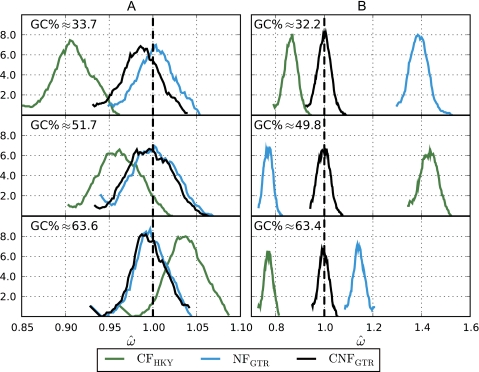
Simulations of neutrally evolving genes confirmed the predicted sensitivity of CF and NF to sequence composition. Simulations were carried out with multiplicative and nonmultiplicative codon frequencies using parameters estimated by fitting GTR variants of the NF and CNF models, respectively, to real sequences with GC% ranging from 30% to 65% (see Theory and Methods). For multiplicative codon frequencies (simulated under NF_GTR(ω = 1)), from the NF and CNF models were similar (fig. 1A) with the largest difference evident for the AT-rich sequences, consistent with the expected bias affecting NF models due to the AT-richness of stop codons (Theory and Methods). As predicted (Lindsay et al. 2008), obtained under the CF model were strongly affected by composition, moving from < 1 to > 1 as sequence composition changed from AT rich to GC rich (fig. 1A). For nonmultiplicative codon frequencies (simulated under CNF_GTR(ω = 1)), both NF and CF models substantially over- or underestimated ω with the direction of departure depending on composition and codon usage (fig. 1B). These results imply that estimates of ω obtained under both CF and NF models do not provide reliable evidence of the mode of natural selection.

FIG. 1.

The effect of nucleotide composition and nonmultiplicative codon frequencies on estimates of ω from simulated neutrally evolving genes. Sequence simulations were based on an AT-rich gene sampled from Borrelia species, a primate gene with AT% ≈ GC%, and a GC-rich gene sampled from Mycobacterium species. Average GC% of the simulated alignments is shown. The x axis is , and the y axis is an estimate of density. (A) Data generated from a NF_GTR(ω = 1) model resulting in multiplicative codon frequencies. (B) Data generated from a CNF_GTR(ω = 1) model with observed (nonmultiplicative) codon frequencies from the sampled genes. The dashed vertical line shows the expected neutral value, ω = 1.

We did not conduct simulations under the CF model because the relationship between ω from the models is shown by equation (3). This relationship establishes, and the above simulations confirm, that ω estimates from the models will differ in a composition-dependent manner. A more suitable benchmark for assessing consistency of ω estimates from the models with the neutral expectation is to analyze real biological sequences that have evolved in a neutral manner with respect to protein-coding content.

Sensitivity to Real Sequence Composition

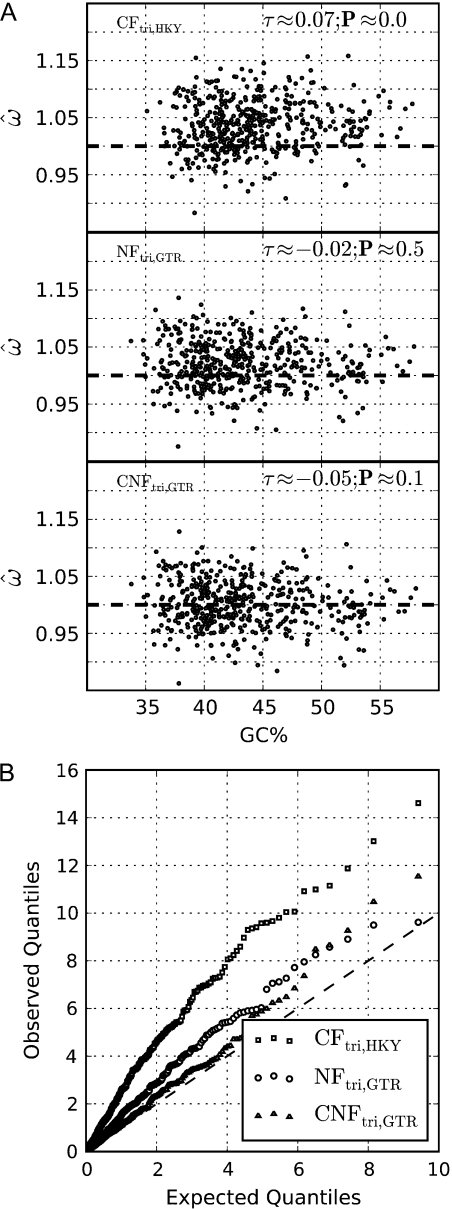
The conditions affecting the evolution of real biological sequences are more complicated than those used for the simulation, with several neutral evolutionary factors, including biased gene conversion (Berglund et al. 2009; Galtier et al. 2009), identified as potentially confounding the estimation of ω from real protein-coding sequences (Supplementary fig. S1, Supplementary Material online). We sought to assess the robustness of the models to these biases. We chose primate introns as they experience the same mutagenic environment as their flanking exons (Green et al. 2003; Duret et al. 2006, Elango et al. 2008), they are not affected by selection for protein-coding content, and they are mostly nonfunctional (Siepel et al. 2005). Using these sequences, we were able to demonstrate that ω = 1 (i.e., no effect of protein-coding selection) from our new model but that previous models led to inaccurate estimates of ω ≠ 1. ω was estimated from intronic sequences using the trinucleotide rather than codon model variants as introns can include trinucleotides that are invalid for codon models (see Theory and Methods). For each model form, the best performing (least correlated) of the parameterizations considered (GTR and HKY; Hasegawa et al. 1985) is shown in figure 2A (see Supplementary fig. S2a, Supplementary Material online, for the remainder). As predicted, ω was significantly correlated with composition even for the best performing CF_tri,s model (fig. 2). Only from NF_tri,GTR,s and CNF_tri,GTR,s did not have a significant association with GC% (fig. 2A). The consistency of the models with the null hypothesis ω = 1 is indicated by the quantile–quantile plots. These confirm that CNF_tri,GTR,s best matches theoretical expectation and that the other models are more prone to false positives (fig. 2B and Supplementary fig. S2b, Supplementary Material online). The strong consistency between CNF_tri,GTR,s and NF_tri,GTR,s in these analyses stems from their being trinucleotide models. The codon NF model will exhibit greater bias due to its treatment of stop codons (Theory and Methods). Our analysis of intronic sequences combined with the relationship between the trinucleotide and codon model forms (Theory and Methods) establishes CNF_GTR as the most robust form for estimating ω.

FIG. 2.

Comparison of the effects of variation in real neutral processes on NF, CF, and CNF models. All alignments were exactly 49,998 nt long (see Theory and Methods). (A) Alignment GC% on the x axis against from the “trinucleotide” models CF_tri,HKY,s, NF_tri,GTR,s, and CNF_tri,GTR,s on the y axis (the best performing [i.e., least correlated] of the parameterizations considered; see Theory and Methods, Supplementary fig. S2, Supplementary Material online). The estimate and significance of Kendall's τ measure of association between GC% and are shown for each panel. The dashed horizontal line is ω = 1. (B) A quantile–quantile plot using quantiles from χ₁² (the expected null distribution) against quantiles of the LRs from testing the alternate (ω ≠ 1) against the null (ω = 1) hypotheses. The dashed diagonal line shows the expected case when the null hypothesis is correct.

These analyses further established that estimates of ω are sensitive to changes in the neutral substitution process. Genomic regions in primates can exhibit pronounced differences in neutral substitution processes (Eyre-Walker and Hurst 2001) which causes substitution model parameters to differ between alignments (Supplementary fig. S1, Supplementary Material online). More general substitution models have a greater capacity to absorb variation in the neutral process between regions. This is borne out by the difference between the HKY and GTR variants; only the CNF_tri,GTR,s variant was sufficiently general to accommodate how the neutral process varied between the alignments, returning ω estimates that were consistent with the null hypothesis. This result further suggests, however, that lineage-specific changes in sequence composition (e.g., Greenbaum et al. 2008) or neutral processes for a single alignment may also affect estimation of ω unless specifically accounted for by the evolutionary model.

Because equilibrium codon frequencies under the NF model are multiplicative, estimates of ω under this model may be biased when this condition is not satisfied (fig. 1B). We tested this on protein-coding genes from bacterial (Borrelia and Mycobacterium), unicellular eukaryote (Plasmodium), and multicellular eukaryote (primates) lineages. The χ² goodness-of-fit statistic between observed codon frequencies and those predicted from nucleotide frequencies was used to measure the magnitude of nonmultiplicative codon frequencies. Bias in ω was determined by comparing estimated from CNF_× (the multiplicative form of CNF) with estimated from the standard CNF form using an LR (see Theory and Methods) with a large LR indicating a large error when multiplicative codon frequencies are assumed. A positive correlation between the χ² and LR statistics was observed for all lineages (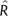² ranged from ∼0.20 for primates to ∼0.58 for Mycobacterium, all P < 10 ^{− 21}; see Supplementary fig. S3, Supplementary Material online) indicating that departure from the assumption of multiplicative CF biases , consistent with the theoretical prediction. By comparison, a parallel analysis using CF showed much weaker associations (Supplementary fig. S4, Supplementary Material online).

Model Discordance in ω Estimates from Pathogens

We assessed the practical significance of model choice by measuring the proportion of loci for which estimates of ω differed substantially between the models. The same LR metric of discordance in was employed, except in this case we used NF or CF instead of CNF_× (see Theory and Methods). Using an LR > 3.84 as indicating a difference between ω estimated from CF/NF and CNF models showed that the three model forms were largely consistent for the primate data but differed markedly for the other lineages (table 3). under both CF and NF differed from under CNF for ∼10% of Mycobacterium loci, although the reasons for the discordance likely differ between the models. The ∼30% discordance between NF and CNF for Borrelia may arise from the bias inherent in NF on AT-rich sequence (fig. 1A, see Theory and Methods). For Plasmodium genomes, NF was highly concordant with CNF, whereas the widely used CF model was ∼15% discordant (table 3). The discordance between the models when codon frequencies were estimated using the typically employed counting procedure emphasized the poorly behaving models; the discordance of NF_GTR increased to ∼40% of Borrelia loci and CF_HKY discordance doubled to ∼30% of Plasmodium loci. These differences may stem from reduced power of the numerical optimization procedure arising from the variability of the π.

Table 3.

Discordance of Estimates of ω between the NF/CF and CNF Models

Lineage	NF%	CF%	Total
Borrelia	30.1	0.0	265
Mycobacterium	9.9	7.9	796
Plasmodium	0.0	14.9	2,840
Primate	1.3	0.9	12,708

NOTE.—Percentage of loci for which under NF/CF models differ (LR > 3.84) from under the CNF model. Total: the number of loci examined for the indicated lineage.

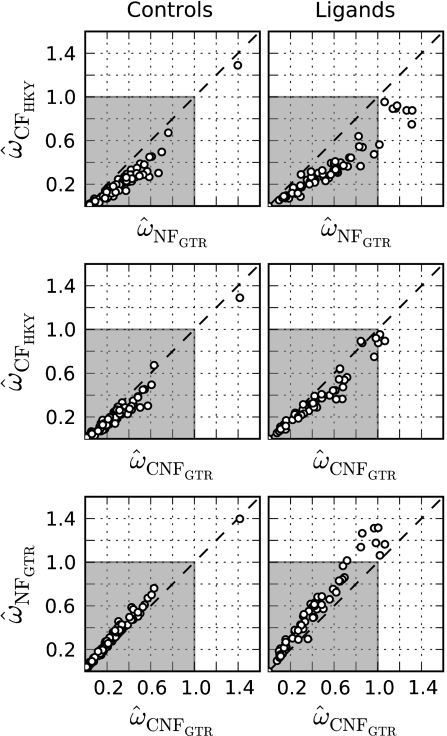
The high error rate for CF applied to Plasmodium (table 3) arises from systematic underestimation of ω, an effect that can cause strong candidates for adaptive evolution to be misclassified. The molecular arms race underway between Plasmodium parasites and their hosts predicts that Plasmodium genes that mediate interactions with the host should exhibit evidence for adaptation. Our results (fig. 1A and table 3) suggested that the low GC% of some Plasmodium genomes, however, will cause CF to systematically underestimate ω, potentially providing false-negative evidence of the involvement of genes in host–parasite interactions. We confirmed this potential in an analysis of Plasmodium genes classified by experimental evidence as ligands or not ligands and thus likely or unlikely candidates for adaptive evolution, respectively (Weedall et al. 2008). Using orthologous gene pairs from Plasmodium species with AT-rich genomes, _CFHKY (ω estimated from CF_HKY) was systematically underestimated for both the control and the adaptive candidate genes (points were typically scattered below the diagonal, fig. 3). In contrast, for a small number of candidate genes, _CNFGTR lay within the zone indicative of adaptive evolution, supporting an adaptive role for these genes. Although from NF and CNF were largely indistinguishable (table 3), a general trend toward overestimation by NF was evident (an excess of points were scattered above the diagonal, fig. 3).

FIG. 3.

Evidence the CF model is prone to underestimating positive natural selection in Plasmodium. Plotted are from the models indicated by subscript on the x and y axes. The gray region corresponds to the realm of ω values representing neutral or purifying natural selection. Values of ω outside this zone indicate positive natural selection. The left and right plot columns are from Plasmodium control and ligand loci, respectively. Dashed diagonal lines correspond to a slope of 1.

Hypothesis Tests Affected by Composition

We have demonstrated that the properties of commonly used substitution models result in systematic errors and that these can affect test results. This finding is based on tests involving the comparison of only two or three sequences. More powerful tests have been developed that compare estimates of ω across lineages in a phylogenetic tree of multiple sequences. Other tests have been developed based on rate heterogeneity at individual sites that overcome the loss of power that results when whole genes are used to estimate ω, but adaptive sequence changes are restricted to a small fraction of codons within genes (Nielsen and Yang 1998; Yang and Nielsen 2002). Combinations of these branch and site tests have also been devised (Zhang et al. 2005).

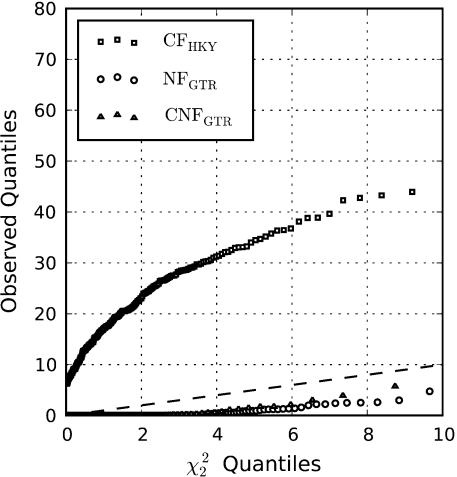
In principle, the biases demonstrated in our simulations should affect all tests for selection that incorporate ω = 1 into the null hypothesis, including these more powerful versions. Using the systematic biases of ω evident in the middle panel of figure 1B, for example, we would predict CF models to give false positives and NF models to give false negatives, irrespective of the specific type of test employed.

We tested this prediction for the case of an alternate hypothesis of among-site heterogeneity of ω, using a simple form of mixture model that specifies two site classes with neutral positions evolving according to 0 ≤ ω ≤ 1 and adaptive positions evolving according to ω > 1. Using the sequences simulated under a single site class CNF model with ∼50% GC (fig. 1B), we found, as predicted, that the CF form was conspicuously prone to false positives, whereas the NF model was weakly conservative (fig. 4).

FIG. 4.

Incorrect Type 1 error rates for CF and NF in testing the null hypothesis of one class of sites against the alternate of two site classes. The sequences were the same as those from figure 1B with GC% ≈ 50—simulated under CNF_GTR(ω = 1). The dashed diagonal line is the expected quantile relationship for χ₂².

Conclusions

Because the inferred mode of natural selection is based on the position of ω relative to 1, the sensitivity of under the CF/NF forms to aspects of sequence composition means that erroneous conclusions can result from use of these model forms. This problem is particularly acute in analysis of pathogen genomes, in which extreme sequence composition biases are common. As we have shown here for a modest number of pathogens, choice of method can alter inference regarding the mode of natural selection. Such erroneous conclusions could impact vaccine design, for instance, by unnecessarily retarding the speed of epitope mapping or prompt a complete rejection of the powerful signature of natural selection from the vaccine development process. The new CNF model we present significantly improves robustness to the diversity of sequence compositions evident in nature by unifying the generality of the CF form with the nucleotide composition independence of NF. Our demonstration of the sensitivity of all models to changes in the neutral process implies, however, that resolving lineage-specific adaptive episodes, such as those underpinning host specificity, may require removing the constraint of time reversibility from this model class.

Supplementary Material

Supplementary figures S1–S4 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).