Inference and Characterization of Horizontally Transferred Gene Families Using Stochastic Mapping

Abstract

Macrogenomic events, in which genes are gained and lost, play a pivotal evolutionary role in microbial evolution. Nevertheless, probabilistic-evolutionary models describing such events and methods for their robust inference are considerably less developed than existing methodologies for analyzing site-specific sequence evolution. Here, we present a novel method for the inference of gains and losses of gene families. First, we develop probabilistic-evolutionary models describing the dynamics of gene-family content, which are more biologically realistic than previously suggested models. In our likelihood-based models, gains and losses are represented by transitions between presence and absence, given an underlying phylogeny. We employ a mixture-model approach in which we allow both the gain rate and the loss rate to vary among gene families. Second, we use these models together with the analytic implementation of stochastic mapping to infer branch-specific events. Our novel methodology allows us to infer and quantify horizontal gene transfer (HGT) events. This enables us to rank various gene families and lineages according to their propensity to undergo gains and losses. Applying our methodology to 4,873 gene families shows that: 1) the novel mixture models describe the observed variability in gene-family content among microbes significantly better than previous models; 2) The stochastic mapping approach enables accurate inference of gain and loss events based on simulations; 3) At least 34% of the gene families analyzed are inferred to have experienced HGT at least once during their evolution; and 4) Gene families that were inferred to experience HGT are both enriched and depleted with respect to specific functional categories.

Introduction

Sophisticated bioinformatics algorithms are required in order to extract meaningful biological information from vast comparative genomic data. Gene-content variation among species is a phenomenon that poses a great research challenge (Berg and Kurland 2002; Mira et al. 2002; Konstantinidis and Tiedje 2004; Koonin and Wolf 2008). Gene content varies among genomes due to both heterogeneity in the number of paralogous members in each gene family and variation in the presence of different gene families (i.e., gene-family repertoire). Investigating the latter is informative for understanding genome biology because variation in the repertoire of gene families is correlated with evolutionary shifts in proteome functionality. Variation of gene families across genomes results from either gene gains or losses. The availability of hundreds of sequenced microbial genomes has led to the realization that such macroevolutionary events are a dominant evolutionary force shaping microbial genomes.

A well-studied mechanism for gene gain is horizontal gene transfer (HGT) (Syvanen 1994; Garcia-Vallve et al. 2000; Ochman et al. 2000; Koonin et al. 2001). The acquisition of novel gene families via HGT is a dominant factor in microbial evolution (Doolittle et al. 1990; Nelson et al. 1999; Gogarten and Townsend 2005; Choi and Kim 2007). Thus, accurate modeling and inference of HGT is vital for understanding such phenomena as speciation, adaptation to new ecological niches, and the evolution of novel functions (Syvanen 1994; Jain et al. 2003; Lake and Rivera 2004).

Several computational methods for detecting HGTs exist today. The first category of such methods uses compositional disagreement between a gene and the genome in which it resides as predictors of horizontal transfer (e.g., atypical G + C content or codon-usage patterns). Notably, due to sequence amelioration, such methods are limited to detecting recent transfers (Lawrence and Ochman 1997), and their success hinges on the donor and recipient having different sequence characteristics (Koski et al. 2001; Wang 2001). The second category utilizes phylogenetic conflicts as predictors of HGT. Gene trees reconstructed from the assembly of specific orthologs are compared with species trees (Lyubetsky and V'yugin 2003). These methods are limited to genes that exist in most members of the phylogenetic group studied, where extreme sequence divergence (saturation) and extreme conservation (no phylogenetic information) hinder HGT detection (Graybeal 1994).

Others and we have developed methodologies for analyzing gene-family gain and loss events in general (e.g., Snel et al. 2002; Mirkin et al. 2003; Hao and Golding 2004; Lake and Rivera 2004; Spencer et al. 2005, Spencer. 2007; Cohen et al. 2008; McCann et al. 2008). In such methodologies, the presence and absence of all gene families in all studied species, that is, the phyletic pattern, are analyzed where presence indicates that at least one homolog from a certain gene family is identified in a given genome. Notably, there are several existing models that take into account the number of members within gene families, but given their computational complexity, they are less common (Gu and Zhang 2004; Hahn et al. 2005; Csuros and Miklos 2006; Spencer et al. 2006; Iwasaki and Takagi 2007). The evolution of phyletic pattern is governed by transitions between presence and absence, where a gain transition reflects either de novo appearance (“birth”) or HGT of a gene from a family previously absent in the acceptor genome. Similarly, a loss transition corresponds to deletions of all members of a gene family. Notably, accurate tests for HGT inference based on probabilistic-evolutionary models of phyletic data are not yet available.

Evolutionary transitions between presence and absence of gene families were first analyzed using the Dollo parsimony criterion (Kunin and Ouzounis 2003; Mirkin et al. 2003) and later using the more statistically justified maximum likelihood (ML) paradigm (Huson and Steel 2004; Zhang and Gu 2004; Hahn et al. 2005; Hao and Golding 2006). In early ML-based models, all gene families were assumed to evolve under the same evolutionary rate (Marri et al. 2007). This is an oversimplified description of gene-family gain and loss dynamics given the high variance in the tendency of various gene families to undergo such events (Nakamura et al. 2004; Lerat et al. 2005). This simplification was recently alleviated by the development of among-gene-family-rate variation models, which were shown to significantly better fit observed phyletic-pattern data (Cohen et al. 2008; Hao and Golding 2008).

Some gene families tend to be more transferred (gained) than others, and the same is true regarding the tendency of gene families to be lost (e.g., Jain et al. 2002; Krylov et al. 2003). This implies that both the gene-family gain rate and loss rate may vary across gene families. Such heterogeneity of gain and loss rates can be described using probabilistic models that allow the stochastic process to vary across gene families, that is, mixture models (MMs). Specifically, accounting for rate variation only, rather than variation of the stochastic process itself, may fail to accurately describe the evolution of gene families with exceptional gain/loss rate ratio. This observation calls for the development of MMs for the analysis of phyletic-pattern data. Notably, MMs were shown to be very helpful in the analysis of DNA and protein-sequence data (e.g., Huelsenbeck and Nielsen 1999; Lartillot and Philippe 2004).

In the analysis of sequence evolution, evolutionary models are used to infer the probability and expectation of branch site–specific transitions using a methodology termed stochastic mapping (Nielsen 2002; Huelsenbeck et al. 2003; Minin and Suchard 2008a). This methodology was shown to be accurate and robust in respect to possible model misspecifications (O'Brien et al. 2009). Here, we utilize our novel models for describing gene family gain and loss dynamics, as well as an analytic implementation of stochastic mapping (Minin and Suchard 2008a), to develop a novel methodology that can reliably infer gain and loss events during the evolution of gene families.

Our methodology is also suitable for accurately quantifying the transferability of gene families. This quantification, in turn, allows studying the selection forces dictating the probability of fixation of a newly transferred gene family. It is usually accepted that the tendency of a gene family to undergo HGT depends on the protein function (e.g., Nakamura et al. 2004). Gene families associated with metabolism were shown to be more transferable than those related to information processing (Rivera et al. 1998; Jain et al. 1999). However, the dependency between transferability and gene function is currently debated as it has also been claimed that HGT is nearly neutral to all gene functions (Choi and Kim 2007).

In this paper, we develop a MM for phyletic-pattern analysis and show that it better fits phyletic-pattern data. This model is integrated in a stochastic mapping method that enables accurate detection of lineage-specific gain and loss events. We use this methodology for HGT inference and show that it can accurately quantify gene-family transferability. We apply our method to analyze 4,873 gene families across 66 genomes and test the dependence between gene-family transferability and function (i.e., biological process).

Materials and Methods

Evolutionary Models of Gene-Family Gains and Losses

The evolution of gene-family content along a given phylogenetic tree is modeled using probabilistic-evolutionary models. The data are represented as a matrix D, in which rows (1,…,S) represent genomes and columns (1,…,F) represent gene families. In this matrix, D_sf = 1 if gene family f is present in the genome of species s, and D_sf = 0, otherwise. All gene families are assumed to evolve along a phylogenetic tree. The evolution of each gene family follows a continuous time Markov process over a two-state alphabet {0,1}, assuming independent evolution among gene families. Notably, in this representation, the evolution of gene families, rather than orthologous genes, is modeled, and thus, a character “1” is assigned to a specific gene family regardless of the number of paralogs in this gene family.

The probability that character i will be replaced by character j along a branch of length t is denoted P_ij(t) and can be computed by [P(t)]_ij = [e^Qt]_ij where Q is the instantaneous rate matrix. More specifically, Q is given in the following form:

(1)

where g ≡ Q_0→1 denotes the gain rate parameter and l ≡ Q_1→0 denotes the loss rate parameter. P_ij(t) in this case is calculated analytically (Ross 1996).

This basic model is most likely unrealistic, because it implicitly assumes that all gene families evolve with the same Q. Adding a gene-family specific rate generalizes this model and allows for a more realistic description of gene-family evolution (Cohen et al. 2008; Hao and Golding 2008). We term this model M1 + Γ.

Gain–Loss Mixture Models

In the above model, the rate matrix Q is assumed to be identical for all gene families, up to a multiplication factor. To alleviate this assumption, we suggest a model, in which a small number of different Q matrices is assumed (Q₁₁,…,$Q_{K_g,K_l}$). Here, K_g represents the number of allowed gain rates, K_l represents the number of loss rates, and thus all K_g × K_l combinations of gain and loss rates are modeled (i.e., the MM is composed of K_g× K_l stochastic process components). We do not estimate all these matrices from the data but rather assume that both the gain and loss rates are sampled from two independent gamma distributions: gain ∼ Γ(α_g, β_g) and loss ∼ Γ(α_l, β_l), where α and β are the shape and scale parameters, respectively, and α/β is the mean of the distribution. Notably, for the loss distribution α_l = β_l. The reason we do not allow β_l to be a free parameter is to avoid redundancy with branch-length optimization. The gamma distribution is used as it is flexible enough to capture a large set of unimodal distributions, yet it requires only a few parameters. This distribution is widely used to model among-site rate variation for sequence analysis (Yang 1993; Rogers 2001; Susko et al. 2003). In practice, a discrete gamma distribution with equal probabilities is assumed, so that the prior probability of each rate matrix is p(Q_ij) = (K_g K_l)⁻¹. All results presented in this work were computed with K_g = K_l = 4, which was found to balance well between running times and accuracy. The stationary frequencies of matrix Q_ij are obtained by π_Qij(1)= g_i/(g_i + l_j) where g_i is the ith gain rate category, and l_j is the jth loss rate category. This model is termed MM1.

Nonstationary Models: Independent Character Frequencies at the Root

The M1 + Γ and MM1 models both assume that the character frequencies at the root are equal to the stationary ones (π_Q = π_ROOT). We have additionally implemented models M2 + Γ and MM2, in which we allow π_ROOT to differ from π_Q, adding a single free parameter to each model. Notably, for the MM1 model, each of the stochastic process components has a different stationary character distribution, and therefore different character frequencies at the root, whereas for MM2, the character frequencies at the root are free to differ from the stationary ones, but the estimated root frequencies are assumed to be the same for all stochastic process components.

Likelihood Computation

The likelihood of gene family f in the data is computed given the tree topology and set of branch lengths denoted by T and t, respectively:

(2)

The log likelihood of the entire data (F gene families) is then

(3)

Likelihood computations are achieved using Felsenstein's (1981) pruning algorithm adapted for nonstationary stochastic models (Yang and Roberts 1995; Galtier and Gouy 1998; Boussau and Gouy 2006). All free parameters of the model are estimated such that they maximize the likelihood of the data using Brent's (1973) optimization scheme. For each model, its free parameters were estimated one at a time in an iterative manner. To avoid local likelihood maxima, random starting points were used during the optimization process.

Likelihood Correction Accounting for Unobservable Data

A column of zeros represents gene families that are absent in all taxa and are not observable. The likelihood must be corrected for these unobservable data (Felsenstein 1992):

(4)

where L⁽⁺⁾_f is the corrected likelihood term for gene family f, L_f is the likelihood as computed in equation (2), and L⁽⁻⁾ is the probability to generate an unobservable pattern given the model and tree. Let D₀ denote a column of zeros (the unobservable pattern). L⁽⁻⁾ is thus the likelihood of obtaining D₀ given the model and tree. For the MMs,

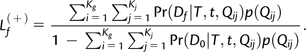(5)

We note that for data extracted from the clusters of orthologous groups of proteins (COG) database (used in this analysis), orthologs are identified by three-way patterns of sequence similarity among genomes, so a gene family does not appear in the COG database unless it occurs in at least three genomes. In these data, in addition to the zeros pattern (D₀), patterns in which the gene family is present in only one or two species are unobservable as well. Let O be the set of all unobservable patterns, that is, the set of all columns, in which there are less than three 1s. To correct for the unobserved data, we must now compute L⁽⁻⁾ accounting for all possible unobservable patterns (for the 66 genomes analyzed here, the set of unobservable patterns includes a column of zeros, 66 columns in which there is a single 1, and all the remaining entries are “0,” and 2,145 columns with exactly two 1s). Denoting by L_p⁽⁻⁾ the probability of the pth unobserved pattern, the probability of obtaining an unobserved pattern becomes

(6)

L⁽⁺⁾_f is thus computed as in equation (4), but in the denominator, we now sum over all unobservable patterns.

Gain and Loss Computation for Each Gene Family

We compute the posterior expectation of the gain and loss rates for each gene family using the following equations:

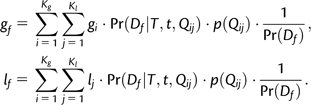(7)

The Posterior Expectation of the Number of Gains and Losses along a Branch

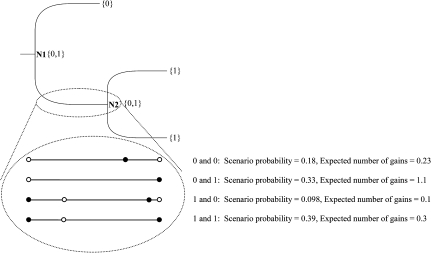
The posterior expectation of the number of gains and losses along a certain branch for a specific gene family can be computed. We first explain the computation for the simple case of a single Q matrix and then extend it to the MM. The computation for a toy example is shown in figure 1. Let b denote a branch connecting nodes n₀ and n_t. Without loss of generality, we only show the computation of the posterior expectation of gain events:

(8)

Here, N₀₁(b) denotes the number of gain events occurring along the branch b. This expression can be computed as follows:

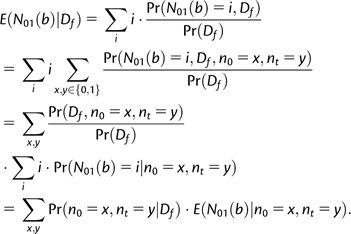(9)

The first factor, $\mathrm{Pr}(n_0=x,n_t=y|D_f)$, is computed using the pruning algorithm (Felsenstein 1981), adapted for nonstationary stochastic models. This factor corresponds to the “scenario probability” in the toy example of figure 1. The second factor, $E\left(N_{01}\right(b\left)\right|n_0=x,n_t=y)$, is computed analytically for stochastic processes with binary alphabet (Minin and Suchard 2008a). This factor corresponds to the “expected number of gains” in the toy example of figure 1. In the MMs, the posterior expectation is computed as a posterior average over all possible Q matrices:

(10)

E(N₀₁(b)|D_f) is an estimate of the number of gain events in a specific lineage b in a specific gene family f. Thus, the total number of gain events for a gene family is the sum of gain events over all lineages and the total number of gain events for a lineage is the sum over all gene families. The posterior probability of at least one gain event in a specific lineage in a specific gene family is computed in a similar fashion (Minin and Suchard 2008a).

FIG. 1.

Toy example. Shown is the computation of the posterior expectation of the number of gain events for the branch connecting nodes N1 and N2. The total expectation equals 0.53 and is computed as the weighted sum over four scenarios: N1 = 0 and N2 = 0, N1 = 0 and N2 = 1, N1 = 1 and N2 = 0, and N1 = 1 and N2 = 1. The gain and loss rates of the Q matrix used for this computation are 0.35 and 0.7, respectively, and π_ROOT=0.5. For each scenario, the most plausible event leading to a gain event is depicted.

Phyletic Pattern Data and Reference Phylogeny

The presence and absence of gene families for each species were extracted from the updated version of the COG database (Tatusov et al. 2003). The data set includes 4,873 gene families spanning 66 species: 50 Bacteria, 13 Archaea, and 3 Eukaryota. The reference tree topology was taken from the “tree of life” (Ciccarelli et al. 2006). Notably, for few species, the COG data set and the Ciccarelli tree used different National Center for Biotechnology Information (NCBI) taxonomy IDs, denoting different substrains. In these cases, we assumed that different substrains have the same placement on the species tree. This assumption was validated by inspecting the positions of both substrains in NCBI's common species tree. For each model, branch lengths were estimated based on the phyletic data using the ML framework. The branch lengths in all models were normalized with respect to the rate matrices, so that a unit branch length corresponds to one expected gain–loss event per gene family at stationarity (e.g., Yang et al. 1994; Yang and Roberts 1995). For the models in which the character frequencies at the root are allowed to differ from the stationary ones, the position of the root must be determined. Thus, for these models, we find the position of the root by maximizing the likelihood of the data given the root position. As a control, we also repeated the analysis with the NCBI taxonomy tree topology (Wheeler et al. 2004).

A Simulation Study—Testing the Accuracy of Gain Inference

We have evaluated the performance of our stochastic mapping–based method to reconstruct gain and loss events using simulations. The simulations were performed by drawing the waiting times and transition events based on the underlying Markov process. All the substitution events were recorded for each gene family, for each branch. The genomes resulting from the simulations were used as input to our methodology for the inference of gain and loss events. To be consistent with the COG data, all resulting patterns with less than three 1s were removed from the analysis. Thus, unobservable patterns in the simulations mimic unobservable patterns in the real data. Based on this scheme, we were able to estimate the accuracy of our model-based mapping method. The stochastic simulations that produced the sequences were based on the same phylogeny we use for analyzing the phyletic patterns. In each simulation run, the gain and loss rates for each gene family were randomly sampled from a uniform distribution over the range [0.01, 2] and [0.01, 5], respectively. The root frequency for each run was sampled uniformly in the range [0.01, 0.99]. Notably, the parameter ranges are assumed to cover most biologically plausible values. The resultant genomes were analyzed under M1 + Γ, M2 + Γ, MM1, and MM2 optimizing the models’ free parameters. Next, the posterior number of gains and losses for each gene family and each branch were computed and compared with the “true” recorded events. In addition, we estimated the accuracy when the gain and loss rates for each gene family were randomly sampled from the gamma distributions estimated for the COG data set.

Testing Whether a Gene Family Had Undergone an HGT Event

We have used the MM2 model to develop a method for testing whether a given gene family had undergone at least one HGT event (although the method can work with any other model). Our test is based on the observation that a single gain event across the entire phylogeny may reflect de novo appearance of a gene family. Thus, our test aims to detect those gene families in which the data suggest at least two gain events. Specifically, for a given gene family, we compute the posterior probability for at least one gain event in each tree branch. If the two highest probabilities are higher than a given threshold—this gene family is classified as “transferable” (undergone HGT). In order to determine this threshold we simulated data sets under MM2, where the gain and loss rates were sampled from the gamma distributions with parameters equal to those estimated from the real data. The threshold was fixed such that on these simulated data, the rate of false positive classification of transferable genes is lower than 0.05.

Program Availability

The evolutionary models and inference methods were implemented in C++. Source code, Windows executable, makefile for Unix machines, and brief manual are available in http://www.tau.ac.il/∼talp/phyletic_patterns.html.

Results

Nonstationary MMs for the Analysis of Phyletic Patterns

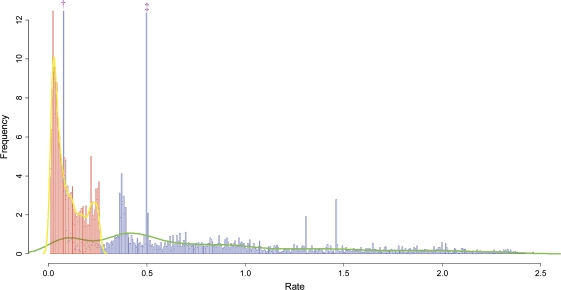
Several probabilistic models in increasing order of complexity were implemented. The simplest (M1 + Γ) assumes a single rate matrix (one free parameter for the gain rate and one for the loss rate). An additional free parameter is used to model rate variability among gene families. On a data set of 4,873 gene families across 66 species, the maximal log likelihood obtained under this model was −91,962.8. This model, however, assumes that the ratio of gain and loss rates is the same across all gene families, although biological intuition suggests that some gene families tend to be either gained or lost significantly more than others. Indeed, the mixture model (MM1) that allows for the gain and loss ratio to vary across gene families fits the data significantly better than M1 + Γ, with maximal log-likelihood differences in the orders of dozens (table 1). The justification for MMs that allow for independent distributions for gain and loss rates is evident in figure 2, where the empirical distributions of gain and loss rates of the COG gene families are presented (the computations of the gain and loss rates are based on eq. 7 above).

Table 1.

Comparison of Evolutionary Models Used for the Analysis of Phyletic Patterns.

Model	Assumptions	MLE of Model Parameters	Maximum Log-Likelihood
M1 + Γ	Rate ∼ Γ(α), πROOT = πQ	g = 0.54	−91,962.8
		l = 6.61
		α = 0.73
M2 + Γ	Rate ∼ Γ(α)	g = 0.12	−90,293.7
		l = 2.08
		α = 0.87
		ΠROOT(1) = 0.45
MM1	Gain ∼ Γ(αg, βg), loss ∼ Γ(αl), πROOT = πQ	αg = 0.35	−91,873.9
		βg = 5.63
		αl = 0.86
MM2	Gain ∼ Γ(αg, βg), loss ∼ Γ(αl),	αg = 0.32	−89,590.1
		βg = 9.87
		αl = 1.0
		ΠROOT(1) = 0.59

MLE denotes maximum likelihood estimate.

FIG. 2.

The empirical distributions of gain and loss rates. The empirical distribution of gain rates (red) and loss rates (blue) were computed for all 4,873 COG gene families. The bins denoted by the symbols “†” and “‡” represent the loss rate of the 63 gene families that are present in all species and the loss rate of the 288 gene families that are present only in the three eukaryotes, respectively.

The MM1 model assumes that the stationary character frequencies are equal to those at the tree root. Allowing the root frequencies to differ from the stationary ones significantly improves the fit of the model to the data (a difference of hundreds of log-likelihood points, comparing models MM1 and MM2, table 1). Interestingly, in one aspect, MM2 is less flexible compared with MM1: The root frequencies of all rate matrices are assumed to be the same in MM2, whereas in MM1, each rate matrix is associated with its own root frequencies. Our results show that in terms of model fitting, the contribution of nonstationary character frequencies at the root (MM2) is more significant than the contribution of allowing different character frequencies at the root for each rate matrix (MM1) (table 1).

Accuracy of Branch-Specific Inference of Gain and Loss Events

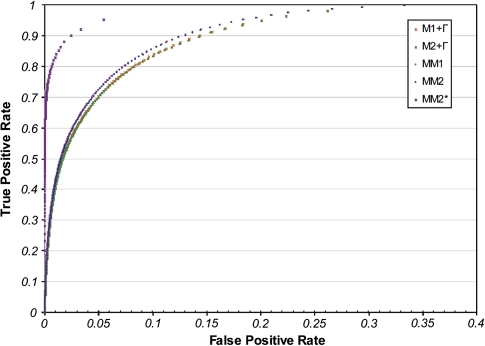
A computational method to infer the posterior expectation of the gain and loss events for each gene family and for each tree branch was developed (see Materials and Methods). This method is especially useful when analyzing microbial genomes as it points to putative HGT (gain) events. We evaluated the accuracy of our novel method to infer gain and loss events for a given gene family along a specific branch using simulations. Generating a data set of the same size as the real data set analyzed above, we tested the performance of our method over a wide range of parameters. Notably, the distributions of the gain and loss rate parameters that were used to generate the data were different from those estimated from the real data (see Materials and Methods). This was done in order to avoid evaluating the method under favorable conditions, in which the model used for the inference is the same as that used to generate the data. For comparison, we also simulated the data with gain and loss rate parameters sampled from the estimated gamma distributions. This comparison allows us to quantify the error under favorable conditions (the inference is done assuming the correct type of distribution used to generate the data, yet the shape and scale parameters are evaluated in each simulation run). Receiver operating characteristic (ROC) curves were used to evaluate the performance of the inference methodology under each of these settings. The performance of the inference under all models ranges from an area under the curve (AUC) of 0.85 (M1 + Γ) to 0.96 (MM2) (fig. 3). Notably, AUC values obtained for the MMs (both over 0.95) are higher than those obtained for models with only rate variability (both 0.85), indicating that accounting for heterogeneity in the gain and loss rate ratio among gene families results in more accurate inference of gain and loss events. In contrast, allowing the root frequency to differ from the stationary one had little impact on the accuracy of the inference (<0.06% change in the AUC).

FIG. 3.

ROC curve for the inference of gain events. The accuracy of the stochastic mapping method to infer gain events for a given gene family along a specific branch was evaluated using simulations.

As expected, an even higher performance (AUC higher than 0.98) is obtained when inference is performed using MM2, and the data simulation is performed by sampling gain and loss rates from gamma distributions (fig. 3, MM2*). Importantly, these performance comparisons under various models demonstrate that the inference of gain and loss events is highly robust to model misspecifications. Because in reality, the true distributions of gain and loss rate parameters are unknown, henceforth, we report performance analysis under MM2, under unfavorable conditions (the data are generated using a different distributions than those used for the inference). Furthermore, in subsequent analyses, we limit the false positive rate to 0.05. This enables a recall rate (true positive gain events) of 0.72. This value corresponds to a posterior probability threshold of 0.2 that at least one gain event has occurred in the specific branch. A similar performance is obtained for the inference of loss events (supplementary material, fig. S1, Supplementary Material online) with AUC over 0.94.

Inference of Events is Robust to Uncertainties in the Species Tree

In our methodology, the topology of the species tree is assumed to be known. It is important to test how robust our results are to possible inaccuracies in the assumed species tree topology. This was estimated by comparing the results obtained using Ciccarelli's underlying topology (Ciccarelli et al. 2006) with the results obtained using NCBI's consensus species tree http://www.ncbi.nlm.nih.gov/Taxonomy/CommonTree/wwwcmt.cgi. Specifically, we inferred the number of gain events for each of the 4,873 gene families under each of the two alternative topologies and computed the Pearson correlation among these two vectors. Reassuringly, high correlation coefficients were found for all four implemented models: 0.93, 0.94, 0.96, and 0.88 for models M1 + Γ, M2 + Γ, MM1, and MM2, respectively. Similar results were obtained when comparing the number of loss events under both tree topologies. These results show that our results are relatively robust with respect to the underlying assumed tree topology.

The Percent of Transferable Genes

Our method for the inference of gain events was utilized to classify each gene family as either transferable (high posterior probability to have undergone HGT, i.e., at least two gain events over the entire tree) or not. The classification methodology ensures a false positive rate of less than 0.05 and enables a recall of 0.85, as determined using simulations.

Of all gene families, 34.23% were classified as transferable. This estimation is highly conservative for several reasons. First, simulations according to which the test threshold was determined (see Materials and Methods) suggest that limiting the false positive rate to 0.05 resulted in an estimate of ∼15% positive cases that were misclassified as nontransferable. Second, we demand at least two gain events, although in fact, in some of the gene families, a single gain event probably reflects HGT rather than de novo birth. Third, our requirement for two branches, each having high posterior gain probability, is somewhat arbitrary and, although proven accurate in simulations, may render some cases of HGT undetected. For example, our definition would miss a case in which there is high probability for a gain event along one branch and small probability for a gain event along several other branches, which taken together may suggest HGT. Finally, phyletic-pattern estimations are conservative because they only consider HGTs that result in the “birth” of a novel gene family. Thus, for example, HGTs resulting in the recipient genomes gaining additional members of existing gene families are ignored.

When we performed the analysis using a less stringent criterion for transferability, demanding only a single gain event, 55.69% of gene families were classified as transferable. This definition implicitly assumes that the vast majority of gain events correspond to HGT. Specifically, it assumes that most cases of a single-gain event reflect HGT from donors not present in the data, rather than de novo appearance. In the following analysis, we adhered to the more stringent criterion, in order to be more conservative.

Biological Function Trends within Transferable Gene Families

Although transferable gene families were found to be 34.23% of the entire set of gene families analyzed, their percentage was substantially different among some functional categories (table 2). Functional classification was based on the COG database, which lists 25 categories grouped into four supercategories: “Information storage and processing,” “Cellular processes and signaling,” “Metabolism,” and “Poorly characterized.” Among the supercategories, the first two were found to be significantly depleted in transferable gene families, whereas the other two were found to be enriched (P values of 0.00023, 0.00053, 0.028, and 0.1, respectively; Fisher's exact test; table 2). Because the enrichment and depletion tests were performed over all 25 COG functional categories, all P values were corrected for multiple testing using false discovery rate (FDR) (Benjamini et al. 2001). The inclination of transferable genes toward metabolic roles rather than information-related roles is in agreement with current views regarding HGT functional bias (e.g., Rivera et al. 1998; Nakamura et al. 2004). The observed trend with respect to “Cellular processes and signaling” and “Poorly characterized” supercategories is currently less discussed in the literature. We speculate that the depletion in “Cellular processes and signaling” may reflect selection against the transfer of housekeeping genes. The enrichment in “Poorly characterized” gene families may reflect the fact that genes with overall sparse taxonomical representation are both frequently inferred as transferable and tend to be poorly characterized.

Table 2.

Percent of Transferable Gene Families in Functional Categories that Significantly Differ from the Background Percent of All Gene Families.

Functional Categories	Transferable Gene Families Out of the Total Number of Gene Families in Each Functional Category (P Value)
(A)
METABOLISM	38.93% (0.028)
POORLY CHARACTERIZED	37.19% (0.1 a)
Carbohydrate transport and metabolism	46.96% (0.011)
Replication, recombination, and repair	46.63% (0.011)
General function prediction only	39.03% (0.092 a)
Energy production and conversion	41.47% (0.1 a)
Depleted Functional categories
(B)
CELLULAR PROCESSES AND SIGNALING	25.9% (0.00053)
INFORMATION STORAGE AND PROCESSING	24.9% (0.00023)
Translation, ribosomal structure, and biogenesis	12.25% (3.72E−09)
Intracellular trafficking, secretion, and vesicular transport	12.03% (1.66E−06)
Transcription	18.61% (0.00015)
RNA processing and modification	4.0% (0.011)
Cell motility	17.71% (0.012)
Cell cycle control, cell division, and chromosome partitioning	19.44% (0.06 a)

(A) Enriched categories (significantly higher than 34.23%). (B) Depleted functional categories (significantly lower than 34.23%). Supercategories are in bold and in upper-case letters. All P values were computed using Fisher's exact test.

^aFunctional categories for which the P value is not significant after FDR correction but lower or equal to 0.1.

Performing this analysis with respect to the entire list of 25 biological process categories enables further understanding of the factors that determine transferability. All functional categories with significant enrichment or depletion of transferable gene families are listed in table 2. The functional category with the highest percentage of transferrable gene families is “Carbohydrate transport and metabolism.” Over 46.9% of the gene families within this functional category were classified as transferable. Interestingly, a few of the enriched functional categories are related to metabolism and energy production. These biological functions were previously suggested to be enriched with transferable gene families (Beiko et al. 2005). We speculate that the high transferability in these functional categories plays a critical role in microbial niche adaptation. The functional category “Replication, recombination, and repair” was also found to be highly enriched in transferable genes, in agreement with previous reports (Hsiao et al. 2005; Mau et al. 2006; Merkl 2006).

Three Information storage and processing functional categories (“Translation, ribosomal structure, and biogenesis,” “Transcription,” and “RNA processing and modification”) and two cellular process and signaling ones (“Intracellular trafficking, secretion, and vesicular transport,” and “Cell motility”) are significantly depleted of transferable gene families. It should be noted that the abovementioned information-related categories comprise only a small fraction of the supercategory Information storage and processing. However, due to the extreme depletion of transferable gene families in some of these categories (especially, the “Translation, ribosomal structure and biogenesis” category), the entire assortment of categories that make the “Information storage and processing” supercategory shows a significant depletion of transferable gene families.

Highly Transferred Gene Families

The group of transferable gene families is not homogenous. Some gene families have experienced many HGT events, whereas some—only one. Notably, the above definition of transferability lacks a quantitative measure of the expected number of HGT events. Our method enables us to infer the posterior expectation of the number of HGT events for each gene family. We therefore ranked all the gene families according to the inferred number of HGT events that have occurred (computed by summing the posterior expectation of the number of HGT events over all branches). The number of HGT events for each gene family is given in supplementary table S1, Supplementary Material online. For the 25 gene families with the highest number of HGT events, the posterior expectation of the number of HGT events exceeded 7.35. Among these gene families, eight were categorized as “Poorly characterized.” Our results thus highlight a subset of the large group of gene families that are poorly characterized, for which our predictions suggest their fixation following HGT may be selected for.

Discussion

In this work, we have devised new probabilistic-evolutionary models to better describe dynamics of gains and losses of gene families. We have further developed inference methodology to reconstruct gain and loss events and to statistically test whether a gene family underwent HGT. This model-based inference methodology allows accurate and robust detection of HGT.

In previous models, it was assumed that the rate matrix is the same for all gene families, up to a scaling factor. Biologically, this means that if one gene family has experienced more losses, it should also experience more gains, to the same extent. However, the validity of this assumption is questionable (e.g., Cole et al. 2001; Jordan et al. 2001). To capture possible deviations from this assumption, we developed a more sophisticated model, in which the evolutionary dynamics are modeled with a mixture of stochastic processes, which in practice allows each gene family to evolve under separate gain and separate loss rate parameters. The evolutionary models were subsequently used to analyze an extensive phyletic-pattern data set. We show that MMs are more suitable to explain phyletic-pattern data compared with simpler models and that an additional improvement is achieved when the model allows the root character frequencies to differ from the stationary ones. Notably, the mixture models (MM1 and MM2) have the same number of free parameters as the simpler models (M1 + Γ and M2 + Γ), strengthening our conclusion that our MMs better capture the dynamics of gene-family evolution.

Both the MM1 and the MM2 models are simplified versions of a true MM, in which the gain and loss rates of each matrix component, the character frequencies at the root, and the weight of each such component are all free parameters of the model. In our approach, the MMs are less flexible; however, the need to estimate too many parameters from the data is avoided, thus alleviating the risk of model overfitting and large errors of estimated parameters. This is avoided by first assuming equal weights for all components of the MM. Moreover, by assuming that the gain and loss rates are gamma distributed, a significant reduction in the number of free parameters is obtained. Finally, when nonstationary character frequencies in the root were allowed, we assumed that these frequencies are the same among the mixture components, again to reduce the number of free parameters.

In the MM2 models, the character frequencies at the root are allowed to differ from the stationary ones, and it is assumed that they are the same among the mixture components. Although this last assumption may be unrealistic, MM2 was still found to be superior to MM1. This could be explained by the substantial differences in the estimated character frequencies at the root. In the stationary models (M1 + Γ and MM1), the frequency of 1 at the root tends to be very low. For M1 + Γ, the root frequency of 1 is obtained by dividing the gain rate by the sum of loss and gain rates and was found to equal 0.082. For MM1, the computation must account for all components in the mixture—the mean gain divided by the sum of mean gain and mean loss rates is 0.035. In biological terms, such a low presence frequency at the root requires rampant gains in most gene families. In contrast, when the character frequencies at the root are allowed to be estimated separately, the frequencies of 1s at the root are much higher: 0.45 and 0.59 for M2 + Γ and MM2, respectively. We thus suggest that the stationary models may “force” unrealistic character frequencies at the root, and the alleviation of this limitation in the nonstationary models resulted in the observed large increase in likelihood.

These evolutionary models were applied in a method to infer gain and loss events using a stochastic mapping approach. Based on a simulation study, we have shown that the inference method is highly accurate in predicting gain and loss events for each gene family and for each branch. Although the probabilistic model described here was implemented in the context of phyletic pattern, it can be readily used to analyze any binary-based characters such as the evolution of restriction sites (Felsenstein 1992), introns (Csuros 2006; Carmel et al. 2007), and morphological characters (reviewed in Ronquist 2004). A possible extension for our suggested models would be to allow for the rate matrix Q to vary along the tree (Marri et al. 2007; Spencer and Sangaralingam 2009). In biological terms, this would allow, for example, a correct description of gene families that are frequently lost in specific branches, whereas seldom lost in others, as in the case of parasitic bacteria (Spencer and Sangaralingam 2009). Similar models that allow for either the rate or the Q matrix to vary along the tree were previously proven justified for modeling sequence evolution (Fitch and Markowitz 1970; Miyamoto and Fitch 1995; Galtier 2001; Yang and Nielsen 2002).

The test developed for HGT inference can point to specific lineages in which a given gene family was gained. More generally, the stochastic-mapping framework also allows computing probabilities and expectations of various scenarios related to the gene family at hand, for example, the global-mapping expectation of gain events along the entire tree (see Minin and Suchard 2008b for details). Notably, the method in itself is not informative regarding the donor of this gene family. Nevertheless, once HGT is determined, it is straightforward to search sequence-based data sets for remote homologs to the newly gained members of the gene family. A subsequent gene-tree reconstruction may reveal the donor.

Our analysis suggests that at least 34.23% of all gene families are transferable. This is a higher estimate than previously reported (e.g., Garcia-Vallve et al. 2000; Beiko et al. 2005; Ge et al. 2005; Choi and Kim 2007), probably reflecting differences in the inference methodologies (Lawrence and Ochman 2002; Ragan 2006). We suggest that phyletic pattern–based estimates tend to be higher than those obtained by analyzing sequence data because methods that detect HGT using atypical “genomic signature” are tailored only toward recent transfers, whereas “phylogenetic incongruence” methods are capable of detecting genes that have sufficient yet not excessive divergence. In support of such a high estimate of the fraction of transferable gene families, a recent paper analyzing gene-sharing networks among prokaryotes suggests that, on average, approximately 81% of genes in all genomes were transferred at least once (Dagan et al. 2008). Additional experimental support for the potential transferability of a large number of gene families is the work of Sorek et al. (2007) that showed that only 61 gene families are highly untransferable into Escherichia coli.

A reliable methodology for the inference of HGT events is a first step toward understanding the evolutionary forces dictating the probability that a newly transferred gene is fixed in the population of the acceptor. Our analysis suggests that the functional category of the gene family can often be highly predictive of its fixation probability and that higher resolution analysis of functional categories may provide additional insights into the dependence between protein function and its probability to undergo HGT. For example, our results suggest that although in general the number of HGT events in information-related protein families is low, in some specific information-related subcategories, the number of HGT events is relatively high (e.g., “Replication, recombination and repair”).

To conclude, the wealth of sequenced microbial genomes has revolutionized our understanding of the role played by HGT in shaping genomes. It is now becoming increasingly established that probabilistic-evolutionary models may offer the needed gateway toward analysis of these data. Methods based on such models that are capable of accurate inference of gain and loss events provide a more quantitative description of the evolution of gene families in general and of HGT in particular.

Supplementary Material

Supplementary figure S1 and table S1 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).