An integrated approach to cause-of-death analysis: cause-deleted life tables and decompositions of life expectancy

Abstract

This article integrates two methods that analyze the implications of various causes of death for life expectancy. One of the methods attributes changes in life expectancy to various causes of death; the other method examines the effect of removing deaths from a particular cause on life expectancy. This integration is accomplished by new formulas that make clearer the interactions among causes of death in determining life expectancy. We apply our approach to changes in life expectancy in the United States between 1970 and 2000. We demonstrate, and explain analytically, the paradox that cancer is responsible for more years of life lost in 2000 than in 1970 despite the fact that declines in cancer mortality contributed to advances in life expectancy between 1970 and 2000.

1. Introduction

When measured for a particular period, life expectancy at birth is a summary measure of the mortality conditions of that period. Estimating the role of causes of death in determining the level of life expectancy, and changes therein, is an active area of demographic research. Two broad research approaches have been employed: analyzing the life-shortening effect of causes of death if a cause were eliminated; and attributing changes or differences in life expectancy to various causes of death. The first approach is focused on a single population and has led to the development of single decrement (often, “cause-deleted”) life tables. The second approach is comparative and has lead to the development of decomposition methods that assign responsibility for mortality variation to particular causes of death.

The approaches are related but the relations have not been demonstrated. In this paper, we develop new expressions for decomposition methods and show that they are related in a straightforward way to expressions characterizing cause-deleted tables. We apply the analytic framework to data for the United States between 1970 and 2000.

2. Background

Although demographers have long used life tables to analyze mortality from all causes combined, the development of life tables that highlight the role of various causes of death is more recent (Brownlee 1919; Fisher, Vigfusson, and Dickson 1922; Pearl 1922; Greville 1948; Jordan 1952; Chiang 1968; Spiegelman 1968, Preston, Keyfitz, and Schoen 1972). The first official decennial life table by cause of death for the United States was published in the late 1960’s (United States. Dept. of Health, Education, and Welfare 1968).

One of the most important products of such life tables is the estimated gain in life expectancy at birth if a particular cause of death were eliminated, i.e., if the death rate from that cause were arbitrarily set to zero while death rates from all other causes remained the same. To recapitulate the mathematics of such a calculation, suppose that there are n mutually exclusive and exhaustive causes of death operating in a population at time t. The probability of surviving from birth to age a at time t if the only cause of death operating were cause i is

$$p_i(a,t)=e^{-\underset{0}{\overset{a}{\int }}{\mu }_i(s,t)\text{d}s},$$

where μ_i(s, t) is the death rate from cause i in the age interval s to s + ss. In the life table for all causes of death combined, the equivalent survival function is

$$p(a,t)=e^{-\underset{0}{\overset{a}{\int }}\mu (s,t)\text{d}s},\text{where}\mu (s,t)=\sum _{i=1}^n{\mu }_i(s,t).$$

For simplicity, let p(a, t) = p(a).

If we assume the n causes of death to be independent, p(a) = p₁(a) · p₂(a) · … · p_n(a). Let $p_{-i}(a)=\frac{p(a)}{p_i(a)}$ be the probability of surviving from all causes except cause i at age a. Given the force of mortality, μ(s), life expectancy at birth is computed as

$$e(0)=\underset{0}{\overset{\omega }{\int }}{e}^{-\underset{0}{\overset{a}{\int }}\mu (s)\text{d}s}\text{d}a=\underset{0}{\overset{\omega }{\int }}p(a)\text{d}a.$$

If there are n mutually exclusive and exhaustive causes of death operating in a population then life expectancy is computed as

$$e(0)=\underset{0}{\overset{\omega }{\int }}{p}_1(a)p_2(a)\dots p_n(a)\text{d}a.$$

Let D_i(0) be the years of life gained at birth if cause of death i were eliminated. Then D_i(0) is computed as:

$$D_i(0)=\underset{0}{\overset{\omega }{\int }}{p}_{-i}(a)\text{d}a-\underset{0}{\overset{\omega }{\int }}{p}_{-i}(a)p_i(a)\text{d}a.$$ (1)

It is important to note that the calculations made by assuming a particular cause of death is “eliminated” are best interpreted as an accounting exercise rather than an epidemiologic prediction. Since the causes of death are mutually exclusive and exhaustive, the death rates by cause add up to the death rate from all causes combined. This additive framework creates an accounting identity analogous to the balancing equation of population growth. The impact of deaths assigned to a particular cause on life table values can be gauged by recalculating the life table without deaths assigned to that cause. The results provide an estimate of how the intensity and age-distribution of deaths assigned to a particular cause affect all life table values, including life expectancy. To function as an epidemiologic prediction, one would have to assume that all deaths from a particular cause were eliminable, which is rarely possible, and that death rates from other causes would not be changed by the elimination. Such an assumption may be tenable as a first approximation for broad causes of death categories such as infectious diseases, violence, cardiovascular disease, and cancer, but it is clearly not tenable for disease processes such as diabetes that manifest themselves in many different causes of death.

3. Decomposition approaches

In the early 1980’s, a technique to decompose changes in life expectancy by age and cause of death was independently developed by Arriaga (1982; 1984), Andreev (1982), Pollard (1982), and Pressat (1985). These versions are mathematically equivalent (Pollard 1988), although their implementation via various discrete approximations can give rise to different results, as shown below. Later developments applied decomposition methods to other demographic measures and introduced dynamic elements (Andreev et al. 2002; Vaupel and Canudas-Romo 2002; Vaupel and Canudas-Romo 2003).

The initial target and main focus of decomposition techniques was not on causes of death but on age. Decompositions of trends or differences in mortality by age preceded cause-decompositions and the latter decompositions were designed along the lines of the former. Had the initial target been cause-decompositions, a more straightforward set of expressions was available, which is now developed.

As shown above, if there are n mutually exclusive and exhaustive causes of death operating in a population then p(a) = p₁(a) · p₂(a) · … · p_n(a). If we assume that the force of mortality (μ(a)) is differentiable with respect to time, then the change in the probability of surviving from birth to age a with respect to time can be written in the following form:

$$\stackrel{.}{p}(a)=\sum _{i=1}^n{\stackrel{.}{p}}_i(a)p_{-i}(a),$$

where a dot over a term represents the derivative with respect to time. Thus, the continuous change in life expectancy at birth is given by⁴

$$\stackrel{.}{e}(0)=\sum _{i=1}^n\underset{0}{\overset{\omega }{\int }}{\stackrel{.}{p}}_i(a)p_{-i}(a)\text{d}a.$$ (2)

Equation (2) is a straightforward expression for decomposing variation in life expectancy into various causes of death. It shows clearly that the contribution of each cause of death to the change in life expectancy is driven by the changes in cause specific survivorship (cause i) weighted by the cumulative probability of surviving from the remaining causes (cause −i). The integral in equation (2) can be subdivided into age-groups to account for the age-contribution to the change in life expectancy. Thus, equation (2) can return both cause- and age-contribution to the change in e(0). Equation (2) is the basis of the connection between decomposition methods and cause-deleted life tables, as shown below.

For discrete time intervals, let e(0) and e^*(0) represent the life expectancy at birth at times 1 and 2, respectively. Then (see Appendix 1 in Beltrán-Sánchez and Preston (2007) for more details):

$$e^{\ast }(0)-e(0)\cong \sum _{i=1}^n\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a.$$

In discrete age intervals the above formula is equivalent to

$$e^{\ast }(0)-e(0)=\sum _{i=1}^n\sum _{x=0,5}^{\omega }({{}_{n}L}_{x,i}^{\ast }-{{}_{n}L}_{x,i})(\frac{{{}_{n}L}_{x,-i}^{\ast }+{{}_{n}L}_{x,-i}}{2n}),$$

where _nL_x,i, _nL_x,−i, ${{}_{n}L}_{x,i}^{\ast },{{}_{n}L}_{x,-i}^{\ast }$ represent the person-years lived between ages x and x + n at times 1 and 2 in the life tables for cause i and cause −i, respectively, using a life table radix of 1 (see Appendix 3 for more details).

Appendix Table A1 compares results from implementing our approach to cause-of-death decompositions to those of Pollard and Arriaga. Differences are found to be minute between our approach and Pollard’s. Relative to the other two approaches, Arriaga’s approach can underestimate the importance of major causes of death heavily concentrated at older ages.

Table A1.

Difference between present method and Pollard’s and Arriaga’s method in the attribution to various causes of death of the change in life expectancy at birth in the United States, 1970 – 2000 (present estimate minus Arriaga’s and Pollard’s, respectively, in years)

Causes of death	Total Population		Total Male		Total Female		Total White		Total Black
	Arriaga	Pollard	Arriaga	Pollard	Arriaga	Pollard	Arriaga	Pollard	Arriaga	Pollard
Heart	0.10	0.00	0.11	−0.01	0.07	0.00	0.09	0.00	0.13	0.02
Cerebrovascular	0.07	0.01	0.08	0.01	0.06	0.01	0.07	0.01	0.09	0.01
Malignant neoplasms	−0.03	0.00	−0.04	0.00	−0.02	0.00	−0.03	0.00	−0.05	0.00
Chronic lower respiratory diseases	−0.03	−0.01	−0.03	−0.01	−0.02	−0.01	−0.03	−0.01	−0.02	0.00
Violence	−0.01	0.01	−0.03	0.01	0.00	0.00	0.00	0.01	−0.02	0.00
Diabetes	0.00	0.00	−0.01	0.00	0.00	0.00	0.00	0.00	−0.02	0.00
Influenza and pneumonia	0.00	0.01	0.00	0.00	0.00	0.01	0.00	0.01	0.00	0.01
Nephritis, nephrotic syndrome and nephrosis	−0.01	−0.01	−0.02	−0.01	−0.01	0.00	0.00	0.00	−0.02	0.00
Septicemia	−0.01	0.00	−0.01	−0.01	−0.01	0.00	0.00	0.00	−0.02	0.00
Chronic liver disease and cirrhosis	0.00	0.00	0.00	0.01	0.00	0.00	0.00	0.00	0.00	0.00
Hypertension and hypertensive renal disease	0.00	0.00	0.00	0.00	−0.01	0.00	0.00	0.00	−0.01	0.00
All other	−0.10	−0.03	−0.07	−0.01	−0.10	−0.04	−0.09	−0.03	−0.07	0.00

Note: The implementation of Arriaga’s formula is taken from equation Arriaga (1989:125) in which the master life tables are closed using the approach described in Appendix 2. The implementation of Pollard’s approach is taken from Pollard (1982:229).

Source: See Tables 1 and 3.

4. Relation between the decomposition approach and cause-deleted life tables

As shown in equation (1), the years of life gained at birth at time t if cause of death i is eliminated is computed as:

$$D_i(0)=\underset{0}{\overset{\omega }{\int }}{p}_{-i}(a)\text{d}a-\underset{0}{\overset{\omega }{\int }}{p}_{-i}(a)p_i(a)\text{d}a.$$

Thus, the change in D_i(0) with respect to time is given by

$${\stackrel{.}{D}}_i(0)=\underset{0}{\overset{\omega }{\int }}{\stackrel{.}{p}}_{-i}(a)q_i(a)\text{d}a-\underset{0}{\overset{\omega }{\int }}{\stackrel{.}{p}}_i(a)p_{-i}(a)\text{d}a,$$ (3)

where q_i(a) = 1 − p_i(a) and a dot over a term represents the derivative with respect to time.

For discrete time intervals, let D_i(0) and $D_i^{\ast }(0)$ represent the gain in life expectancy at birth at times 1 and 2, respectively, by eliminating cause of death i. Then, equation (3) can be written as (see Appendix 2 for more details):

$$D_i^{\ast }(0)-D_i(0)=\underset{0}{\overset{\infty }{\int }}(p_{-i}^{\ast }-p_{-i})(\frac{q_i+q_i^{\ast }}{2})\text{d}a-\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a,$$

where q_i = 1 − p_i.

In discrete age intervals the above formula is equivalent to

$$\begin{array}{l}{D}_i^{\ast }(0)-D_i(0)=\sum _{x=0,5}^{\omega }({{}_{n}L}_{x,-i}^{\ast }-{{}_{n}L}_{x,-i})(1-\frac{{{}_{n}L}_{x-i}+{{}_{n}L}_{x,i}^{\ast }}{2n})\\ -\sum _{x=0,5}^{\omega }({{}_{n}L}_{x,i}^{\ast }-{{}_{n}L}_{x,i})(\frac{{{}_{n}L}_{x,-i}+{{}_{n}L}_{x,-i}^{\ast }}{2n}).\end{array}$$

Thus, the change in the number of years of life lost to a particular cause of death is a function of two terms. The second term in equation (3) is the change in survival from cause i weighted by the cumulative probability of surviving from cause −i. From equation (2), it is precisely the change in life expectancy at birth attributable to changes in cause of death i. Thus, the change in the amount of life expectancy sacrificed to cause i in cause-deleted life tables is closely connected to the change in life expectancy attributable to cause i in decomposition formulas. In fact, the two would be exactly the same if death rates from other causes were constant, because p −_−i(a) in the first term would then be zero. In other words, a positive contribution by a cause of death to changes in life expectancy would exactly equal the reduction in years of life lost to that cause (hence the minus sign on the second term of equation (3)). In general, the first term in equation (3) shows the change in survival from cause −i weighted by the cumulative probability of dying from cause i. It would be large in magnitude only if cause i is an important cause of death and changes in cause −i are large.

To illustrate the meaning of equation (3), we anticipate a later result. Suppose that we attribute changes in mortality between time 1 and time 2 to various causes of death, including cancer. Suppose further that declines in cancer contribute to improvements in life expectancy over the period (the second term in (3) for cancer is negative). Now suppose that we calculate cause-deleted life tables at times 1 and 2. The second term in equation (3) would lead to the prediction that the left-hand side of equation (3) would be negative: cancer should be causing less loss of life at time 2 than at time 1. However, if other causes of death declined enough during the period (i.e., the first term in (3) is strongly positive), cancer could actually be causing a bigger loss of life at time 2 than at time 1. Clearly, changes in its life-shortening effects depend on changes in mortality from other causes, a dependence that is made explicit in equation (3).

5. Application to recent mortality change in the United States

5.1 Decomposition of changes by causes of death

After several decades of slow improvement in mortality, the United States experienced substantial advances in longevity between 1970 and 2000. These are widely believed to reflect primarily reductions in death rates from cardiovascular diseases, facilitated by medical advances such as cardiovascular bypass surgery and expanded use of blood pressure reduction drugs, statins, and beta blockers, as well as by reductions in cigarette smoking (Cutler 2004; Ergin et al. 2004; Ford et al. 2007).

Mortality data for 1970 are drawn from the publicly available multiple cause of death file, 1968–1973, obtained through the Inter-university Consortium for Political and Social Research (National Center for Health Statistics (NCHS) 2001). For the year 2000, we use the multiple cause of death public use file published by the National Center for Health Statistics (2002). The midyear population figures in 1970 and 2000 are drawn from the Census Bureau (U.S. Bureau of the Census 1971; U.S. Bureau of the Census 2005).⁵ For blacks in 1970 we use the size of the African-American population reconstructed by Preston et al. (1998).⁶ The terminal age category in our application is age 100+.⁷ We focus on the eleven leading causes of death in the U.S. for the year 2000 and construct comparable categories in 1970.⁸ We use the following groups: heart disease; cerebrovascular diseases; malignant neoplasms; chronic lower respiratory diseases; violence (accidents (unintentional injuries), intentional self-harm (suicide), and assault (homicide)); diabetes; influenza-pneumonia; nephritis (nephritis, nephrotic syndrome and nephrosis); septicemia; liver cirrhosis (chronic liver disease and cirrhosis); and hypertension (essential (primary) hypertension and hypertensive renal disease). Comparable codes for 1970 were derived from Centers for Disease Control and Prevention (CDC) (2001).

5.1.1 Results

We estimate life expectancy at birth for the total U.S. population in 1970 to be 70.70 years (slightly lower than the value of 70.9 estimated by the NCHS (1974)) and 76.96 years for the year 2000 (slightly higher than the value of 76.9 estimated by Arias (2002)). Thus, life expectancy at birth is estimated to have increased by about 6.26 years between 1970 and 2000 for the total population of the U.S. Comparable figures by race and sex are shown in Table 1.

Table 1.

Change in life expectancy at birth for the U. S. population by race and sex between 1970 and 2000

Year	Total Population			White Population			Black Population
	All	Males	Females	All	Males	Females	All	Males	Females
2000	76.96	74.24	79.56	77.44	74.79	79.99	71.74	68.15	75.06
1970	70.70	66.97	74.62	71.58	67.88	75.46	64.78	61.16	68.66
Difference	6.26	7.27	4.94	5.86	6.91	4.53	6.96	6.99	6.40

Source: Multiple cause of death file (1968–1973), multiple cause of death 2000, and census bureau estimates.

The eleven causes of death selected in this study account for the majority of the deaths in both time periods. In 1970, about 84% of the total deaths were attributed to one of those eleven causes for the total population, and in 2000, the percentage slightly decreased to about 80% (Table 2). Cardiovascular diseases (heart and cerebrovascular) and malignant neoplasms are responsible for 66% of deaths in 1970 and 59% in 2000.

Table 2.

Percentage distribution of deaths by cause for the total U. S. population, 1970–2000

Cause of death	1970	2000
Heart	38.28	29.58
Malignant neoplasms	17.21	23.00
Cerebrovascular	10.78	6.98
Violence	8.08	5.29
Chronic lower respiratory diseases	1.61	5.07
Diabetes	1.99	2.88
Influenza and pneumonia	3.26	2.72
Nephritis, nephrotic syndrome and nephrosis	0.46	1.55
Septicemia	0.18	1.30
Chronic liver disease and cirrhosis	1.63	1.11
Hypertension and hypertensive renal disease	0.43	0.75
All other	16.07	19.79
Sum	100.00	100.00

Source: see Table 1.

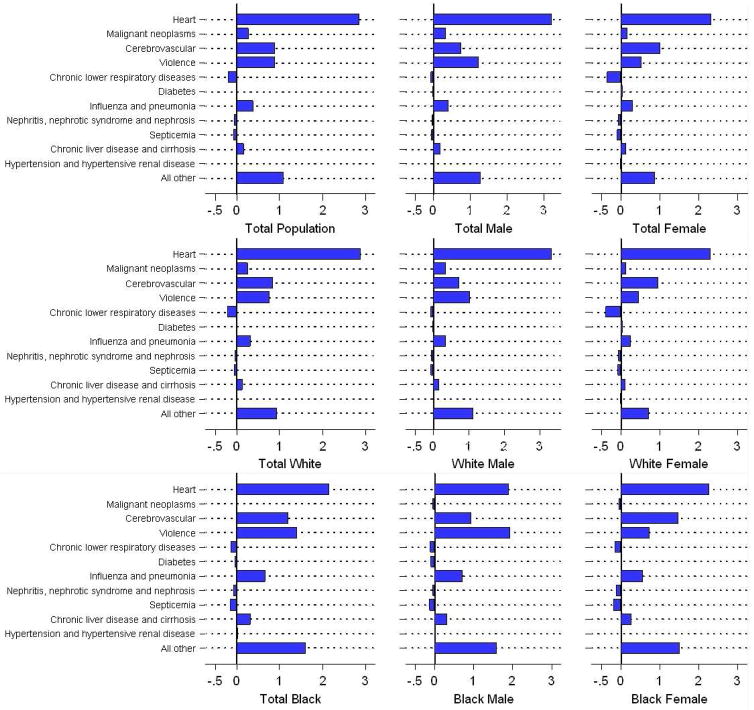
Our estimates of the contribution of each cause of death to the change in life expectancy at birth by race and sex between 1970 and 2000 are shown in Table 3 and Figure 1.⁹ Heart disease contributed the majority of the increase in life expectancy at birth during the 30-year period for all groups except black males, for whom large declines in death rates from violence contributed 1.94 years of life to the total gain of 6.99 years. This exceptionally large decline in violent mortality resulted in a larger gain in life expectancy for black males than for any other race/sex group during the period. Cancers made a positive contribution to life expectancy gains for the total population and for whites but not for blacks. Diabetes also shows a negative contribution but among males only.

Table 3.

Change in life expectancy at birth, 1970–2000, attributable to various causes of death in the United States (in years)

Causes of death	Total Population			White Population			Black Population
	All	Males	Females	All	Males	Females	All	Males	Females
Heart	2.87	3.22	2.33	2.90	3.32	2.30	2.16	1.90	2.27
Malignant neoplasms	0.27	0.35	0.17	0.26	0.36	0.15	−0.02	−0.06	−0.04
Cerebrovascular	0.90	0.77	1.02	0.85	0.73	0.96	1.21	0.94	1.48
Violence	0.90	1.23	0.53	0.77	1.04	0.47	1.42	1.94	0.74
Chronic lower respiratory diseases	−0.21	−0.08	−0.36	−0.23	−0.07	−0.39	−0.14	−0.12	−0.16
Diabetes	0.01	−0.03	0.05	0.01	−0.02	0.05	−0.05	−0.10	0.03
Influenza and pneumonia	0.38	0.42	0.32	0.32	0.36	0.27	0.67	0.73	0.57
Nephritis, nephrotic syndrome and nephrosis	−0.06	−0.05	−0.07	−0.05	−0.05	−0.06	−0.08	−0.06	−0.11
Septicemia	−0.08	−0.07	−0.10	−0.07	−0.06	−0.09	−0.16	−0.13	−0.18
Chronic liver disease and cirrhosis	0.17	0.20	0.14	0.14	0.17	0.12	0.32	0.33	0.28
Hypertension and hypertensive renal disease	0.00	0.01	−0.01	0.00	0.01	−0.01	0.02	0.03	0.00
All other	1.10	1.29	0.88	0.95	1.14	0.73	1.61	1.59	1.5
Sum	6.25	7.26	4.90	5.85	6.93	4.50	6.96	6.99	6.40
Total change in e0	6.26	7.27	4.94	5.86	6.91	4.53	6.96	6.99	6.40

Source: See Table 1 and equation (2).

Figure 1. Change in life expectancy at birth attributable to various causes of death in the United States (in years): 1970 – 2000.

Source: Table 3

5.2 Cause-deleted life tables and changes therein

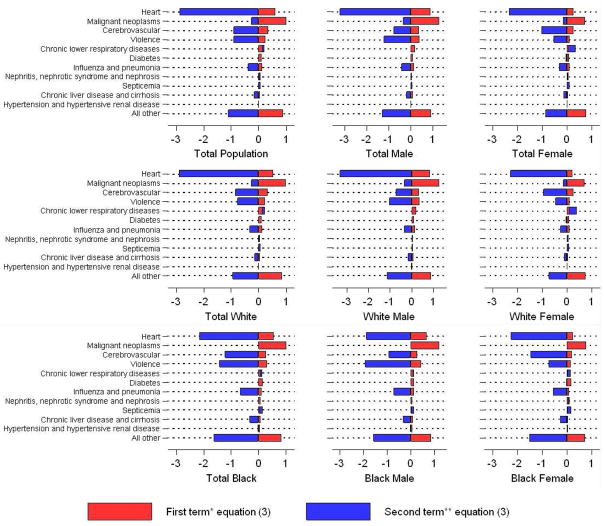
Table 4 and Figure 2 show the estimated gain in life expectancy from eliminating a particular cause of death in 1970 and 2000, using formula (1). Table 4 also shows, in column 3, the change in this quantity between 1970 and 2000. These values correspond to “Ḋ_i(0)” in formula (3). Column 4 (red color in Figure 2) and column 5 (blue color in Figure 2) of the table present the two elements on the right-hand side of formula (3). Column 5 is simply the change in life expectancy attributable to a particular cause of death (i.e., the result of our decomposition of mortality change by cause) while Column 4 represents the changed significance of a cause of death that is introduced by changes in other causes of death during the period. Without such interference from other causes, columns 3 and 5 would be identical.

Table 4.

Decomposition of the change in the gain of life expectancy at birth by eliminating a cause of death for the U. S. population by sex and race: 1970 – 2000

Cause of death	Gain in e0 by eliminating a cause of death (years)		Change in the gain of e0 by eliminating a cause (years)	Equation (3)
	1970 (1)	2000 (2)	(3) = (2)−(1) (3) = (4)+(5)	First Term* (4)	Second Term** (5)
TOTAL POPULATION
Heart	6.20	3.93	−2.27	0.60	−2.87
Malignant neoplasms	2.54	3.27	0.74	1.00	−0.27
Cerebrovascular	1.26	0.70	−0.56	0.34	−0.90
Violence	1.86	1.20	−0.66	0.24	−0.90
Chronic lower respiratory diseases	0.20	0.55	0.35	0.15	0.21
Diabetes	0.25	0.34	0.10	0.11	−0.01
Influenza and pneumonia	0.50	0.25	−0.25	0.13	−0.38
Nephritis, nephrotic syndrome and nephrosis	0.07	0.16	0.09	0.04	0.06
Septicemia	0.03	0.14	0.11	0.02	0.08
Chronic liver disease and cirrhosis	0.29	0.17	−0.12	0.05	−0.17
Hypertension and hypertensive renal disease	0.05	0.07	0.02	0.02	0.00
All other	3.21	2.99	−0.22	0.88	−1.10
TOTAL MALE POPULATION
Heart	6.39	4.07	−2.32	0.91	−3.22
Malignant neoplasms	2.38	3.32	0.94	1.29	−0.35
Cerebrovascular	0.98	0.57	−0.40	0.37	−0.77
Violence	2.51	1.66	−0.84	0.39	−1.23
Chronic lower respiratory diseases	0.26	0.54	0.28	0.20	0.08
Diabetes	0.18	0.32	0.14	0.11	0.03
Influenza and pneumonia	0.50	0.24	−0.26	0.16	−0.42
Nephritis, nephrotic syndrome and nephrosis	0.07	0.16	0.09	0.05	0.05
Septicemia	0.04	0.13	0.09	0.03	0.07
Chronic liver disease and cirrhosis	0.33	0.22	−0.11	0.09	−0.20
Hypertension and hypertensive renal disease	0.05	0.06	0.01	0.02	−0.01
All other	3.24	2.88	−0.35	0.93	−1.29
TOTAL FEMALE POPULATION
Heart	5.67	3.61	−2.07	0.27	−2.33
Malignant neoplasms	2.61	3.17	0.56	0.73	−0.17
Cerebrovascular	1.55	0.79	−0.76	0.26	−1.02
Violence	1.08	0.66	−0.42	0.11	−0.53
Chronic lower respiratory diseases	0.11	0.56	0.45	0.09	0.36
Diabetes	0.32	0.36	0.04	0.09	−0.05
Influenza and pneumonia	0.47	0.25	−0.22	0.10	−0.32
Nephritis, nephrotic syndrome and nephrosis	0.06	0.16	0.09	0.03	0.07
Septicemia	0.03	0.15	0.12	0.02	0.10
Chronic liver disease and cirrhosis	0.23	0.11	−0.12	0.03	−0.14
Hypertension and hypertensive renal disease	0.05	0.07	0.03	0.02	0.01
All other	3.08	2.97	−0.11	0.77	−0.88
TOTAL WHITE POPULATION
Heart	6.22	3.85	−2.36	0.53	−2.90
Malignant neoplasms	2.56	3.27	0.72	0.98	−0.26
Cerebrovascular	1.19	0.66	−0.53	0.32	−0.85
Violence	1.71	1.17	−0.55	0.22	−0.77
Chronic lower respiratory diseases	0.21	0.58	0.38	0.15	0.23
Diabetes	0.23	0.31	0.08	0.10	−0.01
Influenza and pneumonia	0.44	0.24	−0.19	0.13	−0.32
Nephritis, nephrotic syndrome and nephrosis	0.05	0.14	0.08	0.03	0.05
Septicemia	0.03	0.12	0.10	0.02	0.07
Chronic liver disease and cirrhosis	0.27	0.17	−0.09	0.05	−0.14
Hypertension and hypertensive renal disease	0.04	0.05	0.02	0.02	0.00
All other	2.91	2.81	−0.10	0.84	−0.95
WHITE MALE POPULATION
Heart	6.49	4.03	−2.47	0.86	−3.32
Malignant neoplasms	2.39	3.29	0.91	1.27	−0.36
Cerebrovascular	0.92	0.54	−0.38	0.35	−0.73
Violence	2.28	1.60	−0.68	0.36	−1.04
Chronic lower respiratory diseases	0.27	0.56	0.28	0.21	0.07
Diabetes	0.17	0.30	0.13	0.10	0.02
Influenza and pneumonia	0.44	0.23	−0.21	0.15	−0.36
Nephritis, nephrotic syndrome and nephrosis	0.05	0.14	0.09	0.04	0.05
Septicemia	0.03	0.12	0.08	0.03	0.06
Chronic liver disease and cirrhosis	0.31	0.22	−0.08	0.08	−0.17
Hypertension and hypertensive renal disease	0.03	0.05	0.01	0.02	−0.01
All other	2.94	2.69	−0.25	0.89	−1.14
WHITE FEMALE POPULATION
Heart	5.57	3.48	−2.08	0.22	−2.30
Malignant neoplasms	2.64	3.19	0.55	0.70	−0.15
Cerebrovascular	1.46	0.75	−0.71	0.25	−0.96
Violence	1.03	0.66	−0.37	0.10	−0.47
Chronic lower respiratory diseases	0.10	0.60	0.49	0.10	0.39
Diabetes	0.29	0.31	0.03	0.08	−0.05
Influenza and pneumonia	0.42	0.25	−0.17	0.10	−0.27
Nephritis, nephrotic syndrome and nephrosis	0.05	0.13	0.08	0.02	0.06
Septicemia	0.03	0.13	0.10	0.02	0.09
Chronic liver disease and cirrhosis	0.20	0.11	−0.09	0.03	−0.12
Hypertension and hypertensive renal disease	0.04	0.06	0.02	0.01	0.01
All other	2.79	2.80	0.01	0.75	−0.73
TOTAL BLACK POPULATION
Heart	6.02	4.42	−1.60	0.56	−2.16
Malignant neoplasms	2.42	3.44	1.03	1.01	0.02
Cerebrovascular	1.81	0.87	−0.94	0.28	−1.21
Violence	2.60	1.49	−1.12	0.31	−1.42
Chronic lower respiratory diseases	0.14	0.36	0.21	0.08	0.14
Diabetes	0.37	0.58	0.21	0.16	0.05
Influenza and pneumonia	0.80	0.26	−0.55	0.12	−0.67
Nephritis, nephrotic syndrome and nephrosis	0.16	0.32	0.15	0.07	0.08
Septicemia	0.06	0.27	0.21	0.05	0.16
Chronic liver disease and cirrhosis	0.41	0.15	−0.25	0.07	−0.32
Hypertension and hypertensive renal disease	0.14	0.17	0.03	0.05	−0.02
All other	4.84	4.07	−0.77	0.84	−1.61
BLACK MALE POPULATION
Heart	5.40	4.17	−1.23	0.67	−1.90
Malignant neoplasms	2.33	3.59	1.25	1.19	0.06
Cerebrovascular	1.40	0.73	−0.66	0.28	−0.94
Violence	3.72	2.20	−1.51	0.43	−1.94
Chronic lower respiratory diseases	0.17	0.38	0.21	0.10	0.12
Diabetes	0.23	0.45	0.22	0.12	0.10
Influenza and pneumonia	0.85	0.26	−0.59	0.14	−0.73
Nephritis, nephrotic syndrome and nephrosis	0.15	0.28	0.13	0.07	0.06
Septicemia	0.06	0.24	0.18	0.04	0.13
Chronic liver disease and cirrhosis	0.43	0.18	−0.25	0.08	−0.33
Hypertension and hypertensive renal disease	0.13	0.14	0.01	0.05	−0.03
All other	4.82	4.08	−0.74	0.86	−1.59
BLACK FEMALE POPULATION
Heart	6.49	4.45	−2.04	0.23	−2.27
Malignant neoplasms	2.40	3.22	0.82	0.77	0.04
Cerebrovascular	2.26	0.98	−1.28	0.20	−1.48
Violence	1.29	0.69	−0.60	0.14	−0.74
Chronic lower respiratory diseases	0.10	0.31	0.21	0.05	0.16
Diabetes	0.55	0.68	0.14	0.17	−0.03
Influenza and pneumonia	0.72	0.24	−0.48	0.09	−0.57
Nephritis, nephrotic syndrome and nephrosis	0.17	0.35	0.17	0.07	0.11
Septicemia	0.07	0.30	0.23	0.04	0.18
Chronic liver disease and cirrhosis	0.35	0.12	−0.24	0.05	−0.28
Hypertension and hypertensive renal disease	0.15	0.19	0.04	0.04	0.00
All other	4.71	3.91	−0.80	0.72	−1.52

^*Effect of changes in other causes of death on years of life lost to the cause.

^**Effect of changes in the cause itself on years of life lost.

Source: Table 1 and equation (3).

Figure 2. Decomposition of the chaxnge in the gain of life expectancy at birth by eliminating a cause of death for the U.S. population by sex and race: 1970 – 2000.

^* Effect of changes in other causes of death on years of life lost to the cause.

^**Effect of changes in the cause itself on years of life lost.

Source: Table 4

Table 4 highlights the changing significance of cancer and heart disease. In both 1970 and 2000, these are the two causes of death whose elimination would produce the greatest advance in life expectancy at birth (columns 1 and 2). But the relative importance of the two has changed dramatically. In 1970, heart disease for all groups combined was responsible for about 2.4 times the loss of life years of neoplasms. In 2000, the ratio was only 1.2.

Even though the death rate from neoplasms was slowly declining between 1970 and 2000, more years of life were actually sacrificed to neoplasms in 2000 than in 1970. The average number of years of life lost to neoplasms grew by 0.74 for the population as a whole, by far the greatest increase for any cause. This value, shown in column 3, is the results of a contribution of +1.00 years from the “other cause change” term in column 4, partially offset by the −0.27 year term reflecting the decline in death rates from neoplasms themselves. In other words, the sole reason why more years of life are sacrificed to neoplasms in 2000 than in 1970 is the decline in death rates from other causes of death, most notably heart disease. If cancer death rates had not changed, cancer would have been responsible for the loss of 1.00 additional year of life in 2000. Because of the decline in causes of death other than cancer, those who died from cancer in 2000 would otherwise have lived longer, on average, than those who died from cancer in 1970. As a result, cancer caused a greater loss of life in 2000 than in 1970 even though its death rates declined over this period. This result underscores the importance of interactions among diseases in determining longevity. The key interaction is made explicit in equation (3).

While extreme, the result pertaining to cancer is not unusual. In fact, the values in column 4 are positive for every cause of death for each of the race/sex groups. Declines in mortality from other causes of death, ceteris paribus, inevitably increase the years of life lost to any particular cause of death. In the case of heart disease, the declines in other causes of death by themselves increased the number of years lost to heart disease by 0.60 between 1970 and 2000. But the declines in heart disease itself were large enough (2.87 years) to overcome this effect and produce a reduction in the years lost to heart disease by 2.27 years.

6. Summary

Cause-deleted life tables provide a clear measure of the public health significance of a particular disease or injury process. Decompositions of mortality change demonstrate the significance of a particular cause of death for that change. In this paper, we show that these two types of analyses are closely related to one another. In particular, the change in the years of life lost to a particular disease is shown to be equal to the amount of change attributable to that disease in a cause-decomposition, plus a simple additional term that reflects movements in other causes of death. The public health significance of a disease is thus shown to be an outcome of a struggle among causes of death. If one cause declines more rapidly than others, in a manner made explicit in equation (3), that cause will be responsible for fewer years of life lost at the end of the period. Heart disease won that struggle over the period investigated, whereas the decline in cancer death rates was not sufficient to avert its becoming responsible for a greater loss of life at the end of the period than at the beginning.

The simplicity of formulas is complemented by simplicity in calculation. To implement the decomposition framework in equation (2) requires that cause-deleted life tables be constructed. Thus, cause-deleted tables are an important byproduct of the decomposition approach developed here. So the complete accounting framework of equations (2 and 3), illustrated in Table 4, is readily available whenever decompositions are performed. It is also available whenever cause-deleted life tables are calculated at two points in time.

Appendix 1

Relation between our approach and Pollard’s

As noted in the text, equation (2) can be derived from Vaupel and Canudas-Romo (2003:209) equation (36). They show that their formulation is equivalent to Pollard’s (Vaupel and Canudas-Romo (2003:209) equation (38)). Likewise, our equation (2) is equivalent to Pollard’s following from equation (38) in Vaupel and Canudas-Romo (2003).

When applied to the U.S. data, the difference in cause-of-death attributions among our method, Pollard’s, and Arriaga’s is shown in Appendix Table A1. There is virtually no difference between Pollard’s attributions and ours; the greatest difference is about four-hundredths of a year. Except for heart disease, the difference between Arriaga’s and our approach is also very small. For the total population, our method attributes a contribution of heart disease of about 0.1 year higher than Arriaga’s. This difference is of similar magnitude for the total population of males, and somewhat lower for females and whites. For the total black population, black males and black females the difference is about 6%, 6.9% and 5.5% higher, respectively, compared to Arriaga’s formula (data not shown).

Appendix 2

Implementing equations (2) and (3) for discrete time intervals

For discrete time intervals, equation (2) can be approximated as (Beltrán-Sánchez and Preston 2007: Appendix 1):

$$e^{\ast }(0)-e(0)\cong \sum _{i=1}^n\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a.$$ (A1)

In order to produce a discrete time formula for equation (3) we begin with equation (1). The years of life gained at birth at discrete time one and two if cause of death i is eliminated can be computed as:

$$D_i(0)=\underset{0}{\overset{\infty }{\int }}{p}_{-i}(a)\text{d}a-\underset{0}{\overset{\infty }{\int }}{p}_i(a)p_{-i}(a)\text{d}a,$$

and

$$D_i^{\ast }(0)=\underset{0}{\overset{\infty }{\int }}{p}_{-i}^{\ast }(a)\text{d}a-\underset{0}{\overset{\infty }{\int }}{p}_i^{\ast }(a)p_{-i}^{\ast }(a)\text{d}a.$$

For simplicity, let p_i(a) = p_i and $p_i^{\ast }(a)=p_i^{\ast }$. The change, $D_i^{\ast }(0)-D_i(0)$, is then given by:

$$\begin{array}{l}{D}_i^{\ast }(0)-D_i(0)=\underset{0}{\overset{\infty }{\int }}{p}_{-i}^{\ast }\text{d}a-\underset{0}{\overset{\infty }{\int }}{p}_i^{\ast }{p}_{-i}^{\ast }\text{d}a-(\underset{0}{\overset{\infty }{\int }}{p}_{-i}\text{d}a-\underset{0}{\overset{\infty }{\int }}{p}_i{p}_{-i}\text{d}a)\\ D_i^{\ast }(0)-D_i(0)=\underset{0}{\overset{\infty }{\int }}(p_{-i}^{\ast }-p_{-i}\text{)}\text{d}a-(\underset{0}{\overset{\infty }{\int }}{p}_i^{\ast }{p}_{-i}^{\ast }\text{d}a-\underset{0}{\overset{\infty }{\int }}{p}_i{p}_{-i}\text{d}a)\end{array}$$ (A2)

The term in parenthesis of equation (A2) can be written as:

$$\begin{array}{l}\underset{0}{\overset{\infty }{\int }}{p}_i^{\ast }{p}_{-i}^{\ast }\text{d}a-\underset{0}{\overset{\infty }{\int }}{p}_i{p}_{-i}\text{d}a\\ =\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a+\underset{0}{\overset{\infty }{\int }}(p_{-i}^{\ast }-p_{-i})(\frac{p_i+p_i^{\ast }}{2})\text{d}a.\end{array}$$

Then,

$$\begin{array}{l}{D}_i^{\ast }(0)-D_i(0)\\ =\underset{0}{\overset{\infty }{\int }}(p_{-i}^{\ast }-p_{-i})\text{d}a-\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a-\underset{0}{\overset{\infty }{\int }}(p_{-i}^{\ast }-p_{-i})(\frac{p_i+p_i^{\ast }}{2})\text{d}a\\ =\underset{0}{\overset{\infty }{\int }}(p_{-i}^{\ast }-p_{-i})(1-\frac{p_i+p_i^{\ast }}{2})\text{d}a-\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a\\ =\underset{0}{\overset{\infty }{\int }}(p_{-i}^{\ast }-p_{-i})(\frac{q_i+q_i^{\ast }}{2})\text{d}a-\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a\end{array}$$ (A3)

where q_i = 1 − p_i and $q_i^{\ast }=1-p_i^{\ast }$. Thus, for discrete time intervals, equation (3) can be estimated using equation (A3).

Appendix 3

Implementing equations (2) and (3) for discrete age intervals

As shown in Appendix 2, discrete time versions of equations (2) and (3) are given by:

$$e^{\ast }(0)-e(0)\cong \sum _{i=1}^n\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a$$

and

$$D_i^{\ast }(0)-D_i(0)=\underset{0}{\overset{\infty }{\int }}(p_{-i}^{\ast }-p_{-i})(\frac{q_i+q_i^{\ast }}{2})\text{d}a-\underset{0}{\overset{\infty }{\int }}(p_i^{\ast }-p_i)(\frac{p_{-i}+p_{-i}^{\ast }}{2})\text{d}a$$

where q_i = 1 − p_i and $q_i^{\ast }=1-p_i^{\ast }$.

In discrete age the above formulas are equivalent to:

$$e^{\ast }(0)-e(0)=\sum _{i=1}^n\sum _{x=0,5}^{\omega }({{}_{n}L}_{x,i}^{\ast }-{{}_{n}L}_{x,i})(\frac{{{}_{n}L}_{x,-i}^{\ast }+{{}_{n}L}_{x,-i}}{2n})$$

and

$$\begin{array}{l}{D}_i^{\ast }(0)-D_i(0)=\sum _{x=0,5}^{\omega }({{}_{n}L}_{x,-i}^{\ast }-{{}_{n}L}_{x,-i})(1-\frac{{{}_{n}L}_{x,i}+{{}_{n}L}_{x,i}^{\ast }}{2n})\\ -\sum _{x=0,5}^{\omega }({{}_{n}L}_{x,i}^{\ast }-{{}_{n}L}_{x,-i})(\frac{{{}_{n}L}_{x,-i}+{{}_{n}L}_{x,-i}^{\ast }}{2n}).\end{array}$$

for a life table radix equal to 1 (l₀ = 1), where _nL_x,i, _nL_x,−i, ${{}_{n}L}_{x,i}^{\ast },{{}_{n}L}_{x,-i}^{\ast }$ represent the person-years lived between ages x and x + n at times 1 and 2 in the life tables for cause i and cause −i, respectively.

In order to estimate _nL_x,i, we assume that the force of decrement function from cause i is proportional to the force of decrement function from all causes combined within the interval x to x + n (Preston, Heuveline, and Guillot 2001:82). The computation of _nL_x,i also requires the estimation of _na_x,i values, which represent the mean number of person-years lived in the interval x to x + n by those dying from cause i in the interval. These values are obtained through graduation using equations 4.8 for ages 0, 1, 5 and 95 and equation 4.6 for ages 10 to 90 from Preston et al. (2001:82–84).

Having estimated _nL_x,i, we then estimate the person-years lived in the cause-deleted life tables for each cause as:

$${{}_{n}L}_{x,-i}=\left(\frac{{{}_{n}L}_x}{{{}_{n}L}_{x,i}}\right)·n,\text{for}i=1,2,3,\dots ,k.$$ (A4)

where _nL_x are the person-years lived between ages x and x + n in the master life table for all causes of death combined at each time period. The construction of the master life tables for 1970 and 2000 follows the methodology of Preston et al. (2001:Ch. 3), including the use of graduation to determine the values of _na_x as described above.

Equation (A4) preserves the multiplicative property whereby the product of the probabilities of survival to a particular age in the associated single decrement table for cause i and in the cause-deleted table for cause i equals the probability of survival to that age for all causes combined.

We also wish to preserve that multiplicative property when the associated single decrement life tables for each individual cause are combined. We ensure this property through the formula by which we estimate person-years lived in the residual category, the category that includes all causes of death that are not individually modeled. In particular, the person-years lived for the remaining causes (cause k, the residual) are computed as¹⁰:

$${{}_{n}L}_{x,k}=\left(\frac{{{}_{n}L}_x}{{\displaystyle \prod _{m=1}^{k-1}}{{}_{n}L}_{x,m}}\right)·n^{(k-1)}\text{for}t=1,2.$$ (A5)

For the open ended interval, which in our applications begins at age 100, we assume mortality rates to be constant and that no person-years are lived above age 110. In this case, the person-years lived for the master and the associated single decrement life tables are computed as:

$${{}_{+}L}_{100}=l_{100}·\underset{100}{\overset{110}{\int }}{e}^{-M(a-100)}\text{d}a=l_{100}·\left(-\frac{1}{M}(e^{-10M}-1)\right)=l_{100}·\frac{1-e^{-10M}}{M},$$

and

$${{}_{+}L}_{100}^i=l_{100}^i·\frac{1-e^{-10M^i}}{M^i},$$

respectively, where M and Mⁱ represent the death rate above age 100 from all causes and from cause of death i.