Distributed lag and spline modeling for predicting energy expenditure from accelerometry in youth

Abstract

Movement sensing using accelerometers is commonly used for the measurement of physical activity (PA) and estimating energy expenditure (EE) under free-living conditions. The major limitation of this approach is lack of accuracy and precision in estimating EE, especially in low-intensity activities. Thus the objective of this study was to investigate benefits of a distributed lag spline (DLS) modeling approach for the prediction of total daily EE (TEE) and EE in sedentary (1.0–1.5 metabolic equivalents; MET), light (1.5–3.0 MET), and moderate/vigorous (≥3.0 MET) intensity activities in 10- to 17-year-old youth (n = 76). We also explored feasibility of the DLS modeling approach to predict physical activity EE (PAEE) and METs. Movement was measured by Actigraph accelerometers placed on the hip, wrist, and ankle. With whole-room indirect calorimeter as the reference standard, prediction models (Hip, Wrist, Ankle, Hip+Wrist, Hip+Wrist+Ankle) for TEE, PAEE, and MET were developed and validated using the fivefold cross-validation method. The TEE predictions by these DLS models were not significantly different from the room calorimeter measurements (all P > 0.05). The Hip+Wrist+Ankle predicted TEE better than other models and reduced prediction errors in moderate/vigorous PA for TEE, MET, and PAEE (all P < 0.001). The Hip+Wrist reduced prediction errors for the PAEE and MET at sedentary PA (P = 0.020 and 0.021) compared with the Hip. Models that included Wrist correctly classified time spent at light PA better than other models. The means and standard deviations of the prediction errors for the Hip+Wrist+Ankle and Hip were 0.4 ± 144.0 and 1.5 ± 164.7 kcal for the TEE, 0.0 ± 84.2 and 1.3 ± 104.7 kcal for the PAEE, and −1.1 ± 97.6 and −0.1 ± 108.6 MET min for the MET models. We conclude that the DLS approach for accelerometer data improves detailed EE prediction in youth.

a sedentary lifestyle with diminished physical activity (PA) is considered one of the major contributors to the increased prevalence of obesity in youth in recent decades (17, 18, 28). Therefore, precise measurements of PA are important to our understanding of physiological, behavioral, and environmental factors causing energy imbalance and obesity (36). The determinants of PA include type, intensity, frequency, and duration (6). In recent years, PA intensity received considerable attention because of a reported increase in sedentary behaviors characterized by increased sedentary and light PA and decreased moderate and vigorous intensity PA (22).

Among noninvasive, nonintrusive, and low-cost methods, accelerometry has received the most attention, and has been frequently used to characterize PA. The output from commercially available accelerometers is typically reported in arbitrary units such as counts, reflecting body movements over a selected time interval (4, 9). These units do not have physiological meaning and usually are converted to physiological measures such as energy expenditure (EE) using prediction models.

To predict EE from accelerometry output, several approaches and usually monitor-specific prediction models, have been developed for youth (10, 21) and adults (8, 35). The benefits and limitation of using accelerometers for EE prediction have been recently reviewed (7, 15, 19, 24, 32). The major reasons for poor prediction of PA-related EE from accelerometers are 1) most predictive equations are developed from limited data generated in laboratory settings; 2) the variability in the accelerometers' output (counts) is greater than variability in EE measured using a reference standard method; 3) the relationship between measured EE and the accelerometer counts is often assumed to be linear; and 4) most studies used a single monitor placed on the waist or hip, limiting the assessment of arm and leg movement.

To overcome these limitations, we investigated the potential benefits of a distributed lag spline (DLS) modeling approach for the prediction of total daily EE (TEE) and EE spent in sedentary, light, and moderate/vigorous activities in youth using a whole-room indirect calorimetry as the reference standard. We applied a distributed lag model to address the fact that EE rises gradually after starting a PA bout and decreases gradually after finishing the bout. This is in contrast to rapid rises and falls in accelerometer PA counts when starting and ending the PA bout. To establish nonlinear relationships between the measured EE and the accelerometers' counts, we applied spline functions to model EE using PA counts during a wide range of activities. We also examined the benefits of using additional monitors located on the wrist and ankle and developed a series of prediction models. As a secondary goal, we applied the DLS modeling to predict PAEE and metabolic equivalents (MET) during the waking (nonsleeping) period for comparison with previously published and commonly used models for youth (11, 21, 25, 30, 31) and adults (8).

MATERIALS AND METHODS

Study Design and Participants

The study design entailed simultaneous measurements of EE and PA during an ∼24-h stay in a whole-room indirect calorimeter. Seventy-six healthy children (29 boys and 47 girls), 10–17 years old with a range of body mass index (BMI) percentiles from 10 to 99 (BMI 16.1 to 44.0 kg/m²) completed the study protocol. The participating children were healthy as assessed by a physician. Their demographic characteristics are shown in Table 1. Participants were recruited from the Nashville, TN, area using flyers, e-mail distribution, and word of mouth. Before the study, both children and parents or guardians signed informed consent approved by the Vanderbilt University Medical Center Institutional Review Board.

Table 1.

Characteristics of study participants

	All Subjects (n = 76)	Boys (n = 29)	Girls (n = 47)
Age, yr	13.4 ± 2.2 (10–17)	13.4 ± 2.5 (10–17)	13.4 ± 2.1 (10–17)
Ethnicity/race, %w/b/o	36.8/61.8/1.3	41.4/58.6	34.0/63.8/2.1
Height, cm	160.8 ± 9.3 (140.7–187.0)	162.8 ± 12.6 (140.7–187.0)	159.6 ± 6.4 (146.3–176.5)
Weight, kg	67.7 ± 20.0 (38.6–129.5)	71.0 ± 24.4 (38.6–129.5)	65.7 ± 16.7 (39.0–111.5)
BMI percentile	80.7 ± 24.1 (4–99)	82.9 ± 19.3 (38–99)	79.3 ± 26.8 (4–99)
% with BMI >95th percentile	36.8	37.9	36.2

Values are means ± SD. Values in parentheses are ranges. Body mass index (BMI) percentile was calculated using Centers for Disease Control software. w, White; b, black; o, other ethnicities.

Whole-Room Indirect Room Calorimeter Protocol

During the overnight stay (∼24 h) in the room calorimeter, participating youth followed a structured protocol during which activity data were collected. Participants were prompted to begin each required activity with an auditory alert, cuing them to interact with a touch screen interface that recorded start and end times for each activity interval. Morning activities included stretching, pacing, walking, and jogging on a treadmill with various speeds, sorting objects with a dominant hand, and using a computer mouse (solitaire). Afternoon activities included sedentary behaviors such as talking on the phone, handwriting, typing, playing video games, and shuffling cards, as well as sweeping the floor, biking, and stepping. Each prompted activity was performed for 10 min followed by a 10-min rest period. Other activities included eating meals and snacks at the table and self-care activities. During periods when no specific activity was scheduled, the participants were asked to engage in their normal daily routine without specific suggestions. To reflect habitual activity patterns in our study population, the protocol included more sedentary (∼35%) and light (∼55%) than moderate/vigorous (∼10%) intensities during waking period. Data collected during all activities including sleeping were used to develop the DLS models for prediction of TEE and all data except sleeping period were used to develop the DLS models for prediction of PAEE and MET during waking period.

Anthropometric Measurements

Body weight was measured to the nearest 0.01 kg with a monthly calibrated digital scale (Detecto-Medic, Detecto Scales, Northbrook, IL) while the participants wore light clothing and no shoes. Height was measured using a wall-mounted stadiometer calibrated upon wall installation and recalibrated yearly (Perspective Enterprises, Portage, MI).

Measurement of EE

The EE (kcal/min) was measured using the Vanderbilt whole-room indirect calorimeter described previously (26). The room calorimeter is equipped with a treadmill, stationary bike, wooden step, bed, television, DVD player, video game console, laptop computer with internet connection, desk, chair, toilet, and sink. The room calorimeter contains a precision force platform covering most of the floor for movement detection. The EE was calculated from the rates of oxygen (O₂) consumption and carbon dioxide (CO₂) production using measured concentrations of O₂ and CO₂ of the air inside the room calorimeter and multiplying by the flow rate of purged air. Sleeping energy expenditure (SEE; kcal/min) was calculated as the average EE during sleep (34). The waking period was defined as time from entering the room until going to bed in the evening and confirmed by the room calorimeter. The PAEE (kcal/min) was calculated by subtracting SEE from EE. The PA intensity categories were defined using METs calculated minute-to-minute as a ratio of EE and SEE. These PA categories entail sedentary (1.0–1.5 MET), light (1.5–3.0 MET), and combined moderate and vigorous (moderate/vigorous, ≥3.0 MET) intensities.

PA Monitoring

The PA was measured using a commercially available Actigraph GT1M accelerometer (ActiGraph, Pensacola, FL) placed on the hip at the dominant side of the anterior axillary line, the dominant wrist, and dominant ankle. Among commercially used accelerometers, Actigraph provides consistent and high quality data supported by its feasibility, reliability, and validity (9). The monitor measures accelerations 30 times/s in the range of 0.05–2.00 G and reports counts from the summation of the measured accelerations over a specified epoch (1). Actigraph data were collected at a 1-s epoch and summed as counts per minute.

Modeling Approach: Distributed Lag Spline Model

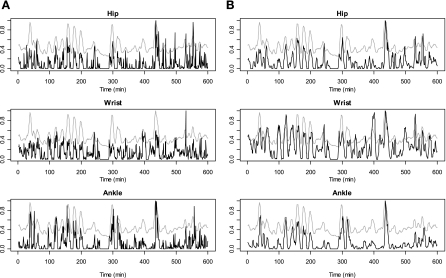
Applying the same distributed lag spline (DLS) modeling approach, we developed models for prediction of TEE (including sleeping), PAEE, and MET (during the waking period). Our modeling approach was based on an exploratory analysis examining the relationships between the room calorimeter-measured EE and the PA counts obtained from accelerometers placed on the hip, wrist, and ankle. Plots for the measured EE and the raw counts were overlaid in a normalized scale from 0 to 1 for each participant to examine the pattern of associations in a continuous time domain. Plots in Fig. 1A show relatively smooth changes in EE magnitude (gray lines) and more abrupt changes in raw PA counts magnitude (black lines) from hip, wrist, and ankle sites. This reflects differences between changes in EE and changes in motion in response to performed activities. Moreover, we found that the adjacent PA counts (lag PA) were strongly associated with both EE and PA measured at the current time point.

Fig. 1.

Normalized overlaid plot for a representative participant (10-year-old boy, weight = 76.5 kg, height = 155 cm) obtained during first 600 min of the ∼24-h stay in the whole-room indirect calorimeter. A: energy expenditure (EE) measured by room calorimetry (gray lines) and the raw physical activity (PA) counts (dark lines) obtained at hip, wrist, and ankle. B: EE measured by room calorimetry (gray lines) and the distributed lag PA counts (dark lines). The distributed lag PA counts were generated by taking the weighted average of the raw PA counts from lag −1 to lag 2.

These observations promoted the use of a distributed lag model as our modeling approach, which belongs to parametric generalized additive models. The model initially included several individual lag PA counts and their average as in models developed by Welty and Zeger (33). The inclusion of individual lag PA counts did not improve the prediction of EE, hence the average variable was chosen for further modeling and termed a distributed lag variable.

Next, we explored a nonlinear relationship between the measured EE and the PA counts (and the distributed lag variable) using nonparametric smoothing curves (5). Since no single equation (e.g., quadratic) could be applicable to modeling the relationship between PA counts and EE across all participants, we modeled smooth nonlinear relationship using restricted cubic splines (12).

Finally, our exploratory analysis showed that a high percentage of “zero” PA counts was associated with activities ranging from sleeping to moderate activities (0.6–6.4 kcal/min), suggesting that the same “zero” counts predict the wide range of EE values. To address this challenge, we generated a nonzero variable, defined as the time span (minutes) of continuous nonzero counts prior to the current PA measurement (counts). The rationale behind this is that the longer the time span of nonzero counts in the past time period, the more likely that it is an active period. Likewise, a shorter time span of nonzero counts in the past time period would more likely correspond to a sedentary or sleeping period associated with low EE.

We also included demographic covariates such as gender (0 for females, 1 for males), age (years), body weight (kg), and height (cm) in the models. Nonlinear relationships between the measured EE and some demographic covariates (age, weight, and height) were modeled using the restricted cubic spline functions. A detailed description of the distributed lag variable and the nonzero variable is provided in Statistical Methods and Analysis.

Comparison with Commonly Used Models

We also compared TEE, PAEE, and MET predicted by the DLS models with the results predicted by several commonly used models for youth (11, 21, 25, 30, 31) and adults (8). The room calorimeter EE measurements were used as a reference standard.

Statistical Methods and Analysis

Distributed lag variable.

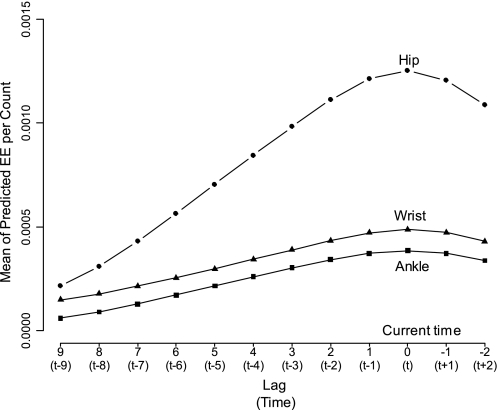
We define lag as the length of time (min) from the current EE measurement: lag 0 is the current time (t), lag 1 is 1 min prior to the current t, lag −1 is 1 min after the current t, and so on (see Fig. 2). The positive sign of the lag represents past time, whereas the negative sign represents future time. To examine the predictive ability for the neighboring PA counts measurements, we estimated the mean of predicted EE per PA count by regressing the measured EE (kcal/min) on the PA raw counts at each lag (Fig. 2). The greater the mean of predicted EE per the PA count, the greater would be the predictability of the PA counts at each lag. The predictive ability for the EE per the PA count persisted up to lag 2 for all sites. This suggested that the PA raw counts measured at lag −2, lag −1, lag 0 (the current time point), lag 1 and lag 2 may be used for each monitor. Thus we defined the distributed lag variable as a weighted average of the individual PA counts from lag a to b obtained from each monitor site, denoting ${\overline{x}}_t={\sum }_{l=t-a}^{t+b}{p}_l{x}_l$, where p_l are weights that sum to one and x_l is PA raw counts at lag l. To determine the appropriate weights and lags, we tested several candidates for a, b, and p_l in the Hip+Wrist+Ankle TEE model using the mean squared errors (MSE; kcal²/min) as the optimization target. The predictive abilities were not significantly impacted by various p_l, and hence the equal weights were chosen for simplicity in the final model.

Fig. 2.

The means of predicted EE (kcal/min) per PA raw count worn at hip, wrist, and ankle against lag and time (min). The predicted means are for lags 9 to −2 from the current measurement (lag 0 or time t), and time (min) is from past (−9 min) to future (+2 min).

Nonzero counts variable.

An automatic algorithm was used to generate the nonzero counts variable. The algorithm examined a sequence of data points (counts/min) acquired before the current measurement (at time t) for a specific search-back time period (i.e., 40 min). Starting from the current data point at t, the number of nonzero data points (counts/min) was found by counting nonzero data points until two consecutive zero counts values were found. The final duration of the search-back period (40 min) was chosen based on the distribution of the nonzero counts variable generated with a larger search-back period of 60-min.

Model validation.

The fivefold cross-validation was used to evaluate all models performance (13). Briefly, the participants were randomly divided into five groups. One group was held out as a test set and the remaining four groups were used as a training set to develop a model. The developed model was used to predict the EE in the held-out test group. This process was repeated five times for each held-out test set and the training set consisting of the remaining four-fifths participants. Thus, although the EE were predicted for all participants, an individual was never used in the prediction of their own EE. To check sensitivity of the results to the choice of fold, we compared the prediction errors from the Hip+Wrist+Ankle TEE model using 5-fold, 10-fold, and 50 times of 10-fold cross-validation. Since there were little differences between the results, we used fivefold cross-validation except for the regression coefficients, which was estimated using the entire data set (see appendix, tables a1, a2, and a3).

Statistical analysis.

Model performance was evaluated using summary statistics summarized for individuals for TEE (kcal) during ∼24-h room calorimeter stay, and PAEE (kcal) and MET (MET min) during the waking period. The minute-to-minute MSE (kcal²/min) was calculated as the average of squared differences between the predicted and measured values per minute for each participant. The means and standard deviations (mean ± SD) of prediction error (measured − predicted), percent prediction error, and the root mean squared error (RMS; the square root of the average of squared prediction error for individuals) were calculated as differences between TEE, PAEE, and MET measured using the room calorimeter and predicted by the DLS models. Note that the square roots of MSE are a minute-to-minute measure of error (e.g., kcal/min), whereas the RMS is an overall measure of error (e.g., kcal/day).

Bland-Altman plots (2) were used to assess agreements between the TEE, PAEE, and MET measured by the room calorimeter and predicted by the DLS models. The differences between the measured and predicted values (measured − predicted) and the 95% limits of agreement are presented against the measured values. The 95% confidence intervals (CI) of the mean differences between measured and predicted values were estimated using Student's t statistics.

Differences (measured − predicted) for EE, PAEE, and MET during waking period at three PA intensity levels (sedentary 1.0–1.5, light 1.5–3.0, and moderate/vigorous ≥3.0 METs) were calculated. The distributions of the differences were examined by strip charts with box plots. The sensitivity analysis (the probability of correct classification) of time spent prediction at each PA intensity was performed by calculating the percent of time points (min) the DLS models correctly categorized PA intensity compared with the room calorimeter (true category).

Wilcoxon signed rank tests, rank sum tests, or the corresponding nonparametric CI were used whenever appropriate due to skewed distributions. Data are presented as means, standard deviations (SD), and ranges. All analyses were performed using STATA 9.2 (StataCorp, College Station, TX) and a programming language R (29).

RESULTS

DLS Model Development

Development of the distributed lag and nonzero variables.

Plots in Fig. 1 illustrate that the distributed lag variables are better associated with the EE measurements compared with the PA raw counts. Direct neighboring measurements at lag +1 to −1 (minutes) had the strongest predictability for EE (Fig. 2). The measurement at lag 2 reduced MSE significantly compared with the model with lag +1 to −1 (P < 0.001). Thus, lags from +2 min to −1 min were chosen as time points for the distributed lag variables.

To generate the nonzero counts variable, the length of the search-back period was examined using its distribution. We chose a 40-min period, which covered the 99^th percentile of the distribution of the variable. Inclusion of the nonzero counts variable in the TEE model significantly reduced MSE compared with the model without this variable (P < 0.05). The nonzero counts variable improved the model by explaining additional variability during periods of low activity.

Development of site and outcome specific DLS models.

DLS models for prediction of TEE during ∼24-h room calorimeter stay were developed separately for Hip+Wrist+Ankle, Hip+Wrist, Hip, Wrist, and Ankle. Prediction models for PAEE and MET during waking period were developed with the same combination of accelerometer sites and modeling approach. Mathematical models are described in the appendix, and the regression coefficients are presented in Tables A-1, A-2, and A-3 for the TEE, PAEE, and MET models, respectively.

Model Performance and Validation

Overall model performance.

The prediction errors (measured − predicted), percent errors, and RMS for TEE, PAEE and MET models are presented in Table 2. Compared with the Hip model, models including wrist and/or ankle reduced RMS and the variability in prediction for all DLS models.

Table 2.

Prediction errors, percent prediction errors, and RMS calculated as differences between TEE, PAEE, and MET measured using the whole-room indirect calorimeter during approximately 24-h room calorimeter stay (TEE) and during approximately 800 min waking (nonsleeping) period (PAEE and MET) and predicted by DLS models

DLS Models	Prediction Error
	Error	Percent error	RMS
	(kcal/day)	TEE model, %	(kcal/day)
Hip+Wrist+Ankle	0.4 ± 144.0	−0.4 ± 6.8	143.0
Hip+Wrist	1.2 ± 156.8	−0.4 ± 7.3	155.8
Hip	1.5 ± 164.7	−0.3 ± 7.7	163.6
Wrist	−0.3 ± 181.8	−0.5 ± 8.0	180.6
Ankle	−2.0 ± 152.2	−0.5 ± 7.3	151.2
	(kcal)	PAEE model, %	(kcal)
Hip+Wrist+Ankle	0.0 ± 84.2	−0.9 ± 10.6	83.6
Hip+Wrist	1.3 ± 97.7	−0.7 ± 11.8	97.1
Hip	1.3 ± 104.7	−0.9 ± 13.4	104.1
Wrist	−0.5 ± 131.9	−1.1 ± 14.6	131.1
Ankle	−2.2 ± 106.4	−1.6 ± 13.8	105.7
	(MET min)	MET model, %	(MET min)
Hip+Wrist+Ankle	−1.1 ± 97.6	−0.3 ± 5.9	97.0
Hip+Wrist	−0.1 ± 102.8	−0.2 ± 6.2	102.1
Hip	−0.1 ± 108.6	−0.2 ± 6.5	107.8
Wrist	−1.9 ± 122.9	−0.3 ± 7.5	122.1
Ankle	−2.7 ± 119.8	−0.5 ± 7.3	119.0

Values are means ± SD. RMS, root mean squared errors; TEE, total energy expenditure; PAEE, physical activity energy expenditure; MET, metabolic equivalent; DLS, distributed lag spline.

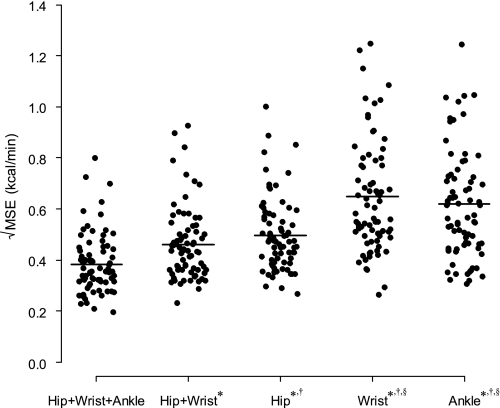
The square roots of the individual MSE for the TEE models are shown in Fig. 3. Adding wrist or/and ankle monitor significantly improved accuracy and precision of minute-to-minute EE prediction. The Hip+Wrist+Ankle predicted EE better than other models (all P < 0.05), while the Hip+Wrist performed better than all single site models (all P < 0.05). The Hip model also performed better than the Wrist and Ankle models (all P < 0.05). We obtained similar results for prediction of PAEE and MET (data not shown).

Fig. 3.

The distributions of the square root of the mean of squared errors (MSE; kcal/min) for prediction of TEE from the distributed lag and spline (DLS) models calculated for each participant. The horizontal bars represent the means. *P < 0.001 vs. Hip+Wrist+Ankle model; †P < 0.001 vs. Hip+Wrist model; ^§P < 0.001 vs. Hip model.

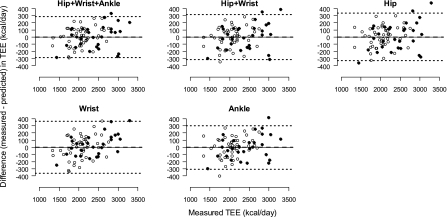
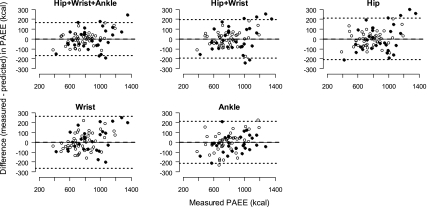
Table 3 summarizes means, SD, and the 95% percentile intervals (2.5^th and 97.5^th percentiles) for TEE, PAEE, and MET predicted by the DLS models and measured by the room calorimeter. Bland-Altman plots for TEE and PAEE models and the Hip+Wrist+Ankle and Hip models for MET are shown in Figs. 4, 5, and 6, respectively. They all show good agreements between the measured TEE, PAEE, or MET and the corresponding predicted values. The TEE, PAEE, or MET predicted by the models were not significantly different from the corresponding room calorimeter measurements (all P > 0.05). All DLS models accurately predicted TEE with good precision (shorter 95% CI) for Hip+Wrist+Ankle (−33 to 33 kcal), Hip+Wrist (−35 to 37 kcal), Hip (−36 to 39 kcal), Wrist (−42 to 41 kcal), and Ankle (−37 to 33 kcal) models. The overall performance of the PAEE and MET models was similar to the TEE models.

Table 3.

TEE, PAEE, and MET measured by the whole-room indirect calorimeter (approximately 24 h) and predicted by the corresponding DLS models for TEE, PAEE and MET for individuals

	TEE, kcal/day	PAEE, kcal	MET, MET min
Room calorimetry	2,200 ± 427 (1,434, 3,023)	817 ± 201 (478, 1,202)	1,642 ± 160 (1,353, 1,974)
Hip+Wrist+Ankle	2,199 ± 408 (1,531, 3,115)	817 ± 190 (478, 1,170)	1,643 ± 149 (1,383, 1,921)
Hip+Wrist	2,199 ± 410 (1,516, 3,045)	815 ± 196 (488, 1,202)	1,642 ± 159 (1,397, 1,956)
Hip	2,198 ± 410 (1,490, 3,047)	815 ± 191 (481, 1,174)	1,642 ± 157 (1,387, 1,948)
Wrist	2,200 ± 419 (1,542, 2,952)	817 ± 210 (508, 1,172)	1,644 ± 171 (1,394, 1,919)
Ankle	2,202 ± 405 (1,549, 3,191)	819 ± 183 (482, 1,147)	1,644 ± 142 (1,405, 1,876)

Values are means ± SD. Values in parentheses are 95% percentile intervals.

Fig. 4.

Bland-Altman agreement plots between total energy expenditure (TEE, kcal/day) measured during ∼24-h stay in the whole-room indirect calorimeter, and TEE predicted from the DLS models using PA measurements (counts) obtained from Actigraph accelerometers. The horizontal dashed line represents the mean difference between the TEE measured by the room calorimeter and predicted by the DLS models, and the upper and lower dotted lines are 95% limits of agreement calculated as mean difference ± 2 SDs. Values above and below the middle horizontal zero line are underestimation and overestimation of TEE, respectively. ● and ○, boys and girls, respectively.

Fig. 5.

Bland-Altman agreement plots between PAEE (kcal) during waking (nonsleeping) period measured during ∼24-h stay in the whole-room indirect calorimeter and PAEE predicted from the DLS models using PA measurements (counts) obtained from Actigraph accelerometers. The horizontal dashed line represents the mean difference between the PAEE measured by the room calorimeter and predicted by the DLS models and the upper and lower dotted lines are 95% limits of agreement calculated as mean difference ± 2 SDs. Values above and below the middle horizontal zero line are underestimation and overestimation of PAEE, respectively. ● and ○, boys and girls, respectively.

Fig. 6.

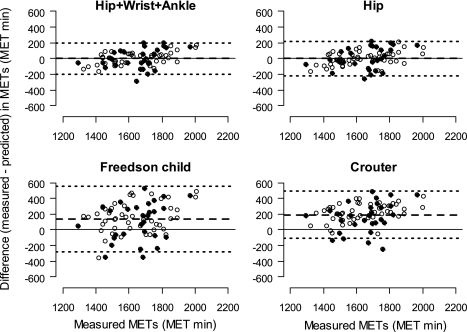
Bland-Altman agreement plots between measured metabolic equivalents (MET) in the whole-room indirect calorimeter calculated as a ratio of EE during waking period and sleeping EE and predicted from models. The METs were summed over waking period (MET min). The METs were predicted from the DLS MET models developed to predict MET during waking period and 2 previously published models, the linear model for children (Freedson child model) (11, 30) and the 2-component regression model (Crouter model) (8). The horizontal dashed line represents the mean difference between the methods, and the upper and lower dotted lines are 95% limits of agreement calculated as mean difference ± 2 SDs. Values above and below the middle horizontal zero line are underestimation and overestimation of METs, respectively. ● and ○, boys and girls, respectively.

EE prediction at PA intensity levels.

As expected, participants spent more waking time in sedentary and light (303 ± 130 and 454 ± 118 min, respectively) compared with moderate/vigorous intensity activities (78 ± 22 min).

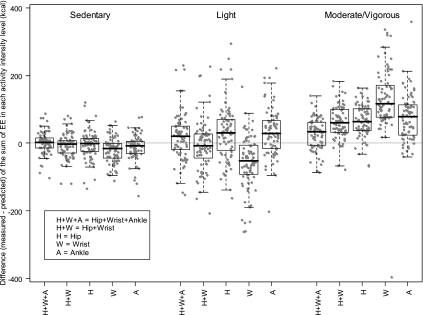
The distribution of EE prediction errors at different PA intensities (measured − predicted) are shown in Fig. 7. Overall, the TEE models predicted EE well at both sedentary and light PA intensities, but underpredicted EE at moderate/vigorous PA intensity. The PAEE models predicted the light PAEE well but slightly overpredicted the sedentary PAEE. This trend was similar for the MET models (data not shown).

Fig. 7.

Box plots of differences (measured − predicted) in EE (kcal) between measurements obtained from the whole-room indirect calorimeter and predicted from the DLS TEE models during waking period in sedentary (1.0–1.5 MET), light (1.5–3.0 MET), and moderate/vigorous (≥3.0 MET) PA intensity levels. ●, individual TEE differences.

The benefits of using additional accelerometers were assessed by comparing prediction errors between the Hip+Wrist+Ankle, Hip+Wrist, and Hip models at the PA intensities. The EE prediction errors from the Hip+Wrist+Ankle were significantly smaller than those from the Hip+Wrist at moderate/vigorous PA intensity (P = 0.001). The prediction errors from the Hip+Wrist at light PA intensity were smaller (P = 0.058) than those from the Hip. The Hip and the Ankle models were not significantly different in prediction errors at all PA intensities (all P > 0.05). The results were similar for the PAEE and MET models except that the prediction errors from the Hip+Wrist at sedentary PA level were significantly smaller than those from the Hip model for the PAEE and MET (P = 0.020 and 0.021, respectively).

Correct classification of time spent in PA intensities during waking (nonsleeping) periods.

Correct classification of time spent by the Hip+Wrist+Ankle TEE model was high at all intensity PA levels (Table 4). Compared with the Hip, the Hip+Wrist increased the correct categorization of time spent at light PA by 10% (P < 0.001). The Hip+Wrist+Ankle increased the correct categorization of time spent at moderate/vigorous PA by 17% compared with the Hip+Wrist (P < 0.001). The Hip+Wrist+Ankle and Ankle models resulted in the highest correct categorization of time spent at moderate/vigorous PA. The Hip+Wrist and the Wrist models had the highest correct categorization of time spent at light PA. Correct categorization of time spent at combined sedentary and light PA levels was very high (> 95%) for all DLS models. The results were similar for the PAEE and the MET models (data not shown).

Table 4.

Correct classification of time spent in sedentary, light, combined sedentary and light, and combined moderate and vigorous PA intensity categories during waking (nonsleeping) period predicted by DLS models for prediction of TEE

	Sedentary (1.0 < METs <1.5)	Light (1.5 ≤ METs <3.0)	Sedentary + Light (1.0 < METs <3.0)	Moderate/Vigorous (3.0 ≤ METs)
Measured by room calorimeter, min	303 ± 130	454 ± 118	756 ± 82	78 ± 22
DLS models, %
Hip+Wrist+Ankle	75	77	98.5	80
	(71,78)	(75,78)	(97.9,99.0)	(77,84)
Hip+Wrist	67	79	97.8	63
	(64,71)	(77,80)	(96.8,98.8)	(59,66)
Hip	76	68	99.0	62
	(73,79)	(65,71)	(98.6,99.	(58,65)
Wrist	63	78	96.5	34
	(59,67)	(76,80)	(95.5,97.5)	(31,40)
Ankle	73	69	99.1	69
	(69,76)	(67,72)	(98.9,99.3)	(65,73)

Values for room calorimeter are means ± SD. Values for the models are medians and 95% confidence intervals in parentheses.

We also examined the effect of PA data smoothing on time spent categorization. Compared with the DLS models, the correct categorization of time spent by models with the raw PA counts was lower at sedentary (72 vs. 75%), light (69 vs.77%) and moderate/vigorous (74 vs. 80%) PA intensities for the Hip+Wrist+Ankle model.

Comparison with Existing Models

Among several commonly used models, the predictions by the linear model for children proposed by Freedson and coworkers (Freedson child model) (11, 30) and the two-component regression model developed by Crouter and coworkers (Crouter model) (8) showed the highest agreement with the room calorimeter measurements, and hence were chosen for the Bland-Altman agreement comparison with the DLS models. Since both the linear and the two-component regression models use data from one-site (hip) monitor and predict METs, we used our MET Hip model and the best performing Hip+Wrist+Ankle model for final comparisons. Both Hip+Wrist+Ankle and Hip models were less biased (all P < 0.001) compared with the two tested models and more precise in the MET prediction (Fig. 6). The Hip model bias was significantly smaller than the bias generated by the two models (95% nonparametric CIs for the difference in bias were 91 to 182 and 172 to 227 MET min, respectively). Similarly, the bias from the Hip+Wrist+Ankle was also significantly smaller than those from the two models (95% nonparametric CIs for the difference in bias were 92 to 187 and 167 to 229 MET min, respectively).

DISCUSSION

The major accomplishment of this study is the development of a new modeling approach to predict TEE and EE in sedentary and light intensity PA categories for youth using PA counts measured by accelerometers and observable characteristics of sex, weight, height, and age. We also showed that EE prediction in sedentary, light, and moderate/vigorous intensity PA categories could be further improved by collecting data from monitors placed on wrist and ankle.

Our approach is novel in predicting EE from PA measurements in several ways. First, we used the distributed lag modeling to improve EE predictions by smoothing PA measurements of body movements, which improved correlation of PA measurements with room calorimeter EE measurements. Second, we used spline functions to model nonlinear relationships between the measured EE and the PA counts while most published models developed for EE prediction from accelerometer data used regression modeling assuming a linear relationship, a quadratic function, or two-regressions with polynomial function (8, 25). It may be possible that these approaches do not have sufficient flexibility to explain variability in a wide spectrum of PA intensities. Third, we generated a nonzero counts variable to improve EE prediction from “zero” PA counts at low intensity activities. Fourth, we examined the benefits of using additional monitors located at wrist and/or ankle to improve the EE prediction. Finally, we applied the DLS modeling to predict PAEE and METs during waking period. To ensure high applicability of our models to other youth populations, participants were heterogeneous in terms of height, weight, BMI (16.1 to 44.0 kg/m²), with a wide range of ages (10 to 17 yr), and were ethnically diverse.

In recent years, more complex modeling approaches for EE prediction have emerged such as two-regression modeling (8), Markov chain pattern recognition (20), and neural network (23) modeling. All these models require data collected at 1- or 10-s epoch, which may not be feasible in many large-scale epidemiological studies (6). Other approaches such as recent cross-sectional time series modeling (36) require simultaneous heart rate measurements. Model performance could be compared across the models and monitors if the prediction error, percent error, and/or RMS are reported. Among a few studies that developed models for youth, Zakeri et al. (36) recently reported prediction errors from the cross-sectional time series models developed using the Actiheart monitor. All DLS 24-h TEE models showed lower RMS than the Actiheart model (143.0 to 180.6 kcal vs. 200.8 kcal). For the prediction of PAEE, all DLS Actigraph models except the Wrist model generated smaller RMS than the Actiheart model (e.g., Hip+Wrist+Ankle: 83.6 kcal, Hip+Wrist: 97.1 kcal, Hip: 104.1 kcal vs. Actiheart: 107.7 kcal). The DLS 24-h TEE models also resulted in lower mean absolute errors and percent errors than the Actiheart model. A younger population, different monitor used, and a single-site approach in the Zakeri et al. (36) study may be a plausible explanation of the differences between the two studies.

Most published models were developed using accelerometers worn on the waist (hip) since this placement is optimal for detecting the central body movements. Single locations, however, may not fully capture low intensity activities performed with limited trunk movements (i.e., playing computer games, using computer mouse, talking or “texting” using cellular phone, or internet browsing). Few studies have examined the benefits of using additional monitoring sites, and the findings were not consistent between studies. Swartz et al. (27) and Leenders et al. (14) showed that the additional wrist Actigraph did little in improving the prediction of EE, whereas Melanson and Freedson (16) reported that the additional monitor improved the EE prediction. In our previous study, using different types of accelerometers, we showed benefits of using hip and wrist worn monitors (3) in predicting EE. In the present study, the Hip model was accurate in overall prediction of TEE, PAEE, or MET, and addition of wrist and ankle monitors did not significantly improve the overall prediction. Therefore, in studies designed to measure group averages of TEE, PAEE, or MET in youth, using a monitor placed at the waist (hip) and appropriate prediction equation might be sufficient.

However, the benefit of additional monitors is apparent when the prediction errors and RMS at PA levels were compared. The means and SD of the prediction errors and the RMS were reduced in the Hip+Wrist and Hip+Wrist+Ankle models. Compared with the Hip model, addition of a wrist monitor improved the prediction of EE, PAEE, or MET at light and sedentary PA intensity levels. A plausible explanation is the ability of the wrist monitor to measure hand movements associated with some sedentary behaviors. Addition of an ankle monitor to the Hip+Wrist model resulted in further improvement in the prediction of EE at moderate/vigorous PA intensity. Overall, the Hip+Wrist+Ankle model had smaller bias and variance than any other models at tested PA intensity levels. Thus, in studies focused on predicting EE of sedentary behaviors, the additional wrist or wrist and ankle monitors could improve the prediction of the EE, PAEE, or METs. Regarding the correct prediction of time spent in PA intensity categories, our results showed that wrist and ankle monitors could help in more accurate prediction of time spent at light and moderate/vigorous PA intensities, respectively. However, feasibility of using more than one monitor site in the free-living environment should be investigated, and the optimal balance between validity and feasibility of such approach should be assessed.

We also compared the prediction from our models with those from several commonly used models developed for Actigraph data. Our DLS models predicted METs more accurately and precisely than the best performing model for children (30) and the two-component regression model (8). It is also important to note that our modeling approach is general and could be modified for the prediction of EE from data generated by other types of accelerometers.

There are some limitations to our study and the developed DLS models. We used the room calorimeter generated EE data for modeling, including routine activities reflective of activities performed under free-living conditions. Although we included many different types of PA, some activities such as playing basketball or baseball cannot be performed in the room calorimeter. Thus future studies should incorporate doubly labeled water techniques to test the performance of the DLS models in the free living. Although the DLS models were developed for youth with a wide range of age and BMI, they might predict EE less accurately in younger children or adults. The DLS models for the different age groups and populations may need to be validated or optimized with specific model components. In this study, we used 1.5 MET to distinguish between sedentary and light PA intensities, although a clear threshold cut-off between sedentary and light PA intensities has not been well established. We used the 1.5-MET threshold to categorize these two PA levels to examine the benefits of using additional monitors more closely. Since many data points were close to the boundary of sedentary and light PA intensities, our results obtained for these categories may not be definite and should be used with caution. Although the DLS models for PAEE and METs performed satisfactorily compared with the commonly used models, they could be improved further. Finally, we observed that the DLS models have lower predictive power for EE or PAEE at moderate/vigorous than light and sedentary PA intensities, and hence should be used with caution in studies focused on predicting EE in higher (>3 METs) PA intensities.

In summary, we developed a new approach to predict EE from PA counts collected by accelerometers using a distributed lag variable in flexible spline models. The TEE predicted by our DLS models was not significantly different from the TEE measured by the room calorimeter. However, our DLS models should be further validated in an independent data set of children and adolescents in laboratory conditions using calorimetry and in the free living using doubly labeled water. Prediction by the DLS models appeared to be more accurate, precise, and sensitive in sedentary and light PA intensities. Moreover, the prediction of time spent in sedentary and light intensities benefited from the addition of wrist and ankle monitors. These findings may be useful in studies where measuring changes in sedentary behavior is important. Examples include preventive or therapeutic weight regulation programs with a PA component designed for obese or at risk for obesity youth.

GRANTS

This study was supported in part by R01-HL-082988, the Vanderbilt Institute for Clinical and Translational Research (VICTR) Grant 1UL1-RR-024975 from National Institutes of Health (NIH), Vanderbilt Diabetes Research and Training Center Grant DK-20593. L. Choi and M. S. Buchowski were also supported by R01-DK-69465. K. Y. Chen is supported by Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases/NIH (Z01-DK-071044).

APPENDIX: MODEL SPECIFICATION FOR DLS MODELS

General model notations are as follows. The variables ${\overline{x}}_t^{\mathit{hip}}$, ${\overline{x}}_t^{*\mathit{wrist}}$, and ${\overline{x}}_t^{\mathit{ankle}}$ are the distributed lag variables (lags 2 to −1) at time t for Hip, >Wrist, and Ankle multiplied by each participant's body weight. The x̄_t^wrist is the distributed lag variable for Wrist without being multiplied by the body weight. The variable x_t^nonzero.hip is the number of minutes of continuous nonzero Hip counts in the previous 40-min period at time t. A restricted cubic spline function is used with three specified knots. For an example of the weight in the DLS TEE models, the knots are specified at 40, 50, and 75 kg. A predicted value of x is represented by x̂. A notation for a covariate (x −40)₊ represents that the covariate equals to (x − 40) if x ≥ 40 and equals to 0 if x < 40. The knots for the splines were chosen based on the distribution of the covariates and were robust to precise choice of locations.

Table A1.

Regression coefficients for DLS TEE models for prediction of TEE.

	Hip+Wrist+Ankle	Hip+Wrist	Hip	Wrist	Ankle
βsex	1.801e-01	1.791e-01	1.601e-01	1.903e-01	1.606e-01
βheight	4.618e-01	5.131e-01	5.519e-01	5.538e-01	5.711e-01
β1age	0.0098474647	0.011442208	0.010602982	0.015915414	0.010537649
β2age	−0.0020577091	−0.0021616148	−0.0017917301	−0.0029429420	−0.0019240991
β3age	0.0041154183	0.0043232295	0.0035834602	0.0058858839	0.0038481982
β4age	−0.0020577091	−0.0021616148	−0.0017917301	−0.0029429420	−0.0019240991
β1weight	0.012889108	0.013592301	0.012279253	0.010960134	0.011788989
β2weight	−3.9838978e-06	−4.4419523e-06	−3.9764484e-06	−5.4221807e-06	−3.0563212e-6
β3weight	5.577457e-06	6.2187332e-06	5.5670278e-06	7.591053e-06	4.2788497e-6
β4weight	−1.5935591e-06	−1.7767809e-06	−1.5905794e-06	−2.1688723e-06	−1.2225285e-6
β1nonzero	0.016154343	0.037478371	0.067217778
β2nonzero	−0.00031522878	−0.00076250126	−0.0013219342
β3nonzero	0.00063045756	0.0015250025	0.0026438683
β4nonzero	−0.00031522878	−0.00076250126	−0.0013219342
β1hip	6.1038919e-06	3.4802184e-05	0.00010289413
β2hip	3.6955909e-14	−1.4504872e-13	−6.3722528e-13
β3hip	−5.4509965e-14	2.1394686e-13	9.399073e-13
β4hip	1.7554057e-14	−6.889814e-14	−3.0268201e-13
β1wrist	0.00060991711	0.00071803981		1.7003818e-05
β2wrist	−3.756143e-10	−4.99587e-10		−1.5167660e-15
β3wrist	4.8829859e-10	6.494631e-10		2.6543406e-15
β4wrist	−1.1268429e-10	−1.498761e-10		−1.1375745e-15
β1ankle	3.0542383e-05				0.00016025566
β2ankle	−2.0682920e-13				−1.1539739e-12
β3ankle	3.0507308e-13				1.7021115e-12
β4ankle	−9.8243872e-14				−5.481376e-13
β0	−5.908e-01	−7.400e-01	−6.199e-01	−6.531e-01	−6.426e-01

Table A2.

Regression coefficients for DLS PAEE models for PAEE

	Hip+Wrist+Ankle	Hip+Wrist	Hip	Wrist	Ankle
βsex	6.340e-02	6.061e-02	4.285e-02	7.000e-02	5.141e-02
βheight	3.326e-01	4.454e-01	4.462e-01	5.614e-01	3.971e-01
βage	−1.023e-02	−9.043e-03	−7.060e-03	−1.525e-02	−7.231e-03
β1weight	0.0063881575	0.0071198469	0.0062470157	0.0050236536	0.0071413129
β2weight	−3.0779033e-06	−3.5020714e-06	−3.5909033e-06	−6.0810182e-06	−3.5036577e-06
β3weight	4.3090647e-06	4.9029e-06	5.0272646e-06	8.5134255e-06	4.9051208e-06
β4weight	−1.2311613e-06	−1.4008286e-06	−1.4363613e-06	−2.4324073e-06	−1.4014631e-06
β1nonzero	0.0094423991	0.032353784	0.045767961
β2nonzero	−0.00021081922	−0.00069615082	−0.00093777958
β3nonzero	0.00042163844	0.0013923016	0.0018755592
β4nonzero	−0.00021081922	−0.00069615082	−0.00093777958
β1hip	2.0740686e-05	5.0148819e-05	8.8411013e-05
β2hip	−7.2883273e-14	−2.6048381e-13	−5.3001964e-13
β3hip	1.0750283e-13	3.8421361e-13	7.8177897e-13
β4hip	−3.4619555e-14	−1.2372981e-13	−2.5175933e-13
β1wrist	0.00028580228	0.00040005359		1.2198069e-05
β2wrist	−8.9523862e-11	−2.2095764e-10		−7.4097988e-16
β3wrist	1.1638102e-10	2.8724494e-10		1.2967148e-15
β4wrist	−2.6857159e-11	−6.6287293e-11		−5.5573491e-16
β1ankle	2.6366781e-05				0.00013084094
β2ankle	−1.7582419e-13				−9.3607983e-13
β3ankle	2.5934067e-13				1.3807177e-12
β4ankle	−8.3516488e-14				−4.4463792e-13
β0	−4.945e-01	−7.589e-01	−6.098e-01	−6.608e-01	−6.059e-01

Table A3.

Regression coefficients for DLS MET models for prediction of MET

	Hip+Wrist+Ankle	Hip+Wrist	Hip	Wrist	Ankle
βsex	−6.237e-02	−6.547e-02	−8.156e-02	−5.455e-02	−7.435e-02
βheight	1.525e-01	2.639e-01	2.670e-01	3.934e-01	2.208e-01
βage	−3.109e-03	−2.243e-03	−2.042e-05	−9.313e-03	−6.952e-04
βweight	−2.272e-03	−1.940e-03	−2.930e-03	−6.085e-03	−2.069e-03
β1nonzero	0.010773824	0.032365330	0.045856839
β2nonzero	−0.00023613161	−0.00069350054	−0.00093281675
β3nonzero	0.00047226321	0.0013870011	0.0018656335
β4nonzero	−0.00023613161	−0.00069350054	−0.00093281675
β1hip	2.9618283e-05	5.849171e-05	9.5284008e-05
β2hip	−1.5188450e-13	−3.3744338e-13	−5.9390138e-13
β3hip	2.2402964e-13	4.9772898e-13	8.7600453e-13
β4hip	−7.2145138e-14	−1.6028561e-13	−2.8210315e-13
β1wrist	0.00023583468	0.00034666784		1.3678485e-05
β2wrist	−3.0702699e-11	−1.5703812e-10		−1.1114611e-15
β3wrist	3.9913509e-11	2.0414955e-10		1.9450569e-15
β4wrist	−9.2108098e-12	−4.7111435e-11		−8.3359581e-16
β1wrist	2.6873824e-05				0.00013305167
β2wrist	−1.8086133e-13				−9.5560507e-13
β3wrist	2.6677046e-13				1.4095175e-12
β4wrist	−8.5909131e-14				−4.5391241e-13
β0	1.288e+00	1.052e+00	1.186e+00	1.209e+00	1.202e+00

DLS TEE models

1) Hip+Wrist+Ankle model.

2) Hip+Wrist model.

3) Hip model.

4) Wrist model.

5) Ankle model.

DLS PAEE models

1) Hip+Wrist+Ankle model.

2) Hip+Wrist model.

3) Hip model.

4) Wrist model.

5) Ankle model.

DLS MET models

1) Hip+Wrist+Ankle model.

2) Hip+Wrist model.

3) Hip model.

4) Wrist model.

5) Ankle model.