Spatial and Temporal Features of Synaptic to Discharge Receptive Field Transformation in Cat Area 17

Abstract

The aim of the present study was to characterize the spatial and temporal features of synaptic and discharge receptive fields (RFs), and to quantify their relationships, in cat area 17. For this purpose, neurons were recorded intracellularly while high-frequency flashing bars were used to generate RFs maps for synaptic and spiking responses. Comparison of the maps shows that some features of the discharge RFs depended strongly on those of the synaptic RFs, whereas others were less dependent. Spiking RF duration depended poorly and spiking RF amplitude depended moderately on those of the underlying synaptic RFs. At the other extreme, the optimal spatial frequency and phase of the discharge RFs in simple cells were almost entirely inherited from those of the synaptic RFs. Subfield width, in both simple and complex cells, was less for spiking responses compared with synaptic responses, but synaptic to discharge width ratio was relatively variable from cell to cell. When considering the whole RF of simple cells, additional variability in width ratio resulted from the presence of additional synaptic subfields that remained subthreshold. Due to these additional, subthreshold subfields, spatial frequency tuning predicted from synaptic RFs appears sharper than that predicted from spiking RFs. Excitatory subfield overlap in spiking RFs was well predicted by subfield overlap at the synaptic level. When examined in different regions of the RF, latencies appeared to be quite variable, but this variability showed negligible dependence on distance from the RF center. Nevertheless, spiking response latency faithfully reflected synaptic response latency.

INTRODUCTION

The receptive field (RF) concept is at the core of our understanding of the physiology of the nervous system. Following the original studies by Hubel and Wiesel (1959, 1962), the spatial organization of discharge RFs in primary visual cortex (V1) has been characterized in exquisite detail through the use of static flashing stimuli and quantitative analyses (Baker Jr and Cynader 1986; Chen et al. 2007; Dean and Tolhurst 1983; DeAngelis et al. 1993a; Emerson and Gerstein 1977a; Emerson et al. 1987; Field and Tolhurst 1986; Glezer et al. 1982; Heggelund 1981a,b, 1986; Jones and Palmer 1987a,b; Malone et al. 2007; Mata and Ringach 2005; McLean and Palmer 1989; Movshon et al. 1978a,b; Palmer and Davis 1981; Pernberg et al. 1998; Ringach 2002; Rust et al. 2005; Sasaki and Ohzawa 2007; Shevelev et al. 1992; Smyth et al. 2003; Suder et al. 2002; Szulborski and Palmer 1990; Touryan et al. 2005; Usrey et al. 2003; Wörgötter et al. 1998). Similarly, temporal properties of discharge RFs—visual response latency in particular—have been examined in a large number of studies (reviewed in DeAngelis et al. 1995; Lamme and Roelfsema 2000; Nowak and Bullier 1997; Schroeder et al. 1998). Beyond this quantitative description, the spatiotemporal features of the static RF have been particularly important for testing the contributions of linear and nonlinear mechanisms in the genesis of various RF properties such as orientation tuning (Chen et al. 2007; Gardner et al. 1999; Heggelund and Moors 1983; Jones and Palmer 1987b; Szulborski and Palmer 1990; Touryan et al. 2005; Usrey et al. 2003), spatial frequency tuning (Andrews and Pollen 1979; DeAngelis et al. 1993b; Field and Tolhurst 1986; Jones and Palmer 1987b; Kulikowski and Bishop 1981; Movshon et al. 1978a,b; Touryan et al. 2005), direction selectivity (Baker Jr 2001; Baker Jr and Cynader 1986; Conway and Livingstone 2003; DeAngelis et al. 1993b; De Valois et al. 2000; Emerson and Gerstein 1977b; Emerson et al. 1987; Horwitz and Albright 2005; Humphrey and Saul 1998; Livingstone 1998; McLean and Palmer 1989; McLean et al. 1994; Pack et al. 2006; Peterson et al. 2004; Reid et al. 1991; Saul et al. 2005), disparity tuning (Anzai et al. 1997; DeAngelis et al. 1991; Ohzawa et al. 1997; Tsao et al. 2003), or color coding (Conway and Livingstone 2006; Horwitz and Albright 2005; Horwitz et al. 2007). Static RF maps and latencies have also been instrumental in studies aimed at determining the flow of information transfer in the visual cortex (Alonso and Martinez 1998; Alonso et al. 2001; Ghose et al. 1994; Martinez and Alonso 2001; Reid and Alonso 1995).

The principal aim of the present study was to examine how synaptic RFs are transformed into discharge RFs. Although the spatiotemporal organization of discharge RFs has been amply documented, the way these discharge RFs are generated through their synaptic inputs is not well characterized. A better understanding of the elaboration of cortical neurons RFs requires the examination of their synaptic counterparts. Both the spatial and temporal organizations of cortical neurons RFs at the membrane potential level have been addressed in a number of studies (Borg-Graham et al. 1998; Bringuier et al. 1999; Cardin et al. 2005; Creutzfeldt and Ito 1968; Ferster 1988; Finn et al. 2007; Hirsch et al. 1998, 2002, 2003; Lampl et al. 2001, 2004; Martinez et al. 2002, 2005; Nelson et al. 1994; Nowak et al. 2005; Pei et al. 1994; Priebe and Ferster 2005; Priebe et al. 2004; Volgushev et al. 1995, 1996), yet these studies have usually provided either no or only partial examination of the relationship between synaptic and discharge RFs. A quantitative comparison of features of discharge and synaptic RFs in the same cells is still lacking. Importantly, since most mapping studies are based on extracellular recording, such a comparison would also allow determining how much of the subthreshold RF might be inferred on the basis of extracellularly recorded responses.

In the present investigation, we used bars flashed at high temporal frequency to quantitatively examine the spatial and temporal properties of, and the transformation between, synaptic and discharge RFs. Our results demonstrate that some features of the discharge RFs are poorly predicted from those of the synaptic RFs, whereas others appear to be directly inherited from the synaptic RFs. Comparison of RF size and temporal properties with the known spatiotemporal features of inputs to V1 suggests that the synaptic RF, as revealed with high-frequency flashing bars, is constructed mostly through thalamocortical and short-distance intracortical connections.

METHODS

Surgical procedure

A detailed account of the protocols for cat preparation, electrophysiological recordings, and data acquisition can be found in Sanchez-Vives et al. (2000) and is summarized here. Experiments were performed on adult cats (2.5–3.5 kg). Anesthesia was induced with ketamine (12–15 mg/kg, administered intramuscularly [im]) and xylazine (1 mg/kg, im). Atropine (0.05 mg/kg, administered subcutaneously) was given to reduce secretions. Wires were placed through the skin for electrocardiographic recording. A cannula was inserted into a forelimb vein for intravenous perfusion and an endotracheal tube was inserted for artificial respiration. The cat was set in a stereotaxic frame and ventilated with nitrous oxide and oxygen (2:1) with halothane (1.5% during surgery). Epidural electroencephalographic (EEG) recording was performed through wires inserted over the frontal cortex. A cisternal drainage and a bilateral thoracotomy were made to minimize brain movements resulting from respiration and from heartbeat. The animal was suspended by the rib cage to the stereotaxic frame. A small craniotomy was made to gain access to area 17.

Following surgery, the animal was paralyzed with Pavulon (0.3 mg/kg for induction followed by a continuous perfusion of 0.3 mg·kg⁻¹·h⁻¹) or Norcuron (0.15 mg/kg for induction followed by a continuous perfusion of 0.1 mg·kg⁻¹·h⁻¹). The nictitating membranes were retracted using ophthalmic phenylephrine. The pupils were dilated and accommodation was paralyzed with ophthalmic atropine. The area centralis and optic discs were localized by back projection. Corrective, gas-permeable contact lenses were used to protect and focus the eyes onto a computer monitor at 114 cm.

During recording, anesthesia was maintained with 0.4–1% halothane in nitrous oxide:oxygen (2:1). The heart rate, expiratory CO₂ concentration, rectal temperature, and blood O₂ concentration were monitored throughout the experiment and maintained at 150–180 bpm, 3–4%, 37–38°C, and >95%, respectively. The EEG and the absence of reaction to noxious stimuli were regularly checked. This protocol was approved by the Yale University Institutional Animal Care and Use Committees and conforms to the guidelines recommended in Preparation and Maintenance of Higher Mammals During Neuroscience Experiments (National Institutes of Health publication No. 91-3207).

Recording

Intracellular recordings were obtained with sharp micropipettes filled with potassium acetate (2 M). The micropipettes were beveled to obtain a resistance of 50–100 MΩ. Recordings were accepted only if the membrane potential was more negative than −55 mV at rest, the input resistance was >20 MΩ, and the neuron able to discharge trains of action potentials during the whole duration of depolarizing current pulses (≥200 ms). Spikes were extracted on-line as time series (resolution: 10 μs) through a window discriminator after band-pass filtering of the raw signal.

Receptive field mapping

RF location was assessed by using light bars that were moved by hand. Subsequently, preferred orientation and spatial frequency were quantitatively assessed from peristimulus time histograms (PSTHs) calculated on-line. Visual stimuli were generated through a VSG-Series 3 computer system (CRS, Cambridge, UK) and displayed on a 19-in. color monitor (80-Hz noninterlaced refresh, 1,024 × 768 resolution). All stimuli were delivered through the dominant eye. For orientation tuning (Nowak et al. 2008), we used light or dark bars drifting at 4–8°/s and presented with eight different orientations and two motion directions (16 stimuli total; angular resolution: 22.5°). For spatial frequency tuning, we used drifting gratings (40% contrast) presented within a circular patch (3–10° diameter) centered on the RF. The remainder of the screen was a gray background with a luminance equal to the mean grating luminance. The drift temporal frequency was 1.56 or 3.12 cycles/s. Spatial frequencies varied between 0.125 and 2.83 cycles/deg in logarithmic steps (increment by $\sqrt{2}$).

We used stimuli flashed one at a time at high frequency (“sparse noise”; adapted from DeAngelis et al. 1993a; Jones and Palmer 1987a) to activate the discharge and synaptic RFs. The stimulus was a bar that was either darker or brighter than the background. Background luminance was halfway between that of the bright and dark bars and the contrast between the bright and dark bars was 80%. For each presentation, which lasted 50 or 62.5 ms, the bar occupied one randomly chosen position among 16 available. Randomization protocol was “blockwise,” with no repeats of a given stimulus until all 32 stimuli were presented. The bar orientation was chosen to match that preferred by the neuron under study and the bar positions varied along the axis perpendicular to the preferred orientation. The mapping was therefore restricted to this single dimension. Adjacent positions were spaced apart by a distance equal to the bar width, such that bars in adjacent positions were adjacent but not overlapping. The bar width was a fraction (one fourth to one seventh) of the inverse of the preferred spatial frequency. The bar width was 0.62 ± 0.23° (mean ± SD; range: 0.17–1.33°) and the stimulated area represented 9.93 ± 3.69° of visual angle (range: 2.67–21.33°).

To facilitate the comparison of RFs based on membrane potential deviations and spike rates, we replaced each spike with a raised cosine bell (10-ms width at half-height), forming a spike density function. The spike density function and membrane potential were sampled at a rate of 200 Hz. Spikes were clipped from the membrane potential trace at the spike threshold level. For each bar polarity and position, we calculated an average of the membrane potential and of the spike density function over a period of −125 to +225 ms, with time 0 corresponding to stimulus onset. The averaged spike density function is strictly similar to a classical PSTH, except with reduced high-frequency noise. To further reduce noise, the averaged spike density function and averaged membrane potential were smoothed with a Gaussian filter (width: 3.6 ms). This smoothing was applied in the time domain and thus did not affect the data in the spatial domain.

The data are represented as space–time maps (DeAngelis et al. 1993a; McLean and Palmer 1989), which allow the decomposition of the response in both temporal (x-axis in figures) and spatial (y-axis) dimensions; the response strength (z-axis) is represented by a color code (Figs. 1 and 2). In simple cells, third map was obtained by subtracting the dark bar response map from the bright bar response map (Fig. 2).

Fig. 1.

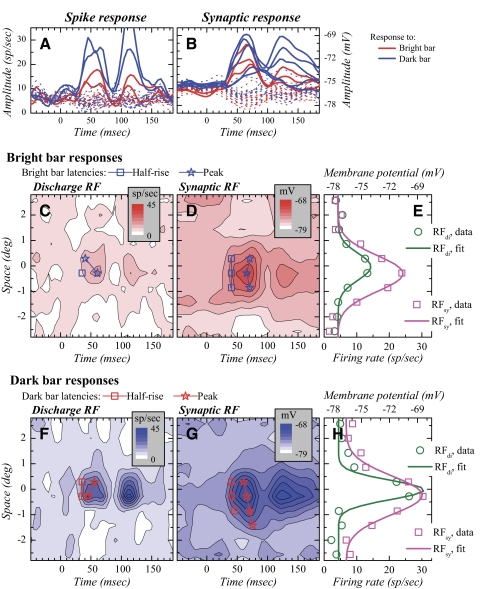
Discharge and synaptic receptive fields (RFs) in complex cells. A: time course of the spiking response to the presentation of the bright (red traces) and dark bars (blue traces) in 16 spatial positions across and beyond the RF. Solid lines correspond to responses that were significant by our criteria and dotted lines to responses that were not. Time 0 corresponds to stimulus onset. The first peaks (30–100 ms) correspond to the responses to the onset of the stimulus (“on” response) and the second peaks (>100 ms) to the responses to stimulus extinction (“off” response). B: time course of the synaptic responses in the same cell. C: response to the bright flashing bar shown as a space–time map for the spiking response. D: response to the bright flashing bar shown as a space–time map for the membrane potential response. In C and D, half-rise and peak latencies are represented as a function of space by squares and stars, respectively. E: bright bar RF profiles taken at the time of the maximum “on” response in the maps. Experimental data are shown as circles (spiking response) and squares (synaptic response). Continuous lines correspond to Gaussians fitted to the data. F–G: same as C–E for the response to the dark bar.

Fig. 2.

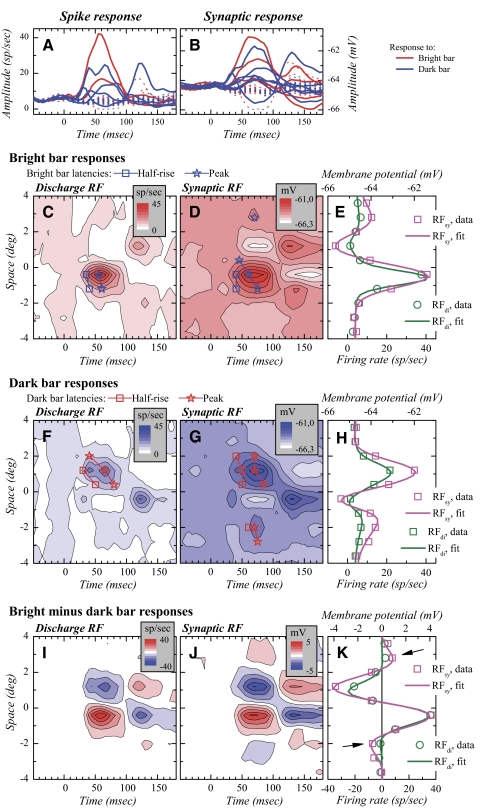
Discharge and synaptic RFs in a simple cell. Conventions for A–H as for Fig. 1. In E and H, experimental data have been fitted using pairs of difference-of-Gaussians (DOGs). I and J: subtraction of the dark bar response map from the bright bar response map. In these subtracted maps, an increase in red saturation represents increased response to the bright bar and an increase in blue saturation represents increased response to the dark bar, scaled negatively due to the subtraction. K: synaptic and discharge RF profiles taken at the time of maximal “on” response in the subtracted maps. The data have been fitted with Gabor functions.

The amplitude of the largest bin in the baseline (−125 to 0 ms) was determined in each map. Responses were considered significant if, for three consecutive bins, their amplitude was >1.1-fold the largest baseline bin. This approach allowed us to dismiss false positives, irrespective of the statistics underlying the noise distribution. This is a conservative approach; if the amplitude of the baseline bins was distributed in a Gaussian fashion, as often happened for the synaptic responses, then the P value associated with our criteria would be extremely low (P ≪ 0.01).

The quantitative analysis of RF spatial features was performed on the response averaged over a time period of ±10 ms centered on the peak response in the space–time plots. In complex cells, subfield amplitude and extent were determined using Gaussian functions fitted to the bright and dark bar responses

$$y=y_0+A_{\max \hspace{0.17em}}\exp \hspace{0.17em}\left[\frac{-{(x-x_c)}^2}{2{\sigma }^2}\right]$$

where y₀ corresponds to the baseline firing rate (in spikes/s) or to the baseline membrane potential (in mV), A_max represents the maximal amplitude of the response (in spikes/s or in mV), x_c represents the center of the subfield (in deg), and σ represents its SD (in deg).

In simple cells, we also examined the subfields using a Gaussian-based fitting procedure. Studies have previously shown that the RF profiles and contrast sensitivities of simple cells may be well accounted for by combinations of Gaussians or difference-of-Gaussians (DOGs) (Hawken and Parker 1987; Soodak 1986). Depending on the cells, we found that different combinations of Gaussians were necessary. Initially, one Gaussian curve was fitted to each subfield.¹ In some other cells, the RFs also included hyperpolarizing responses and firing rate decreases in addition to depolarizing responses, which were taken into account by including additional Gaussian curves with negative amplitude. Finally, in a small number of cells, we found that the best fit was obtained using a single DOG or pairs of DOGs. RFs of retinal ganglion cells and dorsal lateral geniculate nucleus (LGNd) neurons exhibit a center–surround structure that is well described by DOGs (Enroth-Cugell and Robson 1966; Rodieck 1965). DOGs thus seemed to be an obvious choice for fitting subfields in simple cells and, indeed, worked well in many cases (Fig. 2). However, not all subfields could be fitted with a DOG because surrounds were not always apparent (Supplemental Fig. S2).² This may result from the fact that flashing bars are not always efficient for activating the surround in LGNd neurons, especially when bars are short compared with the surround size (Bullier et al. 1982). When characterized by DOGs, the center position, amplitude, and width of the “center” Gaussian were used for comparing synaptic and discharge subfields in simple cells. The parameters associated with the “surround” Gaussian of the DOGs were not studied further. With a couple of exceptions, we always used the same fitting procedure for both spiking and synaptic responses. Different combinations of functions were tested for each data set. The choice of the combination that best fit the data was based on the reduced chi-square value. The fit quality was evaluated with an r² value. The mean r² values for Gaussian fits on discharge and synaptic RFs were 0.93 ± 0.08 and 0.93 ± 0.07, respectively.

The entire RF of simple cells with more than one subfield was quantified using the profile taken from the subtracted maps at the time of peak response amplitude, which was fitted with a Gabor function (Field and Tolhurst 1986; Jones and Palmer 1987b; Marcelja 1980)

$$y=y_0+A_{\max }\exp \left[\frac{-{\left(x-x_c\right)}^2}{2{\sigma }^2}\right]\times \cos \left\{\left[2\pi F_{\mathrm{opt}}\left(x-x_c\right)\right]+\phi \right\}$$

In addition to the parameters A_max, x_c, and σ corresponding to the Gaussian envelope, F_opt is the frequency of the RF (in cycles/deg), and φ is its phase (in radians). The mean r² values obtained with Gabor fits were 0.97 ± 0.02 for the discharge RFs and 0.95 ± 0.04 for the synaptic RFs.

Latency and response duration measurements

Two different latency measures were used: 1) the half-rise latency (Levick 1973; Lu et al. 1995), which corresponds to the time between stimulus appearance and the time at which the response for each stimulus position reaches a value representing half the peak amplitude for that position; and 2) the peak latency, which corresponds to the time at which spiking or synaptic responses reached their maximal values for each stimulus position, relative to stimulus appearance.

Beyond peak latency, we also calculated the latency at which the response decreased back to half the peak amplitude (half-fall latency). Response duration was calculated by subtracting this latency from the half-rise latency.

Latencies were determined for bright and dark bar responses, but not in subtraction maps, to avoid interference between the “push” and the “pull” in the latency domain.

Because stimulus frequency was 20 Hz (more rarely 16 Hz), latencies longer by 50 ms than the shortest latencies were not taken into account because they most likely reflected responses to stimuli extinction (“off” responses). “Off” response latency has not been examined in this study.

Statistics

Population data are given as means ± 1SD. Comparisons were made using nonparametric tests (Mann–Whitney and Wilcoxon tests for unpaired and paired comparisons, respectively). Except when mentioned, linear regression analysis was used to characterize the transformation from synaptic RF to discharge RF. Except when noted, the R² values given in text correspond to those obtained using linear regression analysis. Nonparametric correlation tests (Spearman rank correlation) were performed to rule out effects of outliers.

RESULTS

We used a sparse-noise stimulation technique to characterize the spatiotemporal features of discharge and synaptic RFs of intracellularly recorded neurons in cat area 17 (n = 38). Simple (n = 25) and complex (n = 13) cells were distinguished on the basis of the space–time maps calculated for spiking responses. Simple cells were characterized either by the presence of “on” and “off” responses that were well separated in space (Hubel and Wiesel 1962) (n = 20) or by the presence of a single “on” subfield (n = 5).³ Complex cells, on the other hand, showed bright and dark bar responses that overlapped extensively in both space and time.

Examples of RF maps are presented in Figs. 1 and 2 and in Supplemental Figs. S1 and S2. Segments of raw data from the same cells are shown in Supplemental Fig. S3. The orientation of the flashing bar used to map the RF was the one found to be optimal for the cell under study. The bar width corresponded to one fourth to one seventh of the inverse of the preferred spatial frequency determined using drifting gratings. Orientation and spatial frequency tuning curves are illustrated for the same cells in Supplemental Fig. S4.

Figures 1A and 2A show the averaged spike discharge for each stimulus position. Red lines correspond to the responses to the bright bar presented on a gray background and blue lines to the responses to the dark bar presented on a gray background. Solid lines correspond to responses that were significant by our criteria (see methods) and dotted lines to responses that were not. Panel B in each figure illustrates the averaged membrane potential, using the same conventions.

The map in Fig. 1C represents the spiking response to the bright bar in a complex cell. Conversely, the map in Fig. 1F represents the spiking response to the dark bar. In these space–time maps, the x-axis corresponds to time and the y-axis to space. The z-axis, corresponding to response strength, is color coded: an increase in red saturation represents increased response to the bright bar (Fig. 1C) and an increase in blue saturation represents increased response to the dark bar (Fig. 1F). In both maps, two “blobs” are visible, approximately centered on 50 and 110 ms, representing the “on” and “off” responses to the stimuli: the “on” response is the response to stimulus appearance and the “off” response is the response to stimulus withdrawal. As is typical of complex cells, the “on” and “off” responses occupy the same spatial position. Following DeAngelis et al. (1993a), in the remainder of this study we call “bright excitatory subfield” (BES) the subfield presenting an “on” response to the bright bars and “dark excitatory subfield” (DES) the subfield presenting an “on” response to the dark bars. As is typical of complex cells, BES and DES occupy the same spatial position (Fig. 1, C and F). The synaptic RF for the same cell also possessed BES and DES responses that occurred in the same spatial positions (Fig. 1, D and G). Half-rise and peak latencies are represented as a function of space overlaid on the four RF maps. The synaptic RF was considerably broader than the discharge RF and lasted longer.

The squares and circles in Fig. 1, E and H correspond to the RF profiles taken at the time at which the “on” response was the largest in the space–time maps and represent response amplitude as a function of space. The continuous lines represent the fits made to these data. As in all complex cells, the data were fit with Gaussians (see methods). The fitted Gaussians show that the synaptic subfields were larger than the discharge subfields.

Space–time RF maps of a simple cell are shown in Fig. 2. Figure 2, A, C, and F illustrates the spiking responses to the bright bar and to the dark bar. In both maps, regions of significant activation are visible but—in contrast to those of the complex cells (Fig. 1)—these regions are spatially separated. The space–time map shown in Fig. 2I was obtained after subtraction of the dark bar map from the bright bar map. The discharge RF obtained this way displays two well-defined subfields between 40 and 100 ms, one corresponding to the BES and the other one to the DES (in red and blue, respectively). After 100 ms, the response polarity is reversed. This reversal, observed in a majority of simple cells, occurs after the end of the stimulus presentation. It corresponds to the response to the bright bar extinction (a local contrast decrement) in the DES and to the response to the dark bar extinction (a local contrast increment) in the BES. Since the contrast change associated with bar offset is the opposite of that obtained with bar onset, the spatial pattern of the responses is also reversed.

Space–time maps for the synaptic responses are displayed for the bright bars, for the dark bars, and for the response difference in Fig. 2, D, G, and J, respectively. As expected from the push–pull organization of cortical simple cells (Ferster 1988; Palmer and Davis 1981), the bright bar response map shows, in addition to the depolarization associated with the spiking response, a hyperpolarization, whose spatial and temporal position coincides with the DES. The dark bar synaptic response map shows the opposite pattern. Furthermore, as can be more clearly seen in the subtracted map (Fig. 2J), the synaptic RF shows two additional subfields in addition to the two principal ones, which were not visible in the spiking response map.

As for complex cells, we quantified the spatial features of simple cell subfields by examining the RF profiles at the time where the response displayed its largest amplitude (Fig. 2, E and H). Subfield organization in simple cells was more complex than that in complex cells. For this reason, different combinations of Gaussian functions were tested to quantify the amplitude and spatial features of both bright bar and dark bar responses (see methods). Compared with other Gaussian combinations, a pair of DOGs (Hawken and Parker 1987; Soodak 1986), used in opposition, provided the best description of the organization of discharge and synaptic subfields for the cell in Fig. 2. For the synaptic subfields, the largest depolarization peaks corresponded to the “center” of one of the two DOGs, whereas the largest hyperpolarization peak corresponded to the “center” of the second DOG (Fig. 2, E and H). Note that the side peaks were well included by the dual DOG fit. As for most of the cells examined, the fit functions and combinations that were used for the synaptic response were also used for the spiking response (Fig. 2, E and H). A feature of the maps is that regions of hyperpolarization in the synaptic RFs were consistently associated with regions of reduced firing rate in the discharge RFs, although the firing rate reduction was relatively less prominent than the hyperpolarization.

We also quantified the entire RF of simple cells using the profile taken from the subtracted maps at the time of peak response amplitude (Fig. 2K). For all simple cells with at least two subfields peaking within a similar time range (n = 18), this quantification was achieved by fitting the response profile with a Gabor function (see methods). For the cell in Fig. 2, the Gabor fit describes the two main subfields of the discharge RF. The Gabor fit to the synaptic RF includes two additional, smaller subfields (Fig. 2K, arrows), which were subthreshold for spike generation, making the synaptic RF larger than the discharge RF.

Subfield composition

The subfield in which the strongest response was obtained will be referred to as the “dominant” subfield and the second one in strength as the “secondary” subfield. Some simple cells (Fig. 2) eventually showed additional subfields that will be referred to as “tertiary” and “quaternary.” The number of excitatory subfields (that have been fitted in bright and/or dark bar RF profiles) was always 2 in complex cells (one BES and one DES). In simple cells, it varied between 1 and 4, with an average of 2.20 subfields for discharge RFs and 2.44 for synaptic RFs. The difference between synaptic and discharge RFs was nearly significant (P = 0.06).

Receptive field amplitude

Synaptic RF to discharge RF amplitude transformation in the dominant subfields.

We examined how the amplitude of depolarizing synaptic subfields was transformed into firing rate in the discharge subfields. This analysis was restricted to the “dominant” subfield. The amplitude (“A_max”) of the dominant synaptic subfield varied considerably between cells, from 0.9 to 19.6 mV (Fig. 3A). The average maximum depolarization produced by our RF mapping stimuli was 4.6 ± 3.7 mV. Simple (4.5 ± 4.4 mV; median, 2.9 mV) and complex cells (4.7 ± 1.5 mV; median, 4.8 mV) showed slightly different distributions for this feature (P = 0.03; Fig. 3A). For the spiking response, the maximal amplitude of the dominant subfield also varied considerably among cells, ranging from 5 to 143 spikes/s (Fig. 3B). At the population level, the mean was 31 ± 27 spikes/s. There was no significant difference between simple and complex cells (P = 0.18).

Fig. 3.

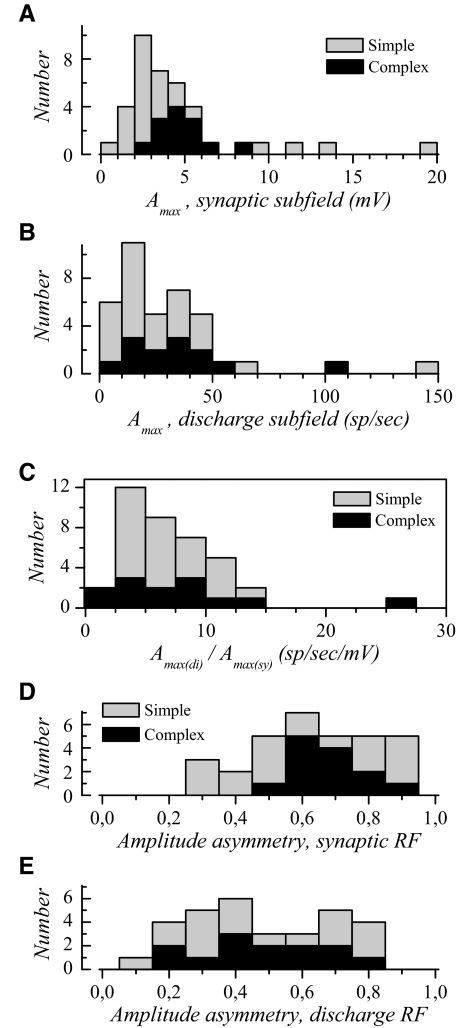
Amplitude of visual responses in synaptic and discharge RFs. Data in A and B correspond to the amplitude of the Gaussian curves fitted to the dominant subfield in simple and complex cells (A_max). A: distribution of A_max in the dominant synaptic subfield in simple (gray bars) and complex cells (dark bars). B: distribution of A_max in the dominant discharge subfield. C: distribution of the ratio of peak firing rate divided by maximal depolarization amplitude. D: ratio of secondary to dominant A_max distribution for the synaptic subfields. E: ratio of secondary to dominant A_max for discharge subfields.

The synaptic to discharge amplitude transformation was examined through the ratio, A_max(di)/A_max(sy), with the indices “di” and “sy” referring to discharge and synaptic RFs, respectively. This ratio represents the gain of the synaptic to firing rate transformation and indicates how much firing rate is gained per millivolt of depolarization. This ratio applies only to the peak response and is likely to be different before and beyond the peak due to different time courses for spiking and synaptic responses (see following text). The amplitude ratio (Fig. 3C) was not significantly different between simple and complex cells (P = 0.9) and the mean was 7.3 ± 4.6 spikes·s⁻¹·mV⁻¹. This ratio varied widely from one cell to the next. In parallel, regression analysis of A_max(di) versus A_max(sy) (not illustrated) revealed a moderate relationship (R² = 0.482).

Synaptic RF to discharge RF amplitude transformation in simple cells fitted with a Gabor function.

The analysis presented earlier concerned the dominant subfield of the RFs. Although this description is adequate to account for the full RF of complex cells, it does not account for the synaptic to discharge amplitude transformation that operates in simple cells when the subtracted maps are fitted with a Gabor function.

In Gabor fits, the parameter A_max (amplitude of the Gaussian envelop) overestimates the actual maximal amplitude of the RF. The largest response amplitude, hereafter called “y_max,” was derived analytically from the parameters extracted from the Gabor fit. The mean y_max for synaptic and discharge RFs (4.8 ± 4.3 mV and 30.9 ± 32.8 spikes/s; not illustrated) appears to be similar to the y_max obtained in Gauss-fitted dominant subfields (Fig. 3, A and B). The mean amplitude ratio for Gabor-fitted simple cells was 6.9 ± 3.2 spikes·s⁻¹·mV⁻¹. The regression analysis of Y_max(di) versus Y_max(sy) yielded an R² value of 0.612 (not illustrated).

Response strength asymmetry in discharge and synaptic subfields.

As shown previously (Heggelund 1986; Sasaki and Ohzawa 2007; Spitzer and Hochstein 1985), and as illustrated in Figs. 1 and 2, response amplitudes in BES and DES were rarely identical. We quantified this response amplitude difference using the amplitude of the fitted Gaussians. Only cells that responded to both bright and dark bars within the same time range were considered for this analysis (n = 31). We calculated an “asymmetry index” in which the amplitude for the dominant subfield was used as the denominator and the amplitude of the secondary subfield was used as the numerator (Heggelund 1986). This ratio is close to 1 when the response amplitudes are similar for the two bar contrasts and close to zero for strongly asymmetric response amplitudes.

The mean asymmetry index for discharge RFs was 0.48 ± 0.21 (Fig. 3E). A comparable asymmetry in response strength has been documented in Heggelund (1986). The asymmetry index for synaptic RFs averaged 0.64 ± 0.19 (Fig. 3D). There was no significant difference between simple and complex cells (synaptic RFs: P = 0.3; discharge RFs: P = 0.9). These data show that a balance of BES and DES strength is the exception rather than the rule, even in complex cells.

The asymmetry was more pronounced for the discharge subfields compared with that calculated for the synaptic subfields (P = 0.0004). Thus asymmetry of response strength was already present in the synaptic RF, but appears to be exacerbated in the discharge RFs. This suggests that spike threshold and input–output nonlinearity amplified this asymmetry.

Receptive field width

Comparison of discharge and synaptic subfield widths.

The fact that synaptic RF width is larger than that of the discharge RF is widely reported (Bringuier et al. 1999; Creutzfeldt and Ito 1968; Martinez et al. 2005; Pei et al. 1994; Priebe et al. 2004), although the relationship between the two has not been examined in detail. We first examined the widths of the dominant subfield in simple and complex cells. To calculate a width parameter that is close to the full extent of the subfields, we used the width of the Gaussian at 5% of the peak height (w_5%), calculated as

$$w_{5\%}=2\times {\left[2\times \ln \left(20\right)\right]}^{0.5}\times \sigma$$

that is, w_5% ≈ 4.896σ.

The distribution of w_5% for the dominant discharge subfields is presented in Fig. 4B. Mean widths for simple (2.6 ± 1.4°) and complex cells (3.3 ± 1.5°) did not differ significantly (P = 0.13). However, the w_5% for the synaptic subfields was significantly larger in complex cells compared with that in simple cells (P = 0.02); w_5% for the dominant synaptic subfield averaged 3.5 ± 1.8° in simple cells and 5.4 ± 2.6° in complex cells (Fig. 4A).

Fig. 4.

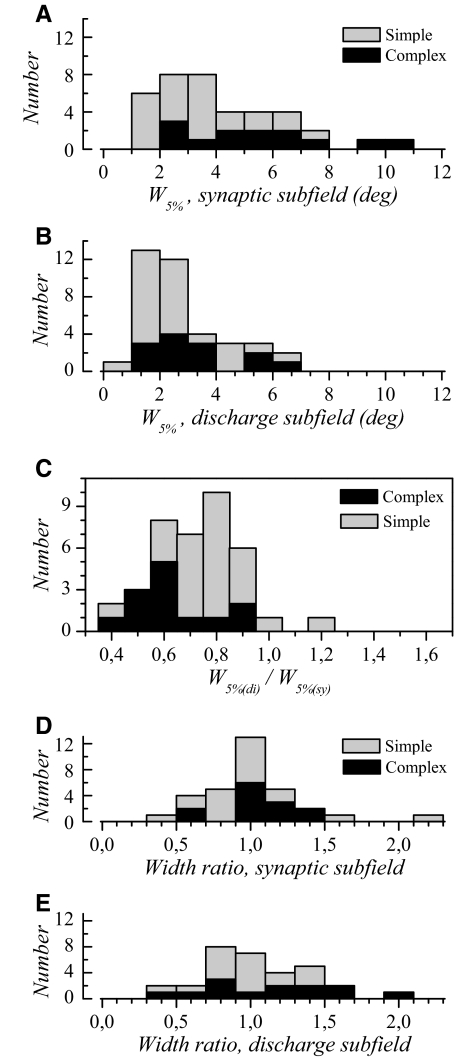
Subfield widths for synaptic and spiking responses. A: distribution of the widths (w_5%) determined for dominant synaptic subfields in simple (gray bars) and complex cells (dark bars). B: distribution of w_5% for dominant discharge subfields in simple and complex cells. C: discharge to synaptic subfield width ratio. Almost all values are <1, indicating that synaptic subfields are larger than discharge subfields. D and E: primary and secondary subfields are on average of similar width. Width ratio distribution is shown in D for the synaptic responses and in E for the spiking responses.

As expected, synaptic subfields were significantly larger than discharge subfields (P < 0.0001 in simple cells and P = 0.0015 in complex cells).

To further characterize differences between synaptic and discharge subfields, we calculated a width ratio as w_5%(di)/w_5%(sy). It can be seen that the distribution of the ratio values is rather broad (Fig. 4C), with values ranging between 0.43 and 1.18. This means that the width of the dominant synaptic subfield is close to that of the discharge subfield width in some cells, but can be up to 2.3-fold larger in others. Note that, since we generated one-dimensional maps, these measurements apply only to the width dimension and may be different for the length dimension.

The discharge-to-synaptic RF width ratios were significantly (P = 0.009) larger in simple cells compared with those in complex cells (Fig. 4C). The means were 0.78 ± 0.16 for simple cells and 0.63 ± 0.16 for complex cells. In other words, the difference between synaptic and spiking subfield width was smaller in simple cells compared with that in complex cells. This indicates that the transition from synaptic to discharge subfields is somehow “steeper” in simple cells than that in complex cells. This difference in synaptic to discharge width transformation helps to explain why simple and complex cells possess subfield widths that are different at the synaptic response level (Fig. 4A), but not at the spiking response level (Fig. 4B).

Entire RF width for spiking and synaptic responses in simple cells.

A strong overlap of BES and DES is the defining characteristic of a complex RF, which has the consequence that the width of the dominant subfield is close to that of the whole RF. This is not the case for simple cells, since BES and DES are more separated spatially. Therefore to characterize differences between synaptic and discharge RFs in simple cells, we also examined their whole RF width. This was calculated as w_5%, using the width of the Gaussian envelope of the Gabor fits. The mean w_5% was 4.3 ± 2.0 for the discharge RF (not illustrated). The w_5% for the full synaptic RF of simple cells was significantly larger than that of the discharge RF (P = 0.0005). Synaptic RF w_5% averaged 5.1 ± 2.3° (range: 2.0–11.8°).

The discharge-to-synaptic w_5% ratio was 0.84 ± 0.12 (range: 0.61–1.07; Fig. 6C). This value is clearly larger than that when dominant subfields were examined alone (Fig. 4C). The implication of this result is that, when considering their full extent, the synaptic RFs of simple cells were, on average, only 1.2-fold wider than their discharge RFs (range: 0.93–1.65).

Fig. 6.

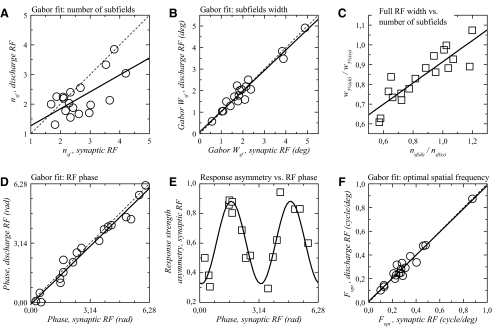
A: number of subfields (n_sf) in synaptic and discharge RFs of Gabor-fitted simple cells. The scatterplot and linear regression analysis illustrate the dependence of discharge n_sf on synaptic n_sf. For the majority of cells, the values are below the equality line (dashed line), implying that synaptic RFs in a majority of simple cells possessed subfields that were subthreshold for spike generation. B: subfield widths derived from Gabor function fitted to simple cell RFs (w_sf). In contrast to those determined from Gaussian fits (Fig. 4), subfield widths are very similar for synaptic and discharge RFs. Regression equation: w_sf(di) = 0.083 + 0.951 × w_sf(sy). C: ratio of the spiking to synaptic whole RF width (w_5%) plotted against spiking to synaptic number of subfields ratio. The significant correlation indicates that, in simple cells, the variability in the discharge to synaptic RF width ratio is well explained by the number of synaptic subfields that did not induce spiking responses. D: phases of synaptic and discharge RFs of simple cells fitted with Gabor functions. The scatterplot and regression analysis demonstrate that the discharge RF phase is almost completely determined by the phase of the synaptic RF. The regression equation is: φ_di = −0.102 + 0.979 × φ_sy. E: relationship between responses strength asymmetry (Fig. 3D) and synaptic RF phase. The data have been fitted with a sinusoid. One cell from D does not appear due to lack of measurable response with individual Gaussian fit for one of the two bar contrasts. F: optimal spatial frequency (F_opt) determined from Gabor fits in simple cells. The regression equation is: F_opt(di) = −0.008 + 0.978 × F_opt(sy). Dashed lines in A, B, D, and F represent equality line.

The w_5% for the spiking RF in Gabor-fitted simple cells did not differ significantly from the w_5% of the dominant synaptic subfield in complex cells (P = 0.21). This suggests that complex cells inherit most of their synaptic RF width from simple cells belonging to the same vertical “column.”

Comparison of dominant and secondary subfield width.

We next examined whether dominant and secondary subfields possessed similar widths. The width in the secondary subfield was expressed relative to the width of the dominant subfield (Heggelund 1986). The ratios thus calculated (Fig. 4, D and E) were not significantly different between simple and complex cells (P = 0.5 and 0.3 for synaptic and discharge subfields, respectively). At the population level, BES and DES presented the same width, the mean ratio values being 1.01 ± 0.33 for the synaptic subfields and 1.05 ± 0.35 for the discharge subfields.

Subfields overlap in discharge and synaptic RFs

We quantified the overlap between BES and DES using a modified version of the “overlap index” (OI) of Schiller et al. (1976), which takes differences in subfield amplitude into account. First, the width of the secondary subfield was recalculated, so that this width (w_re) corresponded to that measured at 5% of the maximal amplitude in the dominant subfield

$$w_{\mathrm{re}}=2{\left\{-2\ln \left[\frac{0.05}{A_{\max \left(\sec \right)}/A_{\max \left(\mathrm{dom}\right)}}\right]\right\}}^{0.5}\times {\sigma }_{\sec }$$

For example, if the secondary subfield amplitude was half that of the dominant subfield, then the recalculated width would correspond to that measured at 10% of the secondary subfield amplitude. The overlap index was then calculated as

$$\mathit{OI}=\frac{0.5\times \left[w_{5\%\left(\mathrm{dom}\right)}+w_{\mathrm{re}}\right]-\left|x_{c\left(\mathrm{dom}\right)}-x_{c\left(\sec \right)}\right|}{0.5\times \left[w_{5\%\left(\mathrm{dom}\right)}+w_{\mathrm{re}}\right]+\left|x_{c\left(\mathrm{dom}\right)}-x_{c\left(\sec \right)}\right|}$$

A value of 1 is obtained when the BES and DES overlap completely, a value of 0 indicates that the two subfields are immediately adjacent without overlapping, and a value of 0.33 indicates that subfields are separated by a distance equivalent to half their widths.⁴

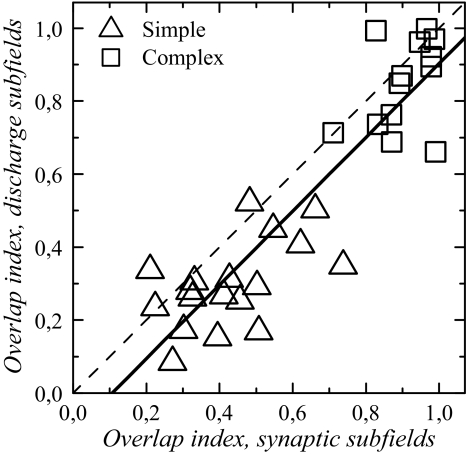
For simple cells, the mean OI for spiking response was 0.30 ± 0.12. The range was large, with the largest value being 0.52 (Fig. 5). For complex cells, the mean was 0.85 ± 0.12 and the lowest value was 0.66 (Fig. 5).

Fig. 5.

Subfield overlap indices (OIs) for spiking and discharge RFs are well correlated. Solid line: regression line. The regression equation is: OI_(di) = −0.108 + 1.011 × OI_(sy), with the indices “di” and “sy” referring to discharge and synaptic RFs, respectively. Dashed line represents equality line.

The OI values for synaptic subfields were significantly different between simple and complex cells (P < 0.0001). The means were 0.43 ± 0.15 in simple cells and 0.90 ± 0.08 in complex cells. Distributions for simple and complex cells show little overlap (Fig. 5). OI in simple cells reached a maximal value of 0.74, whereas the minimum value for complex cells was 0.71.

OI at the spiking response level was well predicted by the OI at the synaptic response level: the synaptic OI was significantly (P < 0.0001) correlated with the discharge OI, with an R² of 0.81 and a slope close to 1 (Fig. 5).

When comparing synaptic and discharge subfields, the OIs were not found to be significantly different in complex cells (P = 0.06), but they were significantly different in simple cells (P = 0.0014). This means that, in simple cells, BES and DES overlapped more extensively in the synaptic RF, as expected, given the larger synaptic subfield widths compared with discharge subfield widths.

Hyperpolarizing subfields

We did not observe hyperpolarizing subfields in any of the complex cells, whereas this was a prominent feature in 11 of the 25 simple cells.⁵ To keep with the terminology used thus far, the hyperpolarizing subfields have been abbreviated as “BIS” for “bright inhibitory subfield” when the hyperpolarization was induced by a bright bar and “DIS” for “dark inhibitory subfield” when the hyperpolarization was evoked by a dark bar, although we acknowledge that there is some difficulty in equating hyperpolarization and inhibition. Hyperpolarization may result from the withdrawal of tonic excitation. In addition, hyperpolarization could have been missed if the membrane potential was near the reversal potential for inhibition. Different methods (Borg-Graham et al. 1998; Hirsch et al. 1998; Monier et al. 2003) are required for a more precise examination of the involvement of inhibition in RF generation. Our analysis nevertheless provides an insight into the potential organization of putative inhibitory subfields in simple cells.

As expected from the push–pull arrangement (Ferster 1988; Palmer and Davis 1981), the position of the center of hyperpolarizing subfields evoked with one stimulus polarity corresponded closely to the center of the depolarizing subfields obtained with the opposite stimulus polarity. For BES versus DIS center positions, the relationship was highly significant (P < 0.0001, R² = 0.981; not illustrated). For DES versus BIS center positions, the relationship was slightly less good (P = 0.01, R² = 0.793). In both cases, the regression slopes were close to 1 (0.941 and 1.112, respectively).

Not only subfield center positions, but also subfield widths were similar. DIS width, measured at 5% of peak amplitude, was slightly but significantly (P = 0.02) less than the BES width and the width ratio w_5%(DIS)/w_5%(BES) averaged 0.86 ± 0.12 (not illustrated). BIS width did not differ significantly from DES width (P = 0.8), but data were more variable; w_5%(BIS)/w_5%(DES) averaged 1.05 ± 0.53. When bright bar and dark bar responses were pooled together, width ratio for hyperpolarizing versus depolarizing responses averaged 0.94 ± 0.36. Given similarities for both subfield center position and subfield width, it is no surprise that the hyperpolarizing response evoked for one stimulus polarity overlaps extensively with the depolarizing response evoked with the opposite polarity (overlap index, BES vs. DIS: 0.91 ± 0.08; DES vs. BIS: 0.80 ± 0.16; not illustrated).

Given the strong similarity of hyperpolarizing versus depolarizing subfield width and position, on the one hand, and the overlap of BES and DES, on the other hand, it can be concluded that inhibition evoked by one bar contrast will extend into approximately half the excitatory area for the same bar contrast. This corresponds well with results obtained in an extracellular recording study using interaction between stimuli (Heggelund 1981a). This large overlap of excitatory and inhibitory subfields might be of relevance for RF properties in simple cells (e.g., Heggelund and Moors 1983).

Additional parameters for Gabor-fitted simple cells

Number of subfields in discharge and synaptic RFs.

In simple cells whose RFs have been fitted with Gabor functions, the number of sinusoid half-cycles that are included in the Gaussian envelope provides an evaluation of the number of subfields (n_sf) contained in the RF, calculated as follows (DeAngelis et al. 1993a)

$$n_{\mathrm{sf}}=2\times w_{5\%}\times F_{\mathrm{opt}}$$

n_sf is a continuous variable, whereas the count presented earlier, corresponding to the number of excitatory subfields that were fitted with Gaussians, was a discrete measure. However, the two estimates are quite close. Mean n_sf was 2.2 ± 0.6 (range: 1.3–3.8) for the discharge RF and 2.65 ± 0.7 (range: 1.7–4.2) for the synaptic RF (vs. 2.15 and 2.44, respectively, obtained with the discrete measures in the same cells). The mean number we report here for spiking response is similar to that reported by DeAngelis et al. (1993a) (2.45 in adult cats).

The n_sf value was found to differ consistently between discharge and synaptic RFs (Fig. 6A); this parameter was significantly larger for synaptic RFs than that for discharge RFs (P = 0.012).

Regression analysis indicated a significant dependence of n_sf(di) on n_sf(sy) (P = 0.003; Fig. 6A). However, the R² value of 0.396 was relatively low. This shows that the number of subfields exhibited by the synaptic RFs is larger than that found in the discharge RFs, but also indicates that it is not a very good predictor of the number of subfields found in the discharge RFs.

Width of the subfields extracted from a Gabor fit.

There are two ways of measuring subfield width in simple cells. The first one, presented earlier, was derived from the responses to either bright or dark bar responses fitted with Gaussians. Another way of measuring subfield width can be applied to the bright minus dark bar responses fitted with Gabor functions. This second subfield width measure (“w_sf”) was calculated as w_5%/n_sf. The mean value was 2.09 ± 1.10° for synaptic RFs (Fig. 6B). Subfield width for discharge RFs (2.07 ± 1.07°; Fig. 6B) was nearly identical (P > 0.9). w_sf values for spiking and synaptic responses were significantly (P < 0.0001) and strongly correlated (R² = 0.946) with a slope close to unity (Fig. 6B).

With a Gaussian fit on either DES or BES, the subfield width was, for the same population of simple cells, significantly larger than that determined here from the Gabor fit in the subtracted maps (2.49 ± 1.36° for discharge subfields and 3.35 ± 1.76° for synaptic subfields; P = 0.0004 and 0.0002, respectively). This difference is due to the partial overlap of BES and DES in simple cells. This overlap is erased by the bright bar minus dark bar response subtraction procedure. Estimates of subfield width based on subtracted maps fitted with a Gabor function may thus underestimate the actual subfield width. The difference is relatively minor, on average, for the discharge RFs (83 ± 12%), but becomes quite large for the synaptic RFs (63 ± 11%).

Receptive field width and number of subfields.

In simple cells whose RF profile was fitted with a Gabor function, we have shown that the full width of the discharge RFs represented between 61 and 107% of the full width of the synaptic RFs (Fig. 6C). This variability cannot be explained by differences in subfield widths (Fig. 6B). We next examined whether this variability could be explained by a related variability in the relative number of synaptic and discharge subfields (Fig. 6A). In other words, is there a relationship between the ratio of synaptic RF to discharge RF width and the presence of subthreshold synaptic subfields in simple cells? As shown in Fig. 6C, we found there is indeed a significant correlation between the two ratios, n_sf(di)/n_sf(sy) and w_5%(di)/w_5%(sy). The R² value (0.77) indicates that more than three quarters of the width ratio variability can be explained by the variability of the number of subfields ratio. In other words, the simple cells that show larger synaptic RF than discharge RF width are also those for which the number of subfields in the synaptic RF is larger than the number of subfields in the discharge RF.

Receptive field phase and response strength asymmetry.

The phase of the RFs, given by Gabor fits in simple cells, reflects the organization of the subfields within the RF and indicates, at the population level, whether subfields may be arranged in a stereotyped fashion, corresponding to odd symmetric RFs, in which the phase is an integer multiple n, of π, and even symmetric RFs, in which the phase is nπ + 0.5π. Similar to previous studies performed in cat area V1 (DeAngelis et al. 1993a; Field and Tolhurst 1986; Jones and Palmer 1987a), the phase values for discharge RFs did not show any clustering (Fig. 6D), indicating no obvious segregation between odd and even symmetric RFs. We found that this was also the case for the spatial phase of the synaptic RFs (Fig. 6D). This indicates that the flat distribution found at the spiking level does not result from the addition of some noise on an initially odd-and-even symmetric synaptic phase distribution. Furthermore, the phase for synaptic and discharge RFs showed a highly significant correlation (R² = 0.968; Fig. 6D).

Earlier we showed that response amplitudes in BES and DES are often asymmetric (Fig. 3, D and E). This response strength asymmetry can be related to the phase of the RF. Figure 6E represents response strength asymmetry for the synaptic subfields, plotted against the phase measured for the same RFs. Note that these two variables were determined independently: the phase was given by the Gabor fit on the bright bar minus the dark bar subtracted responses, whereas response strength was measured on the dominant and secondary subfields fitted with Gaussians. The data have been fit with a sinusoid and the goodness of fit (r² = 0.82) indicates that the cells with the most asymmetrical responses possessed rather odd symmetric RFs, whereas more symmetrical response strengths were obtained in cells with rather even synaptic RFs.

Optimal spatial frequency.

Gabor fits on simple cells provide another parameter, the spatial frequency of the RF (F_opt). F_opt ranged between 0.1 and 0.87 cycle/deg for both discharge and synaptic RFs (Fig. 6F). Means and SD obtained for synaptic and discharge RFs were identical: 0.31 ± 0.18 cycle/deg for both. Regression analysis showed a strong dependence of discharge F_opt on synaptic F_opt (Fig. 6F; R² = 0.957, slope = 0.978; R² = 0.878, slope = 0.949 without the outlier near 0.9 cycle/deg). This suggests that the optimal spatial frequency of the discharge RFs is inherited almost completely from that of the synaptic RFs.

Spatial frequency tuning predicted from synaptic RFs is sharper than that predicted from discharge RFs in simple cells

Extracellular recording studies have shown that the preferred spatial frequency exhibited by simple cells corresponds very precisely with the one that can be determined from the static RF (Andrews and Pollen 1979; DeAngelis et al. 1993b; Field and Tolhurst 1986; Jones and Palmer 1987b; Kulikowski and Bishop 1981; Movshon et al. 1978a). Similar results have been obtained for membrane potential responses in intracellularly recorded cells (Lampl et al. 2001). Nevertheless, it has also been shown that the width of the spatial frequency tuning curve predicted from the static discharge RF is systematically broader than the one actually measured (DeAngelis et al. 1993b; Field and Tolhurst 1986; Kulikowski and Bishop 1981). It has been proposed that this discrepancy results from a larger number of subfields in the synaptic RFs (Andrews and Pollen 1979; Field and Tolhurst 1986; Kulikowski and Bishop 1981). Because we demonstrated that the number of subfields n_sf is indeed larger in the synaptic RFs (Fig. 6A), we also explored the consequences of this difference on the spatial frequency selectivity that can be predicted from both synaptic and discharge static RFs.

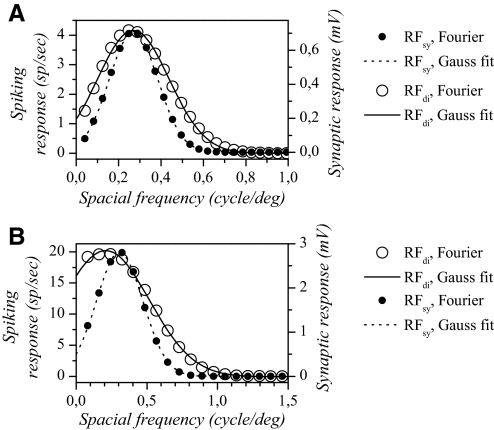
Predicted spatial frequency selectivity of simple cells (n = 18) was determined by applying Fourier analysis to the Gabor fitted on discharge and synaptic RFs (DeAngelis et al. 1993b; Field and Tolhurst 1986; Kulikowski and Bishop 1981). The resulting spatial frequency selectivity profile was fit with a Gaussian (DeAngelis et al. 1993b). Two examples are shown in Fig. 7, A and B, which correspond to the example simple cells shown in Fig. 2 and in Supplemental Fig. S2, respectively. In both cases, the predicted tuning appears broader for the spiking response than that for the synaptic response. In addition, the cell in Fig. 7B appears low-pass when considering the spike response, but appears band-pass when considering the synaptic response.

Fig. 7.

Examples of spatial frequency tuning curves predicted from synaptic and discharge static RFs in 2 simple cells. A: predicted tuning for the simple cell shown in Fig. 2. B: predicted tuning for the simple cell shown in Supplemental Fig. S2. Open symbols represent the result of the Fourier transform on the Gabor used to fit the discharge RFs and closed symbols the result of the Fourier transform on the Gabor used to fit the synaptic RFs. Continuous lines represent the Gaussian fits made on the Fourier transforms of the discharge RFs and dashed lines those made on the Fourier transforms of the synaptic RFs. For both cells, the spatial frequency tuning width predicted from the synaptic RF appears narrower than that predicted from the discharge RF.

The frequency at which the Gaussian shows its maximum amplitude corresponds to the predicted optimal spatial frequency pF_opt. As expected, pF_opt was nearly identical to that determined from Gabor fits (Fig. 6F). Mean values obtained for synaptic and discharge RFs were again nearly identical: 0.31 ± 0.18 cycle/deg for the synaptic RFs and 0.30 ± 0.18 cycle/deg for the discharge RFs (range: 0.1–0.87 cycle/deg for both discharge and synaptic RFs; not illustrated).

For three other parameters, however, the predicted spatial frequency selectivities for discharge and synaptic RFs were found to differ significantly. The first of these parameters is the high spatial frequency cutoff (or corner frequency), pF_high, which corresponds to the spatial frequency for which half the maximum response was attained (Derrington and Fuchs 1979). It was determined, using the SD of the Gaussian σ, as pF_low = pF_opt + 1.177σ. We found that pF_high was slightly but significantly larger for the discharge RFs than that for the synaptic RFs (P = 0.006). Mean values were 0.56 ± 0.26 cycle/deg for the discharge RFs and 0.51 ± 0.25 cycle/deg for the synaptic RFs (Fig. 8, A and B). The ratio between the two reached an average of 1.09 ± 0.07 (not illustrated). In the regression analysis (Fig. 8C), the two parameters were strongly correlated and the slope was 1.02 (all cells, R² = 0.982) or 1.09 (with the outlier at 1.35 cycles/deg excluded, R² = 0.962). In other words, it is predicted that simple cells would respond to higher spatial frequency on the basis of the Fourier transform of their discharge RFs, compared with the Fourier transform of their synaptic RFs.

Fig. 8.

A–C: predicted high-frequency cutoff (pF_high) is smaller for tuning curves predicted from synaptic RFs compared with that predicted from discharge RFs. A: distribution of pF_high for synaptic RFs. B: distribution of pF_high for discharge RFs. C: correlation between synaptic and discharge pF_high values. D–F: low spatial frequency cutoff (pF_low) is higher for tuning curves predicted from synaptic RFs compared with that predicted from discharge RFs. D: pF_low distribution for synaptic RFs. E: pF_low distribution for discharge RFs. F: correlation between synaptic and discharge pF_low values. G–J: bandwidths of predicted spatial frequency tuning curves (pBWs) are smaller when predicted from synaptic RFs compared with those predicted from discharge RFs. G: distribution of pBW for synaptic RFs. H: pBW distribution for discharge RFs. I: correlation between bandwidth predicted from synaptic and spiking RFs. J: distribution of predicted discharge to synaptic bandwidths ratios. K: ratio of the number of subfields exhibited in discharge vs. synaptic RFs is plotted against the ratio of discharge to synaptic pBW. The difference between synaptic and discharge pBW values is well explained by the difference in subfield number in synaptic and spiking RFs. The significant correlation and negative slope indicate that the difference in pBW values increases when the difference in subfield number between synaptic and discharge RFs increases. Dashed lines in C, F, and I represent equality line.

The spatial frequency predicted from the discharge RF also predicted a lower spatial frequency cutoff, compared with that predicted from the synaptic RF. The predicted low spatial frequency cutoff pF_low was calculated as pF_low = pF_opt − 1.177σ. In a number of cases, pF_low was <0 and, in these cases, pF_low was set to 0 cycle/deg. Interestingly, the number of low-pass cases was 8 for discharge RFs, but 4 for synaptic RFs (Fig. 8, D and E). On average, pF_low was lower for discharge than that for synaptic RFs (0.07 ± 0.11 and 0.10 ± 0.11, respectively; Fig. 8, D and E), and the two differed significantly (P = 0.02). In a regression analysis, pF_low predicted from the spiking response was significantly (P = 0.003, R² = 0.866) dependent on pF_low predicted from the synaptic response, but with a slope of 0.888 (Fig. 8F).

The third parameter that was significantly different between synaptic and discharge RFs was the width of the predicted spatial frequency tuning curve. The bandwidth (BW) of the predicted spatial frequency-tuning curve (pBW) was calculated as log₂ (pF_high/pF_opt).⁶ The BW was significantly (P = 0.02) larger for tuning curves predicted from the discharge RFs (0.95 ± 0.27 octave) compared with that predicted from the synaptic RFs (0.79 ± 0.18 octave) (Fig. 8, G and H). The mean ratio of discharge to synaptic pBW averaged 1.22 ± 0.33; in other words, the BW for the discharge RF is predicted to be 22% larger than that for the synaptic RFs (Fig. 8J). It is to be emphasized that the pBW ratio was quite variable from cell to cell (Fig. 8J). This is also reflected in the fact that the regression analysis between pBW for synaptic and discharge tuning curves was at the limit of significance (P = 0.051) (Fig. 8I).

The difference in predicted spatial frequency selectivity we observed here appears to be directly related to the difference in the number of subfields n_sf exhibited by synaptic and discharge RFs. This is illustrated by the significant correlation between the two ratios, n_sf(di)/n_sf(sy) and pBW_(di)/pBW_(sy) (Fig. 8K; P = 0.0005, r² = 0.502). This indicates that the difference between synaptic and discharge BWs are in part the consequence of differences in the number of subfields. In other words, discharge and synaptic static RFs predict similar spatial frequency tuning when they possess a similar number of subfields, whereas a narrower tuning is found in synaptic RFs when they possess additional (subthreshold) subfields.

Comparison of latencies in discharge and synaptic receptive fields

Extracellular recording studies performed in area V1 revealed widely varying visual latencies (e.g., Nowak and Bullier 1997). One question we sought to answer is whether this variability is already present in the synaptic responses or whether it results from a more or less sluggish integration of synaptic inputs by cortical neurons. The latencies presented in this section (Fig. 9) correspond to those determined for the largest response in both dominant and secondary subfields. In other words, each subfield is characterized by one latency measure. Spiking response latencies did not differ significantly between simple and complex cells (P = 0.4 and 0.8 for half-rise and peak latencies, respectively), which are thus treated as a homogeneous sample.

Fig. 9.

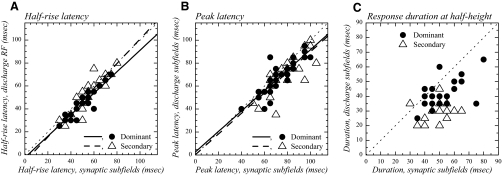
Half-rise latency, peak latency, and response duration. Dominant subfields are represented by black circles and secondary subfields by open triangles. A: half-rise latency in discharge subfields as a function of half-rise latency in synaptic subfields. The continuous line corresponds to the regression line for the dominant subfields and the dashed line is the regression line obtained for the secondary subfields. B: peak latency in discharge subfields is strongly correlated with peak latency in synaptic subfields. Continuous and dashed lines: regression lines for dominant and secondary subfields, respectively. C: response duration in discharge subfields as a function of response duration in synaptic subfields. The two variables are weakly correlated. The dotted line is not a regression line and represents duration equality, to help illustrate the fact that discharge RF durations are nearly systematically lower than synaptic RF durations. The numbers of data points in A, B, and C may appear lower than the sample sizes given in text because latencies were determined in 5-ms steps, such that cells displaying identical latencies or durations are represented by points that overlap.

Response latency at half-rise.

Half-rise latencies are presented in Table 1 and in Fig. 9A. Half-rise latency for the spike discharge in the dominant subfields averaged 44.2 ± 11.5 ms and ranged between 25 and 70 ms. In the secondary subfields, half-rise latency averaged 53.2 ± 15.8 ms. For membrane potential responses, the dominant subfields displayed half-rise latency between 30 and 75 ms, with a mean of 51.5 ± 16.6 ms. The mean half-rise latency for the synaptic responses in the secondary subfields was 55.7 ± 14.5 ms.

Table 1.

Latencies, latency differences, and response durations for the strongest responses in dominant and secondary subfields of V1 neurons

	Dominant Subfield		Secondary Subfield
	Synaptic RF	Discharge RF	Synaptic RF	Discharge RF
Half-height latency	51.5 ± 11.6 [55] (n = 37)	44.2 ± 11.5 [45] (n = 36)	55.7 ± 14.5 [55] (n = 29)	53.2 ± 15.8 [55] (n = 19)
Half-height latency difference (di − sy)	−5.7 ± 4.4 [−5.0] (n = 35)		−2.1 ± 7.5 [0] (n = 19)
Peak latency	72.2 ± 13.5 [70] (n = 36)	67.6 ± 13.8 [70] (n = 38)	80.3 ± 14.4 [80] (n = 31)	70.9 ± 16.1 [75] (n = 27)
Peak latency difference (di − sy)	−5.3 ± 7.0 [−5.0] (n = 36)		−7.8 ± 9.9 [−5.0] (n = 27)
Response duration	50.6 ± 10.2 [50] (n = 32)	41.6 ± 9.9 [40] (n = 35)	49.6 ± 9.6 [50] (n = 26)	38.4 ± 7.6 [40] (n = 19)
Ratio of response duration (di/sy)	0.81 ± 0.16 [0.80] (n = 31)		0.84 ± 0.21 [0.82] (n = 17)

Values are means ± SD. Numbers between brackets correspond to the median. Numbers between parentheses correspond to sample size. All values are in milliseconds, except response duration ratio.

We examined how half-rise latency for spike responses is related to half-rise latency for synaptic responses (Fig. 9A). Synaptic and discharge half-rise latencies were significantly (P < 0.0001) and well correlated for both dominant and secondary subfields (n = 35 and 19 paired observations, respectively). For the dominant subfields, the slope was 0.94, the constant term was −2.5 ms (not significantly different from 0), and R² was 0.845; for the secondary subfields, the slope was 1.07, the constant term was −5.9 ms (not significantly different from 0), and R² was 0.765. Although the constant terms did not differ significantly from zero, half-rise latencies differed significantly between synaptic and spiking response in the dominant subfields (P < 0.0001). The mean difference was −5.7 ms, implying that responses reach their half-height amplitude faster in the spiking than in the synaptic response.

The high correlation coefficients and slopes close to 1 indicate that longer discharge latencies are due to longer synaptic latencies and not to some slowness in the integration of the synaptic inputs. In addition, there was no significant correlation between half-rise latency and response strength (not illustrated), indicating that longer half-rise latencies are not associated with more sluggish responses.

Peak response latency.

For both dominant and secondary subfields, the peak latency was significantly longer in the synaptic RFs than that in the discharge RFs (Fig. 9B, Table 1) (P < 0.0001 and P = 0.0004, respectively). Maximal firing rate was achieved, on average, 5.3 ± 7.0 ms earlier than the maximal depolarization in dominant subfields and 7.8 ± 9.9 ms earlier in the secondary subfields.

Discharge and synaptic peak latencies were significantly correlated (Fig. 9B, R² = 0.750, P < 0.0001 for dominant subfields; R² = 0.613 and P < 0.0001 for secondary subfields). For both dominant and secondary subfields, constant terms (2.7 and 0.4, respectively) were not significantly different from 0. The slopes were close to 0.9 (0.890 and 0.896, respectively).

Response duration.

In most cells, the time course of the response showed two successive peaks, corresponding to the response to stimulus appearance and withdrawal (Figs. 1 and 2). Here we examined response duration for the “on” response only. RF duration corresponds to the duration measured at half of the peak response height. Several cells have been excluded because the “off” response merged with the “on” response, such that it was not possible to determine a half-fall latency for the end of the “on” response.

The mean response duration for the dominant subfields of the synaptic RFs was 50.6 ms (Table 1, Fig. 9C). It was significantly (P < 0.0001) longer than that for discharge RFs, which averaged 41.6 ms. When expressed as a ratio (Table 1), the discharge RF duration represented 81% of the synaptic RF duration. Similar differences (P = 0.004) were observed for the secondary subfields (Table 1).

Regression analysis revealed a surprisingly weak dependence of discharge RF duration on synaptic RF duration (Fig. 9C; R² = 0.25, P = 0.002 for dominant subfields; not significant for secondary subfields: P = 0.36). This weak relationship suggests that the discharge RF duration is not simply a scaled-down version of the synaptic RF duration and that other factors are involved in this transformation (see discussion). This also suggests that synaptic RF duration cannot be easily retrieved from the spiking RF duration.

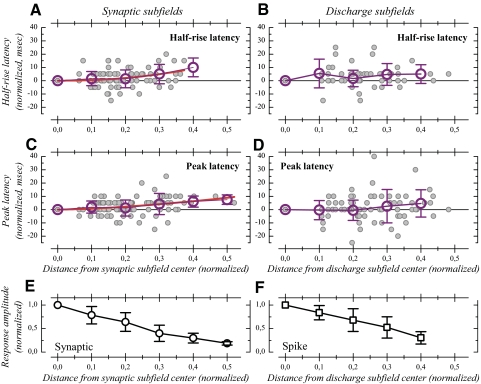
Latencies as a function of distance within the receptive field

We next examined quantitatively how latency varied with respect to distance from the subfield center. This analysis revealed that half-rise and peak latencies depended very little, if at all, on distance.

To allow normalization of response latency across cells (Bringuier et al. 1999), we first shifted stimulus positions to reassign a position of 0° to the strongest response. Second, the latency of the strongest response was subtracted from the latency for all the responses, such that the latency for the strongest response is zeroed and latencies in other regions of the subfields are expressed relative to this zero latency. Results of these first two normalizations are presented in Supplemental Fig. S5, representing latency versus distance for all the cells together and for dominant, secondary, tertiary, and quaternary subfields. To examine more precisely the relationship between latency and space, we further normalized the spatial spread of the responses by dividing the stimuli position by the width (w_5%) of the subfields (Fig. 10). This procedure allowed normalization of subfield extent across cells. Latencies for synaptic responses were normalized by synaptic subfield width (Fig. 10, left column) and latencies for spiking responses were normalized by spiking subfield width (Fig. 10, right column). Negative distance values were replaced by their absolute values (this allowed us to test for the presence of a significant relationship with nonparametric correlation tests). In this normalized scale, the full extent of the subfields is comprised between 0 and +0.5. Data presented in Fig. 10 correspond to the dominant subfields. Due to the smaller number of data points, the weak tendencies found for the dominant subfields were even weaker for the secondary subfields and are not illustrated.

Fig. 10.

Normalized latencies as a function of normalized space. A and C: half-rise and peak latency for membrane potential responses as a function of distance from subfield center expressed in fraction of synaptic subfield width. B and D: half-rise and peak latency for spiking responses as a function of distance expressed in fraction of spiking subfield width. In A–D, individual latency values are indicated by gray dots; open symbols and associated error bars show the means ± 1SD of the latencies calculated for different bins of the normalized subfield width: 0–0.05, 0.05–0.15, 0.15–0.25, and so forth. For synaptic responses (A, C), the relationship between distance and latency (individual data) has been examined with a power function and the best-fit line is shown in red. E: means and SDs of the normalized amplitude of synaptic responses represented as a function of normalized distance for synaptic responses. F: same as E for discharge subfields.

The filled dots in the scatterplots in Fig. 10A represent synaptic half-rise latencies, normalized by synaptic subfield width. Figure 10B illustrates, in a similar fashion, the half-rise latency as a function of distance for the discharge subfields. This shows that the shortest half-rise latencies were not systematically associated with the strongest response: beyond subfield center, half-rise latency either did not change or increased or decreased by up to 20 ms. To further illustrate the space–latency relationship at the population level, the normalized spatial scale was binned in 0.1-unit-wide increments and the mean ± 1SD of the latency were calculated within each interval. This corresponds to the open dots and error bars in Fig. 10, A and B. For synaptic subfields, a tendency for increased latency with increased distance is visible in the binned and averaged latency versus distance plots. Further analysis revealed that half-rise latency increased significantly with distance in both the synaptic and discharge subfields (Spearman rank correlation, P = 0.001 for dominant synaptic subfields and P = 0.0005 for dominant discharge subfields). As illustrated in Fig. 10A, the mean half-rise latency for synaptic responses was longer by 5 ms at a distance corresponding to 60% of the subfield width (0.3 on normalized distance). At this distance, amplitude of the synaptic responses was 40% of the maximal amplitude (Fig. 10E). Similarly, the mean half-rise latency was longer by 5 ms at positions corresponding to 60–80% of the width of discharge subfields (Fig. 10B), where spiking responses represented 30–50% of the maximal response (Fig. 10F).

Although a significant trend is observed, a large variability is also found when comparing different cells (Fig. 10, A and B). We therefore examined the strength of the relationship between distance and latency. To allow for more flexibility in the relationship, we used a power function of the form: latency = a × (distance)^b, rather than a linear relationship. The relationship appears to be extremely weak: for the spiking response, the r² was 0.08 and the r² was 0.10 for the synaptic responses (Fig. 10A). In other words, the distance from RF centers explains only 10% at best of the half-rise latency variance in the subfields.

Similar analysis was conducted for the peak latency (Fig. 10, C and D). Spiking response latency did not depend significantly on the distance from subfield center (Spearman rank correlation, P = 0.13). For synaptic response, peak latency was poorly related to distance within the subfields: latency depended significantly on distance (Spearman rank correlation, P < 0.0001), but the power function fitted to the data (Fig. 10C) was again associated with a very low r² value (0.12).

DISCUSSION

In this study, we characterized the relationship between synaptic and discharge RFs in the spatial and temporal domains. We found that some discharge RF features, such as response amplitude, depended modestly on those exhibited by the underlying depolarization. Other features, such as subfield and RF width, were more dependent. Other features of the spiking response—such as RF phase and optimal spatial frequency, subfield latencies, and subfield overlap—depended strongly on those of the synaptic RFs. These results indicate that the transformation from synaptic to spiking activity is variable and complex in sensory processing—this must be taken into account in our understanding of cortical networks.

Variability in synaptic to discharge RF amplitude transformation

To relate the transformation from synaptic to discharge response amplitudes, we calculated a synaptic to discharge amplitude ratio (Fig. 3C), which averaged 7.3 ± 4.6 spikes·s⁻¹·mV⁻¹ (6.9 ± 3.2 spikes·s⁻¹·mV⁻¹ for Gabor-fitted simple cells). Carandini and Ferster (2000) reported a mean ratio of 7.2 spikes·s⁻¹·mV⁻¹ for their simple cells, a value very similar to ours, although the stimulus they used (drifting sinewave gratings) probably possessed more energy than that of the thin bars we used. This suggests the presence of gain-control mechanisms whose recruitment depends on the stimuli being used, as recently demonstrated by Cardin et al. (2008).

The synaptic to discharge amplitude ratio appears to be quite variable from cell to cell. In other words, when considering two different cells, it appears that the same depolarization amplitude does not necessarily translate into the same firing rate. Conversely, it shows that those neurons that were only slightly depolarized were not necessarily those that discharged the least. There are many possible, nonexclusive explanations for this variability. 1) The distance between resting membrane potential and spike threshold varies considerably between cells (Azouz and Gray 2000; Nowak et al. 2008; Volgushev et al. 2002), such that a given depolarization amplitude might reach, or might not reach, spike threshold. In a previous study (Nowak et al. 2005), we showed in individual cells that hyperpolarizing the membrane potential by DC injection effectively reduces discharge RF amplitude. 2) Neurons exhibit variable amounts of noise, either stimulus induced or related to spontaneous activity, which may also affect firing probability (e.g., Anderson et al. 2000; Azouz and Gray 2003). When considering a population of cells, the presence of high-amplitude membrane potential fluctuations in some cells will bring a visually evoked depolarization of small amplitude close to firing threshold often enough to evoke firing, whereas a larger visually evoked depolarization in other cells that show a lower noise level may generate less firing. In a recent study, Haider et al. (2007) effectively demonstrated at the single-cell level that the RF amplitude is twofold larger during the up-state of spontaneous slow cortical oscillations, due in part to increased synaptic potentials (Reig and Sanchez-Vives 2007). 3) Visually evoked depolarizations are not purely excitatory; they also include variable amounts of inhibitory conductance (Borg-Graham et al. 1998) that may shunt, to a variable extent, the firing of action potentials. Similarly, K⁺ conductances associated with spike firing also introduce a strong shunt (Schwindt et al. 1988) that may counteract the excitatory drive. 4) A last possible explanation is that cortical cells vary widely in their action potential discharge properties (e.g., McCormick et al. 1985; Nowak et al. 2003): some cells generate high-frequency bursts (chattering and intrinsically bursting cells) and other cells series of action potentials that adapt either strongly (regular-spiking cells) or weakly (fast-spiking cells). In support of this explanation, Contreras and Palmer (2003) showed that visually evoked depolarization of comparable amplitudes induce considerably larger firing rates in fast-spiking cells compared with those in regular-spiking cells.

Synaptic to discharge RF width transformation

The widths of subfields and whole RFs we report here for spiking responses (Fig. 4) are similar to those reported in studies based on quantitative mapping of RFs (Bringuier et al. 1999; DeAngelis et al. 1993a; Heggelund 1981a,b, 1986; Hetherington and Swindale 1999; Jones and Palmer 1987b; Li and Li 1994; Palmer and Davis 1981). The large range of values can be attributed to increased RF extent with eccentricity (Albus 1975; Heggelund 1986) and to the cortical layers in which the neurons were recorded (Gilbert 1977; Hetherington and Swindale 1999; Leventhal and Hirsch 1978).

We found that discharge RF widths were not significantly different between simple and complex cells. Other studies in which RFs have been quantitatively mapped also reported no significant differences, or only marginal differences, between simple and complex cells (Heggelund 1986; Hetherington and Swindale 1999; Li and Li 1994; Pernberg et al. 1998; Sasaki and Ohzawa 2007). When examining the relationship between spiking and synaptic responses, we found that in complex cells the width of the discharge RF was about 60% of the width of the synaptic RF (Fig. 4C). In simple cells, the width of individual discharge subfields represented more than three quarters of the corresponding synaptic subfield width (Fig. 4C). When the whole of the RF of simple cells was examined, there appeared to be even less difference between synaptic and discharge RF widths (Fig. 6C): ratio values show that >80%, on average, of the synaptic RF width is transferred to the discharge RF.

That synaptic RFs are not so extended compared with discharge RFs, especially in simple cells, has one important consequence: the width of the discharge RFs may be scarcely affected by changes in the membrane potential. That is to say, to use a metaphor, the walls of the iceberg may be rather steep, such that its width may not increase much when more of it is exposed above the water line. This provides one possible explanation as to why discharge RF width is weakly affected by manipulations, such as RF surround stimulation (Palmer and Nafziger 2002) or contrast adaptation (Nowak et al. 2005), which nevertheless have strong effects on the amplitude of discharge RFs.

There was some variability in the width transformation (Figs. 4C and 6C). The putative sources for this variability are likely to be the same as those discussed for the variability in response gain (spike threshold, noise, shunting conductance; see preceding text). Additionally, we showed that, in simple cells, this width ratio variability was strongly determined by the number of synaptic subfields that were subthreshold for spike generation (Fig. 6C). It is possible that, under natural physiological conditions or with different stimuli, these subfields could form part of the discharge RF (e.g., with dense noise; Alonso et al. 2001).

Subfield overlap in simple cells was more pronounced for synaptic than that for spiking RFs (Fig. 5). Thus threshold nonlinearity likely plays a role in decreasing subfield overlap in the spiking response (Martinez et al. 2005; Priebe et al. 2004). Nevertheless, we found that subfield overlap in spiking RFs was well correlated with subfield overlap in synaptic RFs (Fig. 5).

Subfields in Gabor-fitted simple cells and predicted spatial frequency tuning

Discharge RFs of Gabor-fitted simple cells are made of a variable number of subfields (Fig. 6A). The number of synaptic subfields (2.65 on average) appears to be significantly larger than the number of spiking subfields (2.2 on average). This difference may be of importance in a linear model of spatial frequency tuning. Indeed, studies have shown that the preferred spatial frequency exhibited by simple cells corresponds very precisely with the one that can be determined from the static RF (Andrews and Pollen 1979; DeAngelis et al. 1993b; Field and Tolhurst 1986; Jones and Palmer 1987b; Kulikowski and Bishop 1981; Lampl et al. 2001; Movshon et al. 1978a). However, it has also been shown that the spatial frequency tuning predicted by the static, extracellular RF is systematically broader than that actually measured with drifting gratings (DeAngelis et al. 1993b; Field and Tolhurst 1986; Kulikowski and Bishop 1981). It has been proposed (Andrews and Pollen 1979; Field and Tolhurst 1986; Kulikowski and Bishop 1981) that this difference resides in a larger number of subfields in the synaptic RFs, which we demonstrated here (Fig. 6A).

We showed that the spatial frequency tuning that can be predicted from the static discharge RF is broader, compared with that predicted from the static synaptic RF (Fig. 8). Interestingly, the difference in tuning width we report here (∼20%) between tuning predicted from synaptic and discharge RFs is similar to the difference reported earlier between the tuning predicted from the discharge RF and the tuning actually measured in the same neurons (DeAngelis et al. 1993b; Field and Tolhurst 1986; Kulikowski and Bishop 1981). Moreover, we showed that the difference between spiking and synaptic tuning width is significantly correlated with the difference in the number of subfields (Fig. 8K). This suggests that the spatial frequency tuning curves conventionally determined using drifting gratings mostly reflects the subfield composition of the synaptic RF, rather than that of the spiking RF.

Latency

With respect to spiking responses, the latencies we report here are similar to those obtained in other cat studies (Best et al. 1986; Creutzfeldt and Ito 1968; DeAngelis et al. 1993a; Dinse and Krüger 1994; Duysens et al. 1985; Eschweiler and Rauscheker 1993; Ikeda and Wright 1975; Minke and Auerbach 1972; Shevelev et al. 1992; Swindale and Mitchell 1994). The latencies and response durations reported here for synaptic responses are comparable to those reported by Hirsch et al. (1998, 2002). As in previous studies (Hirsch et al. 2002; Ikeda and Wright 1975; Minke and Auerbach 1972; Shevelev et al. 1992), latencies for simple and complex cells were not found to differ significantly.

One important result of this study is that spiking response latency faithfully reflected synaptic response latency, irrespective of the latency measure considered. Indeed, spiking response latencies were strongly correlated with synaptic latencies and regression analyses showed slopes close to unity in all cases (Fig. 9, A and B). In other words, cells with late spiking responses were also cells displaying late synaptic responses.

We found that half-rise latency and peak latency for spiking responses were, somehow unexpectedly, shorter than those of the synaptic responses (Fig. 9, A and B). We also showed that response duration was longer in the synaptic responses than that in the spiking responses (Fig. 9C). Accordingly, Tanaka (1983) observed that the response of simple cells was more transient than that of the thalamic neurons projecting onto them. Differences between synaptic and action potential responses in both half-rise latency, peak latency, and response duration might be due to the recruitment of stronger inhibitory conductance in the later part of the synaptic response (Borg-Graham et al. 1998). Alternatively, the intrinsic properties of cortical neurons might explain these differences (e.g., McCormick et al. 1985; Nowak et al. 2003): for example, a fast intrinsic adaptation mechanism might reduce firing rate before the summation of synaptic potentials is able to bring the membrane potential depolarization to its climax. Alternatively, the presence of burst firing might result in a high concentration of spikes earlier in the synaptic response.

Latency versus space

We found that response latency in different parts of the RFs can be quite variable, possibly as a consequence of the variability in response latency at the subcortical stages (e.g., Bolz et al. 1982; Sestokas and Lehmkuhle 1986; Wolfe and Palmer 1998). The maximal distance over which we have obtained significant responses was ±3° from the subfield center. Within this distance, the latency scatter we obtained is appreciably comparable with that reported by Bringuier et al. (1999). Within and beyond this distance, we occasionally recorded significant responses that were sometimes extremely delayed (Supplemental Fig. S5), but these corresponded to ternary and quaternary subfields, which, at least in some cases, likely reflected the activation of LGNd RF surrounds that are known to be delayed with respect to LGNd RF centers (Bullier et al. 1982; Cai et al. 1997).

We found that latency variability depended only marginally on where the flashing bar was positioned relative to the position that evoked the strongest response (r² ≤ 0.12; Fig. 10). This weak latency–distance relationship may be due to a slow propagation of activity within intracortical connections. On the other hand, it might also be inherited directly from the retina: indeed, Levick (1973) showed increased latency as a function of distance for the spiking response of a retinal ganglion cell, with a 5-ms difference between the central and most peripheral stimulation site in the cell's RF.

At first sight, the weak latency–distance relationship we obtained may appear to be at variance from that reported in the studies by Kitano et al. (1994) for local field potentials, by Suder et al. (2002) for spiking responses, by Bringuier et al. (1999) for synaptic responses, and by Jancke et al. (2004) with voltage-sensitive dyes, which all showed a significant increase in latency with increased distance from the middle of the RFs. There are several possible reasons for this discrepancy. First, the latencies were not measured the same way in all studies (see Bair et al. 2003 for a related topic). Second, the use of stimuli with different energy may result in the activation of different sets of connections; thus it is possible that the thin bars we used to map the RFs possessed less energy and thus were less capable of activating remote regions of the subthreshold RFs, than the flashing gratings used by Kitano et al. (1994) or by Bringuier et al. (1999) in some of their experiments.

However, the discrepancy may not be so great if the temporal frequency of the stimulus is taken into account. Stimulus presentation rate in the study by Suder et al. (2002) was 3.3 Hz. In the study by Bringuier et al. (1999) the subthreshold RF showed slowly propagating, long-distance responses when the stimulus rate was about 1 Hz, but not when using a stimulus rate (20–30 Hz) compared with the one we used (20 Hz). Similarly, Kitano et al. (1994) disclosed two components in their field potentials: a fast one, whose spatial spread did not exceed 5–7°; and a slow one (propagation speed <1 m/s), whose spatial distribution could be extremely wide (≤15° from the RF center). Importantly, this slow component was markedly reduced or completely suppressed when the stimulation rate was >8 Hz. Altogether, these different results suggest that the extent of the subthreshold RF—and possibly suprathreshold RF—strongly depends on stimulus temporal frequency. Distant synaptic influences may be gated by adaptation mechanisms turned on at high temporal frequency. In support of this possibility, we previously found that long-distance synaptic responses to artificial scotoma may be visible at stimulus onset, but adapted rapidly thereafter (Nowak et al. 2005).

Connections generating the receptive field revealed by high-frequency flashing bars in V1

By examining the spatiotemporal properties of synaptic and discharge RFs, we may try to infer what connections are involved in their generation. The size of the aggregate RF produced by converging thalamocortical axons can be estimated from previous anatomical and electrophysiological studies. Our recordings were obtained between 0 and 10° eccentricity. Given the magnification factor in the LGNd for these eccentricities (0.1–0.6 mm/deg; Sanderson 1971), the convergence of thalamocortical projection (0.4 mm; Salin et al. 1989) and the size of the center of LGNd neuron RFs (0.1 to 5°, depending on eccentricity and the RF type of LGNd neurons; e.g., Bullier and Norton 1979; Cai et al. 1997; Hoffmann et al. 1972; Spear et al. 1989; Wolfe and Palmer 1998), it can be calculated that the synaptic RF in a cortical simple cell could “see” an area of visual space, which is between 0.8° (X inputs near the area centralis) and ≤9° (Y inputs at 10° eccentricity). These estimates correspond quite well to the widths we measured in simple cells (subfield width: 1.0–8.0°, Fig. 4A; whole RF width: 2.0–8.8°, except one case at 11.8°). This suggests that the width of the synaptic RFs in simple cells can be well accounted for by the size of the aggregate RF provided by their thalamic inputs.

Interestingly, the average discharge RF width of simple cells did not differ significantly from the synaptic RF width in complex cells. Assuming a hierarchical model of the information transfer of simple to complex cells (Hubel and Wiesel 1962), this suggests that simple to complex cell inputs spatially diverge very little, at least under our experimental conditions. Results obtained by Sasaki and Ohzawa (2007) also suggest there is little spatial pooling of the “subunits” that compose RFs of complex cells.

Long-range horizontal connections show less spatial precision than that of thalamocortical connections, such that they allow interactions between neurons whose discharge RFs do not overlap (Das and Gilbert 1995; Salin et al. 1992). In cat visual cortex, intrinsic horizontal connections allow one neuron to interact with other neurons located ≤3 mm away (Buzás et al. 2006; Crook et al. 2002; Das and Gilbert 1995; Gilbert and Wiesel 1983; Kennedy et al. 1994; Kisvarday et al. 1997; Luhmann et al. 1990; Martin and Whitteridge 1984; Salin et al. 1992). Intrinsic connections are characterized by their slow conduction velocities (0.1 to 1 m/s, means near 0.3 m/s; Girard et al. 2001; Gonzalez-Burgos et al. 2000; Komatsu et al. 1988; Lohmann and Rörig 1994; Luhmann et al. 1990; Murakoshi et al. 1993; Nowak and Bullier 1998; Salin and Prince 1996). Since latencies of global responses are imposed by the fastest conducting inputs, and conservatively taking an axonal velocity of 0.3 m/s, it can be calculated that inputs originating at 3 mm from the subfield center should induce responses delayed by 10 ms and by 5 ms for a 1.5-mm separation. This is less than the fluctuation in latency we observed (Fig. 10). Therefore using latency as an indicator, we cannot firmly tell whether horizontal connections contributed to generation of the discharge RF and of the underlying synaptic RF.

On the other hand, given the retinotopic organization of area 17 (Tusa et al. 1978), it is possible to calculate that horizontal connections should allow the pooling of visual signals over a diameter of 2.5° near the area centralis (including callosal connections) and about 15° at 10° eccentricity. Including the spiking RF size of the neurons, horizontal connections should generate responses over diameters that are about 3.5° at 0° eccentricity and ≥17° at 10° eccentricity. However, in all but two cases, the synaptic RFs we measured were between 2 and 10° wide. This suggests that the most distal horizontal inputs were not visible in our experimental conditions.

In addition to thalamic and intrinsic inputs, area 17 receives inputs from “higher” cortical areas via feedback connections (e.g., Bullier et al. 1984; Symonds and Rosenquist 1984). Feedback inputs display relatively high conduction velocities (median: 3.5 m/s; Girard et al. 2001). They are widely divergent and are issued from neurons with RFs larger than those found in area 17 (Angelucci et al. 2002; Salin et al. 1992). This allows the integration of very large regions of the visual space (>10° for area 18 to area 17 projection; Salin et al. 1992). Therefore feedback inputs, if involved in the synaptic RF generation, should have generated temporally homogeneous responses over wide regions of the visual field, which we did not observe.

Altogether, our results suggest that the synaptic and spiking RFs of cortical neurons—as revealed by high-frequency flashing stimuli—are generated essentially by thalamocortical and short-distance intracortical connections. We emphasize that this conclusion is valid for high-frequency stimulation only, given that previous studies (Bringuier et al. 1999; Kitano et al. 1994) showed that stimulus temporal frequency has a strong impact on spatiotemporal integration in cat area 17. The consequences of these dynamic adjustments require further investigations.

GRANTS

This research was supported by grants from the National Institutes of Health to D. A. McCormick, the Centre National de la Recherche Scientifique to L. G. Nowak, and the Spanish Ministry of Science and Innovation to M. V. Sanchez-Vives.