Rectification of the EMG Signal Impairs the Identification of Oscillatory Input to the Muscle

Abstract

Rectification of EMG signals is a common processing step used when performing electroencephalographic–electromyographic (EEG–EMG) coherence and EMG–EMG coherence. It is well known, however, that EMG rectification alters the power spectrum of the recorded EMG signal (interference EMG). The purpose of this study was to determine whether rectification of the EMG signal influences the capability of capturing the oscillatory input to a single EMG signal and the common oscillations between two EMG signals. Several EMG signals were reconstructed from experimentally recorded EMG signals from the surface of the first dorsal interosseus muscle and were manipulated to have an oscillatory input or common input (for pairs of reconstructed EMG signals) at various frequency bands (in Hz: 0–12, 12–30, 30–50, 50–100, 100–150, 150–200, 200–250, 250–300, and 300–400), one at a time. The absolute integral and normalized integral of power, peak power, and peak coherence (for pairs of EMG signals) were quantified from each frequency band. The power spectrum of the interference EMG accurately detected the changes to the oscillatory input to the reconstructed EMG signal, whereas the power spectrum of the rectified EMG did not. Similarly, the EMG–EMG coherence between two interference EMG signals accurately detected the common input to the pairs of reconstructed EMG signals, whereas the EMG–EMG coherence between two rectified EMG signals did not. The frequency band from 12 to 30 Hz in the power spectrum of the rectified EMG and the EMG–EMG coherence between two rectified signals was influenced by the input from 100 to 150 Hz but not from the input from 12 to 30 Hz. The study concludes that the power spectrum of the EMG and EMG–EMG coherence should be performed on interference EMG signals and not on rectified EMG signals because rectification impairs the identification of the oscillatory input to a single EMG signal and the common oscillatory input between two EMG signals.

INTRODUCTION

Temporal binding mechanisms are very important in synchronizing the communication of higher centers with the periphery and significantly influence performance of various systems (Engel et al. 2001). This temporal binding also occurs for the motor system in which muscle activity contains specific oscillations that may be a consequence of neural synchronization of action potentials from higher centers with functional implications in motor control (Brown 2000; Farmer et al. 1997; Mima and Hallett 1999a; Salenius and Hari 2003). The synchronization of action potential discharge times between motor units (often termed short-term synchrony) has been shown in the time (Semmler 2002) and frequency domains (Christou et al. 2007; Farmer et al. 1997). Interestingly, the synchrony in the time domain appears to be due to common oscillations between motor units from about 16 to 32 Hz (Christou et al. 2007; Farmer et al. 1997; Lowery et al. 2007).

The origin of common oscillations from about 16 to 32 Hz at the motor unit level is most likely due to oscillatory input from the motor cortex (Brown 2000; Conway et al. 1995; Farmer et al. 1997). The initial evidence in humans comes from Conway et al. (1995), which demonstrated significant coherence between the motor cortex and surface electromyography of the first dorsal interosseus (FDI) muscle during constant isometric contractions. Since then, a number of studies have demonstrated a functional oscillatory coupling (corticomuscular coherence; electroencephalographic–electromyographic [EEG–EMG] coherence) between the motor cortex and muscle activity of the FDI muscle (Kilner et al. 1999, 2000, 2004; Yao et al. 2007) and between the motor cortex and other muscles (Halliday et al. 1998; Mima and Hallett 1999b; Schoffelen et al. 2005). Interestingly, the coherent activation between different muscles or different electrodes within the same muscle (EMG–EMG coherence) appears to provide similar results to the EEG–EMG coherence (Grosse et al. 2003a; Kilner et al. 1999; Richardson et al. 2006).

Rectification of surface EMG signals is a common processing step used prior to performing EEG–EMG coherence and EMG–EMG coherence. The reasoning for performing such processing is based on the assumption that full-wave rectification of EMG demodulates (see discussion for an explanation) the neural activation signal to the muscle (Mima and Hallett 1999a; Myers et al. 2003; Yao et al. 2007). Despite the wide use of EMG rectification when examining EEG–EMG coherence or EMG–EMG coherence, the scientific evidence for using EMG rectification is based primarily on two studies. One study (Yao et al. 2007), using experimental data, demonstrated that EEG–EMG coherence was similar when the EMG signal was rectified or not (interference EMG; often referred to as the “raw” EMG). Another study (Myers et al. 2003), using simulations, demonstrated that the mean motor unit discharge rate of simulated EMG coincides with the peak of the rectified EMG power spectrum (cf. Farina et al. 2002, 2004). Although the mean discharge rate of the motor units was evident in the simulated interference EMG power spectrum (e.g., a peak at 15 Hz), it was more apparent in the rectified EMG power spectrum relative to other frequencies. Myers et al. (2003) argued that the peak in the power spectrum associated with the mean discharge rate was less evident in the interference EMG power spectrum because of the greater power at higher frequencies (100–200 Hz), which is associated with the shape of the action potential of the motor units. Both of the above-cited studies, however, are limited because the EMG signal was never manipulated experimentally—i.e., frequency bands were never removed or made stronger to determine whether rectification of EMG would be sensitive enough to identify changes of the oscillatory input. In addition, it is possible that inputs to the motor neuron pool can occur at frequencies other than the mean discharge rate of the motor units (see Brown et al. 2000), which is the case with the frequency band (16–32 Hz) associated with motor unit synchronization (Christou et al. 2007).

Because there is evidence that the results from EMG–EMG coherence compared with those from EEG–EMG coherence may be superior in identifying changes in the cortical drive to the muscle (Grosse et al. 2003a), the purpose of this study was to determine whether rectification of the EMG signal influences the capability to make predictions about the oscillatory input to a single EMG signal and common oscillations between two EMG signals. Our approach was to experimentally reconstruct recorded EMG signals from the FDI muscle and, consequently, manipulate different frequency bands either by removing or doubling their power. Additionally, several pairs of reconstructed signals were manipulated to have a common input at various frequency bands. Part of the experimental recordings were previously reported (Baweja et al. 2009).

METHODS

Twenty young adults (10 men and 10 women; 20–32 yr) volunteered to participate in the experiment. All subjects reported being healthy without any known neurological problems, were right-handed according to a standardized survey (Oldfield 1971), and had normal or corrected-to-normal vision. The Institutional Review Board at the Texas A&M University approved the procedures and subjects provided written informed consent before participation in the studies.

Experimental arrangement

Subjects were seated comfortably in an upright position facing a 22-in. computer screen (NEC MultiSync LCD 2180 UX, NEC Display Solutions, Itasca, IL) that was located 1 m away at eye level. The monitor was used to display the force produced by the abduction of the index finger. All subjects affirmed that they could clearly see the display. The left arm was abducted by 45° and flexed to about 90° at the elbow. The left forearm was pronated and secured in a specialized padding (Versa Form, AB Germa, Kristianstad, Sweden). The thumb, middle, ring, and fifth fingers of the left hand were restrained with metal plates and there was approximately a right angle between the index finger and thumb. Only the left index finger was free to move. The left index finger was placed in an adjustable finger orthosis to maintain extension of the middle and distal interphalangeal joints (for a schematic, see Taylor et al. 2003). This arrangement allowed abduction of the index finger about the metacarpophalangeal joint in the horizontal plane, a movement produced almost exclusively by contraction of the FDI muscle (Chao et al. 1989; Li et al. 2003).

EMG measurement

FDI muscle activity was recorded with gold disc electrodes (4-mm diameter; Model F-E6GH, Grass Technologies, West Warwick, RI) and taped on the skin distally to the innervation zone (Homma and Sakai 1991). The recording electrodes were placed in line with the muscle fibers. The center-to-center distance between the two electrodes was 5 mm. The reference electrode was placed over the ulnar styloid. The EMG signal was amplified (×2,000) and band-pass filtered at 3–1,000 Hz (Grass Model 15LT system; Grass Technologies). The EMG signal was sampled at 2 kHz with a Power-1401 A/D board (Cambridge Electronic Design [CED], Cambridge, UK) and stored on a personal computer.

Constant isometric force task

Subjects were instructed to accurately match a target force at 15% of their maximal isometric force with abduction of the index finger. The subjects had visual feedback with gain equal to 12.8 pixels/N (visual angle: ∼0.34°). The subjects were instructed to gradually push against a force transducer and increase their force to match the target force within 3 s. When the target was reached, subjects were instructed to maintain their force on the target as accurately and as consistently as possible for 19 s.

Experimental data analysis

Data were acquired with Spike2 software (Version 6.02; CED) and analyzed off-line using custom-written programs in Matlab (The MathWorks, Natick, MA).

Reconstructed signals

To determine the accuracy of estimating the oscillatory drives from the interference and rectified EMG signals, we reconstructed EMG signals from the recorded EMG of the FDI muscle. A custom-written program in Matlab was used to reconstruct the EMG signals.

To construct the signals, two 5-s sections were cut from each selected recorded signal. One section contained the EMG signal during the voluntary contraction (subjects were matching a target force at 15% maximal voluntary contraction), whereas the other section contained the noise of the recorded EMG signal (subjects were producing zero force). These two sections were used to estimate the signal-to-noise ratio (SNR) of the recorded EMG signal as the ratio of the root mean square of the EMG signal during the task relative to the root mean square of the noise.

Fourier transform of each EMG signal was calculated with a 0.2-Hz resolution using the fast Fourier transform (fft) algorithm with a window length of 5,000. The first set of reconstructed signals (Eq. 1) consisted of the linear summation of sine waves (one for each amplitude–frequency pair calculated by the Fourier transform) and a Gaussian noise (whose amplitude was chosen so that the SNR of the reconstructed signal was similar to that from the original EMG signal; Eq. 2)

$$\text{Reconstructed EMG}=\sum \{A(n)\sin \hspace{0.17em}[2\pi f(n)t]+\text{krand}(n)\}$$ (1)

where A(n) is the amplitude (square root of the power), corresponding to the frequency f(n) obtained by the Fourier transform of the original signal; t is an array of 5,000 equally spaced values from 0 to 5; k is a constant obtained by Eq. 2; and rand(n) is an array of n random numbers whose elements are uniformly distributed in the interval from 0 to 1

$$k=\sqrt{\frac{\sum {\{A(n)\sin \hspace{0.17em}[2\pi f(n)t]\}}^2}{\sum [\text{rand}{(n)}^2(2{\text{SNR}}^2-1)]}}$$ (2)

By using Eqs. 1 and 2, 20 different EMG signals were reconstructed from the recorded EMG signals. The reconstructed signals contained similar peak frequencies and similar amplitude distribution to the recorded EMG signals and thus represent signals that are equally as complex as the recorded EMG signals (Fig. 1).

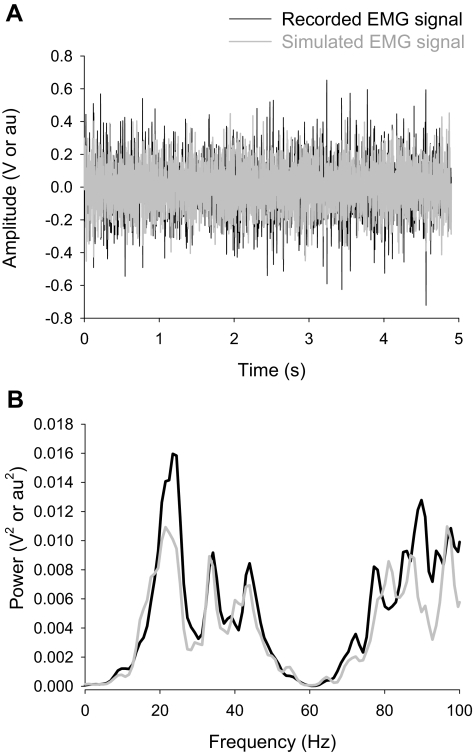
FIG. 1.

Representative example of a reconstructed (simulated) electromyographic (EMG) signal. An EMG signal was reconstructed based on a recorded EMG from the first dorsal interosseus (FDI) muscle when the subjects exerted a constant isometric force equal to 15% maximal voluntary contraction. The top panel (A) demonstrates the interference EMG signal recorded from the FDI muscle (black line) and the reconstructed interference EMG signal (gray line) from the same subject. The bottom panel (B) demonstrates the power spectrum for each signal. It is evident that the reconstructed signal contains peak frequencies and amplitudes similar to those of the recorded EMG signal and thus represents a signal that is as complex as an EMG signal. Note that power at 60 Hz (noise) was very small in the recorded signal and was not due to a notch filter set at 60 Hz in the hardware or software.

Manipulation of reconstructed EMG signals

To change the oscillatory content at various frequency bands we constructed an additional 400 EMG signals (2 manipulations × 10 frequency bands × 20 subjects). The content of each reconstructed EMG signal was changed by manipulating the amplitude (input) from the following 10 different frequency bands (in Hz): 0–12, 12–30, 30–50, 50–100, 100–150, 150–200, 200–250, 250–300, 300–350, and 350–500. The boundaries of the frequency bands vary in the literature [e.g., Farmer et al. (1997) used 16–32 Hz, whereas Brown (2000) used 10–30 Hz] and are used as broad guidelines of where the significant peaks may occur in the coherence between the motor cortex and muscle. The expectation (see Brown 2000) is that significant coherence peaks will occur between EEG and EMG or between two EMG signals at about 8 Hz (mean discharge rate of motor units), about 20 Hz (beta drive), about 40 Hz (low-gamma drive), and about 75 Hz (high gamma drive). Most studies are interested in frequency bands <100 Hz because these frequencies reflect carrying frequencies of the EMG signal (Myers et al. 2003; see also discussion). In this study, however, we also wanted to examine whether there was an association between lower-frequency bands (<100 Hz) and higher-frequency bands (>100 Hz). Therefore the boundaries used for lower-frequency bands (<100 Hz) were based on the literature (see Brown 2000), whereas the boundaries used for higher-frequency bands (>100 Hz) were arbitrary. The first manipulation consisted of zeroing all amplitudes corresponding to the frequencies within each of the predefined bands, one at a time. The second manipulation consisted of doubling all amplitudes corresponding to the frequencies within each of the predefined bands, one at a time.

To impose a common input at various frequency bands we reconstructed an additional 76 EMG signals (2 frequency bands × 19 pairs). The common input was introduced at 12- to 30- and at 100- to 150-Hz bands, one frequency band at a time, for constructing 38 different pairs of reconstructed EMG signals (e.g., reconstructed EMG 1 vs. reconstructed EMG 2, reconstructed EMG 2 vs. reconstructed EMG 3, and so on). The common input was accomplished for a pair of reconstructed signals by replacing the amplitudes within the manipulated band (12–30 or 100–150 Hz) of the first signal with the amplitudes used to construct the second reconstructed signal. Therefore the amplitude (input) within the manipulated band was similar (but not identical because of Gaussian noise) for the two reconstructed EMG signals.

Variables

Three different variables were calculated from each reconstructed EMG signal within each frequency band: integral, normalized integral, and peak power. The integral of a frequency band was estimated by the Riemann sum (integral) of the power values within the band. The normalized integral of a frequency band was calculated in two steps: first, we calculated the integral of the band and divided by the integral of the whole spectrum (0–500 Hz); then the result was divided by the band's frequency range (i.e., 18 Hz, for the 12- to 30-Hz frequency band). Peak power was quantified as the maximum value within each frequency band.

Coherence analyses

Correlations in the frequency domain were examined with the coherence spectrum (Amjad et al. 1989). Data for each of the 38 pairs of reconstructed signals with a common input in either 12- to 30- or 100- to 150-Hz frequency bands and 19 pairs of correspondent reconstructed signals with no common input were transformed into the frequency domain with a resolution of 1 Hz. Auto- and cross-spectra were estimated and a coherence estimate was computed. Significant peaks were identified as values that exceeded the 95% confidence intervals (CIs) relative to the mean value (similar findings with CIs quantified relative to zero values). Peak coherence from each of the following 10 frequency bands was estimated (in Hz): 0–12, 12–30, 30–50, 50–100, 100–150, 150–200, 200–250, 250–300, 300–350, and 350–500.

Statistical analysis

To compare the power spectra of the interference EMG and rectified EMG relative to the actual input to the reconstructed EMG (three conditions) we quantified the integral, normalized integral, and peak power within 10 frequency bands (in Hz: 0–12, 12–30, 30–50, 50–100, 100–150, 150–200, 200–250, 250–300, 300–350, and 350–500). A two-way ANOVA (3 conditions × 10 frequency bands) with repeated measures on all factors compared the integral, normalized integral, and peak power for the different conditions across the 10 frequency bands. To compare the change in power spectra of the interference EMG and rectified EMG (two conditions) when the actual input to the reconstructed EMG was manipulated, we quantified the normalized integral within six frequency bands (in Hz: 0–12, 12–30, 30–50, 50–100, 100–150, 150–200). Results were similar with other measurements (integral and peak power) and are thus not shown here. We examined frequencies ≤200 Hz because there is little power at >200 Hz in surface EMG signals. A two-way ANOVA (2 conditions × 6 frequency bands) with repeated measures on all factors compared the normalized integral for the rectified and interference EMGs across the six frequency bands. Similar two-way ANOVAs with repeated measures (2 conditions × 6 frequency bands) were used to compare the change in coherence of pairs of interference EMG and pairs of rectified EMG signals. Analyses were performed with the SPSS 16.0 statistical package (SPSS, Chicago, IL). Significant interactions from the ANOVA models were followed by appropriate post hoc analyses. For example, differences among conditions and frequencies were followed with paired t-tests and one-way ANOVAs. Multiple t-test comparisons were corrected using Bonferroni corrections. The alpha level for all statistical tests was 0.05. Data are reported as means ± SD within the text and as means ± SE in the figures. Only the significant main effects and interactions are presented, unless otherwise noted.

RESULTS

Oscillatory input and power spectra of the interference and rectified reconstructed EMG signals

The power spectra of the interference and rectified reconstructed EMG signals were different, as can be seen in an example in Fig. 2. Specifically, there was a significant condition × frequency band interaction for the integral [F_(2,18) = 27.7, P < 0.001], normalized integral [F_(2,18) = 32.3, P < 0.001], and peak power [F_(2,18) = 12.8, P < 0.001]. Post hoc analyses indicated that the power spectrum of the interference reconstructed EMG signal matched (P > 0.3) the power values of the input [A(n)²] at all frequency bands. In contrast, and as expected, the power spectrum of the rectified reconstructed EMG signal was significantly different (P < 0.001) from both the interference reconstructed EMG signal and power values of the input. For the integral and peak power the differences occurred at frequencies between 12–200 and 250–500 Hz, whereas for the normalized integral they occurred at 0–12, 30–50, and 100–500 Hz (Fig. 3). An interesting finding from the comparison of the power spectra of the interference and rectified reconstructed EMG signals, however, was that the power of the normalized integral was similar between the interference and rectified reconstructed EMG signals from 12 to 30 Hz. This frequency band is important because it has been associated with the cortical drive to the muscle (Brown 2000).

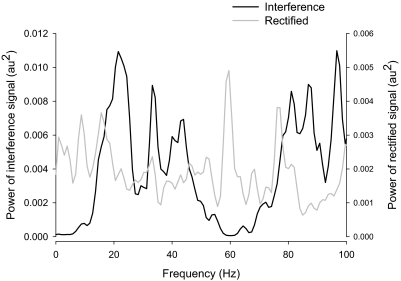
FIG. 2.

Representative example of interference and rectified power spectra of a reconstructed EMG signal. This figure demonstrates the power spectra of the interference (black line) and rectified (gray line) EMGs from a reconstructed EMG signal. Although the power spectrum of the interference EMG and rectified EMG appear to have similar peaks (20, 35, and 80 Hz, all approximate values), it is clear that the power spectra of the 2 signals are different for the following reasons: 1) the rectified reconstructed EMG exhibits peaks at different frequencies (e.g., 5, 10, and 60 Hz) and 2) the interference reconstructed EMG has distinct peaks at 40, 85, and 95 Hz, which were part of the reconstructed EMG signal but are not evident in the power spectrum of the rectified reconstructed EMG signal.

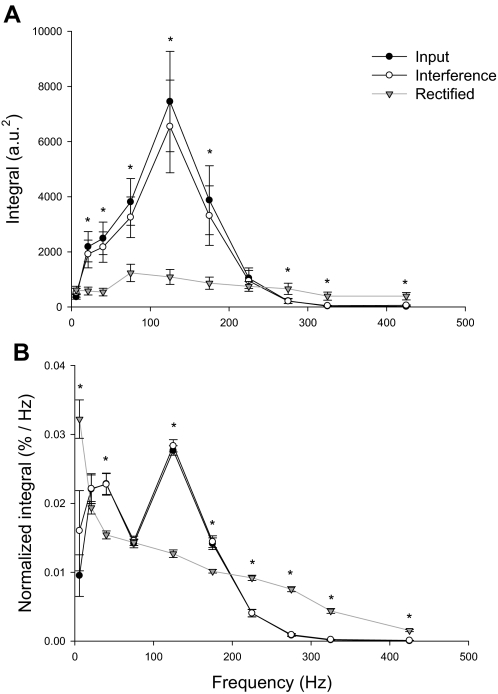
FIG. 3.

Comparison of input, interference, and rectified power spectra of reconstructed EMG signals. This figure demonstrates the integral (A) and normalized integral (B) of predetermined frequency bands within the input signal (black line, black circles), the power spectra of interference reconstructed EMG signal (black line, white circles), and the power spectra of the rectified reconstructed EMG signal (gray line, gray triangles). The integrals (A) and normalized integrals (B) of the reconstructed interference EMG signals were not significantly different (P > 0.2) from those obtained from the input. In contrast, the integrals (A) and normalized integrals (B) of the reconstructed rectified EMG signal were significantly different from the input and interference EMG signals at all frequency bands (P < 0.001), except from 0 to 12 and 200 to 250 Hz (P > 0.2). The asterisk (*) indicates significant differences between the rectified EMG signal and the input and interference EMG.

Manipulation of the oscillatory input

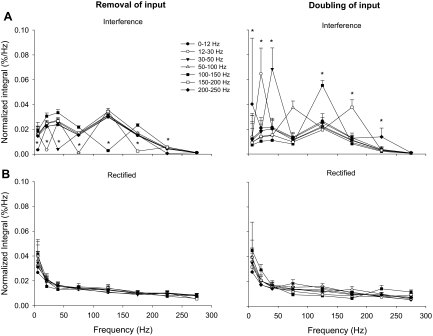
To determine whether the similarities in the 12- to 30-Hz frequency band of the normalized integral between the interference and rectified EMG signals were not random, we manipulated the reconstructed EMG signal by removing and doubling power from each frequency band. Figure 4 demonstrates an example of a reconstructed EMG signal both with and without power in 12–30 Hz (Fig. 4, A and C). The power spectrum of the interference EMG captured the removal of power from 12 to 30 Hz (Fig. 4B), whereas the power spectrum of the rectified EMG did not significantly change from the original reconstructed rectified EMG signal (Fig. 4D). The overall results demonstrated that there was a significant condition × frequency band interaction on the normalized integral (integral and peak power results were similar) for each frequency band manipulation [F_(1,5) >10, P < 0.001; Fig. 5]. It is clear from Fig. 5 that removal or doubling of input at various frequency bands was captured with the use of the interference EMG signal but not with the use of the rectified EMG signal.

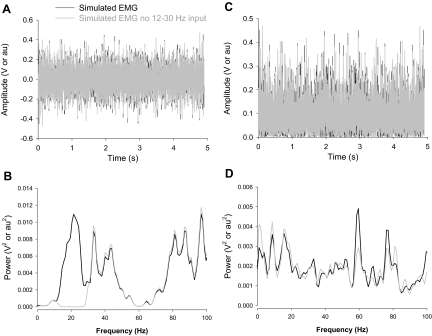
FIG. 4.

Representative example of reconstructed EMG signals with and without input from 12 to 30 Hz. The column on the left (A and B) demonstrates the interference (A) and associated power spectra (B) of the reconstructed EMG signals. The column on the right (C and D) demonstrates the rectified (C) and associated power spectra (D) of the same reconstructed EMG signals. It is evident from the comparison of B and D that the power spectrum of only the interference EMG captures the lack of power from 12 to 30 Hz (gray line).

FIG. 5.

Manipulation of power to the reconstructed EMG signals. This figure demonstrates the change in power spectra for the interference reconstructed EMG signal (top row; A) and rectified reconstructed EMG signal (bottom row; B) when the input was removed (left column) or doubled (right column) at various frequency bands (0–12, 12–30, 30–50, 50–100, 100–150, 150–200, 200–250 Hz). Removal or doubling of input was accurately captured in the power spectrum of the interference reconstructed EMG signal (A), whereas the power spectrum of the rectified reconstructed EMG signal did not change significantly with any manipulation (B). The unmodulated signal is reflected in the average of all the lines, excluding the points of manipulation (see also Fig. 3B). The asterisk (*) indicates significant differences (P < 0.001) between the modulated and unmodulated frequency band.

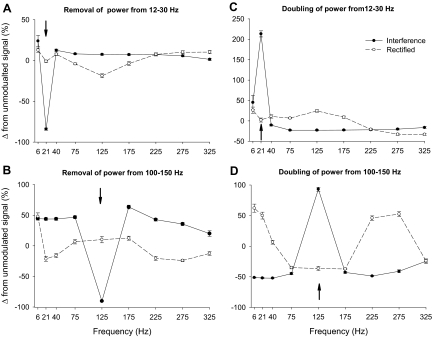
The most engaging findings, in terms of relative change, occurred when we manipulated the 12- to 30- and 100- to 150-Hz bands. This is demonstrated in Fig. 6, which shows the relative change in the normalized integral of these two bands from the unmodulated signal. For example, when power was removed from 12 to 30 Hz the power spectrum of the interference EMG signal was sensitive enough to demonstrate the removal of power from 12 to 30 Hz, whereas the power spectrum of the rectified EMG signal did not change from 12 to 30 Hz (Fig. 6A). Interestingly, the power spectrum of the rectified EMG signal decreased from 100 to 150 Hz (Fig. 6A). When power was doubled from 12 to 30 Hz, the power spectrum of the interference EMG signal was sensitive enough to demonstrate the increase of power from 12 to 30 Hz, whereas the power spectrum of the rectified EMG signal did not change from 12 to 30 Hz, but increased from 50 to 200 Hz (Fig. 6C). Similarly, when the manipulation was performed on the 100- to 150-Hz frequency band, the power spectrum of the interference EMG signal was accurate in demonstrating the removal and doubling of power at the 100- to 150-Hz band. In contrast, removal of power from 100 to 150 Hz did not influence the power spectrum of the rectified EMG signal at 100–150 Hz but decreased power from 12 to 50 Hz. Doubling of power from 100 to 150 Hz did not influence the power spectrum of the rectified EMG signal at 100–150 Hz, but increased power from 0 to 50 and 200 to 300 Hz (Fig. 6D). In summary, these results demonstrate the following two findings: 1) the power spectrum of the interference EMG signal is accurate in demonstrating changes in the oscillatory nature of the signal, whereas the rectified EMG signal is not; 2) the 0- to 30-Hz band in the power spectrum of the rectified signal is influenced by changes in the input from 100 to 150 Hz and the power in the 100- to 150-Hz band is influenced by changes in the input from 0 to 30 Hz.

FIG. 6.

Relative change in power with manipulation from 12 to 30 and 100 to 150 Hz of the reconstructed EMG signal. The column on the left (A and B) demonstrates the change in power spectra relative to the not manipulated signal when power was absent from 12 to 30 (A) and 100 to 150 Hz (B) in the input signal, whereas the column on the right (C and D) demonstrates the change in power spectra when power was doubled from 12 to 30 (C) and 100 to 150 Hz (D) of the input signal. This figure demonstrates the following: 1) The relative change in power spectra for the interference reconstructed EMG signal (black solid line) accurately captured the removal and doubling of the manipulated frequency bands, whereas the change in power spectra of the rectified reconstructed EMG signal (dashed line) did not. 2) For the rectified reconstructed EMG signal when the input was manipulated from 12- to 30-Hz and 100- to 150-Hz power significantly changed in other frequencies (primarily from 100 to 150 Hz for the 12- to 30-Hz manipulation and 0–50 and 200–300 Hz for the 100- to 150-Hz manipulation). The arrows indicate the manipulated frequency band in each panel.

Manipulation of the common input

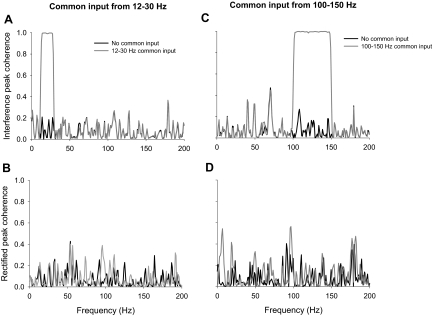
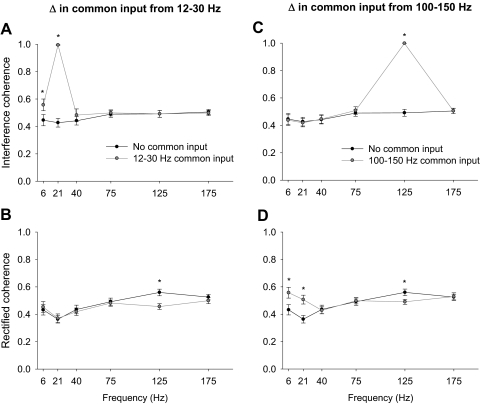
To determine the accuracy of estimating the common oscillatory input in two reconstructed EMG signals using the interference and rectified methods, we manipulated the common input from 12 to 30 and 100 to 150 Hz. Because the two signals were similar at either of those two frequency bands, we expected that a coherence analysis would indicate strong coherence between the two signals at 12–30 and 100–150 Hz. Figure 7 demonstrates examples of peak coherence between a pair of EMG signals both with and without common input at 12–30 Hz (interference EMG signal, Fig. 7A; rectified EMG signal, Fig. 7B) and 100–150 Hz (interference EMG signal, Fig. 7C; rectified EMG signal, Fig. 7D). It is evident that coherence of the interference EMG signals captured the common input from 12 to 30 (Fig. 7A) and 100 to 150 Hz (Fig. 7C). In contrast, coherence of the rectified EMG signals did not (Fig. 7, B and D). The overall results exhibited a significant condition × frequency band interaction on the peak coherence (integral and normalized integral results were similar) for each common input manipulation [F_(1,5) >10, P < 0.001; Fig. 8]. Similar to the single pair example, the overall coherence results demonstrated that coherence between interference signals was accurate in identifying a common input at 12–30 (Fig. 8A) and 100–150 Hz (Fig. 8C). When using the rectified EMG signal a common input at 12–30 Hz exhibited a decrease in peak coherence from 100 to 150 Hz (Fig. 8B), whereas a common input from 100 to 150 Hz exhibited an increase in peak coherence from 0 to 30 Hz and a decrease from 100 to 150 Hz (Fig. 8D). Thus these results extend the findings of the individual power spectrum to the coherence between two signals.

FIG. 7.

Representative example of EMG–EMG coherence with and without common input at 12–30 and 100–150 Hz. This figure demonstrates the change in EMG–EMG coherence for the interference (A, C) and rectified (B, D) approach when a pair of independent reconstructed EMG signals was manipulated to contain a common input at 12–30 (A, B) and 100–150 Hz (C, D). A common input from 12 to 30 (A) and 100 to 150 Hz (B) was accurately captured in the change of the EMG–EMG coherence when interference EMG signals were used, whereas the EMG–EMG coherence when rectified EMG signals were used did not change from 12 to 30 (A) or from 100 to 150 Hz (D).

FIG. 8.

EMG–EMG coherence with and without common input at 12–30 and 100–150 Hz. This figure demonstrates the change in EMG–EMG coherence for the interference (A, C) and rectified (B, D) approach when 19 pairs of independent reconstructed EMG signals were manipulated to contain a common input at 12–30 (A, B) and 100–150 Hz (C, D). A common input from 12 to 30 Hz was accurately captured in the change of the EMG–EMG coherence when interference EMG signals were used (A), whereas the EMG–EMG coherence when rectified EMG signals were used did not change from 12 to 30 Hz but decreased from 100 to 150 Hz (B). A common input from 100 to 150 Hz was accurately captured in the change of the EMG–EMG coherence when interference EMG signals were used (C), whereas the EMG–EMG coherence when rectified EMG signals were used significantly decreased from 100 to 150 Hz and increased from 0 to 30 Hz (D). The asterisk (*) indicates significant differences (P < 0.001) between the modulated and unmodulated signal.

DISCUSSION

Rectification of the surface EMG signal is often used as a processing step prior to the quantification of the EMG power spectrum, EEG–EMG coherence, and EMG–EMG coherence (Conway et al. 1995; Grosse et al. 2003a,b; Kilner et al. 1999, 2000, 2004; Lowery et al. 2007; Mima and Hallett 1999a; Myers et al. 2003, 2004; Yao et al. 2007). Because rectification of the EMG changes the power spectrum of the recorded EMG signal (interference EMG; Yao et al. 2007), we aimed to determine whether rectification can influence identification of the input to a reconstructed EMG signal and the capability to make predictions about common oscillations between two EMG signals. We addressed this question by manipulating signals that were reproduced from experimentally recorded EMG signals. In summary, our findings demonstrate that rectification of the EMG signal significantly impairs the accuracy of estimating the original input to the signal and the common oscillations between two EMG signals. In contrast, when we used the interference EMG signal we were able to accurately capture the input to a signal and the common input between two EMG signals. Therefore our results provide novel evidence that power spectrum analysis and coherence analysis should be performed with interference EMG signals and not with rectified EMG signals.

Rectification of EMG and identification of oscillatory input in a single EMG signal

EMG rectification is an appropriate processing step to identify the overall strength of the neural drive to the muscle and is correlated with the strength of muscle contraction and its output (Merletti et al. 2001). However, it is well established that rectification alters the frequency content (power spectrum density) of the recorded interference EMG signal (Yao et al. 2007). The reasoning for performing rectification to identify the oscillatory input to the muscle is based on the assumption that full-wave rectification of EMG demodulates the neural activation signal to the muscle (Mima and Hallett 1999a; Myers et al. 2003; Yao et al. 2007). Demodulation refers to the enhancement of underlying low-frequency components of the signal (“carrying” frequencies), which may not be easily observed due to the greater power of higher-frequency components of the signal. For the EMG signal, it is assumed that the carrying frequencies occur at <40 Hz and may represent common oscillatory inputs from the motor cortex, whereas power at higher frequencies is associated with the shape of the action potential (Brown 2000; Myers et al. 2003). The evidence that rectification enhances the existing low-frequency component in the interference EMG signal comes from a single study by Myers et al. (2003), which demonstrated that rectification amplifies the frequency content associated with the reconstructed mean discharge rate of the motor units (e.g., a peak at the EMG power spectrum at 15 Hz). Therefore we asked whether manipulations of oscillatory input at various frequencies (including the frequency band associated with the mean motor unit discharge; Christou et al. 2007) would be captured best with the rectified or interference EMG signal.

Our results do not support the use of rectification as a processing step to identify the oscillatory input to a single EMG signal. This was demonstrated by manipulating the input to the reconstructed muscle activity (removed or doubled the power at various frequency bands). The most relevant frequency bands appear to be from 12 to 30 and from 100 to 150 Hz. We showed that when there was no input from 12 to 30 Hz to the muscle activity, the power spectrum of the interference EMG captured the lack of power in that frequency band, whereas the power spectrum of the rectified EMG did not significantly change from 12 to 30 Hz (contained significant peaks from 12 to 30 Hz; Figs. 4–6). Similarly, when we doubled the power from 12 to 30 Hz to the reconstructed muscle activity, the power spectrum of the interference EMG captured the increase of power in that frequency bin, whereas the power spectrum of the rectified EMG did not significantly change from 12 to 30 Hz (Figs. 4 and 5). We also showed that the power from 0 to 30 Hz in the rectified EMG power spectra was related to changes in the input to the reconstructed EMG signals from 100 to 150 Hz (Figs. 5 and 6). These findings provide evidence that the power spectrum of the rectified EMG may not be accurate in capturing changes to the oscillatory activation of the muscle. In contrast, the power spectrum of the interference EMG appears to be accurate in capturing the oscillatory activation of muscle.

Our findings are thus contradictory to the findings of Myers et al. (2003) who demonstrated that rectification enhances the mean discharge rate of the simulated motor units compared with the interference EMG power spectrum and thus the potential use of the rectified EMG for coherence. The following results from our study challenge the findings by Myers et al. (2003). 1) EMG rectification does not enhance detection of the oscillatory input from 12 to 30 Hz. For example, we showed that the rectified EMG power spectrum did not change from 12 to 30 Hz when we removed the same frequency band (12–30 Hz) from the input signal. 2) Peaks within the 0- to 30-Hz band in the rectified EMG power spectrum were not associated with changes from 0 to 30 Hz to the input signal but with changes to the input at higher frequencies (e.g., 100–150 Hz). Therefore it is possible that the 15-Hz peak observed in the study by Myers et al. (2003) in the rectified EMG power spectrum (which they associated with the mean motor unit discharge) was related to higher-frequency bands of the input signal (e.g., 100–150 Hz).

In addition, a method that enhances only the peak of the power spectrum that corresponds to the mean motor unit discharge (8–12 Hz in physiological data) is limited because oscillatory activation of motor units also occurs at different frequency bands. For example, there is evidence that coherence of motor units occurs at about 1 Hz (Christou et al. 2007; De Luca and Erim 1994; Lowery et al. 2007) and from 12 to 30 Hz (Christou et al. 2007; Farmer et al. 1997; Lowery et al. 2007; Moritz et al. 2005). In fact, the most interesting band may be the one from 12 to 30 Hz (beta band) because it is associated with motor unit synchronization from the motor cortex (Christou et al. 2007; Farmer et al. 1997; Lowery et al. 2007; Moritz et al. 2005). Therefore in addition to the lack of power manipulation, the findings by Myers et al. (2003) are limited because they show that rectification enhances only the peak in the power spectrum that is associated with mean motor unit discharge. In contrast, our findings clearly demonstrate that the power spectrum of the interference EMG and not the rectified EMG is the method to accurately capture changes in the oscillatory input to the muscle, including frequency bands that may be associated with the mean motor unit discharge.

Rectification of EMG and EMG–EMG coherence

Coherence between two EMG signals has been used as an alternative way to EEG–EMG coherence to demonstrate the oscillatory input to muscle from higher centers (Boonstra et al. 2008; Grosse et al. 2002, 2003a, 2004; Kilner et al. 1999, 2004). Indeed, there is evidence that EMG–EMG coherence may be superior in identifying changes in the descending drive to the muscle compared with EEG–EMG coherence (Grosse et al. 2003a). In all previous studies the EMG–EMG coherence was performed on the full-wave rectified EMG signals. Therefore we wanted to determine whether EMG rectification is an appropriate processing step to the EMG signal prior to identifying changes to the common oscillatory input between two EMG signals.

Similar to the findings from the single EMG signal analysis, our results do not support the use of EMG rectification as a processing step to identify the common oscillations between two EMG signals (EMG–EMG coherence). We demonstrated that when there was common input from 12 to 30 or 100 to 150 Hz to the two reconstructed muscles, the coherence between the two interference EMGs captured the changes in common input (Figs. 7 and 8). In contrast, coherence between the rectified EMG signals did not significantly change at the manipulated frequencies (Figs. 7 and 8). If anything, a common input from 12 to 30 Hz amplified the coherence from the 100- to 150-Hz band (from 0.4 to 0.6), whereas a common input from 100 to 150 Hz increased the coherence from 0 to 30 Hz (∼0.4 to 0.55) and decreased the coherence from 100 to 150 Hz (∼0.6 to 0.5). These findings thus clearly indicate that the common input between two EMG signals cannot be captured when the EMG signals are rectified. Coherence between two interference EMG signals, however, appears to be a sensitive way to quantify the common input between two EMG signals.

In addition, we show that the 0- to 30-Hz band in the EMG–EMG coherence between two rectified EMG signals is influenced by the common input from 100 to 150 Hz. This finding is important because the common oscillations identified at 0–30 Hz from two rectified EMG signals do not correspond to a constructed common input at 0–30 Hz but rather to the constructed common input at 100–150 Hz. Therefore previous studies (Boonstra et al. 2008; Grosse et al. 2003a, 2004; Kilner et al. 1999, 2004) that show significant EMG–EMG coherence with various manipulations may not demonstrate a change in the oscillatory drive from 0 to 30 Hz but rather a change at higher-frequency bands (e.g., 100–150 Hz). The change in input at higher frequencies may potentially reflect the following: 1) a change of oscillatory input at that frequency band and 2) an increase in the motor unit discharge rate (Myers et al. 2003) or the number of motor units recruited with similar shape. In the interference EMG power spectrum this band is associated with the shape of the action potential. Therefore an increase in motor unit discharge or an increase in the number of motor units recruited with similar frequency structure can potentially change the input to higher frequencies (e.g., from 100 to 150 Hz) and consequently influence EMG–EMG coherence from 0 to 30 Hz when the rectified EMG signals are used.

Interaction between the 0- to 30- and the 100- to 150-Hz bands

We have not been able to determine the exact mechanism that causes the interaction of 0- to 30- and 100- to 150-Hz bands between the interference and rectified EMG signals in both the individual power spectra and coherence. The harmonics of the interference EMG signal can explain part of the shift in power with rectification. When we constructed a simple sinusoidal signal with power only at 21 Hz (middle of the 12- to 30-Hz band), the power spectrum of the rectified signal exhibited power at the harmonics of the original interference signal (e.g., 42, 84, and 168 Hz). Nonetheless, it also exhibited peaks at nonharmonic frequencies (e.g., 125 and 210 Hz), which indicates the nonlinearity in the transformation from the interference to the rectified signal (Yao et al. 2007). Furthermore, in a complex signal that contains multiple frequencies, such as the EMG signals reconstructed for this experiment, the importance of the harmonics to explain the shift in power diminishes. For example, if the harmonics provided the sole explanation to the shift in power, then there would be an interaction between the 30- to 50- and the 50- to 100-Hz bands in our data. However, such an interaction did not occur, thus limiting our ability to explain this shift with harmonics.

Rectification of EMG and EEG–EMG coherence

Numerous high-quality studies demonstrate corticomuscular coherence, typically quantified as the coherence between EEG or magentoencephalography (MEG) and rectified EMG (Grosse et al. 2002; Halliday et al. 1998; Kilner et al. 1999, 2000; Mima and Hallett 1999a; Salenius and Hari 2003; Schoffelen et al. 2005; Yao et al. 2007). Although our study indicates that rectification of the EMG signal may be inappropriate for EMG–EMG coherence, our findings cannot directly challenge the EEG–EMG coherence for two reasons: 1) our findings are limited to manipulation of input to one or two reconstructed EMG signals and not of manipulation of EEG relative to EMG signals and 2) there is evidence to suggest that when the interference EMG or rectified EMG signal is used in the quantification of corticomuscular coherence (EEG–EMG or MEG–EMG coherence) the results are similar (Yao et al. 2007). The results of the study by Yao et al. (2007), however, did not manipulate the EEG and EMG signals and thus did not examine whether the sensitivity of the EMG to capture changes in the oscillatory input would be the same with the interference and rectified EMG. Based on the current findings we expect that the interference EMG will be more sensitive to identify changes associated with the EEG signal. In addition, it is possible that EMG rectification, which amplifies the power in frequency bands not associated with the input, may impose coherence with EEG at inappropriate frequency bands. Future studies should compare the use of the interference and rectified EMG in quantifying EEG–EMG coherence when the EEG and/or EMG signals are reconstructed and manipulated.

In summary, we demonstrate that full-wave rectification of the recorded surface EMG signal (interference EMG signal) is not an appropriate processing step prior to EMG power spectral analysis and EMG–EMG coherence to quantify the oscillatory input to the muscle. However, our findings demonstrate that the interference EMG can accurately capture the manipulation of the input to muscle activity (EMG power spectrum) and the common input between two EMG signals (EMG–EMG coherence). We also found that the 0- to 30-Hz band in the rectified EMG power spectrum does not relate to input from 0 to 30 Hz but is influenced by the input from 100 to 150 Hz. It is concluded that the oscillating input to an EMG signal (EMG power spectrum) and common input to two EMG signals (EMG–EMG coherence) can be accurately captured with the interference EMG but not with the rectified EMG signals. Further research is needed to identify whether EMG rectification is appropriate for EEG–EMG coherence.

GRANTS

This work was supported by National Institute on Aging Grant R01 AG-031769 to E. A. Christou.