Abstract
Blood-oxygenation-level-dependent (BOLD) functional magnetic resonance imaging (fMRI) is currently the dominant technique for non-invasive investigation of brain functions. One of the challenges with BOLD fMRI, particularly at high fields, is compensation for the effects of spatiotemporally varying magnetic field inhomogeneities (ΔB0) caused by normal subject respiration, and in some studies, movement of the subject during the scan to perform tasks related to the functional paradigm. The presence of ΔB0 during data acquisition distorts reconstructed images and introduces extraneous fluctuations in the fMRI time series that decrease the BOLD contrast-to-noise ratio. Optimization of the fMRI data-processing pipeline to compensate for geometric distortions is of paramount importance to ensure high quality of fMRI data. To investigate ΔB0 caused by subject movement, echo-planar imaging scans were collected with and without concurrent motion of a phantom arm. The phantom arm was constructed and moved by the experimenter to emulate forearm motions while subjects remained still and observed a visual stimulation paradigm. These data were then subjected to eight different combinations of preprocessing steps. The best preprocessing pipeline included navigator correction, a complex phase regressor, and spatial smoothing. The synergy between navigator correction and phase regression reduced geometric distortions better than either step in isolation, and preconditioned the data to make them more amenable to the benefits of spatial smoothing. The combination of these steps provided a 10% increase in t-statistics compared to only navigator correction and spatial smoothing, and reduced the noise and false activations in regions where no legitimate effects would occur.
INTRODUCTION
Blood-oxygenation-level-dependent (BOLD) functional magnetic resonance imaging (fMRI) [1–3] is sensitive to spatial and temporal perturbations in magnetic field homogeneity within the brain due to movement outside the imaging field of view (FOV) [4]. In addition to unavoidable sources of movement due to respiration [5–8], cardiac pulsatility [5,9,10], and sporadic swallowing [11], more elaborate paradigms require subjects to perform tasks that include, but are not limited to, speaking, deliberate swallowing, jaw clenching, and tongue movement [11,12], as well as movement of the forearm to reach or grasp an object [e.g., 13]. Such paradigms may also require movement of equipment or the experimenter within or adjacent to the bore during scans. Bodily movements of the subject may also lead to head movements, an area of study that has produced numerous algorithms that provide partial compensation [14,15]. However, even in the absence of head motion, bodily motion can lead to severe artifacts [16] because movements of masses outside the FOV perturb magnetic field homogeneity and create significant geometric distortions [4,11]. When k-space is acquired using echo-planar imaging (EPI), geometric distortions are primarily pixel intensity fluctuations and shifts in the phase-encode direction [17,14]. This problem is exacerbated when movement is correlated with the paradigm, creating geometric distortions that are also correlated with the paradigm and resulting in false regions of activation [4].
A review by Strother [18] summarizes the bountiful repository of algorithms and methodologies available to improve the quality and interpretation of BOLD fMRI data. The choice of preprocessing algorithms, the order in which they are applied, and the statistical analysis used to interpret the data has been denoted as the fMRI data-processing pipeline [19]. A critical step in the preprocessing pipeline is compensation for dynamic field inhomogeneities (primarily caused by respiration and cardiac pulsatility), which apply corrections to either k-space [6,20,21] or image space [22,23]. The benefit of using navigator correction to compensate for other sources of B0 fluctuations has also been presented [24]. Other strategies for compensating for subject movement have been utilized, including the use of event-related designs [12,13] with the removal or modeling of artifact-contaminated volumes [e.g., 25], artifact removal using independent components analysis [e.g., 26], and reweighting of images based on the likelihood of noise contamination [27]. However, it may be more effective to reduce the artifacts at earlier stages of processing, before they interact with other post-processing steps, particularly motion correction, which can be misled by the geometric distortions that accompany subject movement [28,16].
In this study, hybrid two-dimensional (2D) navigator correction [29] was used to compensate for spatially varying field inhomogeneities. This navigator estimates 2D field inhomogeneities in complex image space after each radiofrequency pulse, and then applies the required corrections to low-frequency k-space. The navigator does not assume that frequency offsets are uniform in an axial slice [30], does not require the respiratory cycle to be quasi-periodic, and does not require external monitoring equipment. The only requirement of this technique is that the navigator echo line (i.e., the central line of k-space in the absence of phase encoding gradients) is acquired before the start of each echo train. In the context of the preprocessing pipeline, another advantage of this navigator (like other k-space techniques that could have been used in its place) is that corrections applied to k-space preserve the complex data representation, thus permitting further processing or analysis that require phase information [31].
Since gradient-echo fMRI is sensitive to BOLD signal changes in large veins that can be several millimeters away from the primary site of neural activity [32], a complex phase regressor was proposed by Menon [33] (and further validated by Nencka and Rowe [31]) to reduce the signal contribution from large vessels and increase spatial specificity of BOLD activation. Within a high-resolution functional voxel a few mm3 in volume, vessels larger than the smallest intracortical veins (> 25 µm radius) may be considered to be orientated and contribute to both phase and magnitude changes during activation; in comparison, capillaries and venuoles (< 25 µm radius) are randomly orientated [34] and only produce magnitude changes [33]. A maximum likelihood estimator from a linear fit of the phase and magnitude time series is used to estimate and remove BOLD signal contributions from large vessels [33]. The phase regressor may be applied to fMRI data acquired using any gradient echo EPI sequence that permits the retention of the complex representation.
The use of complex phase regression (PR) to suppress BOLD changes from large vessels has been demonstrated, but as mentioned in the original manuscript [33], this algorithm does not discriminate between phase and magnitude correlation originating from large vessel activation and other mechanisms causing correlated phase and magnitude changes within a voxel. It was proposed that PR could also remove extraneous phase and magnitude fluctuations in BOLD fMRI caused by scanner instabilities, respiratory-induced physiological noise, and geometric distortions caused by movement outside the FOV of interest. Indeed, a swallowing and tongue movement study [35] noted that the PR significantly reduced regions of false activation (Type I errors) along the edge of the brain, around the ventricles, and in inferior slices (closest to the movement). These observations suggest that PR may be particularly useful in compensating for extraneous phase fluctuations caused by subject movement required to perform the paradigm.
The goal of this paper is to investigate the effect of three preprocessing steps (navigator correction, complex phase regression, and spatial smoothing) in reducing geometric distortions due to subject movement in echo-planar fMRI. We collected echo-planar fMRI images while subjects participated in a visual stimulation paradigm with or without uncorrelated motions of a phantom arm (PA). Because the PA was physically independent of the subject’s body, head motion should be comparable between runs with and without PA motions. Two analyses quantified the effects of preprocessing steps upon data quality: 1) the average t-statistics in occipital cortex, where legitimate activation is expected; and 2) the temporal variability through the ventricles and in signal void outside the head, where no legitimate activation is expected.
MATERIALS AND METHODS
Subjects
Eleven subjects participated in this study. Two of these subjects did not complete the experiments, and data from another subject were discarded due to excessive head movement. Each of the eight remaining subjects (5 male and 3 female) completed ten functional runs. All subjects provided written informed consent through a protocol approved by the University of Western Ontario’s Health Sciences Research Ethics Board.
Imaging parameters
Experiments were performed on a Varian Unity INOVA whole-body 4 Tesla MRI scanner (Palo Alto, CA) with a Siemens Sonata gradient coil (Erlangen, Germany). Functional planes were planned parallel to the calcarine sulcus, and a 2-shot EPI sequence (64 × 64, TE = 15 ms, TR = 1000 ms, volume acquisition time = 2 s, FOV (in-plane) = 19.2 cm, θ = 40°, 17 × 3 mm slices, voxel size = 3 × 3 × 3 mm3) was used to acquire 105 volumes (15 per each baseline or activation segment) during a 3.5-minute run. A multi-shot EPI sequence was used in this 4T study to improve image quality by decreasing T2* blurring. Although single-shot acquisitions are becoming increasingly more standard, it must be emphasized that the preprocessing methodologies discussed in this paper are not specific to either multi-shot trajectories or high-field fMRI, and are therefore relevant to a wide range of fMRI studies.
Phantom Arm Set-up
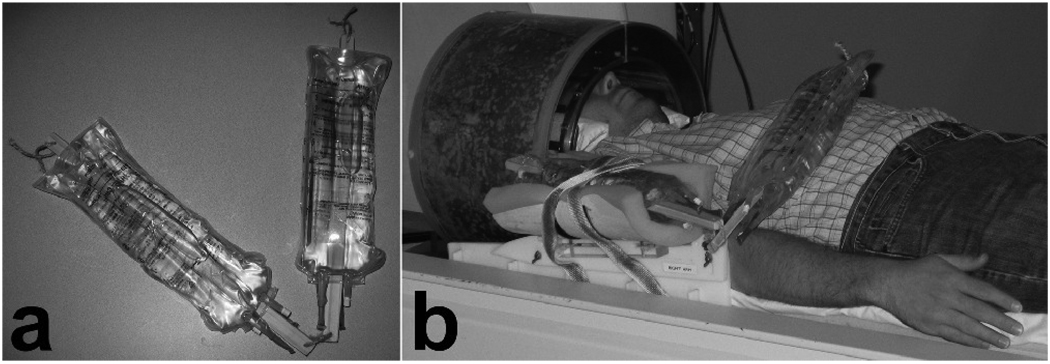
The PA constructed for this study (shown in Fig. 1a) modeled the humerus and ulna bones as two identical pieces of wood (each 30 cm in length and 2 cm in diameter), connected with a cable tie to allow movement at the “elbow” joint. Soft tissues were modeled by securing 1 L of distilled water (approximately the volume of a typical subject’s hand and forearm) to each piece of wood using two half-filled 1 L intravenous bags (to create a relatively uniform distribution of water along the entire length of the “bone”). In the experimental set-up (Fig. 1b), one end of the PA was securely fastened in a right arm restraint with foam padding and Velcro straps so that it did not move during the experiments, and the other end remained in its resting position on the abdomen (where the subject’s arm would have been had it been a real reaching/grasping experiment). The position of the arm restraint was centered on the bicep muscle so that movement of the phantom arm would be a realistic distance from the subject’s head.
FIG. 1.
(a) Phantom arm and (b) the experimental set-up to replicate the movement of the subject’s arm during a reaching/grasping paradigm.
Another cable tie was used to loop the free end of the PA around a length of twine tautly secured to the top of the bore liner to suspend the PA off the subject’s abdomen. The end of a wooden pole (1.5 m in length) was attached to the cable tie suspending the PA. During runs that required PA movement, an experimenter stood beside the subject and moved the pole along the twine in the superior-inferior direction to replicate the desired reaching/grasping motion of a human forearm (leading to arm movements comparable to those from past studies such as Culham et al. [13]).
Visual Stimulation Paradigm and Phantom Arm Movement
The visual paradigm utilized a block design to present seven alternations between 30 s of baseline (blank screen) and 30 s of visual stimulation (a radial checkerboard flickering at 8 Hz). Subjects were instructed to maintain fixation on a central point throughout all runs.
Each session consisted of alternating control runs and movement runs. In control runs, the PA remained in its resting position (as shown in Fig. 1b); in movement runs, the PA was moved between its resting and grasping positions by the experimenter. Movement of the PA was continuous but aperiodic to maximize geometric distortions, and the translational distances varied at the experimenter’s discretion (up to 40 cm away from the resting position) to simulate the random grasping of objects at varying distances. At no time were subjects required to move their arms or any other part of their body.
Data Preprocessing
All EPI data first underwent a non-linear reference phase correction [36] to align even and odd k-space lines and significantly reduce N/2 ghosting artifacts. Although a wide variety of preprocessing options were possible [18], only the following three steps were considered in this paper to focus the analysis on validating the use of phase regression for purposes other than vessel suppression: (1) hybrid 2D navigator correction (NC) to compensate for image-to-image intensity fluctuations due to respiratory-induced physiological noise and other sources of dynamic field inhomogeneities; (2) complex phase regression (PR) to remove correlated phase and magnitude fluctuations; and (3) in-plane spatial smoothing (SS) using a 7.5 mm full-width-at-half-maximum (FWHM) Gaussian kernel to locally average thermal noise and increase the signal-to-noise ratio (SNR).. Since NC and PR are both applied to complex data, but the data become magnitude-only after PR, NC must be performed before PR. Furthermore, since SS should be performed after all possible corrections for physiological noise and other susceptibility-related fluctuations, there is only one logical order in which these steps may be applied: NC, PR, SS. Each step was either performed or not performed, resulting in eight (23) unique processing pipelines: raw, NC, PR, SS, NC+PR, NC+SS, PR+SS, NC+PR+SS. The NC and PR steps were performed with custom software written in Matlab and C, respectively. In-plane spatial smoothing was applied with Analysis of Functional NeuroImages (AFNI) software [37].
A recent study by Strother et al. [19] investigated the impact of no smoothing and 7 Gaussian kernels between 3.4 mm and 27.5 mm FWHM on the prediction and reproducibility of fMRI data. Strother et al. state that the most striking observation across this range is a steep rise in both prediction and reproducibility when the kernel size increases from 3.4 mm to 6.9 mm FWHM. We used this finding to set a lower bound of 7 mm FWHM on our choice of kernel size. The maximum values for prediction and reproducibility occurred at 13.8 mm and 20.6 mm FWHM, respectively, which set a very high upper bound of 21 mm FWHM. Firstly, it is important to note that the peaks for these metrics (with reference to Fig. 3 and Fig. 4 in [19]) are both broad and shallow, and that most of the benefit to prediction and reproducibility provided by smoothing is realized with a kernel size of only 6.9 mm FWHM. Secondly, although a wide kernel of 14 mm to 21 mm FWHM may maximize prediction and/or reproducibility, it is unlikely to be acceptable for the majority of fMRI studies, where reasonable spatial resolution is desirable. Since current practices for group analyses suggest that a kernel size between 6 mm and 9 mm FWHM may be appropriate to decrease functional heterogeneity between subjects, a kernel size of 7.5 mm FWHM was selected for our study because it is in the middle of this range and also benefits from significant increases in prediction and reproducibility.
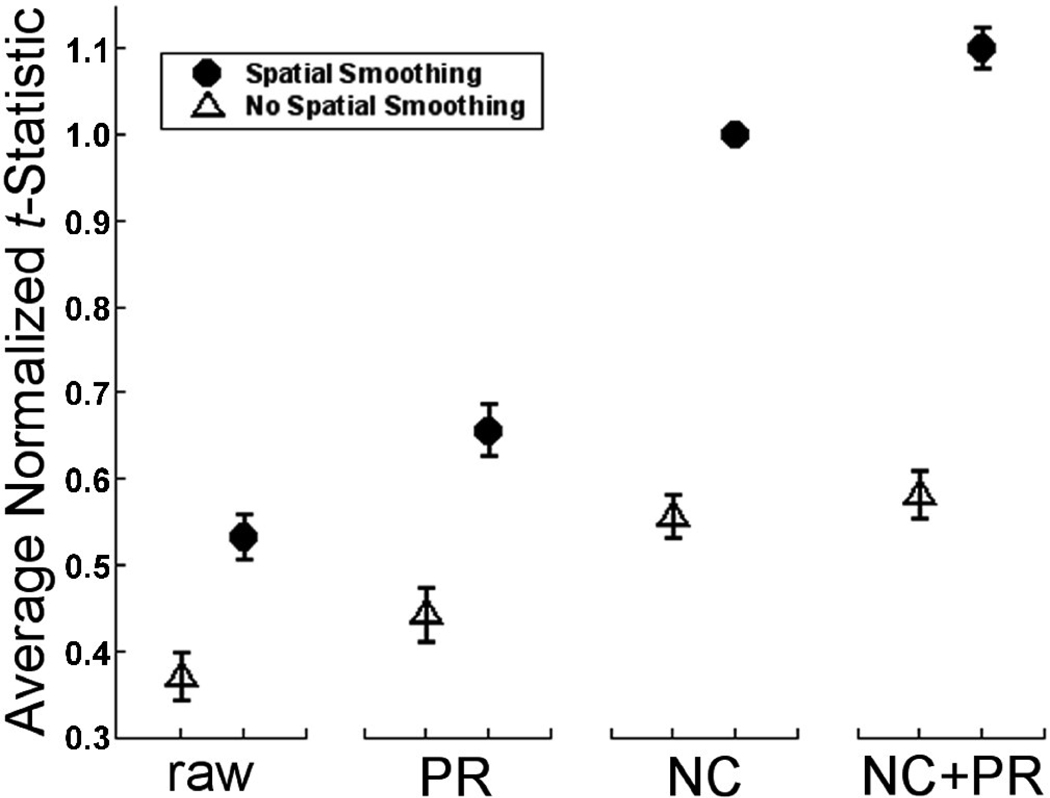
FIG. 3.
Average t-statistic for 40 movement runs normalized with respect to NC+SS (FWHM = 7.5 mm) for each run. Although there is no significant difference between NC and NC+PR, there is a 10.1% increase between NC+PR+SS and NC+SS. Error bars represent the 95% confidence intervals (CI). [NC = navigator correction; PR = phase regression; SS = spatial smoothing; raw = neither NC nor PR]
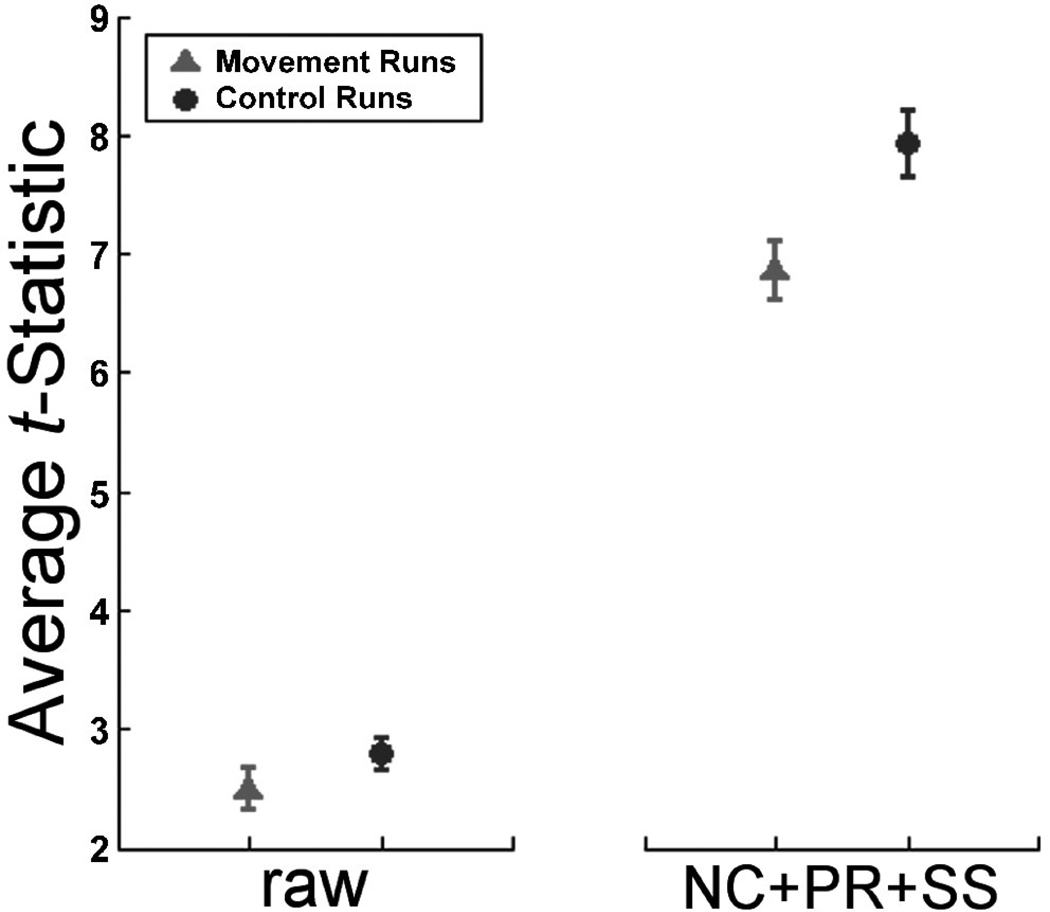
FIG. 4.
Average t-statistic in control and movement runs for the raw (unprocessed) and NC+PR+SS (navigator correction, phase regression, and spatial smoothing) pipelines. Error bars represent the 95% CI. Statistically significant differences exist between the two groups both before (p < .01) and after (p < .0001) processing.
Statistical processing of data
BrainVoyager QX 1.9 (Brain Innovation, Maastricht, The Netherlands) was used to perform the functional analysis upon the interpolated 3D volumetric data. Activation maps were generated using a general linear model with a predictor formed by convolving a boxcar waveform coincident with the visual stimulation paradigm with the software’s default double-Gamma hemodynamic response function (HRF). Statistical comparisons were performed using SPSS 16 software.
To examine the effect of the preprocessing pipeline upon Type II (false rejection) statistical errors, we computed the average t-statistics within a volume of interest (VOI) in the occipital cortex. Because genuine activation is expected within visual cortex, an increase of t-statistics would indicate a reduction in the likelihood of Type II errors. For each of the 80 runs (40 control and 40 movement), we selected a 3D VOI containing contiguous pixels in the occipital cortex with t-statistics ≥ 4.0 using data that had undergone navigator correction and spatial smoothing. Voxels containing large vessels that had BOLD signal change suppressed by the PR algorithm were excluded from the VOI.
We also examined the noise variance within VOIs where no legitimate activation would be expected: through the ventricles and corpus callosum, and in signal void outside the cranium. The VOIs were selected within the middle 2D functional slice for each subject, and the noise variance was recorded in each of the 80 runs for the NC and NC+PR pipelines. Such noise, if spuriously correlated with the paradigm, can lead to false activations, so we also examined the activation maps within these regions.
RESULTS
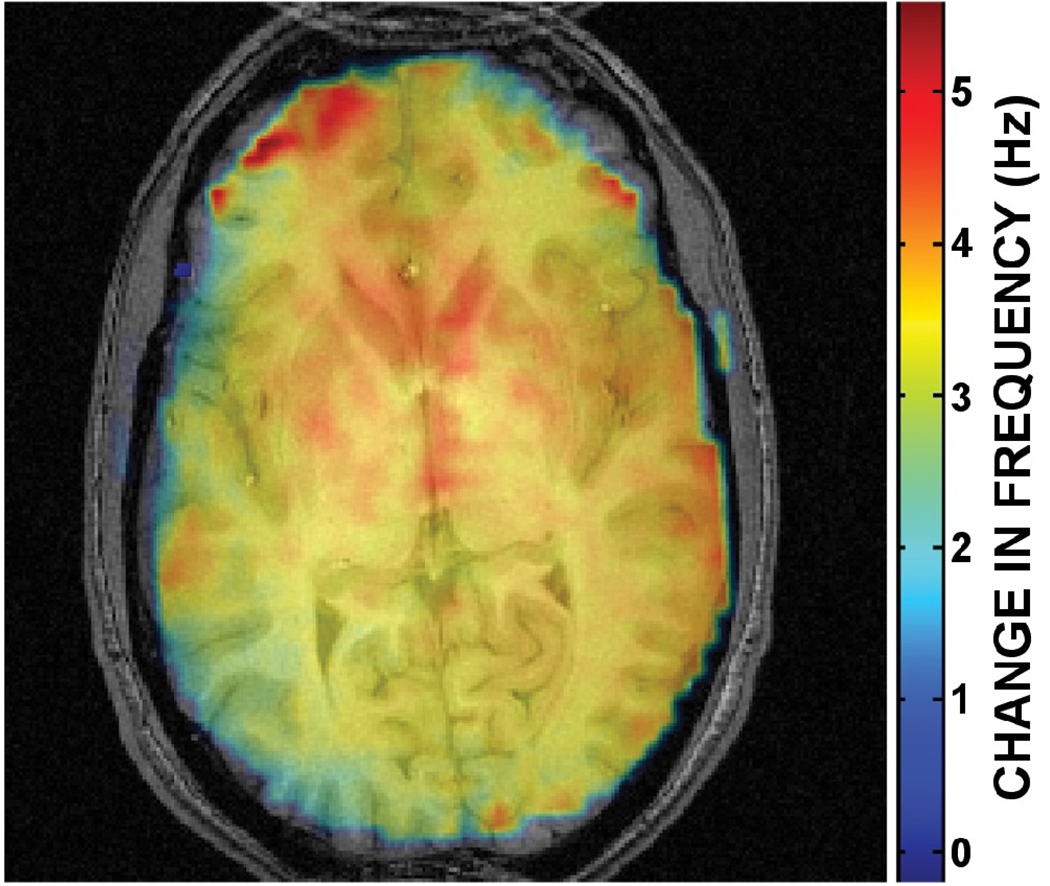
Figure 2 displays the spatially varying magnetic field inhomogeneities in a mid-axial slice caused by PA movement between the grasping and resting positions, calculated as the average of three separate measurements of phase differences in the 3D field maps (acquired using RASTAMAP [38]). Previous field map measurements between full inhalation and exhalation have revealed the magnitude of frequency offsets to be up to 1 Hz in posterior brain regions at 4 T [30]. In comparison, movement of the PA produced field offsets of 6 Hz peak-to-peak in the selected mid-axial slice, with a 3 to 4 Hz frequency shift throughout much of the occipital cortex. Since the magnetic field was shimmed with the PA in its resting position, these additional inhomogeneities are not present in control runs. Thus, in movement runs, data are acquired in the presence of complicated spatiotemporally varying magnetic field inhomogeneities from both respiration and PA movement, leading to frequency offsets at least four times greater than expected during control runs.
FIG. 2.
Spatially varying magnetic field inhomogeneities (6 Hz peak-to-peak) in a mid-axial slice caused by the change in position of the phantom arm between its resting and grasping positions. Frequency offsets are between 3 and 4 Hz throughout much of the occipital cortex, which are at least three times the magnitude of field offsets expected from normal subject respiration.
We began by comparing the effects of the eight (23) combinations of preprocessing on the movement runs. These data are shown in Fig. 3, in which data points have been normalized such that the t-values for the standard processing step, NC+SS, were set to 1.0 for each run and all other values were scaled accordingly. Note that the highest relative t-statistics were observed for the NC+PR+SS combination, which provide an average improvement of 10.1% in t-statistics across all voxels compared to NC+SS (without PR).
Table 1 summarizes the following analysis of variance (ANOVA) findings. Statistical analysis revealed that each of the three preprocessing steps led to a significant improvement in t-statistics for occipital cortex and, moreover, that all two-way combinations of these steps demonstrated interactions. Specifically, to evaluate the statistical differences between the eight conditions, a 2 (NC vs no NC) × 2 (PR vs no PR) × 2 (SS vs no SS) repeated measures ANOVA was performed on the raw (unnormalized) tavg for the eight subjects. Significant main effects were observed for NC, PR, and SS. From these main effects, along with posthoc tests, it is clear that each of the steps improved the tavg values. Although there was no significant three-way interaction (NC × PR × SS), all three two-way interactions were significant. First, the interaction NC × PR showed that the effect of PR was smaller when the data had undergone NC than when they had not; second, the interaction NC × SS showed that the effect of SS was larger when the data had undergone NC than when they had not; third, the interaction PR × SS showed that the effect of SS was larger when the data had undergone PR than when they had not. Post hoc comparisons with a Tukey correction for multiple comparisons revealed significant differences (p<0.01) in tavg between all pairs of pipelines, with one exception, NC vs NC+PR. The pipeline with the highest tavg was NC+PR+SS, which had significantly higher tavg values than NC+SS (a common processing approach).
Table 1.
Summary of repeated measures ANOVAs.
| Region of Interest | Main Effect or Interaction | F(1,7) | P value |
|---|---|---|---|
| Occipital Cortex | |||
| NC | 110.6 | *** | |
| PR | 87.4 | *** | |
| SS | 542.4 | *** | |
| NC × PR × SS | 0.9 | 0.378 | |
| NC × PR | 51.1 | *** | |
| NC × SS | 176.0 | *** | |
| PR × SS | 163.3 | *** | |
| Movement | 30.2 | *** | |
| Preprocessing | 296.6 | *** | |
| Movement × Preprocessing | 43.6 | *** | |
| Ventricles | |||
| PR | 28.7 | *** | |
| Movement | 9.4 | * | |
| PR × Movement | 2.3 | 0.176 | |
| Signal Void | |||
| PR | 12.8 | ** | |
| Movement | 5.9 | * | |
| PR × Movement | 6.2 | * | |
p < 0.05
p < 0.01
p < 0.001
Statistical analysis also revealed that the full complement of preprocessing steps was also highly effective in improving tavg in the occipital cortex for runs in which there was no PA movement; in fact, it was more effective than for runs with PA movement (see Fig. 4). Specifically, we performed a 2×2 repeated measures ANOVA to compare the effect of NC+PR+SS vs no preprocessing (raw) for the movement vs no control runs. As expected, tavg values were lower for movement runs than control runs, a main effect that was significant. Also as expected, the full preprocessing led to higher tavg values than no preprocessing, a main effect that was also significant. In addition, there was a two-way interaction between preprocessing and movement. Surprisingly, there was a greater improvement in tavg values for control runs compared to movement runs, contrary to our initial expectations of the converse pattern. Post hoc Tukey tests indicated that all comparisons between conditions were significant (p<0.01).
The t-statistic is a useful metric to quantify meaningful signal change due to BOLD activation because it incorporates both the change in signal intensity and the noise variance. When considering VOIs where no BOLD signal change is expected (such as in cerebrospinal fluid, white matter, and air), the temporal variance is an appropriate metric to characterize the noise level. In addition to reducing the likelihood of discovering true activations (Type II statistical errors), such noise can also lead to false activations (Type I statistical errors) in these locations if it happens to be spuriously correlated with the paradigm. In the noise analyses, the temporal variance in two VOIs (through the ventricles and in signal void) was measured for the NC and NC+PR pipelines in both control and movement runs. Spatial smoothing was not applied so that the analyses may focus solely on the efficacy of phase regression to reduce Type I errors.
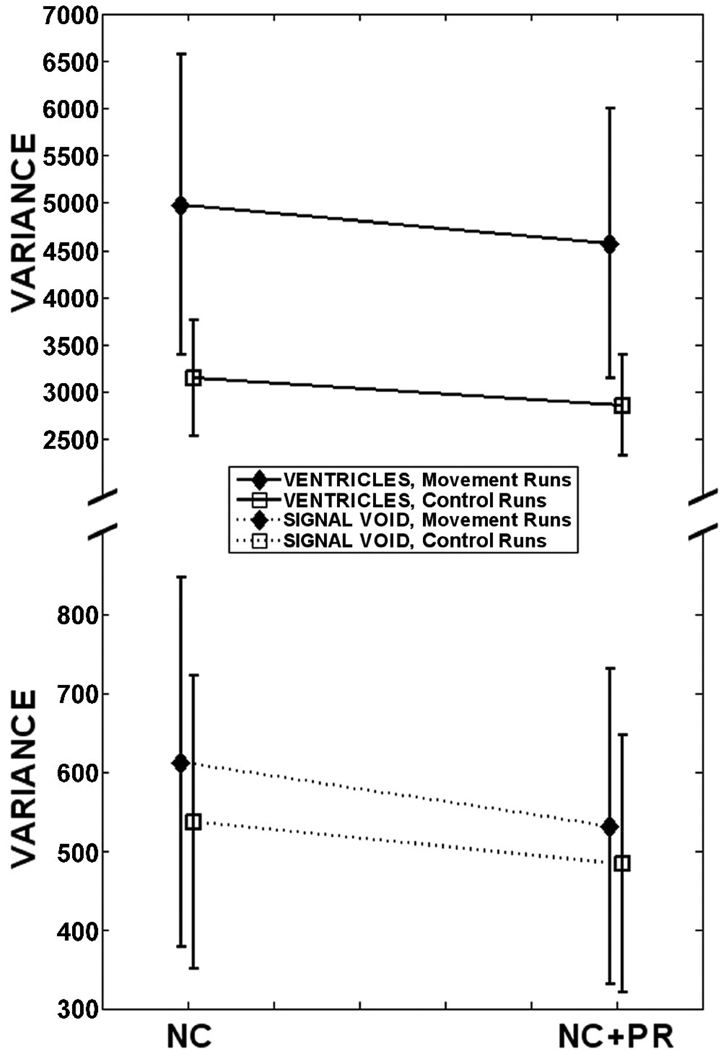
Figure 5 illustrates how the addition of PR (NC+PR vs NC) reduced the variance in the noise VOIs (ventricles and signal void) for both control and movement runs (where the latter group has higher noise to begin with). Specifically, for each of the two VOIs, we performed a 2 (PR vs no PR) × 2 (control vs movement) repeated measures ANOVA. For the ventricles VOI, there was a significant main effect of PR, a significant main effect of movement, but no significant interaction. In short, the PR algorithm was beneficial in reducing noise variance in all functional runs, regardless of whether or not there was movement outside the FOV. For the signal void VOI, there was also a significant main effect of PR and a significant main effect of movement. However, in this case there was also a significant interaction, which occurred because PR was more effective at reducing noise for movement runs than control runs. The fact that PR reduced noise in the signal void for either control or movement runs may initially appear surprising because thermal noise does not have correlated phase and magnitude changes. However, the edge of the signal void VOIs included space containing residual N/2 ghosting artifacts (caused by subtle shifts between even and odd k-space lines that persisted after non-linear reference phase correction [36]). Unlike thermal noise, these ghosting artifacts exhibited correlated phase and magnitude changes, and thus may be reduced via phase regression. These artifacts are also caused by ΔB0, which explains why the variance in signal void VOIs was significantly higher in movement runs than control runs.
FIG. 5.
Average noise variance in VOIs through subjects’ ventricles and corpus callosum, and in signal void outside the head. Error bars represent the 95% CI. Application of PR decreased noise variance in both movement and control runs. For clarity, the vertical axis is scaled differently for each VOI. [NC = navigator correction; PR = phase regression]
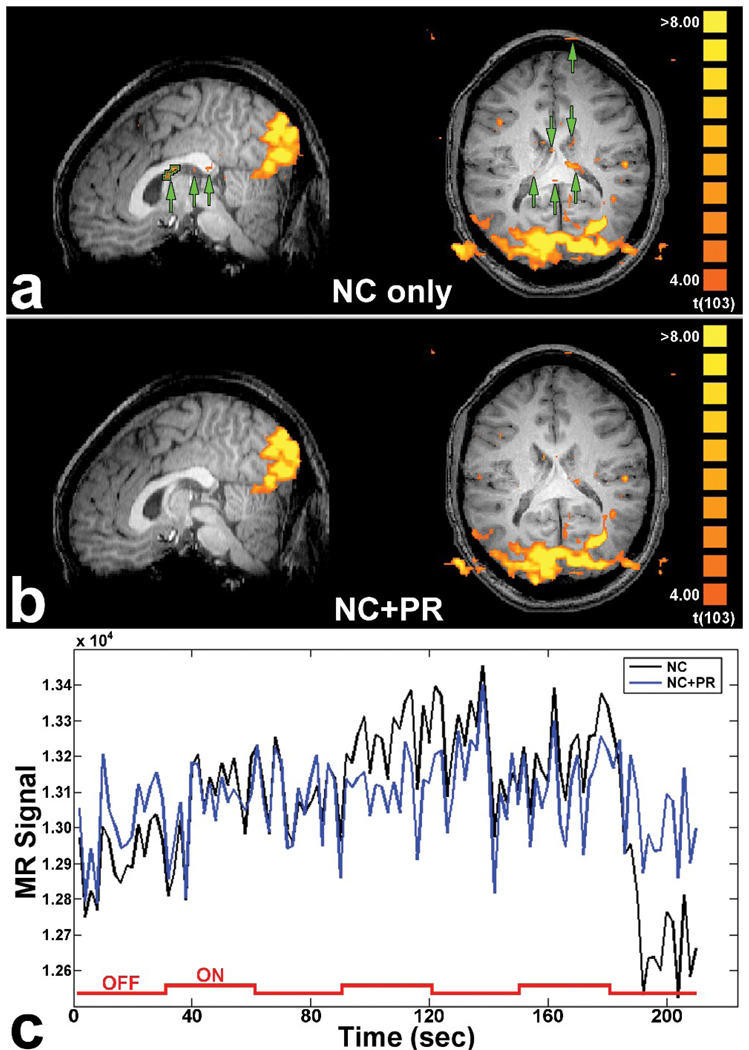
The reduction of extraneous susceptibility-related fluctuations within regions without legitimate activation would be expected to lead to false positives if spuriously correlated with the paradigm. As shown in Fig. 6a, a representative activation map for movement runs from one subject suggests that the noise reduction achieved by NC+PR vs NC does indeed eliminate or reduce false activations in white matter and the ventricles. The time course for falsely activated voxels in the fornix (outlined in green in Fig. 6a, sagittal view) is shown in Fig. 6c. This VOI has a t-statistic of 4.88 in the NC pipeline, which is mostly attributed to the sudden change in phase (and thus magnitude) beginning around 180 seconds, coinciding with the time in which the HRF would be expected to drop following offset of the visual stimulus. (If this change were present in only the magnitude, then the NC and NC+PR time series would be virtually identical.) The PR corrected this phase discontinuity and decreased the noise variance by a factor of three (from 4.39 × 104 to 1.48 × 104), resulting in a non-significant t-statistic of 1.57 in the NC+PR pipeline.
FIG. 6.
Activation maps for a movement run from one subject processed using (a) NC and (b) NC+PR. Green arrows show regions of false activation (Type I error) that are suppressed using the PR algorithm. (c) Raw time course for the white matter VOI outlined in (a). The timing of the visual stimulus is superimposed. The noise variance is decreased by a factor of three in the white matter VOI due to the correction of the phase discontinuity beginning around 180 seconds. [NC = navigator correction; PR = phase regression]
DISCUSSION
We have shown that statistical errors caused by bodily movements can be compensated by a combination of preprocessing techniques. We found that simulated arm movements (in the absence of yoked head movements) led to a reduction in the average t-statistics in a region of legitimate activation and an increase in temporal noise and false positive activations in regions where no legitimate activation was found. Both of these problems, corresponding to Type II and Type I statistical errors, respectively, were considerably reduced with data preprocessing. The full combination of NC+PR+SS improved data quality over all other combinations of preprocessing steps, including NC+SS, which is a more standard combination. Moreover, in some cases, interactions occurred. Specifically, the benefits of SS were amplified by the inclusion of either NC or PR while the combination of NC+PR led to smaller benefits than would be expected by the sum of the two components alone.
The inclusion of PR was beneficial not only for movement-contaminated runs, but also for control runs. Presumably this occurred because the PR algorithm reduced other artifacts that affect ΔB0, including respiration and small head movements. The PR algorithm is therefore not only useful for suppressing the contributions from large vessels, but it also improves the quality of data with or without movement artifacts. A modest improvement of only 10% between NC+SS and NC+PR+SS may be explained by a reduction in activation levels (and thus t-statistics) from the exclusion of large vessels. Similarly, the lack of a statistically significant difference in tavg between NC+PR and NC pipelines is likely to be due to the opposing effects of vessel suppression (which reduces tavg) and artifact suppression (which increases tavg). Indeed, NC+PR led to a significantly greater reduction in noise in the ventricles and outside the head compared to NC alone. In short, though the addition of PR to the processing pipeline (before spatial smoothing) may not increase the significance levels of legitimate activations, it excludes vessel contributions with no significant decrease in statistical power, thus making the spatial localization of activation more closely coupled to the neural events. The benefits of PR may be even greater in other areas of the brain. We chose to examine t-statistics in the visual cortex, a standard VOI for methodological studies; however, given that geometric distortions may be particularly problematic in anterior (Fig. 2) and inferior regions closer to the bodily motion, greater improvements in statistics with PR may be expected.
Even with the combination of all three preprocessing steps, data from movement runs was still poorer than non-movement runs (lower t-statistics and higher noise). This result is consistent with our previous findings from simulations exploring the effect of spatially and temporally varying field inhomogeneities due to respiratory-induced physiological noise on the time course of pixels in reconstructed images [29]. Even though those simulations were conducted in the absence of additive thermal noise, the residual geometric distortions persisted in simulated images after navigator correction (global, 1D, or 2D), indicating that none of the navigator techniques considered were able to completely compensate for spatially varying magnetic field inhomogeneities – even under artificially ideal circumstances. Thus, residual distortions persist in real fMRI data after NC, and are more severe in movement data than control data. The efficacy of the subsequent PR and SS steps is unfortunately diminished by these distortions, which explains why NC+PR+SS is more effective in control runs than movement runs.
The most striking feature of Fig. 3 is the positive impact that the chosen spatial smoothing kernel has on all of the pipelines. For example, data that have undergone only SS have tavg that is not significantly different from NC. With the aim of choosing the best pipeline (for the three steps considered), the most significant benefits of spatial smoothing are realized when this step is applied to data that have already undergone NC+PR. Although there is no difference in tavgbetween NC+PR and NC, there is a significant improvement in NC+PR+SS over NC+SS due to the fact that the sequential application of NC and PR suppresses geometric distortions better than either NC or PR alone, which preconditions the data to make them more amenable to the well-recognized benefits of spatial smoothing [39,19].
The engineering of an algorithm to perform a specific task is typically done under ideal circumstances or in isolation from other algorithms. However, in reality, there are interactions between algorithms in the preprocessing pipeline because the output of one algorithm is also the input of the next algorithm. A limitation of k-space correction algorithms (such as the 2D navigator) stated in the literature is that they are only useful in low-frequency k-space where there is sufficient SNR; however, a significant advantage of k-space techniques is that they can apply different corrections to segments of k-space, which is important for multi-shot sequences. An advantage of PR is that it operates on individual pixels in image space and can correct temporal fluctuations that have high spatial frequencies. By combining NC and PR, data first undergo a correction for field inhomogeneities with low spatial frequencies, followed by a complementary correction for the highest spatial frequencies based on correlated phase and magnitude changes. Since PR by itself is barely an improvement over the pipeline with no preprocessing, another way of looking at this relationship is that uncorrected geometric distortions result in pixels with phase and magnitude changes that are influenced by the shifting of adjacent pixels in the phase-encode direction. In the presence of geometric distortions, phase and magnitude changes for each pixel become less correlated, and the PR algorithm is no longer able to accurately compensate for these unwanted fluctuations.
In addition to suppressing BOLD activation from larger vessels [33] and increasing tavg via interactions with NC and SS, the third benefit of the PR algorithm is decreasing spurious activations (Type I errors) by reducing extraneous noise fluctuations. Although false activations are more easily identified when they appear in white matter, cerebrospinal fluid, or at the edge of the brain, they may, without careful scrutiny, be mistaken as genuine activation in gray matter. Sources of extraneous fluctuations include physiological noise and field inhomogeneities caused by bodily movements. Although this paper considered a specific example of subject movement caused by movement of a subject’s forearm during reaching/grasping experiments, it must be emphasized that the benefits of PR are applicable to all fMRI experiments where unaliased complex data are retained.
The findings in this paper may also improve the reliability of motion correction algorithms. Despite the best efforts of the MR technician to immobilize a subject’s head in the RF coil and the good intentions of the subject to remain completely stationary, some degree of physical head movement is inevitable during scans. Head motion degrades the quality of fMRI data by obscuring regions of real activation and creating regions of false activation [40,41]. Even small movements of less than 1 mm translation or 1° rotation can create false regions of activation if the movement is correlated with the paradigm [42].
The use of an algorithm to estimate and correct for rigid-body head motion is generally believed to improve the quality of fMRI data [15], although such algorithms can create spurious activations in the absence of subject motion [28]. Motion correction can actually lead to erroneous corrections [16] and create false regions of activation when the cost function used to estimate motion is sensitive to spatially varying changes in signal intensity due to BOLD activation and geometric distortions caused by ΔB0. Future work can include rigid-body motion correction in the preprocessing pipeline to investigate the influence that steps to reduce geometric distortions (e.g., navigator correction and complex phase regression) have on the efficacy of the motion correction algorithm to compensate for genuine head motion without introducing additional artifacts.
In conclusion, an approach to compensate for spatiotemporally varying magnetic field inhomogeneities has been presented that combines complementary techniques of navigator correction and complex phase regression. The first step is applied to low-frequency k-space while the second step operates on individual pixels in complex image space, and their synergy in the preprocessing pipeline precondition the data to make them more amenable to the benefits of spatial smoothing. An fMRI study was performed that emulated magnetic field distortions expected from a reaching/grasping paradigm by moving a human arm phantom outside the imaging FOV. An analysis in the occipital lobe demonstrated a 10% increase in t-statistics when phase regression is included between 2D navigator correction and spatial smoothing, leading to a decrease in Type II errors. Analyses in regions other than gray matter revealed a decrease in noise variance after phase regression, providing better control of Type I errors. As residual geometric distortions persisted in reconstructed images, future work can investigate the inclusion of additional steps in the preprocessing pipeline (for example, the Stockwell transform filter [43]) to further compensate for non-trivial magnetic field inhomogeneities. Finally, since the scope of this study was limited to spatial smoothing for typical group analyses (a single kernel width used for all data sets), future work can also consider the role that phase regression may play in optimized spatial smoothing for both single-subject and group fMRI analyses.
ACKNOWLEDGMENTS
The authors thank Dr. Marc Joanisse and Adam McLean for discussions regarding AFNI scripting, and Jeff Mason and Laura Gee for their assistance in the construction of the phantom arm. This research was supported by funding from the National Institutes of Health (Grant # 1R01EB002739), the Canadian Institutes of Health Research (Grant # MOP-64399), the Canada Research Chairs Program to RSM, and the Natural Sciences and Engineering Research Council of Canada (Grant # 249877-2006 RGPIN) to JCC.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R, Cheng H-M, Brady TJ, Rosen BR. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci USA. 1992;89:5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ogawa S, Tank DW, Menon R, Ellermann JM, Kim S-G, Merkle H, Ugurbil K. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci USA. 1992;89:5951–5955. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. Time course EPI of human brain function during task activation. Magn Reson Med. 1992;25:390–397. doi: 10.1002/mrm.1910250220. [DOI] [PubMed] [Google Scholar]
- 4.Yetkin FZ, Haughton VM, Cox RW, Hyde J, Birn RM, Wong EC, Prost R. Effect of motion outside the field of view on functional MR. AJNR Am J Neuroradiol. 1996;17:1005–1009. [PMC free article] [PubMed] [Google Scholar]
- 5.Weisskoff RM, Baker J, Belliveau J, Davis TL, Kwong KK, Cohen MS, Rosen BR. Power spectrum analysis of functional-weighted MR data: what’s in the noise? Proc SMRM. 1993:7. [Google Scholar]
- 6.Hu X, Kim S-G. Reduction of signal fluctuation in functional MRI using navigator echoes. Magn Reson Med. 1994;31:495–503. doi: 10.1002/mrm.1910310505. [DOI] [PubMed] [Google Scholar]
- 7.Noll DC, Schneider W. Respiration artifacts in functional brain imaging: sources of signal variation and compensation strategies. Proc SMRM. 1994:647. [Google Scholar]
- 8.Noll DC, Schneider W. Theory, simulation, and compensation of physiological motion artifacts in functional MRI; Proc IEEE Intern Conf Image Process; 1994. pp. 40–44. [Google Scholar]
- 9.Hu X, Le TH, Parrish T, Erhard P. Retrospective estimation and correction of physiological fluctuation in functional MRI. Magn Reson Med. 1995;34:201–212. doi: 10.1002/mrm.1910340211. [DOI] [PubMed] [Google Scholar]
- 10.Le TH, Hu X. Retrospective estimation and correction of physiological artifacts in fMRI by direct extraction of physiological activity from MR data. Magn Reson Med. 1996;35:290–298. doi: 10.1002/mrm.1910350305. [DOI] [PubMed] [Google Scholar]
- 11.Birn RM, Bandettini PA, Cox RW, Jesmanowicz A, Shaker R. Magnetic field changes in the human brain due to swallowing or speaking. Magn Reson Med. 1998;40:55–60. doi: 10.1002/mrm.1910400108. [DOI] [PubMed] [Google Scholar]
- 12.Birn RM, Bandettini PA, Cox RW, Shaker R. Event-related fMRI of tasks involving brief motion. Hum Brain Mapp. 1999;7:106–114. doi: 10.1002/(SICI)1097-0193(1999)7:2<106::AID-HBM4>3.0.CO;2-O. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Culham JC, Danckert SL, DeSouza JFX, Gati JS, Menon RS, Goodale MA. Visually guided grasping produces fMRI activation in dorsal but not ventral stream brain areas. Exp Brain Res. 2003;153:180–189. doi: 10.1007/s00221-003-1591-5. [DOI] [PubMed] [Google Scholar]
- 14.Andersson JLR, Hutton C, Ashburner J, Turner R, Friston K. Modeling geometric deformations in EPI time series. NeuroImage. 2001;13:903–919. doi: 10.1006/nimg.2001.0746. [DOI] [PubMed] [Google Scholar]
- 15.Oakes TR, Johnstone T, Ores Walsh KS, Greischar LL, Alexander AL, Fox AS, Davidson RJ. Comparison of fMRI motion correction software tools. NeuroImage. 2005;28:529–543. doi: 10.1016/j.neuroimage.2005.05.058. [DOI] [PubMed] [Google Scholar]
- 16.Culham JC. Functional neuroimaging: Experimental design issues. In: Cabeza R, Kingstone A, editors. Handbook of Functional Neuroimaging of Cognition. 2nd ed. Cambridge MA: MIT Press; 2006. pp. 53–82. [Google Scholar]
- 17.Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med. 1995;34:65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- 18.Strother SC. Evaluating fMRI preprocessing pipelines. IEEE Eng Med Biol Mag. 2006;25:27–41. doi: 10.1109/memb.2006.1607667. [DOI] [PubMed] [Google Scholar]
- 19.Strother S, La Conte S, Kai Hansen L, Anderson J, Zhang J, Pulapura S, Rottenberg D. Optimizing the fMRI data-processing pipeline using prediction and reproducibility performance metrics: I. A preliminary group analysis. NeuroImage. 2004;23:S196–S203. doi: 10.1016/j.neuroimage.2004.07.022. [DOI] [PubMed] [Google Scholar]
- 20.Wowk B, McIntyre MC, Saunders JK. k-Space detection and correction of physiological artifacts in fMRI. Magn Reson Med. 1997;38:1029–1034. doi: 10.1002/mrm.1910380625. [DOI] [PubMed] [Google Scholar]
- 21.Pfeuffer J, Van de Moortele P-F, Ugurbil K, Hu X, Glover GH. Correction of physiologically induced global off-resonance effects in dynamic echo-planar and spiral functional imaging. Magn Reson Med. 2002;47:344–353. doi: 10.1002/mrm.10065. [DOI] [PubMed] [Google Scholar]
- 22.Glover GH, Li T-Q, Ress D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn Reson Med. 2000;44:162–167. doi: 10.1002/1522-2594(200007)44:1<162::aid-mrm23>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 23.Chuang K-H, Chen J-H. IMPACT: Image-based physiological artifacts estimation and correction technique for functional MRI. Magn Reson Med. 2001;46:344–353. doi: 10.1002/mrm.1197. [DOI] [PubMed] [Google Scholar]
- 24.Durand E, van de Moortele P-F, Pachot-Clouard M, Le Bihan D. Artifact due to B0 fluctuations in fMRI: correction using the k-space central line. Magn Reson Med. 2001;46:198–201. doi: 10.1002/mrm.1177. [DOI] [PubMed] [Google Scholar]
- 25.Cavina-Pratesi C, Goodale MA, Culham JC. fMRI reveals a dissociation between grasping and perceiving the size of real 3D objects. Public Library of Science (PLoS) ONE. 2007;2(5):e424. doi: 10.1371/journal.pone.0000424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kochiyama T, Morita T, Okada T, Yonekura Y, Matsumara M, Sadato N. Removing the effects of task-related motion using independent-component analysis. NeuroImage. 2005;25:802–814. doi: 10.1016/j.neuroimage.2004.12.027. [DOI] [PubMed] [Google Scholar]
- 27.Diedrichsen J, Shadmehr R. Detecting and adjusting for artifacts in fMRI time series data. NeuroImage. 2005;27:624–634. doi: 10.1016/j.neuroimage.2005.04.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Freire L, Mangin J-F. Motion correction algorithms may create spurious brain activations in the absence of subject motion. NeuroImage. 2001;14:709–722. doi: 10.1006/nimg.2001.0869. [DOI] [PubMed] [Google Scholar]
- 29.Barry RL, Klassen LM, Williams JM, Menon RS. Hybrid two-dimensional navigator correction: a new technique to suppress respiratory-induced physiological noise in multi-shot echo-planar functional MRI. NeuroImage. 2008;39:1142–1150. doi: 10.1016/j.neuroimage.2007.09.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Barry RL, Menon RS. Modeling and suppression of respiration-related physiological noise in echo-planar functional magnetic resonance imaging using global and one-dimensional navigator echo correction. Magn Reson Med. 2005;54:411–418. doi: 10.1002/mrm.20591. [DOI] [PubMed] [Google Scholar]
- 31.Nencka AS, Rowe DB. Reducing the unwanted draining vein BOLD contribution in fMRI with statistical post-processing methods. NeuroImage. 2007;37:177–188. doi: 10.1016/j.neuroimage.2007.03.075. [DOI] [PubMed] [Google Scholar]
- 32.Segebarth C, Belle V, Delon C, Massarelli R, Decety J, Le Bas J-F, Décorps M, Benabid AL. Functional MRI of the human brain: predominance of signals from extracerebral veins. NeuroReport. 1994;5:813–816. doi: 10.1097/00001756-199403000-00019. [DOI] [PubMed] [Google Scholar]
- 33.Menon RS. Postacquisition suppression of large-vessel BOLD signals in high-resolution fMRI. Magn Reson Med. 2002;47:1–9. doi: 10.1002/mrm.10041. [DOI] [PubMed] [Google Scholar]
- 34.Duvernoy HM. The Human Brain: Surface, Blood Supply, and Three-Dimensional Sectional Anatomy. 2nd ed. New York: Springer-Verlag; 1999. [Google Scholar]
- 35.Martin RE, MacIntosh BJ, Smith RC, Barr AM, Stevens TK, Gati JS, Menon RS. Cerebral areas processing swallowing and tongue movement are overlapping but distinct: a functional magnetic resonance imaging study. J Neurophysiol. 2004;92:2428–2443. doi: 10.1152/jn.01144.2003. [DOI] [PubMed] [Google Scholar]
- 36.Bruder H, Fischer H, Reinfelder H-E, Schmitt F. Image reconstruction for echo planar imaging with non-equidistant k-space sampling. Magn Reson Med. 1992;23:311–323. doi: 10.1002/mrm.1910230211. [DOI] [PubMed] [Google Scholar]
- 37.Cox RW. AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- 38.Klassen LM, Menon RS. Robust automated shimming technique using arbitrary mapping acquisition parameters (RASTAMAP) Magn Reson Med. 2004;51:881–887. doi: 10.1002/mrm.20094. [DOI] [PubMed] [Google Scholar]
- 39.LaConte S, Anderson J, Muley S, Ashe J, Frutiger S, Rehm K, Kai Hansen L, Yacoub E, Hu X, Rottenberg D, Strother S. The evaluation of preprocessing choices in single-subject BOLD fMRI using NPAIRS performance metrics. NeuroImage. 2003;18:10–27. doi: 10.1006/nimg.2002.1300. [DOI] [PubMed] [Google Scholar]
- 40.Hajnal JV, Myers R, Oatridge A, Schwieso JE, Young IR, Bydder GM. Artifacts due to stimulus correlated motion in functional imaging of the brain. Magn Reson Med. 1994;31:283–291. doi: 10.1002/mrm.1910310307. [DOI] [PubMed] [Google Scholar]
- 41.Friston KJ, Williams S, Howard R, Frackowiak RSJ, Turner R. Movement-related effects in fMRI time-series. Magn Reson Med. 1996;35:346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- 42.Field AS, Yen Y-F, Burdette JH, Elster AD. False cerebral activation on BOLD functional MR images: study of low-amplitude motion weakly correlated to stimulus. AJNR Am J Neuroradiol. 2000;21:1388–1396. [PMC free article] [PubMed] [Google Scholar]
- 43.Goodyear BG, Zhu H, Brown RA, Mitchell JR. Removal of phase artifacts from fMRI data using a Stockwell transform filter improves brain activity detection. Magn Reson Med. 2004;51:16–21. doi: 10.1002/mrm.10681. [DOI] [PubMed] [Google Scholar]