Electron traps and their effect on the surface chemistry of TiO₂(110)

Abstract

Oxygen vacancies on metal oxide surfaces have long been thought to play a key role in the surface chemistry. Such processes have been directly visualized in the case of the model photocatalyst surface TiO₂(110) in reactions with water and molecular oxygen. These vacancies have been assumed to be neutral in calculations of the surface properties. However, by comparing experimental and simulated scanning tunneling microscopy images and spectra, we show that oxygen vacancies act as trapping centers and are negatively charged. We demonstrate that charging the defect significantly affects the reactivity by following the reaction of molecular oxygen with surface hydroxyl formed by water dissociation at the vacancies. Calculations with electronically charged hydroxyl favor a condensation reaction forming water and surface oxygen adatoms, in line with experimental observations. This contrasts with simulations using neutral hydroxyl where hydrogen peroxide is found to be the most stable product.

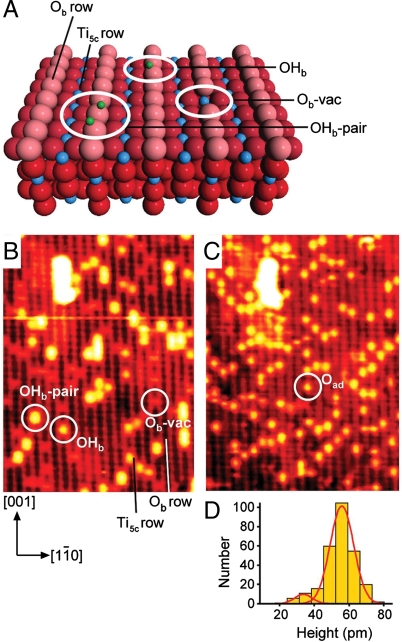
The rutile TiO₂(110) surface, which we use as a model photocatalytic system here, is displayed as a ball model in Fig. 1 A. It is characterized by alternate rows of fivefold coordinated Ti (Ti_5c) and bridging-O atoms (O_b) that run in the [001] direction. Fig. 1 B shows a typical scanning tunneling microscopy (STM) image of the surface. The Ti_5c rows appear bright, and the O_b rows appear dark. Point defects are common on this surface, the vast majority being O_b vacancies (O_b-vac) and surface hydroxyls (OH_b). As can be seen in Fig. 1 B, these defects appear as bright spots between the bright Ti_5c rows. O_b-vac are known to be particularly reactive, with STM images providing compelling evidence that O₂ dissociates at O_b-vac (1, 2) leaving a healed vacancy and one oxygen adatom (O_ad) on Ti_5c according to ref. 3:

[1]

where the reduction of one oxygen atom of O₂(g) to one bridging oxide species (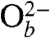) is accomplished by oxidation of the two Ti³⁺ sites associated with O_b-vac to Ti⁴⁺ (3), on the basis of a purely ionic model. (Formal charges are written in reactions 1 and 2 to highlight the redox processes involved.)

Fig. 1.

Reaction of O₂ with TiO₂(110). (A) Ball model of TiO₂(110). Red and blue spheres denote O and Ti, respectively. The pink spheres are bridging O atoms, which lie in the [001] azimuth of the substrate. Parallel Ti rows that lie between the bridging-O rows are fivefold coordinated Ti atoms. Green spheres indicate H atoms (from OH_b). (B) 130 × 170 Å ² STM image (V = 1.5 V, I = 0.25 nA) of an as-prepared TiO₂(110) surface that contains O_b-vac and OH_b. OH_b forms from dissociation of water from the residual vacuum at O_b-vac. An O_b-vac, an OH_b, and an OH_b pair are indicated. (C) The surface in B after exposure to ∼90 L O₂ at 300 K. One of the bright spots assigned to O_ad is circled. B and C have been smoothed using Image SXM (12) v.1.75. (D) A histogram showing the height distribution of 276 bright spots found on the Ti_5c rows fitted to two Gaussian curves. The data are taken from an unsmoothed, larger version of the image in C. The histogram indicates that the reaction products are almost entirely from one species.

The interaction of O₂ with OH_b, on the other hand, is still a matter of controversy. Following the reaction of these species at temperatures ≤ 240 K, water is seen to desorb at ∼310 K in temperature programmed desorption (TPD) spectra (3, 4). Henderson et al. (3) concluded that this water evolution is a consequence of the formation of oxygen adatoms (O_ad) at the surface as follows:

[2]

where the two Ti³⁺ species provide the two electrons necessary to reduce one oxygen atom of O₂(g) to H₂O(g) (3). In stark contrast to the TPD results, previous calculations find H₂O₂ to be by far the most stable product (5). Moreover, on the basis of these calculations, water desorption is not expected up to the highest temperature computed, 350 K (5). This discrepancy provided the initial motivation for the present work.

Results and Discussion

We use STM to provide an additional experimental test of the picture that has emerged thus far. Fig. 1 B shows a surface containing both O_b-vac and OH_b, alongside the same surface in Fig. 1 C after it was exposed to 90 Langmuirs (L) O₂ at 300 K (1 L = 1.33 × 10^-6 mbar·s, 1 mbar = 100 Pa). A number of small, bright spots can be seen on the Ti_5c sites (bright rows) in the latter image. The histogram of the height distribution of these bright spots, shown in Fig. 1 D, indicates that these bright spots are almost entirely due to one final product.

It should be noted that at lower O₂ exposures we see a number of different types of species on Ti_5c rows that are likely to arise from terminal hydroxyls (OH_t) and other metastable species such as O₂H. These latter results are consistent with previous work (4, 6).

Analysis of the images in Fig. 1 shows that before the reaction with O₂ there were about 72 OH_b species and 38 O_b-vacs. Following the reaction with O₂, about 118 new bright spots are seen on the bright Ti_5c rows in Fig. 1 C. As it is well known that O_ad form after exposure of O_b-vac to O₂ (1, 2, 7 –9), we conclude that O_ad also forms from exposure of OH_b to O₂, in line with the conclusions of Henderson et al. (3). Moreover, the availability of only 72 H atoms rules out the possibility that the products in the present case are OH_t (4, 6).

There is, however, a subtle but crucial discrepancy between our observations and the conclusions of Henderson et al. (3). With a starting point of 38 O_b-vacs and 72 OH_b, we would expect each O_b-vac to yield one O_ad (reaction 1) and each OH_b to yield half an O_ad (reaction 2), i.e., only 74 O_ad in total compared to the 118 found in the experiment. Because the availability of electrons from reduced TiO₂ is a prerequisite for O₂(g) dissociative adsorption on TiO₂(110) (3, 5), the extra O_ad found in Fig. 1 C require the TiO₂ sample to supply more electrons than expected on the basis of the number of O_b-vac (2Ti³⁺) and OH_b (1Ti³⁺) initially present.

Thus, the assignment of the adsorbates in Fig. 1 C to O_ad and the interpretation of TPD results (3) challenge the current theoretical understanding of the surface chemistry of TiO₂(110). Even using a hybrid HSE06 approach (10, 11), which is expected to describe more accurately than other functionals the electronic structure of metal oxides, we also predict that H₂O₂ is overwhelmingly the most stable product of the reaction between O₂ and OH_b. This result, which is inconsistent with the TPD data, mimics that found in previous simulations (5).

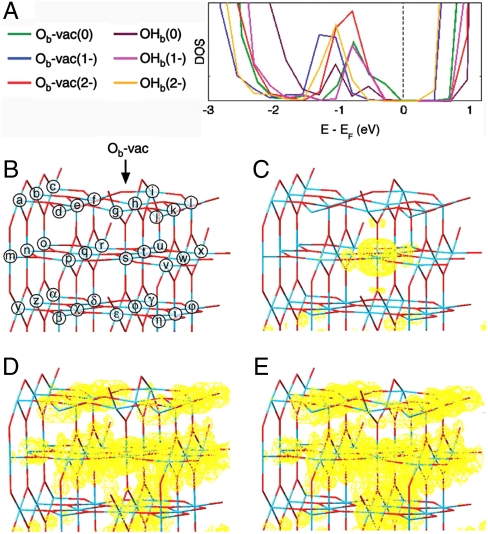
It turns out that we can only model O_ad as the most stable product when we allow excess electronic charge to accumulate at the O_b-vac and OH_b (see Fig. 2), the latter being formed by reaction of water molecules with O_b-vac. The presence of extra electrons at O_b-vac/OH_b originates from occupation of additional 3d electron states arising from polaronic distortion at both O_b-vac and OH_b sites. As we discuss later, the excess electronic charge is not pinned directly at the O_b-vac but is rather found localized at a number of reduced Ti sites around the vacancy (see also Fig. S1). High affinities for both surface and bulk electron polaron trapping have been reported for substrates such as HfO₂ (13) and SiO₂ (14). This has been used to explain a number of surface properties, such as SiO₂ discharge phenomena, although not the surface chemistry.

Fig. 2.

Calculated electronic structure of O_b-vac and OH_b. (A) The total density of states for the optimized layers in the presence of different amounts of extra electronic charge. (B) The TiO₂(110) surface shown as a stick model where the blue intersections indicate Ti sites and the red intersections indicate O sites. The arrow points at the O_b-vac and each Ti atom is labeled. The global charge density of the BGS is shown in yellow (10^-6 e Å ^-3) for O_b-vac(0), O_b-vac(1 - ), and O_b-vac(2 - ) in C, D, and E, respectively.

Various spectroscopies suggest that O_b-vac introduces electronic states into the band gap about 1 eV below the conduction band (CB) onset (3, 15, 16). These band gap states (BGS) are known to have d character (15). The BGS persist even when the O_b-vac are replaced with OH_b formed by water dissociation at the O_b-vac (3, 15). In our calculations, regardless of the number of electrons occupying the BGS [2 electrons (e) for O_b-vac(0), 3e for O_b-vac(1 - ), 4e for O_b-vac(2 - ), 1e for OH_b(0), 2e for OH_b(1 - ), 3e for OH_b(2 - )] we find that the energy remains close to 1 eV below the CB onset (Fig. 2 A). The extra electrons, however, drastically affect the spatial distribution of the associated 3d electronic density. While for O_b-vac(0), the simulations suggest a subsurface localization immediately beneath the defect site (Ti_s in Fig. 2 B), the presence of one and two extra electrons induces an electronic reorganization that moves electronic charge away from the O_b-vac site and the corresponding O_b row (see Fig. 2 D and E). In line with other hybrid DFT results for O_b-vac in high-k dielectrics (13, 17), an analysis of the O_b-vac induced changes in the global electronic distribution reveals symmetry breaking at the defect site (details are shown in Fig. S2). This is discussed in more detail below.

We now consider the possible origin of the additional electronic charge. Given the ease of electron transfer in TiO₂ (18, 19) with reported barriers as low as 0.09 eV and mobilities as high as 5.24 × 10^-2 cm² V^-2 s^-1, it is reasonable to expect interstitial Ti (Ti_int)-donated electrons to diffuse comparatively freely within the system (20). To test the hypothesis that they will, in this case, diffuse toward the O_b-vac/OH_b sites at the surface, we also modeled a much larger unit cell (8 trilayers) with inclusion of one initially neutral Ti_int atom. The increased size of the simulated systems here (288 atoms for the clean slab) prevent us from applying HSE06 so we chose instead to use a local spin density approximation (LSDA) + U scheme already successfully applied to O_b-vac on TiO₂(110) (21).

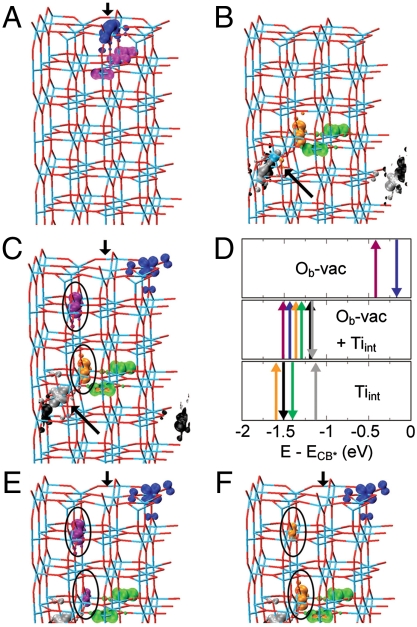
Fig. 3 shows the BGS spatial distribution for O_b-vac both isolated and in the presence of one Ti_int. Recently, Ti_int species have been suggested as the main origin of titania BGS (9) with negligible importance of O_b-vac (or OH_b) sites. In contrast, our results shown in Fig. 3 C and D demonstrate that a combination of Ti_int and O_b-vac induce new BGS. For isolated O_b-vac, the BGS (and the associated Ti³⁺ sites) are symmetrically localized at or immediately beneath the defect site (Fig. 3 A). For one isolated Ti_int (Fig. 3 B), the calculations suggest an asymmetric localisation of the BGS at the Ti_int site (one state) and on other separate, regular lattice Ti sites across the slab. Following refs. 22 and 23, we assign the appearance of localized BGS, and the ensuing local rehybridization to the chemical reduction of specific Ti sites from their stoichiometric oxidation state (i.e., reduction from Ti⁴⁺ to Ti³⁺ in an oversimplified ionic model).

Fig. 3.

Electronic charge density distribution (10^-5 e Å ^-3) for the BGS of the considered 8 trilayer systems. (A) O_b-vac, (B) one Ti_int between the fourth and fifth trilayers, (C) O_b-vac modeled together with one Ti_int between the fourth and fifth TiO₂(110) trilayers (O_b-vac + Ti_int). Blue intersections indicate Ti atoms and red intersections O atoms. Ti_int is shown as a blue sphere. The positions of O_b-vac and Ti_int are marked by the black arrows. Different colors have been used to distinguish between Ti_int-donated (black, gray, green, orange), and surface O_b-vac induced (purple, blue) BGS. (D) Single-state energy level diagram with respect to the CB onset (E-E _CB^∗ = 0) for the BGS in A–C after vacuum level electrostatic alignment. Up and down arrows refer to the modeled spin of the specific state. The same BGS color labelling has been used for all the displayed A–F panels. (E and F) For clarity, the hybridized BGS of O_b-vac + Ti_int (orange and purple) circled in C, are redisplayed with the omission of the orange in E and purple in F BGS.

Upon consideration of an O_b-vac together with one Ti_int, coupling between the vacancy site and the Ti_int-donated electrons is evidenced by the large changes in the BGS eigenvalues (Fig. 3 D). By comparing the formation energies of an isolated O_b-vac (+5.11 eV) and a Ti_int-coupled vacancy (+2.72 eV), the simulations suggest a net stabilization of 2.39 eV for O_b-vac within the adopted simulation cell. The concentration of Ti_int modeled is about an order of magnitude higher than experimental estimates from the literature (20). This allows us to capture the qualitative behavior but prevents us from addressing quantitatively the number of electrons globally transferred to the surface. Given that the Ti_int concentration simulated is about an order of magnitude greater than experimental estimates (20), this coupling should be even more favorable in reality because the electrostatic repulsion between BGS is expected to be much lower.

This BGS coupling drastically affects both the energy and, as was the case for the HSE06 modeling for O_b-vac(2 - ) (Fig. 2), the spatial distribution of the BGS of O_b-vac. The presence of Ti_int-donated BGS induces an electronic reorganization that moves electronic charge away from the vacancy site and the corresponding O_b row (Fig. 3 C). Note that this is a different role for Ti_int than that claimed in an earlier study, where electronic states associated with Ti_int were responsible for the BGS (9).

Analysis of the individual BGS for the coupled systems provides insight into how the Ti_int-donated electrons couple to O_b-vac sites. As shown in Fig. 3 C–F, when Ti_int-donated electrons are modeled together with O_b-vac, hybridization between specific BGS (circled in Fig. 3 C, E, and F) make Ti_int-donated electrons available at the O_b-vac site thus locally charging O_b-vac with the extra electrons necessary to account for the additional O_ad imaged in Fig. 1 C. The same mechanism is also found for the interaction of Ti_int-donated electrons with OH_b. In this case, comparison between the formation energies of OH_b (+0.32 eV) and OH_b/Ti_int (-1.05 eV) suggests a net stabilization of 1.37 eV. As with the O_b-vac/Ti_int system, the Ti_int electronic surplus is also characterized by symmetry breaking and hybridization between specific BGS (circled in Fig. S3).

Although we are unable to address directly the number of electrons globally transferred to the surface, we can make estimates based on the upper limit of reported Ti_int concentration: 2 × 10¹⁹ cm^-3, i.e., one per 800 TiO₂ unit cells (20). In our estimation, we assume typical O_b-vac/OH_b defect concentrations of 5 × 10¹³ cm^-2 on a 1.0 × 0.5 × 0.1 cm³ sample, and we consider that each Ti_int generates four Ti³⁺ sites (Fig. 3 B and ref. 24). This means that to singly (doubly) charge O_b-vac/OH_b would only require the participation of 0.0017% (0.0034%) of the global number of Ti_int-donated electrons.

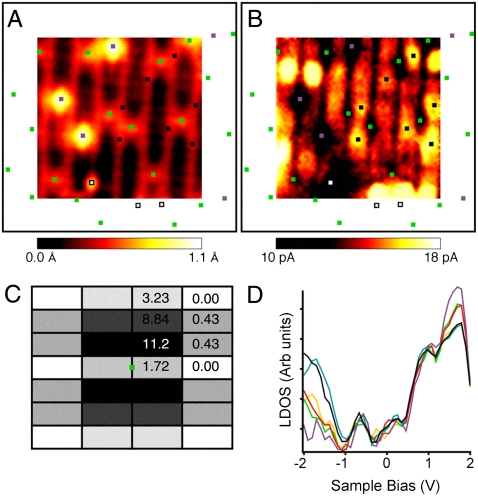
To further validate our model of the electronic structure, we probed the electronic charge distribution associated with O_b-vac experimentally using scanning tunneling spectroscopy (STS) at ∼5 K. This low temperature was chosen to deliberately freeze out polaronic hopping effects that are thought to average out asymmetries that are predicted to arise at 0 K (17, 18, 25). During the acquisition of the STM image shown in Fig. 4 A, the tip was immobilized at each point of the scan while tunneling current versus bias voltage (I-V) spectra were recorded. This method of recording I-V spectra alongside STM images is known as current imaging tunneling spectroscopy (CITS) (16), and it allows the I-V spectra to be displayed as current maps at each voltage.

Fig. 4.

Experimental STM and STS data. (A) (44 Å)² STM image recorded simultaneously with the STS. (B) (44 Å)² CITS current map at -2 V. The squares in A and B show the positions of O_b-vac (green), OH_b (purple), and some bright features associated with O_b-vac (black). One impurity is also present and marked with a white square. Using a larger-scale image, the positions of O_b-vac, OH_b, and other impurities outside the area imaged in A and B are also indicated. A and B have been smoothed using Image SXM (12) v.1.75. (C) A correlation map between O_b-vac and bright features in B. The center of the map represents the position of an O_b-vac shown as a green square. The black rectangles represent unit cells centered on Ti_5c atoms that surround O_b-vac. The results are averaged between the four quadrants with the numbers shown only in one quadrant. The results are expressed as percentages that add to 100% when the numbers in all four quadrants are summed. The darker the shading, the greater the probability of finding a bright feature at the separation indicated by the map. (D) STS spectra represented as LDOS plots by plotting (dI/dV) × (V/I) vs V (26). The LDOS plots are taken from the bright features associated with O_b-vac (black), O_b-vac (green), OH_b (purple), Ti_5c (yellow), and O_b (red). Each curve is averaged from 180 individual spectra taken from the CITS set shown in this work and another 180 individual spectra taken from an equivalent CITS set recorded in an identical area of the surface. The black squares in A and B indicate which bright features contribute to the curves for bright features associated with O_b-vac; none were counted when they were also diagonally adjacent to OH_b or in close vicinity to impurities.

The STM image in Fig. 4 A was acquired at a sample bias of +2 V with a tunneling current of 0.03 nA. It clearly shows both OH_b and O_b-vac as bright spots between bright Ti_5c rows. The current map at +2 V has a similar appearance to the STM image, as one would expect. However, the current map at -2 V (Fig. 4 B) has a very different appearance. O_b-vac and OH_b both appear as dark spots centered between two bright rows. Bright features can be seen on the bright Ti_5c rows and a correlation analysis (Fig. 4 C) shows that these lie diagonally adjacent to the O_b-vacs in the positions of the second nearest Ti_5c neighbors. Each O_b-vac tends to be surrounded by one or two brighter features rather than four equally bright features. Fig. 4 D shows normalized conductance spectra (dI/dV) × (V/I) that approximate the local density of states. Each curve represents an average of 360 spectra corresponding to the bright features, O_b-vac, OH_b, Ti_5c, and O_b. Similar spectra were recorded using the same tip with the tunneling current set between 0.015 nA and 0.7 nA. We also recorded some spectra using an iridium tip. In neither case did we observe a shift of features, which suggests that the effect produced by tip-induced band-bending is negligible. These STS data are in broad agreement with recently reported 78 K results (27).

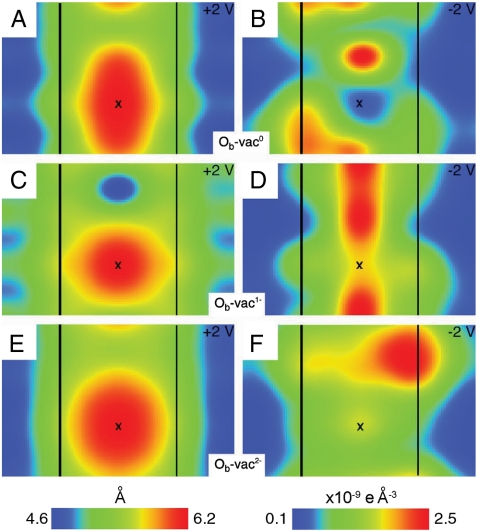
Fig. 5 shows our STM and current map simulations of O_b-vac at +2 V and -2 V, respectively. These are derived from the HSE06 density of states. The simulations at +2 V are similar to each other, the highest current being found at the O_b-vac (Fig. 5 A, C, and E). In contrast, the simulations at -2 V are strongly dependent on the O_b-vac charge. For both O_b-vac(0) and O_b-vac(1 - ), the highest current is found in a spot (or spots) directly in line with the bridging O row, inconsistent with the experimental contrast. The experimental distribution of the defect states is only reproduced in simulations of O_b-vac(2 - ) where the highest current is found on a second nearest Ti_5c neighbor with little current along the O_b row. The current map for O_b-vac(2 - ) at -2 V was deconstructed by separating the contributions into “slices” with energy windows of 0.2 eV (Fig. S4). In this way, we find that the asymmetry originates between energies of 1.1 and 1.5 eV, with the majority signal between 1.1 and 1.3 eV. This identifies the asymmetry in the current map with the BGS introduced by O_b-vac(2 - ). This asymmetry is not observed in data recorded at 78 K (27). Presumably this arises because of significant polaronic hopping of the type recently identified at room temperature (25).

Fig. 5.

Modeled STM and CITS appearance for O_b-vac. Simulated STM images (+2 V, 10^-7 e Å ^-3) and current maps (-2 V, same height above the surface as from the corresponding left-side topography) are shown for O_b-vac(0) in A and B, for O_b-vac(1 - ) in C and D, and for O_b-vac(2 - ) in E and F. Ti_5c rows are indicated by black lines, and an X marks the O_b-vac. STM simulations were performed with a tip-surface distance of ∼5 Å [the detailed procedure can be found in ref. (28)].

STM and current map simulations based on the LSDA + U treatment of Ti_int/O_b-vac introduced above (Fig. 3 C) also fit the experimental results well. The asymmetry can again be traced to the BGS of O_b-vac, in this case coupled to the Ti_int donated electrons (Fig. S5, S6).

We are now in a position to reexamine the theoretical description of the reactivity of O₂ with O_b-vac and OH_b in the presence of Ti_int-donated electron surplus. The use of the HSE06 (10, 11) approach allows us to accurately describe the relative energies of molecular H₂O(g), O₂(g), H₂(g). Consequently, the level of accuracy of the calculated chemical potential and then the grand-canonical formation energies are expected to be sufficiently high to quantitatively address the thermodynamic stability of the considered systems (SI Text, Table SI).

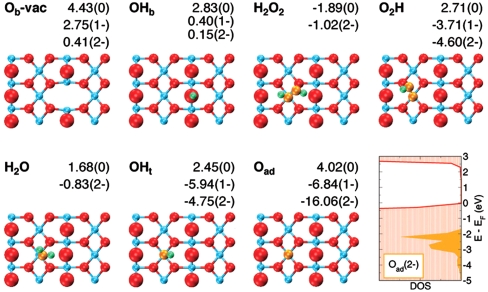
To match with our STM experiments, we use the results of our calculations from a simulated temperature of 300 K, but we note that the same trends are found at a large range of temperatures around 300 K. The formation energies of the pertinent adsorbates (H₂O₂, H₂O, O₂H, OH_t, and O_ad) are shown in Fig. 6 alongside those for O_b-vac and OH_b. We stress that owing to the necessity of enforcing a compensating background in the simulation cells, only relative energy differences for one specific charge state can be meaningfully compared. To illustrate this point, the energy of H₂O₂(2 - ) can be compared with O_ad(2 - ) or O₂H(2 - ) but not with H₂O₂(0) or O_ad(0).

Fig. 6.

Plan view of surface species together with their grand-canonical formation free energies (T = 300 K, P _O2 = 1.3 × 10^-8 mbar, P _H2O = 1 × 10^-11 mbar). Ti is shown blue, lattice O red, O from adsorbates orange, and H green. Bridging oxygen (O_b) atoms are shown larger to highlight them. The energies are in eV and the brackets after the energies indicate the electronic charge of the surface species. Geometries are optimized (3 × 2 supercell) for the neutral state. The total density of states for the optimized layers (filled red) of O_ad(2 - )/TiO₂(110) is displayed together with the O_ad(2 - )-projected density of states (PDOS, filled orange) in the bottom-right panel.

The calculations indicate that when O₂ reacts with O_b-vac(2 - ) (ΔG_f = 0.41 eV), O₂ dissociates, filling the vacancy and forming one O_ad(2 - ) (ΔG_f = -16.06 eV) with ΔG = -16.47 eV [O_b-vac(2 - ) + O_b(g) → O_ad(2 - ) + O_b], consistent with experiments (1, 2). As for the reaction of O₂ with OH_b, we find that whereas formation of O₂H(2 - ) from OH_b(2 - ) is spontaneous (OH_b(2 - ) + O₂(g) → O₂H(2 - ) + O_b, ΔG = -4.75 eV), the formation of H₂O₂(2 - ) (ΔG_f = -1.02 eV) is strongly unfavoured with respect to O_ad(2 - ) (ΔG_f = -16.06 eV). Thus the reaction between O₂ and OH_b must take place via formation of O₂H(2 - ) that, as with other O_xH_y(2 - ) intermediates, eventually reacts to form O_ad(2 - ). O₂ acts to scavenge all the initially available electron excess. Consistent with available spectroscopic data (3, 9, 15) where exposure to O₂ quenches the BGS, sample oxidation in the calculation is accompanied by removal of Ti³⁺ BGS and localisation of O_ad(2 - ) states in the valence band, VB (Fig. 6). Similar results are obtained by simulating one Ti_int in the presence of two O_ad, as shown in Fig. S7. No BGS are found associated with the O_ad; instead the electronic charge density contributes to the lattice VB. A Bader charge analysis reveals a difference of 10% between the modeled atomic charges of these O_ad products (0.9e) and the bridging O_b atoms (1e), thus highlighting the same oxide hybridization (22, 23) for both species in the simulation cell.

Hence, by accounting for TiO₂(110) surface-trapped electron-polarons, and the ensuing increase in the actual number of Ti³⁺ species available at the surface, the experimentally observed formation of O_ad from the reaction of O₂ with OH_b can be correctly described by theory. Furthermore, the same electron traps could be involved in trapping photogenerated electrons with potential implications for the photocatalytic activity of the surface. We expect that electron trapping will be important in dictating the reaction pathways on other dielectric metal oxide surfaces. This will have important consequences in areas such as corrosion, catalysis, and microelectronics.

Methods

Experimental.

O₂ reactions were performed at room temperature with a variable temperature Omicron ultra high vacuum (UHV) STM. STS measurements employed a liquid helium bath cryostat Omicron UHV STM in order to maximize stability. CITS were imaged with 100 × 100 pixels, the component I-V spectra comprising 40 equally spaced points between +2 and -2 V. Positive bias indicates tunneling into empty sample states, with negative bias corresponding to tunneling out of filled sample states. Tungsten tips were always used unless otherwise stated. Standard sample preparation procedures were employed that are described elsewhere (1).

Computational.

Grand-canonical (μVT) formation energies (29) were calculated within a DFT-PAW approach implemented in the VASP program (30). LSDA + U simulations were carried out on the basis of 3 × 2 8 trilayers (8L) slabs with a local U_eff = 5.5 eV correction for Ti atoms, as suggested from embedded cluster configuration interaction results (21). As for the smaller 3 × 2 4 trilayer (4L) slabs, exchange and correlation terms were calculated at PW91-GGA (31) level for geometrical relaxation and on a hybrid HSE06 (10, 11) basis for final single point calculations and STM simulations. Ti 3p and 3s semicore states were treated as valence states. A 3 × 4 × 1 (Γ only) special k-points grid, 15 Å vacuum range, and 400 eV plane-wave energy cutoff were used for all the 4L (8L) simulations. The Γ-only finite sampling error on BGS dispersion (8L) was found to be converged within 0.1 eV against the finer 3 × 4 × 1 grid. The two (six) topmost trilayers and the adsorbates were relaxed to maximum atomic forces of 0.01 e Å ^-1. Spin polarization was enforced accounting for the number of extra electrons and optimising for the highest spin multiplicity.

As in previous investigations (28), STM and STS simulations were performed with a Tersoff-Hamann approach (32) implemented in the bSKAN program (33). The calculated HSE06 Fermi energy was used as the zero voltage point.

Bader charge analysis (34) was carried out on the basis of the total charge density i.e. accounting for both the electronic and ionic core charge.