A COMPARISON OF METHODS FOR IDENTIFYING THE JACOBIAN FOR UNCONTROLLED MANIFOLD VARIANCE ANALYSIS

Abstract

Uncontrolled Manifold (UCM) analysis has been used to identify a component of joint variance leading to pointer-tip position variability and a component representing motor abundant joint combinations corresponding to an equivalent hand position. A Jacobian is required for UCM analysis, typically derived from an analytic model relating joint postures to pointer-tip position. Derivation of the Jacobian is often non-trivial, however, because of the complexity of the system being studied. In this article, we compared the effect of different methods of deriving the Jacobian on results of UCM analyses during reaching. Jacobian matrices were determined at each percentage of the reach across trials using one of the three methods: (M1) partial derivatives of the geometric model relating ten joint postures, segment lengths and pointer length to the position of a hand-mounted pointer tip; or (M2–M3) as the coefficients of linear regression between the ten joint postures and either (M2) the pointer tip position measured directly from motion capture or (M3) the pointer-tip position estimated from the geometric model. For all methods, motor abundant joint variance (V_UCM) was larger than joint variance leading to a variable pointer-tip position (V_ORT). Results did not differ among methods prior to the time of peak velocity. Thereafter, M2 yielded lower V_ORT and slightly higher V_UCM compared to M1. Method M3 was used to disambiguate the possible effect of estimating model parameters for the geometric model on the M1–M2 comparison. The advantages of the use of linear regression method in the UCM approach are discussed.

1. Introduction

The Uncontrolled Manifold (UCM) hypothesis proposes that the nervous system takes advantage of abundant degrees of freedom (DOF) when performing motor acts (Scholz & Schöner, 1999; Schöner, 1995). The UCM method recently was used to investigate reaching to targets with a hand-mounted pointer, involving ten joint DOFs (Freitas et al., 2007; Freitas and Scholz, 2009). Across-trials joint variance at each percentage of the reach was partitioned into a component reflecting the use of motor abundant joint combinations to achieve the same pointer-tip position (variance within the UCM, V_UCM) and a component leading to different pointer-tip positions (variance orthogonal to the UCM, V_ORT). Significantly greater V_UCM than V_ORT indicated that motor abundance was used to achieve the required pointer-tip position.

This ‘typical’ UCM analysis requires an analytic model of the Jacobian derived from a geometric model relating joint postures and segment and pointer lengths to the pointer-tip position. The null space of this Jacobian provides a linear estimate of the UCM, a subspace in joint space where changes in the joint configuration have no effect on the pointer-tip position. Although a formal geometric model exists in most situations, it may be too complex to analytically solve for the null space in some contexts, e.g. if additional constraints need to be considered as when the hand is fixed on an external object that limits some hand orientations.

Analytical estimation of a Jacobian for elemental variables other than joint angles (e.g. muscle firing patterns) also is non-trivial. To overcome this problem, for example, the Jacobian has been estimated by linear regression between the EMG patterns and a task-level variable such as the center of foot pressure (Krishnamoorthy, Latash, Scholz, & Zatsiorsky, 2003) or moments of force (Krishnamoorthy, Scholz, & Latash, 2007).

A recent analysis investigated the use of a regression approach to derive the Jacobian in the space of joint angles and found equivalent UCM results compared to those obtained using an analytically derived (Freitas, Scholz, & Latash, in submission). However, the task involved only three planar joint angles, making unclear whether a regression approach would be as consistent when analyzing more complex three-dimensional (3D) tasks where a regression approach could have more value. We investigate this question here by analyzing a 3D, ten joint DOF reaching task. Initially, results of UCM analysis using a Jacobian derived with the typical analytic approach (M1) were compared with results using a Jacobian derived from linear regression of joint angles on the measured pointer-tip position obtained from motion analysis (M2). Those results were comparable, although a slight discrepancy was found late in the trajectory. To investigate whether this discrepancy was due to estimation errors of parameters required for the geometric model, the regression approach was repeated but using the pointer-tip position estimated from the geometric model (M3). The results suggest that the regression approach to estimating the Jacobian is a reasonable alternative when investigating complex movement tasks and may also have advantages when accurate estimates of geometric model parameters are difficult.

2. Method

Eleven right-hand-dominant adults, averaging 26.5 (± 10.5) years old, 171 (± 11) cm in height, with 62 (± 4) cm arm lengths and weighing 66 (± 13) kg, participated in the study after giving informed written consent according to the Declaration of Helsinki.

Participants wore a hand splint with attached pointer. They sat in front a computer monitor placed at a distance corresponding to 95% of their extended arm length. Forty reaches were performed to a 1.5-cm diameter target “as fast and as accurately as possible” from a controlled initial arm posture (Freitas, Scholz, & Stehman, 2007).

A six-camera (M-13) VICON system tracked (120-Hz) movement of four reflective markers mounted on four rigid bodies placed on (1) the upper scapula, midway along the (2) lateral arm and (3) forearm, and (4) on the hand splint. The markers were low-pass filtered at 5-Hz with a bidirectional 2^nd order Butterworth filter in Matlab™. Individual markers were placed on the pointer tip, sternal notch, below the acromion, and medial and lateral sides of both elbow and wrist joints to estimate the joint centers. One static arm calibration trial was recorded with the arm extended forward. The positive axes of each joint coordinate system in this position pointed laterally (X), anteriorly (Y), and vertically upward (Z). Rotation matrices required to take rigid bodies at each sample of movement back into their position in the static calibration trial were estimated using the method of Söderkvist and Wedin (1993). Euler angles then were extracted from the product of the rotation matrices from adjacent segments to define three rotational DOFs each at the scapula and shoulder and two DOFs each at the elbow and wrist. Kinematic variables of each trial were time-normalized to 100% in 0.5% increments starting at movement onset and ending at movement termination, defined respectively as 3% and 5% of the peak velocity of the pointer-tip trajectory.

Across-trials UCM analyses were performed at each percentage of the reach. For method M1, the Jacobian (J̲) was computed analytically based on the geometric model relating the 10 joint postures to the 3D pointer-tip position (ṟ):

$$\begin{array}{l}\underset{¯}{r}={{\mathrm{R}}_{\theta \mathit{1}}}^{*}{{\mathrm{R}}_{\theta \mathit{2}}}^{*}{{\mathrm{R}}_{\theta \mathit{3}}}^{*}{\mathrm{P}}_1+\dots \hfill \\ {{\mathrm{R}}_{\theta \mathit{1}}}^{*}{{\mathrm{R}}_{\theta \mathit{2}}}^{*}{{\mathrm{R}}_{\theta \mathit{3}}}^{*}{{\mathrm{R}}_{\theta \mathit{4}}}^{*}{\mathrm{P}}_2+\dots \hfill \\ {{\mathrm{R}}_{\theta \mathit{1}}}^{*}{{\mathrm{R}}_{\theta \mathit{2}}}^{*}{{\mathrm{R}}_{\theta \mathit{3}}}^{*}{{\mathrm{R}}_{\theta \mathit{4}}}^{*}{{\mathrm{R}}_{\theta \mathit{5}}}^{*}{\mathrm{P}}_3+\dots \hfill \\ {{\mathrm{R}}_{\theta \mathit{1}}}^{*}{{\mathrm{R}}_{\theta \mathit{2}}}^{*}{{\mathrm{R}}_{\theta \mathit{3}}}^{*}{{\mathrm{R}}_{\theta \mathit{4}}}^{*}{{\mathrm{R}}_{\theta \mathit{5}}}^{*}{{\mathrm{R}}_{\theta \mathit{6}}}^{*}{\mathrm{P}}_4+\dots \hfill \\ {{\mathrm{R}}_{\theta \mathit{1}}}^{*}{{\mathrm{R}}_{\theta \mathit{2}}}^{*}{{\mathrm{R}}_{\theta \mathit{3}}}^{*}{{\mathrm{R}}_{\theta \mathit{4}}}^{*}{{\mathrm{R}}_{\theta \mathit{5}}}^{*}{{\mathrm{R}}_{\theta \mathit{6}}}^{*}{{\mathrm{R}}_{\theta \mathit{7}}}^{*}{\mathrm{P}}_5+\dots \hfill \\ {{\mathrm{R}}_{\theta \mathit{1}}}^{*}{{\mathrm{R}}_{\theta \mathit{2}}}^{*}{{\mathrm{R}}_{\theta \mathit{3}}}^{*}{{\mathrm{R}}_{\theta \mathit{4}}}^{*}{{\mathrm{R}}_{\theta \mathit{5}}}^{*}{{\mathrm{R}}_{\theta \mathit{6}}}^{*}{{\mathrm{R}}_{\theta \mathit{7}}}^{*}{{\mathrm{R}}_{\theta \mathit{8}}}^{*}{\mathrm{P}}_6+\dots \hfill \\ {{\mathrm{R}}_{\theta \mathit{1}}}^{*}{{\mathrm{R}}_{\theta \mathit{2}}}^{*}{{\mathrm{R}}_{\theta \mathit{3}}}^{*}{{\mathrm{R}}_{\theta \mathit{4}}}^{*}{{\mathrm{R}}_{\theta \mathit{5}}}^{*}{{\mathrm{R}}_{\theta \mathit{6}}}^{*}{{\mathrm{R}}_{\theta \mathit{7}}}^{*}{{\mathrm{R}}_{\theta \mathit{8}}}^{*}{{\mathrm{R}}_{\theta \mathit{9}}}^{*}{\mathrm{P}}_7+\hfill \\ {{\mathrm{R}}_{\theta \mathit{1}}}^{*}{{\mathrm{R}}_{\theta \mathit{2}}}^{*}{{\mathrm{R}}_{\theta \mathit{3}}}^{*}{{\mathrm{R}}_{\theta \mathit{4}}}^{*}{{\mathrm{R}}_{\theta \mathit{5}}}^{*}{{\mathrm{R}}_{\theta \mathit{6}}}^{*}{{\mathrm{R}}_{\theta \mathit{7}}}^{*}{{\mathrm{R}}_{\theta \mathit{8}}}^{*}{{\mathrm{R}}_{\theta \mathit{9}}}^{*}{{\mathrm{R}}_{\theta \mathit{10}}}^{*}({\mathrm{d}}_{\mathrm{i}}+{\mathrm{I}}_{\mathrm{h}}),\hfill \end{array}$$ (1)

R_θi = rotation matrices associated with each joint axis; P_θi = translation vectors from the sternum marker (the base frame) to each joint center; d_i = distance from the sternum marker to the wrist joint; l_h = length from wrist to pointer marker. The mean joint configuration (θ̠₀) across trials at each percentage of the reach was used to estimate numerical values of J̲ for M1.

For the second method (M2), J̲ was estimated as coefficients of multiple linear regression between across-trials joint configurations and the measured pointer-tip position. The third method (M3) estimated J̲ from a regression between joint configurations and the pointer-tip position estimated from the geometric model, requiring estimates of the joint centers.

For each method (M_i={1,2,3}), the UCM was estimated as the null space (ε̠_ii) of each J̲.

$$0=\underset{¯}{\underset{¯}{J}}({\underset{¯}{\theta }}_{\mathit{0}}{)}^{*}{\underset{¯}{\epsilon }}_{\mathit{\text{ii}}}$$ (2)

At each percentage of the reach, deviations of each trial’s 10-dimensional joint configuration vector from the mean joint configuration (θ̠₀), Δθ̠ = θ̠ − θ̠₀, were projected parallel (θ̠_para = ε̠_i * Δθ̠) and perpendicular (θ̠_para − ε_i * Δθ̠) to the null space. The variance of the length of these projections was computed across the N-trials as:

$${\mathrm{V}}_{\text{UCM}}={(\mathit{n}-\mathit{d})}^{-1}\sum ({\displaystyle \sum _{i=1}^n{{\epsilon }_j}^{*}\mathrm{\Delta }\theta {)}^2/N}$$ (3)

$${\mathrm{V}}_{\text{ORT}}={\mathit{d}}^{-1}\sum (\mathrm{\Delta }\theta -{\displaystyle \sum _{i=1}^n{{\epsilon }_j}^{*}\mathrm{\Delta }\theta {)}^2/N}$$ (4)

where d=3 and n=7 are the number of dimensions of task space and of the UCM, respectively. V_UCM and V_ORT results obtained for each method were averaged across each 25% of the normalized reach duration for statistical purposes (repeated measures analysis of variance and linear regressions, p<0.05).

3. Results

All methods had V_UCM greater than V_ORT (e.g., Fig. 1A), which did not differ across methods early in the reach (p>0.05; Fig. 1C). After 50% of the reach, V_ORT was lower and V_UCM (Fig. 1B) was slightly higher for M2 (F(2,20)>15.72; p<0.002), while M1 and M3 did not differ (p>0.05).

Figure 1.

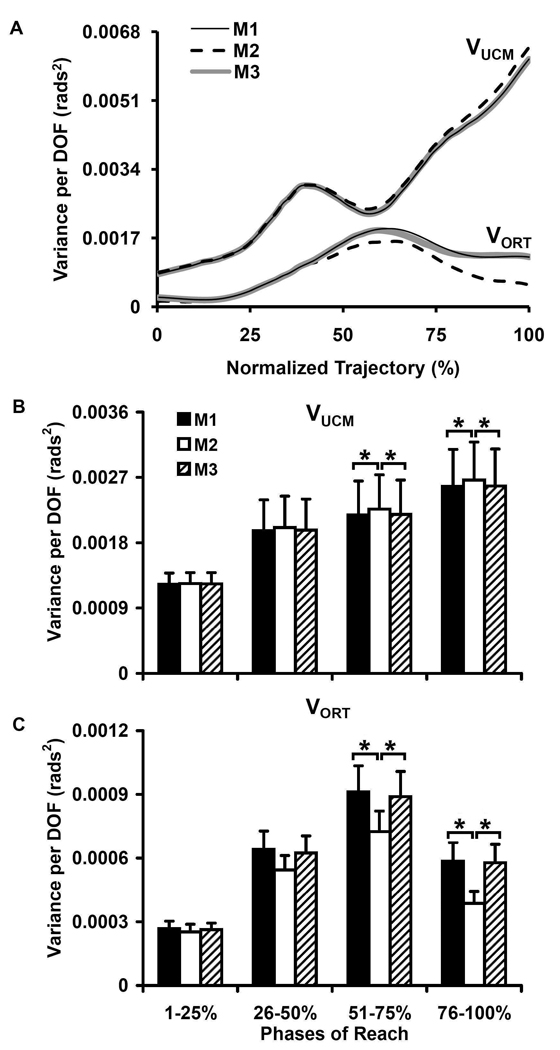
Time-series of V_UCM and V_ORT results for a representative participant (A) and V_UCM (B) and V_ORT (C) results averaged-across participants obtained from each method within four periods of the reaching trajectory. The asterisks represent statistical significant differences with a level of significance set at p<0.05.

Regression analyses between pairs of methods (Fig. 2) reveal excellent agreement between methods for estimating V_UCM (R² = 1) and V_ORT, although the regression coefficients were lower (R² > 0.86) when comparing M2 to either M1 or M3.

Figure 2.

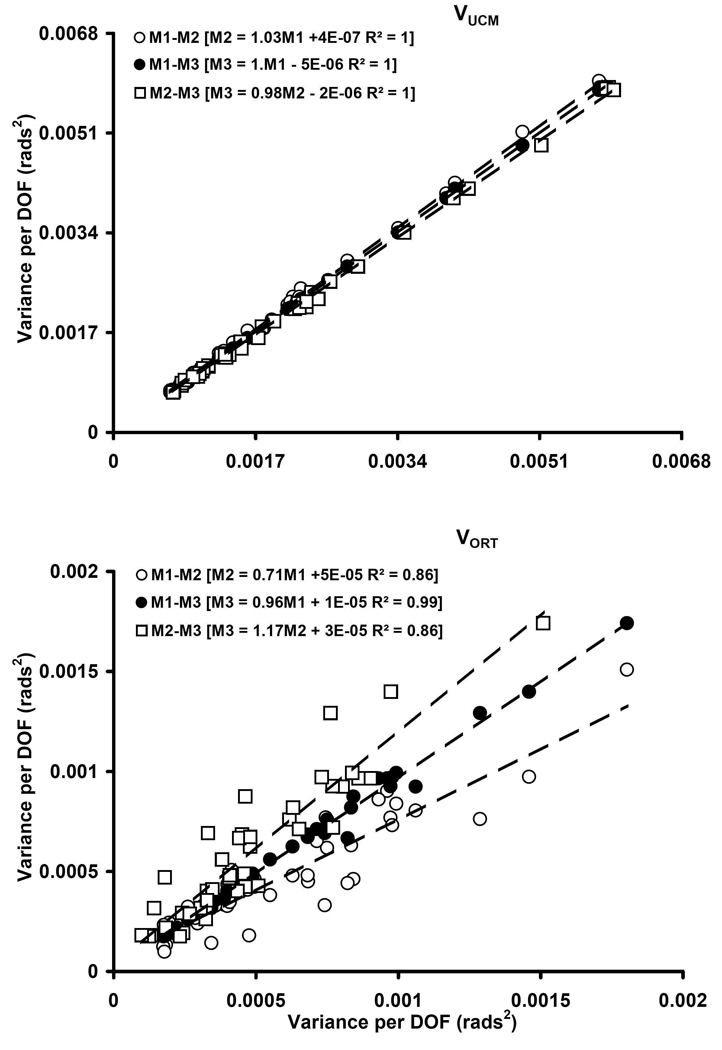
Regressions of V_UCM and V_ORT between each pair of methods for estimating the Jacobian based on values for all participants (white circles, M1–M2; black circles, M1–M3 and white squares, M2–M3).

4. Discussion

The main comparison of interest was between M1 (analytic estimate) and M2 (regression estimate) and resulted in excellent agreement for V_UCM (Figure 2, top panel) and V_ORT up to the time of peak velocity (Figure 1). After this time, however, V_ORT differed between the two approaches. Because the Jacobian was derived for M2 by regressing joint configurations on the measured pointer-tip position obtained from VICON, we hypothesized that the M1–M2 discrepancy could be due to errors in estimating the joint centers when using the geometric model (M1). This may be a particular problem for estimates of glenohumeral and clavicular joint centers. Errors in estimating the translation vectors also might be exacerbated when the arm is further extended because only a single marker was used to estimate these joint centers in the calibration position, and the sternum marker, the base frame, had a greater tendency to move slightly when the shoulder was more horizontally adducted.

We tested this hypothesis by using method M3, regressing the joint angles on the pointer-tip position estimated from the geometric model rather than its measured position. This analysis confirmed our hypothesis. Results for M1 and M3 were equivalent throughout the movement while both approaches differed significantly from M2 during the late phase of reaching. Thus, the discrepancy between M1 and M2 was not due to the regression approach but errors in estimating parameters for the geometric model. Thus, our findings suggest that a linear regression approach provides a reasonable alternative to the geometric model for identifying a Jacobian when it is difficult to define analytically in joint space and may even provide advantages over the geometric approach by reducing the influence of estimation errors. Further studies are required to determine if the same conclusion would apply to analyses performed in kinetic spaces.