Abstract
The commonly used simulation techniques, Metropolis Monte Carlo (MC) and molecular dynamics (MD) are of a dynamical type which enables one to sample system configurations i correctly with the Boltzmann probability, PiB while the value of PiB is not provided directly; therefore, it is difficult to obtain the absolute entropy, S ~ -ln PiB, and the Helmholtz free energy, F. With a different simulation approach developed in polymer physics, a chain is grown step-by-step with transition probabilities (TPs), and thus their product is the value of the construction probability; therefore, the entropy is known. Because all exact simulation methods are equivalent, i.e. they lead to the same averages and fluctuations of physical properties, one can treat an MC or MD sample as if its members have rather been generated step-by-step. Thus, each configuration i of the sample can be reconstructed (from nothing) by calculating the TPs with which it could have been constructed. This idea applies also to bulk systems such as fluids or magnets. This approach has led earlier to the “local states” (LS) and the “hypothetical scanning” (HS) methods, which are approximate in nature. A recent development is the hypothetical scanning Monte Carlo (HSMC) (or molecular dynamics, HSMD) method which is based on stochastic TPs where all interactions are taken into account. In this respect HSMC(D) can be viewed as exact and the only approximation involved is due to insufficient MC(MD) sampling for calculating the TPs. The validity of HSMC has been established by applying it first to liquid argon, TIP3P water, self-avoiding walks, and polyglycine models, where the results for F were found to agree with those obtained by other methods. Subsequently, HSMD was applied to mobile loops of the enzymes porcine pancreatic α-amylase and acetylcholineesterase in explicit water, where the difference of F between the bound and free states of the loop was calculated. Currently HSMD is being extended for calculating the absolute and relative free energy of ligand-enzyme binding. We describe the whole approach and discuss future directions.
Keywords: entropy, free energy, computer simulation, polymers, proteins
INTRODUCTION
The absolute entropy, S and the absolute Helmholtz free energy, F (F =E-TS, where E is the energy and T is the absolute temperature) are fundamental thermodynamic quantities which are important in all the physical sciences — chemistry, physics, engineering, and biology, but play a special role in structural biology. Thus, S - the measure of order, is the main driving force in protein folding and F — the criterion of stability, is essential for determining the structure and function of peptides, proteins, nucleic acids and other biological macromolecules. However, calculation of F and S by computer simulation is extremely difficult, and considerable attention has been devoted in the last 50 years to this subject. While significant progress has been made (see the reviews, Beveridge and DiCapua, 1989; Kollman, 1993; Jorgensen, 1989; Meirovitch, 1998; Gilson et al., 1997; Boresch et al., 2003; van Gunsteren et al., 2006; Meirovitch, 2007; Gilson et al., 2007), in many cases the efficiency (or accuracy) of existing methods is unsatisfactory and the need for new ideas has kept this field highly active.
The difficulty lies in the fact that the commonly used (exact) simulation methods, Metropolis Monte Carlo (MC) (Metropolis et al., 1953) and molecular dynamics (MD) (Alder and Wainwright, 1959; McCammon et al., 1977) are of a dynamical character. Thus, these methods enable one to sample system configurations i correctly with the Boltzmann probability, PiB, however, the value of PiB is not provided and S ~ -lnPiB is thus unknown,
| (1) |
where kB is the Boltzmann constant and Z is the partition function,
| (2) |
The problem is to calculate Z from a finite sample while Z is defined over the entire ensemble. This discussion, which is described in terms of a discrete system, also applies to an N-atom continuum system, where Ei is replaced by E(xN) (xN is a 3N vector of the Cartesian coordinates) and the summations become integrations.
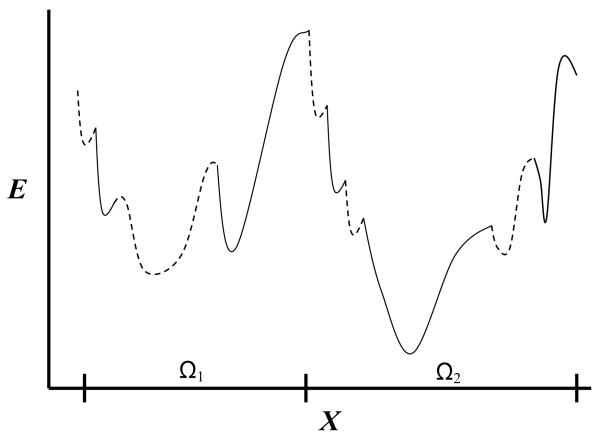
Calculation of F and S, which is difficult for any non-trivial system, becomes even more challenging in structural biology due to the inhomogeneity, flexibility, and strong long-range interactions characterizing bio-macromolecules such as proteins. The potential energy surface of a protein [E(xN)] is rugged “decorated” with a tremendous number of localized energy wells and ‘wider’ wells defined over regions, Ωm called microstates, where each wider well consisting of many localized ones (see Figure 1). A microstate Ωm, which constitutes only a tiny part of the entire conformational space, Ω (e.g., an α-helical region of a peptide) can in principle be represented by a local MD trajectory starting from a structure belonging to Ωm (however, this definition is not straightforward as discussed later). MD studies have shown that a molecule will visit the region of a localized well only for a very short time (several femtoseconds (fs)) while staying for a much longer time within a microstate (Stillinger and Weber, 1984; Elber and Karplus, 1987), meaning that the microstates are of a greater physical significance than the localized wells. Typically, one would seek to find the most stable microstates, i.e. those with the lowest free energy, Fm, Fm= − kBTlnZm= −kBTln∫mexp[−E/kBT]dxN, where the partition function Zm is integrated over Ωm (rather than over the entire space). The daunting task of protein folding is to identify the microstate with global minimum Fm.
Figure (1).
Schematic one-dimensional representation of part of the energy surface of a peptide or a protein, as a function of a coordinate X. The two large potential energy wells are defined over the corresponding microstates denoted Ω1 and Ω2. Each microstate consists of many localized potential wells denoted intermittently by solid and dashed lines. The partition function Zm of microstate m is obtained by integrating exp[−E/kBT] over Ωm where Fm = − kBT lnZm is the microstate’s free energy. The figure suggests that the second microstate is the more stable among the two due to lower energy and higher entropy (Ω2 is larger than Ω1) hence lower free energy. If F2 is also the global free energy minimum of a protein, Ω2 is expected to describe the native microstate (assuming a perfect force field) and a simulation started from Ω2 will keep the protein in this microstate for a long time. On the other hand, a peptide can populate significantly several of the most stable microstates in thermodynamic equilibrium.
Unlike protein folding, where the interest is in a single microstate, flexible protein segments (e.g. sidechains and surface loops), cyclic peptides and ligands bound to proteins can populate significantly several Ωm in thermodynamic equilibrium, which should be identified and their populations, pm = exp[−Fm/kBT] calculated. It is of interest to know whether the conformational change adopted by a loop (a sidechain, ligand, etc.) upon ligand binding has been induced by the ligand (induced fit, Getzoff et al., 1987; Rini et al.,1992) or alternatively whether the free loop interconverts among different microstates, one of which is selected upon binding (selected fit, Constantine et al.,1998). (Notice again that not only is the calculation of pm difficult, but also defining a microstate in the high-dimensional conformational space is not straightforward.) Finally, the free energy (typically of microstates) determines the binding affinity of protein—protein interactions, is an important factor in enzymatic reactions, electron transfer and ion transport through membranes.
CONVENTIONAL METHODOLOGIES FOR CALCULATING S AND F
In most cases one is interested in differences of free energy and entropy, ΔF and ΔS rather than in the absolute values themselves and the related methods can be divided into two classes, according to whether they provide the relative or the absolute F and S. Our review below covers only the commonly used techniques in these categories (for more information see for example, Meirovitch, 2007).
Thermodynamic integration
Differences ΔF and ΔS commonly calculated by thermodynamic integration (TI) over physical quantities such as the energy, temperature, and the specific heat, as well as non-thermodynamic parameters (other computational alchemy methods can also be included in this category; see, Beveridge and DiCapua, 1989; Kollman, 1993; Jorgensen, 1989; Meirovitch, 1998; Gilson et al., 1997; Boresch et al., 2003; Meirovitch, 2007; Gilson et al., 2007). This is a robust and highly versatile approach, which enables one calculating a small difference in the binding F of two ligands a and b in the active site of a large enzyme solvated by water. (This approach is based on mutating a to b within the framework of a thermodynamic cyle.) However, while the mutation process is well controlled by TI, conformational changes in the entire protein (i.e., “jumps” of side chains among rotamers) occur constantly and therefore the results might not converge for long simulation times. Also, it is sometimes difficult to control the size and shape of the active site after mutation and the correct position of b in it (Miyamoto and Kollman, 1993a; 1993b). In many cases one is interested in calculating ΔFmn between two microstates Ωm and Ωn (for brevity, these microstates will be denoted m and n, respectively); however, if the structural variance between m and n is significant the integration from m to n becomes difficult and for large molecules unfeasible.
These drawbacks of the TI approach can be overcome to a large extent by methods that provide the absolute Fm and Sm from a given sample; thus, one is required to carry out (only) two separate local MD simulations of microstates m and n, calculating directly the absolute Fm and Fn hence their difference ΔFmn = Fm — Fn, where the complex TI process is avoided (For a more extensive discussion on TI and other techniques for calculating ΔF and ΔS, see Meirovitch, 2007.)
Methods for calculating the absolute entropy
The harmonic approximation
The first approach for estimating the absolute S is based on the harmonic approximation which was introduced to biomolecules by Gō and Scheraga, 1969; 1976. They obtained
| (3) |
where Hessian is the matrix of second derivatives of the force field with respect to internal coordinates around an energy minimized structure; in other words, a localized energy well is represented by a parabola. A related approach, “the second generation mining minima” method (M2) has been developed by Gilson’s group (Chang and Gilson, 2003; Chen et al., 2005). With M2, low energy minimized structures (within a microstate) are initially identified, the free energies of the corresponding local potential wells are calculated with a method that considers both harmonic and an-harmonic effects, and the contribution of the individual wells is then accumulated.
The quasi-harmonic approximation
An important development has been the introduction of the quasiharmonic (QH) method by Karplus and Kushick, 1981, where the Boltzmann probability density of structures defining a microstate (rather than only a localized energy well) is approximated by a multivariate Gaussian. Thus,
| (4) |
where the covariance matrix, σ, is obtained from a local MD (MC) sample and N is (usually) the number of internal coordinates. Anharmonic contributions can be considered (Friesner and Levy, 1984; van Gunsteren et al., 2006), but QH is not suitable for treating several microstates, a random coil polymer or diffusive systems such as water (even though attempts to extend QH to argon have shown success (Schäfer, et al., 2000; Reinhard and Grubmüller, 2007)). Some of the above mentioned studies are based on the ad-hoc quantum mechanical approximation of Schlitter (Schlitter, 1993; Schäfer et al., 2000), where σ is defined in Cartesian coordinates; this method was followed by the exact quantum mechanical derivation of QH (Andricioaei and Karplus, 2001). These versions were studied further (van Gunsteren et al., 2006) and their performance has been compared (Carlsson and Åqvist, 2005).
QH has been used extensively during the years. A systematic study of its performance carried out by Gilson’s group (Chang et al., 2005) concludes that it can be accurate for a highly populated single microstate where the calculation is based on internal coordinates, while the use of Cartesians leads to errors of several kcal/mol. When the simulation covers several microstates the errors of QH(internal coordinates) can increase to tens of kcal/mol and are significantly larger with QH(Cartesians). This study also finds that the convergence of the QH results is slow.
In this context it should be pointed out that the absolute F can also be obtained with TI provided that a reference state R with known F is available and an efficient integration path R→m can be defined. A classic example is the calculation of F of liquid argon or water by integrating the free energy from an ideal gas reference state, where TI is very efficient (see later). However, for non-homogeneous systems such an integration might not be trivial, and in models of peptides and proteins defining adequate reference states and integration paths is not straightforward (see, Stoessel and Novak, 1990; Tyka et al., 2006; Meirovitch, 2007 and references cited therein).
GROWTH PROCEDURES FOR POLYMERS
Ideal chains
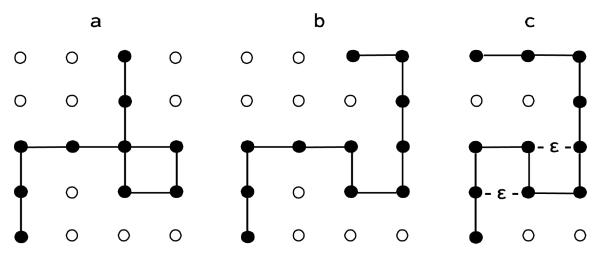
Whereas the dynamical MC and MD methods and the TI approach have become the main tools for studying fluids and biological macromolecules, an additional approach has been developed for synthetic polymers, where a chain configuration is grown step-by-step (from nothing) with the help of transition probabilities (TPs). A trivial example is an ideal chain of N steps (bonds), i.e., N+1 monomers starting from the origin on a (large) square lattice. In this chain model the excluded volume (EV) interaction is not considered, i.e., the chain can cross itself and go on itself, and no attraction is defined between the monomers; therefore, the chains are equally probable (see Figure 2).
Figure 2.
(a) An ideal chain of N=10 bonds (steps) and 11 monomers (full spheres) on a large square lattice, which only a limited part of it appears in the figure. The chain can intersect itself and go on itself. Because attraction energy is not defined all chains have the same Boltzmann probability, PiB (equation (5)). The ensemble of ideal chains can be generated (as random walks) step-by-step (from nothing) where a direction (out of 4 available directions) is selected blindly with transition probability (TP) 1/4. Therefore, the Boltzmann probability of an ideal chain is PiB =(1/4)N and the entropy is kBNln4. (b) A self-avoiding walk (SAW); here the excluded volume interaction is applied, i.e., self-intersections are not allowed. Thus, the ensemble of SAWs constitutes a partial group of the ideal chains. Again, all SAWs have the same Boltzmann probability, however PiB is unknown exactly. One can build the ensemble of SAWs step-by-step blindly, discarding the produced self-intersection chains and retaining only the SAWs; the entropy can be calculated but the procedure is extremely inefficient; in practice, SAWs of length larger than N=100 cannot be generated because the number of self-intersecting walks increases exponentially with N. With the exact scanning method, the transition probabilities (TPs) at each step are calculated by scanning all possible (SAW) continuations of the chain in future steps. This guarantees that the chain will not get into traps (dead ends) in future steps; the entropy is calculated exactly as a logarithm of the product of the transition probabilities (equation (10)). (c) A self-interacting SAW. Two (non-bonded) monomers that are nearest neighbors on the lattice interact with a negative energy ε (ε = −| ε|) (see equation (14) and equations (20)-(35)).
An ideal chain can be simulated by the usual Metropolis method (e.g., by applying small successive conformational changes to an initial chain conformation); in this case the sample generated is correlated and the value of PiB (in principle) is unknown. Alternatively, one can treat an ideal chain as a random walk, which is generated from the origin step-by-step and because self-intersections are allowed, a direction is chosen blindly with equal TP=1/4 for each direction. The members of a random walks sample are statistically independent and the value of PiB is known, and as required it is the same for all configurations i,
| (5) |
Therefore, the partition function is Zid=4N and the entropy is, S=kBNln4. Notice that a sample of random walks and a large enough (correlated) Metropolis sample are equivalent in the sense that they both lead to the same averages and fluctuations (e.g. for the end-to-end- distance) within the statistical errors. This equivalence is essential for our methodology and we shall return to it later.
Self-avoiding walks
A much more realistic model of a polymer is a self-avoiding walk (SAW) where the EV interaction is considered, i.e., self-intersections are forbidden (Figure 2); again, the SAW starts from the origin of a large square lattice. Thus, the SAWs constitute a subgroup of the ideal chains; because of the lack of finite interactions the partition function, ZSAW (equation (2)) is the total number of SAWs,
| (6) |
and all SAWs i are equally probable with a Boltzmann probability (equation (1)),
| (7) |
and
| (8) |
where j is any SAW. The summations (denoted with i) in equations (6) and (8) and in the rest of the paper are over the entire ensemble of SAWs. Equation (8) demonstrates that because PiB is constant, F (and S for this particular model) has zero fluctuation, σ, which is a general property of the correct free energy of any system. In other words, if the Boltzmann probability of any single SAW (j) is known, F (and S for this particular model) is known as well. On the other hand, the fluctuation of a free energy functional based on an approximate probability distribution (see below), denoted σA is expected to be finite (Meirovitch and Alexandrowicz, 1977).
As for an ideal chain, a sample of SAWs can be obtained by the Metropolis MC method as-well-as by various step-by-step construction procedures, such as the method of Rosenbluth and Rosenbluth, 1955 or its extension - the scanning method, which is described below (Meirovitch, 1982; 1988a).
The complete scanning method
With the complete scanning method a SAW (on a square lattice) is grown from the origin step-by-step with (exact); thus, at step k of the process, k−1 directions (bonds), ν (ν=1,4) will have already been constructed (they are denoted ν1,..,ν(k-1)) and the direction νk should be determined (in principle, out of 4 possible directions, ν, but in practice only out of three directions because an immediate reversed step is forbidden). To calculate TP(νk) one enumerates all of the possible continuations of the chain in the N-k+1 (remaining) future steps that start from ν at step k,; the number of these future chains defines a future partition function (compare with equation (6)) denoted Zkν(N-k+1) or for brevity, Zkν. The exact TP(ν)=p(ν|ν(k-1),..,ν1)] is proportional to Zkν)
| (9) |
Using these TPs, the kth step is determined by a random number and the process continues. The construction probability Pi of SAW i is the product of the TPs with which the steps have been chosen, and it is exact (=PiB)
| (10) |
Thus, like for the ideal chain, the value of PiB can be obtained exactly, which leads to the exact partition function and entropy (see equation (8)).
Incomplete scanning method
For a long chain a complete scanning is unfeasible, and therefore in practice one enumerates all of the possible continuations, of the chain in f future steps (f << N, typically, f ≤ 15 on a square lattice with present computers), where is a partial future partition function and f is the scanning parameter. Notice that the Rosenbluth method is based on f=1; this incomplete scanning procedure is usually referred to as the scanning method. defines the TPs
| (11) |
and the construction probability Pi0(f) of SAW i is approximate, i.e., it differs from PiB,
| (12) |
Due to the “incomplete” scanning, the chain can get trapped in a dead end during construction, meaning that the number, nsuccess of constructions succeeded (i.e., completed) is smaller than nstart, the number of SAWs started. In other words, Pi0(f) is normalized over a subgroup of the random walks that includes all the SAWs and part of the self-intersecting walks. Also, Pi0(f) is biased, i.e. (unlike PiB), one can show that it is larger for the compact SAWs than for the open ones. This bias can be decreased systematically by increasing f, where for a complete future scanning, i.e., fmax=N-k+1, the TPs (equation (11)) become exact (equation (10)) and no trapping occurs. In practical applications the bias is removed by an importance sampling procedure, which leads to an unbiased estimation, for the entropy that is exact within the statistical error
| (13) |
The scanning method can easily be extended to a chain model with finite interactions (Figure 2); in this case the interaction energy of the future chain j that starts from ν with itself and with the rest of the chain is calculated and the corresponding Boltzmann factor contributes to , rather than 1,
| (14) |
In this case PiB and Z are defined by equations (1) and (2), respectively.
HOW TO EXTRACT S FROM AN MC SAMPLE
Exact hypothetical scanning method
As for an ideal chain, a Metropolis MC sample of SAWs and a sample generated by the complete scanning method are equivalent. Therefore, one can assume that a given sample of SAWs obtained by the Metropolis procedure (or any other exact method, e.g., MD) has (hypothetically) been generated with the exact scanning method (the sample does not carry a memory of the simulation method with which it has been generated). Under this assumption one can reconstruct each chain configuration i of the Metropolis sample step-by-step by the complete scanning method calculating for each step νk(i) the (scanning) TP(νk(i)) (equation(9)). The product of these TPs leads to PiB (equation (10)) and thus to the correct entropy (equation (8)). This is the exact hypothetical scanning (HS) method.
The (incomplete) HS method
However, because the complete scanning procedure is impractical for large N, one has to resort to approximations. One approximation is the local states (LS) method described in the Appendix (Meirovitch, 1977). With another approximation an incomplete scanning is applied (like in the incomplete scanning method) based on a finite scanning parameter, f which leads to approximate p(ν|ν(k−1),..,ν1,f) (equation (10)) and approximate Pi0(f) (equation (12)), where Pi0(f) is nonzero also for a part of the self-intersecting chains. This approximate hypothetical scanning (HS) method enables one to define an entropy functional, SA, over the ensemble of SAWs, where SA can be shown rigorously (using Jensen’s inequality) to be an upper bound for the correct S (see Appendix and Meirovitch, 1985a; 1985b),
| (15) |
Thus, a random variable ln Pi0(f) is assigned to each SAW i of the ensemble (which is selected correctly with PiB). SA is estimated by from a finite (MC) sample of size n,
| (16) |
where t runs over the n SAWs of the sample. In this paper a summation over i denotes a summation over the whole ensemble, whereas t is used in a summation over a sample, and the estimated property appears with a bar. Clearly, the larger is f the better the approximation (i.e., the smaller is SA). Also, the fluctuation, σA(f) of the approximate entropy
| (17) |
is not zero but is expected to decrease as the approximation improves. Thus, one can calculate in the same HS run several approximations SA(f) and σA(f) and estimate the correct S from the correlation between SA(f) and σA(f) (Meirovitch, 1999, see also below).
THE HYPOTHETICAL SCANNING MONTE CARLO METHOD - THEORY
Due to the exponential growth (with f) of the number of future SAWs it is unfeasible to improve the TPs of the HS method beyond a maximal value of f. Thus, while the TPs defined by HS are deterministic (based on all of the future SAWs of f bonds at step k), the method is always approximate.
The hypothetical scanning Monte Carlo (HSMC) method overcomes this limitation by seeking to estimate the exact TP at step k (equation (10)). This is achieved by carrying out a Metropolis MC simulation of the entire future part of the chain (i.e., steps k, k+1,…,N) in the presence of the “frozen past” (ν1,..,ν(k−1)). The TP, pHSMC of the actual direction, νk(i) of the reconstructed SAW i is obtained from the number of times, , the direction νk(i) was visited during the simulation of nf (entire future) MC steps. Because later we shall also define HSMD (based on molecular dynamics rather than MC) we denote the TP, pHSMC by pHSM , which will define both cases,
| (18) |
and the reconstruction probability of chain i is
| (19) |
where, for simplicity, i has been omitted from the TPs. Thus, the deterministic TPs of the HS method are replaced by stochastic TPs for HSMC. The fact that the entire future is considered is important for systems with strong long-range interactions such as SAWs, proteins, etc. Still, pHSM hence are approximate, but as the MC simulation is increased, their estimation improves, i.e., pHSM→pexact (=p(ν|ν(k−1),..,ν1), equation (8)) and → PiB (equation (7)) (see proofs in the Appendix of White and Meirovitch, 2004); this means that S can be estimated by reconstructing a single SAW (see previous discussion following equation (8)). Notice that unlike HS, is defined only over the set of SAWs, a distinction which enables one to define a set of entropy and free energy functionals with specific relations to the correct F and S (e.g., upper and lower bounds). (It should be pointed out that stochastic TPs were implemented previously within the framework of the double scanning method in Meirovitch, 1988a).
A lower bound for the free energy
To express these functionals in a way that applies to a general system, they will be derived for a model of SAWs with attractive interactions, as defined in equation (14) (see Figure 2); thus, every SAW i has potential energy Ei. For this model, PiB and the partition function, Z are defined by equations (1) and (2) (rather than by equations (7) and (6), respectively). Thus, the exact free energy is
| (20) |
where its fluctuation is zero, because substituting PiB by its expression in equation (1) leads to [Ei + kBT ln PiB] = kBT ln Z , i.e., the random variable defined in the brackets is the same for all i.
Notice that for this model, pHSM and are still obtained by equations (18) and (19), respectively (however, the simulation of the future chains is carried out with an MC procedure based on SAWs with attractions). Also, SA ( ) , defined by replacing Pi(f) with in equations (15) and (16) is an upper bound because (as stated above) in practice is approximate. Therefore, the free energy functional, FA is a rigorous lower bound (see Appendix in White and Meirovitch, 2004),
| (21) |
FA is estimated by the arithmetic average, from a sample of size n generated with PiB (compare with equation (16)),
| (22) |
It is important to note that the quantity in equation (21) is not the same for all i, meaning that the fluctuation, σA in FA is not zero. This fluctuation, which is defined by
| (23) |
is, however, expected to decrease as the approximation improves, meaning that for very good approximations of the free energy can be very accurately determined by averaging Fi over just a handful of configurations (or even a single one) (compare with equation (17)).
Upper bounds for the free energy
One can define another approximate free energy functional denoted FB (Meirovitch, 1985b), where Pi is any probability distribution
| (24) |
The minimum free energy principle (Gibbs, 1902) states that FB as a function of P satisfies, FB(P) ≥ F becoming minimal for PiB, FB(PiB)= F (equation (20)). Thus, FB is an upper bound which approaches the correct free energy, F, when Pi→PiB (equation (1)). Notice that the relation FB(P) ≥ F is rigorously correct only if Pi and PiB are defined on the same space. Thus, Pi0(f) defined earlier by the HS method (equation (12)) does not lead to this free energy inequality because it is also defined on a partial group of the ideal chains, and one can only show that FB[Pi0(f)] ≥ FA (Meirovitch, 1985b). It is necessary to rewrite equation (24) such that FB can be estimated by importance sampling from a (Boltzmann) sample of configurations generated with PiB (rather than Pi). Applying the identities Σi Pi =1 and PiB/(exp[−Ei /kBT] /Z)=PiB / PiB =1 one obtains for
| (25) |
In practice FB is estimated by as the ratio of simple arithmetic averages, which are accumulated for each of the quantities in the brackets in equation (25) (compare with equations (16) and (22)),
| (26) |
Notice, however, that the statistical reliability of this estimation (unlike the estimation of FA) decreases sharply with increasing system size, because the overlap between the probability distributions PiB and decreases exponentially (see Meirovitch et al., 1994), therefore the samples required for a reliable estimation of FB are significantly larger than those required for FA. In practice is verified to be an upper bound if it decreases as the approximation is improved (Meirovitch, 1985b; White and Meirovitch, 2004).
Another way to estimate FB is by using a “reversed-Schmidt procedure” (Meirovitch, 1985b; White and Meirovitch, 2004) which enables one to extract from the given unbiased sample of size n generated with PiB an effectively smaller biased sample generated with Pi. However, for brevity we do not describe this procedure here and the reader is advised to check Meirovitch, 1985b, or section II.B of White and Meirovitch, 2004. With values for both FA and FB, their average, FM defined by
| (27) |
often becomes a better approximation than either of them individually. This is provided that their deviations from F (in magnitude) are approximately equal, and that the statistical error in FB is not too large. Typically, several improving approximations for FA, FB, and FM are calculated and their convergence enables one to determine the correct free energy with high accuracy.
A Gaussian estimation of FB
We shall now present the result for a Gaussian estimate for the free energy upper bound, FB (equations (25) and (26)), which can effectively overcome the statistical limitations associated with the standard evaluations of FB described in the previous section. It is noted that this approximation is mainly applicable for the HSMC(D) method and to emphasize this we define . Again, the complete derivation appears in section II.C, and the Appendix of White and Meirovitch, 2004. We begin by rewriting equation (25) as
| (28) |
Equation (28) emphasizes an explicit dependence of FB on the variable, , a quantity that is directly related to the average, FA (equation (21)) and the fluctuation, σA (equation (23)). Let us now assume that when configurations (i) are sampled from the Boltzmann distribution (i.e. with PiB), their corresponding values occur with a Gaussian probability. That is, the resulting values are described by the Gaussian distribution,
| (29) |
which is thus determined solely by the two parameters, FA (the mean) and σA (the standard deviation). Now, rather than summing over the configurations i with their weights, PiB, as in equation (25), we can sum (integrate) over all values of weighted with . The result is a Gaussian estimation of FB, denoted (for details see section II.C of White and Meirovitch, 2004)
| (30) |
We see that depends only on FA and the fluctuation, σA. This is an advantage of because these quantities are typically easier to estimate than FB from equation (26). Provided that the Boltzmann sample of values is approximately Gaussian, then . Our results show that this Gaussian distribution is a very good approximation as there is excellent agreement of with FB for cases where FB is well converged. Similar to equation (27) we define the average,
| (31) |
An exact expression for the free energy
The denominator of FB in equations (25) and (26) defines an exact expression for the partition function,
| (32) |
which is based on , where ; therefore, equation (32) will hold for any approximation Pi as long as it is normalized over the same space as PiB. An exact expression for the correct free energy F, denoted by FD is
| (33) |
In practice, the efficiency of estimating F by FD depends on the fluctuation of this statistical average, which is determined by the fluctuation of Fi exponentiated. That is, if the fluctuations in Fi are small, the values for exp[Fi /kBT] do not vary drastically, and the averages for FD (and FB) can be estimated reliably from a relatively small sample size n. Notice, however, that for large enough n, FD → F for any Pi, while which is always approximate. Also (as for FB), the direct calculation of F through FD will not be as statistically reliable as the corresponding calculation for the lower bound estimate, FA. Obviously, as Fi → F (i.e. ) all fluctuations become zero and F can be obtained from a single configuration. Again notice that the identity, FD =F is rigorously correct only if and PiB are defined on the same space. This point will become important in application of HSMC(D) to peptides or loops in proteins.
It should be pointed out that equation (32) with was suggested for a lattice gas long ago by Salsburg et al., 1959 (N is the number of particles and V is the volume.) This choice, however, leads to an extremely inefficient estimation at room temperature and works only at very high T where the Boltzmann probability is represented more faithfully by 1/VN.
The correlation between σA and FA
The zero fluctuation property of the correct free energy can be exploited directly through the extrapolation of a series of FA values, which are derived from a set of improving approximations. Here the fluctuations are expected to decrease systematically as the approximation improves, and we write FA as FA(α) [and σA as σA(α)] thus emphasizing the effect of the general parameter set, α, which controls the level of approximation and therefore the quality of the free energy estimate (α depends on nf (equation (18) and for a continuum system also on a bin size; see below). It has been suggested (Meirovitch, 1999) to express the correlation between FA(α) and σA(α) by the approximate function,
| (34) |
where Fextp is the extrapolated value of the free energy (i.e., Fextp ~F) and C and γ are parameters to be optimized by best-fitting results for FA(α) and σA(α) for different approximations α. This relation (and verifying that FA(α) is a concave-down function) enables one to also define an upper bound, Fup for F. Thus, Fextp and FM2,
| (35) |
(compare with equations (27) and (31)) have been found to provide better estimates for the correct F than FA (equation (21)) (Meirovitch,1999; 2001; White and Meirovitch, 2003, 2004).
All the equations defined above for the free energy of SAWs with attractions also apply to the entropy of SAWs without attractions because F / kBT = −S / kB (equation (8)).
Results for SAWs on a square lattice
It should first be pointed out that it is significantly more difficult to simulate SAWs on a square lattice than on a simple cubic lattice due to the stronger excluded volume interactions in 2D than in 3D. In our previous study (White and Meirovitch, 2005, White et al., 2005) HSMC was applied to SAWs on a square lattice. To generate a sample of SAWs (and for the reconstruction process) we used an MC procedure based on 50% pivot moves (Madras and Sokal, 1987) and 50% corner moves (Verdier and Stockmayer, 1962), which provide global and local conformational changes, respectively. While one can envisage more efficient procedures, we did not attempt to optimize the above MC method further because our main objective has been to check the applicability of the theoretical predictions rather than to provide the most accurate results for SAWs. In White and Meirovitch, 2005 two sets of results are presented, obtained by reconstructing an MC sample of size n of (predominantly different) SAWs, and by reconstructing a single (straight) chain n times. To emphasize the capability of HSMC to provide F (S for SAWs) by reconstructing any single chain, we present in Table 1 some of the results obtained for the straight chain. The HSMC values are compared to TI results (STI) and to those obtained by series expansion (exact enumeration), Sseries, (Guttmann and Enting, 1988; Conway et al., 1993). We also provide entropy results, Sscan obtained long ago by the scanning method based on a scanning parameter f=6 (Meirovitch, 1985a), and HS results, SHS, obtained by reconstructing the sample of SAWs with f=8.
Table 1.
HSMC results for the entropy per bond of N-bond SAWs on a square lattice obtained in White and Meirovitch, 2005a
| nf | SA / kB | σ A | SB / KB | SM / kB | SD / kB | n | ||
|---|---|---|---|---|---|---|---|---|
| N = 99 SSCAN = 0.987726 (5) | ||||||||
| 500 | 0.99294 (2) | 0.01030 (3) | 0.9826 (1) | 0.98243 (6) | 0.98775 (5) | 0.98769 (4) | 0.98773 (5) | 250000 |
| 5000 | 0.98826 (2) | 0.00324 (3) | 0.98722 (5) | 0.98722 (3) | 0.98774 (3) | 0.98774 (2) | 0.98774 (3) | 25000 |
| 50000 | 0.98777 (2) | 0.00101 (3) | 0.98767 (4) | 0.98767 (2) | 0.98772 (2) | 0.98772 (2) | 0.98772 (3) | 2500 |
| S HS | 0.98994 (1) | 0.00507 (1) | 0.9856 (2) | 0.9874 (1) | 0.9878 (1) | 0.9887 (1) | 0.98817 (5) | 250000 |
| S TI | 0.987727 (3) | 0.987727 (3) | 0.987727 (3) | 0.987727 (3) | 0.987727 (3) | 0.987727 (3) | ||
| S series | 0.987730 (3) | 0.987730 (3) | 0.987730 (3) | 0.987730 (3) | 0.987730 (3) | 0.987730 (3) | ||
| N = 399 SSCAN = 0.97567 (4) | ||||||||
| 500 | 0.98138 (6) | 0.00540 (5) | 0.9710 (5) | 0.9697 (2) | 0.9762 (3) | 0.9756 (1) | 0.9759 (3) | 9500 |
| 5000 | 0.97625 (4) | 0.00170 (5) | 0.9751 (1) | 0.97509 (8) | 0.97567 (5) | 0.97567 (5) | 0.97567 (5) | 2000 |
| 50000 | 0.97568 (4) | 0.00053 (5) | 0.97557 (7) | 0.97557 (5) | 0.97563 (4) | 0.97563 (4) | 0.97563 (5) | 225 |
| S HS | 0.98141 (5) | 0.00335 (5) | 0.9743 (5) | 0.9769 (3) | 0.9779 (3) | 0.9792 (2) | 0.9782 (2) | 5500 |
| S TI | 0.975655 (8) | 0.975655 (8) | 0.975655 (8) | 0.975655 (8) | 0.975655 (8) | 0.975655 (8) | ||
| S series | 0.975652(1) | 0.975652 (1) | 0.975652 (1) | 0.975652 (1) | 0.975652 (1) | 0.975652 (1) | ||
For SAWs, F/kBT = −S/kB (equation (8)), therefore, an upper bound for F becomes a lower bound for S and vise versa. The results were obtained from n reconstructions of a straight chain. SA (equations (15) and (21)) is an upper bound, and σA is its fluctuation (equations (17) and (23)). SB (equations (25) and (26)) and its Gaussian approximation, (equation (30)) are lower bounds, and their averages with SA are denoted SM (equation (27)) and (equation (30)), respectively. SD (equation (33)) is an exact entropy functional. nf is related to the number of MC steps per bond. The results for STI were obtained by thermodynamic integration, and those for Sscan (equation (13)) by the scanning method (f=5) in Meirovitch, 1985a. The results for Sseries were obtained by a series expansion formula (equation (20) of White and Meirovitch, 2005), and those for SHS (equations (15) and (16)) by the HS method (f=8). The statistical error is defined by parentheses: 1.00(3) = 1.00 ± 0.03.
The best results in the table are for Sseries, and STI, which are very close to each other. The table shows that for each chain length N, increasing the future sample size, nf (from 500 to 5000, and to 50,000) leads to the expected behavior: i.e., the upper bound, SA and its fluctuation σA decrease monotonically, while the lower bounds, SB and monotonically increase; the best result for SA (for n =50,000) is always larger than Sseries, while the best results for SB and are always smaller than Sseries. For each chain length N, the results for SM, SD, and are comparable and equal to Sseries, but within error bars that are larger than that of Sseries. It should be noted that the HS results are always worse than the corresponding best HSMC values (e.g., SA(HSMC) < SA(HS), σA(HSMC) < σA(HS), etc.). The fact that the results for the upper and lower bounds approach each other from both sides as a function of nf demonstrate the “self checking” property of HSMC, which enables one to determine the accuracy of S (i.e., S is located between SA and SB) without the need to know the correct answer.
APPLICATION OF HSMC(D) TO FLUIDS
Step-by-step construction procedures, which are natural for chain models can also be devised for bulk systems, such as 3D magnets or fluids, by defining suitable chain-like growth procedures where particles (or spins) are added gradually to an initially empty volume. In fact, such ideas were suggested for the Ising model first by Kikuchi, 1951 and later by Alexandrowicz, 1971 without relating them to polymer chains. Also, the scanning method was developed initially for the 2D Ising model (Meirovitch, 1982), the HS method was introduced for calculating the entropy to the 3D Ising model (Meirovitch, 1983), and HSMC was applied originally to argon and water (White and Meirovitch, 2003; 2004). However, presenting this approach as applied to SAWs (rather than to a bulk system) has didactic and theoretical advantages, as our main goal is to extend it to biological macromolecules.
Initially, HSMC was developed (for argon and water) as an “excluded volume” (EV) procedure that has been simplified later by a “free volume” (FV) procedure. We shall describe both procedures as applied to argon represented by the standard Lennard-Jones potential, where the extension to water is straightforward.
Statistical Mechanics of liquid models
Argon is represented by the standard Lennard-Jones potential with the parameters ε/kB=119.8 K and σ =3.405 Å; water is represented by the three site TIP3P potential (Jorgensen et al., 1983). We consider N atoms (molecules) enclosed in a periodic box of volume, V, at temperature, T [(NVT) ensemble]. The configurational partition function is given by
| (36) |
where E(xN) is the potential energy, xN is the set of Cartesian and orientational (for water) coordinates and dxN is the corresponding differential (including any necessary Jacobian factors). The integration is carried out over the configurational space, VN for argon, and (8π2V)N for water. Using the Boltzmann configurational probability density ρ(xN),
| (37) |
the total entropy, S, is
| (38) |
where SIG is the entropy of the ideal gas at the same temperature and density, and Se is the excess entropy. The factor, (8π2)N, would be replaced by unity for argon. The corresponding excess Helmholtz free energy is,
| (39) |
where <E> is the average potential energy. For water we present results for Fe; however, to be consistent with the literature (Li and Scheraga, 1988), for argon the configurational free energy, Ac is provided,
| (40) |
where σ is the van der Waals parameter from the Lennard-Jones potential.
A complete growth construction and exact HS procedures for fluids
It should first be pointed out that like the complete scanning method described for SAWs, each MC(MD) argon configuration, in principle, could have been generated by an alternative exact (complete) build-up procedure where argon atoms are added step-by-step to the initially empty volume (box) using TPs. Thus (like for SAWs), one can envisage an exact HS method where a given MC sample is assumed to have been generated by this exact build-up procedure, and thus each configuration is reconstructed with the build-up procedure, the TPs are calculated, and their product leads to ρ(xN) and to the absolute entropy ~ln ρ(xN) (compare with SAWs).
In the first stage of the exact HS method the box is divided into L3=LхLxL cubic cells with a maximal size that still guarantees that no more than one center of a spherical argon molecule occupies a cell. During the reconstruction of configuration i, the cells are visited orderly line-by-line layer-by-layer starting from one corner of the box until all of them have been treated. The calculation of TPk for the target cell k [which could be a vacant (−) or a populated cell (+)] is outlined as follows. At step k of the process, Nk atoms and k−1-Nk vacant cells have already been treated, i.e., their TPs have been calculated. These Nk atoms are now positioned at their coordinates of configuration i and together with the already visited vacant cells they define the (frozen) “past”; the L3-(k−1) as yet unvisited cells (including target cell k) define the “future volume”. To determine the TP of target cell k two future canonical partition functions are calculated, Z−(k) and Z+(k) for vacant and occupied cell k, respectively, by scanning (integrating) all of the possible configurations of the remaining N-Nk (future) atoms in the future volume, while the past volume is excluded; for Z−(k), the target cell k is excluded as well.
The sum, Z+(k)+Z−(k), covers all possible future atomic arrangements at step k, therefore if cell k is vacant the TPk is, p(k,-)=Z−(k)/[Z+(k)+Z−(k)]. If cell k is occupied, then the future partition function, Z+(k,x’), is calculated where one of the future atoms is fixed at the position, x’, the exact location (inside the target cell k) at which an atom was exhibited in configuration i. Z+(k,x’) thus covers a portion of the total configurational volume spanned by Z+(k). TPk for an occupied cell is the probability density, Z+(k, x’)/{[Z+(k)+Z−(k)]}. After cell k has been treated it becomes a past cell, empty or occupied according to configuration i. In this HS procedure all the L3 TPs are calculated exactly (where the periodic system is considered as well) and their product leads exactly to ρ(xN) (equation (37)). However, in practice scanning the entire conformational space is unfeasible.
The HSMC-EV procedure
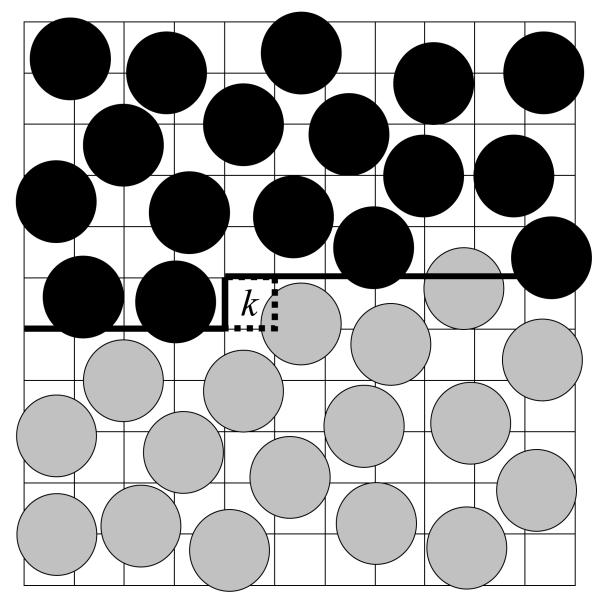
As for SAWs, with HSMC-EV, instead of calculating (integrating) exact future partition functions, the future atoms are simulated at each step by MC and the TPs are obtained from the number of counts of atoms in the target cell. This method is capable, in principle, of yielding the exact HS result (described above) in the limit of infinite future MC sampling. For finite future sampling, HSMC provides approximations ρHSM (xN) for the Boltzmann density, ρ(xN) that improve as the sampling is increased, thus giving rise to narrowing rigorous bounds for F and S (e.g., SA, FA, and FB, etc.) as discussed earlier. HSMC-EV is conducted as follows: At step k, the previously defined Nk atoms, are held fixed in their assigned positions (in configuration i), while all the remaining N-Nk future atoms are moved by the MC method (with the exception that regions inside previously defined cells are excluded, i.e. any trial move that would place a future atom into this previously assigned volume is rejected). If k is an occupied cell a small cube of size, Vcube is defined at the atomic position; the TP is determined from atom counts in the target cell k and its cube (see Figure 3). For more details and enhancements see White and Meirovitch, 2004.
Figure 3.
A two-dimensional (2D) illustration of the main simulation (periodic) box at the kth step of the HSMC-FV reconstruction of argon. The 2D “volume” is divided into cells, where k−1 of them have already been considered in previous steps (starting from the upper left corner). These k−1 cells comprise the “past volume” (the region above the heavy lines) which contains previously treated fixed atoms that are denoted by full black circles defined by the van der Waals radius. This region is excluded from the moveable future atoms (denoted by full grey circles) which are thus simulated in the “future volume” below the heavy lines, while in the presence of the fixed atoms. The future atoms can visit the target cell k (depicted by dotted lines) and their counts in this cell lead to the transition probability of an empty cell or the transition probability density of an occupied one. Note that for the case of an occupied target cell, counts are actually accumulated for visitations to a smaller region, Vcube located inside the target cell but not shown in the figure.
The HSMC(D)-FV procedure
The HSMC-EV procedure is not conveniently applicable to MD. Therefore, we have developed an alternative simpler free volume (FV) procedure where instead of treating vacant and occupied cells, only the N atoms are considered (White and Meirovitch, 2006). Thus, at step k, k−1 atoms have already been treated and they are fixed in their positions in configuration i. A small cube (sphere) is defined at the position of atom k at i, future atoms k, k +1⋯N are simulated by MC(MD), and TPk is calculated (as for HSMC-EV) from atom counts in the cube. Notice that while with EV the future atoms are excluded from the past volume, with FV they are allowed to move in the entire volume. In principle, the FV method (like EV) is exact for infinite simulation and does not depend on the order in which the atoms are treated; in practice, however, some “past” regions with low accessibility might not be visited during a finite simulation and the results might be slightly distorted. To minimize this effect we treat the atoms in the same order as in the EV procedure. The FV procedure is easy to implement even in a rugged shaped volume, where it would be difficult to define an adequate set of cells for the EV procedure. Thus, FV would be useful for implementation of HSMC(D) to a loop capped with explicit water; however, FV needs further optimization before such an implementation can be carried out (see later).
Results for argon and water
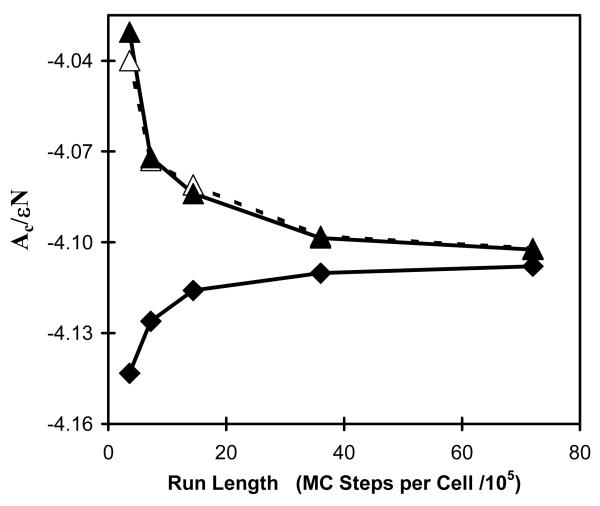
In Table 2 HSMC results are presented for various free energy functionals calculated for N=125 argon atoms (enclosed in a box) as a function of the average number of MC steps per cell, . n is the sample size. In Table 3 similar results are presented for N=64 TIP3P water molecules (Jorgensen et al., 1983). All these results were obtained by The HSMC-EV procedure (White and Meirovitch, 2004). As in Table 1, the results demonstrate the expected behavior, i.e., FA increase, while and σA decrease as is increased. The results for FB are less accurate than those for and their expected decrease is masked by relatively large statistical errors. The best values of FA are always smaller and those of FB and , are always larger than the corresponding TI results that are expected to be exact within the error bars. The results for FM, , and FD are equal within the error bars to the TI values, where those for are the most accurate with statistical errors of 0.02 and 0.14% for argon and water, respectively. Figure 4 exhibits the approach of the results for FA and those for FB and , from both sides towards the correct value as a function of .
Table 2.
HSMC results for 125 argon moleculesa
| − FA | σ A | − FB | − FM | − FD | n | |||
|---|---|---|---|---|---|---|---|---|
| 1,000,000 | 4.139 (1) | 0.0246 (5) | 4.08 (2) | 4.045 (4) | 4.11 (2) | 4.092 (2) | 4.10 (1) | 362 |
| 2,000,000 | 4.124 (1) | 0.0175 (6) | 4.06 (2) | 4.077 (4) | 4.09 (2) | 4.100 (2) | 4.09 (1) | 179 |
| 4,000,000 | 4.116 (1) | 0.0110 (9) | 4.10 (1) | 4.097 (3) | 4.11 (1) | 4.107 (2) | 4.108(7) | 125 |
| 10,000,000 | 4.1124 (6) | 0.0083 (5) | 4.10 (1) | 4.102 (1) | 4.10 (1) | 4.1070 (9) | 4.105 (6) | 170 |
| 20,000,000 | 4.1102 (6) | 0.0060 (5) | 4.10 (1) | 4.105 (1) | 4.11 (1) | 4.1074 (8) | 4.107 (4) | 99 |
| TI | 4.108 (1) | 4.108 (1) | 4.108 (1) | 4.108 (1) | 4.108 (1) | 4.108 (1) |
Free energy values are given as Ac/εN where Ac is the configurational freeenergy (equation (40)), ε is the standard Lennard-Jones energy parameter (see text) and N is the number of atoms FA (equation (21)) is a lower bound of the free energy and σA (equation (23)) is its fluctuation. FB (equations (25) and (26)) is an upper bound and (equation (30)) is its corresponding Gaussian approximation. FM (equation (27)) and (equation (31)) are the averages of FA with FB and , respectively. FD (equation (33)) is the direct estimate for the free energy. is the average number of MC steps per cell, and n is the number of configurations analyzed (the sample size), where a single HSMC reconstruction was performed on each configuration. Results obtained by thermodynamic integration are denoted as TI. The statistical error appears in parenthesis; for example, 4.108(1) = 4.108±0.001.
Table 3.
| − FA | σ A | − FB | − FD | n | |||
|---|---|---|---|---|---|---|---|
| 5,312,000 | 5.736 (5) | 0.064 (5) | 5.58 | 5.29 (7) | 5.52 (4) | 5.62 (4) | 147 |
| 13,280,000 | 5.679 (4) | 0.040 (4) | 5.61 | 5.51 (4) | 5.59 (2) | 5.63 (3) | 94 |
| 26,560,000 | 5.636 (3) | 0.027 (3) | 5.59 (3) | 5.555 (18) | 5.595 (9) | 5.607 (15) | 100 |
| 53,120,000 | 5.627 (3) | 0.024 (3) | 5.57 (3) | 5.565 (16) | 5.596 (8) | 5.595 (15) | 87 |
| TI | 5.599 (2) | 5.599 (2) | 5.599 (2) | 5.599 (2) | 5.599 (2) |
Free energy values are given as the excess free energy, Fe (equation (39)) in units of kcal/(mol). FA, σA, FB, , , FD, , n, TI, and the statistical error are defined in Table 2.
Though the values for FB are reasonably close to the correct free energy, the expected upper bound trends are not exhibited due to lack of convergence and thus no statistical errors are given.
Figure 4.
Free energy bounds as a function of HSMC-FV run length for argon, N = 125 atoms. The HSMC run length on the horizontal axis is given as , the average number of MC steps per cell. Shown are the free energy lower bound FA (equation (20)) (diamonds and solid lines), the upper bound FB (equations (25 and (26)) (open triangles and dashed lines), and the Gaussian upper bound (equation (30)) (solid triangles and solid lines). Free energies are given as Ac/εN, where Ac is the configurational free energy defined in (equation (28)), ε is the standard Lennard-Jones energy parameter, and N is the number of atoms.
Based on the correlation between σA and FA (equations (34) and (35)) White and Meirovitch, 2004 also obtained for N=125 argon particles the upper bound, −Fup=4.1036 (7), and the estimations −FM2=4.1075 (6) and −Fextp=4.1065 (10) for the correct value, −FTI=4.108 (1)) (the error of the last digit appears in parenthesis, thus, 4.10 (2) is 4.10 ±0.02). As for SAWs, very good results for the free energy functionals, FA, FB, and FM were obtained for each of five single argon configurations (N=64) by applying to each configuration many HSMC reconstructions. It should be pointed out again that unlike F, reconstructing a single configuration does not lead to the entropy (and the energy) which requires averaging over a Boltzmann sample. Results for the entropy of argon are given in White and Meirovitch, 2003.
The expected (theoretical) behavior of the various free energy functionals has also been demonstrated for 64 argon particles reconstructed with the HSMC-FV and the HSMD-FV procedures; these results, summarized in a table similar to Table 2, are not provided here (see, White and Meirovitch, 2006). These HSMC(D)-FV results together with the above HSMC-EV results for argon and water and those presented earlier for SAWs show that FA, which is statistically the most reliable functional, provides a good approximation for F; as discussed later, this leads to very accurate estimates, and for free energy and entropy differences. The fact that the theoretical predictions of HSMC(D) have been validated for highly non-trivial systems, gives reasons to believe that HSMC(D) can be applied reliably to more complex systems, such as peptides and loops where no exact results for comparison are available.
HSMC(D) APPLIED TO PEPTIDES
Initially we applied HSMC to models of polyglycine, NH2(Gly)NCONH2 (or simply (Gly)N) for N=10 and 16 in vacuum where the potential energy E is defined by the AMBER96 force field (Cornell et al., 1995), which is implemented in the program TINKER (Ponder, 2004). However, replacing MC by MD has led to an increase in efficiency by a factor of ~100. Therefore, we are mainly interested in the application of HSMD (rather than HSMC) to peptides or mobile loops in proteins. A peptide is most conveniently described by internal coordinates - dihedral and bond angles, and bond lengths (with the corresponding Jacobians); thus, in the case of an MD simulation the Cartesian coordinates should be transferred into internal ones. Notice that while the bond lengths contribute significantly to the absolute entropy, to a good approximation, their contribution is equal for different microstates and thus get cancelled in differences ΔSmn, which are our main interest. Therefore, the effect of bond lengths is ignored (i.e., they are considered as constants); we have also shown that the contribution of the Jacobians of the bond angles are cancelled in differences, ΔSmn and they are ignored as well (Cheluvaraja and Meirovitch, 2006; 2008). Thus, a chain conformation is defined by the backbone dihedral angles φi,ψi, and ωi and the corresponding bond angles (θk) ordered along the chain, which for (Gly)N are denoted for simplicity by αk, k=1,6N=K, where N is the number of residues; however, sidechain angles can be ordered as well, where the total number of variables is denoted by K.
Theoretical considerations
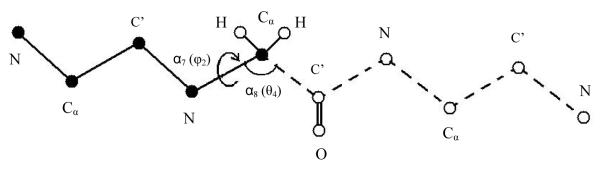
In should be pointed out that typically a peptide is not simulated over the entire conformational space, Ω but over a limited microstate m (e.g., an α-helical region); in this respect peptides are similar to SAWs, which constitute a subgroup of the ideal walks. However, while it is straightforward to distinguish between a SAW and a self-intersecting walk, a practical definition of a microstate is not trivial. Before discussing this subject in detail, we define the reconstruction transition probability, TP(HSM) for a peptide, which is an extension of the SAWs equation (18) for a continuum chain model.
Thus, at step k, k-1 angles αk−1 ⋯α1 of conformation i have already been reconstructed and the TP density of αk , ρ(αk αk−1, ⋯ ,α1) is calculated from an MD sample of nf conformations (generated in Cartesian coordinates), where the entire future of the chain, i.e., the atoms defined by αk ,⋯,αK are moved, while the past - the loop atoms defined by α1,⋯,αk−1 are held fixed at their values in conformation I (see Figure 5). A small segment (bin) δαk is centered at αk(i) and the number of visits of the future chain to this bin during the simulation, nvisit, is calculated; one obtains,
| (41) |
where ρHSM (αk|αk−1,⋯, α1) becomes exact for very large nf (nf → ∞) and a very small bin (δαk→ 0).(Notice that the HSMC theory developed previously for a lattice polymer (equations (20-35)) applies also to a continuum model of a peptide.) Equation (41), which differs from equation (18) by δαk is suitable for HSMC. However, for practical reasons, with HSMD a pair of angles should be treated simultaneously, where each pair consisting of a dihedral angle and its successive bond angle (e.g., φ and the bond angle N-Cα-C’). Thus, at each step both αk and αk+1 are considered and nvisit is increased by 1 only if αk and αk+1 are both located within the limits of δαk and δαk+1, respectively; also, for Arg we have treated 3 consecutive χ angles (ignoring the bond angles; Mihailescu and Meirovitch, 2009) and in the future we plan to treat 4 angles. Therefore, for l consecutive angles equation (41) becomes
| (42) |
where we have shown that δαk and δαk+1can be optimized (Cheluvaraja and Meirovitch, 2006). The corresponding probability density is
| (43) |
Notice that the future conformations simulated by MD (MC) at each step k should remain within the limits of m defined by the analyzed sample - a condition which will be satisfied in general. However, if nf is too large the future chains might move to other regions of conformational space and certain procedures should be applied to avoid this situation (see later).
Figure 5.
Illustration of the HSMD reconstruction process of conformation i of a peptide consisting of three glycine residues. At each step the transition probability (TP) of a dihedral angle and the successive bond angle is determined and the related atoms are then fixed in their positions in i. The figure describes step 4 where the dihedral and bond angles considered are φ2 (of the second residue) and the successive θ, respectively; these coordinates are also denoted α7 and α8, respectively (see text). In this process the already reconstructed part (the past) is depicted with solid lines and solid spheres (atoms); for simplicity the oxygens and most of the hydrogens are discarded. The TP is obtained by carrying out an MD simulation of the as yet unreconstructed part of the peptide (the future) which is depicted with dashed lines and empty spheres. In this simulation the “past” atoms remain fixed at their positions in i while the conformations of the future part should remain within the limits of the microstate; future-past interactions are taken into account. Small bins δφ2and δθ are centered at the values of φ2 and θ in i. The TP is calculated from the number of simultaneous visits of the future part to δφ2 and δθ during the simulation (see equation (42)). After TP(4) has been determined the coordinates of the two hydrogen atoms of Cα (2) and those of C’(2) are fixed at their positions in i and the process continues.
On the definition of a microstate
This discussion brings us back to the problematic issue of the definition of a microstate for a peptide - a subject that has been given considerable thought by us over the course of the years (Meirovitch et al., 1987; 1992; 1994; Meirovitch and Meirovitch, 1996; Meirovitch and Hendrickson, 1997; Baysal and Meirovitch, 1999; 2000; Celuvaraja and Meirovitch, 2004: 2005; 2006; 2008; Celuvaraja et al., 2008). For simplicity, we consider again (Gly)N with rigid geometry, i.e., with constant bond lengths and bond angles where ωk is fixed at 180°; thus, a conformation is defined by φk and ψk, k=1,N. For a helical microstate (Ωh), these angles are expected to vary within relatively small ranges Δφk and Δψk around φk = −60° and ψk = −50° (we ignore for a moment the possible effect of side chains). However, if N is not too small, the correct limits of Ωh in the [φk,ψk] space are unknown even for this simplified model since they constitute a complicated narrow “pipe” contained within the (larger) region defined by the product, Δφ1xΔψ1xΔφ2xΔψ2 ⋯·· ΔφNxΔψN due to the strong correlations among the dihedral angles. Obviously, these correlations are taken into account by an exact simulation method and thus, in practice, Ωh can be defined (or more correctly, represented) by a local MD (MC) sample of conformations initiated from an α-helical structure, as mentioned earlier.
However, this definition should be used with caution. Thus, a short simulation will span only a small part of Ωh which will grow constantly as the simulation continues; correspondingly, the calculated average potential energy, Eh and the entropy Sh (obtained by any method) will both increase and the free energy, Fh is expected to change as well. As the simulation time is increased further, side chain dihedrals will “jump” to different rotamers, which according to our definition should also be included within Ωh; for a long enough simulation the peptide is expected to ”leave” the α-helical region and move to a different microstate. Thus, in practice, the microstate size and the corresponding thermodynamic quantities can depend on the simulation time t used to define the microstate. In some cases, one can better define Ωh by discarding structures with dihedral angles beyond predefined Δφk and Δψk values or structures that do not satisfy a certain number of hydrogen bonds; one can also apply energetic restraints where their bias should be removed. However, these restrictions are somewhat arbitrary and are difficult to apply for calculating the differences ΔFmn and ΔSmn between microstates m and n. Therefore, one should bear in mind that in practice there is always some arbitrariness in the definition of a microstate, which affects the calculated averages. This arbitrariness is severe with some methods and can be controlled (minimized) by others.
To reliably estimate ΔSmn (ΔFmn, etc.) we simulate both m and n for the same t looking for a range of t values where ΔFmn(t), ΔSmn(t) and ΔEmn(t) are stable within the statistical errors [due to typically simultaneous increase of Em(t), En(t), etc.]. For the QH method (equation (4)) such stable results constitute the best final answer. For HSMC(D) one can also calculate improved approximations [and ] for increasing sample sizes nf and decreasing bins, δαk (equation (42)); if these differences (for the better approximations) converge within the statistical errors, the converged values are considered to be the correct differences (see below).
Obviously, if m is less stable than n the t values should be adjusted (i.e., decreased) to fit the stability of m. If m is significantly larger than n, t should be large enough to allow an adequate coverage of m. However, if ΔSmn(t) increases monotonically it constitutes a lower bound. If the microstate is restrictive, e.g., side chains should populate a single rotamer, the MD sample can be composed of several smaller samples, each starting from the same structure (seed) with a different set of velocities. It should be pointed out that with the QH method relatively large samples are required for obtaining a converged correlation matrix σ (equation (4)) (Chang, 2005). Therefore, one should verify that the sample remains in the original microstate and has not “escaped” to neighboring ones. We have developed methods which enable one to analyze the stability of a microstate by calculating distribution profiles of dihedral angles (Meirovitch and Meirovitch, 1996; Baysal and Meirovitch, 1999; 2000). Some information about the representation of a microstate by a sample can be obtained by calculating αk(max) and αk(min), which are the maximum and minimum values of αk found in the sample, respectively and the variability ranges,
| (44) |
Sampling strategies for peptides and loops
Unlike QH (and LS), HSMC(D) is not based on gathering statistics from the studied sample; therefore, the required sample size is relatively small; moreover, F[HSMC(D)] (but not E and S[HSMC(D)]) can be obtained from a very small sample (even from a single conformation) as has been demonstrated earlier (White and Meirovitch, 2004; 2005). Therefore, in our studies of peptides and loops which populate significantly different microstates (Cheluvaraja and Meirovitch, 2004; 2006; 2008; Cheluvaraja et al., 2008) the sample size for HSMC(D) is relatively small and has been determined by the range of t values for which the average of Em (En) is approximately constant (typically a 0.5 ns trajectory). For peptides we reconstructed ~600 conformations selected from such trajectories; however, more recently we have found that already 80 loop/protein/water configurations are sufficient if chosen homogeneously along the trajectory (Mihailescu and Meirovitch, 2009). Again, one can envisage extreme cases where m is significantly larger than n, which would require increasing the sample size for m as discussed above.
This discussion also applies to the future samples generated in the reconstruction process; thus, one has to verify that microstate m is adequately covered, i.e., that the future chains do not span a too small part of the entire region (this applies in particular to the side chain rotamers) and that they do not “overflow” to neighboring microstates due to too small or too large nf values, respectively. (Note that even at step k, where the “past” segment of the peptide/loop is kept fixed, the (future) unfixed part can leave the microstate during long MD simulations - an overflow that is more likely to happen for small k and for small residues such as Gly.) Therefore, the MD simulation of the future chain at step k starts from the reconstructed conformation i, and every g fs (typically, g=10 fs) the current conformation is considered, while the ninit initial considered conformations are discarded for equilibration. The next nf (considered) future conformations are represented in internal coordinates and their contribution to nvisit (equation 41) is calculated. To be able to control the extent of coverage of m the following procedure has been applied: nf has been divided into several (j) shorter repetitive procedures (“units”), each based on n’f < nf conformations where nf=jn’f, and each unit starts from the reconstructed structure i with a different set of velocities followed by equilibration of size, ninit; obviously, one would seek to determine the minimal values for n’f, j, and ninit, which would keep the future chains within m while allowing its adequate sampling. A similar procedure was first suggested by Brady & Karplus, 1985 within the framework of the QH method, and was also used in implementations of the local states method to peptides (Meirovitch and Meirovitch, 1996: Baysal and Meirovitch, 1999).
Analysis of results
In our application of HSMC(D) to argon, water and SAWs the primary goal has been to calculate the absolute F. However, in the study of peptides (and loops) the focus is on calculating ΔFmn (ΔSmn) between microstates which has led us to ignore the effects of bonds stretching and the Jacobians related to the bond angles: thus, the absolute F (and S) is inherently approximate. Still, it is important to verify that the various free energy functionals change as the approximation improves according to the theoretical predictions. Indeed, in general FA has been found to increase as nf is increased and δαk is decreased but the correlation sometimes has not been perfect because it also depends on a third parameter, the unit size, n’f , which determines to a large extent, the coverage of a microstate by the future chains. However, if the FA (and SA) results converge for the better approximations the converged values are considered to be exact (neglecting the bond stretching and the Jacobians) within the statistical errors.
On the other hand, with HSMD the behavior of FB (and FD), which needs relatively large samples for both the peptide conformations and the future chains, did not show the expected pattern - a decrease as the approximation improves. This might also be a result of the imbalance introduced to the exponents, defining FB and FD (equations (25) and (33)) where the AMBER potential, Ei includes the bond stretching energy while the effect of bond stretching is ignored in .
In this context we note that for a model of (Gly)10 based on constant bond lengths and bond angles in the extended, helix, and hairpin microstates (m) (where the above mentioned imbalance does not exist) both FA and FB have shown the expected increase and decrease, respectively, as the approximation improves (Cheluvaraja and Meirovitch, 2004); similarly, in this HSMC study the fluctuation, σA (as expected) always decreased and (which depends on FA and σA (equation (30)) but was not calculated in this paper) can be shown to decrease as well. Correspondingly, reliable results were obtained for FD (equation (33)), FM (equation (27)) and (equation (31)); also, results for FA and FB obtained from two single conformations are close to those obtained from the entire sample of (Gly)10. Moreover, results for the difference based on the best approximation, and results for all approximations of , , and are equal within the error bars; this demonstrates a convergence of the differences of each of the last three functionals, strongly suggesting that the converged values are equal to the correct ΔFmn (and ΔSmn) within the error bars. Furthermore, this support our working assumption that the correct ΔFmn (and ΔSmn) can be estimated accurately from the converging results of (and ), which are computationally the most reliable.
These calculations describe an important case where (unlike SAWs, argon, and water) reliable results from other methods are unavailable for comparison and the “self-checking” property of HSMC alone guarantees that the correct F is confined within the small region between the best results for FB and FA. For this model we also calculated the quasi-harmonic entropy, SQH (equation (4)) which provides an overestimation; indeed, the SQH results were always larger than the S(HSMC) values, but the results were equal within the error bars to those of ΔSmn(HSMC), providing an additional support for the reliability of HSMC.
Still, one would like to be able to estimate FB (and FD) also with HSMD. In previous publications (Cheluvaraja and Meirovitch, 2006) we have argued that the bond stretching entropy can be taken into account approximately within the framework of HSMD; this enhancement, which has not been implemented as yet, might improve the behavior of FB (and FD). Notice, however, that for a loop capped with explicit water the configurations of water are currently not reconstructed by HSMD but their contribution to the free energy is calculated with a more efficient TI procedure (see next section).
HSMD-TI EXTENDED TO LOOPS IN EXPLICIT SOLVENT
HSMD has been applied to a 7-residue mobile loop 304-310 (Gly-His-Gly-Ala-Gly-Gly-Ser) of the enzyme porcine pancreatic α-amylase (Cheluvaraja and Meirovitch, 2008) in vacuum and in the GB/SA implicit solvent (Qiu et al., 1997), again within the framework of TINKER (Ponder, 2004) using the AMBER force field (Cornell et al., 1995); later the same loop capped with 70 TIP3P water molecules (Jorgensen et al., 1983) was treated by HSMD-TI, a method that is a combination of HSMD and TI (Cheluvaraja et al., 2008). Very recently a short mobile loop in the protein Acetylcholine esterase (AChE) was studied where the main objective of this study has been to estimate the required number of water molecules which would lead to systematic free energy results that are also in agreement with experimental data (Mihailescu and Meirovitch, 2009). Typically, one analyzes two x-ray structures (taken from the Protein Data Bank - PDB) of the free and bound protein, where the structure of a mobile loop in the free protein is not well defined, or is resolved with large B factors. When the ligand binds to the active site, the loop moves significantly towards the active site sometime creating a “lid” above the ligand protecting it from water. Thus, the two templates, i.e., the protein structures excluding the loop, might be very similar, which justifies attaching the bound loop structure to the free template for free energy studies. One might be interested not only in comparing the stability of the free and bound loop microstates but also whether the process is of a selected fit type (Constantine et al.,1998), i.e., whether the microstate of the bound loop is included within those visited by the (flexible) loop in the free protein (or otherwise the process is of an induced-fit type, Getzoff et al., 1987; Rini et al.,1992).
Initial optimization of the template-loop-water system
We describe here the implementation of HSMD to a mobile loop capped with explicit water. Notice first, that taking into account the whole protein would be computationally prohibitive; therefore, the template size is reduced to the Ntemp atoms closest to the loop, where the rest of the atoms of the protein are ignored. More specifically, the center of mass of the backbone atoms of the free loop is calculated as a (3D) reference point denoted xcmb and a distance (Rtemp) is chosen. If the distance of any atom of a residue from xcmb is less than Rtemp, the entire residue is included in the template; otherwise, the residue is eliminated. Moreover, the template’s coordinates are fixed, i.e., the template-template interactions are not considered, while template-loop and template water interactions (defined by the AMBER force field) are taken into account.
To add water, we define a sphere centered at xcmb with a radius, Rwater (Rwater=Rtemp+1 Å) where waters are added at random to the hemisphere oriented towards the exterior of the template. To hold these waters around the loop they are restrained with a flat-welled half-harmonic potential (with a force constant of 10 kcal mol−1Å−2) based on their distance from xcmb. That is, if the distance of a water oxygen from xcmb is greater than Rwater a harmonic restoring force is applied, otherwise the restraining force is zero. To these “random” waters one can add crystal waters that reside in crevices of the protein structure.
These systems for the free and bound loop structures (connected to the free template) undergo several rounds of optimization. First, to relax atomic overlaps in the crystal structure, harmonic forces are applied to the crystal positions of all heavy atoms, and the energy of the protein is minimized. Second, the orientations of the polar hydrogens in the loop and template are optimized by carrying out a sequence of optimization steps each consists of a high temperature MD simulation followed by energy minimization. During these optimizations the structure of the loop and template are held fixed. In the next step, the positions (and orientations) of the water molecules are optimized by rounds of high temperature MD simulations and energy minimizations.
In this context it should be pointed out that we seek to simulate the loop in solution, hence it is not clear whether the positions of the crystal waters are relevant for the solution environment. In particular, water molecules that are caged within the crystal structure are expected to stay there during the MD simulations, and thus can be considered as part of the template. Therefore, the number and arrangement of these waters should be globally optimized, which is a non-trivial task (for more details, see Cheluvaraja et al, 2008, Mihailescu and Meirovitch, 2009). Finally, the energy of the system is minimized where the coordinates of the loop are allowed to change.
Each of the optimized “free” and “bound” structures becomes a “seed” for an MD run at 300 K, where only the loop and water atoms are moved, while the template atoms are kept fixed. An equilibration run of 0.5 ns is initially generated, followed by a 0.5 ns production run, from which 1000 loop/water configurations are collected by retaining a configuration every 0.5 ps; these configurations represent the corresponding microstates. The total potential energy Etotal is the sum of partial energies related to the loop and water (the template-template energy is constant and thus is ignored),
| (45) |
where Eloop-loop is the intra loop energy, Eloop-temp is the energy due to loop-template interactions; these energies define the total loop energy Eloop, and the interactions related to water are defined in a similar way, where their total is denoted by Ewater. From these samples (of size 1000) two smaller samples of ~100 configurations are chosen homogenously along the sample for reconstruction and free energy calculations.
Reconstruction of the loop structure
The reconstruction of the loop-water system is based on an exact construction procedure, where a loop conformation is built first (in the presence of the fixed template) by defining the angles αk step-by-step using TPs; water molecules are added in a second stage in the presence of a fixed loop structure and a fixed template.
The reconstruction of the loop structure is carried out in the same way described for a peptide with one difference: at sep k, the future consists, not only of all of the future loop conformations (within m) defined by αk…. αK but also of all the possible configurations of the N water molecules, defined by xN; this combined future is simulated by MD, leading to the TP, ρHSM (αk|αk−1,⋯, α1) (equation (42)) and to the loop probability density, ρHSM (αK ,⋯,α1) (equation (43)). ρHSM (αK ,⋯,α1) defines an approximate entropy functional for microstate m (bound or free) denoted , which can be shown (using Jensen’s inequality, see Appendix) to constitute a rigorous upper bound for Sloop (m)
| (46) |
where for brevity [αk] = (αK ,⋯, α1) and the correct Sloop (m) is obtained by replacing in equation (46) ρHSM ([αk]) by the Boltzmann probability, ρB([αk]).
Reconstruction of water
To reconstruct the water configuration one can use in principle the procedures HSMC(D)-FV or HSMC-EV described earlier for fluids, where the already reconstructed loop is held fixed in its structure ([αk]) in i. The product of the TPs of water would lead to the water probability density, and then to the water configuration to the free energy
| (47) |
where Ewater is defined in equation (45). However, these procedures for fluids have not been optimized as yet and are relatively time consuming.
Alternatively, one can obtain Fwater ([αk],xN) by a TI procedure based on the same reference state for all the free and bound loop structures. Thus, imagine that the loop-water interactions are switched off, while the water-water and template-water interactions are kept intact. Under this condition, and because the water molecules in the free and bound microstates “see” the same template, they will define the same (reference) state. Therefore, one can increase gradually the loop-water interactions (from zero) in an MD-based TI procedure where the loop structure remains fixed at [αk]. For each system configuration, this TI procedure will lead to the contribution of water to the free energy, integrated from the same reference state, and therefore can be used in free energy differences. This TI procedure is highly efficient because only the water molecules are moved while the protein atoms are held fixed. In practice, the integration is carried out in two stages but in an opposite direction to that described above, i.e., first the charges are gradually decreased to zero, followed by a similar decrease of the Lennard Jones (LJ) potential, which leads to and , respectively.
The total free energy of configuration i (loop and water) is denoted, FiA (m) to emphasize that in practice it is approximate,
| (48) |
where Eloop is defined in equation (45) and ρHSM ([αk]) in equations (43) and (46). The FiA (m) values are averaged over a sample of size n for the free and bound microstates leading to ,
| (49) |
The converged values of lead to the correct ΔFmn =Ffree - Fbound.
HSMD-TI results for a loop of AChE
The loop 287-290 (Ile, Phe, Arg, and Phe) of the protein AChE changes its structure upon interaction of AChE with diisopropylphosphorofluoridate (DFP). Reversible dissociation measurements suggest that the free energy penalty for the loop displacement is ΔF=Ffree — Fbound ~ −4 kcal/mol. Therefore, this loop has been the target of two studies by Olson’s group for testing the efficiency of procedures for calculating F (Carlacci et al., 2004; Olson, 2004). In a recent study (Mihailescu and Meirovitch, 2009) we have tested for the first time the performance of HSMD-TI and the validity of the modeling described above for a loop with bulky sidechains in explicit water. We have found that consistent results for the free energy (which agree with the experimental data above) require a template larger than a minimal size, and a number of water molecules which lead approximately to the experimental density of bulk water in the sphere. For example, we obtained ΔFtotal = ΔFwater +ΔFloop = −3.1 ± 2.5 and −3.6 ± 4 kcal/mol for a template consisting of 944 atoms and a sphere containing 160 and 180 waters, respectively. Our calculations demonstrate the important contribution of water to the total free energy. Namely, for water densities close to the experimental value, ΔFwater is always negative leading thereby to negative ΔFtotal (while ΔFloop is always positive). Also, the contribution of the water entropy TΔSwater to ΔFtotal is significant.
Efficiency issues
An inherent inefficiency of HSMC(D) lies in the need to carry out N simulations for reconstructing an N-bond SAW, a peptide with N dihedral and bond angles, or an N-particle fluid treated by HSMC(D)-FV; on the other hand, with HSMC-EV the number of reconstructed cells is much larger than N, and indeed for N=64 argon atoms calculations with HSMC-FV required three times less computer time than with HSMC-EV (White and Meirovitch, 2004; 2008). In all these cases application of HSMC was found to be time consuming, where HSMC is the least efficient method among those applied; for SAWs the best method appears to be the scanning method (White and Meirovitch, 2005). For argon and water TI was found to be ~100 time more efficient than HSMC-EV. As emphasized in the relevant papers, HSMC(D) can still be optimized significantly, but it is fair to say that if one is interested in the absolute free energy of a homogeneous system where the free energy, FR of an “ideal” reference state R is known (e.g., ideal gas for a fluid, or an ideal chain for a SAW) and an efficient integration path from R to the state of interest is available, TI would be a much better choice than HSMC(D). For us the above systems (fluids and SAWs) constitute convenient tools for verifying the theoretical predictions of HSMC(D) as compared to results obtained by other known methods. In this context we note that the integration of is efficient because FR for the free and bound microstates is the same (hence it get canceled in free energy differences) and only the water-loop interaction (based on a fixed loop) is integrated.
The advantage of HSMC over TI will become evident for inhomogeneous systems where a reference state with calculable FR is not available, such as for a long SAW enclosed in small volume with an inhomogeneous shape, for water molecules enclosed in crevices within a protein structure, or for peptides (as mentioned earlier).
However, our main interest is in the difference ΔSmn (and ΔFmn) between microstates, rather than in the absolute S (and F) itself. As has already been pointed out, for any practical set of nf, (or equivalently n’f, and j) and bin sizes, δαk the calculated (and ) will be approximate, and thus the corresponding difference, might be approximate as well. However, if is found to be stable for significantly improving sets of parameters, the stable value can be considered as the correct difference (within the statistical errors). Indeed, in the application of HSMD to peptides (Cheluvaraja and Meirovitch, 2006) and loops (Cheluvaraja and Meirovitch, 2008; Cheluvaraja et al., 2008; Mihailescu and Meirovitch, 2009) relatively small values of n’f and j have already led to stable differences, meaning that the systematic errors in both and are comparable and thus are cancelled in (for convenience we define the deviation, as the systematic error.) For example, for (Gly)10, the nf values studied are between 500 and 24000, where already nf =500 (5 ps) leads to the correct results, as demonstrated in Table 4. (Cheluvaraja and Meirovitch, 2006). In Table 5, it is shown that for the loop of α-amylase results for (equation (46)) decrease systematically (as expected) as the approximation improves (i.e., as δ is decreased and nf is increased), while results for are very stable for all approximations, as has also found for the other systems studied. This cancellation of relatively large systematic errors makes HSMD a relatively efficient procedure for peptides and loops.
Table 4.
Differences in entropy, TΔSA (kcal/mol) between the extended, helical and hairpin microstates of (Gly)10 obtained by HSMDa
| Unit=1500 n=400 | Unit=500 n=400 | Unit=2000 n=200 | Flexible model | ||||
|---|---|---|---|---|---|---|---|
| nf = 24000 | nf = 6000 | nf = 2000 | nf = 1000 | nf = 500 | nf = 6000 | ||
| T(Sextend - Shairpin) | 2.9 (1) | 2.9 (2) | 2.9 (2) | 2.9 (2) | 2.9 (2) | 2.8 (3) | 3.0 (3) |
| T(Sextend - Shelix) | 4.0 (1) | 4.0 (1) | 4.0 (1) | 4.0 (1) | 4.0 (1) | 3.9 (2) | 4.0 (3) |
| T(Shairpin -Shelix) | 1.1 (1) | 1.2 (1) | 1.2 (1) | 1.1 (1) | 1.1 (1) | 1.2 (1) | 1.0 (2) |
The simulations were carried out in vacuum at a low temperature, T=100 K - to keep the system in the three microstates (Cheluvaraja and Meirovitch, 2006). n is the size of the reconstructed MD sample; nf is the sample size of the future chains, nf =jn’f where n’f is the unit size. The statistical error is defined in Table 1. The table shows that the results for TΔSA are very stable i.e., they are equal (within the error bars) for a range of nf values between 24000 and 500. The results for nf=24000 are considered to be the correct results for TΔS. The HSMD results are very close to those obtained by Cheluvaraja and Meirovitch, 2004 using HSMC for the “flexible model” of (Gly)10 where the bond lengths are constant but the bond angles are allowed to change.
Table 5.
HSMD results (in kcal/mol) for the entropy, (equation (46)) and at T=300 K for the free and bound microstates of the loop of α-amylase in explicit watera
| Free loop | Bound loop | |||
|---|---|---|---|---|
| Bin size | nf (j) | |||
| Δαk/15 | 250 (1) | 67.18 (4) | 68.72 (4) | −1.5 |
| “ | 500 (2) | 66.48 (7) | 67.86 (8) | −1.4 |
| “ | 750 (3) | 66.17 (4) | 67.58 (8) | −1.4 |
| “ | 1250 (5) | 65.74 (4) | 67.19 (8) | − 1.4 |
| Δαk/30 | 250 (1) | 67.04 (9) | 68.61 (7) | −1.6 |
| “ | 500 (2) | 66.22 (7) | 67.61 (7) | −1.4 |
| “ | 750 (3) | 65.77 (4) | 67.15 (8) | −1.4 |
| “ | 1250 (5) | 65.19 (4) | 66.49 (3) | − 1.3 |
| Δαk/45 | 250 (1) | 67.03 (4) | 68.60 (5) | −1.6 |
| “ | 500 (2) | 66.17 (7) | 67.56 (7) | −1.4 |
| “ | 750 (3) | 65.69 (4) | 67.08 (8) | −1.4 |
| “ | 1250 (5) | 65.06 (4) | 66.36 (8) | − 1.3 |
| TS QH | 78.6 (1) | 87 (6) | −.8 (7) | |
| TS LS | 87.4 (1) | 90 (7) | −2.6 (8) |
The results are taken from Cheluvaraja et al., 2008. The bin sizes are δ=Δαk/l(equation (44)). nf denotes the sample size of the future chains used in the reconstruction process, nf = unit×j, where j is the number of simulations of unit size applied at each reconstruction step. Generation of the samples (of 600 conformations) and their reconstruction is based on the AMBER force field and 70 TIP3P water molecules. The statistical error in defined in Table 1; for the errors are smaller than ±0.1. SQH (equation (4)) is the quasi-harmonic entropy and SLS is obtained by the local states method using b=2 and the discretization parameter, l=10 (see Appendix). These results that were obtained from larger samples are strongly inaccurate. The entropy is defined up to an additive constant that is expected to be the same for both microstates. As anticipated, the results for decrease systematicallyas the approximation improves (i.e., as δ is decreased and nf is increased). The results for are stable converging to 1.3±0.2 kcal/mol.
The reason for the close systematic errors is the fact that with MD the atoms are moved along their potential gradients and the conformational changes are therefore induced with the same efficiency on both microstates; thus, the extent of coverage of the microstates by the corresponding trajectories is similar. Because HSMD takes all interactions into account, this also applies to the future chains, that for a given nf are treated with the same level of approximation in both microstates. Again, as was noted in a previous section, if one microstate is significantly “flatter” than the other, the required nf value for obtaining convergence of will be determined mainly by the flatter microstate. For peptides treated by HSMD, the systematic errors become comparable for much smaller nf than with HSMC because the efficiency of our MC procedure depends on the compactness of a structure (e.g., an open extended microstate is simulated more efficiently than a compact hairpin microstate and therefore relatively large nf is needed to achieve systematic errors that are equal within the statistical errors). Thus, for (Gly)10, HSMD with nf=500 is ~100 times more efficient (in terms of computer time) than HSMC (Cheluvaraja and Meirovitch, 2004; 2005; 2006). For the loop of AChE we have found that already nf=200 and a relatively small sample of 80 structures (rather than a sample size of ~600 used previously) has led to converging ΔS values. Thus, a reconstruction (based on nf=200) of a single loop conformation surrounded by 160 and 180 water molecules requires 0.92 and 1.05 h CPU, respectively on a 2.1 GHz Atlon processor, which demonstrates a further increase in the efficiency of HSMD by factor of ~20. The computer time for integrating water is, respectively 9.2 and 10.5 h CPU, meaning that the total computer time required is 10.1×80=810 and 11.6×80=924 h CPU. It should be added that calculation of the different reconstruction steps is completely independent and these calculations are also independent of the integration of water. Therefore, the computation of these components can be fully parallelized and the entire calculation can be completed in one day using 75 2.1 GHz Atlon processors. While this time might not be considered short, it should be noted that we are not aware of other studies of the free energy of microstates of loops where the contribution of (explicit) water to F and S has been calculated.
In summary. While HSMC(D) is inherently a time consuming method, one can increase its efficiency dramatically by applying strong approximations (e.g., small nf values) as long as the resulting systematic errors get cancelled in entropy (free energy) differences. The severity of such approximations depends on the specific system and on the statistical errors. Clearly, one has to verify that the future chains do not overflow to neighbor microstates, which can be achieved by verifying that FA increases and σA decreases monotonically as the approximation improves, by analyzing results for Δαk (equation (44)), and by other means.
SUMMARY AND CONCLUSIONS
In this paper we have described the problems involved in calculating the entropy and free energy with the commonly used dynamical MC and MD methods, and discussed in some detail the advantages and disadvantages of the thermodynamic integration (TI) approach. In particular, path-based limitations in TI have led to the development of techniques for computing the absolute F and S, which enable one to calculate ΔFmn=Fm-Fn, from two local simulations of microstates m and n, without the need to carry out a complex reversible (or non-reversible) thermodynamic integration. We then reviewed methods, based on harmonic and quasi-harmonic approximations, for calculating the absolute S (F) and discussed the inherent difficulty to define a microstate in practice.
Based on growth procedures in polymer physics, such as the scanning method, the hypothetical scanning (HS) method was developed, where the growth procedure is used to extract the entropy from an MC sample. After discussing HS, the theoretical basis of the more recent HSMC(D) method was described in detail, together with its application to (non trivial) systems, argon, TIP3P water, and self-avoiding walks (SAWs). In these studies, various theoretical predictions have been verified computationally and by comparison with TI results (and for SAWs by comparison with results of other techniques). Application of HSMC to models of polyglycine with rigid geometry (i.e., constant bond length and bond angles) provided further computational validation of the theory.
Finally, we described the application of HSMD-TI to loops capped with explicit (TIP3P) water, where the contribution of the loop to F is calculated first, followed by calculating F(water) in the presence of a fixed loop structure. However, F(water) was not calculated with HSMD but with a significantly more efficient TI procedure. The most recent application of HSMD-TI to a loop of acetylcholineesterase have led to results which are very close to the experimental value Ffree-Fbound ~ 4 kcal/mol.
Comparing the different techniques, it is fair to state that TI is the most general methodology, which in many cases is also the easiest to implement. Furthermore, various versions of TI (in particular procedures for calculating the relative free energy of ligands bound to an active site) are already programmed in the commonly used molecular mechanics/molecular dynamics software packages. The methods for calculating the absolute F overcome some of the weaknesses of TI, however, they have their own limitations; thus, for an N-atom system the fluctuation in Sm (and practically also in an approximate Fm) is ~N1/2 and for large N estimating small ΔFmn values would be unfeasible. Also, the harmonic approximation (Gō and Scheraga, 1969) and the quasi-harmonic (QH) approximation (Karplus and Kushick, 1981) for calculating the absolute Fm (Sm) are not applicable (at least as yet) to diffusive systems (e.g., water) and further developments in this direction are needed. Moreover, these methods and others do not provide criteria for estimating their accuracy and the QH method should be used with caution (Chang et al., 2005).
In this respect HSMC(D) (White and Meirovitch, 2004; Cheluvaraja and Meirovitch, 2004; 2006) (which still needs further development) has clear advantages: it is applicable to diffusive systems and to any chain flexibility (microstates as well as the random coil state), and it provides self-checking means for estimating its accuracy. The efficiency of HSMC(D) has been improved significantly in recent years and further improvements are anticipated (in particular for fluid systems). For example, HSMC(D) which has been developed thus far within the framework of the TINKER package (Ponder, 2004), is being implemented now within the MM/MD AMBER software (Cornell et al., 1995) in expectation of gaining better efficiency. Our next goal is to extend HSMD-TI for calculating the relative and absolute binding free energies of ligands to enzymes, where HSMC(D) (in the protein environment) will provide a new independent tool, which in some respects, might be better than existing methods. We are studying now the interaction of biotin (and other ligands) to streptavidin,
Finally one should emphasize the strong effects of modeling (in particular of electrostatic interactions) on the results for F (and S) and other thermodynamic and structural properties. In fact, incompatibility of theoretical results with experimental data due to unreliable modeling can be much more severe than method-related inaccuracies in the calculation of F (and S). Therefore, to gain progress in computational structural biology, the existing force fields and solvation models should be improved, more efficient techniques for simulating biological macromolecules should be devised, as well as better techniques for calculating F (and S).
ACKNOWLEDGMENTS
This work was supported by NIH grant 2-R01 GM066090-4 A2.
APPENDIX
The Jensen inequality
The Jensen inequality states that if g is a concave function and then
| (A1) |
The function g(x) = −x ln (x) is a concave function for x > 0 (since its second derivative −1/x is always negative). Defining, xi = PiB / Pi and substituting xi in equation (A1) leads to
| (A2) |
Because Pi0 is also defined over part of the self—intersecting chains, we define a function Pi which is normalized only over the set of SAWs,
| (A3) |
where , 0 < A < 1, and - ln A > 0. Substituting Pi in equation (A2) leads to
| (A4) |
The local states method
The local states (LS) method enables one to calculate the entropy from an MC sample. The method was introduced initially to an Ising model (Meirovitch, 1977). However, we describe it here as applied to a peptide, and for simplicity to (Gly)N of 1≤ αk ≤6N=K dihedral and bond angles, αk ordered along the chain. In the first step the MC sample (of a given wide microstate) is visited and the variability range Δαk (see equation (44)) is calculated. Next, the ranges Δαk are divided into l equal segments, where l is the discretization parameter. We denote these segments by νk, (νk=1,l). Thus, an angle αk is now represented by the segment νk to which it belongs and a conformation i is expressed by the corresponding vector of segments [ν1(i), ν2(i), …, ν6N (i)]. Under this discretization approximation ρ(αk|αk−1 ⋯α1) can be estimated by
| (A5) |
where n(νk ,⋯,ν1) is the number of times the local state [i.e., the partial vector (νk ,⋯,ν1) representing (αk ,⋯,α1)] appears in the sample. Because the number of local states increases exponentially with k one has to resort to approximations based on smaller local states that consists of νk and the b angles preceding it along the chain, i.e., the vector (νk,νk−1,…,νk−b) ; b is called the correlation parameter. The sample is visited for the second time and for a given b one calculates the number of occurrences n(νk,νk−1,…,νk−b) of all the local states from which a set of transition probabilities p(νk| νk−1,…, νk−b) are defined. The sample is then visited for the third time and for each member i of the sample one determines the K local states and the corresponding transition probabilities, whose product defines an approximate probability density ρi(b,l) for conformation i
| (A6) |
the larger are b and l the better the approximation (for enough statistics). ρi(b,l) allows defining an approximate entropy functional, SA, which constitute a rigorous upper bound
| (A7) |
SA leads to a free energy functional, FA, which is a lower bound and its fluctuation decreases as the approximation improves (see equations (15), (21) and (23) and the related discussion). The LS method has been applied to peptides and loops (Meirovitch et al., 1987; 1992; 1994; Meirovitch and Hendrickson, 1997).
REFERENCES
- Alder BJ, Wainwright TE. Studies of molecular dynamics. I. General method. J. Chem. Phys. 1959;31:459–466. [Google Scholar]
- Alexandrowicz Z. Stochastic models for the statistical description of lattice systems. J. Chem. Phys. 1971;55:2765–2779. [Google Scholar]
- Andricioaei I, Karplus M. On the calculation of entropy from covariance matrices of the atomic fluctuations. J. Chem. Phys. 2001;115:6289–6292. [Google Scholar]
- Baysal C, Meirovitch H. Free energy based populations of interconverting microstates of a cyclic peptide lead to the experimental NMR data. Biopolymers. 1999;50:329–344. doi: 10.1002/(SICI)1097-0282(199909)50:3<329::AID-BIP8>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- Baysal C, Meirovitch H. Ab initio structure prediction of a cyclic pentapeptide in DMSO based on an implicit solvation model. Biopolymers. 2000;53:423–433. doi: 10.1002/(SICI)1097-0282(20000415)53:5<423::AID-BIP6>3.0.CO;2-C. [DOI] [PubMed] [Google Scholar]
- Beveridge DL, DiCapua FM. Free energy via molecular simulation: applications to chemical and biomolecular systems. Annu. Rev. Biophys. Biophys. Chem. 1989;18:431–492. doi: 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- Boresch S, Tettinger F, Leitgeb M, Karplus M. Absolute binding free energies: A qualitative approach for their calculation. J. Phys. Chem. B. 2003;107:9535–9551. [Google Scholar]
- Brady J, Karplus M. Configuration entropy of the alanine dipeptide in vacuum and in solution: A molecular dynamics sdudy. J. Am. Chem. Soc. 1985;107:6103–6105. [Google Scholar]
- Carlacci L, Millard CB, Olson MA. Conformational energy landscape of the acyl pocket loop in acetylcholinesterase: A Monte Carlo-generalized Born model study. Biophys. Chem. 2004;111:143–157. doi: 10.1016/j.bpc.2004.05.007. [DOI] [PubMed] [Google Scholar]
- Carlsson J, Åqvist J. Absolute and relative entropies from computer simulation with applications to ligand binding. J. Phys. Chem. B. 2005;109:6448–6456. doi: 10.1021/jp046022f. [DOI] [PubMed] [Google Scholar]
- Chang CE, Gilson MK. Tork: Conformational analysis method for molecules and complexes. J. Comput. Chem. 2003;24:1987–1998. doi: 10.1002/jcc.10325. [DOI] [PubMed] [Google Scholar]
- Chang CE, Chen W, Gilson MK. Evaluating the accuracy of the quasiharmonic approximation. J. Chem. Theory. Comput. 2005;1:1017–1028. doi: 10.1021/ct0500904. [DOI] [PubMed] [Google Scholar]
- Cheluvaraja S, Meirovitch H. Simulation method for calculating the entropy and free energy of peptides and proteins. Proc. Natl. Acad. Sci. USA. 2004;101:9241–9246. doi: 10.1073/pnas.0308201101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheluvaraja S, Meirovitch H. Calculation of the entropy and free energy by the hypothetical scanning Monte Carlo Method: Application to peptides (2005) J. Chem. Phys. 2005;122:054903–14. doi: 10.1063/1.1835911. [DOI] [PubMed] [Google Scholar]
- Cheluvaraja S, Meirovitch H. Calculation of the entropy and free energy of peptides by molecular dynamics simulations using the hypothetical scanning molecular dynamics method. J. Chem. Phys. 2006;125:024905–13. doi: 10.1063/1.2208608. [DOI] [PubMed] [Google Scholar]
- Cheluvaraja S, Meirovitch H. Stability of the free and bound microstates of a mobile loop of α-amylase obtained from the absolute entropy and free energy. J. Chem. Theory Comput. 2008;4:192–208. doi: 10.1021/ct700116n. [DOI] [PubMed] [Google Scholar]
- Cheluvaraja S, Mihailescu M, Meirovitch H. Entropy and free energy of a mobile loop in explicit water. J. Phys. Chem. 2008;112:9512–9522. doi: 10.1021/jp801827f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W, Chang CE, Gilson MK. Concepts in receptor optimization: targeting the RGD Peptide. J. Am. Chem. Soc. 2005;128:4675–4684. doi: 10.1021/ja056600l. [DOI] [PubMed] [Google Scholar]
- Constantine KL, Friedrichs MS, Wittekind M, Jamil H, Chu CH, Parker RA, Goldfarb V, Mueller L, Farmer BT. Backbone and side chain dynamics of uncomplexed human adipocyte and muscle fatty acid-binding proteins. Biochemistry. 1998;37:7965–7980. doi: 10.1021/bi980203o. [DOI] [PubMed] [Google Scholar]
- Conway AR, Enting IG, Guttmann, AJ. Algebraic techniques for enumerating self-avoiding walks on the square lattice. J. Phys. A. 1993;26:1519–1534. [Google Scholar]
- Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A second generation force field for the simulation of proteins,nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- Elber R, Karplus M. Multiple conformational states of proteins - a molecular dynamics analysis of myoglobin. Science. 1987;235:318–321. doi: 10.1126/science.3798113. [DOI] [PubMed] [Google Scholar]
- Friesner RA, Levy RM. An optimized harmonic reference system for the evaluation of discretized path integrals. J. Chem. Phys. 1984;80:4488–4495. [Google Scholar]
- Getzoff ED, Geysen HM, Rodda SJ, Alexander H, Tainer JA, Lerner RA. Mechanisms of antibody binding to a protein. Science. 1987;235:1191–1196. doi: 10.1126/science.3823879. [DOI] [PubMed] [Google Scholar]
- Gibbs W. Elementary Principles in Statistical Mechanics. Yale University Press; 1902. Chapter XI. [Google Scholar]
- Gilson MK, Given JA, Bush BL, McCammon JA. The statistical thermodynamic basis for computing of binding affinities: A critical review. Biophys. J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson MK, Zhou H-X. Calculation of protein-ligand binding affinities. Ann. Rev. Biophys. Biomol. Struct. 2007;36:21–42. doi: 10.1146/annurev.biophys.36.040306.132550. [DOI] [PubMed] [Google Scholar]
- Gō N, Scheraga HA. Analysis of the contribution of internal vibrations to the statistical weights of equilibrium conformations of macromolecules. J. Chem. Phys. 1969;51:4751–4767. [Google Scholar]
- Gō N, Scheraga HA. On the use of classical statistical mechanics in the treatment of polymer chain conformation. Macromolecules. 1976;9:535–542. [Google Scholar]
- Guttmann AJ, Enting IG. The size and number of rings on the square lattice. J. Phys. A. 1988;21:L165–172. [Google Scholar]
- Jorgensen WL. Free energy calculations: a breakthrough for modeling organic chemistry in solution. Acc. Chem. Res. 1989;22:184–189. [Google Scholar]
- Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- Karplus M, Kushick JN. Method for estimating the configurational entropy of macromolecules. Macromolecules. 1981;14:325–332. [Google Scholar]
- Kikuchi R. A theory of cooperative phenomena. Phys. Rev. 1951;81:988–1003. [Google Scholar]
- Kollman PA. Free energy calculations: applications to chemical and biochemical Phenomena. Chem. Rev. 1993;93:2395–2417. [Google Scholar]
- Li Z, Scheraga HA. Monte Carlo recursion evaluation of free energy. J. Phys. Chem. 1988;92:2633–2636. [Google Scholar]
- Madras N, Sokal AD. Nonergodicity of local, length-conserving Monte Carlo algorithms for the self-avoiding walk. J. Stat. Phys. 1987;47:573–595. [Google Scholar]
- McCammon JA, Gelin BR, Karplus M. Dynamics of folded proteins. Nature. 1977;267:585–590. doi: 10.1038/267585a0. [DOI] [PubMed] [Google Scholar]
- Meirovitch H. Calculation of entropy with computer simulation methods. Chem. Phys. Lett. 1977;45:389–392. [Google Scholar]
- Meirovitch H. An approximate stochastic process for computer simulation of the Ising model at equilibrium. J. Phys. A. 1982;15:2063–2075. [Google Scholar]
- Meirovitch H. Methods for estimating the entropy with computer simulation. The simple cubic Ising lattice. J. Phys. A. 1983;16:839–846. [Google Scholar]
- Meirovitch H. The scanning method with a mean-field parameter: Computer simulation study of the critical exponents of self-avoiding walks on a square lattice. Macromolecules. 1985a;18:563–569. [Google Scholar]
- Meirovitch H. Scanning method as an unbiased simulation technique and its application to the study of self-attracting random walks. Phys. Rev. A. 1985b;32:3699–3708. doi: 10.1103/physreva.32.3699. [DOI] [PubMed] [Google Scholar]
- Meirovitch H. Computer simulation of the free energy of polymer chains with excluded volume and with finite interactions. Phys. Rev. A. 1985c;32:3709–3715. doi: 10.1103/physreva.32.3709. [DOI] [PubMed] [Google Scholar]
- Meirovitch H. Statistical properties of the scanning simulation method for polymer chains. J. Chem. Phys. 1988a;89:2514–2522. [Google Scholar]
- Meirovitch H. Calculation of the free energy and entropy of macromolecular systems by computer simulation. In: Lipkowitz KB, Boyd DB, editors. Reviews in Computational Chemistry. Vol. 12. Wiley-VCH; New York: 1998b. pp. 1–74. [Google Scholar]
- Meirovitch H. Simulation of a free energy upper bound, based on the anti-correlation between an approximate free energy functional and its fluctuation. J. Chem. Phys. 1999;111:7215–7224. [Google Scholar]
- Meirovitch H. Recent developments in methodologies for calculating entropy and free energy of biological systems by computer simulation. Curr. Opinion in Struct. Biol. 2007;17:181–186. doi: 10.1016/j.sbi.2007.03.016. [DOI] [PubMed] [Google Scholar]
- Meirovitch H, Alexandrowicz Z. On the zero fluctuation of the microscopic free energy and its potential use. J. Stat. Phys. 1976;15:123–127. [Google Scholar]
- Meirovitch H, Vásquez M, Scheraga HA. Stability of polypeptides conformational states as determined by computer simulation of the free energy. Biopolymers. 1987;26:651–671. doi: 10.1002/bip.360260508. [DOI] [PubMed] [Google Scholar]
- Meirovitch H, Kitson DH, Hagler AT. Computer simulation of the entropy of polypeptides using the local states method: Application to Cyclo-(Ala-Pro-D-Phe)2 in vacuum and the crystal. J. Am. Chem. Soc. 1992;114:5386–5399. [Google Scholar]
- Meirovitch H, Koerber SC, Rivier J, Hagler AT. Computer simulation of the free energy of peptides with the local states method: Analogues of gonadotropin releasing hormone in the random coil and stable states. Biopolymers. 1994;34:815–839. doi: 10.1002/bip.360340703. [DOI] [PubMed] [Google Scholar]
- Meirovitch H, Meirovitch E. New theoretical methodology for elucidating the solution structure of peptides from NMR data. III. Solvation effects. J. Phys. Chem. 1996;100:5123–5133. doi: 10.1002/(sici)1097-0282(199601)38:1<69::aid-bip6>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- Meirovitch H, Hendrickson TF. The backbone entropy of loops as a measure of their flexibility. Application to a ras protein simulated by molecular dynamics. Proteins. 1997;29:127–140. [PubMed] [Google Scholar]
- Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953;21:1087–1092. [Google Scholar]
- Miyamoto S, Kollman PA. Absolute and relative binding free energy calculations of the interaction of biotin and its analogs with streptavidin using molecular dynamics/free energy perturbation approaches. Proteins. 1993a;16:226–245. doi: 10.1002/prot.340160303. [DOI] [PubMed] [Google Scholar]
- Miyamoto S, Kollman PA. What determines the strength of noncovalent association of ligands to proteins in aqueous solution. Proc. Natl. Acad. Sci. USA. 1993b;90:8402–8406. doi: 10.1073/pnas.90.18.8402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson MA. Modeling loop reorganization free energies of acetylcholinesterase: A comparison of explicit and implicit solvent models. Proteins. 2004;57:645. doi: 10.1002/prot.20294. [DOI] [PubMed] [Google Scholar]
- Prazen E. Modern Probability Theory and its Application. Wiley; New York: p. 434. [Google Scholar]
- Ponder JW. TINKER - software tools for molecular design. version 4.2. 2004. [DOI] [PMC free article] [PubMed]
- Qiu D, Shenkin PS, Hollinger FP, Still WC. The GB/SA continuum model for solvation. A fast analytical method for the calculation approximate Born radii. J. Phys. Chem. 1997;101:3005–3014. [Google Scholar]
- Reinhard F, Grubmüller H. Estimation of absolute solvent and solvation shell entropies via permutation reduction. J. Chem. Phys. 2007;126:014102–7. doi: 10.1063/1.2400220. [DOI] [PubMed] [Google Scholar]
- Rini JM, Schulze-Gahmen U, Wilson IA. Structural evidence for induced fit as a mechanism for antibody- antigen recognition. Science. 1992;255:959–965. doi: 10.1126/science.1546293. [DOI] [PubMed] [Google Scholar]
- Rosenbluth MN, Rosebluth AW. Monte Carlo calculation of the average extension of molecular chains. J. Chem. Phys. 1955;23:356–359. [Google Scholar]
- Salsburg ZW, Jacobson JD, Fickett W, Wood WW. Application of the Monte Carlo method to the lattice-gas model. I.Two dimensional triangular lattice. J. Chem. Phys. 1959;30:65–72. [Google Scholar]
- Schäfer H, Mark AE, van Gunsteren WF. Absolute entropies from molecular dynamics simulation trajectories. J. Chem. Phys. 2000;113:7809–7817. [Google Scholar]
- Schlitter J. Estimation of absolute and relative entropies of macromolecules using the covariance matrix. Chem. Phys. Lett. 1993;215:617–621. [Google Scholar]
- Stillinger FH, Weber TA. Packing structures and transitions in liquids and solids. Science. 1984;225:983–989. doi: 10.1126/science.225.4666.983. [DOI] [PubMed] [Google Scholar]
- Stoessel JP, Novak P. Absolute free energies in biomolecular systems. Macromolecules. 1990;23:1961–1965. [Google Scholar]
- Tyka MD, Clarke AR, Sessions RB. An efficient path-independent method for free energy calculations. J. Phys. Chem. B. 2006;110:17212–17220. doi: 10.1021/jp060734j. [DOI] [PubMed] [Google Scholar]
- van Gunsteren WF, Bakowies D, Baron R, Chandrasekhar I, Christen M, Daura X, Gee PJ, Geerke DP, Glättli A, Hünenberger PH, Kastenholz MA, Oostenbrink C, Schenk M, Trzesniak D, van der Vegt NFA, Yu HB. Biomolecular Modeling: Goals, Problems, Perspectives. Angew. Chem. Int. Ed. 2006;45:4064–4092. doi: 10.1002/anie.200502655. [DOI] [PubMed] [Google Scholar]
- Verdier PH, Stockmayer WH. Monte Carlo calculations on the dynamics of polymers in dilute solution. J. Chem. Phys. 1962;36:227–235. [Google Scholar]
- White RP, Meirovitch H. Absolute entropy and free energy of fluids using the hypothetical scanning method.. II. Transition probabilities from canonical Monte Carlo simulations of partial systems. J. Chem. Phys. 2003;119:12096–12105. [Google Scholar]
- White RP, Meirovitch H. Lower and upper bounds for the absolute free energy by the hypothetical scanning Monte Carlo method: Application to liquid argon and water. J. Chem. Phys. 2004;121:10889–10904. doi: 10.1063/1.1814355. [DOI] [PubMed] [Google Scholar]
- White RP, Meirovitch H. Calculation of the entropy of random coil polymers with the hypothetical scanning Monte Carlo method. J. Chem. Phys. 2005;123:214908–11. doi: 10.1063/1.2132285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White RP, Meirovitch H. Free volume hypothetical scanning molecular dynamics method for the absolute free energy of liquids. J. Chem. Phys. 2006;124:204108–13. doi: 10.1063/1.2199529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White RP, Funt J, Meirovitch H. Calculation of the entropy of lattice polymer models from Monte Carlo trajectories. Chem. Phys. Lett. 2005;410:430–435. doi: 10.1016/j.cplett.2005.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]