Abstract
Using the external noise plus training paradigm, we have consistently found that two independent mechanisms, stimulus enhancement and external noise exclusion, support perceptual learning in a range of tasks. Here, we show that re-weighting of stable early sensory representations through Hebbian learning (Petrov et al., 2005, 2006) can generate performance patterns that parallel a large range of empirical data: (1) perceptual learning reduced contrast thresholds at all levels of external noise in peripheral orientation identification (Dosher & Lu, 1998, 1999), (2) training with low noise exemplars transferred to performance in high noise, while training with exemplars embedded in high external noise transferred little to performance in low noise (Dosher & Lu, 2005), and (3) pre-training in high external noise only reduced subsequent learning in high external noise, whereas pre-training in zero external noise left very little additional learning in all the external noise conditions (Lu et al., 2006). In the augmented Hebbian re-weighting model (AHRM), perceptual learning strengthens or maintains the connections between the most closely tuned visual channels and a learned categorization structure, while it prunes or reduces inputs from task-irrelevant channels. Reducing the weights on irrelevant channels reduces the contributions of external noise and additive internal noise. Manifestation of stimulus enhancement or external noise exclusion depends on the initial state of internal noise and connection weights in the beginning of a learning task. Both mechanisms reflect re-weighting of stable early sensory representations.
Keywords: Re-weighting, Hebbian learning, Stimulus enhancement, External noise exclusion, Mechanisms of perceptual learning
1. Introduction
Perceptual learning—performance improvements through training or practice in perceptual tasks—has been documented over a wide range of tasks in all sensory modalities (Fahle & Poggio, 2002). Many studies on perceptual learning have focused on the specificity or transfer of perceptual learning to assess the functional locus of learning (Ahissar & Hochstein, 1996; Ball & Sekuler, 1982; Fahle & Edelman, 1993; Fiorentini & Berardi, 1980; Karni & Sagi, 1991; Liu & Vaina, 1998; Poggio, Fahle, & Edelman, 1992; Seitz, Kim, & Shams, 2006; Shiu & Pashler, 1992; Vogels & Orban, 1985; Xiao et al., 2008). Increasingly, there is also interest in understanding the mechanisms of perceptual learning, that is, what is learned during perceptual learning (Chung, Levi, & Tjan, 2005; Crist, Li, & Gilbert, 2001; Dosher & Lu, 1998, 1999; Fahle & Daum, 2002; Ghose, Yang, & Maunsell, 2002; Gold, Bennett, & Sekuler, 1999; Law & Gold, 2008; Lu et al., 2008; Saarinen & Levi, 1995; Schiltz et al., 1999; Schoups, Vogels, Qian, & Orban, 2001; Schwartz, Maquet, & Frith, 2002; Seitz et al., 2006). Understanding the mechanisms of perceptual learning may provide insights into the nature of plasticity in the adult brain, and may also have profound implications for remediation of perceptual functions in clinical populations (Huang, Zhou, & Lu, 2008; Levi & Li, 2009; Polat, Ma-Naim, Belkin, & Sagi, 2004; Zhou et al., 2006).
Motivated by principles in signal processing and neurophysiology, we developed the external noise plus attention/training paradigm and a theoretical framework based on the perceptual template model (PTM; Fig. 1a) to distinguish mechanisms of attention and perceptual learning (Dosher & Lu, 1998; Lu & Dosher, 1998; see Lu and Dosher (2008) for a recent review). In this approach, perceptual inefficiencies are attributed to three limitations in perceptual processes: imperfect perceptual template(s), internal additive noise, and multiplicative noise. Systematic measurements of human performance as a function of both the amount of external noise added to the signal stimulus and training received by the observers enable us to analyze how perceptual inefficiencies improve over the course of perceptual learning and therefore identify mechanisms of perceptual learning. There are three potential mechanisms. Stimulus enhancement increases the gain to both the signal and external noise in the stimulus and is associated with reduction of absolute threshold and performance improvements in the absence or presence of low external noise (Fig. 1b). External noise exclusion improves the perceptual template(s) to exclude external noise and is associated with performance improvements only in the presence of high external noise (Fig. 1c). Internal multiplicative noise (or gain control) reduction increases system response to stimulus contrast and is associated with improvements throughout the full range of external noise levels (Fig. 1d). Measurements of performance at multiple criterion performance levels (a proxy for full psychometric functions) throughout the course of perceptual learning are necessary to distinguish pure mechanisms and mechanism mixtures (Dosher & Lu, 1999).
Fig. 1.
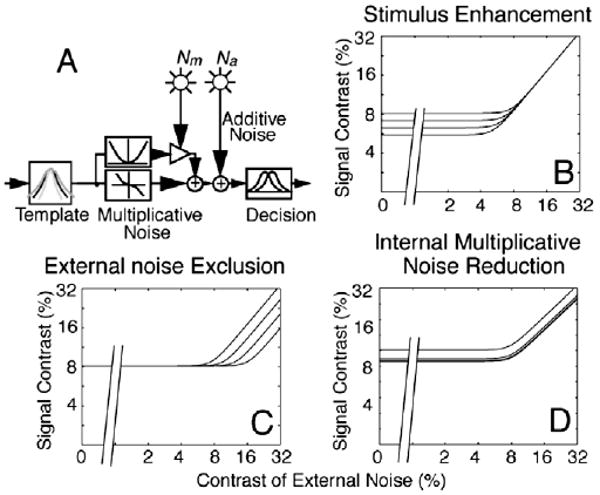
(A) Schematics of the perceptual learning model (PTM). (B) Stimulus enhancement improves performance at low and zero external noise. (C) External noise exclusion improves performance only at high levels of external noise. (D) Internal multiplicative noise improves performance at all levels of external noise, but slightly more so as external noise increases.
In the first application of the external noise plus training paradigm, Dosher and Lu (1998, 1999) investigated mechanisms of perceptual learning in an orientation identification task in the periphery. Virtually identical magnitudes of performance improvements (contrast threshold reduction) were observed at two performance levels. They concluded that the mechanism of perceptual learning consists of a mixture of stimulus enhancement and external noise exclusion rather than multiplicative noise reduction. Essentially the same pattern of results was observed by Gold et al. (1999) at a single performance level in a face identification task, although they came to a different interpretation (see Lu and Dosher (2009) for detailed discussion). Mixtures of stimulus enhancement and external noise exclusion have been reported in other tasks (Lu, Chu, Dosher, & Lee, 2005; Lu, Chu, & Dosher, 2006).
Two additional studies tested the separability of stimulus enhancement and external noise exclusion (Dosher & Lu, 2005; Lu et al., 2006). Using an orientation identification task similar to Dosher and Lu (1998, 1999), Dosher and Lu (2005) found that training in a simple Gabor orientation identification task exhibited an asymmetric pattern of transfer. Training with low noise exemplars transferred to performance in high noise, while training with high noise exemplars – in which target objects were embedded in white external noise – transferred little to performance in low noise. In the other study, Lu et al. (2006) trained their observers in a motion direction identification task in fovea. They found that: (1) Without pre-training, perceptual learning significantly reduced contrast thresholds by about the same amount across all the external noise levels. (2) Pre-training in either zero or high external noise condition significantly reduced contrast thresholds in the corresponding external noise condition. (3) Pre-training in high external noise greatly reduced subsequent learning in high external noise but left subsequent learning in low external noise essentially intact. (4) Pre-training in zero external noise left only little residual learning in all the external noise conditions. To explain the asymmetric pattern of transfer of perceptual learning in clear and noisy displays and different effects of pre-training in low and high external noise conditions, Dosher and Lu (2005) and Lu et al. (2006) hypothesized that (1) the two mechanisms of perceptual learning, external noise exclusion and stimulus enhancement, are independent, and (2) whereas training in high external noise could only improve external noise exclusion, training in zero external noise may substantially improve external noise exclusion and enhance the stimulus.
Based on the results of their initial external noise study on perceptual learning and existing results in the literature, Dosher and Lu (1998) postulated the re-weighting hypothesis in perceptual learning: “perceptual learning primarily serves to select or strengthen the appropriate channel and prune or reduce inputs from irrelevant channels. The connections between the most closely tuned visual channel and a learned categorization structure are maintained or strengthened, while input from other channels is reduced or eliminated.” This claim was also consistent with an earlier commentary made by Mollon and Danilova (1996). Although the re-weighting hypothesis was first outlined in the context of an external noise study of perceptual learning, its focus on the architecture and process of perceptual learning is quite different from that of the external noise/mechanisms studies, which primarily focus on the impact of perceptual learning on intrinsic limitations of perceptual processes. Whether and how channel re-weighting can lead to the various observed patterns of results in the empirical external noise studies on perceptual learning needs to be evaluated. The current study is our first computational investigation of the re-weighting hypothesis in relation to the empirical studies on perceptual learning that explicitly manipulated the amount of external noise.
Our investigation is based on the Augmented Hebbian Re-weighting Model (AHRM) developed by Petrov, Dosher & Lu, (2005). The model is a full multi-channel implementation of the channel re-weighting hypothesis outlined in Dosher and Lu (1998). Originally, the AHRM was developed to provide a computational instantiation of the re-weighting hypothesis and to model the detailed learning dynamics and recurring switch costs of perceptual learning in non-stationary contexts (Petrov et al., 2005). It has since been used to model perceptual learning in non-stationary contexts with and without feedback (Petrov, Dosher & Lu, 2006), interactions between feedback and training accuracy (Liu, Lu, & Dosher, 2008), and the Eureka effect in perceptual learning (Ahissar & Hochstein, 1997, Liu, Lu, & Dosher, 2009; Rubin, Nakayama, & Shapley, 1997). These previous applications all involved tests in high external noise, but did not address the mechanisms of perceptual learning in different external noise environments. In this study, we test the AHRM against empirical results on mechanisms of perceptual learning by applying the AHRM to data from experiments in which external noise was explicitly manipulated. Data from Dosher and Lu (1998, 1999, 2005), and Lu et al. (2006) are considered.
2. AHRM for orientation identification
The multi-channel AHRM is a neural network model of perceptual learning (Petrov et al., 2005, 2006). It consists of four types of units (Fig. 2): representation units that encode input images as activation patterns, task-specific decision units that receive weighted inputs from the representation units, an adaptive bias unit that accumulates a running average of the response frequencies and balances the frequency of the responses, and a feedback unit that makes use of external feedback if feedback is available. Learning in the model occurs exclusively through incremental Hebbian modification of the weights between the representation and decision units, while the early processing pathway that constructs representations from the retinal image remains fixed throughout training. Detailed descriptions of the AHRM can be found in Petrov et al. (2005, 2006). Here we briefly review the major computations in the model.
Fig. 2.
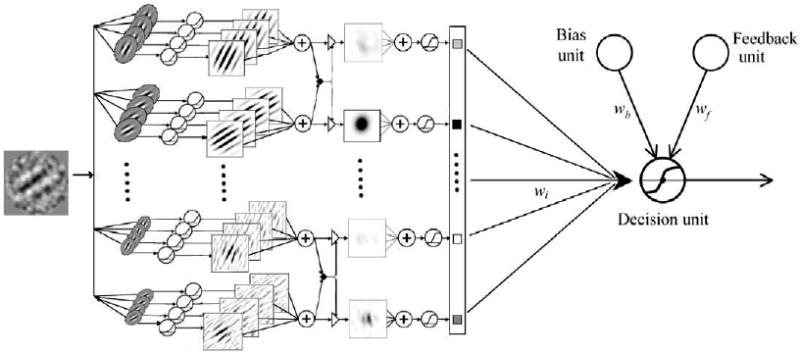
The Augmented Hebbian Re-weighting Model (AHRM). It consists of four types of units: representation units, task-specific decision units, an adaptive bias unit, and a feedback unit. Learning in the model occurs exclusively through incremental Hebbian modification of the weights between the representation and decision units (After Petrov et al., 2005, Fig. 6.).
2.1. Representation subsystem
The representation subsystem consists of 5 × 7 orientation- and frequency-selective units (Fig. 2). The activation A(θ, f) of each of the 35 representation units encodes the normalized spectral energy in the corresponding orientation and frequency channel. First, units tuned to seven different orientations θ (with half-amplitude full-bandwidth hθ), five spatial frequencies f (with half-amplitude full-bandwidth hf), and four spatial phases φ ∈ {0°, 90°, 180°, 270°} compute a set of phase-sensitive maps S(x, y, θ, f, φ) of the input image I(x, y):
| (1) |
Because spatial phase is not relevant in orientation identification tasks, the model aggregates across phases in each channel at each spatial location and uses shunting inhibition to obtain normalized outputs (Heeger, 1993):
| (2) |
| (3) |
where ε1 represents a Gaussian-distributed internal noise source with mean 0 and standard deviation σ1, the normalization pool N(f) is a weighted sum of S(x, y, θ, f, φ). It is assumed to be essentially independent of orientation and modestly tuned for spatial frequency, a is a scaling factor, and k is the saturation constant that is relevant only at near-zero contrasts.
The energy maps were then pooled across space, weighted by a radial symmetric Gaussian kernel Wr with full-width at half-height hr, commensurate with the size of the target signal:
| (4) |
where ε2 represents another Gaussian-distributed noise source with mean 0 and standard deviation σ2.
Finally, an activation function with gain parameter γ was used to limit the dynamic range of the representation units.
| (5) |
2.2. Task-specific decision subsystem
The decision unit aggregates the sensory information using the current weights wi and the current top-down bias b:
| (6) |
where Gaussian-distributed noise εd with mean 0 and standard deviation σd models the random fluctuations in the decision process. Although the bias unit is very important in accounting for human performance following learning context switches in Petrov et al. (2005, 2006), it was not necessary for modeling the tasks under consideration in this study. We set wb = 0.
The early activation o′ of the unit is a sigmoidal function of the early input u with gain γ:
| (7) |
| (8) |
2.3. Augmented Hebbian learning
Following the response of the task-dependent re-weighting system, feedback—if present—is encoded by the feedback unit and sent as a top-down input to the decision unit. This new input F adds to the early input u in driving the decision unit, which changes its activation to a new, late level o according to the following equation:
| (9) |
The impact of feedback depends upon the weight wf on the feedback input. The late activation is driven to ±Amax = ± 1.0 when feedback F = ± 1 is present and the feedback weight wf = 1.0. When no feedback signal is present (F = 0), the late decision activation is the same as the early decision activation (o = o′), which typically is in the intermediate range.
In the AHRM, the only mechanism for long-term changes operates on the connection weights (wi) between the sensory and decision units. The Hebbian rule is exactly the same both with and without feedback. Each weight change depends on the activation A(θi, fi) of the pre-synaptic sensory unit and the activation o of the post-synaptic decision unit relative to the baseline ō:
| (10) |
| (11) |
| (12) |
Eq. (10) corrects the post-synaptic activation o by its long-term average ō. Thus, the Hebbian term δi tracks systematic stimulus–response correlations rather than mere response bias. Eq. (11) keeps the weights within bounds by scaling δi down in proportion to the remaining range (O'Reilly & Munakata, 2000).
2.4. Model implementation
The AHRM was implemented in MATLAB programs. The model takes the actual stimuli (grayscale images) used in the experiments as inputs, produces binary (left/right) responses as outputs, and learns on a trial-by-trial basis by running exactly the same training procedure, with identical stimuli and schedule, as the human observers in the original empirical studies.
There are a total of 15 parameters in the AHRM. Nine of them were fixed by values used and evaluated in Petrov et al. (2005, 2006). The other six were qualitatively adjusted to approximately match the general data pattern in each empirical study. Our aim was to test whether the AHRM can reproduce the general patterns in the empirical data, with tests in both low and high external noise. Data of representative subjects from each empirical study was overlaid on model results. We did not attempt to computationally optimize fits to any particular dataset; further efforts would only improve the match to the data. For groups with different training procedures in each empirical study, we kept most of the model parameters, especially the learning rate, the same. Only the gain factor and standard deviations of the internal noises were adjusted to obtain the different overall ranges of thresholds for different subjects. Following Petrov et al. (2005), we set the initial weights of the AHRM in proportion to the preferred orientation of the units: wi = (θi/30°)winit to represent subjects' prior knowledge of the orientations. Testing with different magnitude and shape of initial weights showed that the simulation results are largely invariant. The AHRM was simulated 100 times in each experimental procedure. We report the mean and standard deviation of the model performance.
To gauge the time course of the learning process, i.e., the quality of the connection weights in each trial wi(t), we computed the following metric:
| (13) |
where are the “optimal” weights obtained by training the AHRM in the zero external noise condition for 200,000 trials, long after the weights reach their asymptotic levels.1 R(t) quantifies the similarity of the weights wi(t) to the optimal weights in trial t.
3. Simulation studies
3.1. A Mixture of stimulus enhancement and external noise exclusion
Dosher and Lu (1998, 1999) investigated mechanisms of perceptual learning in an orientation identification task in the periphery. Observers identified the orientations of peripheral Gabor patches embedded in eight levels of external noise while performing a concurrent letter identification task at fixation. Accuracy feedback for both tasks was presented on every trial. Perceptual learning was measured in terms of changes of contrast thresholds using two interleaved adaptive staircases yielding 79.3% and 70.7% accuracies in every external noise condition. Four observers ran a single session per day for 10 days, with 1440 trials per session, consisting of 100 trials for each 3:1 staircase and 80 trials for each 2:1 staircase. For the average observer, practice reduced contrast thresholds at both 79.3% and 70.7% correct by about 63.8 ± 1.8% and 69.1 ± 1.6% in the four lowest and two highest external noise conditions, respectively. According to the PTM, the strong invariance of the log magnitude of perceptual learning for the two criterion performance levels implies no change in multiplicative noise or non-linearity. Dosher and Lu (1998, 1999) concluded that a mixture of stimulus enhancement and external noise exclusion underlies the observed perceptual learning.
The signals in the perceptual learning task in Dosher and Lu (1998, 1999) were Gabor patterns tilted ±12° (or of vertical (Fig. 3A):
Fig. 3.
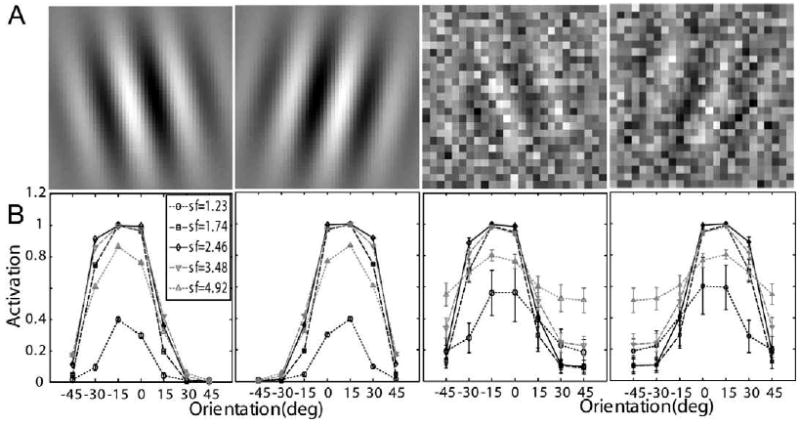
(A) Representative stimuli used in Dosher and Lu (1998, 1999): left and right titled Gabors with 100% contrast embedded in zero and high external noise. (B) Corresponding neural network activation patterns (Eq. (5)) of the stimuli shown in (A).
| (14) |
where background luminance l0 = 71.0 cd/m2, Gabor center frequency f = 2.3 c/deg, Gabor spatial window σ = 0.385°. The peak contrast c was set by the adaptive staircase procedures. The Gabors were rendered on a 64 × 64 pixel grid, extending 1.54 × 1.54° of visual angle. The center of the Gabor was displaced from the fixation by 2.4° vertically and 3.3° horizontally. External noise images (1.54 × 1.54°) were constructed from 0.048 × 0.048° pixel patches with identically distributed contrasts drawn independently from Gaussian distributions with mean 0 and standard deviation Next ∈ {0, 0.02, 0.04, 0.08, 0.12, 0.16, 0.25, 0.33}. A sample with the maximum standard deviation of 0.33 conforms reasonably well to a Gaussian distribution. External noise and signal Gabors were combined via temporal integration. In each trial, the peripheral stimulus consisted of two frames (16.7 ms/frame) of external noise images, a signal frame with a Gabor patch tilted either left or right, and two additional frames of external noise images. All noise samples in each trial were independent samples with the same variance.
We simulated the ARHM using exactly the same experimental procedure in Dosher and Lu (1998, 1999). Perfect summation of the signal and external noise frames was assumed in the simulation. The parameters of the AHRM are listed in Table 1. The scaling factor and half saturation point of contrast-gain control, the noise variances, and the learning rate were qualitatively adjusted to approximately match the general data pattern of one typical subject (KM) in Dosher and Lu (1999).
Table 1.
Model parameters.
| Parameter | Value | |||
|---|---|---|---|---|
| Parameters set a priori | Orientation spacing, Δθ | 15°, 15°, 30° | ||
| Spatial frequency spacing, Δf | 0.5 octave | |||
| Maximum activation level, Amax | 1 | |||
| Weight bounds, wmax, wmin | ±1 | |||
| Initial weights scaling factor, winit | 0.0563 | |||
| Activation function gain, γ | 5 | |||
| Orientation bandwidth, hθ | 30° | |||
| Frequency bandwidth, hf | 1.0 octave | |||
| Radial Kernel width, hr | 2.0 dva | |||
| PNAS'98 | PNAS'05 | VR'06 | ||
| Parameters adjusted for the data | Normalization constant, k | 6e–7 | 1e–7 | 3e–6 |
| Scaling factor, a | 0.175 | 0.17, 0.35 | 0.033,0.5,0.13 | |
| Internal noise 1, σ1 | 1.05 × 10−7 | (4.8, 13) × 10−8 | (1.5, 2.0, 1.5) × 10−6 | |
| Internal noise 2, σ2 | 0 | 0.0005, 0.0006 | 0.04, 0, 0.05 | |
| Decision noise, σd | 0.0875 | 0.0006, 0.014 | 0 | |
| Learning rate, η | 0.00015 | 0.0006 | 0.0001 | |
Rendering of the sample perceptual learning stimuli with and without external noise are shown in Fig. 3A. Activation levels (Eq. (5)) of the 35 channels of the AHRM for a signal Gabor with 100% contrast and embedded in zero and 33% external noise are plotted in Fig. 3B. The activation pattern in the high external noise condition is much broader and with much larger standard deviations (0.033 vs. 0.092 in the zero and highest external noise conditions, respectively), reflecting contributions of external noise.
Performance of the AHRM matched the general data pattern of KM: averaged over 70.7% and 79.3% correct, ten sessions of perceptual learning reduced AHRM's contrast thresholds by 39.4 ± 2.6% and 45.5 ± 2.7% in the four lowest and two highest external noise conditions, respectively. In comparison, ten sessions of perceptual learning reduced KM's contrast thresholds by 49.8 ± 5.1% and 56.7 ± 4.5% in those conditions. The AHRM also exhibited a major property observed by Dosher and Lu (1998, 1999)—the amount of threshold reduction was about the same at the 70.7% and 79.3% correct performance levels: 38.1 ± 3.8% and 40.6 ± 3.6% in the lowest four external noise conditions, and 43.7 ± 3.7% and 47.3 ± 3.7% in the two highest external noise conditions. The invariance of the magnitude of perceptual learning at the two criterion performance levels has been used by Dosher and Lu (1998, 1999) to imply no change in multiplicative noise or non-linearity based on the PTM. Although the AHRM has not been systematically optimized for the particular dataset, but just qualitatively for the level of the initial measurements, the model accounted for 95.3% of the variance in the data (Fig. 4).
Fig. 4.
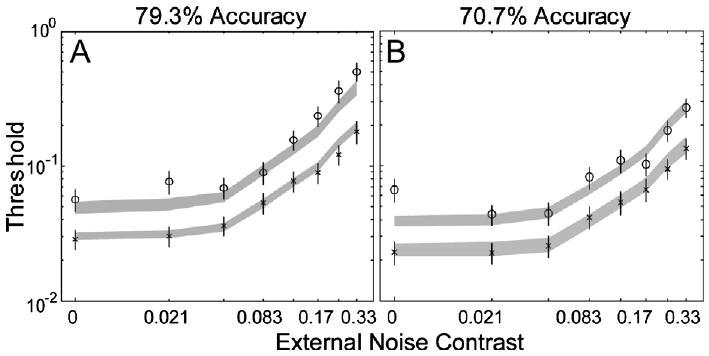
Average threshold vs. external noise (TvC) functions in day 1/2 (circles) and day 9/10 (crosses) at 79.3% (A) and 70.7% (B) correct performance levels. The data points are adopted from (Dosher and Lu (1999); subject KM). The shaded regions represent the confidence interval (±1 SD) of the AHRM predictions.
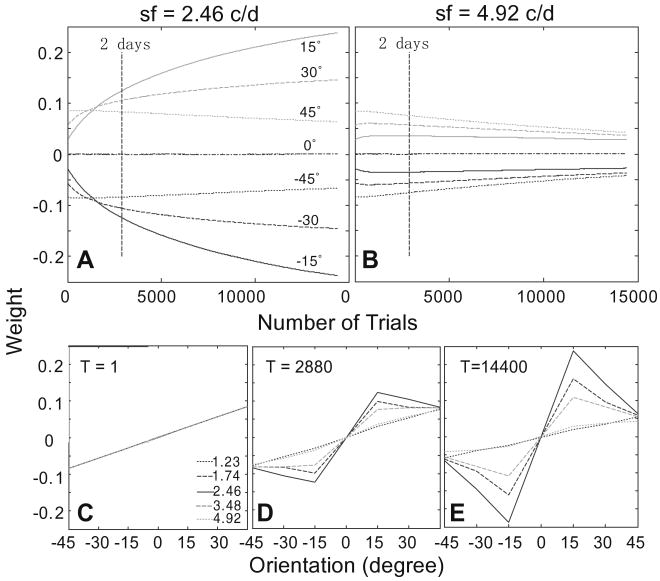
The time courses of the weights of the AHRM units tuned to the target spatial frequency (2.46 c/deg) and to an irrelevant spatial frequency (4.92 c/deg) are plotted in the top row of Fig. 5. Throughout the course of training, the weights of the relevant channels increased and the weights of the irrelevant channels decreased. Snapshots of the weights in all the 35 channels are plotted in the bottom row of Fig. 5, showing weights in the beginning (T = 1 trial), after 2 days (T = 2880 trials), and 10 days (T = 14,400 trials) of training. The time course of weight improvements can be clearly seen in Fig. 6A: similarity to the optimal weights, R(t), improved from 0.17 in the beginning of training to 0.67 in the end of training through a protocol matched to the extent of training in the experiment.
Fig. 5.
(A and B) The time courses of the weights of the AHRM units tuned to the target spatial frequency (A) and to an irrelevant spatial frequency (B). (C–E) Snapshots of the AHRM weights in all the 35 channels in the beginning (C), after 2 days (D), and 10 days (E) of training.
Fig. 6.
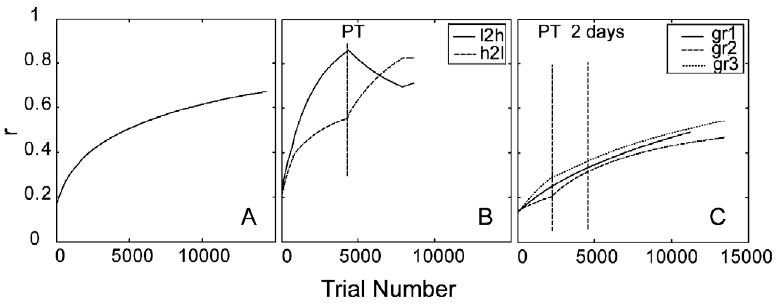
Similarity of the weights to optimal weights as a function of trial number for simulation study 1 (A), study 2 (B), and study 3 (C).
Through Hebbian learning in a wide range of external noise levels, the ARHM re-tuned its weights to better match the input signals, i.e., the difference between the activation patterns of the left- and right-oriented Gabors aggregated across external noise levels. In the ARHM, re-weighting may lead to distinct forms of improvement in different external noise conditions because increasing the weights of all of the channels will decrease the impact of the internal decision noise and increasing the impact of the signal channel relative to the irrelevant channels will reduce the impact of external noise and the other two internal noise sources (ε1 and ε2). Therefore, in zero and low external noise conditions, re-weighting amplifies the internal representations of the Gabor signals relative to the internal noises in the model, corresponding to stimulus enhancement in the PTM. In high external noise conditions, re-weighting reduces the impact of external noise through reduction of the weights of the irrelevant channels, corresponding to external noise exclusion in the PTM. The ARHM is also able to reproduce a key feature of the data in Dosher and Lu (1998, 1999) (and in the PTM model)—the magnitude of learning was essentially the same in two performance accuracy levels.
3.2. Asymmetric transfer of perceptual learning between high and low external noise
Using a task very similar to Dosher and Lu (1998, 1999), Dosher and Lu (2005) investigated whether improvements in the two external noise regimes could be trained separately. Six observers discriminated the orientation of peripheral Gabor patches embedded in either zero or high external noise while performing a concurrent central letter identification, fixation task. Perceptual learning was assessed by measuring contrast thresholds at two criterion performance levels (70.7% and 79.3% correct) using two interleaved staircases, with 100 trials in the 3:1 staircase and 80 trials in the 2:1 staircase in each experimental block. Observers were divided into two groups. Both groups ran two intermixed pre-test blocks of zero and high external noise in the beginning of the study. This was followed by 20 blocks of training in either the zero external noise condition (Group 1) or the high external noise condition (Group 2), and then 10–20 blocks of transfer tests in the other noise condition.
Observers in both groups showed substantial perceptual learning. Described as a linear function of log 10 contrast threshold vs. log 10 practice blocks, the slope of the learning curves were between −0.12 and −0.65 for observers trained in zero noise, and between −0.24 and −0.64 for observers trained in high external noise. Training in zero external noise strongly benefited performance in high external noise. The difference between thresholds in the pre-test blocks and the first block of the transfer test averaged 0.42 log units. Additional training in high external noise during the transfer test did not further reduce contrast thresholds. However, training in high external noise did not reliably benefit performance in zero external noise. Subsequent training in zero noise during the transfer test resulted in additional learning, with an average slope of −0.12, typical of initial low-noise training.
The signals in the perceptual learning task in Dosher and Lu (2005) were Gabor patterns tilted ±8° (or ) of vertical (Fig. 7A):
Fig. 7.
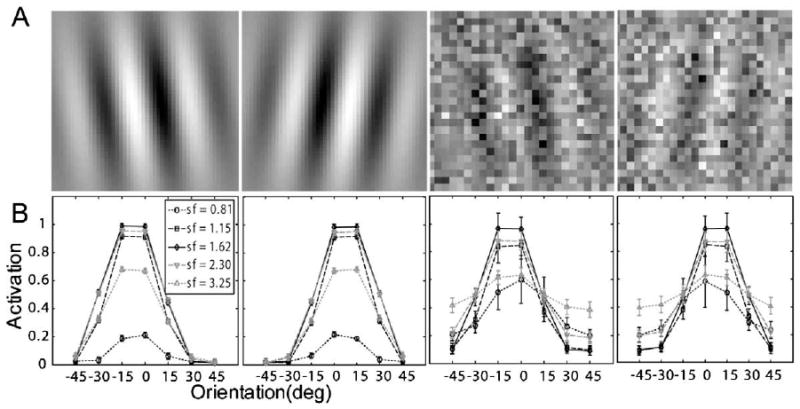
(A) Representative stimuli used in Dosher and Lu (2005): left and right titled Gabors with 100% contrast embedded in zero and high external noise. (B) Corresponding neural network activation patterns (Eq. (5)) of the stimuli shown in (A).
| (15) |
where background luminance l0 = 19.5 cd/m2, center frequency f = 1.6 c/deg, spatial window σ = 0.6°. The peak contrast c was set by the adaptive staircase procedures. The Gabors were rendered on a 64 × 64 pixel grid, extending 2 × 2° of visual angle. The center of the Gabor was displaced from the fixation by 2.4° vertically and 3.3° horizontally. External noise images (2 × 2°) were constructed from 0.063 × 0.063° pixel patches with identically distributed contrasts drawn independently from Gaussian distributions with mean 0 and standard deviation Next ε {0, 0.33}. External noise and signal Gabors were combined via temporal integration. In each trial, the peripheral stimulus consisted of two frames (16.7 ms/frame) of external noise images, a signal frame with a Gabor patch tilted either left or right, and two additional frames of external noise images. All noise samples in each trial were independent samples with the same variance.
We applied the same experimental procedure in Dosher and Lu (2005) to the simulated ARHM model. Perfect summation of the signal and external noise frames was assumed in the simulation. The parameters of the AHRM are listed in Table 1. Of the 15 parameters, nine were fixed and the other six were adjusted to match the general data patterns of one typical subject (JC) in the low to high condition, and another typical subject (KL) in the high to low condition in Dosher and Lu (2005).
Sample stimuli with and without external noise are shown in Fig. 7A. Activation levels (Eq. (5)) of the (seven orientations by five spatial frequencies) 35 channels of the AHRM for signal stimuli embedded in the zero and high external noise conditions are plotted in Fig. 7B. The activation pattern in the high external noise condition is much broader and with much larger standard deviations (0.028 vs. 0.088 in the zero and 33% external noise conditions, respectively), reflecting contributions of external noise. The representation system is fixed during the learning process, while the contributions of the activations of different units to the decision process is re-weighted.
Following Dosher and Lu (2005), a single AHRM threshold at 75% correct in each training block was obtained by averaging the thresholds at 70.7% and 79.3% correct. Learning curves of the AHRM, plotted as log10 (threshold) vs. log10 (block of practice), along with data from representative subjects in Dosher and Lu (2005), are shown in Fig. 8. The learning curves were fit with a linear function of log10 contrast threshold as a function of log10 practice blocks through regression analysis. This is generally consistent with a power law function of practice (Anderson & Fincham, 1994; Logan, 1988). To evaluate if there is significant transfer of learning from training in one (training) external noise condition to the other (transfer) external noise condition, we statistically tested whether learning curves obtained before training and in transfer tests can be described by a single linear function vs. two linear functions. Nested F-tests (Wannacott & Wannacott, 1981) were used: with degrees of freedom kfull − kreduced and n − kfull, where RSS is the residual sum of squared errors for the model. For the full model (two linear functions), kfull = 4; for the reduced model (a single linear function), kreduced = 2.
Fig. 8.
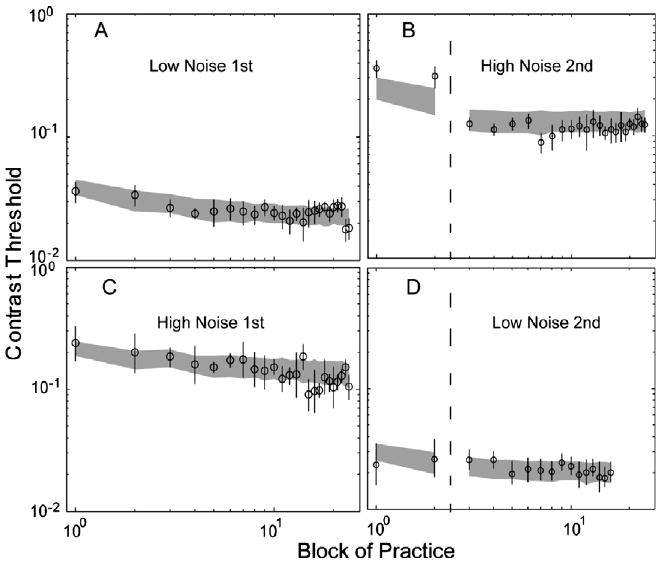
Learning curves—threshold at 75% correct vs. training blocks for subject JC who was trained in zero external noise and then transferred to high external noise (A and B), and subject KL who was trained in high external noise and then transferred to zero external noise (C and D). The data points are adopted from Dosher and Lu (2005). Squares and circles represent data in zero, and high external noise conditions. The shaded regions represent the confidence interval (±1 SD) of the AHRM predictions.
Low to high
The slopes of the AHRM learning curves are −0.15 ± 0.04 and −0.01 ± 0.03 in zero external noise training and high external noise transfer, respectively, comparable to corresponding values of JC: −0.12 ± 0.02 and 0.01 ± 0.02. The small slope during transfer indicates no significant further learning in the high external noise condition after training in low external noise. There is also comparable transfer of learning in the data and the model: contrast threshold in the high external noise condition was reduced by 59.3 ± 4.9% (JC) and 47.5 ± 11.0% (AHRM) between the last block of the pre-test and first block of the transfer, indicating significant transfer of learning in zero external noise to high external noise. For both the AHRM and the subject, two linear functions, one for the pre-training data and the other for the transfer data, provided significantly better fits to the thresholds in high external noise than the single linear function, with F(2, 20) = 46.58 and 11.10 for the data and the model, respectively, and both p < 0.001. This indicates that contrast thresholds in the high external noise condition during transfer tests are not continuations of the learning curve in the pre-test. We conclude that the AHRM generated data patterns closely parallel those of the empirical data. Although the model parameters were only approximately set and not formally optimized for the particular data set, it can account for 96.4% of the variance in JC's data.
The time courses of the weights of the AHRM units tuned to the target spatial frequency (1.62 c/deg) and to an irrelevant spatial frequency (3.25 c/deg) are plotted in the top row of Fig. 9. Training in zero external noise greatly increased the weights of the relevant channels and also decreased the weights of the irrelevant channels. However, further training in high external noise in the transfer phase did not further increase the weights of the most relevant channels, although it did continue to decrease the weights in some irrelevant channels. Snapshots of the weights in all the 35 channels are plotted in the bottom row of Fig. 9, showing weights in the beginning of training (T = 1 trial), after initial training in zero external noise (T = 4680 trials), and after transfer training in high external noise (T = 8640 trials). The weights after initial training in zero external noise (R(1) = 0.22, R(4680) = 0.84) are more similar to the optimal weights than those in the end of the transfer training (R(8640) = 0.71) in high external noise (Fig. 6B). Training in high external noise in the transfer phase actually made the weights less optimal.
Fig. 9.
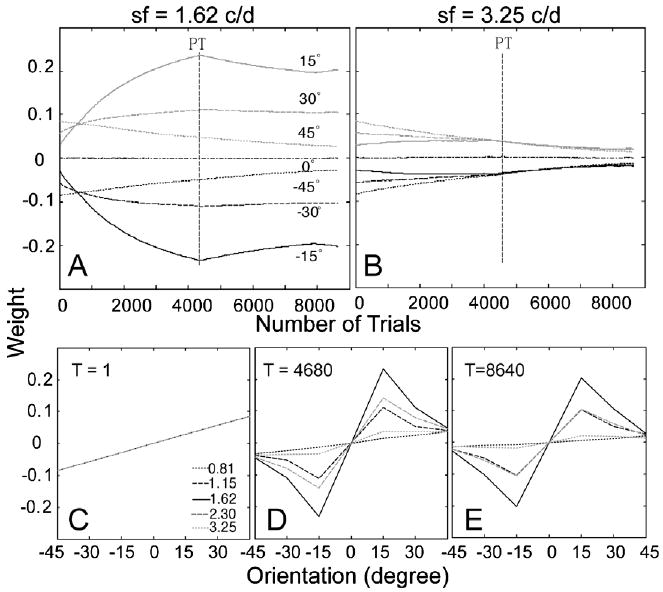
(A and B) The time courses of the weights of the AHRM units tuned to the target spatial frequency (A) and to an irrelevant spatial frequency (B) in the low to high training condition. (C–E) Snapshots of the AHRM weights in all the 35 channels in the beginning of training (C), after initial training in zero external noise (D), and after transfer training in high external noise (E).
High to low
The slopes of the AHRM learning curves are −0.15 ± 0.04 and −0.15 ± 0.03 in high external noise training and zero external noise transfer, respectively, not significantly different from those of KL: −0.23 ± 0.04 and −0.10 ± 0.06 (p > 0.10). The relatively large negative slope during transfer indicates significant further learning in the low external noise condition after training in high external noise. For the AHRM, although there is a 18.7 ± 14.3% of threshold reduction between the last block of pre-training and the first block of transfer in zero external noise, a single linear function provided statistically equivalent fit to the entire learning curve, including data from both pre-training and transfer, compared to the double-linear function (F(2, 12) = 2.70, p > 0.10). The same F-test on KL's data resulted in an F(2,12) = 1.88, p > 0.15. This indicates that, for both the AHRM and the subject, contrast thresholds in the zero external noise condition during the transfer test are statistically indiscriminable from the continuation of a single learning curve in the pre-test, as though the training in high external noise did not happen. We conclude that the AHRM generated data patterns that are qualitatively consistent with the empirical data. Although the model parameters were only approximately adjusted and not formally optimized for the particular data set, it can account for 97.1% of the variance in KL's data.
The time courses of the weights of the AHRM units tuned to the target spatial frequency (1.62 c/deg) and to an irrelevant spatial frequency (3.25 c/deg) are plotted in the top row of Fig. 10. Compared to training in zero external noise (Fig. 9), training in high external noise increased the weights of the relevant channels at a slower pace, although it decreased the weights of the irrelevant channels at about the same rate. Further training in zero external noise in the transfer phase accelerated the increase of the weights of the most relevant channels. Snapshots of the weights in all the 35 channels are plotted in the bottom row of Fig. 10, showing weights in the beginning of training (T = 1 trial), after initial training in high external noise (T = 4680 trials), and after transfer training in zero external noise (T = 8640 trials). Compared to the low to high training protocol, the weights after initial training in high external noise (R(1) = 0.21, R(4680) = 0.61) is less similar to the optimal weights. Training in zero external noise during transfer further improved the weights (R(8640) = 0.83).
Fig. 10.
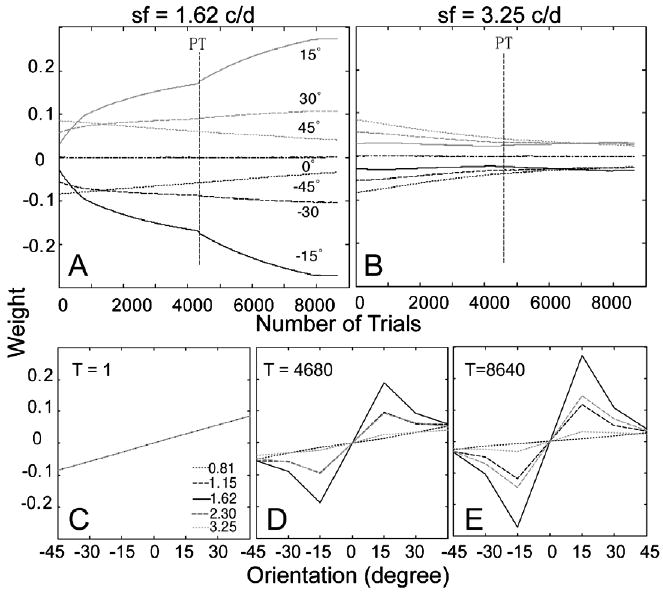
(A and B) The time courses of the weights of the AHRM units tuned to the target spatial frequency (A) and to an irrelevant spatial frequency (B) in the high to low training condition. (C–E) Snapshots of the AHRM weights in all the 35 channels in the beginning of training (C), after initial training in high external noise (D), and after transfer training in low external noise (E).
Training in either zero or high external noise improves the weights in the AHRM and thus performance in both zero and high external noise conditions. However, the efficiency of the improvements under the two training conditions is quite different. Sufficient training in zero external noise can lead to optimal weights, while training in high external noise can never lead to the optimal weights because the external noise in the input stimuli causes the weights to migrate around an approximately optimal state. Although the weights are not optimal following training in zero external noise in the simulation because of the finite number of training trials used in Dosher and Lu (2005), the weights are much better than those following training in high external noise, especially in the region of the signal stimulus. Further training in high external noise adds variability to the convergence to the optimal weights. This explains why there is no further learning in the transfer phase in the low to high condition. On the other hand, the weights following training in high external noise, even after sufficient number of trials, are much less optimal. Additional training in zero external noise can therefore further improve the weights. That is why further learning was observed in the transfer phase in the high to low condition.
3.3. Different effects of pre-training in low and high external noise
Lu et al. (2006) used pre-training manipulations to evaluate the separability of stimulus enhancement and external noise exclusion. In the main experiment, observers were trained to identify the motion direction of a moving sine-wave grating in fovea in eight levels of superimposed external noise in ten daily sessions. Accuracy feedback for both tasks was presented on every trial. Perceptual learning was measured in terms of changes of contrast thresholds using two interleaved adaptive staircases yielding 79.3% and 70.7% accuracies in every external noise condition. Each training session consisted of 1120 trials, with 80 and 60 trials for each of the eight 3/1 and 2/1 staircases, respectively. Prior to the main experiment, the observers were divided into three groups that either received no pre-training (Group I, three observers), pre-training in high external noise (Group II, three observers), or pre-training in zero external noise (Group III, four observers) in the same task. During pre-training, thresholds at 70.7% and 79.3% correct were measured using two interleaved staircases with 160 trials per staircase in a single external noise condition in each session. Observers ran seven sessions on separate days.
Seven sessions of pre-training reduced contrast thresholds by 36.9 ± 5.3% and 44.1 ± 13.0% in Groups II and III, respectively. For Group I, who received no pre-training, virtually identical magnitudes of threshold reduction (40.7 ± 4.5%) were observed in the low and high external noise conditions across 10 days of training, analogous to the prior findings in Gabor orientation identification (Dosher & Lu, 1998, 1999). For Group II, who were pre-trained in high external noise, different magnitudes of threshold reduction were observed in the low and high external noise conditions: contrast thresholds were reduced by 54.9 ± 1.6% and 25.5 ± 5.0% in the four lowest and two highest external noise conditions, respectively, across ten training sessions in the main experiment, although training reduced contrast threshold by a total of 51.8 ± 4.7% in the highest external noise condition from the first day of pre-training to the last day of the main experiment, comparable to the amount of learning in the low noise conditions. Pre-training accounted for about 64.6% of the total threshold reduction in the two highest external noise condition. For Group III, who were pre-trained in the zero external noise condition, only a small amount of threshold reduction (4.7 ± 3.2%) was obtained during the 10 training sessions in the main experiment. Pre-training in zero external noise left very little further performance improvements in the main experiment. Because the magnitudes of threshold reduction were essentially the same at the two criterion performance levels in all the conditions, we concluded that perceptual learning in this study did not lead to any change in multiplicative noise or non-linearity, and a mixture of stimulus enhancement and external noise exclusion underlie the observed perceptual learning in all three groups. We speculated that although stimulus enhancement and external noise exclusion are independent, “pre-training in high external noise only impacted the external noise external noise mechanism, but pre-training in zero noise impacted both stimulus enhancement and external noise exclusion” (Lu et al., 2006, p. 2325).
The motion stimuli used in Lu et al. (2006) consisted of five-frames of moving sinusoidal luminance gratings with 90° phase-shifts between successive frames (Fig. 11A):
Fig. 11.
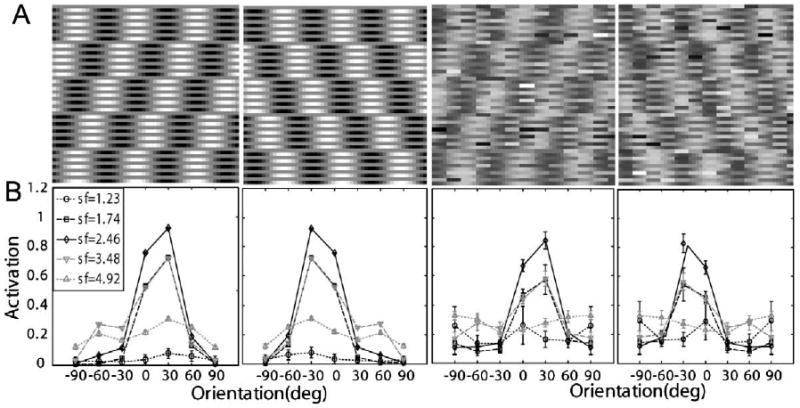
(A) Representative stimuli used in Lu et al. (2006): left and right moving sinewaves with 100% contrast embedded in zero and high external noise. The motion stimuli are shown as texture in x–t space. (B) Corresponding neural network activation patterns (Eq. (5)) of the stimuli shown in (A).
| (16) |
where l0 = 27 cd/m2, f = 3 c/deg, contrast c was determined by the adaptive staircases, and the initial phase (θ ε [0, 2π)) and the direction of motion (λ = ±1) were chosen randomly across trials. The sine-wave gratings were rendered on a 50 × 50 pixel grid, extending 1.54 × 1.54° of visual angle. For each frame of the motion stimuli, an independent external noise image frame of the same size was constructed. Made of 1 by 4 pixels (0.03 × 0.12°), the luminance of each independent patch in the external noise image was drawn independently from a Gaussian distribution with mean l0 and standard deviation σextl0, where σext ∈ {0; 0.02; 0.04; 0.08; 0.12; 0.16; 0.25; 0.33} was determined by the chosen external noise level in a given trial. Signal and external noise images were combined via spatial and temporal sub-sampling and integration: in a given frame, signal and external noise were displayed in alternating 0.03° rows; across frames, the pixels in a given row were alternately drawn from signal and noise images. Each frame lasted 33 ms. The corresponding motion is therefore at 7.5 Hz—a relatively high temporal frequency at which motion is primarily processed by the first-order motion system (Lu & Sperling, 1995, 2001).
Although the original ARHM was developed for an orientation identification task, we can apply the same model to the motion direction identification task in Lu et al. (2006). This is because the computation of motion direction in x–t is equivalent to that of texture orientation in x–y (Adelson & Bergen, 1985), although different orientations in the x–t representation of motion stimuli represent different velocities instead of spatial orientations. Here, we first generated x–y representations of the motion stimuli used in Lu et al. (2006) (Fig. 11A) and then simulated the ARHM with the same experimental procedure. The parameters of the AHRM are listed in Table 1. Of the 15 parameters, nine were fixed and the other six were adjusted to qualitatively match the general data pattern of one typical subject in each of the three groups in Lu et al. (2006). Orientation spacing was set to 30° instead of 15° to model the range of motion directions in the stimuli. It is important to note that the learning rate parameters in the model (η) are the same for the three groups.
Activation levels (Eq. (5)) of the (seven orientations by five spatial frequencies) 35 channels of the AHRM for signal stimuli with 100% contrast and embedded in the zero and the highest level of external noise are plotted in Fig. 11B. The activation pattern in the high external noise condition is much broader and with much larger standard deviations (0.016 vs. 0.099 in the zero and 33% external noise conditions, respectively), reflecting contributions of external noise.
Group I (no pre-training)
Performance of the AHRM matched the general data pattern of TJ: averaged over 70.7% and 79.3% correct performance levels, 10 sessions of perceptual learning reduced the AHRM's contrast thresholds by 47.5 ± 2.3% and 45.8 ± 2.4% in the four lowest and two highest external noise conditions, respectively, comparable to the corresponding values for TJ (46.1 + 5.6% and 39.0 + 6.3%) in those conditions. Similar to the first simulation study, the amount of the AHRM's threshold reduction is about the same at 70.7% and 79.3% performance levels: 45.8 ± 3.9% vs. 49.1 ± 3.3% in the four lowest external noise conditions, and 45.5 ± 3.8% vs. 46.1 ± 3.5% in the two highest external noise conditions. Although only approximately optimized for the particular dataset, the model accounted for 86.7% of the variance in the data (Fig. 12).
Fig. 12.
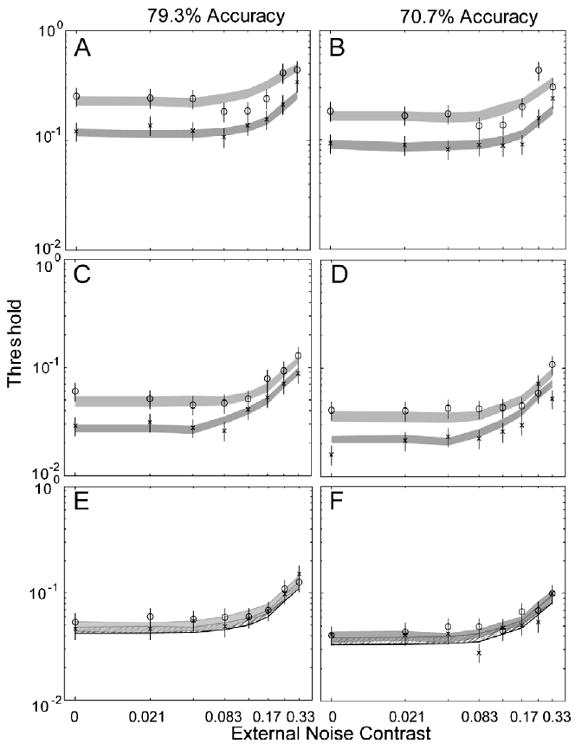
(A and B) Average threshold vs. external noise (TvC) functions in day 1/2 (circles) and day 9/10 (crosses) at 79.3% (A) and 70.7% (B) correct performance levels for subject TJ, who received no pre-training. (C and D) Average threshold vs. external noise (TvC) functions in day 1/2 (circles) and day 9/10 (crosses) at 79.3% (C) and 70.7% (D) correct performance levels for KK during post-training. (EF) Average threshold vs. external noise (TvC) functions in day 1/2 (circles) and day 9/10 (crosses) at 79.3% (E) and 70.7% (F) correct performance levels for IB during post-training. The data are adopted from Lu et al. (2006). The shaded regions represent the confidence interval (±1 SD) of the AHRM predictions.
The time courses of the weights of the AHRM units tuned to the target spatial frequency (2.46 c/deg) and to an irrelevant spatial frequency (4.92 c/deg) are plotted in the top row of Fig. 13. Similar to the first simulation study, simultaneous training in all eight levels of external noise increased the weights of the relevant channels and decreased the weights of the irrelevant channels. Snapshots of the weights in all the 35 channels are plotted in the bottom row of Fig. 13, showing weights in the beginning (T = 1 trial), after 2 days (T = 2240 trials), and 10 days (T = 11,200 trials) of training. Similarity of the weights to the optimal weights improved from R(1) = 0.13 to R(11,200) = 0.49 through 10 days of training (Fig. 6C).
Fig. 13.
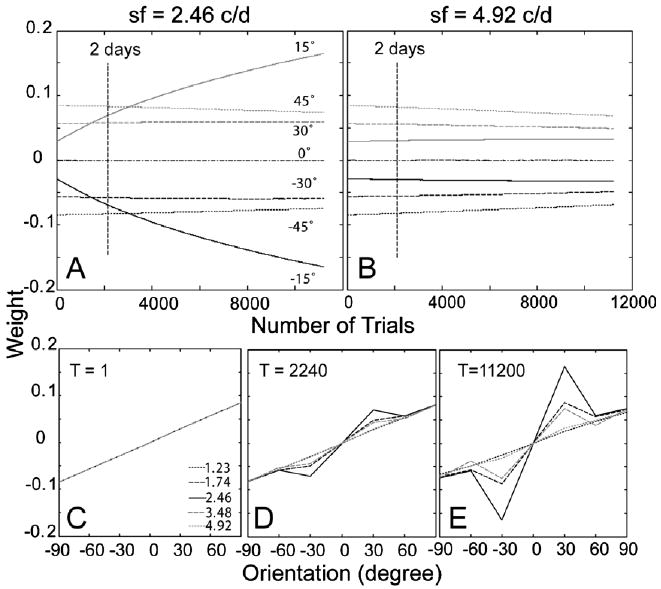
(A and B) The time courses of the weights of the AHRM units tuned to the target spatial frequency (A) and to an irrelevant spatial frequency (B) for Group I (no pre-training). (C–E) Snapshots of the AHRM weights in all the 35 channels in the beginning (C), after 2 days (D), and 10 days (E) of training.
Group II (pre-training in high external noise)
Averaged over 70.7% and 79.3% correct performance levels, pre-training in high external noise reduced the AHRM's contrast thresholds in the highest external noise condition by 24.8 ± 5.3%, comparable to effects of pre-training on KK (26.6 ± 10.8%). Ten sessions of perceptual learning in all eight levels of external noise further reduced AHRM's contrast thresholds by 40.5 ± 2.8% and 23.1 ± 3.3% in the four lowest and two highest external noise conditions, respectively, comparable to the corresponding values for KK (47.1 ± 5.5% and 21.3 ± 8.1%) in those conditions. Consistent with the data, following pre-training in high external noise, the amount of the AHRM's threshold reduction in the highest two external noise levels is much smaller than that in the four lowest external noise conditions (47.1 ± 5.5% vs. 21.3 ± 8.1% for the data, and 40.5 ± 2.8% vs. 23.1 ± 3.3% for the model). The amount of threshold reduction in the highest external noise condition after pre-training accounts for 56.9 ± 3.0% (data) and 46.9 ± 4.5% (model) of the total amount of learning in the highest external noise conditions. Although it has not been optimized for the particular dataset, the model accounted for 90.2% of the variance in the data (Fig. 12).
The time courses of the weights of the AHRM units tuned to the target spatial frequency (2.46 c/deg) and to an irrelevant spatial frequency (4.92 c/deg) are plotted in the top row of Fig. 14. Pre-training in high external noise increased the weights of the relevant channels and decreased the weights of the irrelevant channels. It decreased contrast thresholds in the high external noise condition by 24.8%. Further training in the eight levels of external noise accelerated the increase of the weights of the most relevant channels. Snapshots of the weights in all the 35 channels are plotted in the bottom row of Fig. 14, showing weights after pre-training in high external noise (T = 2240 trial), after first 2 days of training in eight levels of external noise (T = 4480 trials), and in the end of the experiment (T = 13,440 trials). The similarity between the weights and the optimal weights is R(1) = 0.14 in the beginning of training, R(2240) = 0.20 after pre-training in high external noise, and R(13,440) = 0.47 in the end of the experiment (Fig. 6C).
Fig. 14.
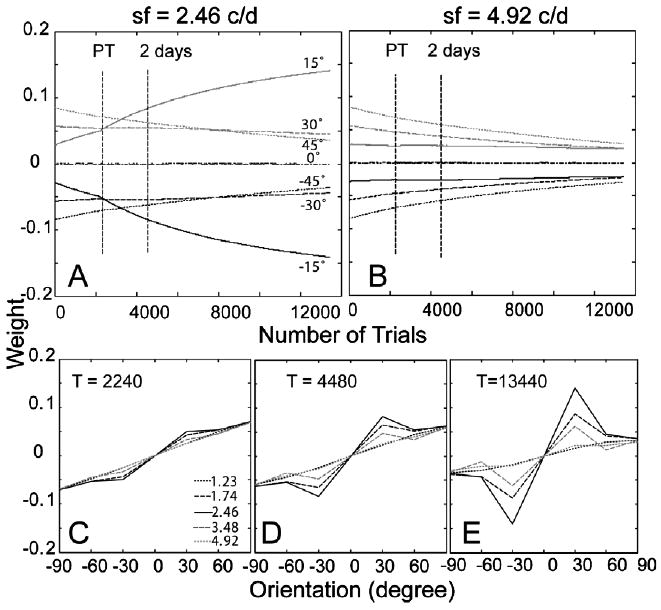
(A and B) The time courses of the weights of the AHRM units tuned to the target spatial frequency (A) and to an irrelevant spatial frequency (B) for Group II (pre-training in high external noise). (C–E) Snapshots of the AHRM weights in all the 35 channels after pre-training in high external noise (C), after 2 days of training in eight levels of external noise (D), and in the end of the experiment (E).
Group III (pre-training in zero external noise)
Averaged over 70.7% and 79.3% correct performance levels, pre-training in zero external noise reduced the AHRM's contrast thresholds in the zero external noise condition by 49.2 ± 3.6%, comparable to its effect on IB (51.2 ± 7.1%). Ten sessions of perceptual learning in all eight levels of external noise further reduced the AHRM's contrast thresholds by 7.5 ± 4.4% and 8.2 ± 4.3% in the four lowest and two highest external noise conditions, respectively, comparable to the corresponding values for IB (15.4 ± 8.7% and 3.9 ± 9.9%) in those conditions. Consistent with the data, following pre-training in zero external noise, there was not much learning left in all the external noise conditions. Although it has not been optimized for the particular dataset, the model accounted for 90.6% of the variance in the data (Fig. 12).
The time courses of the weights of the AHRM units tuned to the target spatial frequency (2.46 c/deg) and to an irrelevant spatial frequency (4.92 c/deg) are plotted in the top row of Fig. 15. Training in zero external noise increased the weights of the relevant channels at a much higher rate. It also decreased the weights of the irrelevant channels. Pre-training decreased contrast threshold by 49.2% in the zero external noise condition. Additional training in eight levels of external noise in the transfer phase further increased the weights of the most relevant channels, but at a slower rate compared to pre-training in zero external noise. Snapshots of the weights in all the 35 channels are plotted in the bottom row of Fig. 15, showing weights after pre-training in high external noise (T = 2240 trial), after first 2 days of training in eight levels of external noise (T = 4480 trials), and in the end of the experiment (T = 13,440 trials). The similarity between the weights and the optimal weights is R(1) = 0.13 in the beginning of training, R(2240) = 0.29 after pre-training in high external noise, and R(13,440) = 0.54 in the end of the experiment (Fig. 6C). Compared to Group II, training in zero external noise (R(2240) = 0.29) is more effective than training in high external noise (R(2240) = 0.20).
Fig. 15.
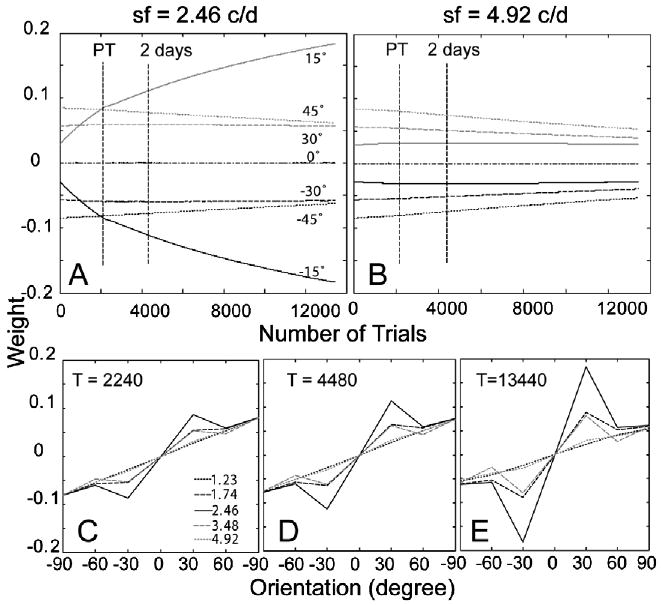
(A and B) The time courses of the weights of the AHRM units tuned to the target spatial frequency (A) and to an irrelevant spatial frequency (B) for Group III (pre-training in zero external noise). (C–E) Snapshots of the AHRM weights in all the 35 channels after pre-training in zero external noise (C), after 2 days of training in eight levels of external noise (D), and in the end of the experiment (E).
Similar to the second simulation study, training in either zero or high external noise improved the weights in the AHRM, benefiting performance in both zero and high external noise conditions. However, the efficiency of the improvements was quite different. Training in zero external noise was much more efficient than training in high external noise. This explains why there was little learning left in the transfer phase after pre-training in zero external noise but quite some learning left in the transfer phase after pre-training in high external noise.
4. Discussion
In this computational study, we simulated the performance of the Augmented Hebbian Re-weighting Model (AHRM; Petrov et al., 2005, 2006) in several experimental procedures that have been developed to evaluate the mechanisms of perceptual learning. The AHRM had previously been used in those studies to model the dynamics of learning and the role of feedback in perceptual learning in the presence of external noise. The focus of the current study was the ability of the AHRM to account for patterns of perceptual learning in different levels of external noise that are associated with the mechanisms of stimulus enhancement and external noise exclusion. We found that the AHRM model can predict a range of data patterns observed in all these empirical studies, including a mixture of stimulus enhancement and external noise exclusion (Dosher & Lu, 1998, 1999), asymmetric transfer of perceptual learning between high and low external noise conditions (Dosher & Lu, 2005), and different impact of pre-training in low and high external noise on the family of threshold vs. external noise contrast functions in subsequent perceptual learning in a full range of external noise conditions (Lu et al., 2006).
The AHRM is a multi-channel implementation of the re-weighting hypothesis outlined in Dosher and Lu (1998). Performance of the AHRM, like that of the perceptual template model (PTM; Dosher & Lu, 1998), is limited by internal noises and non-optimal weights of sensory information. Although the only way to improve performance in the AHRM is through incremental Hebbian modification of the weights between the representation and decision units, the model is capable of predicting all three mechanisms of perceptual learning in the perceptual template model. Improved weights through incremental learning in the AHRM are reflected in terms of contrast threshold reductions in low or high amount of external noise, depending on the initial state of the observer.
In simulation study 1, we showed that strengthening the weights of the relevant channels in the AHRM amplifies the signal in zero and low external noise, corresponding to a stimulus enhancement mechanism of perceptual learning. Over the same time period, trimming the weights of the irrelevant channels in the AHRM reduces the impact of external noise in the high external noise conditions, corresponding to the external noise exclusion mechanism of perceptual learning. The magnitudes of performance improvements in low and high external noise conditions are determined not only by the weights but also differential impacts of internal noises in different external noise conditions and therefore need not be correlated.
We conjecture that different initial weights are necessary for the AHRM to account for the pure mechanism of external noise exclusion observed in a foveal orientation identification task in (Lu & Dosher, 2004) and the pure mechanism of stimulus enhancement observed in a second-order character identification task in (Dosher & Lu, 2007). For example, an AHRM with initial weights wi(1) that are more broadly tuned than the optimal weights yet have the property predicts a pure mechanism of external noise exclusion. An AHRM with initial weights that are nearly optimal in high external noise (such as after pre-training in high external noise) but suboptimal in zero external noise can predict a pure mechanism of stimulus enhancement. These conjectures are currently being tested in new simulation studies.
Because re-weighting is the only way for the AHRM to improve its performance, training in either zero or high external noise may improve the weights if they are suboptimal in both noise conditions. On the other hand, the rates of weight improvements\through training in zero and high external noise conditions are generally quite different – even with an identical learning parameter in the model. These differences reflect the differences in the evidence provided by the different training conditions. With the same internal learning parameter controlling the Hebbian process, the weights in the AHRM improve much more following training in zero external noise than following the same amount of training in high external noise. Sufficient training in zero external noise can lead to weights that are matched to the signal stimuli and optimal, while training in high external noise can never lead to stable and optimal weights because of the external noise in the input stimuli. Once the weights are optimized through training in zero external noise, additional training in high external noise may cause the weights to become suboptimal again. This offers a somewhat different account of the asymmetric transfer between training in high and zero external noise from that of Dosher and Lu (2005) and Lu et al. (2006). In the AHRM, the asymmetry is attributed to the different learning efficiencies in zero and high external noise.
Many researchers have associated perceptual learning with persistent plasticity of sensory representations in early visual cortex (Gilbert, Sigman, & Crist, 2001; Karni & Sagi, 1991; Seitz & Watanabe, 2006; Tsodyks & Gilbert, 2004). However, there is increasing evidence (Ghose et al., 2002; Law & Gold, 2008; Yang & Maunsell, 2004) supporting the proposal that specificity in perceptual learning in the visual system instead reflects re-weighting of stable visual sensory representations to decisions (Dosher & Lu, 1998, 1999; Mollon & Danilova, 1996). In the visual domain, re-weighting or altered readout at higher levels of the visual system is perhaps the dominant mode of perceptual learning (see Dosher & Lu (2009), for a review).
A number of models have been proposed in perceptual learning (Herzog & Fahle, 1998; Petrov et al., 2005, 2006; Vaina, Sundareswaran, & Harris, 1995; Vallabha & McClelland, 2007; Weiss, Edelman, & Fahle, 1993; Zhaoping, Herzog, & Dayan, 2003) (see Tsodyks & Gilbert (2004), for a review). All these models assume an appropriate stimulus representation and postulate incremental learning; none proposes systematic changes in representation. The ARHM (Petrov et al., 2005, 2006) belongs to this class of incremental re-weighting models. In developing and applying the ARHM, we have focused on standard representations, biological plausibility, explicit top-down inputs, and quantitative testing against complex data sets. The ARHM has been used to successfully model the detailed learning dynamics and recurring switch costs of perceptual learning in non-stationary contexts (Petrov et al., 2005), perceptual learning in non-stationary contexts with and without feedback (Petrov et al., 2006), interactions between feedback and training accuracy (Liu et al., 2008), and the Eureka effect in perceptual learning (Liu et al., 2009). Here, we show that the AHRM can also predict the various data patterns in external noise studies of perceptual learning. From a theoretical point of view, integrating the two levels of analysis on perceptual learning, changes of observer limitations in the PTM analysis and the learning process and algorithms in the AHRM, provides support for both theoretical frameworks.
The AHRM has been developed to model perceptual learning in a relative confined spatial region. Although it has been used to model specificity and transfer of perceptual learning across different contexts (Petrov et al., 2005, 2006) and different tasks in a single spatial region (Huang, Lu, & Dosher, 2008), the AHRM needs further development to model specificity and transfer of perceptual learning in different retinal locations. Whereas complete retinal specificity (e.g., (Karni & Sagi, 1991)) suggests completely independent connection weights in different retinal locations and is relatively easy to implement in an AHRM (Dosher & Lu, 2009; Petrov et al., 2005), partial or complete transfer of perceptual learning requires specifications of the relationship between weights in different retinal locations.
Two recent studies provided some important constraints on the architecture of multi-location AHRMs. In one study, Jeter, Dosher, Petrov, and Lu (2009) found that specificity, or conversely transfer, is primarily controlled by the precision demands (i.e., orientation difference) of the transfer task: for an orientation discrimination task, transfer of performance improvement is observed in low-precision transfer tasks, while specificity of performance improvement is observed in high-precision transfer tasks, regardless of the precision of initial training. The results suggest that only the relatively coarse weights common to low- and high-precision tasks transfer. In another study, Xiao et al. (2008) developed a novel double-training paradigm that employed conventional feature training (e.g., contrast) at one location, and additional training with an irrelevant feature/task (e.g., orientation) at a second location, either simultaneously or at a different time. They showed that this additional location training enabled a complete transfer of feature learning (e.g., contrast) to the second location. The authors concluded that perceptual learning could take place in a more central site, but is not transferable to a new location because of the local noise at the new location. We are currently investigating mutli-location AHRMs that incorporate these and other constrains.
Acknowledgments
This research was supported by NEI, NIMH, and NSF.
Footnotes
wi(t) obtained by training the AHRM in the highest external noise conditions for 200,000 trials are inferior to . Contrast thresholds in zero external noise based on wi(t) are about 8% higher than those based on ; Contrast thresholds in the highest external noise condition are about 15% higher.
References
- Adelson EH, Bergen JR. Spatio-temporal energy models for the perception of apparent motion. Journal of the Optical Society America A. 1985;2:284–299. doi: 10.1364/josaa.2.000284. [DOI] [PubMed] [Google Scholar]
- Ahissar M, Hochstein S. Learning pop-out detection: Specificities to stimulus characteristics. Vision Research. 1996;36(21):3487–3500. doi: 10.1016/0042-6989(96)00036-3. [DOI] [PubMed] [Google Scholar]
- Ahissar M, Hochstein S. Task difficulty and the specificity of perceptual learning. Nature. 1997;387(6631):401–406. doi: 10.1038/387401a0. [DOI] [PubMed] [Google Scholar]
- Anderson JR, Fincham JM. Acquisition of procedural skills from examples. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:1340–1372. doi: 10.1037//0278-7393.20.6.1322. [DOI] [PubMed] [Google Scholar]
- Ball K, Sekuler R. A specific and enduring improvement in visual motion discrimination. Science. 1982;218(4573):697–698. doi: 10.1126/science.7134968. [DOI] [PubMed] [Google Scholar]
- Chung STL, Levi DM, Tjan B. Learning letter identification in peripheral vision. Vision Research. 2005;45(11):1399–1412. doi: 10.1016/j.visres.2004.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crist RE, Li W, Gilbert CD. Learning to see: Experience and attention in primary visual cortex. Nature Neuroscience. 2001;4(5):519–525. doi: 10.1038/87470. [DOI] [PubMed] [Google Scholar]
- Dosher B, Lu ZL. Level and mechanisms of perceptual learning: Learning in luminance and texture objects. Vision Research. 2007;46:1996–2007. doi: 10.1016/j.visres.2005.11.025. [DOI] [PubMed] [Google Scholar]
- Dosher B, Lu ZL. Hebbian reweighting on stable representations in perceptual learning. Learning and Perception. 2009;1:37–58. doi: 10.1556/LP.1.2009.1.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosher BA, Lu ZL. Perceptual learning reflects external noise filtering and internal noise reduction through channel reweighting. Proceedings of the National Academy of Sciences of the United States of America. 1998;95(23):13988–13993. doi: 10.1073/pnas.95.23.13988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosher BA, Lu ZL. Mechanisms of perceptual learning. Vision Research. 1999;39(19):3197–3221. doi: 10.1016/s0042-6989(99)00059-0. [DOI] [PubMed] [Google Scholar]
- Dosher BA, Lu ZL. Perceptual learning in clear displays optimizes perceptual expertise: Learning the limiting process. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(14):5286–5290. doi: 10.1073/pnas.0500492102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahle M, Daum I. Perceptual learning in amnesia. Neuropsychologia. 2002;40(8):1167–1172. doi: 10.1016/s0028-3932(01)00231-7. [DOI] [PubMed] [Google Scholar]
- Fahle M, Edelman S. Long-term learning in vernier acuity: Effects of stimulus orientation, range and of feedback. Vision Research. 1993;33(3):397–412. doi: 10.1016/0042-6989(93)90094-d. [DOI] [PubMed] [Google Scholar]
- Fahle M, Poggio T. Perceptual learning. Cambridge, MA: MIT Press; 2002. [Google Scholar]
- Fiorentini A, Berardi N. Perceptual learning specific for orientation and spatial frequency. Nature. 1980;287(5777):43–44. doi: 10.1038/287043a0. [DOI] [PubMed] [Google Scholar]
- Ghose GM, Yang T, Maunsell JHR. Physiological correlates of perceptual learning in monkey V1 and V2. Journal of Neurophysiology. 2002;87(10):1867–1888. doi: 10.1152/jn.00690.2001. [DOI] [PubMed] [Google Scholar]
- Gilbert CD, Sigman M, Crist RE. The neural basis of perceptual learning. Neuron. 2001;31(5):681–697. doi: 10.1016/s0896-6273(01)00424-x. [DOI] [PubMed] [Google Scholar]
- Gold J, Bennett PJ, Sekuler AB. Signal but not noise changes with perceptual learning. Nature. 1999;402(6758):176–178. doi: 10.1038/46027. [DOI] [PubMed] [Google Scholar]
- Heeger DJ. Modeling simple-cell direction selectivity with normalized, half-squared, linear operators. Journal of Neurophysiology. 1993;70(5):1885–1898. doi: 10.1152/jn.1993.70.5.1885. [DOI] [PubMed] [Google Scholar]
- Herzog MH, Fahle M. Modeling perceptual learning: Difficulties and how they can be overcome. Biological Cybernatics. 1998;78:107–117. doi: 10.1007/s004220050418. [DOI] [PubMed] [Google Scholar]
- Huang CB, Lu ZL, Dosher B. Co-learning analysis of two perceptual learning tasks with identical input stimuli supports the reweighting hypothesis. Journal of Vision. 2008;8(6):1123. doi: 10.1016/j.visres.2011.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang CB, Zhou Y, Lu ZL. Broad bandwidth of perceptual learning in the visual system of adults with anisometropic amblyopia. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(10):4068–4073. doi: 10.1073/pnas.0800824105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeter PE, Dosher B, Petrov A, Lu ZL. Task precision at transfer determines specificity of perceptual learning. Journal of Vision. 2009;9(3):1–13. doi: 10.1167/9.3.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karni A, Sagi D. Where practice makes perfect in texture-discrimination – Evidence for primary visual-cortex plasticity. Proceedings of the National Academy of Sciences of the United States of America. 1991;88(11):4966–4970. doi: 10.1073/pnas.88.11.4966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Law CT, Gold JI. Neural correlates of perceptual learning in a sensory motor, but not a sensory, cortical area. Nature Neuroscience. 2008;11:505–513. doi: 10.1038/nn2070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levi DM, Li RW. Perceptual learning as a potential treatment for amblyopia: A mini-review. Vision Research. 2009 doi: 10.1016/j.visres.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Lu ZL, Dosher B. Augmented Hebbian learning hypothesis in perceptual learning: Interaction between feedback and training accuracy. Journal of Vision. 2008;8(6):1124. doi: 10.1167/10.10.29. [DOI] [PubMed] [Google Scholar]
- Liu J, Lu ZL, Dosher B. Augmented Hebbian learning accounts for the Eureka effect in perceptual learning. Journal of Vision. 2009;9(8):851. [Google Scholar]
- Liu Z, Vaina LM. Simultaneous learning of motion discrimination in two directions. Cognitive Brain Research. 1998;6(4):347–349. doi: 10.1016/s0926-6410(98)00008-1. [DOI] [PubMed] [Google Scholar]
- Logan GD. Toward an instance theory of automatization. Psychological Review. 1988;95:492–527. [Google Scholar]
- Lu ZL, Chu W, Dosher BA. Perceptual learning of motion direction discrimination in fovea: Separable mechanisms. Vision Research. 2006;45:2500–2510. doi: 10.1016/j.visres.2006.01.012. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Chu W, Dosher BA, Lee S. Independent perceptual learning in monocular and binocular motion systems. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:5624–5629. doi: 10.1073/pnas.0501387102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu ZL, Dosher B. External noise distinguishes attention mechanisms. Vision Research. 1998;38(9):1183–1198. doi: 10.1016/s0042-6989(97)00273-3. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Dosher B. Characterizing observer states using external noise and observer models: Assessing internal representations with external noise. Psychological Review. 2008;115(1):44–82. doi: 10.1037/0033-295X.115.1.44. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Dosher B. Mechanisms of perceptual learning. Learning and Perception. 2009;1:19–36. doi: 10.1556/LP.1.2009.1.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu ZL, Dosher BA. Perceptual learning retunes the perceptual template in foveal orientation identification. Journal of Vision. 2004;4:44–56. doi: 10.1167/4.1.5. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Sperling G. The functional architecture of human visual motion perception. Vision Research. 1995;35(19):2697–2722. doi: 10.1016/0042-6989(95)00025-u. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Sperling G. Three-systems theory of human visual motion perception: Review and update. Journal of the Optical Society of America A – Optics Image Science and Vision. 2001;18(9):2331–2370. doi: 10.1364/josaa.18.002331. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Xu P, Wang X, Dosher BA, Zhou J, Zhang D, et al. Category and perceptual learning in subjects with treated wilson's disease. Journal of Vision. 2008;8(6):977. doi: 10.1371/journal.pone.0009635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollon JD, Danilova MV. Three remarks on perceptual learning. Spatial Vision. 1996;10(1):51–58. doi: 10.1163/156856896x00051. [DOI] [PubMed] [Google Scholar]
- O'Reilly RC, Munakata Y. Computational explorations in cognitive neuroscience. Cambridge, MA: MIT Press; 2000. [Google Scholar]
- Petrov A, Dosher B, Lu ZL. Comparable perceptual learning with and without feedback in non-stationary contexts: Data and model. Vision Research. 2006;46:3177–3197. doi: 10.1016/j.visres.2006.03.022. [DOI] [PubMed] [Google Scholar]
- Petrov A, Dosher BA, Lu ZL. Perceptual learning through incremental channel reweighting. Psychological Review. 2005;112(4):715–743. doi: 10.1037/0033-295X.112.4.715. [DOI] [PubMed] [Google Scholar]
- Poggio T, Fahle M, Edelman S. Fast perceptual learning in visual hyperacuity. Science. 1992;256(5059):1018–1021. doi: 10.1126/science.1589770. [DOI] [PubMed] [Google Scholar]
- Polat U, Ma-Naim T, Belkin M, Sagi D. Improving vision in adult amblyopia by perceptual learning. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(17):6692–6697. doi: 10.1073/pnas.0401200101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin N, Nakayama K, Shapley R. Abrupt learning and retinal size specificity in illusory-contour perception. Current Biology. 1997;7(7):461–467. doi: 10.1016/s0960-9822(06)00217-x. [DOI] [PubMed] [Google Scholar]
- Saarinen J, Levi DM. Perceptual learning in vernier acuity: What is learned? Vision Research. 1995;35(4):519–527. doi: 10.1016/0042-6989(94)00141-8. [DOI] [PubMed] [Google Scholar]
- Schiltz C, Bodart JM, Dubois S, Dejardin S, Michel C, Roucoux A, et al. Neuronal mechanisms of perceptual learning: Changes in human brain activity with training in orientation discrimination. NeuroImage. 1999;9:46–62. doi: 10.1006/nimg.1998.0394. [DOI] [PubMed] [Google Scholar]
- Schoups A, Vogels R, Qian N, Orban G. Practising orientation identification improves orientation coding in V1 neurons. Nature. 2001;412(6846):549–553. doi: 10.1038/35087601. [DOI] [PubMed] [Google Scholar]
- Schwartz S, Maquet P, Frith C. Neural correlates of perceptual learning: A functional MRI study of visual texture discrimination. Proceedings of the National Academy of Sciences. 2002;99:17137–17142. doi: 10.1073/pnas.242414599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seitz A, Watanabe T. A unified model for perceptual learning. Trends in Cognitive Science. 2006;9:329–334. doi: 10.1016/j.tics.2005.05.010. [DOI] [PubMed] [Google Scholar]
- Seitz AR, Kim R, Shams L. Sound facilitates visual learning. Current Biology. 2006;16(14):1422–1427. doi: 10.1016/j.cub.2006.05.048. [DOI] [PubMed] [Google Scholar]
- Shiu LP, Pashler H. Improvement in line orientation discrimination is retinally local but dependent on cognitive set. Perception and Psychophysics. 1992;52(5):582–588. doi: 10.3758/bf03206720. [DOI] [PubMed] [Google Scholar]
- Tsodyks M, Gilbert C. Neural networks and perceptual learning. Nature. 2004;431:775–781. doi: 10.1038/nature03013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaina LM, Sundareswaran V, Harris JG. Learning to ignore: Psychophysics and computational modeling of fast learning of direction in noisy motion stimuli. Cognitive Brain Research. 1995;2(3):155–163. doi: 10.1016/0926-6410(95)90004-7. [DOI] [PubMed] [Google Scholar]
- Vallabha GK, McClelland JL. Success and failure of new speech category learning in adulthood: Consequences of learned Hebbian attractors in topographic maps. Cognitive, Affective and Behavioral Neuroscience. 2007;7:53–73. doi: 10.3758/cabn.7.1.53. [DOI] [PubMed] [Google Scholar]
- Vogels R, Orban GA. The effect of practice on the oblique effect in line orientation judgments. Vision Research. 1985;25(11):1679–1687. doi: 10.1016/0042-6989(85)90140-3. [DOI] [PubMed] [Google Scholar]
- Wannacott TH, Wannacott RJ. Regression: A second course in statistics. New York: Wiley; 1981. [Google Scholar]
- Weiss Y, Edelman S, Fahle M. Models of perceptual learning in vernier hyperacuity. Neural Computation. 1993;5(5):695–718. [Google Scholar]
- Xiao L, Zhang J, Wang R, Klein S, Levi DM, Yu C. Complete transfer of perceptual learning across retinal locations enabled by double training. Current Biology. 2008;18(24):1922–1926. doi: 10.1016/j.cub.2008.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang T, Maunsell JHR. The effect of perceptual learning on neuronal responses in monkey visual area V4. Journal of Neuroscience. 2004;24(7):1617–1626. doi: 10.1523/JNEUROSCI.4442-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhaoping L, Herzog MH, Dayan P. Quadratic ideal observation and recurrent preprocessing in perceptual learning. Network: Computation in Neural Systems. 2003;14:223–247. [PubMed] [Google Scholar]
- Zhou YF, Huang CB, Xu PJ, Tao LM, Qiu ZP, Li XR, et al. Perceptual learning improves contrast sensitivity and visual acuity in adults with anisometropic amblyopia. Vision Research. 2006;46(5):739–750. doi: 10.1016/j.visres.2005.07.031. [DOI] [PubMed] [Google Scholar]