Behavioral Impact of Graduated Driver Licensing on Teenage Driving Risk and Exposure

Abstract

Graduated Driver Licensing (GDL) is a critical policy tool for potentially improving teenage driving while reducing teen accident exposure. While previous studies demonstrated that GDL reduces teenage involvement in fatal crashes, much remains unanswered. We explore the mechanisms through which GDL influences accident rates as well as its long term effectiveness on teen driving. In particular, we investigate; 1) whether GDL policies improve teenage driving behavior, or simply reduce teenage prevalence on the roads; 2) whether GDL exposed teens become better drivers in later years. We employ a unique data source, the State Data System, which contains all police reported accidents (fatal and non-fatal) during 1990–2005 for twelve states. We estimate a structural model that separately identifies GDL s effect on relative teenage prevalence and relative teenage riskiness. Identification of the model is driven by the relative numbers of crashes between two teenagers, two adults, or a teenager and an adult. We find that the GDL policies reduce the number of 15–17 year-old accidents by limiting the amount of teenage driving rather than by improving teenage driving. This prevalence reduction primarily occurs at night and stricter GDL policies, especially those with nighttime driving restrictions, are the most effective. Finally, we find that teen driving quality does not improve ex-post GDL exposure.

I. Introduction

…“By reducing the risk exposure of teenage drivers and allowing them time to mature before we give them the keys and unlimited use of the car, we will increase the likelihood that they will safely make it through their early driving years. And by creating safer teen drivers today, we also are helping them become safer, more responsible young adult drivers tomorrow…”²

Motor vehicle crashes are the leading cause of death among teenagers. In 2005, a total of 5,300 teenagers 13–19 died in a motor vehicle crash, representing thirty-three percent of deaths among this age group.³ Various studies have attributed this increased risk level to factors such that teenagers have little driving experience, tend to drive at riskier times (nighttime), and usually carry other teenage passengers in their car leading to a distracting environment for the driver.⁴ There is also emerging neurological evidence that regions of the brain governing impulse control, prioritization, and strategy (the dorsal lateral prefrontal cortex) are still “under construction” during teen years and do not develop fully until early 20s (Giedd, 2004). Ultimately, biological or behavioral immaturity may be contributing to teen crash risk.

Over the last 12 years, almost all U.S. states have adopted graduated driver licensing (GDL) policies which have been previously implemented in Australia, New Zealand, and several Canadian provinces as tools to reduce traffic hazards for teenagers. These policies introduce three distinct licensing stages: learner s permit, intermediate license, and full licensure. The first two stages typically involve requirements on the minimum number of hours of supervised driving as well as driving restrictions especially in high risk situations (night-time and with teen passengers). These restrictions are gradually lifted as teen drivers mature and advance to the next stage. The final stage, “full licensure”, removes all the restrictions. The purposes of these policies include expanding the learning process, reducing risk exposure, improving driving proficiency and encouraging safe driving.

The National Committee on Uniform Traffic Laws and Ordinances has developed an ideal system based on the suggestions of the Insurance Institute for Highway Safety. This model recommends that youth are at least 16 to acquire a learner s permit and before advancing to the intermediate license, spend at least 6 months on the learner s permit and log 30–50 hours of supervised driving during this phase. It suggests that the intermediate stage extends until age 18, allows a maximum of one teen passenger, and restricts driving starting at 9 pm or 10 pm. Currently most states have some form of a GDL policy but there is significant variation in their implementation. Some states have introduced all elements of the suggested model while others have introduced only a few components.

Previous literature evaluating the impact of GDL policies of the 1990s has demonstrated the policies effectiveness on reducing teenage involved fatal crashes. However, the mechanisms through which these reductions are achieved are unexplored. In particular, does GDL help improve teen driving, or does it simply limit the number of teens on the road especially in high risk situations? Knowing these mechanisms are fundamental to further improving the design of GDL as well as complementing it with other policies targeted at teen driving. If GDL policies are effective in limiting the amount of teenage driving, then observed reductions in teenage involved crashes may simply be due to this behavioral change rather than to any improvement in teen driving skills. While this may strengthen the case for policies aimed at directly reducing the amount of teen driving as a reliable method for reducing teen accidents, it does trigger the need for further investigation of how other GDL components could be improved to make teens safer drivers. Perhaps GDL policies can be improved by enhancing measures that focus on allowing teens more practice opportunities behind the wheel. For example, the period of time between the first permit and the issuance of the final license could be lengthened. Similarly, supervised driving period could be extended. Moreover, driver improvement courses could be adapted to fit each GDL stage with more basic skills emphasized in the beginner stage and advanced skills in the intermediate stage.

The difficulty in investigating how GDL policies reduce teen fatalities and crashes is due to the unavailability of good estimates of how many teenage drivers are on the roads at any given time, and how that varies with the GDL policies. The Nationwide Personal Transportation Surveys collect self-reported vehicle miles traveled (VMT) data for drivers of all ages but there are two major problems with these surveys. First, the sample sizes are too small to produce reliable geographical estimates for the age group of interest. Second, the surveys are collected only every five years and therefore, the surveys could not capture the variation in the number of drivers due to states adoption of the GDL policies at any given year.

In this paper, we estimate a structural model that separately identifies GDL s effect on the relative teenage prevalence and relative teenage riskiness. We also distinguish between states that implement stricter GDL policies. Finally we evaluate whether GDL policies have long term effects on teenage driving. Our model, similar to Levitt and Porter (2001), relies on data from two-car crashes and the information contained in the relative numbers of crashes between two teenagers, two adults versus a teenager and an adult. These crash frequencies are modeled as a function of the teenage driving exposure and driving risk, both relative to those of adults. Next the relative amount of teenage driving and teenage driving risk are related to the GDL policies as well as other state-year level driving related laws and demographic information. The model is estimated jointly in a two-level hierarchical modeling framework. The primary data source is the State Data System which contains all police reported accidents (fatal, injury and property damage) for 12 states⁵ that provide the data. The study period is from 1990 to 2005.

We find that the GDL policies have reduced the number of 15–17 year-old accidents by limiting the amount of teenage driving rather than by improving teenage driving. More specifically, GDL reduces relative teen prevalence by 5% during the day and 15% during the night. Stricter GDL policies, especially those with night-time restrictions have been significantly more effective in limiting teenage driving at night. Finally, we find that GDL policies do not make teenagers become better drivers in later years. However, future research should revisit this issue as more teens graduate from the GDL policies.

II. Related Literature

Studies to date have primarily focused on understanding the impact of GDL policies on outcomes such as teenage fatalities and teenage crash involvement focusing on 15–17 year olds, or 16-year olds. Based on this literature, there is little doubt that GDL reduces young driver crashes, injuries and deaths. In the United States, earlier studies have examined the effects of GDL policies in a particular state. For example, Ulmer et al (1999) studied Florida, Shope et al (2001) studied Michigan, and Foss et al (2001) studied North Carolina. These three studies report reductions of 9%, 25% and 57% in the crash rates of 16 year-olds respectively. McKnight and Peck (2002) provide an excellent review of GDL related research for specific countries (Sweden, Ontario, Quebec, Nova Scotia, New Zealand) and states (California, Ohio, Connecticut, Florida, Kentucky, Louisiana, Michigan). The general conclusion is that overall crash rates of 16–17 year-olds decline.

More recently, Shope (2007) and Hedlund et al (2006) provide comprehensive reviews of studies that evaluate GDL since 2002. For example, Eisenberg (2003) uses state-by-year panel data for 1982–2000 to primarily study drunk-driving laws, but attributes 4% of the reduction in fatal crash rates involving 16–20 year olds to GDL policies of the states. Dee et al (2005) also use state-by-year panel data from the Fatal Analysis Reporting System (FARS), focusing on the period of significant adoption of the GDL policies between 1990–2002. They report at least a 5.6% reduction in fatal crash rates involving 15–17 year olds and larger crash reductions were achieved in states with more restrictive policies. Chen et al (2006) rely on the same data and find approximately a 20% reduction in the 16-year-old drivers fatal crash involvement rates in states with comprehensive GDL policies. Morrisey et al (2006) apply the same data and framework to rural areas and report an 8% reduction in teenage fatalities among 15–17 year olds on rural roads. Baker et al (2007) study injury crashes as well as fatal crashes and find an 11% reduction in fatal crash involvement and a 19% reduction in injury crash involvement of 16-year olds. Reductions reach up to 40% for both fatal and injury crashes in states with stricter GDL policies. Morrisey et al (2006) study the GDL impact on the number of teenage fatalities in crashes that occur at night-time as well as in crashes with passengers present. Their results suggest a 10–12% reduction in night-time fatalities but this finding has weak statistical power. Restrictions of GDL policies on the number of passengers do not seem to have a strong impact on reducing the number of teen driver fatalities but they reduce the number of passenger fatalities.

The limitation of all the previous literature is the limited evidence they provide on how these reductions are achieved. In particular these studies do not effectively control for GDL s effect on the number of teenagers on the road. It is possible that GDL policies increase the amount of teenagers on the road by increasing the required number of supervised and unsupervised hours driven in learner and intermediate stages. Similarly, the presence of GDL policies might signal safer driving environment and parents might look more favorably to allowing their teens to become younger drivers and take on the road more frequently. On the other hand, the policies may limit the amount of teenage driving by imposing minimum age requirements into each stage, by restricting night-time driving and/or driving with passengers.

Most studies tackle the relative reduction in teenage driving rate by using indices such as “per licensed driver” and “per capita”. For example, they find that per capita crash rates decline up to 30% for 16 year olds and half or more of this figure results from decreases in the proportion of drivers who are licensed since the length of the learner stage is increased. However, per-capita rates and licensed drivers are not good measures. The 16–17 year old population does not change significantly within a state, making it difficult to interpret the effectiveness of the GDL policy using within state variation in the adoption of GDL policy. The annual number of young licensed drivers is not ideal either since before GDL there were only two types of licenses (permit or full license), while after GDL, there are different license types one can have and teens change these license types by month.⁶

III. GDL Policies in the U.S

Currently most states have some form of a GDL policy but there is significant variation in their implementation. Baker et al (2007) dichotomize the main components of the GDL policies similar to suggestions of the Insurance Institute for Highway Safety (IIHS). The IIHS tracks and lists detailed descriptions of GDL policies in the U.S. since 1996. We obtained the data on state GDL laws from Baker et al (2007)⁷ who verified the data with the state government web sites and made edits to reflect changes in GDL programs.

Table 1 lists important components and presents variation across state-year observations regarding the characteristics of the GDL policies for all states (column 1) and for the 12 states used in the analysis (column 2). In all states, 12% of the policies require a minimum age of 16 for obtaining a learner s permit and 76% require at least 6 months of holding the learner permit before being able to advance to the intermediate stage. About half of the GDL policies (55%) require at least 30 hours of supervised driving during the learner stage. In the intermediate stage, 89% have some form of nighttime driving restriction (for example after midnight), and 38% restrict driving in the presence of more than one teenage passenger. The variation in GDL components among the 12 states used in the analysis is similar to the U.S.-wide variation, slightly more restrictive in some aspects such as minimum holding periods, required supervised driving and minimum age of entry into the final stage.

Table 1.

Variation in Components of GDL policies, Conditional on GDL presence

	All States	12-States used in the analysis
Learner Stage
Minimum age of 16	12%	9%
Minimum holding period of 6 months	76%	82%
Minimum 30 hours of supervised driving	55%	69%
Intermediate Stage
Minimum age of 16.5	11%	9%
Restriction on unsupervised night-time driving	89%	91%
No unsupervised driving with >1 passenger <20	38%	36%
Final Stage
Minimum age of 17	69%	79%

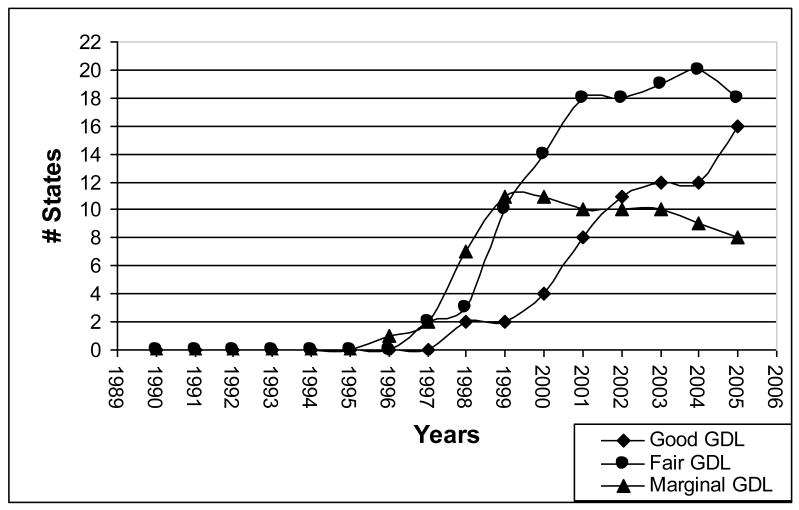
The Insurance Institute of Highway Safety (IIHS) rates each state as “Good”, “Fair”, “Marginal”, or “Poor” based on their licensing system. All states with an intermediate licensing stage are rated at least “Marginal”. Table 2 lists the IIHS criteria for its ratings. Following this scoring system together with the annually updated components of the GDL policies presented in Table 1, we constructed scores and ratings for each of the state-year observations. Figure 1 presents the number of states with each rating over time across the U.S. As the figure shows, adoption of GDL policies dramatically increases over time. While more states implement “Fair” GDL policies than “Good” policies for all years, the number of states with “Marginal” GDL policies decreases over time, suggesting that states move toward stricter policies. By 2005, all states except for six (Arizona, Kansas, Kentucky, Montana, North Dakota and Oklahoma) have implemented a GDL policy.

Table 2.

IIHS Criteria for Ranking GDL policies

Components	IIHS points
Learner’s Entry Age
minimum age of 16	1
Learner’s Holding Period
min. 6 months	2
3–5 months	1
less than 3 months	0
Practice Driving Certification
min. 30 hours	1
Night Driving Restriction
not allowed after 9 pm	2
not allowed after 10 pm	1
Passenger Restriction
1 or less underage passanger	2
1–2 passengers	2
3 passengers or more	0
Duration of Restrictions
min. unrestricted license age minus the min. intermediate license age is more than 12 months	1

Good systems score at least 6 points; Fair systems 4–5 points; Marginal systems 2–3 points; Poor Systems <2 points

Figure 1.

GDL Policies and Ratings across the U.S.

IV. Benchmark Model and Methodology

IV.2. Overview

The primary structural parameters of interest are the relative crash risks and the relative exposure between two age groups: teens and adults. We adopt a methodology building on the model developed in Levitt and Porter (2001), which identified the risks posed by drunk drivers separately from the number of drunk drivers on the road using data on fatal crashes. Our ability to identify the relative crash risks and relative exposure relies on data from two-car crashes and the information contained in the counts of teen/teen, teen/adult, and adult/adult crashes. There are only certain relative risks and exposures that would make a particular collection of crash counts plausible. If many of the accidents involve teen/teen collisions then either the teen relative risk is high or there are many teens on the road relative to adults. The counts of teen/adult and adult/adult crashes can be used to identify how much the number of teen/teen crashes depends on risk and how much depends on exposure.

Let I be an indicator that equals one if two cars interact with the potential for a crash to occur and zero otherwise. For any two drivers of type i and j, Levitt and Porter assume that drivers are equally mixing on the road so that, given that two cars interact, the type of driver in one of the cars is independent of the type of driver in the other car. Specifically,

$$Pr(i,j\backslash I=1)=Pr(i\backslash I=1)Pr(j\backslash I=1)$$

where $Pr(i\backslash I=1)=\frac{N_i}{N_{\mathit{Total}}}$ with N_i denoting the number of drivers of type i on the road and N_Total denoting the total number of drivers of all types on the road.

Equal mixing requires that there is no “clumping” of driver types in space or time. This will be violated if, for example, adult drivers are more likely to interact with other adult drivers for each mile driven, perhaps because they frequent the same locations or drive at the same times of day. The equal mixing assumption is likely valid for a fine enough partition of space and time but will be violated if clumping occurs as the level of aggregation increases. For each state-year, we slice the time scale by hour of the day and by weekday/weekend when modeling prevalence to mitigate the risk of violating this assumption. In addition, we conduct analyses to investigate the sensitivity of our results to this assumption.

Let θ_T represent the probability that a teen causes a two-car accident and θ_A represent the probability that an adult driver causes a two-car accident. The probability of a crash (C) given that two cars interact with the potential for a crash is P(C=1|I=1, i, j) = θ_i + θ_j − θ_i θ_j. Since the probability that both drivers cause an accident is small, the product θ_i θ_j can be dropped. From this probability calculation and the equal mixing assumption we can construct a multinomial likelihood for the counts of teen/teen accidents, teen/adult accidents, and adult/adult accidents. While neither the individual accident rates, θ_T and θ_A, nor the rates of driving exposure, N_T and N_A, are identifiable, Levitt and Porter (2001) show that the relative accident rate, $\theta =\frac{{\theta }_T}{{\theta }_A}$, and the relative exposure, $N=\frac{N_T}{N_A}$, are identifiable from just the two car accident data yielding the likelihood in (1)

$$(C_{TT},C_{TA},C_{AA})\sim \text{Multinomial}\left(C_{\mathit{total}},\left[\frac{N^2\theta }{1+N(1+\theta )+N^2\theta },\frac{N(1+\theta )}{1+N(1+\theta )+N^2\theta },\frac{1}{1+N(1+\theta )+N^2\theta }\right]\right)$$ (1)

where C_ij are the observed counts of each of the three types of accidents: between two teenage drivers, a teenage and an adult driver, and two adult drivers respectively. ⁸

IV.3. Evaluating the Impact of GDL Policies

In principle, for each state by year, one could estimate the relative accident rate, θ, and relative exposure, N, using the method described above. Next, these estimates could be used as dependent variables and regressed on state GDL policies as well as other state-year varying covariates. Levitt and Porter use this two-stage approach to assess the impact of alcohol policies on drunk driving, although they do not account for the potential measurement error on the estimated dependent variables. If the measurement on the left-hand-side variable has a common variance across all observations a correction would not be necessary, but since θ and N are estimated for each state-year pair based on a different number of crash observations, the variance of the measurement error potentially varies by state-year.

We instead take a joint-estimation approach that is not subject to the problem mentioned above and is also more efficient. In particular, we construct a hierarchical model building off of the likelihood in (1) with second level models of the form

$$log({\theta }_{s,t})={\text{GDL}}_{s,t}{\gamma }^{(\theta )}+X_{s,t}{\beta }^{(\theta )}+{\eta }_t^{(\theta )}+{\alpha }_s^{(\theta )}$$ (2)

$$log(N_{s,t})={\text{GDL}}_{s,t}{\gamma }^{(N)}+X_{s,t}{\beta }^{(N)}+{\eta }_t^{(N)}+{\alpha }_s^{(N)}$$ (3)

In (2) and (3), GDL_s,t represents the presence of a GDL policy and its characteristics in state s in year t. X_s,t represents state specific characteristics that vary over time such as the presence of other driving related policies and other macro level variables such as the share of teenage population. The η_t and α_s represent year and state fixed effects to control for time specific and state specific factors unobserved to the researcher. For notational ease, equations (2) and (3) specify the unit of observation to be a state-year pair. In our analysis we expand this framework and allow for θ to vary by state-year-night-time, and equation (2) differentiates the GDL effect by night-time, and includes an indicator variable for night-time observations. The unit of variation for N is specified to be state-year-hour-weekend. Similarly, equation (3) also distinguishes the GDL effect by night time, and includes hour fixed effects as well as weekend fixed effects.⁹

We estimate (1), (2) and (3) jointly using maximum likelihood estimation. Following Bertrand et al. (2004), we cluster standard errors at the state level to account for the potential presence of serial correlation.

IV.3. Data

We use a relatively new dataset called the State Data System (SDS) which has data from 1990–2005. This data is very similar to the Fatal Analysis Reporting System (FARS) data used extensively by previous research on traffic safety. While FARS reports only fatal accidents, SDS includes all police reported crashes and provides information on all persons involved in the crash (age, gender, drinking status etc) as well as detailed information on the crash (location, time, road type, road conditions, number of vehicles involved etc) and on all the vehicles involved (make, model, year).¹⁰

Unfortunately, not all states report to SDS and some that do report do not make the data available for research use. Department of Transportation listed that 22 states report to SDS. We contacted each state, three states responded that data are not available for research purposes, and 12 states responded favorably to our data request. Other states did not respond. Table 3 reports data availability and GDL adoption of the 12 states used in the analysis. Forty-three percent of state-year observations included in the analysis for the 12 states have an effective GDL policy, 32% of these policies are rated “Good”, 28% “Fair” and 40% “Marginal”.

Table 3.

GDL Policies and Data availability for the 12 states used in the analysis

States	Years of Data Availability	Year of GDL Adoption	IIHS Ranking	Notes
AR	1998–2005	2002	Marginal
CA	1991–2004	1998	Good
FL	1991–2004	1996	Marginal	in 2000 changed to Fair
IL	1991–2003	1998	Marginal
MD	1991–2005	1999	Marginal	in 2005 changed to Good
MI	1991–2005	1997	Fair
MO	1991–2005	2001	Marginal
MT	1994–2005	no GDL until 2005		adopted GDL in 2006
NM	1990–2005	2000	Good
PA	1991–2005	1999	Fair
VA	1991–2004	1999	Fair	in 2001 changed to Good
WA	1999–2005	2001	Good

Notes:

1. Illinois, 1996 is not used in the analysis since it contains only “state maintained road crashes” (page B-2 of user manual)

2. Washington 1999–2000 are not used in the analysis since they contain only “state route crashes” (page 4 of user manual)

Given that our identification heavily relies on the different accident types (between two teens, a teen and an adult versus two adults), fatal accidents in FARS did not give us the sufficient sample size on each accident type. Therefore, we decided to use the SDS data despite the fewer number of states responding to our data request.¹¹

We investigated differences between 12 states in our analysis and the remaining states. As Table 4 reports, average population is higher in states used in the analysis relative to those excluded. We did not find any statistically significant difference in the share of men, while excluded states had slightly higher and significantly different representation of teens. Overall fatality rates and teen fatality rates were similar in included and excluded states. Similarly, two groups of states were similar in GDL laws as well as other drinking and driving related laws.

Table 4.

Comparison of 12 states used in the analysis to excluded states (1990–2005)

	States in SDS		States not in SDS		Ho: Means are equal p-values
	Mean	Std. Deviation	Mean	Std. Deviation
Population
Total Population	7,187,904	6,490,368	3,475,646	3,402,268	0
Share of men	0.483	0.007	0.484	0.009	0.18
Share of teens (15–17)	0.054	0.005	0.055	0.007	0.01
Fatalities
Overall fatality rate (per 1,000 individuals)	0.219	0.073	0.221	0.078	0.8
Teen fatality rate (per 1,000 teens)	0.247	0.092	0.260	0.097	0.1
Driving Laws
GDL	0.369	0.474	0.316	0.458	0.18
GDL rated “Good”	0.107	0.308	0.084	0.274	0.37
License Revocation Law	0.762	0.423	0.807	0.392	0.19
BAC 0.08 Law	0.495	0.499	0.439	0.493	0.18
Zero Tolerance Law	0.686	0.456	0.643	0.466	0.26

We define teen drivers as those between ages 15–17 (age cohort directly impacted by GDL policies), and adult drivers as those older than 18. We extract data on the number of two-vehicle crashes by driver type (two teen drivers, a teen and an adult driver, and finally two adults drivers) for each state, year, hour and weekend/weekday observations.

Three different characterizations of the GDL policy are used. First, we use a binary variable indicating the presence of a GDL policy at a given year and state. Second, we examine GDL policies with night-time restrictions and those with no night-time restrictions. Third, we distinguish GDL policies based on the IIHS rating as discussed earlier. In each case, we allow the GDL effect to vary by state-year-night for the relative teen crash risk θ. The relative number of teens on the road, N, is allowed to vary by state, year, hour, and weekend.

We use a set of variables related to the presence of additional driving-related state policies for each year as state specific controls in the estimation of (2) and (3). Similar to Dee (2002), Eisenberg (2003), and Dee et al (2005), we use binary variables that indicate whether it is illegal per se to drive with a blood alcohol concentration (BAC) of 0.08, whether the state has a “zero-tolerance” law,¹² and whether there is a license revocation policy.

We aggregated two-car crashes reported in SDS for each state-year by crash characteristics (driver type, severity, time of day and day of week) to describe our data for each state-year pair. As Table 5 shows, an average state has 99,000 two-car crashes annually of which about 10% occur at night-time (between 9 pm–5 am) and a third of the night-time crashes occur during the weekend. Fatal crashes make up about 0.4% of total crashes while injury crashes constitute 27% and property damage accidents account for the majority with 67%. ¹³

Table 5.

Summary Crash Statistics at the State-Year level for 12 States Included in the Analysis

	Mean	Std. Dev.	Min	Max
Total # of Two-Car Crashes
All	99109	71882	8835	270693
Night-time	9928	7123	651	25736
Night and Weekend	3630	2637	232	9372
Fatal	417	321	42	1201
Injury	26912	14279	954	53652
Property Damage-Only	66638	51090	7687	190581
Two Teen Drivers	714	545	84	2098
A Teen and an Adult Driver	10074	6903	1585	24898
Two Adult Drivers	88320	65085	6878	250105
Fatal, Two Teen Drivers	1	1	0	7
Fatal, A Teen and an Adult Driver	33	23	2	102
Fatal, Two Adult Drivers	383	299	36	1127

Notes:

1. Night-Time is characterized as 9 pm–5am

2. There are 160 state-year observations

Among all two-car accidents, 88,320 (89%) involve two adult drivers, 10,074 (10%) involve one-teen and one adult driver, and about 714 (1%) involve two teen drivers. This suggests that overall 11% of the two car accidents involve at least one teenage driver between ages 15–17. If we restrain the analysis to fatal crashes, only 1 crash in a state-year observation on average involves two teen drivers and 33 involve a teen and an adult. This supports our argument earlier on why we chose to estimate the model using all crashes in SDS instead of just relying on fatal crashes provided in FARS.

V. Results

Table 6 presents three different models that estimate parameters of slightly modified equations (2) and (3), the “risk equation” and the “prevalence equation” respectively. In the risk equation the dependent variable can be viewed as log(θ), teens likelihood of causing an accident relative to adults. The prevalence equation specifies the number of teens on the road relative to adults, log(N), as the dependent variable. As discussed earlier, these two equations are estimated simultaneously embedded in a hierarchical maximum likelihood framework which specifies probabilities of observing crashes by two teens, one teen and an adult, and two adults. The unit of observation is a two-car crash, but in practice the likelihood function uses the number of accidents of different driver types for each state-year-hour-weekend cell.

Table 6.

Joint Hierarchical Maximum Likelihood Estimation - Allowing for Night-Time Interactions

	Panel A: Coefficient Estimates
	Risk Equation		Prevalance Equation		Risk Equation		Prevalance Equation		Risk Equation		Prevalance Equation
	(1a)		(1b)		(2a)		(2b)		(3a)		(3b)
	Coeff.	Std. Err.	Coeff.	Std. Err.	Coeff.	Std. Err.	Coeff.	Std. Err.	Coeff.	Std. Err.	Coeff.	Std. Err.
GDL	0.002	(0.06)	−0.05 **	(0.02)
GDL×Night-Time	0.03	(0.07)	−0.11 **	(0.05)
GDL without Night Restriction					0.11	(0.28)	−0.07	(0.12)
GDL with Night Restriction					−0.02	(0.06)	−0.05 *	(0.03)
GDL without Night Restriction×Night					−0.004	(0.04)	−0.04	(0.07)
GDL with Night Restriction×Night					0.03	(0.07)	−0.11 **	(0.05)
Good GDL									0.58	(0.39)	−0.44	(0.27)
Fair GDL									−0.05	(0.07)	−0.03	(0.05)
Marginal GDL									−0.16	(0.13)	0.08	(0.08)
Good GDL×Night-Time									−0.04	(0.06)	−0.12 ***	(0.04)
Fair GDL×Night-Time									0.02	(0.04)	−0.10 **	(0.04)
Marginal GDL×Night-Time									−0.01	(0.03)	−0.07 ***	(0.02)
Teen Pop./Adult Pop.	5.08	(20.40)	2.68	(6.8)	6.24	(21.97)	2.55	(7.39)	−30.00	(28)	23.34	(20)
License Revocation Law	−0.07	(0.23)	−0.05	(0.08)	−0.08	(0.24)	−0.05	(0.09)	−0.03	(0.08)	−0.03	(0.06)
BAC 0.08 Law	−0.08	(0.23)	0.16	(0.10)	−0.09	(0.23)	0.17 *	(0.10)	0.28 **	(0.12)	−0.09	(0.09)
Zero Tolerance Law	0.11	(0.26)	−0.03	(0.12)	0.12	(0.25)	−0.03	(0.11)	−0.03	(0.06)	0.02	(0.03)
Night-Time	−0.01	(0.04)			−0.02	(0.03)			0.02	(0.02)
Weekend			0.09 ***	(0.02)			0.08 ***	(0.02)			0.09 ***	(0.02)
Weekend×Night-Time			0.14 ***	(0.02)			0.14 ***	(0.02)			0.14 ***	(0.02)
Hour fixed effects			Included				Included				Included
Year fixed effects	Included		Included		Included		Included		Included		Included
State fixed effects	Included		Included		Included		Included		Included		Included
	Panel B: Estimates for Night-Time Observations
	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value
GDL during Night-Time
GDL+GDL×Night-Time	0.03	(0.77)	−0.16 ***	(0.00)
GDL without Night Restriction during Night					0.11	(0.68)	−0.11	(0.36)
GDL with Night Restriction during Night					0.01	(0.91)	−0.16 ***	(0.00)
Good GDL during Night-Time									0.54	(0.12)	−0.56 **	(0.03)
Fair GDL during Night-Time									−0.03	(0.63)	−0.13 *	(0.06)
Marginal GDL during Night-Time									−0.17	(0.13)	0.01	(0.92)

1. Standard errors are clustered at the state level

2. ***, **, and * denote statistical significance at 0.01, 0.05, and 0.10 respectively

3. Data represents 7,680 state-year-hour-weekend cells

The first model in Table 6 includes a binary indicator to represent the presence of GDL policy and allows for its differential effect by day-time and night-time. The first column in the first specification, (1a), presents estimates of the risk equation, and suggests no statistically significant impact of GDL on relative teenage driving behavior. The predictions using these estimates suggest that on average teens were 14% more risky than adults in Non-GDL states regardless of time of day (mean θ of 1.137 during day time and 1.135 during night time) and in GDL states during the day time (mean θ of 1.138), while 15% more risky in GDL states during the night time (mean θ of 1.145).

The second column, (1b), corresponds to the prevalence equation and the coefficient on GDL represents a 5%¹⁴ statistically significant reduction in the relative number of teens during day-time observations. Panel (B) at the bottom of Table 6 presents GDL s impact on night-time observations, wherein we add the coefficient on GDL and the coefficient on GDL s interaction with night-time. We find a 15% reduction¹⁵ in the relative number of teens on the road during night time with a p-value less than 0.001. ¹⁶

The second model in Table 6 identifies different effects of GDL policies with nighttime restrictions versus those with no night-time restrictions. As we showed that GDL s primary influence is on teen prevalence during night-time, we should expect to see a stronger reduction in the number of teens during night-time in states with GDL policies that restrict night-time driving. As column (2b) outlines, GDL policies with no night-time restrictions do not have a statistically significant impact on the relative number of teens on the road, neither during day-time nor during night-time. GDL policies with night-time restrictions, on the other hand, reduce relative teen prevalence during day-time by 5% and during night-time by 15%. The 5% reduction during day-time is most likely due to the fact that GDL policies with night-time restrictions tend to be more restrictive policies in general. The finding that such policies reduce night-time driving by even more than those without night-time restrictions supports the hypothesis that night-time restrictions by themselves play an important role. As before, neither the policies with night-time restrictions nor those without them have any impact on relative teenage risk.

The third model in Table 6 differentiates GDL policies by their IIHS rating and identifies the impact of good, fair, and marginal policies relative to the reference category of no GDL policy. This model also allows for different impact during day-time and nighttime. Regardless of the policy s rating, we find no influence on the relative teen prevalence of GDL during day-time. However, during night-time, good GDL policies reduce relative teen prevalence by 43%¹⁷ (with p-value 0.03), fair GDL policies reduce it by 12%¹⁸ (with p-value 0.06), and marginal GDL policies have no statistically significant effect. Again, we find no statistically significant effect of any kind of GDL policies on relative teenage risk, neither during day-time nor during night-time.

In models not reported here, we repeated the same analysis as Table 6 except allowing the GDL effect to also vary by weekend. Qualitatively and quantitatively the results were consistent with those reported in Table 6, with only slightly larger magnitudes of the GDL effects.

We also investigated whether GDL policies trigger immediate or more gradual changes in relative teen risk and prevalence. Table 7 distinguishes GDL effect by proximity to its enactment year and shows that the GDL effect is more gradual. While, relative teen prevalence reduces by a statistically insignificant amount of 6%¹⁹ during the year of GDL implementation, corresponding reductions in the first three years and four or more years post enactment are all statistically significant at 9%, 12%, 10% and 21% respectively²⁰. On the other hand, we found no evidence in these data that GDL influences relative teen risk immediately after implementation or gradually in later years.

Table 7.

Joint Hierarchical Maximum Likelihood Estimation - GDL Over Time

	Panel A: Coefficient Estimates
	Risk Equation		Prevalance Equation (log(N))
	(1a)		(1b)
	Coeff.	Std. Error	Coeff.	Std. Error
GDL - year of implementation	0.09	(0.71)	−0.06	(0.05)
GDL - 1 year post implementation	0.003	(0.03)	−0.09 **	(0.03)
GDL - 2 year post implementation	0.27	(0.28)	−0.13 ***	(0.03)
GDL - 3 year post implementation	0.07	(0.52)	−0.1 **	(0.05)
GDL - 4 or more years post implementation	0.45	(1.16)	−0.24 **	(0.12)
Teen Pop./Adult Pop.	−2.6	(25.9)	4.73	(8.5)
License Revocation Law	−0.16	(0.12)	−0.02	(0.05)
BAC 0.08 Law	−0.008	(0.15)	0.14	(0.07)
Zero Tolerance Law	0.1	(0.12)	−0.02	(0.05)
Night-Time	0.04	(0.04)
Weekend			0.08 ***	(0.02)
Weekend×Night-Time			0.14 ***	(0.02)
Hour fixed effects			Included
Year fixed effects	Included		Included
State fixed effects	Included		Included

1. Standard errors are clustered at the state level

2. ***, **, and * denote statistical significance at 0.01, 0.05, and 0.10 respectively

3. Data represents 7,680 state-year-hour-weekend cells

One possible explanation for increased GDL effect over time after the first implementation could be due to increased awareness with the policy provisions, improved compliance by parents and teens, and stronger law enforcement over time in states that adopt GDL. Unfortunately there is no systematic study that reviews GDL law enforcement, which is a major gap in the literature. Anecdotally, some states have, over time, incorporated GDL specific training into their general officer recruit training which increased enforcement (Scott, 2007).

An additional explanation is the direct strengthening of the GDL policies over time since their initial enactment. Three of the twelve states in this study, Florida, Maryland and Virginia, improved their rating after first GDL implementation as noted in Table 3. For example in Virginia, GDL policy was strengthened two years after the first implementation in several dimensions. The mandatory number of months in the learner stage was extended from 6 months to 9 months, and a minimum of 40 hours of supervised driving was implemented. In the intermediate stage, driving was prohibited from midnight to 4 am, and the maximum number of allowed passengers younger than 18 was decreased from three to one for drivers under age 17. Two years afterwards, passenger restriction policy was refined further by endorsing the maximum of one passenger younger than 18 for all teen drivers regardless of age during the first year in the intermediate stage. In addition to the three states with major improvements in their GDL policies, California and Illinois among the 12 states we study also improved several characteristics of their policy during the study period. California, five years after the first implementation, extended the period of passenger restriction in the intermediate stage from 6 months to 12 months. Similarly, Illinois introduced passenger restrictions in the intermediate stage for the first time six years after the GDL implementation.²¹

V.1. Robustness Analyses

In this section, we present our robustness analyses. First, we assess the sensitivity of our results to a critical assumption of our model. Second, we introduce the possibility that adults can avoid the crashes. Next, we alter the definition of “teens” to test the validity of our specifications. Finally, we discuss other issues such as potential reporting bias of accidents and GDL policy endogeneity.

V.1.1 Equal Mixing Assumption

Our model assumes that drivers are equally mixing on the road so that there is no “clumping” of driver types in space or time. Our assumption will be violated if, for example, adult drivers are more likely to interact with other adult drivers for each mile driven. This could happen because they frequent the same locations or drive at the same times of day. The equal mixing assumption is likely valid for a fine enough partition of space and time but will be violated if clumping occurs as the level of aggregation increases. Our benchmark specification s unit of observation is a state-year-hour-weekend, which we believe to be a small enough partition of space and time.

We conduct a sensitivity analysis to assess whether our results are sensitive to different units of observation. In particular, we repeat our joint estimation of (1), (2) and (3) allowing for different restrictions on the units of observation over which “equal-mixing” is imposed. We consider state-year-night-weekend, and state-year-night as alternative units of observations. For example, state-year-night-weekend assumes equal mixing only within a given state-year pair, night and weekend status. Formally, we restrict the relative crash risk θ to be the same for a given state-year-night observation but we allow the relative exposure N to vary by state-year-night-weekend. In addition to varying the unit of observation across the time dimension, we also conduct a sensitivity analysis by varying the unit of observation spatially. In particular, we differentiate between metropolitan areas and rural areas within each state, still allowing the time variation across year, weekend and hour.

Table 8 reports our original estimation that differentiates GDL by its IIHS rating allowing N to vary by state-year-hour-weekend (our original specification) as well as the three new specifications that use a different unit of observation. Estimates are very similar across GDL policies, having no impact on relative teenage risk, good GDL policies reducing the night-time relative teen prevalence by 41%–43%²², and fair GDL policies reducing the night-time relative teen prevalence by 10%–15%²³. The similarity in estimates between these specifications increase our confidence that further relaxing the equal mixing assumption will likely not lead to significantly different findings.

Table 8.

Joint Hierarchical Maximum Likelihood Estimation -Equal Mixing Assumption

	Estimates of GDL
	Vary N by state, year, hour, weekend				Vary N by state, year, night, weekend				Vary N by state, year, night				Vary N by state, urban, year, hour, weekend
	Risk Equation (log(θ))		Prevalance Equation (log(N))		Risk Equation (log(θ))		Prevalance Equation (log(N))		Risk Equation (log(θ))		Prevalance Equation (log(N))		Risk Equation (log(θ))		Prevalance Equation (log(N))
	(1)		(2)		(1)		(2)		(1)		(2)		(1)		(2)
	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value
Good GDL during Day-Time
Good GDL	0.58	(0.14)	−0.44	(0.11)	0.51	(0.21)	−0.40	(0.14)	0.51	(0.21)	−0.40	(0.14)	0.57	(0.15)	−0.42	(0.12)
Fair GDL during Day-Time
Fair GDL	−0.05	(0.45)	−0.03	(0.47)	−0.05	(0.43)	−0.03	(0.44)	−0.05	(0.44)	−0.04	(0.43)	−0.08	(0.29)	0.002	(0.98)
Marginal GDL during Day-Time
Marginal GDL	−0.16	(0.19)	0.08	(0.31)	−0.15	(0.21)	0.08	(0.32)	−0.15	(0.21)	0.08	(0.32)	−0.15	(0.27)	0.079	(0.33)
Good GDL during Night-Time
Good GDL+Good GDL×Night-Time	0.54	(0.12)	−0.56 **	(0.03)	0.48	(0.18)	−0.53 **	(0.04)	0.48	(0.18)	−0.53 **	(0.04)	0.17	(0.13)	−0.53 **	(0.03)
Fair GDL during Night-Time
Fair GDL+Fair GDL×Night-Time	−0.03	(0.63)	−0.13 *	(0.06)	−0.03	(0.65)	−0.15 **	(0.03)	−0.03	(0.65)	−0.16 **	(0.03)	−0.07	(0.44)	−0.096	(0.21)
Marginal GDL during Night-Time
Marginal GDL+Marginal GDL×Night-Time	−0.17	(0.13)	0.01	(0.92)	−0.16	(0.15)	−0.01	(0.93)	−0.15	(0.15)	−0.01	(0.92)	−0.16	(0.17)	0.001	(0.99)

1. Standard errors are clustered at the state level

2. ***, **, and * denote statistical significance at 0.01, 0.05, and 0.10 respectively

3. Data represents 7,680 state-year-hour-weekend cells

4. State and Year fixed effects are used in all specifications.

5. Other driving related laws and the ratio of teen population to adult population are included as covariates in all specifications

V.1.2 Possibility of Crash Avoidance

Our benchmark model assumes that drivers are not able to avoid crashes caused by others. This assumption may hold for teen drivers, but it is likely that experienced adult drivers not at fault can avoid crashes more successfully.²⁴ We explore the implications of relaxing this assumption. By letting p denote the probability that an adult driver can avoid accidents, and following the notation introduced earlier, we can write the probability of crashes as:

$$\begin{array}{l}P(C=1\backslash I=1,i=\mathit{teen},j=\mathit{adult})=2{\theta }_T,\\ P(C=1\backslash I=1,i=\mathit{adult},j=\mathit{teen})={\theta }_T(1-p)+{\theta }_A,\\ P(C=1\backslash I=1,i=\mathit{adult},j=\mathit{teen})=2{\theta }_A(1-p).\end{array}$$

Equation (1) in this case would then become:

$$\begin{array}{l}(C_{TT},C_{TA},C_{AA})\sim \mathit{Multinomial}\\ \left(C_{\mathit{total}},\left[\frac{N^2\theta }{1-p+N(1+\theta (1-p))+N^2\theta },\frac{N(1+\theta (1-p))}{1-p+N(1+\theta (1-p))+N^2\theta },\frac{1}{1-p+N(1+\theta )+N^2\theta }\right]\right)\end{array}$$

We followed the framework in Levitt and Porter (2001) and analytically derived the new estimates of θ. Let θ_orig and θ_new denote the estimated relative risk in the original model (p = 0) and the modified model (p >0) respectively. Similarly, let N_orig and N_new denote the estimated relative prevalence in the original model and the modified model. In the original model, the probabilities of teen-teen/teen-adult/adult-adult crashes are

$$\begin{array}{l}{P}_{TT}=\frac{{(N_{\mathit{orig}})}^2{\theta }_{\mathit{orig}}}{1+N_{\mathit{orig}}(1+{\theta }_{\mathit{orig}})+{(N_{\mathit{orig}})}^2{\theta }_{\mathit{orig}}}=\frac{C_{TT}}{C_{\mathit{total}}},\\ P_{TA}=\frac{N_{\mathit{orig}}(1+{\theta }_{\mathit{orig}})}{1+N_{\mathit{orig}}(1+{\theta }_{\mathit{orig}})+{(N_{\mathit{orig}})}^2{\theta }_{\mathit{orig}}}=\frac{C_{TA}}{C_{\mathit{total}}},\\ P_{AA}=\frac{N_{\mathit{orig}}(1+{\theta }_{\mathit{orig}})}{1+N_{\mathit{orig}}(1+{\theta }_{\mathit{orig}})+{(N_{\mathit{orig}})}^2{\theta }_{\mathit{orig}}}=\frac{C_{AA}}{C_{\mathit{total}}}.\end{array}$$

As in Levitt-Porter (2001), to solve for θ_orig, we take the following ratio:

$$\frac{{(P_{TA})}^2}{P_{TT}{P}_{AA}}=\frac{{(C_{TA})}^2}{C_{TT}{C}_{AA}}={\theta }_{\mathit{orig}}+2+\frac{1}{{\theta }_{\mathit{orig}}}.$$

Letting $R=\frac{{(C_{TA})}^2}{C_{TT}{C}_{AA}}$, we can solve for ${\theta }_{\mathit{orig}}=\frac{(R-2)\mp \sqrt{R^2-4R}}{2}$

In the modified model, using the new probabilities of different types of two car crashes, and following the steps above, we obtain

$$R={\theta }_{\mathit{new}}(1-p)+2+\frac{1}{{\theta }_{\mathit{new}}(1-p)}$$

Solving for θ_new, we get

$$\begin{array}{c}{\theta }_{\mathit{new}}(1-p)=\frac{(R-2)\mp \sqrt{R^2-4R}}{2},\text{or}\\ {\theta }_{\mathit{new}}=\frac{{\theta }_{\mathit{orig}}}{1-p}.\end{array}$$

This calculation implies that as p increases, the estimate of θ increases, but by the same multiplicative factor for all observations. For example, if p 0.25, the new θ is 1.33 times the original estimate. We also empirically confirmed this analytical finding. The estimate of θ increases by the same multiplicative factor for all state-year-night cells. Therefore, the effects of GDL policies on θ do not change. Similarly, relative teen prevalence, N, changes with the same multiplicative factor for all observations, thus the effect of GDL on N is the same as in our benchmark model.

V.1.3 Re-Defining Teens

As mentioned earlier, our benchmark specifications classify teen drivers as those between ages 15–17 (age cohorts directly impacted by GDL policies), and adult drivers as those older than 18. We conduct analyses defining the younger age group broader, as those between ages 15–19, which includes 18 and 19 years-olds not subject to the restrictions of the GDL policies in a given state-year pair.

Our benchmark specifications have consistently shown a reduction in relative teen prevalence during night-time, especially in states with stronger GDL policies, and those with GDL policies that restrict night-time driving. By defining teen drivers as those between ages 15–19, we test whether our specifications predict an equal sized GDL effect on relative teen prevalence at night-time. We predict a smaller effect since the 18 and 19 year-olds are not subject to GDL restrictions.

Table 9 compares our benchmark model with the alternative. In both specifications, GDL has no effect on relative teen risk. Moreover, we observe that the magnitude of GDL effect on teen prevalence during night-time reduces significantly in the second specification that uses a broader definition of teens. In particular, good GDL policies reduce night-time relative teens on the road by 11% while fair GDL policies reduce it by 5%²⁵. Corresponding declines in the original specification are 43% and 12% respectively.

Table 9.

Joint Hierarchical Maximum Likelihood Estimation - Teens defined as the 15–19 Year Olds

	Estimates of GDL
	Teen Definition is 15–17 Year-Olds				Teen Definition is 15–19 Year-Olds
	Risk Equation (log(θ))		Prevalance Equation (log(N))		Risk Equation (log(θ))		Prevalance Equation (log(N))
	(1)		(2)		(1)		(2)
	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value
Good GDL during Day-Time
Good GDL	0.58	(0.14)	−0.44	(0.11)	0.00	(0.60)	−0.06 **	(0.04)
Fair GDL during Day-Time
Fair GDL	−0.05	(0.45)	−0.03	(0.47)	0.00	(0.33)	−0.02	(0.29)
Marginal GDL during Day-Time
Marginal GDL	−0.16	(0.19)	0.08	(0.31)	0.00	(0.87)	−0.01	(0.55)
Good GDL during Night-Time
Good GDL+Good GDL×Night-Time	0.54	(0.12)	−0.56 **	(0.03)	0.00	(0.15)	−0.12 ***	(0.01)
Fair GDL during Night-Time
Fair GDL+Fair GDL×Night-Time	−0.03	(0.63)	−0.13 *	(0.06)	0.00	(0.65)	−0.05 *	(0.08)
Marginal GDL during Night-Time
Marginal GDL+Marginal GDL×Night-Time	−0.17	(0.13)	0.01	(0.92)	0.00	(0.82)	−0.05	(0.11)

1. Standard errors are clustered at the state level

2. ***, **, and * denote statistical significance at 0.01, 0.05, and 0.10 respectively

3. Data represents 7,680 state-year-hour-weekend cells

4. State and Year fixed effects are used in all specifications. Prevalance equation includes additional hour fixed effects for model (1). Models (1) and (2) include weekend-night interactions

5. Other driving related laws and the ratio of teen population to adult population are included as covariates in all specifications

V.1.4 Reporting Bias

Since SDS contains data on all police reported accidents, one may worry whether there are significant reporting biases. In particular, teen drivers that get involved in an accident either while carrying other teen passengers or during the night in states with stricter GDL policies that typically have passenger and night time restrictions may choose not to report the accident, especially if the accident is minor.

We investigate this issue by exploiting the information the data contains on the severity of the accident. In particular, an accident that involves a fatality or an injury has to be reported, while an accident that involves only property damage may go unreported. We estimate ordinary least squares regressions where the dependent variable is the ratio of fatal and property damage crashes that involve at least one teen driver and key independent variables are GDL policies (either as binary indicators of policy presence, or by the IIHS rating), and GDL policy interactions with night-time observations. We estimate separate models for two-car accidents with two teen drivers and those with a teen and an adult driver. The unit of observation is a state-year-hour-weekend. As before, specifications also control for other driving related laws, teenage population, indicators for weekend, weekend and night-time observations, hour fixed effects, year fixed effects and state fixed effects.

We find no statistically significant evidence that the GDL policy influences the relative numbers of fatal and property damage teen crashes during the day or night. Coefficient estimates on GDL policies never have a p-value smaller than 0.17. Nevertheless, we use these estimates to compute an upper bound on the extent of underreporting of property damage crashes that involve teen drivers in GDL states.²⁶ Specifically, we focus on the potential underreporting in stricter GDL states with night-time and passenger restrictions (rated “Good”). We consider the coefficient estimate on the GDL coefficients plus one standard deviation as the upper bound on underreporting. Next, considering the mean ratio of fatal to property damage accidents for non-GDL states by year and time of day as the “unbiased” crash statistics, we find that in “Good GDL” states, property damage accidents during night time that involve two teen drivers may need to be inflated by 55% to match the “unbiased” benchmark in non-GDL states.²⁷ The corresponding upward adjustment needed for those that involve a teen and an adult driver is 5%. We re-estimate our models after inflating the two-car teen driver accidents using these upper bound estimates and find that our findings remain robust, although the extent of GDL prevalence effect diminishes. For example, in comparison with the third model in Table 6, we again find no GDL influence on the relative teen risk. Similarly, we find no influence on the relative teen prevalence of GDL during day-time. However, during night-time, good GDL policies reduce relative teen prevalence by 36% (with p-value 0.05) instead of the 43% in the original specification.

V.1.5 Policy Endogeneity

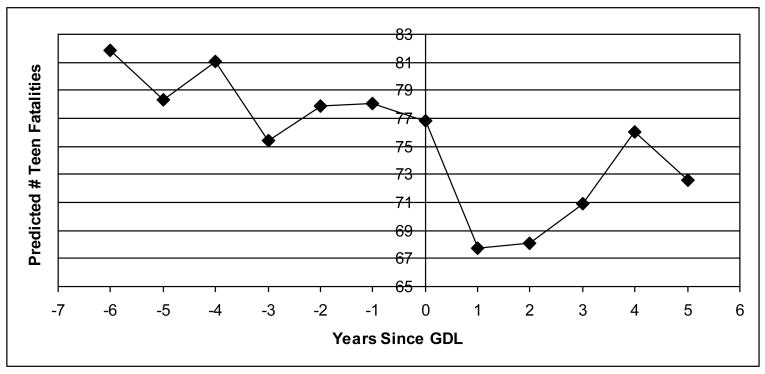
Although all our specifications use state and year fixed effects and other driving related laws, one may still worry that GDL policies are endogenous, and that they are a response to particular trends in teen fatalities and crash involvement. Dee et al (2005) who studied GDL policies for all the states from 1992–2002 provide evidence this is not case. In particular, they relate teen fatalities in state-year observations to 10 indicator variables that indicate whether a given state-year observation falls in the 1–5 years prior to GDL, in the year of GDL enactment, or 1–4 or more years post GDL. They find that teen fatalities in the pre-GDL periods underwent both increases and decreases, not necessarily a monotonic trend, while they were lower in all periods post GDL relative to all periods pre GDL.²⁸ We repeat a similar analysis at the state-year level to check whether similar results hold when we restrict the sample to only the 12 states included in our analysis. The dependent variable is the number of teen fatalities and the independent variables include indicator variables for proximity to GDL enactment, state and year fixed effects, teen population and the presence of other driving related laws used in the benchmark models. Figure 2 plots the predicted number of teen fatalities by proximity to GDL enactment. Our results confirm Dee et al (2005) that there is no distinct trend in teen fatalities in pre-GDL policies and that teen fatalities drop after GDL implementation.

Figure 2. Investigating GDL Policy Endogeneity.

This figure plots predicted number of teen fatalities from an OLS regression of teen fatalities on GDL policy by proximity to enactment

V.2. Dynamics

We have shown that GDL policies do not have significant influence on the driving risk of the teenagers between ages 15–17, but rather achieve observed reductions in teen accidents and fatalities through restricting the amount of teenage driving, especially at night. An interesting question is whether driving under GDL restrictions results in a cohort of drivers that have reduced risks in the future although the effects during the early teen years might be insignificant.

Another question proposed by Dee et al (2005) is whether the GDL regulations shift risky driving to older teens by disallowing them to mature through risky behavior while they are 15–17. Dee et al focus on 18–20 year olds and for each state-year pair, they estimate whether the presence of a GDL policy three years prior has a negative impact on the traffic fatalities of this age cohort. They find a negative but statistically insignificant effect and conclude that such issues should be revisited in the future when more GDL constrained cohorts advance to full licensure and additional FARS data become available.

Here we report analyses aimed at understanding the long-run effects of GDL restrictions while separately identifying the impact on risk exposure and on crash risk. In particular, we re-estimate our benchmark structural model with two key differences. First, instead of defining the young drivers as 15–17 year olds, we define them as 18–20 year olds. Therefore, adults are then defined as the 21 year and older and we drop all accidents that involve 15–17 year old drivers. Second, we construct indicator variables to code whether each state-year observation falls in at least one year prior to GDL enactment or at least four years post GDL. The idea is that the 18–20 year old cohort in years prior to GDL implementation would not be exposed to GDL when they were 15–17,²⁹ while all of the 18–20 year olds in a state with a GDL enacted four years ago would have gone through the GDL program.³⁰

Accordingly, we limit our analyses to state-year observations in which either all or none of the 18–20 year olds were exposed to a GDL at a younger age. We use an indicator variable of “4 Years Post GDL Enactment” as the key independent variable. In an additional specification we focus on teen exposure to GDL policies rated “Good” and limit analyses to state-year observations either at least four years post a “Good” GDL policy or at least one year prior to a “Good” GDL policy. Table 10 reports results for these two models.

Table 10.

Joint Hierarchical Maximum Likelihood Estimation - 18–20 year old cohort

	Compare 18–20 year olds to 21 plus
	Panel A: Coefficient Estimates				Panel A: Coefficient Estimates
	Risk Equation (log(θ))		Prevalance Equation (log(N))		Risk Equation (log(θ))		Prevalance Equation (log(N))
	(1a)		(1b)		(1a)		(1b)
	Coeff.	Std. Error	Coeff.	Std. Error	Coeff.	Std. Error	Coeff.	Std. Error
4 years post GDL enactment (reference category is 1 year or more prior to GDL enactment)	−0.17	(0.11)	0.02	(0.06)
4 years post GDL enactment × Night-Time	0.14	(0.09)	−0.09 *	(0.05)
4 years post Good GDL enactment (reference category is 1 year or more prior to Good GDL enactment)					−0.23	(0.57)	0.14	(0.31)
4 years post Good GDL enactment × Night-Time					−0.17	(0.30)	0.09	(0.16)
18–20 year-old pop./21 plus pop.	21.7	(17.7)	−1.6	(9.6)	3.4	(28.8)	4.13	(13.9)
License Revocation Law	0.14	(0.16)	−0.08	(0.09)	0.01	(0.12)	−0.02	(0.05)
BAC 0.08 Law	0.14	(0.13)	−0.08	(0.07)	−0.08	(0.38)	0.06	(0.19)
Zero Tolerance Law	−0.07	(0.10)	0.06	(0.06)	−0.14	(0.09)	0.09 *	(0.05)
Night-Time	−0.07	(0.07)			−0.02	(0.04)
Weekend			0.06 ***	(0.01)			0.06 ***	(0.01)
Weekend×Night-Time			0.1 ***	(0.01)			0.1 ***	(0.01)
Hour fixed effects			Included				Included
Year fixed effects	Included		Included		Included		Included
State fixed effects	Included		Included		Included		Included
	Panel B: Estimates for Night-Time Observations				Panel B: Estimates for Night-Time Observations
	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value	Coeff.	p-value
4 Years post GDL during Night-Time
4 years post GDL enactment + 4 years post GDL enactment × Night-Time	−0.03	(0.23)	−0.07	(0.17)	−0.4	(0.29)	0.23	(0.24)

1. Standard errors are clustered at the state level

2. ***, **, and * denote statistical significance at 0.01, 0.05, and 0.10 respectively

3. Data represents 5,616 and 6,864 state-year-hour-weekend cells left and right models respectively

Neither of the two models predicts a difference in the relative riskiness of 18–20 year olds observed in state-year pairs post 4 years or more GDL enactment relative to their counterparts in state-year pairs at least one year prior to GDL enactment. This finding suggests that GDL policies, including those rated “Good”, do not necessarily make teens become better drivers in later years. We also find no difference in the relative prevalence between the GDL exposed and the unexposed groups. This finding is consistent with the fact that the restrictions of the GDL apply when the teens are 15–17 year old and should not directly impact the prevalence of 18–20 olds. Ideally, one would like to continue analyses and compare 18–21 year olds to 22 and older and so on. However, since the GDL policies are relatively new, we have very few state-year observations with at least six years post GDL enactment. Future research should revisit this issue as more teens graduate from the GDL policies.

VI. Conclusion

This paper investigated the causal mechanisms through which state GDL policies have been achieving favorable results in reducing accident rates and fatalities of 15–17 year old novice drivers. In particular, we have focused on whether GDL policies reduce relative teenage driving risk, or relative teenage driving prevalence. Using a structural model, we find that the latter is responsible for reducing the observed number of teen crashes. The reductions in relative teenage prevalence are estimated to primarily occur during night-time, due to restrictiveness of the GDL policies during night-time driving. More restrictive GDL policies and those with night-time restrictions achieve greater reductions in teen driving prevalence during the night. We also conducted some analyses to investigate whether the GDL exposed 15–17 year old cohort becomes better drivers in the future, when they are 18–20 year olds, and did not find evidence for reduced riskiness of this cohort. Future research should revisit this issue with more teens graduating from GDL policies each year.

As of August 2008, Arkansas, Kansas and North Dakota still do not have an intermediate stage with night-time or passenger restrictions. Among states that have night-time restrictions, 57% restrict unsupervised driving after midnight and 28% after 11 pm although the IIHS suggests night driving restriction starting at 9 or 10 pm.³¹

From a public health perspective, our findings suggest that more restrictive GDL policies for 15–17 year-old drivers reduce teen accidents and fatalities. Stronger GDL policies defer unrestricted driving thus reducing teens exposure to high risk driving situations. In addition, our findings suggest that GDL policies could benefit from emphasizing stronger measures to improve teen driving proficiency. Such measures could involve increasing the period of time between the first permit and the issuance of the final license. Similarly, required supervised driving period could be extended. Moreover, driver improvement courses could be adapted to fit each GDL stage with more basic skills emphasized in the beginner stage and advanced skills in the intermediate stage.