Efficient Anisotropic Filtering of Diffusion Tensor Images

Abstract

To improve the accuracy of structural and architectural characterization of living tissue with diffusion tensor imaging, an efficient smoothing algorithm is presented for reducing noise in diffusion tensor images. The algorithm is based on anisotropic diffusion filtering, which allows both image detail preservation and noise reduction. However, traditional numerical schemes for anisotropic filtering have the drawback of inefficiency and inaccuracy due to their poor stability and first order time accuracy. To address this, an unconditionally stable and second order time accuracy semi-implicit Craig-Sneyd scheme is adapted in our anisotropic filtering. By using large step size, unconditional stability allows this scheme to take much fewer iterations and thus less computation time than the explicit scheme to achieve a certain degree of smoothing. Second order time accuracy makes the algorithm reduce noise more effectively than a first order scheme with the same total iteration time. Both the efficiency and effectiveness are quantitatively evaluated based on synthetic and in vivo human brain diffusion tensor images, and these tests demonstrate that our algorithm is an efficient and effective tool for denoising diffusion tensor images.

1. Introduction

Magnetic resonance diffusion tensor imaging (DTI) has become established as a primary technique for non-invasive characterization of the structural and architectural features of living tissue [1, 2]. In each voxel, DTI provides a 3×3 symmetric positive definite matrix that describes the local Brownian motion of water molecules. Eigenvalues and eigenvectors of the matrix can be exploited to characterize tissue micro-structure and architecture and assess fiber integrity based on differences in the eigenvalues or orientation of the eigenvectors [3].

As DTI is typically performed with echo-planar imaging sequences, the images acquired usually have very poor signal-to-noise ratio (SNR). High image noise has quite detrimental effects on the accuracy of assessment of diffusion anisotropy (from which tissue structure is characterized), most notably an overestimate of fractional anisotropy (FA) due to sorting bias [4] and erroneous calculations of the principal diffusion direction [5, 6]. To improve SNR, it is a common practice to use time domain signal averaging; this however necessarily incurs other complications such as inter-scan registration and prolonged acquisition time which may worsen the problem of subject motion. A very attractive alternative is noise reduction by image smoothing, which offers an economical and practically feasible means of improving SNR without encumbering the image acquisition procedure.

To date, a plethora of image smoothing techniques have been proposed for reducing noise in DTI data. These include non-linear diffusion filtering [7, 8], B-spline fitting [9], and more sophisticated regularization methods based on a Markovian model [10], stochastic relaxation [11], variational principles [12, 13], differential geometry [14 – 17], and a maximum a posteriori approach [18]. This repository of smoothing techniques, however, have not established their practical utility due, in part, to the somewhat time-consuming numerical implementation especially given the fact that computation complexity increases with the number of weighting directions, or to a lack of rigorous validation with in vivo DTI data to prove their practical value.

Previously we proposed to reduce noise in DTI data by anisotropic filtering of diffusion weighted images [19]. This method improves the nonlinear diffusion filtering by Parker et al. [7] in that the spatially varying diffusion coefficient is replaced with a diffusion tensor, which allows direction dependent smoothing for each voxel. In a typical implementation of diffusion filtering, an explicit finite difference scheme is used to solve the relevant partial differential equation (PDE). Explicit schemes are only stable for very small time step sizes, which imposes a significant restriction on their computational efficiency. Furthermore, explicit schemes are limited to first order accuracy in time, which means the filtering results are less accurate than those from higher order schemes.

The issue of computational efficiency is often addressed by using unconditionally stable semi-implicit schemes, which solve systems of linear equations in each iteration. The linear system is usually split into a sequence of simple ones, each of which can be solved by the efficient Thomas algorithm [20]. For example, Weickert [21] proposed a reliable and efficient additive operator splitting (AOS) scheme that allows larger time step sizes in nonlinear diffusion filtering. The AOS scheme however has the drawback of first order time accuracy only. Barash [22] used an additive and multiplicative operator splitting (AMOS) algorithm, which resembles the classical alternating direction implicit schemes [20]. Although AMOS has second order accuracy in time, it only works for diffusion filters with a scalar diffusion coefficient. In this work we employ an unconditionally stable and second order accurate Craig-Sneyd scheme [23], which improves the anisotropic filtering with respect to both accuracy and efficiency.

In the following, the anisotropic smoothing technique we proposed is first briefly summarized. A semi-implicit Craig-Sneyd scheme for improving both the accuracy and time efficiency of diffusion filtering is then described, followed by detailed implementation procedures for efficient anisotropic smoothing. Comprehensive validations with DTI data synthesized with physiological diffusion parameters and acquired in vivo from a healthy human brain are presented. Explicit and semi-implicit implementations of the anisotropic smoothing algorithm are compared in terms of both the efficiency and effectiveness in restoring the PDD from noise corrupted data. Finally, major contributions of this work are summarized and some technical limitations are discussed so as to guide future research along this line.

2. Methods

2.1. Anisotropic reduction of noise in diffusion tensor images

Noise in DTI data can be reduced by smoothing diffusion weighted images (DWI) from which diffusion tensors are derived. A common smoothing approach is anisotropic filtering, in which the smoothing process is based on the following governing PDE [19]:

$$\frac{\partial I_{\text{m}}}{\partial t}=\mathit{div}(T\nabla I_m),$$ (1)

where I_m is the image intensity in weighting direction m, ∇ is a gradient operator, div is a divergence operator, t is the time. T is a structure tensor that provides the directionality of smoothing. It is constructed from a common gradient tensor G, which is obtained by convolving the sum of outer products of ∇ I_m over all weighting directions with a Gaussian kernel K_ρ:

$$\mathbf{G}=K_{\rho }\ast \sum _m(\nabla I_m\otimes \nabla I_m),$$ (2)

where ⊗ represents the outer product operator. The parameter ρ is the standard deviation of the Gaussian kernel, which determines the spatial scale of the gradient tensor.

To smooth the image isotropically inside structures and anisotropically at structure boundaries, T is defined to be a normalized inverse of G. Denoting v_g1, v_g2, v_g3 as the eigenvectors and λ_g1, λ_g2, λ_g3 as the corresponding eigenvalues of G, the eigenvectors and eigenvalues of T are:

$${\mathbf{v}}_{\text{ti}}={\mathbf{v}}_{\text{gi}},i=1,2,3,$$ (3)

$${\lambda }_{\text{ti}}=1/{\lambda }_{\text{gi}},i=1,2,3.$$ (4)

Therefore, in homogeneous regions, such as inside bundle structures, the magnitudes of the three eigenvalues of the structure tensor are comparable, yielding a similar amount of smoothing along all directions (isotropic smoothing). At the structure boundaries, the eigenvalue of the structure tensor is small across the boundaries (large intensity gradient), and large along them (small intensity gradient), thus permitting greater smoothing along the tangential direction of structure boundaries than perpendicular to it (anisotropic smoothing). To allow equal enhancement to homogeneous regions and structure boundaries, the trace of the structure tensor is normalized to be a constant C; consequently, the total amount of smoothing, whether isotropic or anisotropic, is the same over the entire image.

2.2. Semi-implicit scheme for anisotropic filtering

As mentioned, implementation of the anisotropic filtering typically uses an explicit scheme to solve the diffusion PDE. This however suffers from the limitation of computational inefficiency. As noted before, the computational efficiency can be boosted up by using an unconditionally stable and second order accurate Craig-Sneyd scheme for solving the PDE semi-implicitly. Before introducing this semi-implicit scheme, we first give a brief review of the explicit scheme. In order to approximate Eq. 1 numerically, we replace the time derivatives with forward-time differences and the spatial derivatives with central-space differences as follows,

$$\frac{I^{n+1}-I^n}{\mathrm{\Delta }t}=\sum _{i,j=1}^3{\partial }_{x_i}({\mathit{T}}_{i,j}{\partial }_{x_j}{I}^n),$$ (5)

where ∂_xi represents the central difference operator with respect to axis x_i, one of the spatial coordinates; I ⁿ is the diffusion weighted image at time nΔt or n^th iteration (note that the subscript m to I is suppressed to simplify notation); T_{i, j} is the (i, j) component of 3×3 structure tensor T. The computational cost of each iteration is very low for the above explicit scheme, because I ^{n+ 1} can be directly computed as follows,

$${\stackrel{\sim }{I}}^{n+1}={\stackrel{\sim }{I}}^n+\mathrm{\Delta }t\sum _{i,j=1}^3{L}_{i,j}({\stackrel{\sim }{I}}^n){\stackrel{\sim }{I}}^n,$$ (6)

where Ĩⁿ is a column vector representation of three dimensional image I ⁿ, and L_{i, j} is a linear operator matrix representing ∂ _xi (T_{i, j}∂ _xj) (see Appendix C).

In spite of the simplicity, the explicit scheme however requires a very small time step size in order to ensure its stability [24]. This translates to more iterations needed to reach a specific smoothing effect. Furthermore, as noted before, the above scheme has only first order accuracy in time.

Unlike the explicit scheme, semi-implicit schemes may not approximate time derivatives with forward-time differences. For example, a backward-time difference can also be used to replace the time derivative, and the continuous diffusion equation can be then approximated by:

$$\frac{I^{n+1}-I^n}{\mathrm{\Delta }t}=\sum _{i,j=1}^3{\partial }_{x_i}(T_{i,j}{\partial }_{x_j}{I}^{n+1}),$$ (7)

$$(1-\mathrm{\Delta }t\sum _{i,j=1}^3{L}_{i,j}({\stackrel{\sim }{I}}^n)){\stackrel{\sim }{I}}^{n+1}={\stackrel{\sim }{I}}^n.$$ (8)

For each iteration, a linear system must be solved to compute Ĩⁿ⁺¹, but the stability of the PDE is greatly improved. Note that the tensor T is computed based on Ĩⁿ rather than Ĩⁿ⁺¹, which is the reason why the scheme is called “semi-implicit” instead of “implicit”.

The semi-implicit Craig-Sneyd approach approximates Eq. 1 with the following semi-implicit scheme:

$$A{\stackrel{\sim }{I}}^{n+1}=(A+B){\stackrel{\sim }{I}}^n,$$ (9)

where

$$\begin{array}{l}A=\prod _{i=1}^3(1-\theta \mathrm{\Delta }t{L}_{i,i}),\\ B=\sum _{i,j=1}^{i,j=3}\mathrm{\Delta }t{L}_{i,j},\end{array}$$

and θ is a real number that determines the implicitness of the scheme.

Equation 7 is still first order accurate in time because it has a mixed derivative in space and time [23]. The Craig-Sneyd scheme employs a further iteration to time-center the mixed derivative, and thus gains second order time accuracy even in the presence of the mixed derivative. The two-iteration Craig-Sneyd scheme can be summarized by

$$A{{\stackrel{\sim }{I}}^{\prime }}^{n+1}=(A+B){\stackrel{\sim }{I}}^n,$$ (10a)

$$A{\stackrel{\sim }{I}}^{n+1}=(A+B){\stackrel{\sim }{I}}^n+\lambda M({{\stackrel{\sim }{I}}^{\prime }}^{n+1}-{\stackrel{\sim }{I}}^n),$$ (10b)

where

$$M=\mathrm{\Delta }t\sum _{i,j=1(i\ne j)}^3{L}_{i,j},$$

and λ is a real number.

Equation 10a serves as an estimator that gives an approximate solution for next time step, while Eq. 10b is actually a corrector that uses a part of the estimated solution to calculate its mixed derivative. The parameter λ controls how much of the mixed derivative is computed based on the estimated solution. Such a scheme is unconditionally stable and second order accurate in both time and space for the three dimensional case when λ = ½, θ = ½ [23].

In order to solve the linear system of equations in Eq. 10a efficiently, it is split into the following three parts [23]:

$$(1-\theta \mathrm{\Delta }t{L}_{1,1}){{\stackrel{\sim }{I}}^{\prime }}^{n+1/3}=[1+(1-\theta )\mathrm{\Delta }t{L}_{1,1}+\mathrm{\Delta }t\sum _{i=2}^3{L}_{i,i}+\mathrm{\Delta }t\sum _{i,j=1(i\ne j)}^3{L}_{i,j}]{\stackrel{\sim }{I}}^n,$$ (11a)

$$(1-\theta \mathrm{\Delta }t{L}_{2,2}){{\stackrel{\sim }{I}}^{\prime }}^{n+2/3}={{\stackrel{\sim }{I}}^{\prime }}^{n+1/3}-(1-\theta )\mathrm{\Delta }t{L}_{2,2}{\stackrel{\sim }{I}}^n,$$ (11b)

$$(1-\theta \mathrm{\Delta }t{L}_{3,3}){{\stackrel{\sim }{I}}^{\prime }}^{n+1}={{\stackrel{\sim }{I}}^{\prime }}^{n+2/3}-(1-\theta )\mathrm{\Delta }t{L}_{3,3}{\stackrel{\sim }{I}}^n,$$ (11c)

where Ĩ′^{n+ 1/3} and Ĩ′^{n+ 2/3} denote intermediate variables. All the three linear systems in Eq. 11 are composed of tridiagonal systems that can be efficiently solved by a Thomas algorithm [20].

Similarly, Eq. 10b is split into the three systems below for efficient solutions by the same Thomas algorithm:

$$(1-\theta \mathrm{\Delta }t{L}_{1,1}){\stackrel{\sim }{I}}^{n+1/3}=[1+(1-\theta )\mathrm{\Delta }t{L}_{1,1}+\mathrm{\Delta }t\sum _{i=2}^3{L}_{i,i}+\mathrm{\Delta }t(1-\lambda )\sum _{i,j=1(i\ne j)}^3{L}_{i,j}]{\stackrel{\sim }{I}}^n+\mathrm{\Delta }t\lambda \sum _{i,j=1(i\ne j)}^3{L}_{i,j}{{\stackrel{\sim }{I}}^{\prime }}^{n+1},$$ (12a)

$$(1-\theta \mathrm{\Delta }t{L}_{2,2}){\stackrel{\sim }{I}}^{n+2/3}={\stackrel{\sim }{I}}^{n+1/3}-(1-\theta )\mathrm{\Delta }t{L}_{2,2}{\stackrel{\sim }{I}}^n,$$ (12b)

$$(1-\theta \mathrm{\Delta }t{L}_{3,3}){\stackrel{\sim }{I}}^{n+1}={\stackrel{\sim }{I}}^{n+2/3}-(1-\theta )\mathrm{\Delta }t{L}_{3,3}{\stackrel{\sim }{I}}^n.$$ (12c)

2.3. Implementation

Let σ be the noise standard deviation (SD) and Δt the time step size, set C, the normalization constant for structure tensor, to 3, and set λ = ½, θ = ½. The implementation procedures for one iteration of semi-implicit anisotropic smoothing of DWI data are summarized as follows:

1. Estimate the gradient tensor. Convolve each diffusion weighted image I with a zero mean, SD = σ Gaussian kernel K_σ to stabilize the subsequent gradient calculations, and then calculate the gradient ∇ I. The gradient tensor G is estimated using Eq. 2 with ρ = 2σ.

2. Construct the structure tensor. Construct the structure tensor T using Eq. 3 and 4. As the structure tensor G is a 3×3, symmetric and positive definite matrix, its eigenvalues and eigenvectors are computed analytically (see Appendix A).

3. Implement the first iteration of the Craig-Sneyd scheme. Compute Ĩ′^{n+ 1} according to Eq. 11 by using the Thomas algorithm (see Appendix B and C).

4. Implement the second iteration of the Craig-Sneyd scheme. Similar to step (3) above, Ĩ^{n+ 1} is computed according to Eq. 12 also using the Thomas algorithm.

   Step (3) and (4) are performed for diffusion weighted images along each weighting direction.

2.4. Experiments with synthetic DTI data

The efficient anisotropic smoothing algorithm was first tested with a synthetic DTI dataset. The dataset consisted of two blocks of “fiber” bundles, with each block containing three identical slices of “fibers” along different orientations. Fig. 1a shows the third slice, which lies at the interface of the two blocks. The “fibers” had mean diffusivity (D) of 0.7×10⁻⁵ cm²/s, and fractional anisotropy (FA) of 0.9, comparable to those measured in vivo in the human brain.

Figure 1.

Illustration of the effect of anisotropic smoothing on synthetic data: (a) a middle (third) slice of the original noise free data. The line segments represent the tensor PDD; (b) enlarged view of the PDDs in an ROI demarked in (a); (c) PDDs in the ROI corrupted with zero mean, SD = 0.1 Gaussian noise. (d) PDDs after 40 iterations of explicit anisotropic smoothing with step size dt₀; (e) PDDs after one iteration of semi-implicit anisotropic smoothing with step size 40dt₀.

The DWIs from which diffusion tensors were computed were noise free, but were corrupted with zero mean Gaussian noise at standard deviation (SD) of 0.05, 0.1 and 0.15 times the noise free image intensity respectively. As the maximum step size for stable implementation of 3D nonlinear anisotropic filtering is 3/44 s [24], in this work 3/44 s was used as a basic time unit (dt₀). Anisotropic smoothing with the semi-implicit scheme was performed on the DWIs for a total simulated time of 400dt₀ at all noise levels with step sizes of 20dt₀ and 40dt₀. As a comparison, the same amount of smoothing with an explicit scheme was also performed on the noisy datasets with step size of dt₀ and 20dt₀.

2.5. Experiments with in vivo human DTI data

Performance of the efficient smoothing algorithm on in vivo data was examined with DWIs obtained from a healthy human subject. Prior to imaging, informed consent was given by the subject according to a protocol that was approved by the local ethics committee. The data were acquired with a 3T Philips Intera Achieva MR scanner (Netherlands) and an eight-element sense coil. A volume of 256×256×120 mm³ was scanned using 32 non-collinear weighting directions and a single shot, echo-planar, pulsed gradient spin echo imaging sequence with a diffusion weighting factor (i.e., b value) of 1000 s/mm2. The data matrix had the size of 128×128×60, giving an isotropic resolution of 2×2×2 mm³ in the data. To generate high SNR data used as a “gold standard” for performance evaluation, ten repeated scans were obtained, co-registered, and averaged to yield a volume dataset with an SNR of ~75. This high SNR dataset was corrupted with zero mean Gaussian noise at SD = 0.05, 0.1 and 0.15 times the noise free DWI intensity for smoothing tests. A block of seven slices in the middle of the image volume was smoothed using the semi-implicit scheme with step size of 5dt₀, 10dt₀ and 15dt₀ respectively, each for a total time of 60dt₀. As a comparison, an explicit scheme was also performed on the noisy datasets with step size of dt₀.

2.6. Quantitative measures of smoothing effectiveness and efficiency

Since our primary interest was the restoration of the PDD from noise corrupted images, the effectiveness of anisotropic smoothing was assessed based on the PDD improvement after smoothing. Defining θ₀, θ_N to be the root mean square (RMS) angular difference in the PDD with respect to noise free or “gold standard” data before smoothing and after N iterations of smoothing respectively, the PDD improvement was measured by percent RMS angular difference improvement as:

$$\frac{{\theta }_0-{\theta }_N}{{\theta }_0}\times 100\%.$$ (13)

The Efficiency of smoothing algorithm was evaluated in terms of total computation time required for a designated amount of anisotropic smoothing. Comparison of time efficiency between the semi-implicit and explicit schemes was made on the basis of total computation time cost for the same amount of smoothing.

3. Results

3.1. Experiments with synthetic DTI data

To demonstrate the capability of anisotropic smoothing to preserve structural boundaries while reducing noise, a region of interest (ROI) as demarked in Fig. 1a was chosen for qualitative evaluation. The ROI contains boundaries between “fiber” bundles both within the slice and across slices. Fig. 1(b–e) shows respectively an enlarged view of PDDs in the ROI in the image without noise (b), corrupted with zero mean, SD = 0.1 Gaussian noise (c), after 40 iterations of explicit anisotropic smoothing with step size dt₀ (d), and after one iteration of semi-implicit anisotropic smoothing with step size 40dt₀ (e). As can be seen, there are large variations in the orientation of the PDDs due to noise corruption; these variations are significantly reduced after one iteration of semi-implicit smoothing without appreciable blurring, i.e., mixing of the orientations of neighboring PDDs, at the boundaries. By comparison, the explicit scheme does not restore the orientation of the PPDs as faithfully as the semi-implicit scheme, albeit it has been implemented for the same total iteration time (at the expense of considerably more computation time). This is presumably attributable to its limitation of only first order accuracy.

To quantitatively assess the effectiveness of the semi-implicit smoothing scheme and compare with that of the explicit scheme, RMS angular differences in PDD and signed mean FA differences (relative to the noise free data) after various degrees of smoothing are computed for the entire slice shown in Fig. 1a. Note that the signed FA differences are used to discriminate positive and negative changes of smoothed FA with respect to true FA. Variations of the RMS angular differences and the signed mean FA differences with computation time are plotted respectively in Fig. 2 and 3 for both the explicit and semi-implicit schemes with different step sizes. For the explicit scheme, it can be observed that, after multiple iterations, the RMS angular differences in PDD are greatly reduced and the mean FA difference is stabilized around zero at all noise levels when the step size is dt₀. When the step size is 20dt₀, both the magnitude of the RMS angular differences and FA error increase drastically, indicating that the solution to the diffusion PDE becomes unreliable and unstable. On the other hand, the semi-implicit scheme with all the step sizes removes the vast majority of the RMS angular differences after the first couple of iterations, beyond which the results are quite stable (Fig. 2). Likewise, the mean FA differences also decrease quickly and tend to stabilize around zero after the first couple of iterations (Fig. 3). These results indicate that the semi-implicit scheme is unconditionally stable for the step size up to 40dt₀. Overall, while there are minimal residual RMS errors in the PDD, the mean FA differences tend to drop below zero, particularly for noise SD = 0.15 and step size 40dt₀. Despite this, owing to the second order accuracy, the performance of the semi-implicit scheme with step size 40dt₀ is still superior to that of the explicit scheme with step size dt₀ in the restoration of PDD, and its performance with step size 20dt₀ is comparable to that of the explicit scheme with step size dt₀ in terms of FA.

Figure 2.

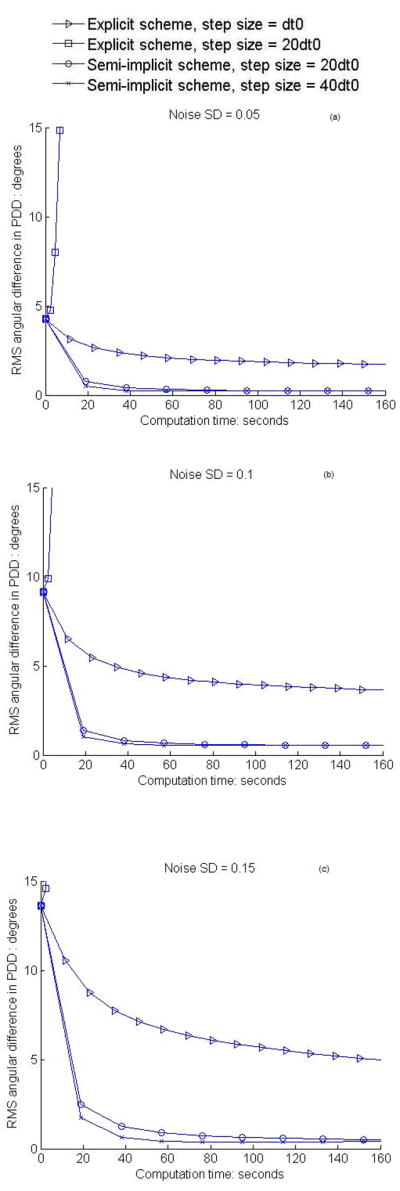
Variations of RMS angular difference in PDD with computation time of smoothing. (a–c) show the results for the synthetic data at the noise level SD = 0.05, 0.1, 0.15 respectively. The portions of the curves with PDD difference above 15 degrees are not shown.

Figure 3.

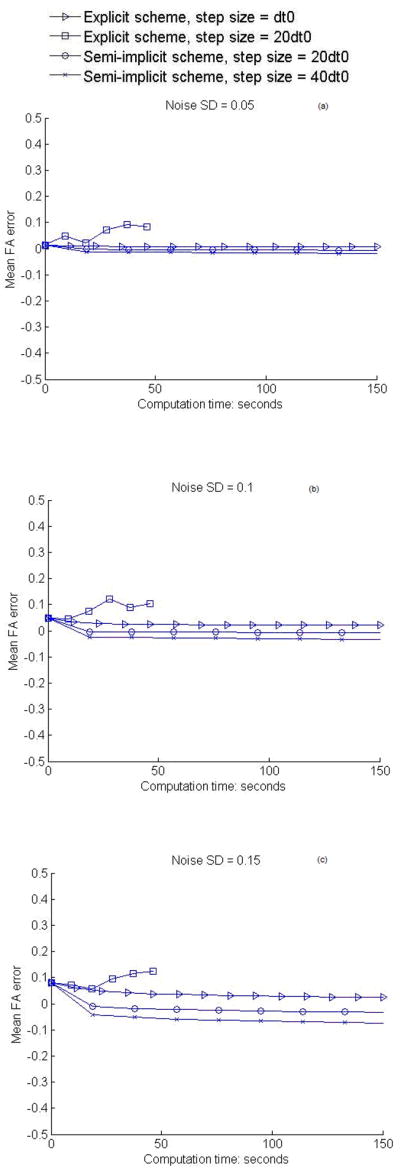
Variations of mean FA difference with computation time of smoothing. (a–c) show the results for the synthetic data at the noise level SD = 0.05, 0.1, 0.15 respectively. The curve of explicit scheme with step size 20dt₀ is shorter than other curves because of the small number of iterations used and the low computation time of each iteration.

In order to quantify the efficiency of the semi-implicit scheme, it was implemented for a total time of 40dt₀ on the synthetic dataset with noise SD = 0.1 at step size dt_0, 10dt₀, 20dt₀ and 40dt_0, respectively. As a comparison, the same total iteration of explicit smoothing with step size dt₀ was also performed on this dataset. The computation times on a COMPAQ Presario laptop (Mobile AMD Sempron 2800) and the PDD improvement from all these tests are summarized in Table 1. It can be seen that, due to the greater number of computations involved, the computation time for one iteration of the semi-implicit scheme is approximately eight times that of one iteration of the explicit scheme. However, the semi-implicit scheme has the advantage that much larger step sizes can be used, which translates to much fewer iterations needed for the same total amount of smoothing. This efficiency gain is clear when the computation time is compared between the semi-implicit scheme with step size 40dt₀ and the explicit scheme with step size dt₀, which shows roughly a five fold speed-up with the semi-implicit scheme. Moreover, the table shows that the semi-implicit scheme with all step sizes is more effective in restoring the PDD than the explicit scheme for the same total iteration time, as it gives a PDD improvement of ~90% whereas the explicit scheme only gives an improvement of ~60%. Our further tests show that, even when the explicit scheme is iterated for 1000 times, which takes a total computation time of 2313 s, the PDD improvement is still below 65%. Therefore, from the point of view of the actual improvement, the efficiency gain from the semi-implicit scheme is much higher.

Table 1.

Comparisons of computation time and percent angular difference improvement of the PDD between the semi-implicit and explicit schemes

Semi-implicit scheme, total time = 40dt0	Computation time	Percent angular difference
Step size = dt0	768 s	90.6%
Step size = 10dt0	76 s	92.3%
Step size = 20dt0	33 s	93.3%
Step size = 40dt0	19 s	93.0%
Explicit scheme, total time = 40dt0
Step size = dt0	92 s	61.0%

3.2. Experiments with in vivo human DTI data

The effect of semi-implicit anisotropic smoothing on in vivo data is examined in the middle (fourth) slice of the test block. The RMS angular difference in PDD and the mean FA difference relative to the “gold standard” data are computed for all voxels with FA>0.3. The voxels with low FA typically reside in the cerebrospinal fluid or gray matter, and thus have a poorly defined PDD regardless of the level of noise. Therefore, they are excluded to avoid their confounding effects on the quantitative analysis. Furthermore, as voxels near the borders of the brain may have artificially high FA values due to misregistration of images, they are removed by morphological erosion operations.

Variations of the RMS angular differences and the mean FA differences of semi-implicit smoothing with iteration time are plotted respectively in Fig. 4 and 5 for all the three noise levels and step sizes used. It can be observed that the RMS angular differences decrease after the first one or two iterations, and then begin to increase. This indicates that the effect of noise on the PDDs can only be partly eliminated by the anisotropic smoothing process. It should be noted that the remaining differences are due in part to the systematic bias in the “gold standard” data, and to the fact that the RMS angular difference in PDD itself is a biased estimator. The mean FA errors, on the other hand, change from positive to negative and tend to stabilize after the first couple of iterations. Like the angular differences, part of the negative FA errors after smoothing is attributable to the systemic bias in the original data which results in higher FA values than the ground truth. Compared to the explicit anisotropic filtering, the semi-implicit smoothing is superior in terms of best RMS PDD differences.

Figure 4.

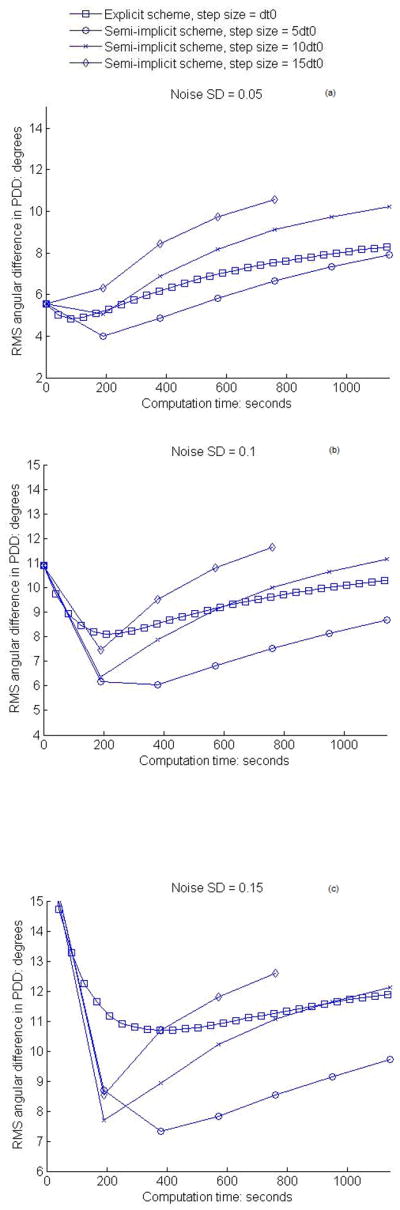
Variations of RMS angular difference in PDD with computation time of smoothing. (a–c) show the results for the in vivo human data at the noise level SD = 0.05, 0.1, 0.15 respectively.

Figure 5.

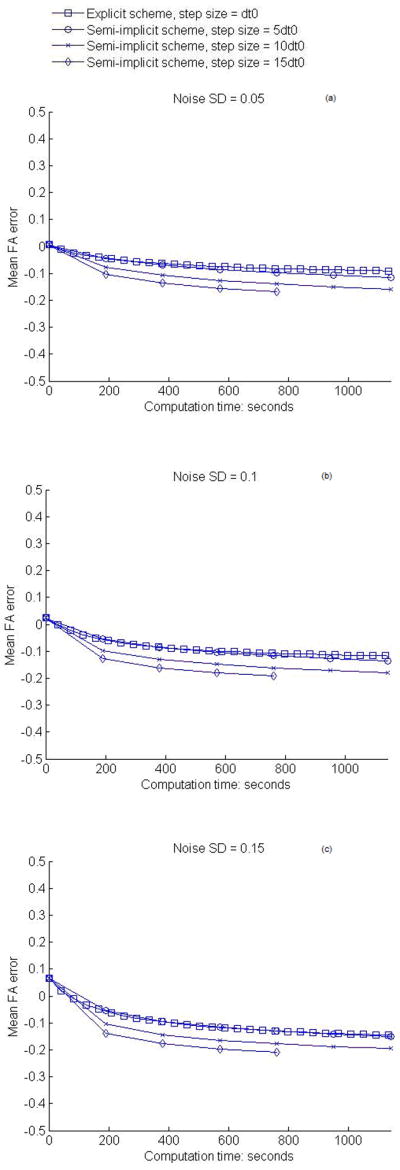
Variations of mean FA difference with computation time of smoothing. (a–c) show the results for the in vivo human data at the noise level SD = 0.05, 0.1, 0.15 respectively.

The gradual increase in the RMS angular differences in PDD and slowly decline in the mean FA values after the first couple of iterations are caused by excessive smoothing that smears out some of the structural details in the DTI data. Therefore, to achieve the best possible smoothing effect, an optimal number of iterations needs to be determined. This problem is in fact common to all diffusion filtering. So a major consideration in iterative smoothing is to obtain a best tradeoff between the extent of noise reduction and the level of artifacts introduced by over-smoothing (25). With this in mind, and taking the computational efficiency into consideration as well, we can readily conclude from Fig. 4 and 5 that one iteration of semi-implicit smoothing with a step size proportional to the level of image noise is optimal. For images with SD = 0.05 Gaussian noise, one iteration of smoothing with step size 5dt₀ is most favorable in terms of both effectiveness and efficiency, whereas for images with SD = 0.1 Gaussian noise, one iteration of smoothing with step size 10dt₀ gives the best overall performance. Using a large step size for a low level of noise would necessarily result in loss of structural details; conversely, using a small step size for a high level of noise, although yielding a slightly better smoothing effect in our case, would entail a proportionally greater number of iterations. Therefore, in applying this anisotropic filtering to the clinical DTI data, the noise level must be estimated a priori to determine the optimal step size.

The effect of anisotropic smoothing on the PDDs in the middle slice using the above parameter settings is illustrated in Fig. 6, in which a shows the PDDs in the original “gold standard” data, b is a enlarged view of demarked region in a, c, e and g are the PDDs corrupted with zero mean Gaussian noise at SD = 0.05, 0.1 and 0.15 respectively, and d, f and h are the corresponding restored PDDs after one step semi-implicit smoothing with step size of 5dt₀, 10dt₀ and 15dt₀ respectively. It is evident that, for all the levels of noise, the disarranged orientations of the PDDs due to noise corruption are largely restored by the smoothing process. Quantitative analysis shows that the PDD improvement is 27% (1 iteration), 41% (1 iteration) and 50% (1 iteration) for noise at SD = 0.05, 0.1 and 0.15 respectively with the semi-implicit scheme. In contrast, the best PDD improvement for noise at SD = 0.05, 0.1 and 0.15 is 12% (5 iterations), 26% (11 iterations) and 37% (21 iterations) respectively for explicit anisotropic filtering.

Figure 6.

Illustration of the effect of semi-implicit anisotropic smoothing on in vivo human data: (a) the middle (fourth) slice from the original high SNR data; (b) enlarged view of the PDDs in an ROI demarked in (a); (c) PDDs corrupted with zero mean, SD = 0.05 Gaussian noise; (d) PDDs after one iteration of smoothing on (c) with step size 5dt₀; (e) PDDs corrupted with zero mean, SD = 0.1 Gaussian noise; (f) PDDs after one iteration of smoothing on (e) with step size 10dt₀; (g) PDDs corrupted with zero mean, SD = 0.15 Gaussian noise; (h) PDDs after one iteration of smoothing on (g) with step size 15dt₀.

4. Discussion and Conclusion

In this paper, we have proposed an efficient anisotropic filtering algorithm for smoothing diffusion tensor images. This efficiency is achieved by using a semi-implicit scheme for solving the diffusion filtering equation. Compared to explicit schemes, the semi-implicit scheme has unconditional stability and second order time accuracy, which allows larger step sizes to be used yet more accurate results to be obtained. This helps improve considerably the efficiency as well as enhance the effectiveness of the anisotropic smoothing algorithm. Experiments with synthetic DTI data demonstrate that the semi-implicit scheme can restore the PDD of the diffusion tensor, the parameter of major interest in this work, from noise corrupted images much more efficiently and effectively than the original explicit scheme, with a five fold speed-up and ~50% improvement in the PDD improvement. Experiments with in vivo DTI data also show a significant reduction of noise effects on the PDDs with a great efficiency. In particular, the in vivo experiments demonstrate that the best overall performance in terms of both efficiency and effectiveness can be achieved by one iteration of semi-implicit smoothing with a step size proportional to the noise level. This in effect turns the iterative smoothing algorithm into a “non-iterative” procedure.

Although in theory our algorithm is stable under any large step size, the step size of our diffusion algorithm needs to be appropriately chosen to guard against potential artifacts introduced by over-smoothing. As alluded to earlier, over-smoothing is in fact a common issue for all PDE-based image denoising methods. Technically, one can either preset the iteration time or incorporate a data fidelity term into the diffusion equation so that artifacts due to large deviations from the unsmoothed image may be prevented. The choice of iteration time and the weighting of the data fidelity term, however, need to be determined with the knowledge of noise level. Usually higher noise level entails longer iteration time and smaller fidelity weighting. In our method, we determine the iteration time similarly on the basis of the noise level, but set the step size to the optimal iteration time thanks to the unconditional stability (this results in a “non-iterative” implementation of iterative diffusion filtering). Our in vivo experiments suggest that 5dt0, 10dt0 and 15dt0 are the optimal step size/iteration time for images with noise level of 0.05, 0.1 and 0.15 respectively.

It should be noted that our anisotropic diffusion filtering is performed on DWIs instead of reconstructed tensor images; therefore the anticipated benefits to tissue characterization are not predicated on any particular reconstruction models (second or higher order models) to be used. A primary consideration for smoothing DWIs is that, since image noise is introduced during the image acquisition process, it is more natural and likely easier to estimate and reduce the noise on the raw DWIs. Furthermore, noise reduction on DWIs can be computationally simpler than on the images reconstructed from them, the latter of which necessarily involves additional constraints that need to be taken into special consideration.

It is worth mentioning that, in this work, construction of the structure tensor is based on analytical solutions to the eigenvalues of the gradient tensor which is positive definite and symmetric. Analytical solutions are at least five times faster than the traditional iterative solutions with negligible loss of accuracy [26]. Furthermore, solving for the eigenvalues and eigenvectors analytically allows convenient matrix operations to be performed which offers a ten fold additional speed-up with certain program languages such as Matlab.

One drawback of the semi-implicit scheme is that Eq. 10 could be split into different linear systems that generate different final outcomes. Future work could be focused on the development of a completely symmetric splitting technique to ameliorate this problem. It should also be noted that the structure tensor plays a pivotal role in anisotropic smoothing. It is constructed from the gradient tensor that is derived from image intensity gradients along the three spatial directions of the image volume. More sophisticated schemes for its estimation may be beneficial to further improvement in the effectiveness of the smoothing algorithm.

Appendix A: Analytical solutions for eigenvalues and eigenvectors of a positive definite, symmetric matrix

Let $D=\left[\begin{array}{l}{D}_{xx},D_{xy},D_{xz}\hfill \\ D_{yx},D_{yy},D_{yz}\hfill \\ D_{zx},D_{zy},D_{zz}\hfill \end{array}\right]$ denote a 3×3 positive definite, symmetric matrix. The eigenvalues and eigenvectors of D can be computed analytically as follows [26]:

1. Determination of the eigenvalues

The eigenvalues (λ ₁ > λ ₂ > λ ₃) can be expressed as

$$\begin{array}{l}{\lambda }_1=I_1/3+2\sqrt{v}cos(\phi )\\ {\lambda }_2=I_1/3-2\sqrt{v}cos(\pi /3+\phi ),\\ {\lambda }_3=I_1/3-2\sqrt{v}cos(\pi /3-\phi )\end{array}$$ (14)

where

$$\begin{array}{l}{I}_1=D_{xx}+D_{yy}+D_{zz}\\ I_2=(D_{xx}{D}_{yy}+D_{xx}{D}_{zz}+D_{yy}{D}_{zz})-(D_{xy}^2+D_{xz}^2+D_{yz}^2)\\ I_3=D_{xx}{D}_{yy}{D}_{zz}+2D_{xy}{D}_{xz}{D}_{yz}-(D_{zz}{D}_{xy}^2+D_{yy}{D}_{xz}^2+D_{xx}{D}_{yz}^2)\\ v={(I_1/3)}^2-I_2/3\\ s={(I_1/3)}^2-I_1{I}_2/6+I_3/2\\ \phi =acos(\frac{s}{v}\sqrt{\frac{1}{v}})/3\end{array}$$

2. Determination of the eigenvectors

For i^th eigenvalue, the corresponding eigenvector e_i = [e_ix, e_iy, e_iz]^T is:

$$\begin{array}{l}{e}_{ix}=(D_{xy}{D}_{yz}-B_i{D}_{xz})(D_{xz}{D}_{yz}-C_i{D}_{xy})\\ e_{iy}=(D_{xz}{D}_{yz}-C_i{D}_{xy})(D_{xz}{D}_{xy}-A_i{D}_{yz})\\ e_{iz}=(D_{xy}{D}_{yz}-B_i{D}_{xz})(D_{xz}{D}_{xy}-A_i{D}_{yz})\end{array}$$ (15)

where

$$\begin{array}{l}{A}_i=D_{xx}-{\lambda }_i\\ B_i=D_{yy}-{\lambda }_i.\\ C_i=D_{zz}-{\lambda }_i\end{array}$$

To guarantee the positive-definite property, the matrix must satisfy the following conditions:

$$\begin{array}{l}{I}_3>0\hfill \\ D_{ii}{D}_{jj}-D_{ij}^2\ge 0\hfill \end{array}\text{for}\text{all}i,j=x,y,orz.$$

The eigenvalues and eigenvectors of matrices that do not satisfy the above conditions need to be calculated using iterative methods.

Appendix B: Thomas algorithm

A tridiagonal system of linear equations can be solved efficiently by Thomas Algorithm [20]. Consider the system of m+1 linear equations with m+1 variables (w₀, w₁…, w_m) below:

$$\begin{array}{l}{a}_i{w}_{i-1}+b_i{w}_i+c_i{w}_{i+1}=d_i,i=1,\dots ,m-1\\ w_0={\alpha }_0{w}_1+{\beta }_0\\ w_{m-1}={\alpha }_m{w}_m+{\beta }_m\end{array}$$ (16)

They can be reduced to

$$w_i=p_{i+1}{w}_{i+1}+q_{i+1},i=0,1,\dots m-1.$$ (17)

The coefficients p_i, q_i, i = 0,1,…m can be obtained with the following code:

$$\begin{array}{l}{p}_0={\alpha }_0,q_0={\beta }_0\\ \mathit{for}i=0,1,\dots ,m-1\\ p_{i+1}=-c_i/(a_i{p}_i+b_i)\\ q_{i+1}=(d_i-a_i{q}_i)/(a_i{p}_i+b_i)\\ \mathit{end}\end{array}$$

The variables w₀, w₁, …,w_m can then be solved with the following code:

$$\begin{array}{l}{w}_m=({\alpha }_m{q}_m+{\beta }_m)/(1-{\alpha }_m{p}_m)\\ \mathit{for}i=m-1,m-2,\dots ,0\\ w_i=p_{i+1}{w}_{i+1}+q_{i+1}\\ \mathit{end}\end{array}$$

Appendix C: Numerical solution for the two-iteration Craig-Sneyd scheme

Let u_i1,i2,i3 and a^{i, j}_i1,i2,i3 denote I_m (i₁h₁, i₂h₂, i₃h₃) and T ^{i, j} (i₁h₁, i₂h₂, i₃h₃) respectively, where h₁, h₂ and h₃ are the spatial step sizes in all the three dimensions and i₁=0…L1, i₂=0…L2, i₃=0…L3.

The central difference approximation of ∂_xi(T_{i, j} ∂ _xj) is given by

$$\begin{array}{l}{\partial }_{x_1}(T_{1,1}{\partial }_{x_1})u_{i1,i2,i3}=\\ (\frac{{a^{1,1}}_{i1-1,i2,i3}+{a^{1,1}}_{i1,i2,i3}}{2{h_1}^2})u_{i1-1,i2,i3}+(-\frac{{a^{1,1}}_{i1-1,i2,i3}+2{a^{1,1}}_{i1,i2,i3}+{a^{1,1}}_{i1+1,i2,i3}}{2{h_1}^2})u_{i1,i2,i3}+(\frac{{a^{1,1}}_{i1+1,i2,i3}+{a^{1,1}}_{i1,i2,i3}}{2{h_1}^2})u_{i1+1,i2,i3},\end{array}$$ (18a)

$$\begin{array}{l}{\partial }_{x_2}(T_{2,2}{\partial }_{x_2})u_{i1,i2,i3}=\\ (\frac{{a^{2,2}}_{i1,i2-1,i3}+{a^{2,2}}_{i1,i2,i3}}{2{h_2}^2})u_{i1,i2-1,i3}+(-\frac{{a^{2,2}}_{i1,i2-1,i3}+2{a^{2,2}}_{i1,i2,i3}+{a^{2,2}}_{i1,i2+1,i3}}{2{h_2}^2})u_{i1,i2,i3}+(\frac{{a^{2,2}}_{i1,i2+1,i3}+{a^{2,2}}_{i1,i2,i3}}{2{h_2}^2})u_{i1,i2+1,i3},\end{array}$$ (18b)

$$\begin{array}{l}{\partial }_{x_3}(T_{3,3}{\partial }_{x_3})u_{i1,i2,i3}=\\ (\frac{{a^{3,3}}_{i1,i2,i3-1}+{a^{3,3}}_{i1,i2,i3}}{2{h_3}^2})u_{i1,i2,i3-1}+(-\frac{{a^{3,3}}_{i1,i2,i3-1}+2{a^{3,3}}_{i1,i2,i3}+{a^{3,3}}_{i1,i2,i3+1}}{2{h_3}^2})u_{i1,i2,i3}+({\mu }_1\frac{{a^{3,3}}_{i1,i2,i3+1}+{a^{3,3}}_{i1,i2,i3}}{2{h_3}^2})u_{i1,i2,i3+1},\end{array}$$ (18c)

$$\begin{array}{l}{\partial }_{x_1}(T_{1,2}{\partial }_{x_2})u_{i1,i2,i3}={\partial }_{x_2}(T_{2,1}{\partial }_{x_1})u_{i1,i2,i3}=\\ (-\frac{{a^{1,2}}_{i1-1,i2-1,i3}}{4h_1{h}_2})u_{i1-1,i2-1,i3}+(-\frac{{a^{1,2}}_{i1-1,i2+1,i3}}{4h_1{h}_2})u_{i1-1,i2+1,i3}(\frac{{a^{1,2}}_{i1+1,i2-1,i3}}{4h_1{h}_2})u_{i1+1,i2-1,i3}+(\frac{{a^{1,2}}_{i1+1,i2+1,i3}}{4h_1{h}_2})u_{i1+1,i2+1,i3},\end{array}$$ (18d)

$$\begin{array}{l}{\partial }_{x_1}(T_{1,3}{\partial }_{x_3})u_{i1,i2,i3}={\partial }_{x_3}(T_{3,1}{\partial }_{x_1})u_{i1,i2,i3}=\\ (-\frac{{a^{1,3}}_{i1-1,i2,i3-1}}{4h_1{h}_3})u_{i1-1,i2,i3-1}+(-\frac{{a^{1,3}}_{i1-1,i2,i3+1}}{4h_1{h}_3})u_{i1-1,i2,i3+1}(\frac{{a^{1,3}}_{i1+1,i2,i3-1}}{4h_1{h}_3})u_{i1+1,i2,i3-1}+(\frac{{a^{1,3}}_{i1+1,i2,i3+1}}{4h_1{h}_3})u_{i1+1,i2,i3+1},\end{array}$$ (18e)

$$\begin{array}{l}{\partial }_{x_2}(T_{2,3}{\partial }_{x_3})u_{i1,i2,i3}={\partial }_{x_3}(T_{3,2}{\partial }_{x_2})u_{i1,i2,i3}=\\ (-\frac{{a^{2,3}}_{i1,i2-1,i3-1}}{4h_2{h}_3})u_{i1,i2-1,i3-1}+(-\frac{{a^{2,3}}_{i1,i2-1,i3+1}}{4h_2{h}_3})u_{i1,i2-1,i3+1}(\frac{{a^{2,3}}_{i1,i2+1,i3-1}}{4h_2{h}_3})u_{i1,i2+1,i3-1}+(\frac{{a^{2,3}}_{i1,i2+1,i3+1}}{4h_2{h}_3})u_{i1,i2+1,i3+1}.\end{array}$$ (18f)

Note that reflecting boundary condition is used when the index exceeds the dimensions of a or u. Using the above central difference approximation, the finite difference equation of Eq. 11 and 12 can then be expressed as follows,

$$(1-\theta \mathrm{\Delta }t\partial x_1(T_{1,1}\partial x_1)){u^{\prime }}_{i1,i2,i3}^{n+1/3}=[1+(1-\theta )\mathrm{\Delta }t\partial x_1(T_{1,1}\partial x_1)+\mathrm{\Delta }t\sum _{i=2}^3\partial x_i(T_{i,i}\partial x_i)+\mathrm{\Delta }t\sum _{i,j=1(i\ne j)}^3\partial x_i(T_{i,j}\partial x_j)]{u^n}_{i1,i2,i3},$$ (19a)

$$(1-\theta \mathrm{\Delta }t\partial x_2(T_{2,2}\partial x_2)){u^{\prime }}_{i1,i2,i3}^{n+2/3}={u^{\prime }}_{i1,i2,i3}^{n+1/3}-(1-\theta )\mathrm{\Delta }t\partial x_2(T_{2,2}\partial x_2){u^n}_{i1,i2,i3},$$ (19b)

$$(1-\theta \mathrm{\Delta }t\partial x_3(T_{3,3}\partial x_3)){u^{\prime }}_{i1,i2,i3}^{n+1}={u^{\prime }}_{i1,i2,i3}^{n+2/3}-(1-\theta )\mathrm{\Delta }t\partial x_3(T_{3,3}\partial x_3){u^n}_{i1,i2,i3},$$ (19c)

$$\begin{array}{l}(1-\theta \mathrm{\Delta }t\partial x_1(T_{1,1}\partial x_1))u_{i1,i2,i3}^{n+1/3}=[1+(1-\theta )\mathrm{\Delta }t\partial x_1(T_{1,1}\partial x_1)+\mathrm{\Delta }t\sum _{i=2}^3\partial x_i(T_{i,i}\partial x_i)+\\ \mathrm{\Delta }t(1-\lambda )\sum _{i,j=1(i\ne j)}^3\partial x_i(T_{i,j}\partial x_j)]u_{i1,i2,i3}^n+\mathrm{\Delta }t\lambda \sum _{i,j=1(i\ne j)}^3\partial x_i(T_{i,j}\partial x_j){u^{\prime }}_{i1,i2,i3}^{n+1},\end{array}$$ (20a)

$$(1-\theta \mathrm{\Delta }t\partial x_2(T_{2,2}\partial x_2))u_{i1,i2,i3}^{n+2/3}=u_{i1,i2,i3}^{n+1/3}-(1-\theta )\mathrm{\Delta }t\partial x_2(T_{2,2}\partial x_2)u_{i1,i2,i3}^n,$$ (20b)

$$(1-\theta \mathrm{\Delta }t\partial x_3(T_{3,3}\partial x_3))u_{i1,i2,i3}^{n+1}=u_{i1,i2,i3}^{n+2/3}-(1-\theta )\mathrm{\Delta }t\partial x_3(T_{3,3}\partial x_3)u_{i1,i2,i3}^n.$$ (20c)

Eq. 19a and 20a consists of (L2+1)×(L3+1) tridiagonal systems of equations, one for each value i₂ and i₃. Because those tridiagonal systems exhibit exactly the same form as Eq. 17, the Thomas algorithm can be used to solve the values of u_{i1, i2, i3} for each value i₂ and i₃, Usually the Thomas algorithm is implemented in a two-loop on i₂ and i₃. Similarly, Eq. 19b and 20b consists of (L1+1)×(L3+1) tridiagonal systems of equations, and Eq. 19c and 20c consists of (L1+1)×(L2+1) tridiagonal systems of equations. Those tridiagonal systems can be solved by the Thomas algorithm in a similar way.