A statistical, formant-pattern model for segregating vowel type and vocal-tract length in developmental formant data

Abstract

This paper investigates the theoretical basis for estimating vocal-tract length (VTL) from the formant frequencies of vowel sounds. A statistical inference model was developed to characterize the relationship between vowel type and VTL, on the one hand, and formant frequency and vocal cavity size, on the other. The model was applied to two well known developmental studies of formant frequency. The results show that VTL is the major source of variability after vowel type and that the contribution due to other factors like developmental changes in oral-pharyngeal ratio is small relative to the residual measurement noise. The results suggest that speakers adjust the shape of the vocal tract as they grow to maintain a specific pattern of formant frequencies for individual vowels. This formant-pattern hypothesis motivates development of a statistical-inference model for estimating VTL from formant-frequency data. The technique is illustrated using a third developmental study of formant frequencies. The VTLs of the speakers are estimated and used to provide a more accurate description of the complicated relationship between VTL and glottal pulse rate as children mature into adults.

I. INTRODUCTION

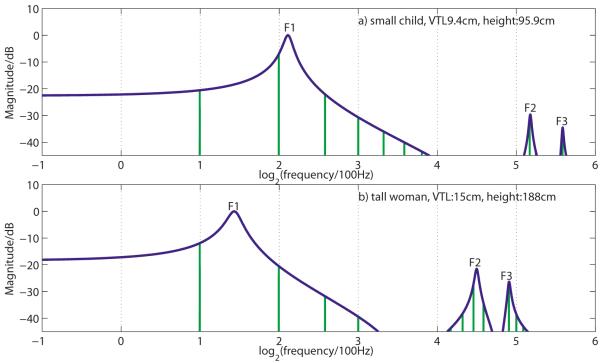
The purpose of this paper is to establish a framework for estimating the vocal-tract length (VTL) of a given speaker from small segments of their voiced speech sounds and thereby to establish a method for continuous estimation of VTL during speech processing. A VTL track, or contour, would assist speaker segregation and vowel normalization in multi-source environments (e.g., Welling and Ney, 2004). The principle is illustrated in Fig. 1 which shows the magnitude spectra (vertical lines) of two synthetic /i/ vowels like those that might be produced by (a) a small child (about 95 cm in height) with a short vocal tract (9.4 cm) and (b) a tall woman (about 188 cm in height) with a long vocal tract (15 cm). The glottal-pulse rate (GPR) and the spectral envelope of a real vowel can be modified in an analogous way using the high quality vocoder referred to as “STRAIGHT” (Kawahara et al., 1999; Kawahara and Irino, 2004). For simplicity, the GPR (the voice pitch) is 200 Hz in both cases; it determines the spacing of the spectral components. The spectral envelopes of the vowels are shown by the smooth lines; they represent the transfer functions of the vocal tracts that produced these vowels. The soft-shouldered peaks in the envelopes represent the vocal-tract resonances which are referred to as formants. The spectra and envelopes are plotted on a logarithmic frequency axis (base 2) and the reference frequency associated with a log value of 0 is 100 Hz.

FIG. 1.

(Color online) Magnitude spectra (vertical lines) and spectral envelopes (smooth lines) of two synthetic /i/ vowels like those that might be produced by (a) a small child and (b) a tall woman. F1, F2, and F3 show the positions of the first, second, and third formants of the vowel. Note that the formant peaks often occur between peaks of the magnitude spectrum.

It is assumed that the child and the adult have formed their vocal tracts into the same shape to produce their /i/ vowels, and as a result, the pattern of formant information is the same for the two tokens of the vowel, on this logarithmic frequency axis. It is only the position of the pattern that differs; the formant pattern for the adult is shifted toward the origin, with respect to that of the child, because the vocal tract of the adult is much longer than that of the child. This very simple model of vowel development is referred to as the fixed-formant-pattern hypothesis in the current paper. It is similar to the uniform scaling hypothesis (e.g., Fant, 1966) and to formant ratio theory (e.g., Miller, 1989). The differences will be discussed below where relevant.

These simple models of vowel development are important because they imply that vowel-type information and VTL information are covariant in the log-frequency vowel spectrum (Patterson et al., 2007), and this, in turn, suggests a relatively simple method for performing VTL estimation in conjunction with vowel identification. The process involves taking the formant pattern for each vowel type, in turn, and shifting it back and forth along the frequency axis to find out which formant pattern (vowel type) leads to the best fit, and the position in which this best fit is achieved. The position specifies the VTL of the speaker to within a fixed constant. Accordingly, the purpose of the paper is to review the developmental data pertaining to the spectral envelopes of vowel sounds to determine the extent to which the formant-pattern hypothesis is true and to investigate the practical implications of estimating VTL from existing developmental data on formant patterns.

Section I A describes a quantitative reanalysis of the classic developmental data of Peterson and Barney (1952) in which the formant pattern is summarized by estimates of the first three formant frequencies, extracted from spectrograms of the vowels by humans. The analysis shows that children and adults produce vowels in which the formant pattern is, at least approximately, fixed, and the main source of variability, after vowel type, is the acoustic counterpart of VTL (i.e., acoustic scale; Cohen, 1993 and Umesh et al., 1999). This suggests that it should be possible to use the formant-pattern principle to estimate VTL as outlined above from formant-frequency data. However, two problems were encountered when attempting to develop a procedure for VTL estimation. (1) There was a small but significant discrepancy from fixed formant patterns in the data of Peterson and Barney (1952) which suggested the presence of another source of variability in the data. Fant (1966, 1975) observed the discrepancy some time ago in the course of investigating the uniform scaling hypothesis. He suggested that the discrepancy might be associated with the fact that the pharyngeal cavity grows proportionately more than the oral cavity as children mature into adults. The extent of the non-uniformity of the growth of the anatomical cavities of the vocal tract is quantified in Sec. I B using the magnetic resonance imaging (MRI) data of Fitch and Giedd (1999). The analysis shows that the non-uniformity is actually much larger than would be required to explain the discrepancy from uniform scaling of formant frequencies in the data of Peterson and Barney (1952). (2) There is also an oddity in the Peterson and Barney (1952) data; there are an excessive number of formant frequencies which are integer multiples of the GPR of the vowel; that is, harmonics of the voice pitch. This suggests that the discrepancy might represent a measurement bias, arising from the well known problem of estimating formant frequencies from the harmonic spectra of voiced vowels. The problem is illustrated in the lower panel of Fig. 1. In this vowel token, there are harmonics (vertical lines) below and above the center of the first formant frequency (which is the first peak of the spectral envelope), but no harmonics right at the formant frequency. The problem is reviewed by de Cheveigné and Kawahara (1999) who concluded that it is inherent in spectrographic representations of speech sounds and extends to automatic transcription methods based on linear predictive coding (LPC).

The purpose of the remainder of the paper is to develop a model of vowel sounds that incorporates a statistical approach to deal with the formant measurement problem. This new approach to formant-frequency data has the distinct advantage that it can determine whether the residual formant variability in the data of Peterson and Barney (1952) is due to errors in formant-frequency estimation or to the non-uniform growth of one or more components of the vocal tract, as suggested by Fant (1975). The result is surprising; once the measurement noise has been properly modeled, it is observed that the formant patterns of the vowel sounds do not vary systematically, either with the size or the sex of the speaker, despite the obvious non-uniformity in the growth of the anatomical cavities (oral and pharyngeal). Moreover, a statistical analysis of the fixed-formant-pattern hypothesis at the heart of the model indicates that more complex growth functions with non-linear terms are less likely than the fixed pattern model, given the data of Peterson and Barney (1952). This means that the formant resonators are not affected by developmental changes in the oral-pharyngeal ratio and that it is reasonable to assume that formant-frequency values are effectively determined by vowel type and VTL, independent of the position of the junction between the oral and pharyngeal cavities, as suggested by McGowan (2006). The results derived from the classic data of Peterson and Barney (1952) are confirmed by replicating the analyses on the massive developmental database reported by Lee et al. (1999). They recorded ten vowels from each of 436 children, ages 5–18, plus 56 adults. Section III shows how the statistical inference model can be used to estimate VTL from a separate set of developmental data reported by Huber et al. (1999) and to illustrate how GPR and VTL evolve from age 4 to adulthood in the human population.

A. Evaluating the fixed-formant-pattern assumption with the data of Peterson and Barney (1952)

The classic formant data of Peterson and Barney (1952) were reanalyzed to quantify the proportions of inter-vowel and intra-vowel variability and to assess the role of speaker size in the intra-vowel variability. Briefly, the analysis reveals that about 80% of the total variability in formant frequencies is accounted for by vowel type, and a second variable, which is referred to as acoustic scale (Cohen, 1993) and which is closely related to VTL and speaker height, accounts for up to 90% of the remaining intra-vowel variability. This indicates the potential value of VTL normalization for speech recognition as noted by, for example, Welling and Ney (2004), and it supports the hypothesis that it should be possible to estimate VTL from vowel sounds.

1. Inter-vowel variability: Vowel type

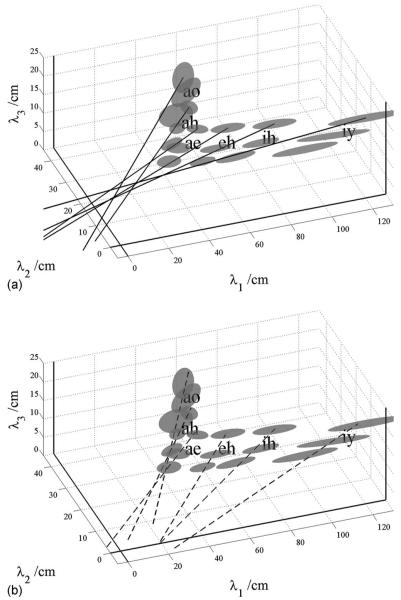
In their classic study, Peterson and Barney (1952) recorded two repetitions of ten American vowels in hVd words (heed /iy/, hid /ih/, head /eh/, had /ae/, hod /aa/, hawed /ao/, hood /uh, who’d /uw/, hud /ah/, and heard /er/) from 76 men, women, and children. From the spectrogram of each recording, they estimated the frequencies of the first three formants (F1, F2, and F3) and the pitch of the vowel (F0). When the data were plotted in F1-F2 space, the tokens of each vowel were found to cluster into relatively well defined regions that Peterson and Barney (1952) delimited with hand-drawn ellipses (their Fig. 8). In order to quantify the analysis, we have fitted three-dimensional Gaussian distributions to the F1-F2-F3 values of all of the tokens in each vowel cluster. The contours of constant probability associated with this distribution are ellipsoids; the contour associated with one standard deviation along each of the axes has been plotted for each of the ten vowels in Fig. 2. The formant frequency values have been converted into their corresponding wavelengths (λ₁,λ₂,λ₃) because the focus of this paper is VTL and the analysis is more direct when presented in terms of wavelengths.

FIG. 8.

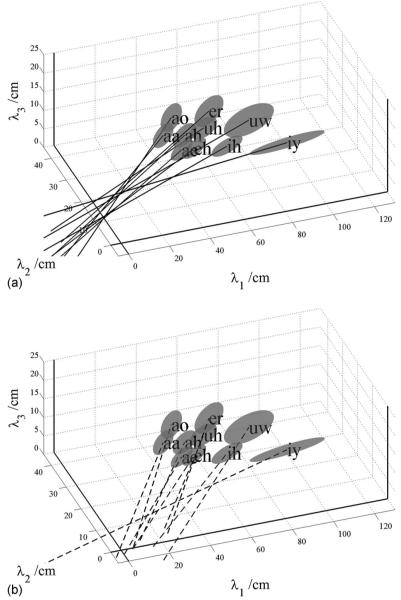
(a) Rotated view of Fig. 3, showing the individual ellipsoids for the population subgroups for six of the vowels in Peterson and Barney (1952). The view emphasizes the bias of the intercepts away from the origin in the λ₁ dimension, and the elongation of the ellipsoids in the λ₁ dimension for vowels /iy/ and /ih/. (b) The same view of the individual ellipsoids using the statistical formant-pattern model with explicit terms for formant measurement error. The bias of the intercepts is considerably reduced.

FIG. 2.

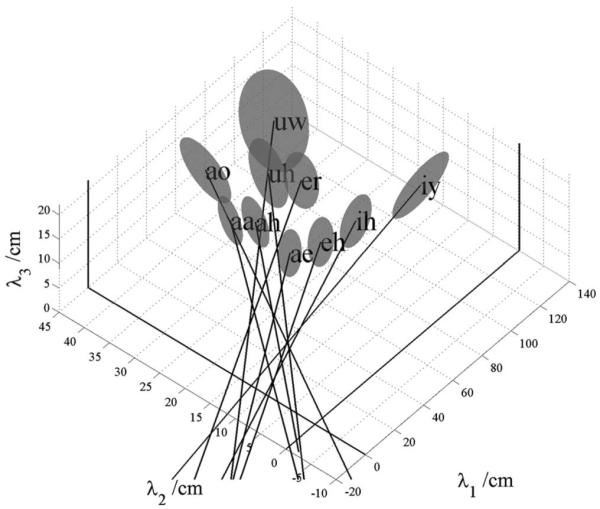
Ellipsoids showing the distribution of formant wavelengths associated with each vowel in the classical formant data of Peterson and Barney (1952). The ellipsoids were derived using PCA; they represent one standard deviation from the mean of the vowel clusters (enclosing 29% of the data points). The lines show the orientation of the major axes of the ellipsoids; their extensions point toward the origin of the space, but there is a consistent bias away from the origin.

The positions of the ellipsoids in wavelength space reveal the established observations concerning inter-vowel variability. (1) There is virtually no overlap between the ellipsoids in this space. (2) The separation between the clusters is significantly greater in the λ₁-λ₂ plane than in the λ₂-λ₃ plane or the λ₁-λ₃ plane, indicating that the first two formants carry most of the vowel-type information. (3) The back vowels and front unrounded vowels occupy different planes in wavelength space due to the relatively high and roughly constant second formant in front unrounded vowels (Broad and Wakita, 1977). The analysis shows that inter-vowel variability accounts for about 80% of the total formant variability in the Peterson and Barney (1952) data.

2. Intra-vowel variability: Vocal tract length

The intra-vowel variability is largely summarized by the eccentricity of the ellipsoid, its orientation, and its distance from the origin. With regard to eccentricity, in each case, one of the three principal axes of the ellipsoid is much longer than the other two. This is basically because the vocal tract increases in length as a child grows up. The eccentricity can be quantified with the aid of a principal components analysis (PCA), and it shows that approximately 90% of the intra-vowel variability lies in the direction of the major axis of the ellipsoid. With regard to the orientation, the ellipsoids all point in the direction of the origin of the space, as illustrated by the lines in Fig. 2; they show the extension of the major axis of each ellipsoid in the direction of the origin (given by the major-eigenvector of the covariance matrix). Together the eccentricities and orientations of the ellipsoids indicate that, within each vowel cluster, the formant pattern is approximately fixed for all members of the population. This is the basis of formant ratio theory (e.g., Lloyd, 1890; Potter and Steinberg, 1950; and Miller, 1989) and the uniform scaling hypothesis (e.g., Fant, 1966; for a review see Adank et al., 2004). The principle has also been used to develop transforms intended to improve the performance of computer speech recognizers (e.g., Irino and Patterson, 2002; Umesh et al., 2002; Welling and Ney, 2004). Similarly, it would appear that if vowel type and VTL account for virtually all of the variability in the formant-frequency data, then it would seem a relatively easy matter to estimate VTL given vowel type, as outlined in the Introduction (Sec. I).

3. Mathematical formulation of the formant-pattern model

The mathematical form for the simplest version of the formant-pattern model is

$${\underset{\_}{\lambda }}_i^v=a_i\langle {\underset{\_}{\lambda }}^v\rangle ,$$ (1)

where v is vowel type, i is the individual speaker, and ${\underset{\_}{\lambda }}_i^v$ is a three-component vector of formant wavelengths, which represents the formant pattern for vowel v of speaker i. $\langle {\underset{\_}{\lambda }}^v\rangle$ is the vector representation of the average formant pattern for vowel v in the population. The scalar, a_i, specifies the length of the individual’s vocal tract relative to the mean of the population. The fixed-formant-pattern model is very simple; there is a single parameter for each formant and a single value of a_i that relates the individual’s formants to those of the population. It is the “acoustic scale” (Cohen, 1993) of the formants relative to that of the population.

Peterson and Barney (1952) were not able to measure the VTL of their speakers; indeed, it is very difficult (Fitch and Giedd, 1999). However, the prediction is that variability in VTL across a population of speakers causes systematic variability in the formant wavelengths of their vowels. Specifically, the fixed-formant-pattern hypothesis predicts that the vowel clusters are ellipsoids and that the orientation of each vowel cluster, which is determined by the direction of the principal component of the variability in the data, will correspond to the direction along which the formant pattern is fixed. This direction, which is the major axis of the ellipsoid, passes through the origin. The eccentricity of the ellipsoid is partly determined by the variability of VTL in the population and partly by the distance of the ellipsoid from the origin of the space. In fact, the relative lengths of the ellipsoids along their major axes are predicted to depend entirely on their relative distances from the origin of the space according to

$${\sigma }^v={\langle {({\lambda }^v-\langle {\lambda }^v\rangle )}^2\rangle }^{1∕2}={\sigma }_a\mid \langle {\underset{\_}{\lambda }}^v\rangle \mid ,$$ (2)

where σ^v is the magnitude of the principal component of the vowel cluster (which is equivalent to the length of the ellipsoid along the major axis), σ_a is the standard deviation of the VTL scalar in the population, and $\mid \langle {\underset{\_}{\lambda }}^v\rangle \mid$ is the magnitude of the vowel-cluster mean or the distance from the origin of the space to the center of the ellipsoid.

Thus, the model predicts that VTL is the largest source of intra-vowel variability and it can be used to assess the accuracy of the fixed-formant-pattern hypothesis. For example, the angle formed between the major axis of each ellipsoid and the line from the center of that ellipsoid to the origin provides a measure of the accuracy of the hypothesis. The angles are presented in Table I for the ten vowels in the Peterson and Barney (1952) database, along with the proportion of the intra-vowel variance accounted for by the principal component. The angles are very small and they show that VTL accounts for about 90% of the variability not attributable to vowel-type. Here, then, is a quantitative basis for the fixed-formant-pattern hypothesis as observed in the classic data of Peterson and Barney (1952).

TABLE I.

Summary statistics for two tests of the fixed-formant-pattern hypothesis: The values in the upper pair of rows are based on a deterministic PCA; those in the lower pair of rows are based on a SFP model. Within each pair, the upper row shows the proportion of variability accounted for by the first component, and the lower row shows the angle that component makes with the uniform scaling line. Notice that the proportion of the variance explained by the principle component for the second analysis is often smaller than that for the first. This is because the second analysis explicitly models the observation noise and, once this contribution has been removed, there is less variability for the principal component to explain

Vowel	/aa/	/ae/	/ah/	/ao/	/eh/	/er/	/ih/	/iy/	/uh/	/uw/	Ave
PCA: variability in direction of the PC	0.91	0.94	0.88	0.84	0.94	0.87	0.97	0.99	0.89	0.91	0.91
PCA: angle deg	11	14	6.0	7.5	8.5	13	6.6	5.6	3.9	8.0	8.4
SFP: variability in direction of the PC	0.85	0.95	0.97	0.85	0.96	0.70	0.96	0.87	0.98	0.83	0.89
SFP: angle deg	5.2	4.6	4.0	7.3	2.6	5.8	1.8	8.2	6.8	6.3	5.2

4. Residual variability

Although the analysis of formant variability indicates that the fixed-formant-pattern hypothesis is largely correct, a detailed examination of Fig. 2 shows that when the main axes of the ellipsoids are extended toward the origin, they actually intercept the λ₁=0 plane at points where λ₂ and λ₃ are slightly, but consistently, positive, and they intersect the λ₃=0 plane at points where the values of λ₁ are consistently negative. This consistent bias in the intercepts suggests that there might be one more factor making a small, but consistent contribution to formant frequency variability. A clue to the form of the remaining variability is provided in Fig. 3 which shows the sub-clusters for men, women, and children plotted separately for six of the vowels in Fig. 2; the centroids of the sub-clusters for men, women, and children are relatively widely separated on the uniform scaling lines. This indicates that VTL variability is greater between speaker groups than within speaker groups—an observation that has been confirmed by Gonzalez (2004). Moreover, the principal axes of the sub-clusters with the more extreme values of λ₁ are more closely aligned with the first-formant axis than with the fixed formant-pattern line; the most obvious examples are the vowels /iy/ and /ih/. This suggests that within speaker sub-clusters, there may be another consistent source of variability which is only revealed in conditions where VTL variability is small.

FIG. 3.

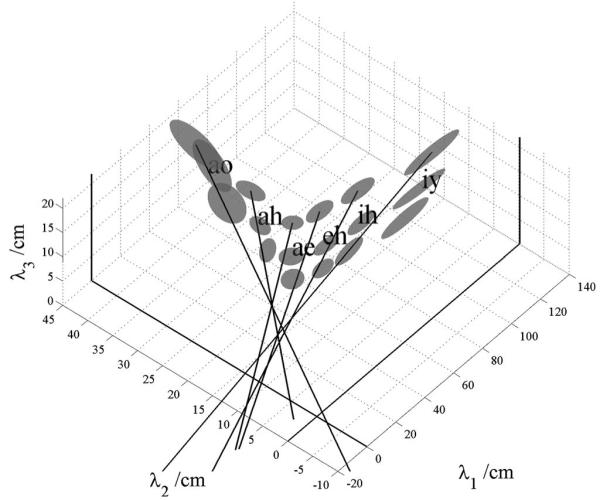
Ellipsoids showing the distribution of formant wavelengths associated with the population subgroups (men, women, and children) for six vowels in the classical formant data of Peterson and Barney (1952).The ellipsoids were derived using PCA; they represent one standard deviation from the mean of the vowel clusters (enclosing 29% of the data points).The lines show the orientation of the major axes of the ellipsoids shown in Fig. 2; the sub-clusters of each vowel are well separated along the scaling line, but the principal axes of these sub-clusters are more closely aligned with the first-formant axis than the scaling line, especially for the vowels with a low first formant (e.g., /iy/).

There are several candidates for the source of this effect: Fant (1966, 1975) suggested that variability in the formant pattern across speakers arises, at least in part, because the pharynx is proportionately larger in men than in women and children. He proposed a non-uniform scaling procedure with separate scale factors for each formant of each vowel to represent the non-uniform growth of the different components of the vocal tract and to take into account the changing formant-cavity-affiliations over vowels. The MRI data of Fitch and Giedd (1999) (reanalyzed below) confirm that the pharynx is proportionately larger in men, but this does not immediately indicate how the scale factors would be affected by VTL. Subsequently, Umesh et al. (2002) showed that Fant’s (1966, 1975) scale factors could be averaged across vowels to form a single non-uniform scaling function that describes the scale factor as a function of formant frequency. In both cases, the implication is that there is one main, latent variable in this system, which is the acoustic scale of the vowel, but that this variable affects different formants in different ways, necessitating extra parameters to be added to the fixed pattern model. In Sec. I B, we develop a statistical model of formant-frequency data that can accommodate more complicated growth dependencies, should they be required, and which has the power to reveal any remaining sources of variability beyond those accounted for by vowel type and the fixed pattern hypothesis. In the event, however, what appears as an “effect” is revealed to be a bias caused by well known problems in formant-frequency estimation (e.g., de Cheveigné and Kawahara, 1999).

B. The form of the non-uniform growth of the oral and pharyngeal cavities

Fitch and Giedd (1999) used MRI to examine the growth of the components of the vocal tract as children mature into adults. The study included 129 men, women, and children ranging in age from 2.8 to 25 years. They recorded each subject’s age, height, and weight, but they did not record samples of their speech sounds. The measurements were made with the subjects in the nasal breathing posture, and care was taken to exclude those who were overweight, or whose families had a history of language or developmental problems. Figure 4 shows VTL as a function of height separately for all of the males (○) (men and boys) and all of the females (+) (women and girls); VTL is effectively a linear function of height in both cases. There are proportionately more men at the tallest heights, but the two populations fall along lines with very similar slopes. It is also the case that the vocal tract grows proportionately slower than height because the head is proportionately larger than the body in children, but the proportionality is the same for the two groups. The growth rate is 0.067 cm/cm.

FIG. 4.

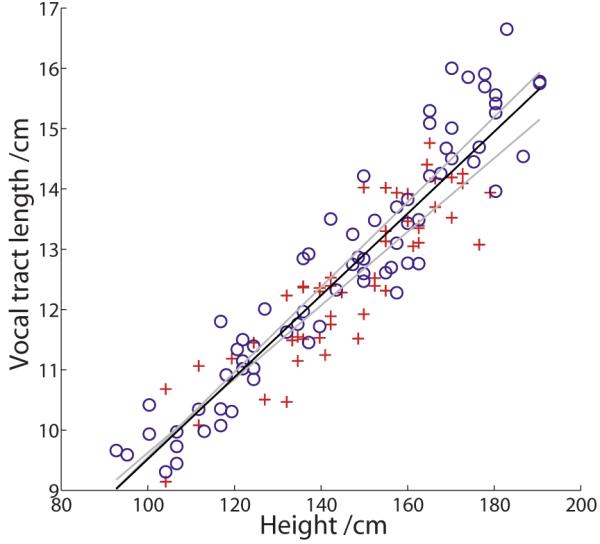
(Color online) VTL as a function of height from the data of Fitch and Giedd (1999). The upper and lower faint trend lines are the fits to the males (circles) and females (crosses), respectively. The solid trend line is the fit to the male and female data combined.

Figure 5 shows the relative lengths of the oral and pharyngeal portions of the vocal tract as a function of VTL, separately for males (○) and females (+). The figure shows that the length of the oral cavity decreases, and the length of the pharyngeal cavity increases, relative to VTL, as VTL increases. This is because the size of the oral cavity is largely determined by the size of the head which decreases as a proportion of body height as a person grows up. The figure makes it clear that the growth of the oral and pharyngeal cavities is decidedly non-uniform. Note, however, that the changes are linear in these coordinates and, for a given VTL, there is no difference between males and females in terms of the proportions of the cavities. This suggests that models, which relate growth in the main vocal tract cavities to the progressive decrease in formant frequencies with age, need not be excessively complex.

FIG. 5.

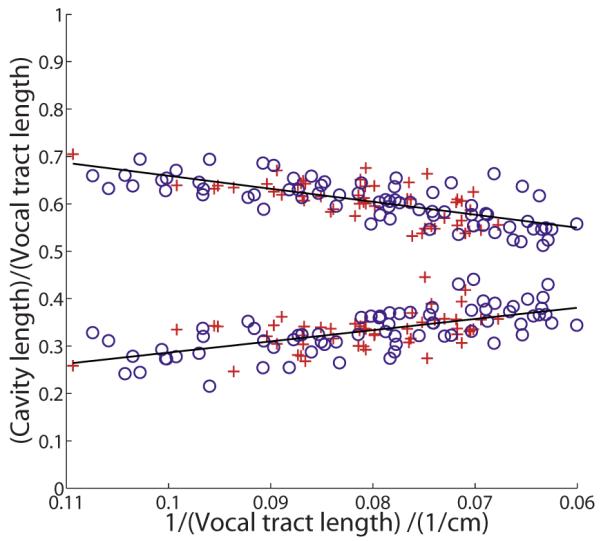
(Color online) Growth functions for the oral cavity (upper cluster) and the pharyngeal cavity (lower cluster) from the data of Fitch and Giedd (1999). The abscissa is the reciprocal of VTL which orders the subjects according to size from left to right across the cluster. The ordinate is the relative length of the cavity and so the figure illustrates the change in the oral-pharyngeal ratio as people grow up. The trend lines show linear fits to the two clusters. The data of the males (circles) and females (crosses) cluster along the same line in both cases.

It is the pronounced non-uniform growth of the oral and pharyngeal cavities that prompts us to avoid the phrase “uniform scaling” when describing formant-frequency variability and to adopt instead the phrase “fixed formant pattern.” The phrase uniform scaling is too readily misinterpreted as implying that the consistency of the formant pattern is the result of uniform growth of the anatomical components of the vocal tract, which is clearly incorrect in the case of the oral and pharyngeal cavities.

The fact that the formant patterns of vowel sounds do not vary markedly, either with the size of the speaker or their sex, may in retrospect seem surprising, given the striking non-uniformity in vocal-tract growth illustrated in Fig. 5. The analysis suggests that the anatomical distinction between the oral and pharyngeal divisions of the vocal tract is immaterial to the acoustic result of speech production. For a given vowel, the tongue constriction is simply positioned where it produces the appropriate ratio of front-cavity length to back-cavity length, independent of the location of the oral-pharyngeal junction

II. A STATISTICAL VERSION OF THE FORMANT PATTERN MODEL

The fact that the growth functions for the oral and pharyngeal cavities are linear suggests that it might be fairly simple to incorporate these growth functions into a model of formant-frequency data and in so doing realize Fant’s (1966, 1975) original ambition. It is necessary, however, to adopt statistical methods to learn the relationship between formant frequency and acoustic scale from the data, and it is necessary to treat the acoustic scale of the vowel as a “latent variable” which is to be inferred from the data. Broadly speaking, the purpose of this section is to construct a statistical model of formant-wavelength data, which can determine the extent to which the complexities in the formant data of Peterson and Barney (1952) are due to non-uniform vocal tract growth, which needs to be included in the model, and the extent to which the complexities are attributable to measurement noise and are therefore artefactual. The development of this statistical formant pattern (SFP) model begins in Sec. II A, where a linear-model is developed to represent the growth functions of the oral and pharyngeal cavities, and the model is shown to be consistent with the developmental data of Fitch and Giedd (1999). Section II B explains why the model has to include explicit terms for the variability of the individual formants and why acoustic scale has to be incorporated as a latent variable. Section II C explains that it is also necessary to include explicit terms for the variability of the components of the measurement noise. Finally, in Sec. II D, the SFP model is applied to the developmental data of Peterson and Barney (1952), and then to the developmental data of Lee et al. (1999), to determine whether non-uniform vocal-tract-growth factors need to be incorporated into formant data models.

A. Modeling vocal tract length

As children mature and their height increases, so does the length of their vocal tract and thus the acoustic scale of their speech sounds. Height, VTL, and acoustic scale also depend on the sex of the speaker beyond about age 12 when VTL and acoustic scale become somewhat greater in males relative to their height. The SFP model employs a latent or hidden variable to represent the general growth factor associated with developmental changes in formant frequencies; that variable is designated a. This general growth factor is directly related to both VTL and to acoustic scale (Cohen, 1993), and it is assumed to be multi-modal in the population with clusters corresponding to men, women, and children.

More specifically, it is assumed that the lengths of the various cavities and components of the vocal tract are linearly related to VTL and therefore to the growth factor, a, via the average length of the cavity, or component, and a weighting factor, which can be thought of as reflecting the growth rate of the cavity or component [see Eq. (3) below]. For cavities like the pharynx, where the proportion changes with growth, the dependence is strong and the weighting factor is large. For components like the lips, where the proportion changes little with growth, the dependence is weak and the weighting factor is small. The weighting factors enable us to construct a model of the vocal tract in terms of VTL, where the growth of the components of the vocal tract is non-uniform but, nevertheless, a linear function of height. Mathematically, the model is

$$L_c^v=\langle L_c^v\rangle +a\frac{d{L}_c^v}{da},$$ (3)

where $\langle L_c^v\rangle$ is the average length for cavity c for people articulating the vowel v, and a is the relative VTL of the individual. $d{L}_c^v∕da$ is a constant that does not depend on the individual. This relationship is consistent with the analysis of vocal-tract component lengths presented by Fitch and Giedd (1999) as will now be shown. If the total length of the vocal tract is written as the sum of the component lengths as follows;

$$L^v=\sum _c{L}_c^v=\sum _c\left[\langle L_c^v\rangle +a\frac{d{L}_c^v}{da}\right]=\langle L^v\rangle +a\frac{d{L}^v}{da},$$ (4)

this expression can be substituted back into Eq. (3) to eliminate the unknown acoustic scale factor, a, and produce an expression for “the ratio of a cavity or component’s length,” L_c, to “the total length of the vocal tract,” L.

$$\frac{L_c^v}{L^v}=\left[\langle L_c^v\rangle -\langle L^v\rangle \frac{d{L}_c^v}{d{L}^v}\right]\frac{1}{L^v}+\frac{d{L}_c^v}{d{L}^v}.$$ (5)

Thus, in this model of vowel production, the growth of the individual cavities and components is predicted to be linear when plotted against the reciprocal of L, which is precisely what was observed in Fig. 3. There is variability in the data that the model does not absorb, but there does not appear to be any consistent deviation as a function of speaker height of the sort that would warrant including quadratic or higher-order terms in the model.

It is now possible to determine quantitatively whether higher-order terms are warranted by fitting Nth-order polynomials to the data, and learning maximum-likelihood parameters for the terms and corresponding error-bars on these inferences. The linear model can then be compared to models of higher order by weighting the best-fit likelihoods of the more complicated models by penalty factors known as Occam factors, which depend both on prior knowledge and the error bars on the maximum-likelihood parameter estimates. In Bayesian statistics, this is a non-arbitrary form of hypothesis test (Mackay, 2003). In the current case, the linear model is found to be much more probable than models with higher-order terms. Moreover, the linear terms in the higher-order approximations were found to have similar values to those of the linear model, and the higher terms were found to contribute little within the range of the data. This, then, is a quantitative justification for using the non-uniform but linear model of VTL variability, and it can now be used to deconvolve the effect of vocal tract changes on vowel formant frequencies.

B. The formant pattern model and the non-uniform growth of the oral and pharyngeal cavities of the vocal tract

The next step in the development of the model is to relate VTL to formant wavelength. Broadly speaking, the higher formants in Peterson and Barney’s (1952) data, F2 and F3, are well modeled as simple standing wave resonances, so they will have wavelengths which are linearly dependent on the length of the vocal tract for a given vowel and formant. A simple standing wave is not, however, a good model of the first formant. To wit, the wavelength of the first formant can be as much as eight times the length of the vocal tract, which is twice the maximum length that would be expected for a simple standing wave resonance. Fant (1966) argued that the first formant is commonly a Helmholtz resonance, in which case, the relationship between the frequency of the first formant and the growth of the vocal tract might be expected to be more complicated. In the event, however, when the correlations between formants for all of the vowels were analyzed (using the Bayesian techniques described in Sec. II A) the relationships were found to be well approximated by a line. As a consequence, any pair of formants in a vowel is linearly related; that is,

$${\lambda }_l^v=m_{l,m}^v{\lambda }_m^v+c_m^v,$$ (6)

where l and m are formant numbers, 1, 2, or 3. This means that a fairly simple model might be expected to capture the majority of the variability in Peterson and Barney’s (1952) data, so long as it incorporates the model of vocal tract growth derived earlier in Sec. II A. A straightforward approach, consistent with the data, is to describe each resonator in terms of an effective wavelength, that is, a simple linear function of VTL, regardless of its physical complexity. That is, ${\lambda }_l^v=n_l^v{L}_l^v$. Each of the effective wavelengths might be expected to develop in exactly the same way as the physical dimensions of the vocal tract [Eq. (3)], in which case the predicted relationship between formant wavelengths is linear, as observed previously in this section. This description can be generalized to the three-component vowel vectors

$${\underset{\_}{\lambda }}^v={\underset{\_}{c}}^v+a{\underset{\_}{m}}^v\text{where}{\underset{\_}{c}}^v={\underset{\_}{n}}^{v_{°}}\langle {\underset{\_}{L}}^v\rangle \text{and}{\underset{\_}{m}}^v={\underset{\_}{n}}^{v_{°}}\frac{d\langle {\underset{\_}{L}}^v\rangle }{da},$$ (7)

where ° denotes the element-wise product. The prediction of this model is that the vowel clusters will form on segments of lines oriented in the direction m^v with centroids at c^v. If the growth rate of the effective lengths is uniform, then m^v and c^v are parallel and the fixed-formant-pattern model is recovered as a simple limit. If the distribution of the acoustic scale factor, a, is Gaussian then this model is equivalent to PCA and the analysis of Sec. I A is recovered. However, as noted earlier, the distribution is not Gaussian; there are three distinct classes of speaker (men, women, and children). Therefore, a more sensible choice is a mixture of Gaussians, with a Gaussian component for each group.

Two versions of the statistical model were developed, distinguished by their assumptions concerning the source of the vowels in each vowel cluster. In the first and simpler version, the vowels in each cluster were treated as if they all came from different speakers, and thus the clusters can be fitted individually. In point of fact, the vowels in the clusters are not independent with respect to VTL; each speaker contributes two tokens to each of the ten vowel clusters. The second version of the model incorporates this constraint, which, in turn, makes it possible to fit all the vowel clusters simultaneously. Although the inferred acoustic scale factors estimated with the second version of the statistical formant pattern model are almost certainly more accurate, the parameter values derived from the two models are very similar. Accordingly the discussion is restricted to the results from the second version of the model, and it is these values that are reported in the lower rows of Table I.

C. The variability of formant measurements

Having included the effects of vowel type and VTL in the statistical version of the formant pattern model, the question is whether the formant-frequency data contain other consistent sources of variability or whether the remaining variability is just due to measurement noise. To answer the question, it is necessary to include an explicit term for the residual noise in the SFP model. When the model, with its noise term, is applied to the data, the result is surprising; most of the remaining variability in the formant wavelength data is due to a consistent measurement error, and when the error is properly modeled, the fixed-formant-pattern model is observed to absorb most of the remaining variability. This indicates that if there is another natural factor, then its effect is limited to a very small contribution—a contribution that would be difficult to characterize because its effect is obscured by measurement noise.

The measurement error arises from the fact that it is difficult to estimate formant-frequency values from a spectrogram, particularly for the first formant, as noted in the Introduction and illustrated in Fig. 1. Formant-frequency estimation based on LPC is also prone to errors in this situation; it can only guarantee accuracy of approximately a quarter of the glottal pulse rate (Monsen and Engebretson, 1983; Vallabha and Tuller, 2002). Peterson and Barney’s (1952) method was less sophisticated; they used a simple weighted average of the harmonics, f_n, in the neighborhood of the formant (see Potter and Steinberg, 1950),

$$\text{formant frequency}=\frac{{\sum }_n{f}_n\times a_n}{{\sum }_n{a}_n}.$$ (8)

Statistically, their method has similar restrictions to those of LPC with respect to accuracy, but the observed errors are somewhat larger. Moreover, an analysis of the data shows that a curiously high proportion of the formant estimates (~20%) are integer multiples of the GPR, as shown in Fig. 6. It appears that the estimate of formant frequency is attracted by a nearby harmonic frequency, which it would only rarely be by chance. It is also clear that many of the formant-frequency estimates were based on a single harmonic frequency. It turns out that this consistent measurement error is the source of much of the remaining variability in the vowel formant data. The measurement noise is roughly the same in absolute terms for all of the formants and so, as a proportion, the effect is largest for the first formant and smallest for the third formant. In wavelength terms,

$$\frac{{\sigma }_{\lambda }}{\lambda }=n\frac{f_0}{f}.$$ (9)

FIG. 6.

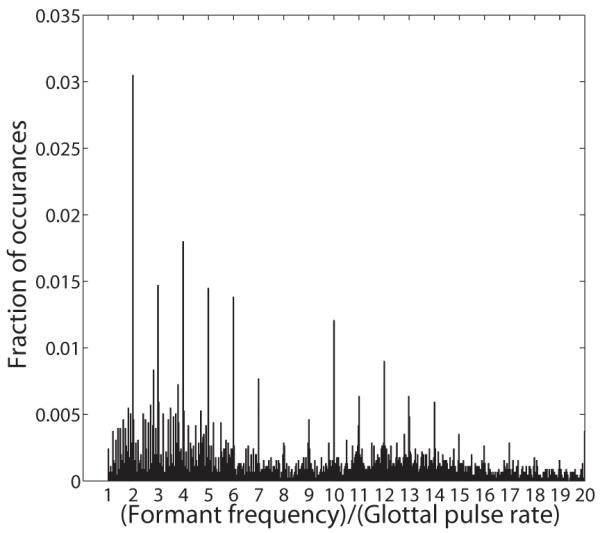
Histogram of formant frequencies normalized to glottal pulse rate, illustrating the over-abundance of formant frequencies which are integer multiples of the GPR (i.e., GPR harmonics).

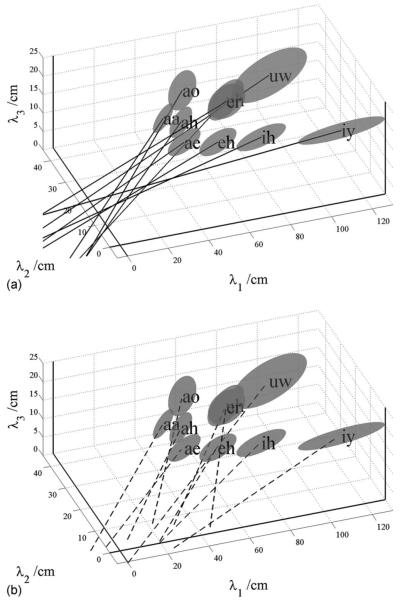
The distortion that the measurement error imparts to the vowel clusters is illustrated in Figs. 7(a) and 8(a), which show views of the respective spaces presented in Figs. 2 and 3, but with the view rotated to emphasize the λ₁-λ₃ plane and thereby to emphasize the variability in λ₁. In Fig. 8(a), for vowels having a large λ₁, such as /iy/ and /ih/, the individual ellipsoids for men, women, and children are observed to be highly elongated in the λ₁ direction. The elongation is a very unusual form of variability, and it is not clear how factors like the non-linear growth of the oral-pharyngeal ratio could explain this form of variability since it does not vary with speaker size. The form of the variability led to the hypothesis that the lack of an explicit noise term in the deterministic formant pattern model (Sec. I A) leads to a bias in formant wavelength estimation that, in turn, produces the elongation of the ellipsoids in Fig. 8(a). It also produces the twisting of the angle of the main axis of the composite ellipsoid, as observed in Figs. 2 and 7(a), which, in turn, causes the intercept of the axis to shift away from the origin. The generation of the bias is illustrated schematically in Fig. 9; Sec. II D shows how to model the noise statistically to eliminate the bias in the full SFP model. The SFP model avoids the bias by introducing explicit terms for the noise associated with each formant,

$${\underset{\_}{\lambda }}^v={\langle \underset{\_}{\lambda }\rangle }^v+a{\underset{\_}{m}}^v+{\underset{\_}{\eta }}^v+\sum _{j=1}^J{b}_j^v{\underset{\_}{n}}_j^v,$$ (10)

where η^v is the formant-specific noise term. It is a vector of zero mean Gaussian noise with covariance given by ${\underset{=}{\Psi }}^v=\mathrm{diag}({\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2)$. A factor, $b_j^v$, was also added to capture any other consistent source of natural variability in the data.

FIG. 7.

(a) Rotated view of Fig. 2, showing the composite ellipsoids for the vowels in Peterson and Barney (1952), to emphasize the bias of the intercepts away from the origin in the λ₁ dimension. (b) The same view of the composite ellipsoids using the statistical formant-pattern model with explicit terms for formant measurement error. The bias of the intercepts is considerably reduced.

FIG. 9.

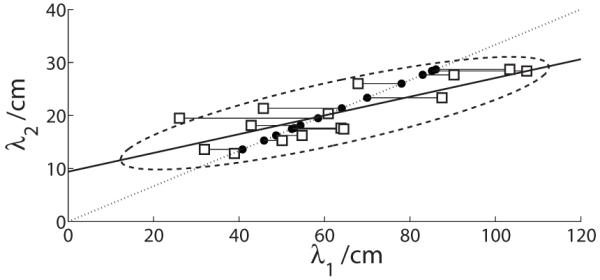
Illustration of how measurement noise can bias the orientation of the major axis of the ellipsoid derived with a traditional deterministic analysis of noisy data. The true data (circles) lie on a uniform scaling line (dotted line), but are corrupted by anisotropic measurement noise (squares). Both the values of the measurement noise and the formant frequencies have been chosen to be typical of the vowel /iy/. A traditional fit with PCA derives a biased ellipse (dotted) with a principal axis which is biased away from the uniform scaling line. The more sophisticated analysis developed in this paper, which can learn the differing contributions from observation noise in each dimension, can recover the true directions, and it is unbiased in this regard.

This model of formant wavelengths is a modified version of factor-analysis (FA) (Roweis and Ghahramani, 1999), where the distribution over the latent variable, p(a), is a mixture of Gaussians (one for each speaker type; man, woman, and child) rather than a single Gaussian. The mixture of Gaussians was used to represent the statistics of the noise, p(b), as well, but the divergence from a simple Gaussian was found to be minimal.

In order to assess the relative contributions of an extra natural factor, on the one hand, and measurement noise, on the other, and to infer the acoustic scale factor of an unknown speaker from their formant data, the values of the model’s parameters must be learned from the data. That is, they must be learned from the statistics of (i) the relative vocal tract lengths, p(a), (ii) the noise, ${\underset{=}{\Psi }}^v$, and (iii) the factor loadings, m^v. The learning and inference is accomplished using probabilistic methods, in particular, the variational expectation-maximization (EM) algorithm of Ghahramani and Hinton (1996). This algorithm repeatedly optimizes a lower bound on the log-likelihood of the parameters in two steps: in the expectation (E) step, the algorithm infers the acoustic scale factors of the speakers, given the current parameter estimates; in the maximization (M) step it finds the most likely parameters given the inferred acoustic scale factors. The iteration of the two steps typically converges in the region of the maximum-likelihood estimate for the parameters (Ghahramani and Hinton, 1996).

D. Application of the statistical, formant-pattern model to developmental formant data

We are now in a position to assess the relative contribution from the hypothetical extra natural factor, ${\underset{\_}{n}}_j^v$, on the one hand, and measurement noise, ${\underset{=}{\Psi }}^v$, on the other hand. The result is illustrated for the Peterson and Barney (1952) data in Figs. 7(b) and 8(b); they showed the major axes of variability for the vowel ellipsoids after they have been corrected for measurement noise. These corrected vectors point more accurately toward the origin of the space, as would be predicted by the fixed-formant-pattern hypothesis, indicating that there is no need for an extra natural factor to explain this data set (that is, ${\underset{\_}{n}}_j^v=0$). The orientation of each component derived with the statistical model was compared to the orientation of the corresponding component derived from the original analysis. The results are presented in the lower rows of Table I; they show that if measurement noise and other sources of natural variability are modeled statistically, the component of variability attributable to VTL becomes more uniform, while the residual noise decreases correspondingly.

In more recent developmental studies of formant frequency, such as those of Hillenbrand et al. (1995) and Lee et al. (1999), the formant-frequency values were estimated automatically from spectral frames of vowel sounds using LPC. The deterministic and statistical versions of the formant-pattern model were fitted to the data of both Hillenbrand et al. (1995) and Lee et al. (1999) to determine (a) whether the extended axes of the vowel ellipsoids would still show the bias away from the origin when the deterministic version of the model was fitted to the LPC data and (b) whether the bias would be reduced when the statistical version was fitted to the data.

The results for the data of Lee et al. (1999) are presented in Fig. 10 in the same format as shown for the data of Peterson and Barney in Figs. 7 and 8. The database of Lee et al. (1999) is far larger than that of Hillenbrand et al. (1995) and it covers a much greater range of ages. Lee et al. (1999) recorded ten vowels spoken by 436 children, ages 5–18, and 56 adults. Figure 10(a) shows the location of the ellipsoids for each vowel in wavelength space. The distribution of the ellipsoids is very similar to that shown for the Peterson and Barney (1952) data in Fig. 7(a), and the extensions of the major axes show the same bias away from the origin. There is also the same pronounced elongation of the ellipsoid for the vowel /iy/ in the λ₁ direction, probably due to the problem of estimating λ₁ which is particularly long in this vowel. The results for the SFP model are presented in Fig. 10(b), where the main axes of the ellipsoids are observed to intercept the λ₁-λ₃ plane at points much closer to the origin, indicating that the average bias is considerably reduced for this version of the formant-pattern model. Similar results were obtained with the data of Hillenbrand et al. (1995) indicating that the LPC method of extracting formant frequencies has a similar problem to that observed with the spectrogram reading method, as would be expected. The figure for the data of Hillenbrand et al. (1995) is omitted for brevity.

FIG. 10.

(a) The composite ellipsoids for the vowels in Lee et al. (1999). The view emphasizes the bias of the intercepts away from the origin in the λ₁ dimension. (b) The same view of the composite ellipsoids using the statistical formant-pattern model with explicit terms for formant measurement error. The bias of the intercepts is considerably reduced.

Finally, the assumptions made in Sec. II B, concerning the distribution of acoustic scale factors and the observation noise, need to be verified. With regard to the distribution of acoustic scale factors, which was modeled as three Gaussian sub-populations for men, women, and children, Fig. 11 shows the inferred scales together with the fitted mixture of Gaussians. The distribution is clearly multi-modal, justifying the assumptions of the model. With regard to the measurement noise, the SFP model learns that the average error is 50 Hz which is consistent with the inherent inaccuracy in the formant extraction process described in Sec. II C.

FIG. 11.

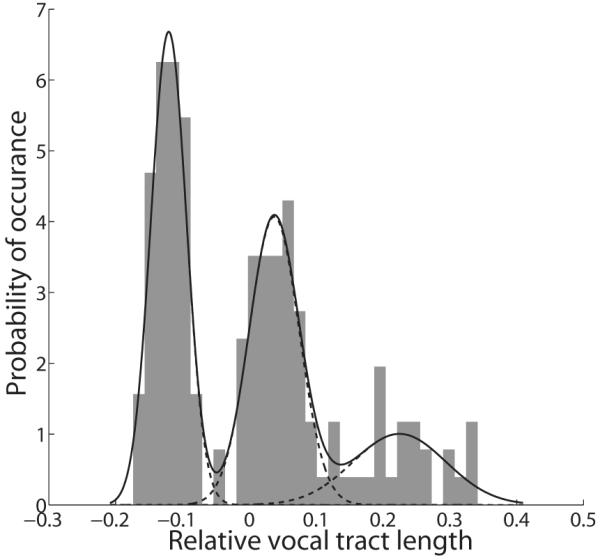
Histogram of VTLs derived from the data of Peterson and Barney (1952) using the statistical formant-pattern model. The mixture of Gaussians derived by the model is shown by the solid line; the Gaussians which make up the fit are shown by dotted lines.

The formant measurement error produces a particular problem for deterministic versions of formant ratio theory (e.g., Miller, 1989), inasmuch as ratios accentuate variability. Moreover, it is traditional to use ratios that have F1 in the denominator, and F1 is the formant estimate that is most prone to error, so the accentuation of the variability is particularly large in the traditional version of formant ratio theory. The variability introduced by the measurement error and the accentuation of the variability associated with the use of ratios are likely to have hampered efforts to normalize for acoustic scale using formant ratios. In the statistical analysis of formant-frequency data, the vectors of formant frequencies are treated as stochastic patterns and the three formants are fitted simultaneously, without the calculation of ratios. This shift in emphasis is important and it is why the model is referred to as a statistical formant-pattern model rather than formant ratio theory. The phrase “formant pattern” is intended to emphasize that the vector of formant wavelengths is a representation of the spectral envelope of the vowel. The shape and position of the spectral envelope are best estimated using a vector of formant peaks which are statistically defined, which is why the acronym for the model includes the “S.” To reiterate, deterministic formant ratios provide a rather unreliable measure of the spectral envelope of a vowel because they amplify the error of the formant in the denominator and, unfortunately, it is common practice to use the most error prone of the formants as the denominator.

III. ESTIMATING VTL FROM FORMANT-FREQUENCY DATA

In this section, the SFP model is extended to produce an algorithm for estimating VTL, which involves calibrating the acoustic scale factors to a measure of absolute size. The algorithm is then applied to the developmental formant data of Huber et al. (1999) to estimate the VTLs of their speaker groups. Huber et al. (1999) reported the average values for the first three formants in /a/, separately, for groups of ten males and ten females in each of nine age bins (4, 6, 8, 10, 12, 14, 16, 18, and adults). Developmental studies of formant frequency often include developmental data on GPR and a comparison of the growth rates for VTL and GPR, since the growth rates change radically at puberty. The study of Huber et al. (1999) includes GPR data which we combine with the VTL estimates to illustrate the complicated developmental relationship between the excitation and resonance components of vowel production.

A. Inferring a speaker’s VTL: Calibration of the data of Huber et al. (1999) to the VTLs of Fitch and Giedd (1999)

The main issue in the VTL estimation algorithm, as in the vowel production model, is to identify and correctly characterize the different components of the variability in the formant-frequency measurements. It is assumed that the measurement noise for individual vowel samples in the data of Huber et al. (1999) has approximately the same form as that in the Peterson and Barney (1952) data. The articulation of the vowels is assumed to be the same in the two studies. Both of these assumptions can be verified retrospectively. The methods developed in Sec. II can now be used to infer the acoustic scale factors for each group of speakers in each age category. In order for these estimates to be converted into absolute VTLs, we need to assume that the studies of Huber et al. (1999) and Fitch and Giedd (1999) were sampling from the same distribution of people, which was modeled as a mixture of Gaussians earlier. In this case, the relative VTLs from the study of Huber et al. (1999) can be scaled using the mean and variance data from Fitch and Giedd (1999). The VTLs inferred from the study of Huber et al. (1999) and the lengths measured by Fitch and Giedd (1999) are presented together in Fig. 12. The correspondence is surprisingly good, particularly for the male speakers. The male values from the study of Huber et al. (1999) seem a little high at 4 and 6 years, and the female values seem a little low for age 16 and above, but the deviations are not large relative to the overall variability.

FIG. 12.

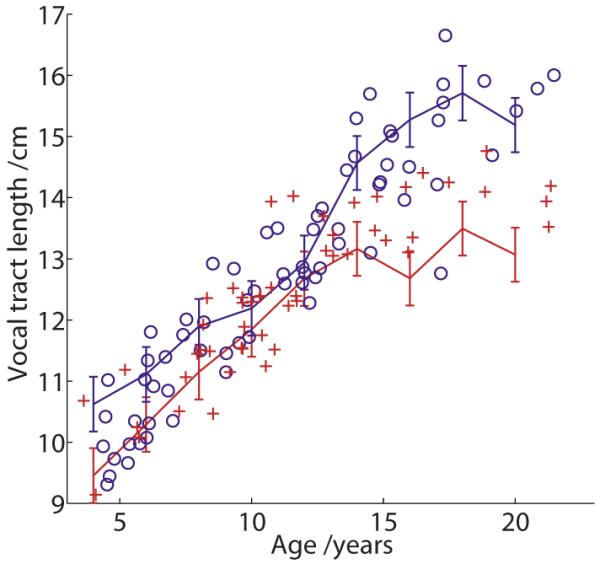
(Color online) VTLs inferred for men and women from the data of Huber et al. (1999), plotted as a function of the speaker’s age. For comparison, the data of Fitch and Giedd (1999) are presented by circles for men and crosses for women. The correspondence is impressive given that the populations in the two studies are not the same.

B. The GPR-VTL plane: Development and natural variability

Finally, the data from Peterson and Barney (1952) and Huber et al. (1999) were combined to characterize the developmental trajectory of vowel sounds in the log GPR-log VTL plane. The domains occupied by men, women, and children in the plane were delineated using the Peterson and Barney (1952) data. The 20 vowel sounds produced by each speaker (two tokens of each of ten vowels) were used to produce an estimate of each speaker’s VTL, using the EM algorithm and the procedure described in Sec. III A; when combined with the corresponding GPR estimates, each individual provides 20 GPR-VTL points on the GPR-VTL plane. Two-dimensional Gaussian distributions were fitted separately to the data of the men, women, and children to characterize the domain of each speaker class on the plane. Contours of constant probability in these distributions are elliptical in form, and the contours that enclose about 80% of the individuals in each speaker class are shown by the three ellipses in Fig. 13. Unfortunately, the record of the Peterson and Barney (1952) data currently available does not contain information regarding the ages of individual children or their heights, and so the VTL estimates of the children had to be calibrated using the values for the adult males. Specifically, the mean and variance for the VTL estimates of the adult males [derived from the Peterson and Barney (1952) data] were equated to the mean and variance of the VTL values for the adult males reported by Fitch and Giedd (1999).

FIG. 13.

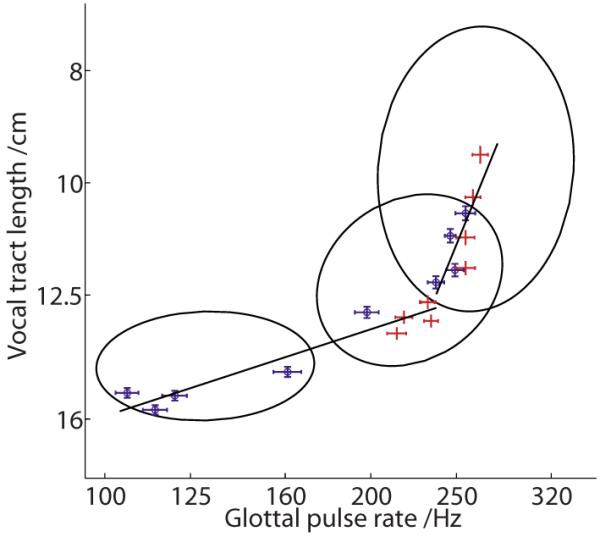
(Color online) Predicting the population distribution over the log GPR-log VTL plane and the path of an average male and female through it as they develop. The distributions of inferred VTLs and GPRs for the data of Peterson and Barney (1952) are characterized by the three ellipses representing men (lower left), women (center), and children (upper right).The ellipses are drawn at two standard deviations about the mean to enclose ~80% of the data points. The developmental paths derived from the data of Huber et al. (1999) for the average female and the average male are shown by circles and crosses, respectively.

The mean VTL value inferred for each age-by-sex group in the data of Huber et al. (1999) was paired with the appropriate mean GPR value and plotted in the logGPR-logVTL plane of Fig. 13 to show the developmental trajectory of the voice for males and females as they mature. The symbols include±one standard deviation in both dimensions. Within each ellipse, the trajectory from the data of Huber et al. (1999) reflects the eccentricity of the ellipse derived from the Peterson and Barney (1952) data. There is good agreement between the developmental data and the positions of the ellipses. It appears that the growth trajectories can be summarized with a pair of straight lines that meet near the center of the ellipse for women. The segment with the steeper slope was fitted to the data of males and females from ages 4 to 10; it has a slope of 1.9, so the VTL of a child is roughly proportional to the square of their GPR. The segment with the shallower slope was fitted to the data of males and females from age 12 upward; it has a slope of 0.25, so the VTL of adults and adolescents is roughly proportional to GPR^1/4. The figure makes it clear that the developmental trajectory for males changes dramatically around puberty and the change in trajectory is mainly due to the sudden drop in pitch that occurs at this time.

With regard to practical application of the VTL estimation process, it is theoretically possible to estimate VTL from all vowels and sonorant consonants on a frame by frame basis, when the vowel type is known. However, VTL would be expected to change at a much slower rate than formant frequency since it mainly changes with the speaker. So a reasonable strategy would probably be to limit VTL estimation to strong vowels where the recognizer is confident of the vowel type.

IV. SUMMARY AND CONCLUSIONS

A PCA was used to cluster the classical formant-frequency data of Peterson and Barney (1952) and provide ellipsoids showing the distribution of formant frequencies associated with each vowel and population subgroup. The analysis revealed that vowel type accounts for 80% of the variability in formant frequencies and 90% of the remaining variability is accounted for by VTL. Sufficient variability remained to support the hypothesis that there might be another consistent source of variability, such as developmental changes in oral-pharyngeal ratio. The MRI data of Fitch and Giedd (1999) were reanalyzed to evaluate this hypothesis, and the analysis confirmed that the growth of the oral and pharyngeal cavities is non-uniform, with the pharyngeal cavity growing faster than the oral cavity. However, the growth functions are linear. Moreover, the growth functions for men, women, and children are all the same. Despite the non-uniform growth of the anatomical cavities of the vocal tract, there is no commensurate non-linearity in the formant-pattern data. Indeed, for a given vowel, the formant pattern is essentially fixed on a log-frequency axis, shifting toward the origin without changing shape as VTL increases. This means that the systematic variability in formant-frequency data (at least the first three formants) is effectively divided between vowel type and VTL, and it suggests that speakers adjust the shape of the vocal tract as they grow to maintain a specific spectral pattern for each vowel type, independent of the relative size of the oral and pharyngeal cavities. The conclusion is important because it means that it should be a straightforward matter to estimate VTL from the voiced sounds in continuous speech.

A statistical formant-pattern model of formant-frequency data was developed with (a) a latent variable to absorb the variability of all size related factors, (b) non-uniform, but linear growth functions for the oral and pharyngeal cavities, and (c) separate measurement-noise terms for each of the formants. A modified version of factor analysis was developed to infer the acoustic scale factor of the vowels and, thus, the VTL of an unknown speaker, from the formant data of a given vowel type. The use of statistical methods to model the measurement noise revealed that the vast majority of the variability not attributable to vowel type is associated with VTL, and if there are any other natural sources of systematic variability their contribution is small with respect to the error in formant frequency estimation. The statistical version of the formant-pattern model was used to correct the biases of the deterministic version of the model, and the effect of the correction was illustrated with the formant-frequency data of both Peterson and Barney (1952) and Lee et al. (1999).

Finally, the SFP model was used to analyze the developmental data of Huber et al. (1999). The mean VTL was estimated for each age group, and the results were used to chart the development of VTL and GPR in children as they mature into adults.