Strict coupling between CFTR’s catalytic cycle and gating of its Cl⁻ ion pore revealed by distributions of open channel burst durations

Abstract

CFTR, the ABC protein defective in cystic fibrosis, functions as an anion channel. Once phosphorylated by protein kinase A, a CFTR channel is opened and closed by events at its two cytosolic nucleotide binding domains (NBDs). Formation of a head-to-tail NBD1/NBD2 heterodimer, by ATP binding in two interfacial composite sites between conserved Walker A and B motifs of one NBD and the ABC-specific signature sequence of the other, has been proposed to trigger channel opening. ATP hydrolysis at the only catalytically competent interfacial site is suggested to then destabilize the NBD dimer and prompt channel closure. But this gating mechanism, and how tightly CFTR channel opening and closing are coupled to its catalytic cycle, remains controversial. Here we determine the distributions of open burst durations of individual CFTR channels, and use maximum likelihood to evaluate fits to equilibrium and nonequilibrium mechanisms and estimate the rate constants that govern channel closure. We examine partially and fully phosphorylated wild-type CFTR channels, and two mutant CFTR channels, each bearing a deleterious mutation in one or other composite ATP binding site. We show that the wild-type CFTR channel gating cycle is essentially irreversible and tightly coupled to the ATPase cycle, and that this coupling is completely destroyed by the NBD2 Walker B mutation D1370N but only partially disrupted by the NBD1 Walker A mutation K464A.

ATP-binding cassette (ABC) proteins bind and hydrolyze ATP, usually to power transport of substrates across membranes. Their common architecture comprises two transmembrane domains (TMDs) and two cytoplasmic nucleotide binding domains (NBDs) containing conserved sequences for interacting with ATP. Once ATP binds to the conserved Walker A and B motifs of each NBD, they dimerize in head-to-tail fashion, burying two ATP molecules in composite interfacial sites (1, 2). Cyclic formation and disruption of the dimer requires hydrolysis of at least one of the ATPs per cycle (3–6).

The ion channel CFTR contains, in addition to canonical ABC protein domains (TMD1, NBD1, TMD2, NBD2), a unique regulatory (R) domain (7) with multiple cAMP-dependent protein kinase (PKA) targets that must be phosphorylated for ATP to activate bursts of channel openings reviewed in ref. 8). But the mechanism of CFTR channel gating remains controversial. Early observations that the gating pattern violates microscopic reversibility suggested that the process underlying bursting operates far from thermodynamic equilibrium (9–11). Building on this, with functional evidence from mutants and nucleotide homologs (12–15) and with structural and biochemical data from prokaryotic NBDs (1–4), a CFTR channel open burst was proposed to be initiated by ATP-mediated formation of a stable NBD1-NBD2 heterodimer, and terminated by dimer dissociation after ATP hydrolysis (16). The ATP hydrolysis was posited to occur at the NBD2 composite site (between NBD2 Walker motifs and NBD1 signature sequence) because the NBD1 composite site in CFTR is catalytically inactive (17, 18). In this model (Fig. 1A, scheme 2), gating cycles are tightly coupled to ATPase cycles (cf. refs. 9, 11–13), and most open bursts include two kinetically distinct steps: ATP hydrolysis (step O₁→O₂) and NBD dimer dissociation (step O₂→C₂).

Fig. 1.

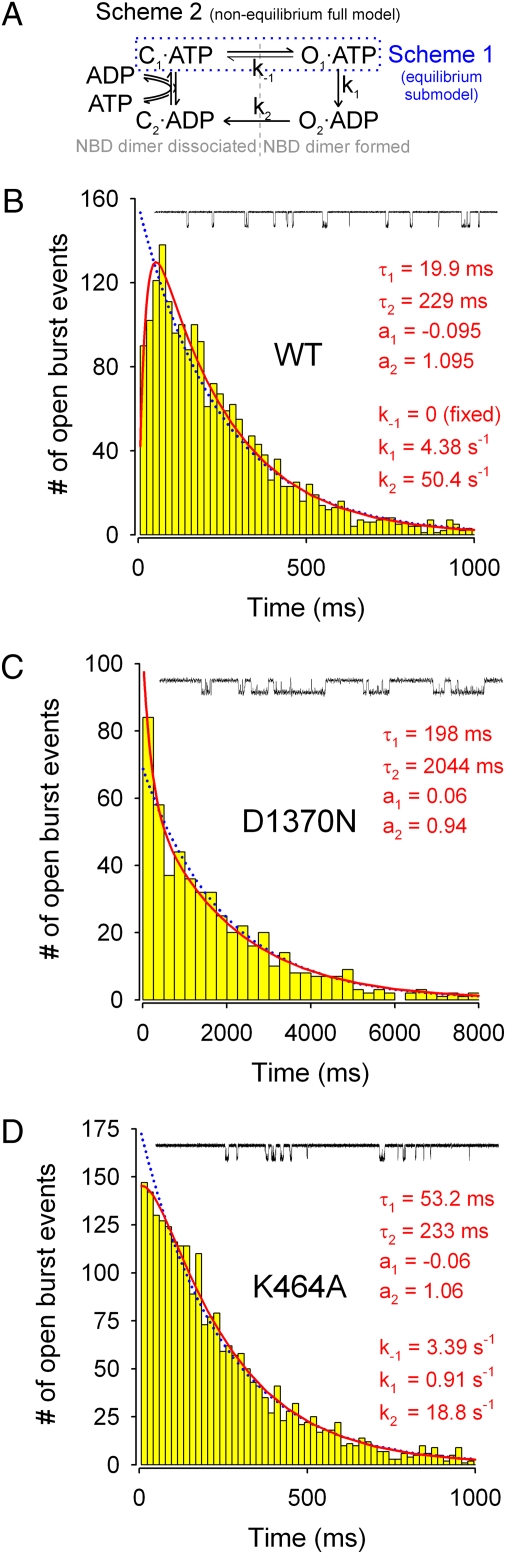
Distributions of burst durations for WT and mutant CFTR channels. (A) Nonequilibrium cyclic full model (scheme 2) proposed to describe CFTR gating. The equilibrium closed-open model (scheme 1, encircled by blue dotted line) is a submodel of scheme 2. (B–D) Histograms of open burst durations for prephosphorylated WT (B), D1370N (C), and K464A (D) CFTR channels; 30-s segments of representative single-channel current recordings are shown above each panel. The lowest bins start at t_low = 6 ms. Blue dotted lines show ML fits to scheme 1. Red solid lines in B and D show ML fits to scheme 2; rate k₋₁ was fixed to zero in B, but left free in D. In C, red solid line shows the ML fit to a double-exponential distribution. Obtained rate estimates, as well as time constants and fractional amplitudes of the resulting exponential components, are printed in red. ATP was 2 mM for WT and D1370N, but 5 mM for K464A.

Energetic coupling of residues across the NBD1-NBD2 interface in CFTR in a gating state-dependent manner (19) supports this model, and it fits with recent structural models of ABC proteins (reviewed in ref. 20). However, it seems hard to reconcile with the puzzling demonstration that mutation of CFTR’s NBD1 Walker-A lysine (K464), in the catalytically incompetent composite site, severely impaired ATPase rate while little altering channel gating at saturating ATP (21). This discrepancy suggested that ATPase and gating cycles are not coupled in CFTR. In apparent corroboration of that interpretation, a reversible equilibrium model of ATP-activated CFTR gating, like that for ligand-gated channels, has been promoted (22, 23).

To solve this conundrum we have exploited the ability, unique among ABC proteins, to record conformational transitions of single CFTR channel molecules. Because only transitions coupled to pore opening or closing are directly observed in current records, and other transitions (e.g., between two open states) go undetected, CFTR gating studies usually report mean opening and closing rates, which are compound functions of several transition rates. Additional information, hidden in the shapes of the distributions of burst and interburst durations, can be extracted using maximum likelihood (ML) optimization (24) to fit them with the most appropriate model and so learn the underlying transition rates (Figs. S1 and S2). Here we adopt this strategy to clarify the transitions that govern closure of CFTR channels, and the influence on them of phosphorylation and of mutations in the two ATP-binding sites. Our analysis reveals that wild-type (WT) CFTR has an essentially irreversible gating cycle tightly coupled to ATP hydrolysis, but that catalytic site mutations can modify the degree of coupling.

Results

CFTR gating is characterized by bursting behavior, due to the presence of two readily distinguishable populations of closed events (25) (Fig. S3 A and B). A series of (one or more) openings separated by brief “intraburst” closures of ∼10 ms is called an open burst, and bursts are flanked by long “interburst” closures of ∼1 s duration. Previous work has established that CFTR phosphorylation by PKA, and ATP binding and hydrolysis, regulate the mean open burst and interburst durations (τ_b and τ_ib). But to dig deeper into the underlying mechanisms of channel gating and how it is coupled to CFTR’s ATPase cycle, we examined the shapes of the burst duration distributions.

Peaked Burst Duration Distributions Reveal Essentially Irreversible Gating Cycle for WT CFTR.

A simple, readily reversible, closed-open equilibrium model of CFTR gating (22, 23) (submodel scheme 1, encircled by the blue dashed line in Fig. 1A) predicts a single-exponential distribution of open burst durations, but the irreversible cyclic model (16) (full model scheme 2 in Fig. 1A) predicts a peaked distribution harboring two components—one with a negative fractional amplitude. This is because the prehydrolytic NBD dimer is very stable (13, 15, 19), and the rate of step O₁→C₁ (k₋₁) is thus very slow. Consequently, the majority of bursts include two sequential steps, ATP hydrolysis (step O₁→O₂) followed by NBD dimer dissociation (step O₂→C₂), and this reduces the incidence of very brief bursts.

To reconstruct the distributions of open burst durations for WT CFTR, we recorded currents from dozens of patches containing a single active channel, collecting 1,441 bursts in 2 mM ATP, following PKA removal. The resulting burst duration distribution (Fig. 1B) showed a clear peak, rather than monotonic decay. This paucity of brief bursts was not due to limited time resolution, because we included only events longer than t_low = 6 ms in our analysis (correspondingly, the lowest bins in Fig. 1 start at 6 ms), whereas the filter dead time was 1.8 ms. Accordingly, when we fitted this distribution, using a maximum likelihood approach, to the single-exponential probability density function (pdf) of scheme 1 (one free parameter; blue dotted line) or to the peaked pdf of scheme 2 with rate k₋₁ fixed to zero (two free parameters; red solid line), the latter fit proved significantly (P = 2·10⁻⁹) better, as shown by the corresponding large log-likelihood ratio ΔLL = 18.01 (cf. ref. 26). This finding provides strong support for a nonequilibrium gating cycle with two sequential open conformations, and so suggests that scheme 2 (in Fig. 1) with a small rate k₋₁ adequately describes the mechanism underlying open bursts of WT CFTR channels.

Burst Duration Distribution of Nonhydrolytic Mutant D1370N Further Supports Irreversible Mechanism for WT.

As a control, we chose to study the NBD2 Walker B mutant D1370N because the analogous mutation completely abolished ATP hydrolysis in other ABC proteins (27–29). The distribution of burst durations of D1370N channels gating in 2 mM ATP (Fig. 1C), reconstructed from 530 bursts, indeed differs qualitatively from that of WT channels (Fig. 1B) in that it decays monotonically. When this distribution was fitted by scheme 2 with k₋₁ fixed to zero, one of the two resulting components was trivially small, and the fit was no better (ΔLL = 0) than that by the equilibrium submodel scheme 1 (Fig. 1, blue dotted line). This finding for a mutant expected incapable of ATP hydrolysis (k₁ = 0) validates our interpretation of the peaked WT CFTR distribution as indicative of a highly nonequilibrium gating cycle.

Interestingly, a combination of two positive-amplitude exponential components slightly improved the fit (ΔLL = 3.24; P = 0.03; Fig. 1C, red solid line; see SI Text for more fitting results), suggesting a mixture of two types of open bursts for D1370N; the major population, with an average lifetime of ∼2 s, seems interspersed with a few brief bursts of ∼200 ms. The latter minor population might reflect the mechanism by which infrequent brief channel openings are observed in the absence of ATP in this mutant (Fig. S3E Inset , asterisks) and even less frequently in WT CFTR (16, 30).

Burst Duration Distribution of K464A Mutant Reveals Profoundly Altered Gating Mechanism.

Although the K464A mutation lowers CFTR ATPase turnover rate ∼10-fold (21), τ_b was essentially unaffected by this mutation (Fig. 1D Inset). However, the shape of the distribution of K464A burst durations (Fig. 1D; reconstructed from 2,327 events) clearly differed from that of WT CFTR. This distribution decayed monotonically, and a fit by scheme 2 (Fig. 1A) with k₋₁ fixed to zero (two free parameters) gave no improvement (ΔLL = 0) over a fit by scheme 1 (one free parameter; blue dotted line), providing no evidence for obligatory sequential progression through two open states. However, because the K464A mutant does carry out some ATP hydrolysis, albeit slowly (21), we also evaluated a partially hydrolytic mechanism by leaving k₋₁ in scheme 2 as a free parameter. This allows some bursts to terminate through reversal of the opening step (rate k₋₁) and others through hydrolysis of ATP, and hence through state O₂. With k₋₁ free, scheme 2 did indeed provide a statistically better fit (P = 0.027; ΔLL = 3.62), evident in the 0–100 ms range (three free parameters; red line). The rate estimates from this fit suggest that in K464A CFTR, the rate of the ATP hydrolysis step (k₁) is slowed by only ∼4-fold compared with WT, consistent with the fact that this mutation is not in the composite NBD2 site, where ATP hydrolysis occurs. But this analysis also indicates that the K464A mutation greatly destabilizes the prehydrolytic dimer (k₋₁ is increased).

Macroscopic Closing Rates of Nonhydrolytic Mutants Provide Estimates of the Rate of Nonhydrolytic Closure of WT CFTR.

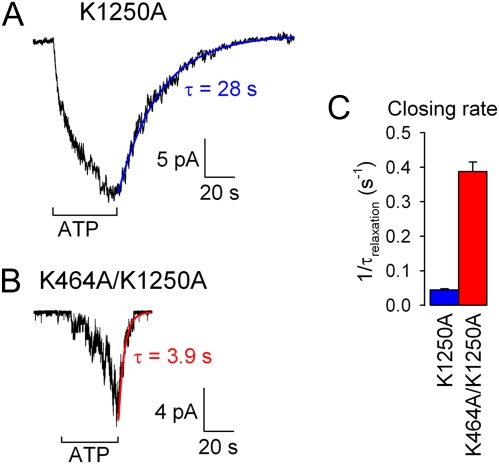
The simplification of making the opening step in scheme 2 irreversible for fitting the burst distribution of WT CFTR (Fig. 1B, red line; k₋₁ was set to zero) rests on experimental evidence that reversal of this step, by dissociation of the prehydrolytic NBD1-NBD2 dimer, is far slower than normal channel closure. For example, mutations of the NBD2 Walker A lysine (K1250) or proposed catalytic carboxylate (E1371), shown to abolish or severely impair ATP hydrolysis in CFTR and other ABC proteins (5, 21, 27), prolong τ_b by several orders of magnitude (9, 11, 16, 19) (Fig. 2). As a three-parameter fit of scheme 2 to the data in Fig. 1B (and also Fig. 3) did not provide a reliable estimate of this small rate (SI Text), to estimate k₋₁ we measured the macroscopic closing rates of prephosphorylated K1250A, K1250R, and E1371S mutant channels (e.g., Fig. 2A) upon sudden removal of ATP. These rates, obtained as the reciprocals of the time constants of fitted single exponentials (e.g., Fig. 2A, blue line), were 0.044 ± 0.004 s⁻¹ (n = 9) for K1250A (Fig. 2C, blue bar), 0.22 ± 0.01 s⁻¹ (n = 17) for K1250R, and 0.036 ± 0.002 s⁻¹ (n = 16) for E1371S. Their variation likely reflects different specific effects of the mutations on the stability of the prehydrolytic NBD1-NBD2 dimer. As we cannot be certain which of these mutant channels, when open, most closely resembles the O₁ state of a WT CFTR channel gating in ATP, we tentatively chose the closing rate of K1250R as an estimate of k₋₁ for WT CFTR (Fig. 4E Right, blue bar) on the grounds that the lysine-to-arginine mutation at least conserves charge in the vicinity of the ATP bound within the NBD2 composite site.

Fig. 2.

Slow nonhydrolytic closing rate and its acceleration by the K464A mutation. (A and B) Macroscopic currents of prephosphorylated K1250A (A) and K464A/K1250A (B) CFTR channels were activated by application of 10 mM ATP. Time courses of current decay upon ATP removal were fitted by single exponentials (colored lines). (C) Mean (±SEM) closing rates estimated as the inverses of the current relaxation time constants (τ_relax), for K1250A (blue) and K464A/K1250A (red).

Fig. 3.

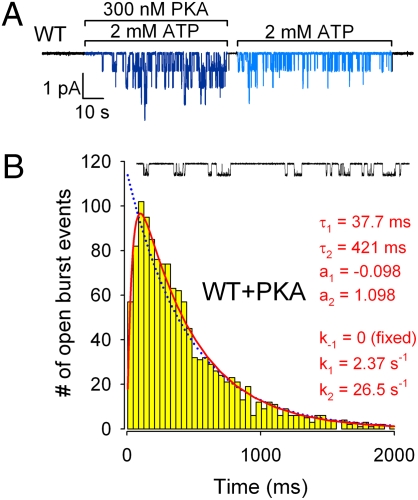
Phosphorylation slows both sequential steps involved in CFTR channel closure. (A) Channel activity of WT CFTR rapidly declines upon PKA removal, but then remains steady for a prolonged period, thereby defining gating patterns for “fully” (in the presence of PKA) and “partially” phosphorylated CFTR (in just ATP, following PKA withdrawal). (B) Histogram of open burst durations for fully phosphorylated WT CFTR channels, and 30-s segment of single-channel current recording. Lowest bin starts at t_low = 6 ms. Blue dotted line is a ML fit to scheme 1. Red solid line is a ML fit to scheme 2 with rate k₋₁ fixed to zero.

Fig. 4.

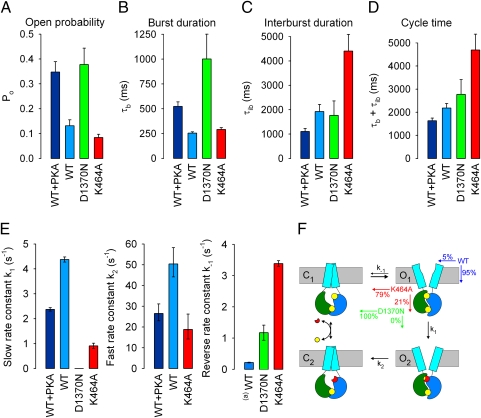
Average gating parameters, gating mechanisms, and microscopic transition rate estimates for WT and mutant CFTR channels. (A–D) Open probabilities (A), mean burst (B), and interburst (C) durations obtained from multichannel fits, and calculated channel cycle times (D) for fully (navy blue) and partially (royal blue) phosphorylated WT, and partially phosphorylated D1370N (green) and K464A (red) CFTR. [ATP] was 2 mM for WT and D1370N, but 5 mM for K464A. Error bars represent SEM. (E) ML estimates of rates k₁ (Left), k₂ (Center), and k₋₁ (Right) for fully (navy blue) and partially (royal blue) phosphorylated WT, and partially phosphorylated D1370N (green) and K464A (red) CFTR channels. Error bars represent 0.5-unit log-likelihood intervals. ^(a)k₋₁ for partially phosphorylated WT is modeled by the closing rate of partially phosphorylated K1250R. (F) Cartoon of gating mechanisms. NBD1, green; NBD2, blue; TMDs, cyan; ATP, yellow; ADP, red. Probabilities for exiting state O₁ (Top Right) in either of two possible directions are printed in color for partially phosphorylated WT (blue), K464A (red), and D1370N (green). Note subtle shape change in TMDs between O₁ and O₂ (see text).

Insofar as ATP hydrolysis is also absent in D1370N (k₁ = 0), for this mutant the rate of channel closure from an open burst reflects the rate of dissociation of the prehydrolytic NBD dimer (k₋₁; Fig. 4E Right, green bar). This rate is accelerated ≥5-fold compared with WT (blue bar), indicating strong destabilization of the prehydrolytic dimer, which is consistent with the proposed role of the Walker B aspartate in Mg²⁺ binding (1, 29, 31).

Acceleration of Nonhydrolytic Channel Closure by the K464A Mutation Supports Microscopic Burst Duration Analysis.

Assuming k₋₁ = 0.22 s⁻¹ for WT, the ML fit of scheme 2 to the K464A burst distribution (Fig. 1D) suggests that rate k₋₁ is increased by ∼15-fold in K464A CFTR. This conclusion from the distribution of microscopic burst durations is corroborated by the fact that closure of nonhydrolytic CFTR mutants and of WT channels “locked” in open bursts by nonhydrolyzable ATP analogs or by orthovanadate is greatly accelerated by the K464A mutation (16, 18, 30, 32). For instance, closure of the catalytically incompetent NBD2 Walker A mutant K1250A is accelerated ∼10-fold in the double-mutant K464A/K1250A, as reported by the rate of macroscopic current decay upon ATP removal (Fig. 2B; red line is a single-exponential fit; Fig. 2C, red bar).

Phosphorylation Slows Both Sequential Steps Involved in Open-Burst Closure in WT CFTR Channels.

The open probability of WT human CFTR channels in inside-out Xenopus-oocyte patches exposed to 300 nM PKA + 2 mM ATP declines by ∼3-fold immediately after removal of PKA (16, 33) (Figs. 3A and 4A). This rapid drop, attributed to partial dephosphorylation by membrane-bound phosphatases, is due to ∼2-fold shortening of τ_b and nearly 2-fold lengthening of τ_ib (Fig. 4 B and C, navy blue vs. royal blue bars; cf. refs. 13, 16, 33).

To dissect the mechanism by which phosphorylation prolongs τ_b, we collected 1,085 bursts from single WT CFTR channels gating in the presence of 2 mM ATP + 300 nM PKA. Just as for partially phosphorylated WT, the burst duration distribution of fully phosphorylated WT CFTR (Fig. 3B) showed a clear peak, rather than monotonic decay, and was significantly (P = 4·10⁻⁹; ΔLL = 17.34) better fitted by scheme 2 (Fig. 1A) with k₋₁ fixed to zero (two free parameters; red line) than by the equilibrium scheme 1 (one free parameter; blue dotted line). Thus, gating of fully and of partially phosphorylated CFTR channels obeys a qualitatively similar, irreversible mechanism. A comparison of the maximum likelihood estimates of the rates k₁ and k₂ for the two conditions reveals that full phosphorylation slows both rates by ∼2-fold, though their ratio k₂/k₁ remains ∼11 (Fig. 4E; k₁, Left; k₂, Center; compare royal blue and navy blue bars). So full phosphorylation slows channel closure from an open burst without altering the fractions of time spent in states O₁ and O₂; regardless of the degree of phosphorylation, ∼92% of the burst duration appears to be spent waiting for ATP hydrolysis to happen, and the final ∼8% can be attributed to the lifetime of the posthydrolytic NBD1-NBD2 dimer. The rapid partial dephosphorylation of CFTR upon PKA removal (Fig. 3A) precludes the use of macroscopic current relaxations (Fig. 2A) to estimate k₋₁ for fully phosphorylated channels.

Perturbations That Profoundly Alter the Mechanism of Gating Need Not Greatly Alter the Cycle Time of CFTR Channel Bursts.

Until now, studies of CFTR gating have focused on extracting open probability and average τ_b and τ_ib, which are readily obtained from patches containing either single (34, 35) or multiple (36) channels. Fig. 4 A-C compares such average parameters for fully (navy blue) and partially (royal blue) phosphorylated WT, and partially phosphorylated D1370N (green) and K464A (red) CFTR channels. Consistent with previous reports, for D1370N CFTR channels gating in near-saturating ATP (2 mM) (16), τ_b is ∼4-fold longer than, but τ_ib is like, that of WT (Fig. 4 B and C, green bars) (cf. refs. 9, 16, 30), whereas for prephosphorylated K464A CFTR channels in saturating ATP (5 mM) (16), τ_b is comparable to, but τ_ib is at least ∼2-fold longer than, that of WT (Fig. 4 B and C, red bars) (9, 14, 16 but cf. ref. 32). However, as the mean length of an entire gating cycle is given by τ_b + τ_ib, the calculated cycle time (Fig. 4D) is only modestly changed by the presence of PKA or by either mutation. In contrast, the rate estimates from our present analysis (Fig. 4E, k₁, Left; k₂, Center; k₋₁, Right) reveal that the same perturbations profoundly alter the microscopic transition rates that determine the mechanism by which bursts are terminated.

Discussion

Maximum likelihood fitting allows quantitative comparison of alternative gating mechanisms, because the log-likelihood ratio for a pair of models provides a measure of their relative applicability, expressible in terms of statistical significance (24, 26). We used this strategy to determine whether the distributions of CFTR open burst durations are more consistent with a reversible equilibrium gating mechanism or with an irreversible nonequilibrium one. The large improvements we found in the fits for WT CFTR (Figs. 1B and 3B) by using a cyclic scheme (scheme 2) as opposed to a closed-open model (scheme 1) strongly support an irreversible mechanism. The interpretation that this irreversible cycle is driven by ATP hydrolysis is validated by the lack of any such fit improvement for the presumed nonhydrolytic D1370N mutant (Fig. 1C). As a bonus, the fits give first estimates for the rates of the two consecutive steps that govern WT CFTR channel closure (Fig. 4E).

Because the pdf for scheme 2 with k₋₁ = 0 (see Methods) is symmetrical with respect to rates k₁ and k₂, the fits to the WT burst duration distributions cannot specify whether k₁ is slow and k₂ fast, or vice versa. We assigned k₁ as the slow rate and k₂ as the fast rate for WT CFTR channels (Fig. 4E Left and Center) on the basis of much previous work that suggests that ATP hydrolysis rate limits closure from an open burst (e.g., refs. 9, 13–15). However, the fit for K464A provides additional support for this assignment. For k₋₁ > 0 the burst pdf for scheme 2 (Methods) is no longer symmetrical with respect to k₁ and k₂, and it can be shown that for any set of rates k₁, k₂, k₋₁, for which k₂ > k₋₁ holds, there exists a single alternative set k₁′, k₂′, k₋₁′ (given by k₁′ = k₂ − k₋₁, k₂′ = k₁ + k₋₁, k₋₁′ = k₋₁), which yields an identical pdf. Thus, the set k₁′ = 15.4 s⁻¹, k₂′ = 4.30 s⁻¹, k₋₁′ = 3.39 s⁻¹ fits the observed pdf for K464A just as well as the set displayed in Fig. 4E (k₁ = 0.91 s⁻¹, k₂ = 18.8 s⁻¹, k₋₁ = 3.39 s⁻¹). But this alternative set can be ruled out as it would yield an essentially hydrolytic mechanism for K464A (with a coupling ratio of ∼82%) in contradiction of the observed severe defect in ATPase turnover rate (21). Together, these findings validate our premise of a slow step O₁→O₂ followed by a faster step O₂→C₂.

The NBD1 Walker A mutant K464A has received much previous attention. That this mutation, in a catalytically inactive binding site (17, 18), affects channel gating only slightly (Fig. 4D; cf. refs. 16, 21, 32) contrasts with its substantial suppression of the rate of ATP hydrolysis of purified K464A CFTR protein (to <10% of WT) (21). The altered shape of the distribution of K464A burst durations (Fig. 1D) now provides a satisfying explanation for this dissociation between channel cycle time and ATPase rate. The ratio k₁/(k₁ + k₋₁) estimated from the scheme 2 fit (Fig.4E Left and Right, red bars) suggests that in K464A approximately one out of every five bursts proceeds through the normal irreversible hydrolytic pathway (Fig. 4F). This “coupling ratio” between channel opening and ATP hydrolysis of ∼21% for K464A CFTR contrasts with that of ≥95% for WT channels (blue bars, Fig. 4E Left and Right and Fig. 4F). Because the cycle time of K464A channels is prolonged ∼2-fold compared with WT (Fig. 4D), the predicted overall ATPase turnover rate is on the order of 10% of WT, which is in very reasonable agreement with the measured value (21). The nonhydrolytic NBD2 mutant D1370N is a more extreme case, with an estimated coupling ratio of 0% (green bars, Fig. 4E Left and Right and Fig. 4F).

The mechanism by which strong phosphorylation by PKA prolongs τ_b (13, 16, 33) has remained a puzzle. We show here that PKA slows closure by decreasing both rates k₁ and k₂ (Fig. 4E), without altering their ratio, and this can explain two poorly understood facts. First, the similar activation enthalpies for closure of partially and fully phosphorylated CFTR suggested that both are rate limited by the same step (37), and we can now identify this step as ATP hydrolysis (k₁). Second, exposing CFTR channels to ATP plus orthovanadate results in long “locked-open” bursts (12, 15), and the rate at which open channels become locked by orthovanadate was found not to depend on τ_b (12). Because orthovanadate must bind to and stabilize the posthydrolytic dimer (O₂), this rate of locking reflects the fraction of the open burst time spent in O₂—which we now show to be independent of τ_b.

In a working transporter, the substrate-binding site is exposed alternately to the two sides of the membrane. For ABC exporters, formation of the tight NBD dimer is believed (20) to flip the transmembrane domains from an inward- to an outward-facing conformation. In CFTR, formation of the NBD dimer opens the channel (16, 19), suggesting that CFTR can be viewed as a “degraded” ABC exporter in which the ATP-bound conformation with outward-facing TMDs somehow allows downhill flow of Cl⁻ ions through a transmembrane pore (Fig. 4F Right). However, we show here that certain severe mutilations of CFTR’s catalytic cycle can leave the superficial gating parameters (τ_b and τ_ib; Fig. 4 B–D) and hence the net rate of Cl⁻ transport not greatly altered. Our analysis of the D1370N mutant, for example, implies that this mutation does not prevent cycling between inward- (closed channel) and outward-facing (open channel) conformations of CFTR (Fig. 4D, green; cf. Fig. 4F). If the D-to-N mutation of the Walker B aspartate were to similarly preserve inward-outward conformation flips in ABC exporters, then why would it abolish their active transport, as observed (27, 28)? To transport substrate uphill, the energy of ATP hydrolysis must be harnessed to convert the substrate binding sites in the transmembrane domain from a high-affinity to the low-affinity conformation needed to ensure substrate release at the higher-concentration side. It seems reasonable to propose that in an ABC exporter, this affinity switch does not coincide with the transition to the outward-facing conformation. In other words, partial cycles reversing from the state corresponding to O₁ do not result in net substrate extrusion. Instead, in ABC exporters, the high- to low-affinity conversion of the substrate-binding site is likely linked to the ATP hydrolysis step itself (transition O₁→O₂). This would explain why catalytic-site mutations in such transporters result in parallel disruption of transport and ATPase turnover rates (27, 28). Intriguingly, in CFTR, a vestige of this affinity-switch conformational change (cartooned as a change in TMD shape between states O₁ and O₂ in Fig. 4F) can be observed, under appropriate conditions, as a subtle change in permeation properties of the CFTR channel pore (9, 10).

Our findings highlight the superior discriminative power afforded by analyzing the distributions of CFTR burst durations rather than just their mean values, and exploit the unprecedented opportunity this approach offers to characterize the steps underlying termination of open-channel bursts in an ABC transporter broken by evolution.

Methods

Molecular Biology.

Mutations were introduced into pGEMHE-CFTR using QuikChange (Stratagene) as previously described (16); cDNA was transcribed in vitro with T7 polymerase (Ambion) and cRNA stored at −80 °C.

Isolation and Injection of Xenopus Oocytes.

Oocytes were isolated from anaesthetized adult female Xenopus laevis and injected with cRNA as described (33). Single-channel and macroscopic recordings were made 2–3 days after injection of 0.03–10 ng cRNA.

Excised Inside-Out Patch Recording.

Patch pipette solution contained (in mM): 136 NMDG-Cl, 2 MgCl₂, 5 HEPES (pH 7.4 with NMDG). Bath solution contained (in mM): 134 NMDG-Cl, 2 MgCl₂, 5 HEPES, 0.5 EGTA (pH 7.1 with NMDG). We added 2–5 mM MgATP from a 400-mM aqueous stock solution (pH 7.1 with NMDG). CFTR channels were activated by 300 nM catalytic subunit of PKA (Sigma). Currents were recorded at a pipette holding potential of +80 mV (V_m= −80 mV), digitized at 10 kHz, and recorded to disk after online Gaussian filtering at 1 kHz.

Kinetic Analysis of Multichannel Records.

Records with 1–8 channels were analyzed as described (33). Currents were digitally filtered at 100 Hz, and idealized by half-amplitude threshold crossing. Events lists were fitted with a simple model in which ATP-dependent slow gating is pooled into a closed-open scheme, and brief closures modeled as pore-blockage events (10). Rate constants (r_CO, r_OC, r_OB, r_BO) of the resulting closed-open-blocked (C↔O↔B) scheme were extracted by a simultaneous ML fit to the dwell-time histograms of all conductance levels, while accounting for the filter dead time (36). τ_ib and τ_b (Fig. 4 B and C) were then calculated as τ_ib = 1/r_CO, and τ_b = (1/r_OC)(1 + r_OB/r_BO).

Burst Analysis of Single-Channel Records.

Individual components of the closed-time distribution were assigned as intra- or interburst based on their ATP dependence (SI Text and Fig. S3). Open bursts were isolated by ignoring closures shorter than a cutoff (t_crit). Two strategies for choosing t_crit are described in refs. 34 (method i) and 35 (method ii). We employed large simulated data sets to study the distortion of the distribution of bursts resulting from these two procedures. Method (ii) proved slightly more accurate for estimating the mean of a single-exponential burst distribution (Fig. S1), but measurably distorted the shape, and the resulting rate estimates, for the peaked distribution characteristic of a cyclic mechanism (Fig. S2). Therefore, although both methods yielded qualitatively similar results, we used the distributions obtained using method (i) for WT and K464A (Figs. 1 B and D, 3B, and 4), and that obtained using method (ii) for D1370N (Fig. 1C).

The distributions of the durations of bursts obtained in this way were fitted to various models using ML (24), by excluding events shorter than t_low = 6 ms. The burst pdf for scheme 1 is given by f(t) = k × exp(−kt); for scheme 2 with k₋₁ = 0 by f(t) = [k₁k₂/(k₁ − k₂)] × [exp(−k₁t) − exp(−k₂t)], and for the full scheme 2 by f(t) = [(k₋₁ − k₂)(k₋₁ + k₁)/(k₋₁ + k₁ − k₂)] × exp[−(k₋₁ + k₁)t] + [k₁k₂/(k₋₁ + k₁ − k₂)] × exp(−k₂t). The improvement of a fit due to introduction of an additional parameter was evaluated using the log-likelihood ratio test (26); a more comprehensive summary of ML fitting results is given in SI Text (Fig. S4).

Fitting of Macroscopic Current Relaxations.

Macroscopic current decay time courses were fit by single-exponential functions using nonlinear least-squares methods (pCLAMP 9; Axon Instruments, Inc.).