Coping without farm location data during a foot-and-mouth outbreak

Despite increasing globalization of agriculture, the last reported outbreak of foot-and-mouth disease (FMD) in the United States was in 1929 (1). Foot-and-mouth disease virus infects cloven-hoofed animals, with cattle and pigs being particularly susceptible. The virus is highly transmissible and causes significant symptoms in many species, with substantial mortality in the young. Therefore, outbreaks of FMD in regions where it has been eliminated (Europe, North and Central America, the Pacific Nations, and the Caribbean) pose immediate challenges for policy makers concerned with animal welfare and continued agricultural productivity (2). In this issue of PNAS, Tildesley et al. (3) use a simulation approach to investigate optimal culling strategies against an outbreak of FMD in the United States.

Since the 2001 outbreak of FMD in the United Kingdom (4, 5), the epidemiology of future similar outbreaks has become a popular example for the application of mathematical models of infectious disease (6–8). In particular, spatially explicit simulation models (9) have helped to quantify the relationship between farm density in the United Kingdom and transmissibility (10). Although similar approaches have been used to describe likely patterns of transmission in the United States (11), Australia (12), Korea (13), New Zealand (14), and the Netherlands (15), analysis of the 2001 United Kingdom outbreak benefits from an unusually rich dataset. Precise locations are available for both affected and unaffected farms; furthermore, the number of infected premises during 2001 was sufficient to permit accurate estimation of key transmission parameters. Together, the rich data from the 2001 United Kingdom outbreak and the development of simulation models have greatly facilitated the investigation of spatially heterogeneous intervention policies. For example, it has been shown that if a well-matched vaccine were available in the United Kingdom during a future outbreak of FMD, once the outbreak had spread to a number of different areas, it would be better to prioritize the vaccination of farms closest to the most recent reported case, rather than adhering to a strict ring-vaccination policy (16).

When large quantities of well-matched vaccine are not available, the main intervention against an outbreak of FMD must be the culling of animals on infected and at-risk farms. The virus spreads effectively in dense populations. Therefore, it is desirable to cull at-risk farms rather than waiting for them to be infected (and be known to be infected). By proactively removing some susceptible farms—those most likely to be infected and fuel the outbreak—the overall number of infected and culled farms (epidemic impact) can be minimized. However, herein lies the principal challenge to any policy-maker during the first days of an outbreak: how aggressively should at-risk farms be culled? Overly aggressive culling will lead to a greater epidemic impact than necessary because of the loss of many never-to-have-been-infected farms. Overly conservative culling will lead to a greater epidemic impact because of an increased outbreak size.

To date, it has not been clear how mathematical models would support such policy decisions during the early stages of a United States FMD outbreak. Methods used for the United Kingdom could not be adapted directly because detailed farm location data are not currently available for the United States. Motivated by this lack of data, in this issue of PNAS, Tildesley et al. (3) present results from an ingenious set of simulation experiments designed to help with early-outbreak decisions. First, to be able to test their methods, they estimated the locations of farms for a handful of counties in the United States using satellite imagery and other data sources. This process gave them credible synthetic populations. Within their simulations, their intervention of interest was ring culling: all farms within a certain distance of a known infected farm were culled. Aggressive ring culling used a large ring, whereas conservative ring culling used a small ring.

Armed with synthetic locations and a well-established simulation framework, Tildesley et al. (3) conducted a number of experiments. First, they simulated an epidemic on the synthetic population of each county with no interventions. Second, they adjusted the parameters of their model so that simulations on a uniformly distributed population of the same size over the same area (with no interventions) gave the same epidemic curve as simulations on the synthetic population. Third, they simulated many epidemics (with the adjusted parameters) on the uniform population with different ring-culling distances to find the optimal distance. Intriguingly, the optimal distance for ring culling using the uniform population density was very close to the optimal distance found using the realistic synthetic location of farms. As further evidence of the generality of this result, they repeated the experiments for counties in the United Kingdom (where exact locations are known) and also for extreme theoretical distributions of farm locations.

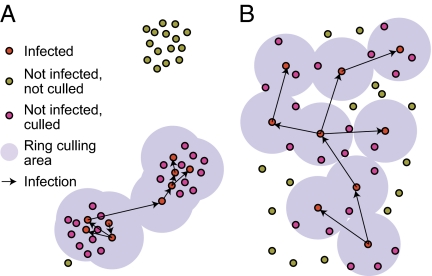
The net result of a transformation of spatial locations (from clustered to uniform) combined with an infection process and ring culling is not immediately obvious. Although it is not too difficult to imagine transformations of the infection kernel that give the same epidemic impact for different population densities (for the same culling radius, Fig. 1), the results reported by Tildesley et al. (3) are stronger than that. Their method of reparameterization seems to conserve the ordering of radial culling distances (by epidemic impact) for transformations of population density from clustered to uniform. The simulation evidence they present is compelling and hints at additional underlying theory. Somehow, by changing the parameters of the realistic spatial infection process to have the same epidemic curve in a uniform population, their method defines an abstract infection-intervention model that relies only on average spatial density. It could be that this particular intervention, in which culling and infection contribute equally to epidemic impact, is somewhat unique. Other intervention processes may not survive the spatial transformation so well. In addition, similar experiments in which outbreaks are simulated on a substantial number of contiguous counties would be of interest. It seems likely that the spatial extent of outbreaks will grow much more rapidly in the transformed simulations (uniform density). Hence, it may become difficult to accurately adjust the simulation parameters so as to conserve county-level epidemic impact data once the outbreak is larger than a single county.

Fig. 1.

Schematic illustration of population density transformation. Similar epidemic impact (infected plus culled farms) can arise for the same ring-culling radius in populations with quite different density distributions. (A) The population is highly clustered and average infection distances are short. The outbreak manages to transition from the seed cluster to a second, but not to the third cluster. (B) The population could have been drawn from a uniform distribution. To obtain a similar epidemic impact as that in A, infection events in B occur over medium distances but without long jumps. The spatial extent of the epidemic is much greater in A than in B.

Detailed farm location data are not currently available for the United States.

In general, mathematical models of infectious disease can be excellent tools for highlighting the value of data in supporting or refuting specific hypotheses. Intuitively, one would have expected the characterization of an optimal spatial intervention to require accurate location data (17). Tildesley et al. (3) have shown that this is not necessarily the case. However, despite the conceptual elegance of these results, some caution is required before celebrating a rare victory of model over data. All of the results by Tildesley et al. (3) rely on a minimum of 2 weeks of epidemic data. Therefore, in the absence of detailed location data, their methods would likely be used only to refine policy that would undoubtedly be initiated during the first few days. This final caveat begs an obvious question. Given the overall insightfulness and scientific quality of current research into transmission dynamics of FMD outbreaks, if detailed location data could be made available for the United States, why not make them available now? The author of this commentary has no intuition with which to assess the potential costs of making commercially sensitive information available for scientific research. Also, there may be concerns of bioterrorism. However, it seems likely that the interests of livestock farmers would be best served by the calibration of current peer-reviewed models with accurate farm location data long before any outbreak actually occurs.