Mixed-power scaling of whole-plant respiration from seedlings to giant trees

Abstract

The scaling of respiratory metabolism with body mass is one of the most pervasive phenomena in biology. Using a single allometric equation to characterize empirical scaling relationships and to evaluate alternative hypotheses about mechanisms has been controversial. We developed a method to directly measure respiration of 271 whole plants, spanning nine orders of magnitude in body mass, from small seedlings to large trees, and from tropical to boreal ecosystems. Our measurements include the roots, which have often been ignored. Rather than a single power-law relationship, our data are fit by a biphasic, mixed-power function. The allometric exponent varies continuously from 1 in the smallest plants to 3/4 in larger saplings and trees. Therefore, our findings support the recent findings of Reich et al. [Reich PB, Tjoelker MG, Machado JL, Oleksyn J (2006) Universal scaling of respiratory metabolism, size, and nitrogen in plants. Nature 439:457–461] and West, Brown, and Enquist [West GB, Brown JH, Enquist BJ (1997) A general model for the origin of allometric scaling laws in biology. Science 276:122 -126.]. The transition from linear to 3/4-power scaling may indicate fundamental physical and physiological constraints on the allocation of plant biomass between photosynthetic and nonphotosynthetic organs over the course of ontogenetic plant growth.

From the smallest seedlings to giant trees, the masses of vascular plants span 12 orders of magnitude in mass (1). The growth rates of most plants, which are generally presented in terms of net assimilation rates of CO₂, are believed to be controlled by respiration (2, 3). Furthermore, many of the CO₂-budget models of plant growth and carbon dynamics in terrestrial ecosystems are based on whole-plant respiration rates in relation to plant size (2, 4–7). Thus far, however, there have been few studies of whole-plant respiration over the entire range of plant size from tiny seedlings to large trees. The purpose of the present study was to quantify the allometric scaling of metabolism by directly measuring whole-plant respiration over a representative range of sizes.

For the past century, the scaling of metabolic rate with body size has usually been described using an allometric equation, or simple power function, for the form (8 –17)

where Y is the respiratory metabolic rate (μmol s⁻¹), F is a constant (μmol s⁻¹ kg^-f), M is the body mass (kg), and f is the scaling exponent. The exponent f has been controversial, and various values have been reported based on studies of both animals and plants (15). Recently, it was suggested that f = 1 for relatively small plants, based on data for a 10⁶-fold range of body mass (16), including measurements using a whole-plant chamber (18, 19). If f = 1, this means that whole-plant respiration scales isometrically with body mass, which may be reasonable in the case of herbaceous plants and small trees because nearly all of their cells, even those in the stems, should be active in respiration. However, it was suggested that f = 3/4 based originally on empirical studies of animal metabolism (8). This idea is consistent with the mechanistic models of resource distribution in vascular systems (10, 11), including the pipe model (20, 21) and models based on space-filling, hierarchical, fractal-like networks of branching tubes.

A recent study showed sample sizes, measurement errors, and statistical analytical methods influence the allometric scaling exponents estimated by metadata syntheses (22). Most data on whole-plant respiration have been acquired using indirect methods of estimation, limited to small plants, or focused on a narrow range of body sizes (2, 5, 15, 16, 18, 19, 23–26). Furthermore, most studies of plant metabolic scaling have been based on the aboveground parts and have ignored respiration of the roots, which is very difficult to measure (23). Furthermore, the flow of dissolved CO₂ in the sap brings into question the accuracy of estimating whole-tree respiration based on measuring small portions of large trees using the standard clamp-on chambers that are commercially available (16, 27–30).

Given the methodological difficulties inherent in whole-plant physiological studies, it is not surprising that there have thus far been no empirical measurements of complete whole-plant respiration, including roots, that have a reasonable sample size and encompass a wide range of plant sizes (2, 22, 26, 31–34). Accurate and efficient methods using whole-plant chambers to measure respiration rates have recently been developed (5, 18, 19, 24–26) and can be applied to assess metabolic scaling (Fig. 1). To determine the metabolic scaling of whole plants, including roots, across ontogenetic stages and species, we measured CO₂ fluxes in a large number of sample plants from tropical to boreal ecosystems (22). These data allow the most comprehensive analysis of scaling of whole-plant metabolic rate undertaken to date.

Fig. 1.

Our methods for measuring whole-plant respiration from seedlings to giant trees using closed-air circulation chamber for all sample plants. (A) Measurement of a standing tree using a dark chamber in Siberia, with air temperature controlled using heat generated from wood fires and permafrost (as schematic representation of the system in Fig. S2, and as exemplification of measured data in Fig. S3). (B) Measurement of a standing tree using a dark chamber in Siberia without an air-temperature controller. (C) Measurement of excised and excavated materials from a large tree using a destructive method. (D) Measurement of excised and excavated materials from a midsize tree using a destructive method. (E) Measurement of excised or excavated seedlings. (F) The roots of midsize trees immediately after rapid excavation.

Results

Using the whole-plant chamber (Fig. 1; detailed description in SI Methods), we measured the respiration of 271 naturally grown whole plants spanning nine orders of magnitude in body mass, from 10⁻⁶ to 10⁴ kg. The plants comprised 64 species from biomes from Siberia to Southeast Asia (Table 1). The diameter, height, and age of the sample plants ranged from ca. 0.05–72 cm, 1–2,900 cm, and 1 week to 240 years of age, respectively.

Table 1.

Plants in this study

Country	City	°N latitude	Species (number of sample trees)
Russia	Tura	64.2	Larix gmelinii(Rupr.) Rupr. (23), Larix gmelinii (Rupr.) Rupr (8), Ledum palustre L (1), Vaccinium uliginosum L (1)
Japan	Nakadomari	40.6	Thujopsis dolabrata Sieb. et Zucc. var. Hondae Makino (7)
Japan	Hachimantai	40.0	Fagus crenata Blume (5)
Japan	Morioka	39.5	Abies firma Sieb. et Zucc (2), Abies sachalinensis (Fr. Schm.) Masters (3), Abies spectabilis (D. Don) Spach (1), Abies veitchii Lindl (1), Alnus firma Sieb. et Zucc (1), Alnus hirsta Turcz (4), Betula ermanii Cham (1), Betula maximowicziana Regel (3), Betula platyphylla Sukatchev var. japonica (Mia.) Hara (11), Chamaecyparis obtusa (Sieb. et Zucc.) Endl (1), Cryptomeria japonica (L. fil.) D. Don (7), Cupressus duclouxiana Hickel (2), Fagus crenata Blume (12), Fraxinus mandshurica Rupr. var. japonica Maxim (4), Larix kaempferi (Lamb.) Carr (4), Liriodendron tulipifera L (3), Pinus densiflora Sieb. et Zucc (7), Pinus koraiensis Sieb. et Zucc (4), Quercus acutissima Carr (5), Quercus cuspidata Blume (2), Thujopsis dolabrata Sieb. et Zucc. var. hondae Makino (7), Zelkova serrata (Thunb.) Makino (2)
Japan	Kawaimura	39.4	Quercus cuspidata Blume (11)
Japan	Ishioka	36.1	Chamaecyparis obtusa(Sieb. et Zucc.) Endl. (5), Cryptomeria japonica (L. fil.) D. Don (5), Pinus densiflora Sieb. et Zucc. (3), Pinus thunbergii Parl. (2), Quercus myrsinaefolia Bl. (1), Quercus serrata Thunb. ex. Muuray (1)
Japan	Kumamoto	32.5	Castanopsis cuspidata (Thunb.) Schottky (2), Camellia sasanqua Thunb. ex Murray (1), Cinnamomum camphora (L.) Presl (1), Dendropanax trifidus (Thunb.) Makino (1), Distylium racemosum Sieb. et Zucc (1), Ficus erecta Thunb (1), Ilex rotunda Thunb (1), Mallotus japonicus (Thunb.) Muell. Arg (1), Melia azedarach L. var. subtripinnata Miq (1), Quercus glauca Thunb. ex Murray (1)
Japan	Nago	26.4	Macaranga tanarius (L.) Muell. Arg (23), Schima wallichii spp. liukiuensis (Nak.) Bloemb (7), Diospyros ferrea Bakh (9)
Japan	Ishigaki	24.3	Calophyllum inophyllum L (1), Castanopsis cuspidata var. sieboldii (1), Dendropanax trifidus (Thunb.) Makino (2), Distylium racemosum Sieb. et Zucc (1), Ficus erecta Thunb (1), Ficus microcarpa L. fil (6), Ficus septica Brumann fil (3), Ficus variegata Blume (1), Fraxinus griffithii C.B.Clarke (1), Kandelia candel (L.) Druce (2), Mallotus japonicus (Thunb.) Muell. Arg (1), Melastoma candidum D. Don (1), Melia azedarach L. var. subtripinnata Miq (1), Neolitsea sericea (Bl.) Koidz (1), Pinus luchuensis Mayr (2), Quercus miyagii Koidz (1)
China	Hong Kong	22.0	Ficus microcarpa L. fil (1)
Thailand	Doi Mae Salong	20.1	Camellia sinensis (L.) O. Kuntze (3), Jasminum sambac (L.) Ait (1)
Thailand	Chiang Rai	19.5	Mangifera indica L (2), Nerium indicum Mill (1)
Thailand	Chiang Mai	18.5	Ficus religiosa L (3)
Thailand	Mukudahan	16.3	Shorea siamensis Miq (4)
Thailand	Ubon Ratchathnai	15.1	Artocarpus heterophyllus Lam (1), Durio zibethinus J. Murr (1), Mangifera indica L (1), Tamarindus indica L (1)
Thailand	Bankok	13.4	Azadirachta indica A. Juss (4), Bouea macrophylla Griff (1), Jasminum sambac (L.) Ait (5)
Indonesia	Samarinda	0.28	Shorea smithiana Sym (6)

Plants are listed by country, city, latitude (^oN), species name, and number of individuals (in parentheses). We used excised materials (plain text, no underline) and intact plants (underlined), as well as materials that were analyzed both destructively and nondestructively (dashed underline).

At first, we tried to fit the relationship between the respiration rate and the whole-plant mass using a simple-power function on log-log coordinates. We found that f = 0.838 (n = 254, 95% CI of f = 0.820–0.855, r = 0.99, P < 0.001, ln F = −0.889) for the aboveground parts and f = 0.844 (n = 183, 95% CI of f = 0.824–0.863, r = 0.99, P < 0.001, ln F = −0.972) based on reduced major axis (RMA) regression of the log transformed version of Eq. 1. These values are significantly different from the exponents of f = 1 and 3/4 reported in previous studies (2, 8–17). Using ordinary least squares (OLS) rather than RMA regression did not change the pattern (Table 2).

Table 2.

The AIC statistics and related constants for Eq. 1, Eq. 2, and a quadratic function

	Simple-power function (Eq. 1) fitted by OLS				Mixed-power function (Eq. 2) fitted by NLS
	n	InF ± SEM	f ± SEM	AIC	G ± SEM	H ± SEM	g ± SEM	h ± SEM	AIC
Aboveground parts	254	−1.001 ± 0.050	0.826 ± 0.009	560.18	6.690 ± 16.320	0.421 ± 0.089	1.082 ± 0.207	0.780 ± 0.037	555.72
Whole plants	183	−0.921 ± 0.057	0.833 ± 0.010	372.12	201.87 ± 734.37	0.410 ± 0.028	1.408 ± 0.341	0.805 ± 0.018	366.33
	Quadric function fitted by OLS
	a ± SEM	b ± SEM	c ± SEM	AIC
Aboveground parts	−0.899 ± 0.063	0.810 ± 0.011	−0.004 ± 0.002	555.31
Whole plants	−0.829 ± 0.070	0.818 ± 0.012	−0.004 ± 0.002	396.18

To compare the goodness of fit for the simple-power function Eq. 1, the mixed-power function Eq. 2, and a quadratic function, the simple power form of ln Y = ln F + fln M, and the quadratic form of ln Y = a + b ln M + c(ln M)², where a, b, and c are coefficients, were fitted to the data by means of ordinary least square regression (OLS). The mixed-power form of ln Y = −ln [1/(GM^g) + 1/(HM^h)] was also fitted to the data using nonlinear least squares regression (NLS), and the AIC values for these functions were calculated. Any differences in AIC values <2 indicate minimal differences between the models. Differences between 4 and 7 led us to conclude that the higher score model was less valid, and a score >10 suggested that the model should be rejected (40).

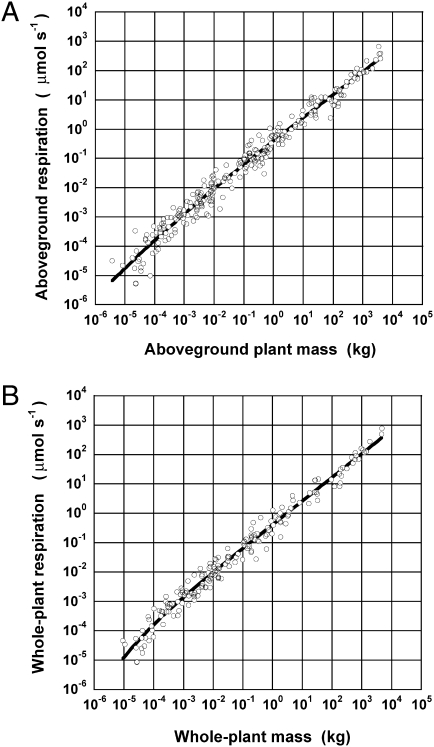
Inspection of the data reveals a convex upward trend and a gradual change in the slope on log-log coordinates. Because there appears to be a systematic change in the value of f, a simple-power function fails to adequately express the relationship between whole-plant respiration and mass across the wide range of body masses that we investigated (Fig. 2).

Fig. 2.

The relationship between respiration Y and mass M for (A) aboveground parts and (B) whole plants, including the roots. Respiration, measured as the net CO₂ efflux under dark conditions, was temperature adjusted to 20 °C, assuming a standard Q ₁₀ = 2. The relationship between ln Y and ln M was fitted to Eq. 2 using a nonlinear least-squares approach.

For a mathematical description of this empirical metabolic scaling, we suggest a mixed-power function, which captures the transition between two simple-power functions, as follows (37):

where G (μmol s⁻¹ kg^-g) and H (μmol s⁻¹ kg^-h) are coefficients, and g and h are exponents. As M varies, Eq. 2 maps onto two asymptotic relationships as follows:

We used Akaike’s information criterion (AIC) (38 –40) to compare the mixed-power function of Eq. 2, the simple-power function of Eq. 1, and a quadratic equation (Table 2). The mixed-power function gave the best fit (the AIC value of 366.33 for Eq. 2 was the less than 372.12 for Eq. 1 and 369.18 for the quadratic function). For aboveground respiration, the AIC value of 555.72 for Eq. 2 was similar to the 555.31 for the quadratic function and less than the 560.18 for Eq. 1. Therefore, we recommend the mixed-power function as the best model for the metabolic scaling of plants.

As shown in Fig. 2 and Table 2, Eq. 2 reflected real trends in both whole-plant and aboveground respiration as a function of plant size well. The slope S that maps ln Y to ln M can be derived as a function of M by differentiating ln Y with respect to ln M in Eq. 2:

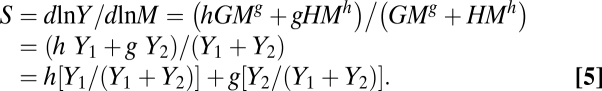Therefore, S is defined as the weighted mean of h and g given the values of Y ₁ and Y ₂, respectively. As M increases, Y ₁/(Y ₁ + Y ₂) and Y ₂/(Y ₁ + Y ₂) change from 0.0 to 1.0 and from 1.0 to 0.0, respectively. The effect of the second term on the first term gradually decreases, and ultimately the slope S converged on h. Thus, Eq. 5 describes a biphasic relationship with two asymptotes, depending on individual mass.

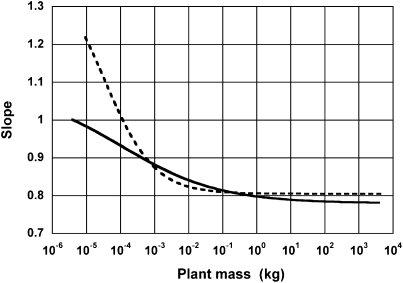
The change in slope is shown in Fig. 3. The value of S changed gradually over the range of M (≈10⁻⁶ to 10⁴ kg), from ≈1.03 to 0.78 in the aboveground parts and from 1.21 to 0.81 in the whole plants. So, for both the aboveground parts and for whole plants, the allometric exponent was close to 1 only for the smallest masses (17) and rapidly converged to a value h = 0.780 ± 0.037 indistinguishable from 3/4 (8, 10, 11) for the aboveground parts, and to a value h = 0.805 ± 0.018, slightly >3/4, for the whole plants (SEM data in Table 2). In summary, we have integrated the two simple-power functions into Eq. 2, and they give two asymptotic slopes of 1 and 3/4 (8, 10, 11, 16) as individual plant mass increases.

Fig. 3.

The relationship between the slope S and the plant mass M in the mixed-power function of Eq. 2. Relationships were calculated for the aboveground parts (solid line) and for whole plants (broken line) using Eq. 5.

Let point P on log-log coordinates denote the intersection between the straight lines representing Eq. 3 and Eq. 4. Also, let point Q be the intersection between the vertical line through P and the curve expressing Eq. 2 on the same coordinates. Then, the slope of a straight line touching this curve at the point Q is (g + h)/2. This is because Y ₁ is equal to Y ₂ at the intersection point P, where the M value is (H/G)^[1/(g−h)]. The value of M at the intersection point P, Y ₁ = Y ₂, was calculated to be 1.054 × 10⁻⁴ kg and 3.429 × 10⁻⁵ kg for aboveground and whole-plant respiration, respectively. Therefore, as shown in Fig. 3, the exponent is close to 1 in only the very smallest plants (M < 1g) converges to 3/4 when M ≈ 0.1 kg (results qualitatively similar but quantitatively somewhat different from ref. 35). The precise transition is likely determined by physicochemical constraints (15) and may be reflect adaptation to various environments.

Discussion

Enquist et al. (35) and Hedin (36) also pointed out the possibility of an ontogenetic shift in the scaling whole-plant respiration over a wide range of body size. An ontogenetic shift from isometric (f = 1) to negatively allometric (f < 1) scaling has also been reported in animals with distinct larval and adult stages (15).

We can provide a biological rationale for this shift in scaling that is described by the mixed-power function and consistent with the morphological/physiological transition from tiny seedlings to giant trees (41, 42). During the earlier stages of ontogeny, a larger fraction of plant biomass is devoted to metabolically active leaf tissue, and a smaller fraction to vascular tissue for transport of water and nutrients. Furthermore, in small plants, such as small herbs and tree seedlings, the entire tissue of stems is metabolically active (43). We conclude that the near-isometric scaling of metabolic rate in herbs and juvenile trees is due to the large proportion of biomass that is metabolically active.

In comparison with small plants, most of the biomass of large trees is in the woody stems, which are much less metabolically active than the leaves and small branches. A large proportion of the trunk and large branches is typically composed of nonliving, metabolically inactive biomass, which serves a mechanical function, supporting the plant against the forces of gravity (11, 35) and wind. Plant respiration is ultimately limited by photosynthesis because plants can only respire compounds that have been fixed. Therefore, photosynthesis and respiration should be closely related to total leaf area (44 –47), and the less-than-linear scaling rate of metabolic plants might reflect a decreased leaf-to-stem ratio with increasing plant size (48). Furthermore, the physiological and morphological changes in stems and leaves between juvenile and mature trees (41, 42) may also affect changes in whole-plant physiology. For all these reasons, with increasing plant size, the allometric exponent should decrease from 1 toward the canonical 3/4.

Conclusions

We conclude that interspecific metabolic scaling of vascular plants can be modeled using a mixed-power function. In Eq. 5, the slope of the mixed-power function is defined as the weighted mean of the slopes of the two asymptotes. Thus, the mixed-power function synthesizes the two previous models that feature slopes of 1 and 3/4 into a single synthetic model. Our proposed function implies a gradual ontogenetic transition in the scaling of metabolism from small seedlings to larger mature plants, a transition that is also seen across species in comparisons of herbaceous and woody plants. Our model can accommodate the variation in the scaling exponent that is observed over the 12 orders of magnitude variation in plant mass in our data. Thus, our function integrates the observed differences between small and large plants into a single statistical model that reflects allocation to photosynthetic and nonphotosynthetic organs during plant growth. Our approach may offer insights into the diversity of plant sizes in the context of physicochemical constraints consistent with the ecological traits of organisms (15).

Materials and Methods

Materials.

We examined 254 aboveground parts, 200 roots, and 183 whole plants to obtain measurements from 271 specimen plants of 64 species, sampled from tropical through boreal ecosystems of Eurasia, as shown in Table 1. At each site, we measured the respiration rates of field-grown plants.

Methods.

We measured whole-plant dark respiration rates during the growing season. We developed two kinds of respiration measurement methods, using a closed-air circulation approach. One system was designed to acquire data using intact aboveground parts of standing trees (Fig. 1 A and B), and the other system was designed to monitor excised aboveground parts (Fig. 1 C–E) or excavated roots (Fig. 1F). As shown in SI Methods, there were no differences in respiration rates of the aboveground parts between the intact and excised materials at the same temperature (Fig. S1). To measure each giant tree, we divided the tree into portions and monitored the respiration of each portion to evaluate whole-plant respiration (see Fig. 1C). The masses of whole plants were measured directly using various balances that could accommodate seedlings to giant trees. Details are given in SI Methods.

Statistical Analysis.

1. To compare the scaling exponents from the present study with previous studies, a simple-power function of the form ln Y = ln F + fln M as shown in Eq. 1 was fitted to the data using both RMA and OLS regression.

2. To compare AIC among Eqs. 1 and 2 and a quadratic function, we analyzed all relationships using nonlinear least squares regressions (NLS) and OLS in Table 2. All analyses were performed using the R software package (49).