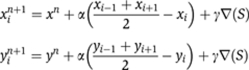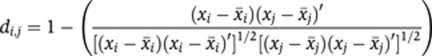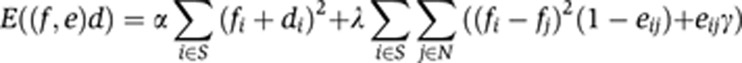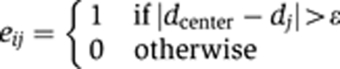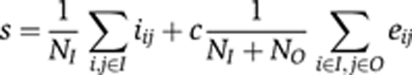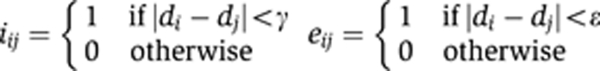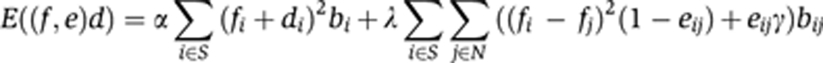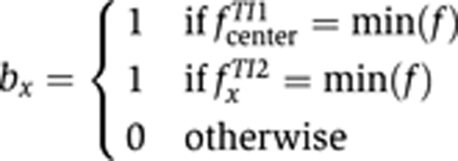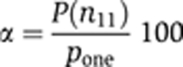Systematic image-driven analysis of the spatial Drosophila embryonic expression landscape

Abstract

Discovery of temporal and spatial patterns of gene expression is essential for understanding the regulatory networks and development in multicellular organisms. We analyzed the images from our large-scale spatial expression data set of early Drosophila embryonic development and present a comprehensive computational image analysis of the expression landscape. For this study, we created an innovative virtual representation of embryonic expression patterns using an elliptically shaped mesh grid that allows us to make quantitative comparisons of gene expression using a common frame of reference. Demonstrating the power of our approach, we used gene co-expression to identify distinct expression domains in the early embryo; the result is surprisingly similar to the fate map determined using laser ablation. We also used a clustering strategy to find genes with similar patterns and developed new analysis tools to detect variation within consensus patterns, adjacent non-overlapping patterns, and anti-correlated patterns. Of the 1800 genes investigated, only half had previously assigned functions. The known genes suggest developmental roles for the clusters, and identification of related patterns predicts requirements for co-occurring biological functions.

Introduction

Almost a decade has passed since the genome sequence of Drosophila melanogaster was published and 13 601 genes identified (Adams et al, 2000), yet well over half of the genes remain poorly characterized. For multicellular organisms, exploring both temporal and spatial gene expression is crucial for understanding the development and regulatory networks. Interacting genes are commonly expressed in overlapping or adjacent domains. Thus, gene expression patterns can be analyzed to infer candidates for gene networks. We are generating a systematic two-dimensional mRNA expression atlas to profile embryonic development of D. melanogaster. We developed a controlled vocabulary (CV) to annotate embryonic expression patterns (Tomancak et al, 2002, 2007). Using controlled conditions, RNA transcripts were detected by hybridization using an antisense DIG-labeled RNA probe and visualized using immunohistochemistry producing a blue stain (Weiszmann et al, 2009). Although not quantitative, the intensity of the staining does vary as a function of expression level. Expression databases are established for a number of model organisms including Ciona (Imai et al, 2004), zebrafish (Sprague et al, 2008), Xenopus (Gilchrist et al, 2009), and mouse (Smith et al, 2007; Richardson et al, 2009). In addition, multiorganism databases allow cross-species expression comparison (Haudry et al, 2008). Our spatial expression data set is among the largest of these and is unique in providing, from a single primary data source, a comprehensive profile of expression patterns for over 40% of all protein coding genes.

Earlier, we used annotated gene-expression profiles to identify genes involved in developmental processes that were missed by traditional genetics (Tomancak et al, 2002, 2007). Human annotation, however, requires an expert curator and the resulting annotation, although rigorous, is neither spatially defined in a coordinate system nor numeric. Here, we address the question of how to best represent a large expression data set in a way that is suitable for computational analysis. Others used image processing to extract information not captured in the annotation (Kumar et al, 2002; Gurunathan et al, 2004; Peng and Myers, 2004; Peng et al, 2007). These image-processing efforts were successful but limited to recognizing similar patterns, predicting CV annotations computationally (Zhou and Peng, 2007; Ji et al, 2008, 2009), clustering a subset of the expression data, and analysis of cis-regulatory sequences (Peng et al, 2006). To date, there have been only limited efforts towards a comprehensive image-based analysis of the spatial expression landscape. In particular, during early development, patterning events take place that require genes to be expressed in defined spatial domains. Misexpression profoundly changes embryonic morphology, and genes known to control early development have been used for modeling transcriptional regulation in early embryogenesis (Reinitz et al, 1995; Segal et al, 2008). These studies predict that many components of these networks remain to be discovered, consistent with our earlier analysis identifying numerous uncharacterized genes with restricted expression in early developmental stages.

Our large data set provides an essential resource for systematic study of patterning events and is well suited for the identification of candidate regulatory genes. How many different regions are there in the embryo and how many distinct pattern categories exist? What links genes with similar expression patterns together? What previously uncharacterized genes have expression patterns that fit directly, partially, or adjacent to known patterning genes? Here, we propose a new, geometry-based, standardized representation of a large-scale expression data set, demonstrate methods and describe novel tools to address these questions. We converted digital embryonic expression patterns to a spatially comparable coordinate representation to enable both visual comparison of patterns among differently shaped embryos, and computational analysis. Our method uses a strategy similar to that used to generate a digital atlas of the mouse brain, a landmark-driven deformable mesh (Ju et al, 2003; Carson et al, 2005). We expanded this system and created a framework for representation and analysis of a developing organism with dynamic changes of gene expression patterns. We then created and applied new methods to relate the patterns generating a systematic, image-driven description of the Drosophila expression landscape. Although our methods are applicable to all but the latest stages of embryonic development, we focused on stages 4–6, corresponding to the blastoderm, a period too early in development for most of the gene expression patterns to be well described by an anatomy-based CV.

Results

Virtual representation of in situ images

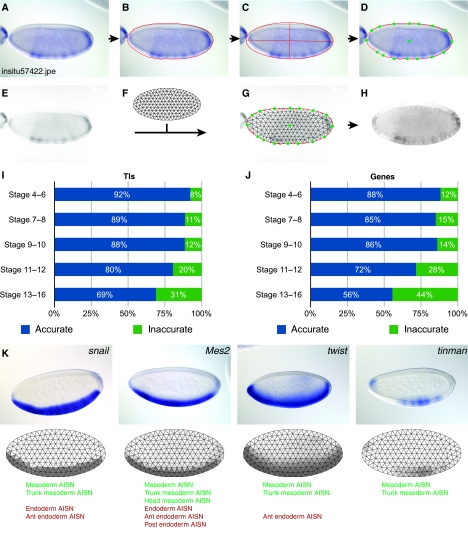
To generate a computational representation of gene expression patterns, we built a fully automated pipeline, TIgen (Figure 1A–H; Supplementary Figure 1, Data set 1). Our data set consists of 66 111 whole embryo images representing 6003 genes (Tomancak et al, 2007). We segmented the embryo in each image using a modified texture-based method (Peng and Myers, 2004). Our method adds three morphological image-processing operations (removal of isolated pixels, dilation, and majority processing), and active contour refinement to generate an outline as close as possible to the embryo. We also added an algorithm to extract individual embryos from images where multiple embryos touch each other (Supplementary Information; Supplementary Figure 2). We generated a virtual representation of the embryo by creating a mesh of 311 equilateral triangles in the shape of an ellipse. This representation fits the multiple angles found in actual expression patterns, and the placement of the triangles corresponds to many embryonic structures such as the epidermal and mesodermal germ layers. To adjust the mesh to the embryo, we used the best fitting ellipse (Figure 1C) to define 16 anchor points on the embryo perimeter and one in the center. We aligned the mesh to the embryo using the anchor points with a customized thin plate spline deformation. To generate a measurement of staining intensity, we applied a customized grayscale conversion algorithm. We eliminated differential interference contrast (DIC) artifacts caused by morphological structures that, in grayscale, are indistinguishable from real staining (Supplementary Information; Supplementary Figure 2). Earlier image-processing attempts on this data set failed to remove DIC induced shadows (Kumar et al, 2002; Peng and Myers, 2004). We used the median of the grayscale pixels in each triangle as the intensity of expression for that triangle. We call these virtual representations ‘triangulated images’ (TIs). The entire following analysis is based on these TIs and all staining intensities reflect the numerical values in the triangles.

Figure 1.

Processflow for converting expression patterns into TIs. (A) Digital photograph of CG10033. (B) Segmentation of the embryo shown in (A) with the boundary indicated by the red line. (C) On the basis of the boundary coordinates in (B), the best fitting ellipse was superimposed on the embryo. (D) Green dots show anchor points. (E) Grayscale image of the embryo in (A) with shadows introduced by DIC microscopy removed. (F) Ellipse in the ratio 4:2 subdivided into equilateral triangles. (G) Alignment of the ellipse from (F) to the embryo using the anchor points. The remaining corner points of the triangles are adjusted with a thin spline deformation algorithm. (H) Virtual representation of the staining intensities in (E) as a TI. Raw intensities of the triangles are enhanced (color saturation increased to 60%) for visualization. (I) Quality assessment of TIs and (J) genes at different developmental stages. Accurate and inaccurate fractions are shown as the percent of samples evaluated. Shown are the results of a random selection of 518 TIs/110 genes (S4–6), 269 TIs/100 genes (S7–8), 266 TIs/109 genes (S9–10), 590 TIs/109 genes (S11–12), and 705 TIs/100 genes (S13–16). (K) Three rows, the top shows four digital photographs, the middle row shows the converted TIs with their superimposed mesh, and the bottom row shows the controlled vocabulary (CV) used to annotate the expression patterns. TIs reveal subtle differences in the patterns not captured by the CV.

To select for TIs that passed this automatic pipeline, we visually compared each TI with the original image and recorded the evaluation in a database using a custom web tool. At the same time, we determined the orientation of each embryo by the addition of unique tags to mark the anterior, posterior, dorsal, and ventral sides. These tags were used to automatically orient each TI and remove failed TIs, thus generating a high-quality curated data set (Supplementary Figure 3). As judged by this visual evaluation of each mesh, our pipeline succeeded in segmenting and converting 60 605 images to TIs corresponding to over 91% of the total. Failed cases group into three categories; multiple embryos in complex arrangements, severely out of focus, and heavily overstained embryos.

To evaluate the accuracy of the successful TIs, we manually scored them as matching the digital image or not (Figure 1I and J; Supplementary Figure 4). For each stage range, we randomly selected at least 100 genes and evaluated a total of 2348 TIs. For a gene to be scored as matching, all its TIs must match their respective digital images. At stages 4–6, 92% of the TIs and 88% of the genes are accurately represented by our geometric representation. The accuracy is slightly lower at stages 7–8 and 9–10 and drops to 69% of TIs and 56% of the genes at the latest stages 13–16. However, even inaccurate TIs give a rough outline of the expression pattern, and we used them for general comparisons.

This geometric representation captured subtle differences in the expression patterns such as those at the anterior pole between snail (sna), Mes2 and twist (twi) (Figure 1K). Moreover, such differences were not accurately represented with the CV annotations due to the lack of reference anatomical landmarks. For example, annotations of sna and tinman (tin) were identical even though their patterns are significantly different (Figure 1K).

TIs as a computationally defined expression pattern representation

Our triangle-based embryo registration simplified the identification of similarly patterned genes by making possible linear representations. We assigned a unique identifier to each triangle and created a data vector so that triangles with the same identifier have the same position in the data vector (Supplementary Figure 5A). Thus, visually similar patterns were readily identified with a correlation distance score. The correlation distance score eliminated the need to correct for overall differences in the intensities between TIs and produced comparable scores independent of the strength of the expression pattern (Supplementary Figure 5B). We used TIs representing different stages of development and consistently identified visually similar expression patterns.

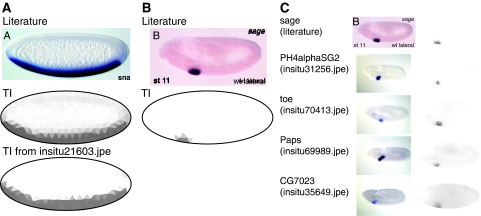
We used TIgen to automatically convert images from the literature to TIs. High-resolution images with no text near the embryo were easily converted (Figure 2A; Supplementary Figure 6A). Lower-resolution images, images in which text touched the embryo, or images with grainy background were converted using TIgen in a manual mode to select the anchor points (Figure 2B; Supplementary Figure 6B–D). A search using the TI generated from a literature image returned TIs for genes with similar expression patterns (Figure 2C).

Figure 2.

Comparing images from the literature to our data set. (A) Image of sna in situ hybridization (top) (Stathopoulos et al, 2002), converted to a TI with the fully automatic pipeline (middle). The TI is nearly identical to the TI from the BDGP collection (bottom). (B) Image of sage in situ hybridization at stage 11 (Abrams et al, 2006), showing expression in the salivary gland (top) and the corresponding TI after manual segmentation (bottom). (C) Similarity search using the TI in (B) showing top hits with other genes expressed in the salivary gland.

Reducing complexity of the expression landscape

For a functional analysis of expression patterns, we used 5745 lateral view TIs captured for stages 4–6. During this stage, axis formation and many of the body patterning events take place, making it a rich choice for comparing gene expression to gene function. Initial attempts of grouping similar TIs revealed a multitude of challenges: (1) a number of embryos showed no or ubiquitous expression, (2) many genes were represented with multiple images showing similar expression patterns, and (3) many images had poorly defined boundaries with little distinction between regions of expression and background. To address these issues, we created an automatic pipeline, TIfilter, to refine the data set for further analysis (Supplementary Figure 1 and Table I; Table I). TIfilter produced two data sets, one containing a compacted and temporally sorted set of all 2693 patterned TIs (1881 genes) and a subset of 553 TIs (365 genes) containing patterns with clearly defined boundaries (Data set 2). The pipeline removed redundant patterns and sorted the images in a developmental time-line (Supplementary Figure 7). We identified 133 genes that are represented by dynamic patterns during this narrow stage range. For example, sloppy-paired 1 (slp1) expression can be grouped into five distinct sets starting with a single narrow stripe at the anterior pole expanding to a seven-stripe pair-rule pattern (Supplementary Figure 7D).

Table 1. Results of filtering TIs at stages 4–6.

Step	No. of TI
Start with all patterns (lateral view)	5745
Remove meshes with no/ubiquitous expression	4454
Remove redundant patterns	2693
Select most distinct patterns	553

Organization of the embryo into co-expressed regions

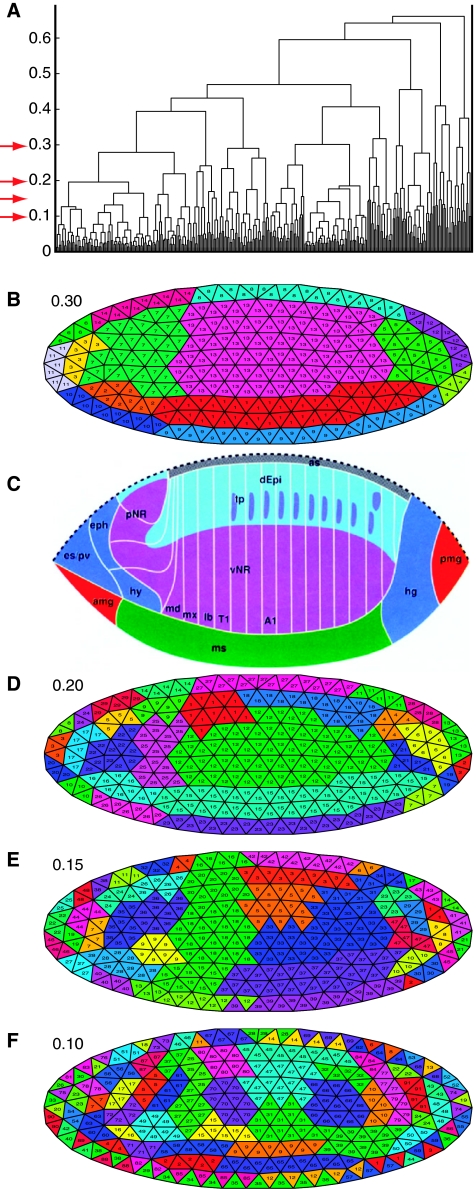
To identify regions in the embryo where genes are expressed similarly, we clustered the 311 triangles across the 553 distinct TIs using hierarchical clustering with the interactive program TIfate. To visualize the clusters, we used different cutoffs (Figure 3). Triangles with similar expression signals are adjacent to each other, revealing subdivisions of the embryo into expression domains. Using a cutoff of 0.3 results in 14 domains (Figure 3B) that show divisions of the embryo that are similar to the embryonic fate map (Hartenstein, 1993) (Figure 3C). Using smaller cutoffs of 0.2, 0.15, and 0.1 (Figure 3D–F) reveals further subdivisions. In particular, the anterior regions of the embryo separate into many small subdomains corresponding to the developing pharynx, procephalic neurogenic region, proventriculus, and anterior midgut. Other tissues such as the developing mesoderm appear more uniform, but we demonstrate that gene expression refines the mesodermal domain into distinct anterior/posterior subdomains with potentially different cell fates.

Figure 3.

Mapping co-expressed genes on the blastoderm embryo. (A) Structure of the hierarchical clustering of the 311 triangles displayed as dendrogram. Triangles 1–311 are shown on the horizontal axis, the distance scores on the vertical axis. The red arrows denote the cut-off values chosen for B, D, E, and F. (B, D, E, F) Clusters at different cut-off values (0.30, 0.20, 0.15, and 0.10, respectively) visualized as TI. Each cluster is labeled with a different color and given a numerical identifier displayed in each triangle. (C) Fate map of the blastoderm after (Hartenstein, 1993). amg, anterior midgut rudiment (endoderm); as, amnioserosa; dEpi, dorsal epidermis; eph, epipharynx; es, esophagus; hg, hindgut; hy, hypopharynx; lb, labium; md, mandible; ms, mesoderm; mx, maxilla; pmg, posterior midgut rudiment (endoderm); pNR, procephalic neurogenic region; pv, proventriculus; vNR, ventral neurogenic region; T1, thoracic segment 1; tp, tracheal placodes.

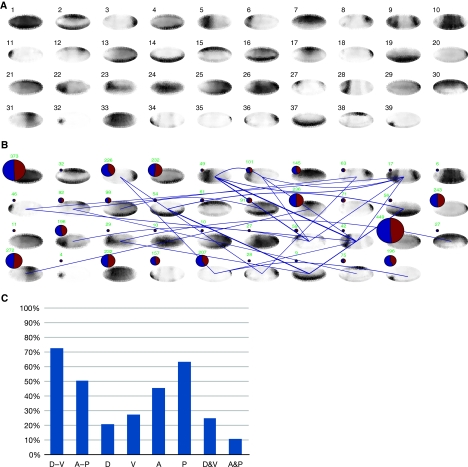
Clustering genes with similar expression patterns

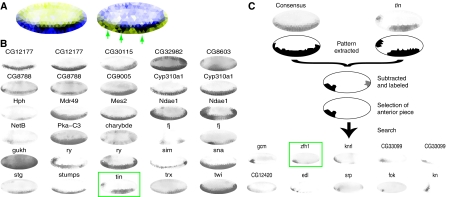
To catalog the expression patterns, we used an unsupervised clustering approach to group related expression patterns into clusters. We cataloged genes using affinity propagation clustering (Frey and Dueck, 2007), using correlation distance to eliminate TI intensity differences. This clustering algorithm sequesters the data set automatically into a computationally optimal number of clusters. While using this algorithm on all 2693 TIs identified over 200 clusters, often with only negligible differences, the 553 distinct TIs generated 39 distinct clusters. The consensus expression pattern for each cluster is shown as a pictogram in Figure 4. The clusters divide the expression landscape into distinct categories, defining clusters of genes with restricted expression, showing staining only anterior, posterior, dorsal, ventral, or combinations of these, and clusters with more broadly expressed genes (see Figure 5B for an example showing patterns in Cluster #14).

Figure 4.

Clustering genes with similar expression patterns. (A) Normalized consensus patterns for each of the Clusters #1 to #39 are displayed. The consensus patterns were computed from the most distinct 553 TIs representing 336 genes. (B) Distribution of genes and relationships among clusters after each pattern was classified. The size of the pie chart on the top of each cluster is proportional to the number of genes in each cluster. The total number is shown in green above each pie chart. The blue area of each pie is proportional to the fraction of characterized named genes and the red area to the fraction of marginally studied genes (CG identifiers only). The blue lines between clusters denote the occurrence of genes that were classified into multiple clusters. (C) Distribution of patterns. D=dorsal, V=ventral, A=anterior, P=posterior. The height of the bars corresponds to the percentage of patterns in the direction D-V, A-P, predominantly D, V, A, or P or combinations of D and V (D&V) or A and P (A&P).

Figure 5.

Targeted mining for differences from the cluster consensus. (A) Single TI shows the consensus Cluster #14 expression pattern, enlarged relative to Figure 4A and in two color schemes. On the left, blue indicates uniform expression, white no expression, and the normalized standard deviation of triangles of expression patterns in the cluster in yellow. Triangles with greater variation are brighter yellow. On the right, for emphasis of the standard deviation, blue and yellow are switched. Darker blue indicates greater variation. The color-coding emphasizes variations in the bandwidth and also reveals three major regions of discontinuous expression (green arrows). (B) First 30 TIs from Cluster #14. Boxed in green is the expression pattern of the gene, tin, highlighted because the pattern is discontinuous at the anterior end. (C) Using the MRF algorithm and the cluster consensus expression pattern, we extracted the tin regions of discontinuity. Both the consensus pattern (as determined by the median of all patterns in the cluster) and the pattern of tin are shown at the top. Shown below the curly bracket are the two extracted regions, the first in black at the anterior and the second in gray at the posterior. The black region was used as bait for a systematic search of the data set. The top 10 results of this search are shown below the arrow. Boxed in green is zfh1, a known interactor of tin. Two distinct patterns were returned for CG33099 as a result of the query.

We extended this initial categorization for 553 TIs to the entire data set of 2693 patterned TIs to include all patterned genes for our subsequent analysis. We used the 39 well-defined clusters as training data to classify all TIs with a binary support vector machine classification algorithm (Supplementary Figure 8, Data sets 3 and 4). We grouped all 2693 TIs including TIs with poorly defined boundaries and TIs annotated with CV terms ‘no staining’ or ‘ubiquitous’ into the 39 clusters because their normalized TI intensities resembled the cluster consensus (Supplementary Figure 8C). The two largest clusters are Cluster #1, with broadly expressed genes, and Cluster #29, with posteriorly expressed genes (Figure 4B). Some clusters had only few members with restricted patterns. Categorizing the clusters reveals that a larger number of genes are expressed posteriorly (P) and ventrally (V) and fewer genes are expressed anteriorly (A) and dorsally (D). Of the A/P and D/V combinations more patterns were located D/V than A/P (Figure 4C). At stages 4–6, there are 25 CV terms describing specific regions of expression. In addition to the differences shown in individual patterns (Figure 1K), our clustering approach reveals subtle differences between patterns that were not captured with an anatomy-based CV. For example, Clusters #8 and #12 and Clusters #18 and #20 share all specific CV terms, respectively, and exhibit similar but distinct patterns.

Next, we investigated the cluster distribution of genes with multiple distinct expression patterns. We identified instances where two clusters share >5% of their genes and visually linked those clusters (Figure 4B). In most of the cases, we linked clusters with narrow expression patterns to clusters with similar but broader expression patterns. For example, Cluster #3 and Cluster #35 share 20 out of the 369 combined genes. Both clusters include genes with expression patterns located at the posterior end of the embryo, but Cluster #3 represents a more broadly expressed pattern group than Cluster #35, consistent with a general trend for patterns of dynamically expressed genes to progress over time from narrow to broader expression. A notable exception is the case of shared genes between Cluster #35, a predominantly posterior grouping, and Cluster #39, a predominantly anterior grouping. The shared genes, Adenosine deaminase-related growth factor A (Adgf-A), Bicaudal D (BicD), CG12420, CG14427, CG7663, CG8289, CG9215, Gasp, HLHm5, argos, anti-silencing factor 1 (asf1), cenG1A, croquemort (crq), numb, screw (scw), sloppy paired 1 (slp1), sanpodo (spdo), yemanuclein α (yemα) show expression patterns that vary in form and intensity from one end of the embryo to the other.

Using the data set to identify co-expressed and potentially interacting genes

Knowing the precise boundary of the expression pattern boundaries was a prerequisite for further study. While simple k-means clustering or other clustering methods such as Gaussian mixture models provided an adequate extraction of the patterns for some of the TIs, those basic clustering methods failed with more complex patterns, and boundaries were not consistently identified between runs (Supplementary Figure 9C). Thus, we developed a more sophisticated algorithm to recognize pattern boundaries much as an expert embryologist would distinguish between a part of the embryo with and without expression. Often, the most reliable indicator of a pattern boundary is a significant change of intensity between neighboring regions. We developed a Markov Random Field (MRF)-based program (Geman and Geman, 1984; Li, 2001), TImrf, that minimizes the global energy score by iteratively labeling each triangle based on its staining intensities in relation to its neighboring triangles. The local energies for each triangle were calculated by either labeling a triangle the same as its neighboring triangles, or introducing an edge, assigning a different label, and computing the difference of the labels from the underlying staining intensities. Using this algorithm, we extracted complex expression patterns (Supplementary Figure 9).

To identify co-expressed genes in each of the 14 domains (Figure 3B), we used the 365 genes with 553 distinctly patterned TIs. We extracted their expression patterns with TImrf and identified all TIs where the extracted pattern covered at least 90% of the triangles for each domain (Supplementary Table II). Consensus TIs and corresponding defined domains are shown in Supplementary Figure 10B. Examination revealed that each domain is the result of combinatorial gene expression and no single gene defines a domain (Supplementary Figure 10C).

To investigate pattern diversity within each of the 39 clusters (Figure 4A), we calculated the standard deviation for each of the triangles and created a composite of the consensus pattern and the normalized standard deviation (Supplementary Figure 11). Most of the significant variations appear at the boundaries of the consensus. Cluster #14 reveals a variability of the pattern at the most dorsal extension of the ventral band (Figure 5A). Similarly, Cluster #36 shows the most variability in the posterior boundary of the expression consensus. This analysis revealed potentially important variations in the consensus patterns themselves. The graph for Cluster #14 (Figure 5A) reveals interruptions in the consensus pattern, further substantiating the results of a non-uniform ventral area of the early embryo suggested in our analysis of co-expressed regions in the embryo (Figure 3F).

Using extracted expression patterns and simple arithmetic subtraction, we identified genes with complementary expression patterns. In Cluster #14, we identified genes whose ventral expression pattern showed discontinuities (Figure 5B). One of the genes with an interrupted pattern was tinman (tin). Using TImrf, we extracted the pattern of tin and the pattern of the cluster consensus. We then subtracted the tin pattern from the consensus, selecting the largest continuous area with all triangles connected by two corners. This identified a small expression domain present in the consensus and absent in tin. We used this small pattern in a systematic search for genes with expression in this domain using TIbin2 and identified six almost perfectly complementary patterns as high scoring hits (Figure 5C). The second highest scoring pattern was the transcription factor zfh1, which previously was shown to interact with tin in the specification of lateral mesodermal derivatives including the gonadal mesoderm (Broihier et al, 1998; Su et al, 1999). In addition, we identified two previously uncharacterized genes, CG33099 and CG12420, which now can be tested for functional interaction with tin.

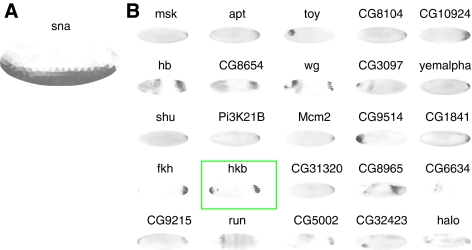
In practice, extracting the exact extent of the pattern boundary was not always possible with the MRF algorithm. Moreover, during blastoderm development, patterns of related genes can completely overlap, can share a boundary with anti-correlation, or overlap but share only a partial boundary (Lawrence and Struhl, 1996). By clustering genes with overall similar patterns, we systematically identified the cases of completely overlapping genes. To find other anti-correlated genes and those that have partial overlapping expression patterns, we developed a modified version of the above MRF program, TImrf2 that uses two TIs. As before, the energy scores for labels were optimized for one TI, and, for the triangles with an edge labeling, the triangles of the second TI included in the computations. The edge triangles of the second TI were assumed to be either, positively or negatively, correlated. The final output was the minimal energy score for the two candidate TIs. A good match of the boundaries of two TIs resulted in a low score, whereas a poor match or no match raised the score. By sorting descending scores for all embryos, we identified the top positively or negatively correlated patterns with matching boundaries (Supplementary Figure 12). We then applied this algorithm to sna and targeted specifically anterior to posterior oriented expression patterns. One of the top hits was the gene huckebein (hkb), which previously was shown to repress the expression of sna at the anterior and posterior poles of the embryo (Reuter and Leptin, 1994) (Figure 6).

Figure 6.

Anti-correlation mining identifies known interacting genes. (A) Single TI showing the sna expression pattern. (B) Using the modified MRF algorithm and filtering for vertically oriented patterns, we used sna, as bait to identify genes with expression patterns that share similar boundaries and do not overlap. One of the top hits of the search was hkb (boxed in green), previously shown to restrict sna expression at the anterior and posterior poles.

Biological functions of clustered expression patterns

Spatial gene expression data have been used to deduce possible gene functions (Hartenstein and Campos-Ortega, 1997). We used our gene expression data set to search for over-represented functions of co-regulated genes and to deduce putative functions of previously uncharacterized genes. We used known genes in each cluster to find enriched gene ontology (GO) terms with a P-value <0.001 and subjected each of the resulting GO terms to a null-hypothesis test for enrichment with respect to the total gene population using a one-sided significance test (Rivals et al, 2007).

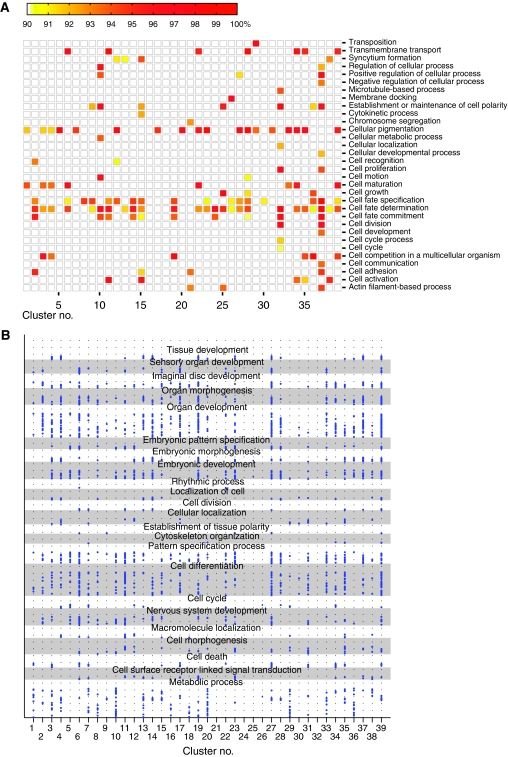
For the limited number of GO terms in the cellular process category (GO:0009987), we filtered for terms with a significance level of >90% and plotted the significance level (Figure 7A). We found 32 cellular processes with enrichments mapping to one or more of the 39 clusters. For example, Cluster #29, a predominantly posterior cluster, has a clear enrichment of genes with transposition function (GO:0032196), and Cluster #32, with a pattern localized at the anterior pole, is highly enriched in cell polarity genes (GO:0007163). Transcription factors were generally not enriched and appear to be evenly distributed among the clusters with the notable exceptions are Clusters #10 and #37, both composed of only a small number of genes and enriched for transcription factors.

Figure 7.

Analysis of clusters for gene ontology (GO) term enrichment in clusters. (A) Enrichment of GO terms in the cellular process (GO:0009987) category (vertical axis) for each of the 39 clusters (horizontal axis). The level of significance is displayed as color intensity between white (90% and below) and red (100%) as indicated by the color bar on the top. (B) Enriched GO terms in each cluster. Clusters are on the horizontal axis, individual GO terms (614 in total) are shown as blue dots on the vertical axis and associated with one or more of the 23 parent terms. Alternating gray and white backgrounds are used to separate parent terms. Identical GO terms are placed at the same vertical height within a parent section.

We found a total of 827 enriched GO terms distributed among the 39 clusters. We computed the correlation of categorical GO terms between each cluster combination as φ correlation coefficient r_φ. We identified only weak correlations (r_φ≈0.5) between the similar Clusters #37, #14, and #19, revealing distinct set of terms for each cluster. To visualize the functional signatures, we manually selected 23 umbrella GO terms (shown on the vertical axis in Figure 7B), which (1) had at least two of the enriched terms as child terms in the acyclic GO tree, (2) represented biological interesting functional categories, and (3) contained the majority of enriched terms as child terms. For example, we selected the umbrella term ‘organ development’ (GO:0048513) to identify clusters involved in early organ specification. We then associated every enriched term with each of the 23 umbrella GO terms where the enriched term is a child of the umbrella term in the GO tree, and then plotted each enriched term as a dot (Figure 7B; Supplementary Figure 13A, Data set 5 for GO terms on the vertical axis). For the earlier example, ‘organ development,’ we associated various organ specific processes such as imaginal disc development, mesoderm formation, or gut development (Data sets 6 and 7 detail the categorized GO terms for each cluster). This resulted in a characteristic signature for each cluster that was reviewed for functional predictive value. The dot density in each GO category is indicative for a potential function of the cluster in that category. For example, Clusters #6 and #27 are enriched in GO terms that map to the sensory organ development class, specifically eye development (Supplementary Figure 13B). The consensus expression patterns of both clusters are localized at the anterior region of the embryo where the eye disc develops. Cluster #11, a cluster with anterior expression exhibited a significant enrichment of A/P axis terms, and Cluster #14, with expression localized to the ventral portion of embryo is enriched in organ development terms especially those terms used to describe mesoderm development (Supplementary Figure 13A). Both known genes in Cluster #32 have restricted expression near the anterior pole and are involved in cell polarity, suggesting a related function for two uncharacterized genes in this cluster. Clusters at the anterior and posterior poles show functional enrichment of cytoskeleton (Clusters #20, 34, and 35). Some clusters at the anterior/posterior/dorsal/ventral poles are enriched in cell cycle genes (Clusters #4, 12, 22, 29, 34, and 39), suggesting an increased mitotic activity at the poles. Interestingly, the patterns restricted at the posterior pole mapping to the pole cells (Clusters #20 and 29) appear also to be enriched in metabolic functions, which, as elaborated below, may suggest an important role of metabolism during pole cell development. We computed r_φ for each category and found only few correlations, mostly among clusters with only 1–2 GO terms (Data set 8). Clustering of genes by spatial expression and analysis of their functions using GO terms allowed us to assign tentative roles to uncharacterized genes.

The enriched GO terms for each cluster support the biological relevance for our approach. As an additional validation, we compared our 39 clusters to the literature curated genetic interaction data set (Yu et al, 2008) and determined enriched genetic interactions (Supplementary Figure 14). We found 15 clusters and 17 cluster pairs with enrichment for genetic interactions.

Discussion

Deformable meshes represent complex and dynamic expression

We developed a method to produce standardized representations of Drosophila embryonic images and demonstrated the usefulness of this method in a framework for analyzing gene function and knowledge discovery. Although it would be ideal to deform the embryos directly to a standardized shape and relate the registered pixels, frequently such deformations result in a misalignment of internal boundaries (Ju et al, 2003). Misalignments make it difficult to compare expression patterns where boundaries are very important. Key image features from the embryonic expression patterns were extracted and simplified using a deformable mesh. Similar meshes have been used extensively for creating characters and shapes for computer-generated movies, medical imaging applications (Yoo, 2004), and also for a digital atlas of sagittal sections from the mouse P7 brain (Ju et al, 2003; Carson et al, 2005).

In contrast to the digital mouse brain atlas, our images were not acquired solely for computational analysis. Data were captured with the intent of describing the expression pattern using CV annotations, and curators collected multiple images for each stage to obtain a comprehensive representation of the pattern. As a consequence, the images presented three challenges: (1) segmenting and separating contacting embryos, (2) reducing the data set to the minimal informative image set, and (3) identifying the canonical forms for genes with dynamic patterns. In place of the subdivision mesh used in the mouse atlas, we used an unbiased equally spaced triangular mesh. By removing redundant patterns and sorting images, we identified genes with dynamic expression patterns. Such genes are often parts of complex regulatory networks and, thus, may prove interesting targets for further studies.

TIs are useful to analyze expression data

Earlier efforts to identify similar expression patterns used methods based on Boolean comparison of extracted patterns (Kumar et al, 2002), comparison of regions based on Gaussian mixtures (Peng and Myers, 2004), Eigenface techniques (Peng et al, 2006), and Haar wavelets (Zhou and Peng, 2007). However, these methods are only capable of detecting similar expression patterns. We represented each image as a data vector and applied many standard algorithms for computational analysis. Biologically related genes were identified either with a straightforward correlation distance measurement or a more sensitive and flexible MRF-based approach. We used pattern variations to identify potential regulatory interactions, such as the repression of sna by hkb at the poles. An advantage of both our correlation distance and MRF approach is that by correlating the expression patterns of two images simultaneously, we can assign a similarity score without prior assumptions about the pattern. As we demonstrated, many pattern boundaries are poorly defined but nonetheless can be identified when placed in context to other patterns (Supplementary Figure 8C). We succeeded in finding correlated patterns even if they shared only small intensity similarities at the same locations.

Currently, there are no benchmarks to evaluate the performance of our similarity search methods or the existing alternatives. Annotations, especially at the studied stages 4–6, are not necessarily applicable as ‘ground truth’ for our data set (Figure 1K; Supplementary Figure 5B). Our method succeeds in finding and clustering biologically related genes. As new protein–protein interaction data becomes available, it will be valuable to compare with our cluster analyses. Currently, a high false positive rate is associated with the yeast two-hybrid data, which limits the value of such comparisons (von Mering et al, 2002). Using a data set of genetically interacting genes that do not necessarily have overlapping expression, we do see non-random enrichments.

Conceptually, our TIs and clustering strategy work with later stage images (Supplementary Figure 15); however, additional parameters and modifications will improve our success rate. During stages 7–9, the germband retracts and thus additional alignments will be needed for accurate pattern comparisons. After stage 11, due to the development of multiple tissue layers, focal planes cannot be collapsed and visually similar patterns are not separable with the information in the images or TIs alone (Supplementary Figure 4B). Thus, for a meaningful biological analysis, layer information will need to be added.

Analysis of co-expressed regions reveals a fate map

Clustering expression patterns can either group correlated regions in the embryo or group correlated expression patterns. Using a standardized spatial representation facilitated the identification of correlated regions of expression in the stages 4–6 embryo. We demonstrated that the fate map created from laser ablation experiments (Lohs-Schardin et al, 1979), HRP labeling, and histological methods (reviewed in Hartenstein and Campos-Ortega (1997)) are correlated and explained by gene expression patterns. By increasing the resolution, we show that gene expression can be used to further refine the domain map. Domains result from combinatorial gene expression (Supplementary Figure 10), and we identified sets of genes that, in combination, define the boundaries for each domain. This is conceptually similar to earlier work that derived ovarian expression patterns from Boolean combinations of primitive domains (Yakoby et al, 2008). Earlier studies and our large number of domains at higher resolution (Figure 3F) imply a more complicated situation in the blastoderm embryo unsuitable for the same manual approach. However, our results suggest that an algorithm could be devised to find a minimal set of primitives that represent most expression patterns and include poorly defined patterns.

Identification of interacting genes by discovering overlapping patterns

Clustering similar expression patterns not only groups genes with overall similar patterns but also reveals pattern diversity within a group. Our analysis of cluster gene composition provides a first systematic insight into pattern progression. Most patterned genes (1516 out of the 1881 studied) do not show precise pattern boundaries but can be categorized with other genes that have clearly defined patterns. Earlier studies have shown that concentration changes of the transcripts or proteins can determine cell identities (e.g. bicoid (Driever and Nusslein-Volhard, 1988)) and genes with indistinct boundaries may act in a similar manner. For processing other large-scale expression sets, a similar pre-processing step using clearly defined patterns, or a more advanced clustering algorithm, will be required to investigate the full diversity of expression patterns. Genes in the same cluster provide a new data set for identifying co-regulated or interacting genes.

Anti-correlation is particularly interesting as it implies transcriptional repression. A well-documented example of blastoderm anti-correlated gene expression involves giant (gt) and Krüppel (Kr) (Lawrence and Struhl, 1996). The posterior boundary of Kr expression matches the anterior boundary of gt expression. Limiting a search for interacting genes to those that share overlapping expression patterns would miss a substantial number of important genes required for a systems level analysis. We developed novel methods for a targeted search to identify interacting gene candidates. We show that patterns are more diverse than simple clustering or CV annotations can capture. Although these differences are not important for a broad categorization, they are vital to explain the biological network surrounding a particular gene. We have used the difference between a particular pattern and the more broadly defined consensus patterns in a cluster to identify known and novel gene regulator candidates in the network surrounding tin. Known repressors are often expressed in domains adjacent to their relative targets. We created a novel implementation of an MRF-based labeling method to score adjacent patterns and showed that we can identify biologically significant patterns such as hkb uncovered for sna.

Elucidating biological functions and their associations from expression

We showed that genes with similar expression patterns have related GO functions. GO functional annotations tend to be fine grained and are unweighted lists of curator associated, evidence-based gene functions. Although this results in comprehensive gene descriptions, it also introduces noise and a substantial number of functions for each cluster. Earlier functional analyses using ontologies collapsed terms to find informative sets (Tomancak et al, 2007). This proved difficult because of the acyclic nature of the ontology tree and the classification of biologically related functions with different ancestors. We developed a novel filtering approach by manually selecting categories and placing the individual terms as a plot. Using this method, we showed that a distinct functional signature characterizes each cluster of related expression patterns and that the broad functional assignments are readily definable by studying this graph. Roughly half of the genes categorized in this way are unnamed and most likely not studied in detail. With this classification, we can suggest putative functions. CV term names at this stage are often inspired by the tissue developing at this location and were frequently selected based on gene expression in the differentiated tissue (Hartenstein, personal communication). In contrast to the anatomy inspired CV, this analysis is solely based on the spatial expression and thus had no prior assumptions.

Our data representation will be useful to elucidate associations between biological functions using overlapping gene expression patterns. Certain biological functions have a tendency to co-occur during development. For example, Clusters #6 and #27 are enriched in genes with the GO functions eye development, and cell death (Figure 7B). This is consistent with the previously demonstrated requirement of programmed cell death during eye development (Bonini and Fortini, 1999). To provide a first systems overview of related biological functions correlated with gene expression during blastoderm development, we created a condensed graphical representation (Supplementary Figure 16). Patterning events are predominant at this stage of development and, indeed, we found many patterning functional terms linked together. Closer examination both of the graphical representation and the individual co-occurrences revealed many previously unidentified relationships that can be considered for future studies (Data set 9). Among the new associations was a link between negative regulation of osk mRNA translation (GO:0007319) to metabolic processes such as glucose metabolic process (GO:0006006) and pyruvate metabolic process (GO:0006090). The link between osk and the pyruvate metabolic process was previously identified in a systematic yeast two hybrid screen (Giot et al, 2003).

Applicability of our methods to other expression data sets

Our TI approach is complementary to the cellular resolution 3D atlas for the Drosophila embryo (Fowlkes et al, 2008). Our method can be used as a rapid, fully automated, high throughput approach to obtain a map of co-expression, which will serve to select specific genes for a detailed multiplex in situ hybridization and confocal analysis for a fine-grain atlas. The higher resolution 3D atlas requires at least double in situ hybridization and far more time-consuming confocal imaging. With our available large low-resolution data set, interesting candidates can be selected for the slower high-resolution approach for further study.

Our data are similar to the data in the literature, and research groups studying reporter constructs, mutant animals, or orthologs can easily produce in situ hybridizations. TIs can be readily created and provide representations that are both comparable to each other and our data set.

Integrating genome-wide expression studies with other data sets has been limited to microarrays and more recently next generation transcriptional profiling, but both only provide temporal information. Our analysis and earlier studies have shown that animal development cannot be studied from temporal data alone. The representation of our expression data in a standard geometric format with a comparable coordinate system will open the spatial data to wider computational analysis similar to microarray analysis. Using appropriate mesh generators, other large spatial expression data sets could be converted into TI representations and used for analyses similar to those described here.

In conclusion, we developed a novel broadly applicable approach to represent spatial expression patterns, created a high-quality data set for Drosophila embryonic expression and developed a tool set for knowledge discovery. We conducted a systems level analysis of our data and found gene candidates for interaction analysis.

Materials and methods

Expression data set

Drosophila embryonic expression patterns were detected by RNA in situ hybridization as described earlier (Weiszmann et al, 2009). We used dioxigenin-labeled RNA probes largely derived from the BDGP cDNA collection for in situ hybridization. Alkaline phosphatase immunohistochemistry was chosen for staining because of its sensitivity compared with other systems and diffusion was mitigated by staining for short times. Images were captured by digital microscopy. Digital images were captured with red/green/blue (RGB) filters on a Spot camera, resized to 1520 × 1080 pixels and stored in JPEG format. The key embryo was placed in the center of the image. Imaged expression patterns and focal planes were manually selected and frequently multiple embryos of the same pattern and or stage were imaged to document patterns in-depth for each gene. No images were captured for genes with exclusively maternal, ubiquitous, or no expression as seen in low-resolution microscopy. For comparable staining intensities between experiments, we stopped the immunohistochemical color reaction of all wells in a 96-well plate at the same time once the staining pattern appeared for three included control probes and most wells of the plates. Imaged embryos were manually assigned to one of six stage ranges. Literature images were downloaded from the journal web sites in the highest resolution available.

Image segmentation

As first part of the TIgen pipeline, we extracted the embryo by resizing the images by half, computing the standard deviation of a 3 × 3 pixel window, and applying a binary threshold with a value of 2.0 to the standard deviation as described by Peng and Myers (2004). This basic texture-based segmentation method applied to the larger data set revealed several major shortcomings. First, it left holes inside the embryo at regions with low texture. Thus, we applied the following morphological operations on the binary image: removal of isolated pixels, dilation, and majority processing. Second, any embryos touching the primary embryo were included in the segmentation result. We developed a heuristic method to detect these cases and calculate the boundary of the touching embryos (Supplementary Figure 2A and B). We then used points at the segmented boundary 2 degrees and 10 degrees away on both sides of the shared boundary and extrapolated the boundary with a cubic spline interpolation constrained by those 4 points. Third, the resulting boundary of the segmentation was up to the equivalent of half a cell layer away from the actual embryo. To refine the boundary, we used the previously computed boundary and refined it with a simple active contour algorithm (snakes). Of the standard deviation values at each pixel in the source image, we created a blurred image S by applying a 3 × 3 Gaussian and calculated the gradient ▿(S). At each iteration n and each x/y coordinate point i=1,…, N for the N points in the boundary, we computed

We performed three iterations with α=0.5 and γ=2. Applying this algorithm brought the boundary into close proximity of the embryo and refined the spline interpolations to the shape of the embryo. We encapsulated all steps in a fully automated pipeline in Matlab 7, used pipeline to extract 360 x/y coordinate points in 1-degree intervals for the circumference of the embryo in each image and saved them in an SQL database and as a flat file. The flat file is available at http://www.fruitfly.org/insitu/FriseMSB.

Creating a geometric database of TIs

For a virtual representation of the embryo, we created a triangular mesh in the shape of an ellipse. To generate this mesh, we used a triangular mesh generator that determines the node locations by iteratively solving for equilibrium in a truss structure and adjusting the topology with a Delaunay triangulation algorithm (Persson and Strang, 2004). With an input of an ellipse in a 4:2 ratio, a preset distance for the initial distribution of points set to 0.2 (referred as h0 in the reference), the algorithm produced an ellipse subdivided into 311 equilateral triangles with 180 corner points.

In the second part of the TIgen pipeline, we aligned this elliptical mesh structure to the shape of the embryo. As landmark alignment points, we selected 16 points corresponding to triangle corners on the boundary of the ellipse so that they were spaced as closely as possible in angular intervals of 22.5 degrees given the constraints of the triangle locations. We then determined the actual angles of the selected points in the meshed ellipse. In addition to the 16 points, we also selected a point at the geometric center, also corresponding to a triangle corner, of the meshed ellipse giving a total of 17 landmark points. To find the corresponding points on the embryo displayed in the image, we fitted an ellipse to the previously calculated outline of the embryo using the least square criterion (fit_ellipse.m at Matlab file exchange http://www.mathworks.com/matlabcentral/fileexchange/3215). We then subdivided the outline of this ellipse into 16 points corresponding to the previously determined angles. We laid lines from the center of the ellipse to the 16 points and intersected the lines with the actual outline of the embryo. Using a thin plate spline deformation algorithm (Bookstein, 1989) modified for the mesh, we deformed the corner points of the triangles so that the selected 16 landmark points at the outline and landmark point at the center fit to the corresponding points on the border of the embryo and at the center of the fitted ellipse.

To calculate the staining intensity within each triangle, we converted the color image into a grayscale eliminating the Normarski/DIC shadows (Supplementary Information; Supplementary Figure 2C–I) and computed the median.

The fully automatic TIgen pipeline in Matlab 7.x performed the computations and the staining intensities for each TI stored as a Matlab matrix and as a flat file.

The orientation of the images and the accuracy of the TI representation were curated by an expert annotator using a custom web tool, pose_editor. This tool presented a set of images and the corresponding TIs with multiple-choice selections for dorsal/ventral/lateral orientation, anterior/posterior/dorsal/ventral re-orientation and accepting/rejecting the mesh. Selections were saved into the primary SQL database (Tomancak et al, 2002). On the basis of the selections, patterns in the TIs were filtered and reoriented accordingly. Reorientation was performed by reassigning identifiers of the triangles. The filtered set of TIs is available at http://www.fruitfly.org/insitu/FriseMSB.

To evaluate TI accuracy, we selected at random at least 100 genes and all corresponding TIs and scored them with an interactive tool. Genes were only scored accurate if all TIs were accurate.

Similarity of two TIs

To determine a similarity score between two TIs, we converted each TI to a data vector x so that identical triangles take identical positions in the data vector and calculated their pairwise correlation distance d_i,j for all TI pairs as data vectors x_i and x_j:

Correlation distance mitigated differences in staining intensity or illumination.

Clustering the triangles and the TIs

To determine the regions of co-expression, we created an interactive tool in Matlab, TIfate, to calculate the pair-wise correlation distance between the triangles and perform hierarchical clustering using unweighted average distance (UPGMA). The program displays a window with the TI, the cluster tree as a dendrogram and a slider to set a cutoff value. We empirically determined suitable values to show varying subdivisions of the co-expressed genes.

To group similar expression patterns, we used affinity propagation clustering with the negative value of the correlation distance. The consensus pattern for each cluster was resolved with the singular value decomposition (SVD):

We assigned the matrix A to all TIs in a cluster and performed the SVD to resolve the U, S, and V components. The first column of U represented the most significant factor in the original matrix A and thus proved to be a reasonably accurate representation of the cluster consensus. To visualize the U column as TI, the values were normalized so that the minimum and maximum value of the vector corresponded to grayscale values of 0 and 255, respectively.

To visualize the diversity of the patterns, we calculated the standard deviation of each triangle after all patterns have been classified, normalized the standard deviation in the same way as the consensus pattern, and superimposed the two in yellow and blue. For blue, we assigned the TI intensity values i to the RGB color space as R=i, G=i, B=255, for yellow as R=255, G=255, B=i, and then superimposed yellow/blue as the min(yellow, blue) for each R, G, B number.

Staining pattern extraction

Extracting the staining was essentially a segmentation problem. In TImrf, we applied an MRF-based algorithm (Li, 2001) that combined both a smoothing term to label continuous neighboring triangles where the staining intensities were similar and a variable term that switched off the smoothing term and introduced a sharp break or edge at neighboring triangles where staining intensity differences exceeded a pre-set threshold. For each triangle with the staining intensity d, the putative label f, the edge e, the set of the triangle and neighboring triangles S and only the neighboring triangles N the posterior energy E((f,e), d) is

With the edge condition e set to

The sets S and N encompassed only connected triangles with two shared edges. α, λ, γ, and ε were parameters that were empirically assigned to values α=5, λ=1, γ=0.1, and ε=10. To minimize the posterior energy over the entire TI, we used a Gibbs sampler with simulated annealing.

Scoring embryos for shared boundaries of their expression patterns

To score boundary matches of two TIs whose expression pattern were extracted and represented as a binary mask, we developed a program TIbin2 using method that was inspired by MRF. For each TI with triangles inside the extracted pattern I, triangles outside the boundary of the extracted pattern O and staining intensities d, we evaluated the number of triangles fitting the source pattern I:

With the internal smoothness i and the edge e set to

N_I and N_O are the number of triangles inside and outside the boundary, respectively. I corresponds to neighboring triangles inside the boundary, and O corresponds to neighboring triangles outside the boundary. As before, neighboring triangles were defined as connected by two shared edges. The parameter γ corresponds to the smoothness threshold for triangles inside the extracted pattern and the parameter ε to the minimum difference for triangles at the boundary. Both parameters were set to 10. The correlation parameter c was set to −1 for positive correlation and +1 for anti-correlation. The resulting scores s were sorted in ascending order with the smallest s being the best fit.

To score boundary matches of two TIs if neither expression pattern was extracted, in TImrf2, we used the MRF method as described, and modified the posterior energy to include all triangles of the first TI (TI 1) and include triangles in the second TI (TI 2) only if a boundary condition b was encountered.

S and N were the sets of triangles for both TI 1 and TI 2. The boundary condition b at i or b at ij was set to

min(f) corresponds to the label f that has the smallest value and thus is the label denoting the staining. To identify anti-correlated pairs, we swapped the values for the label f in TI 2. As before, we applied a Gibbs sampler with simulated annealing to minimize the total posterior energy and returned the sum of the posterior energy for all triangles as score.

To create a data set of anterior-to-posterior oriented patterns, we extracted the pattern by k-means clustering, selected the largest continuous pattern, and subjected the covariance of x/y coordinates of the triangle centroids with the pattern to eigenvalue decomposition. We then calculated the angle of the largest eigen-axis and selected for patterns with angles between 70 and 110 degrees.

GO analysis

We created a custom script to retrieve all enriched GO terms and the raw numbers if they exceeded a P-value <0.001 by batch submitting a list of gene symbols for each cluster to the Amigo web site http://amigo.geneontology.org (GO database release 2008-12-01) and storing the results in a tabulated text file. To find a distribution independent confidence value, each returned GO term was subjected to a null hypothesis test using a hypergeometric distribution. As outlined in Rivals et al (2007), we determined the one-sided P-value p_one:

With N₁₁ denoting the null distribution, n₁₁ the observed number of GO terms in the cluster, K the number of genes annotated with this GO term, and P the hypergeometric distribution with those parameters. We then determined the significance level α:

The significance level α was either used directly to visualize the strength of the null hypothesis or used to accept or reject the null hypothesis by thresholding α values exceeding 10% and only accepting those GO terms.

We performed an equivalent analysis to evaluate the enrichment of genetically interacting genes to the interaction data set from Droid v4.0 (http://www.droidb.org, Yu et al, 2008).

Data sets and software

All described software code and data sets are available as Supplementary Information. Additional data sets, additional code for visualization and analysis, and the most up to date versions of the software in the Supplementary Information are available at http://www.fruitfly.org/insitu/FriseMSB/. Included on the web site are coordinates of the embryo outlines, TIs of the images, and the condensed TIs. TIs are provided in a flat file format and as Matlab matrix.

Supplementary Material

Dataset 1

Compressed file of the software code for TIgen, TIfilter, TIfate, TIbin2, TImrf and TImrf2

Dataset 2

CSV file containing the results of TIfilter at stages 4–6.

Dataset 3

CSV file with the TI assignments to each of the 39 clusters.

Dataset 4

Compressed file with the gene symbols in each cluster.

Dataset 5

List of all GO-terms on the vertical axis of Figure 7B.

Dataset 6

CSV file detailing the GO-terms associated to each cluster in Figure 7B.

Dataset 7

List of GO-terms in each cluster in Figure 7B as human readable version of Dataset 6.

Dataset 8

List of clusters with significant correlation between the categorized GO-terms.

Dataset 9

List of the 869 unique term pairs (199 GO-terms) that are correlated to each other.

Systematic image driven analysis of the spatial Drosophila embryonic expression landscape

Supplementary Information