A model of episodic memory: Mental time travel along encoded trajectories using grid cells

Abstract

The definition of episodic memory includes the concept of mental time travel: the ability to re-experience a previously experienced trajectory through continuous dimensions of space and time, and to recall specific events or stimuli along this trajectory. Lesions of the hippocampus and entorhinal cortex impair human episodic memory function and impair rat performance in tasks that could be solved by retrieval of trajectories. Recent physiological data suggests a novel model for encoding and retrieval of trajectories, and for associating specific stimuli with specific positions along the trajectory. During encoding in the model, external input drives the activity of head direction cells. Entorhinal grid cells integrate the head direction input to update an internal representation of location, and drive hippocampal place cells. Trajectories are encoded by Hebbian modification of excitatory synaptic connections between hippocampal place cells and head direction cells driven by external action. Associations are also formed between hippocampal cells and sensory stimuli. During retrieval, a sensory input cue activates hippocampal cells that drive head direction activity via previously modified synapses. Persistent spiking of head direction cells maintains the direction and speed of the action, updating the activity of entorhinal grid cells that thereby further update place cell activity. Additional cells, termed arc length cells, provide coding of trajectory segments based on the one-dimensional arc length from the context of prior actions or states, overcoming ambiguity where the overlap of trajectory segments causes multiple head directions to be associated with one place. These mechanisms allow retrieval of complex, self-crossing trajectories as continuous curves through space and time.

INTRODUCTION

Episodic memory includes the capacity to internally re-experience the sequence of events that occurred at particular places and times, in what has been termed “mental time travel” (Eichenbaum & Cohen, 2001; Tulving, 2001; 2002). Episodic memory includes the capacity to mentally retrace trajectories through previously visited locations, including re-experiencing specific stimuli encountered on this trajectory, and the relative timing of events. For example, you can probably remember the route you followed when you left your home this morning, with a memory of the locations you visited and the time you spent in individual locations. You can use this memory to remember where you parked the car, who you saw on your trip, or where you left your car keys. This aspect of episodic memory requires some means by which neurons can code continuous trajectories through space with time intervals representing the original episode. This also requires some means for encoding the location and time of specific events or stimuli encountered along this trajectory.

Physiological data shows that hippocampal activity during REM sleep can replay the relative time intervals of spiking activity evoked by different spatial locations during waking (Louie & Wilson, 2001), indicating the capacity to replay spatiotemporal trajectories with the same time scale as actual behavior. Other experiments also show that spiking activity in the hippocampal formation can maintain information about the relative timing of events (Hoehler & Thompson, 1980; Berger et al., 1983; Deadwyler & Hampson, 2006).

Lesion data suggests that encoding and retrieval of previously experienced episodic trajectories involves the entorhinal cortex and hippocampus. In humans, lesions of these structures cause profound impairments of episodic memory, tested both qualitatively and with quantitative measures in verbal memory tasks (Scoville & Milner, 1957; Corkin, 1984; Graf et al., 1984; Rempel-Clower et al., 1996; Eichenbaum & Cohen, 2003). Impairments in formation of object-location associations occur with right hippocampal or parahippocampal lesions (Milner et al., 1997; Bohbot et al., 1998; Bohbot et al., 2000; Stepankova et al., 2004). In rats, hippocampal manipulations impair performance in tasks that can be solved using episodic retrieval of specific recent trajectories, including the 8-arm radial maze (Bunce et al., 2004), delayed spatial alternation (Ennaceur et al., 1996), the Morris water maze with new platform location on each day (Buresova et al., 1986; Steele & Morris, 1999) and a task testing a sequence of spatial locations (Lee et al., 2005). Spatial memory is also impaired by lesions of the entorhinal cortex (Steffenach et al., 2005) and postsubiculum (Taube et al., 1992). Learning of spatial trajectories may be a special case of a general capacity for learning sequences within the hippocampus (Eichenbaum et al., 1999), including the sequential order of sensory stimuli (Kesner & Novak, 1982; Agster et al., 2002; Fortin et al., 2002; Kesner et al., 2002).

Many previous models of hippocampal function focus on its role in spatial navigation to goals (Touretzky & Redish, 1996; Burgess et al., 1997; Foster et al., 2000; Trullier & Meyer, 2000), but not on episodic retrieval of specific trajectories. Most previous hippocampal models that focus on encoding and retrieval of sequences (McNaughton & Morris, 1987; Minai & Levy, 1993; Treves & Rolls, 1994; Jensen & Lisman, 1996a; b; Levy, 1996; Tsodyks et al., 1996; Wallenstein & Hasselmo, 1997; Redish & Touretzky, 1998; Hasselmo & Eichenbaum, 2005; Zilli & Hasselmo, 2008c) focus on encoding associations between discrete sequential states (items or locations). However, recent data on grid cell firing in the entorhinal cortex (Hafting et al., 2005; Sargolini et al., 2006; Barry et al., 2007; Moser & Moser, 2008) suggests a different approach (Hasselmo, 2008b) in which each individual state (place) is associated with an action (the velocity coded by speed-modulated head direction cells).

This model of the episodic encoding and retrieval of trajectories can use either of two main classes of grid cell models. One class of models generates grid cells based on interference patterns (Burgess et al., 2007; Burgess, 2008). This model could use mechanisms of membrane potential oscillations shown in entorhinal neurons (Alonso & Llinas, 1989; Giocomo et al., 2007; Hasselmo et al., 2007; Giocomo & Hasselmo, 2008b; a), or could use mechanisms of stable persistent spiking (Egorov et al., 2002; Fransén et al., 2006; Tahvildari et al., 2007; Hasselmo, 2008a). The other class of models uses attractor dynamics to generate grid cell activity (Fuhs & Touretzky, 2006; McNaughton et al., 2006). The first type of model is used here, but either or both types of models could be used, because both models update grid cell position with a velocity signal from head direction cells. As shown here, a circuit mechanism using grid cells provides a substrate for encoding and retrieval of trajectories defined on continuous dimensions of space and time.

MATERIALS AND METHODS

Model of trajectory encoding and retrieval

The model presented here will consider encoding and retrieval of a trajectory of movement through the environment by an agent over time. The agent could be a human being or other mammal. The circuit model of encoding and retrieval is summarized in Figure 1. The physiological data used to justify the model has primarily been obtained from the rat, including data on entorhinal grid cells (Hafting et al., 2005; Fyhn et al., 2007; Moser & Moser, 2008), head direction cells in structures such as postsubiculum (Taube et al., 1990a; Sharp, 1996; Taube, 1998; Taube & Bassett, 2003), hippocampal place cells (O’Keefe & Burgess, 1996; 2005), and context-dependent firing in hippocampus (Eichenbaum et al., 1999; Ferbinteanu & Shapiro, 2003; Lee et al., 2006; Smith & Mizumori, 2006; Griffin et al., 2007). Analogous neural responses have been demonstrated in non-human primates (Rolls et al., 1997; Robertson et al., 1999) and humans (Ekstrom et al., 2003). The following sections describe how the model uses representations of head direction activity, entorhinal grid cell activity, and hippocampal cell activity to perform episodic encoding and retrieval of trajectories.

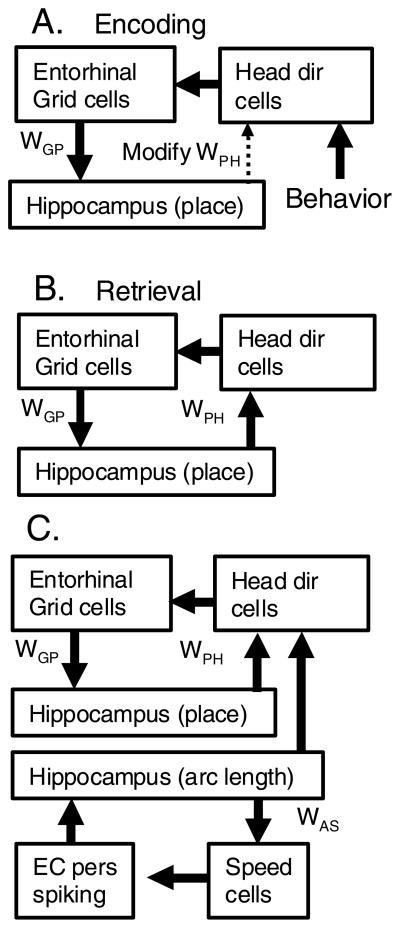
Figure 1.

Proposed circuit for episodic encoding of trajectories. A. During encoding, head direction activity is driven by external behaviour. Head direction input updates grid cells in entorhinal cortex that drive place cell firing in the hippocampus. Associations between state (place) and action (speed and head direction) are formed by strengthening synapses between place cells and head direction cells W_PH. B. During retrieval, place cells drive head direction cells via previously modified synapses W_PH. Head direction cells update grid cells that update place cells to complete the loop driving internal retrieval. C. A parallel circuit generates arc length cells due to input from persistent spiking entorhinal neurons (EC pers spike) that fire near theta frequency and are modulated by input from cells coding rat movement speed (speed cells). Interference patterns generate cells that respond according to arc length along the one-dimensional trajectory. As shown in the figure, this parallel circuit also influences speed-modulated head direction cells to influence grid and place cells.

Encoding associations between location and velocity

The model can encode the trajectory through the environment by encoding associations between location and velocity at each location. The two dimensional location of an animal at one time can be represented with the row vector x⃑ = [x y]. The trajectory through different locations over time can be represented by a sequence of vectors x⃑(t). This representation can be obtained by integration of the velocity row vector v⃑(t) = [dx/dt dy/dt]. Integrating the velocity vector over time yields the current location vector x⃑(t) at time t relative to the starting location vector x⃑₀, as follows:

$$\underset{\tau =0}{\overset{t}{\int }}\stackrel{\rightharpoonup }{v}(\tau )d\tau =\stackrel{\rightharpoonup }{x}(t)-{\stackrel{\rightharpoonup }{x}}_0.$$ (1)

The use of a velocity signal was motivated by data showing that hippocampal spiking activity during REM sleep replays not only the sequence of spatial locations coded by cells, but maintains temporal intervals (Louie & Wilson, 2001), in contrast to the compressed sequences observed during sharp wave/ripples (Skaggs & McNaughton, 1996). Coding of these temporal intervals requires the speed component of velocity in addition to direction.

Head direction cell activity

The encoding of associations between location and velocity requires a representation of velocity. Velocity includes instantaneous direction and speed. These components of velocity can be provided by neural activity coding head direction and translational speed.

Extensive experimental data describes head direction cells in the postsubiculum (dorsal presubiculum) and the anterior thalamus (Taube et al., 1990b; Taube & Burton, 1995; Sharp, 1996; Taube et al., 1996; Sharp et al., 2001; Taube & Bassett, 2003) and in deep layers of the entorhinal cortex (Sargolini et al., 2006). These neurons show selective firing when the rat is facing in a narrow range of directions. In the model, head direction activity is combined with speed modulation. This can be obtained by combining head direction activity with input from cells that are modulated by translational speed, as shown in the postsubiculum (Taube et al., 1990a; Sharp, 1996) and other associated neural structures (O’Keefe et al., 1998; Sharp & Turner-Williams, 2005; Sharp et al., 2006).

In this model, the firing of head direction cells combined with speed modulation is represented with the vector h⃑(t). The model computes the speed-modulated head direction response from the velocity vector of movement in space. These two vectors differ in the model in that the dimensions of the head direction vector are at intervals of 120 degrees, rather than using the 90 degree interval between the x and y dimensions of cartesian coordinates. The head direction vector is obtained by multiplying the velocity vector by the head direction transformation matrix: $H=\left[\begin{array}{ccc}cos({\phi }_1)& cos({\phi }_2)& cos({\phi }_3)\\ sin({\phi }_1)& sin({\phi }_2)& sin({\phi }_3)\end{array}\dots \right]$

In this matrix, φ_ι represents the selectivity of individual head direction cells with index i. This transformation essentially maps x,y coordinates into coordinates relative to dimensions skewed to the angles of head direction preference. This yields the speed- modulated head direction vector: h⃑(t)= v⃑(t)H. As the velocity vector changes over time v⃑(t), this changes the speed modulated head direction vector over time h⃑(t).

Integral of speed modulated head direction vector gives spatial location

Because head direction can be obtained from velocity by the head direction transformation matrix h⃑(t) = v⃑(t)H, this means that integration of the speed modulated head direction over time corresponds to position transformed by the same matrix H: $\underset{\tau =0}{\overset{t}{\int }}\stackrel{\rightharpoonup }{h}(\tau )d\tau =(\stackrel{\rightharpoonup }{x}(t)-{\stackrel{\rightharpoonup }{x}}_0)H$. In the model, the integration of speed modulated head direction is performed by entorhinal grid cells, and provides a mechanism for path integration (O’Keefe & Burgess, 2005; Burgess et al., 2007; Hasselmo et al., 2007; Hasselmo & Brandon, 2008).

In the figures, for the purpose of demonstrating how the entorhinal grid cells represent location, the integral of speed modulated head direction can be transformed back into Cartesian spatial coordinates. This is done by multiplying the integral of head direction activity by the inverse of the head direction transformation matrix: $\underset{0}{\overset{t}{\int }}\stackrel{\rightharpoonup }{h}(\tau )d\tau H^{-1}=\stackrel{\rightharpoonup }{x}(t)-{\stackrel{\rightharpoonup }{x}}_0$. The location coded by grid cell firing phase can be obtained from just two components of the integrated head direction, allowing use of a two component inverse matrix (Strang, 1988) as follows:

$$H^{-1}=\left[\begin{array}{cc}\hfill sin{\phi }_2\hfill & \hfill -sin{\phi }_1\hfill \\ \hfill -cos{\phi }_2\hfill & \hfill cos{\phi }_1\hfill \end{array}\right]/(cos{\phi }_{1}sin{\phi }_2-sin{\phi }_{1}cos{\phi }_2).$$ (2)

Grid cell model

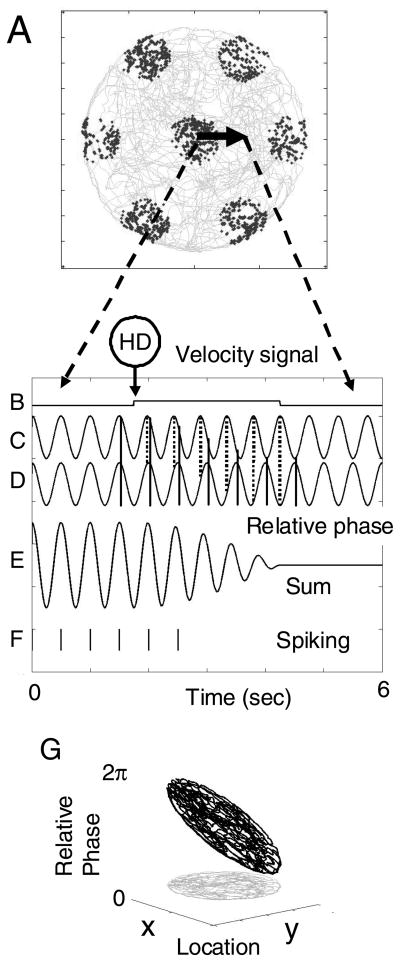
How does the model perform integration of the velocity signal? In the model, the integration necessary to keep track of spatial location is performed by shifts in the relative phase of oscillations in a simulation of entorhinal grid cells. An example of the shift in relative phase of neural oscillations is shown in Figure 2. Oscillations can be described by the instantaneous phase at each time point ϕ = 2πft, which starts with an initial phase at time zero. The relative phase used in this model is the difference between the instantaneous phase of one oscillation and the instantaneous phase of a baseline oscillation at that same time point. Figure 2 shows two oscillations that start out with relative phase of zero. A velocity input then shifts the frequency of one oscillation, causing an additional change in its instantaneous phase that results in a gradual change in relative phase compared to a baseline oscillation. Dashed lines illustrate the phase of the peak of the shifted oscillation relative to the time of the peak of the baseline oscillation with fixed frequency. This mechanism can be used to generate grid cell firing patterns as shown in Figure 2A.

Figure 2.

A. Example of movement of a virtual rat from the middle of a grid cell firing field, to a space between firing fields. B. Trace representing the velocity input from a speed-modulated head direction cell. When the rat is stationary, there is no input. When the rat moves at a constant speed, the velocity input shifts to a higher value until the virtual rat stops again. C.-D. Example of two oscillations contributing to grid cell firing. The velocity input increases the frequency of oscillation C, progressively shifting the phase of C relative to the phase of a baseline oscillation D. The dashed line shows the phase of the peak of the shifted oscillation, and the solid line shows the phase of the peak of the baseline oscillation. E. The sum of the two oscillations is large when the oscillations are in phase (constructive interference in the firing field). As the oscillation trace C shifts in phase relative to trace D, the sum of the oscillations decreases (destructive interference between firing fields). F. Spiking activity occurs when the sum crosses the threshold. This occurs in the firing field (on the left) and stops as the velocity input shifts the relative phase of the oscillations. G. Plot of the relative phase of a single oscillation used to simulate a grid cell, showing the linear relationship between relative phase and spatial location.

The integration of velocity in the model arises due to input from head direction cells depolarizing entorhinal neurons. As shown in Figure 2, depolarizing input in the model causes a shift in the frequency of membrane potential oscillations in the model, thereby shifting their relative phase. This change in relative phase of oscillations could underlie the pattern of entorhinal grid cell firing, as initially shown in the model developed by Burgess and colleagues (Burgess et al., 2005; O’Keefe & Burgess, 2005; Burgess et al., 2007). Experimental data from entorhinal cortex suggests that intracellular membrane potential oscillations could provide this mechanism of the model (Giocomo et al., 2007; Hasselmo et al., 2007; Giocomo & Hasselmo, 2008b). The model is based on data showing that entorhinal stellate cells exhibit membrane potential oscillations around theta frequency (Alonso & Llinas, 1989; Alonso & Klink, 1993; Dickson et al., 2000; Erchova et al., 2004; Giocomo et al., 2007; Engel et al., 2008; Giocomo & Hasselmo, 2008b), and these membrane potential oscillations appear with different frequencies at different membrane potentials (Giocomo & Hasselmo, 2008a). There are excitatory projections to entorhinal cortex stellate cells from the postsubiculum (Caballero-Bleda & Witter, 1993) and deep layers of entorhinal cortex (Sargolini et al., 2006), both of which contain head direction cells. Thus, active head direction cells can directly depolarize entorhinal stellate cells.

If we consider a pure velocity input, then the instantaneous phase of shifted oscillations s would depend upon the baseline frequency f and the shift in frequency due to velocity, as follows: ${\varphi }_s(t)=2\pi (ft+\underset{\tau =0}{\overset{t}{\int }}\stackrel{\rightharpoonup }{v}(\tau )d\tau )$. The relative difference in instantaneous phase between the shifted oscillation (with index s) and an oscillation with the baseline frequency (index b) will be: ${\varphi }_s(t)-{\varphi }_b(t)=2\pi (\underset{\tau =0}{\overset{t}{\int }}\stackrel{\rightharpoonup }{v}(\tau )d\tau )=2\pi (\stackrel{\rightharpoonup }{x}(t)-{\stackrel{\rightharpoonup }{x}}_0)$. As shown in Figure 2, the shift in relative phase of the oscillations depends upon the magnitude and duration of the velocity input.

The Burgess model (Burgess et al., 2007) uses the speed modulated head direction h⃑(t) to regulate different oscillation frequencies as summarized by the following equation:

$$g_{jk}(t)=\mathrm{\Theta }[\prod _i\{cos(2\pi ft)+cos((2\pi f(t+B_j\underset{0}{\overset{t}{\int }}{\stackrel{\rightharpoonup }{h}}_i(\tau )d\tau )+\overrightarrow{\varphi }{(0)}_{ik})\}]$$ (3)

In most simulations presented here, this grid cell model equation was replaced with an equation that computes the relative phase difference more rapidly, and generates denser grid cell firing and more effective place cell formation. Rather than computing the full sum of multiple oscillations, this equation directly computes the relative phase difference caused by head direction input as follows:

$$g_{jk}(t)=\mathrm{\Theta }[\prod _{i}cos(2\pi f{B}_j\underset{0}{\overset{t}{\int }}{\stackrel{\rightharpoonup }{h}}_i(\tau )d\tau +\overrightarrow{\varphi }{(0)}_{ik})]$$ (4)

Where g(t) represents the firing of a single grid cell over time. Π_i represents the product of the different dendritic oscillations receiving input from different components of the head direction vector with index i, and Θ represents a Heaviside step function output (the model has output 1 for any value above a threshold). The intrinsi oscillations change in frequency in proportion to a constant B. The oscillations each have an initial phase ϕ(0)_ik. Figure 3 shows simulations from the model of different grid cells with differences in size and spacing of fields (due to different values of B_j) and different initial phases ‘i’ and ‘k’. These differences in spacing and phase of grid cells are essential to the coding of spatial location and generation of place cell responses in the model. The grid cell spacings shown here prove effective for coding location. Even though the grid cells have repeating fields, the combination of input from different grid cells can result in place cells that are selective over large distances. This mechanism can function on a larger scale as well, as some cells receiving output from these grid cells will respond on the basis of the least common integer multiple of the spacing of a single grid cell (Gorchetchnikov & Grossberg, 2007), so that spacings of 30, 40 and 50 cm can drive selective coding at a scale of 450 cm. The scale of spatial specificity can be further expanded by including grid cells with larger spacing intervals up to 10 meters as shown in more ventral regions of entorhinal cortex (Brun et al., 2008).

Figure 3.

A. Examples of the tuning properties of head direction cells used in the model. B. Examples of firing fields produced by 45 grid cells in the model during an extended period of rat exploration in an open field environment, selected from a total of 75 grid cells in the model. The difference in spacing and size of firing fields arises from differences in the value of the constant B. The difference in spatial offset results from differences in initial phase. C. Examples of the firing fields produced by 16 place cells created in the model through random selection of inputs from groups of three grid cells.

The difference in size and spacing of grid cell firing fields depends upon differences in the effect of depolarization on intrinsic frequency that have been shown along the dorsal to ventral axis of medial entorhinal cortex (Giocomo et al., 2007; Hasselmo et al., 2007; Giocomo & Hasselmo, 2008b). The original Burgess model proposes that grid cells arise from interference, but is open to different mechanisms for the oscillations undergoing interference. The equation could represent the interaction of membrane potential oscillations within a single neuron (Giocomo et al., 2007; Hasselmo et al., 2007), or it could represent the interaction of phasic synaptic input from neurons firing rhythmically due to persistent spiking (Hasselmo, 2008a) or due to oscillatory network dynamics. The progressive scaling of neural responses proves essential to this model, and could prove to be a more general phenomenon that appears in other areas such as medial prefrontal cortex and piriform cortex.

The stability of grid cell and place cell firing over multiple sessions requires sensory input. The velocity input alone only maintains the stability of firing response during the time the velocity is present. To main stability of firing across different sessions, sensory cues are necessary to set the phase of firing to the same starting point. In the simulations presented here, the sensory cues representing specific items are associated with specific sections of the trajectory, and then these sensory cues can cue retrieval of the trajectory. This influence of sensory cues is summarized in the section on Associations with Sensory Stimuli.

Phase of grid cell oscillations maps linearly with location

The phase of oscillations changes linearly with location, as shown in Figure 2G, which plots the phase of a single modelled oscillation as the simulated rat moves along a complex trajectory through the environment. The plot of phase shows a single plane of activity that is related linearly to the two-dimensional location of the animal. Thus, the internal representation of location relative to starting position can be extracted directly from the phase of two oscillations bymultiplying the relative phase of the oscillations by the inverse of the head direction transformation matrix (H) and dividing by the beat frequency (2πfB) as follows:

$$\stackrel{\rightharpoonup }{x}(t)-{\stackrel{\rightharpoonup }{x}}_0=({\stackrel{\rightharpoonup }{\varphi }}_s(t)-{\varphi }_b(t))H^{-1}/2\pi fB.$$ (5)

This process is used to create figures showing how the activity of the model represents spatial location over time, allowing plotting of the trajectory retrieved by internal activity over time. This also indicates that for return to a familiar environment or for off-line retrieval of a trajectory, associative retrieval based on sensory cues or internal spread can cue the correct initial phase of the dendritic oscillations ϕ⃑(0), which is the initial location of the rat multiplied by the head direction transformation matrix scaled by the phase of the beat frequency 2πfB. Thus, the initial phase: ϕ⃑(0) = 2πfBx⃑₀H.

The grid cell firing fields are stable in a familiar environment, indicating that the initial phase of oscillations can be set by familiar stimuli in the environment. This setting of phase could be provided by the angle or distance of stimuli viewed in the environment.

Place cells

The phase of grid cell oscillations effectively represents location, but how can this be accessed by other neural structures? The read-out of spatial location can be provided by hippocampal place cells. Thus, the next stage of the model involves grid cell effects on place cells. Examples of place cells that can be generated by the model are shown in Figure 3.

The influence of grid cells on place cells has been modelled in different ways (Fuhs & Touretzky, 2006; McNaughton et al., 2006; Rolls et al., 2006; Solstad et al., 2006; Gorchetchnikov & Grossberg, 2007), but research has not converged on a single model. In general, the place cell representation p(t) arising from the grid cell representation g(t) in entorhinal cortex would depend upon the synaptic connectivity W_GP from grid cells to place cells.

In the model, place cells are created by selection of random subsets of three grid cells inputs and computation of the overlap in firing for these three grid cells. The place cell is assumed to fire anywhere these three grid cells fire simultaneously. This generates a spatial firing pattern for each place cell that is evaluated by taking the standard deviation of spiking location in the x and y dimension. If the standard deviation of spiking location is smaller than a previously set parameter in both dimensions, then this place cell is selected for inclusion. The input synapses from the randomly selected subset of three grid cells to this place cell are then strengthened according to the outer product equation:

$$W_{GP}=\sum \stackrel{\rightharpoonup }{g}{(t)}^T\stackrel{\rightharpoonup }{p}(t)$$ (6)

Where g⃑(t)^T is a column vector of presynaptic grid cell activity including the three currently selected grid cells, and p⃑(t) is a row vector of place cell activity with only the currently selected place cell active. This ensures that the same place cells are reliably activated in the same location dependent on the pattern of grid cell spiking induced by the phase of grid cells. Examples of place cell firing generated by the model are shown in Figure 3.

During both encoding and retrieval of an episode, the place cell row vector p⃑(t) results from the pattern of activity in the grid cell vector g⃑(t) dependent upon multiplication by the previously modified synaptic connectivity W_GP between these regions as follows:

$$\stackrel{\rightharpoonup }{p}(t)=\stackrel{\rightharpoonup }{g}(t)W_{GP}$$ (7)

Encoding of trajectory: modifying synapses between place and HD cells

How does the model encode a trajectory? This depends upon sequentially encoding associations between place cells and velocity, and later sequentially retrieving these associations. The third stage of the model plays the primary role in encoding of a new trajectory.

This encoding is performed by modification of synaptic connections between active hippocampal place cells and active head direction cells. This synaptic modification allows formation of associations between individual states (spatial locations) and the actions (movements) performed in those states.

During initial encoding of a trajectory, the activity of all cells is determined by the actual velocity of the animal during movement. The sensory input about actual speed and head direction drives the head direction cell activity vector h(t). The head direction input updates the grid cells according to the grid cell model in equation 3, and the grid cells activate individual place cells according to equation 7.

Initial encoding of a trajectory involves strengthening a set of synapses W_PH associating each location (coded by place cells p(t)) and the associated movement action performed at that location (coded by the speed modulated head direction cell vector h(t)). Thus, a trajectory is stored by formation of associations via synaptic modification of the synaptic connectivity matrix W_PH between the population of place cells p⃑(t) and the population of head direction cells h⃑(t), as follows:

$$W_{PH}(t+1)=(W_{PH}(t)+\stackrel{\rightharpoonup }{p}{(t)}^T\stackrel{\rightharpoonup }{h}(t))/2$$ (8)

This synaptic modification during encoding of the trajectory completes the circuit shown in Figure 1A & 1B that forms the basis for later retrieval of the trajectory.

The synaptic connections between place cells and head direction cells could correspond to direct projections from region CA1 of the hippocampus to the postsubiculum (van Groen & Wyss, 1990), or to polysynaptic effects of projections from the hippocampus to subiculum (Swanson et al., 1978; Amaral & Witter, 1989), combined with anatomical projections from the subiculum to the postsubiculum and medial entorhinal cortex (Naber & Witter, 1998).

Retrieval of the trajectory

The cue for retrieval can take a number of forms. The cue can be the actual current location of the rat, coded by place cells updated by grid cells. The cue could also be environmental stimuli that have been associated with a particular pattern of place cells, that can reactivate the place cell pattern. Sensory stimuli are used to cue retrieval in the examples shown later, using the mathematical representation of associations between sensory stimuli representing items or events and places, as described below in equations 15 and 16. Finally, a cue that does not correspond to the actual current stimulus or location in the environment could be activated by internal mechanisms.

Whatever the source, the place cell cue can initiate retrieval of a trajectory by activating the associated action. Thus, activity h(t) can be retrieved from the current place cell activity as follows:

$$\stackrel{\rightharpoonup }{h}(t)=\stackrel{\rightharpoonup }{p}(t)W_{PH}/\sum \stackrel{\rightharpoonup }{p}(t)$$ (9)

This forms one component of a functional loop for retrieval in the model. This loop retrieves trajectories via three stages: 1.) place cells activate associated head direction activity via matrix W_PH (equation 9), 2.) head direction cells update the phase of entorhinal grid cells (equation 3 or 4), and 3.) grid cells g(t) update place cells via matrix W_GP (equation 7). The new place cell activity then activates the associated head direction pattern, and the loop continues driving retrieval of the trajectory. This loop is summarized in Figure 1B.

Retrieval activity in the model can be summarized with the following equation:

$$p(t+\mathrm{\Delta }t)=W_{PG}g(\underset{0}{\overset{t}{\int }}{W}_{HP}p(\tau )d\tau )$$ (10)

The previous place cell activity spreads across the matrix W_HP to drive activity in the head direction cells. The grid cell function g(t) from equation 3 integrates this activity to update grid cell phase. Then the grid cell activity is transformed through a matrix W_PG representing the synaptic drive of grid cells on hippocampal place cells. Thus, the pattern of activity in these two matrices encodes the episodic memory for the trajectory in the model.

The effect of head direction on grid cell activity during retrieval requires that the head direction vector (coding a velocity vector corresponding to rat action) needs to maintain activity for the period Δt until a new place cell representation causes retrieval of the next head direction response. This is justified by graded levels of persistent firing that have been shown in intracellular recording from neurons in deep layers of entorhinal cortex slice preparations (Egorov et al., 2002; Fransén et al., 2006) and intracellular recording in the postsubiculum (Yoshida & Hasselmo, 2009). This suggests that head direction cells in the deep layers of entorhinal cortex (Sargolini et al., 2006) and postsubiculum (Taube et al., 1990a; Sharp, 1996) may be involved in encoding and retrieval of trajectories.

Note that retrieval has different dynamics from encoding, as shown in Figure 1A and 1B. During encoding, the sensory input of velocity determines activity of head direction cells, which then drive grid cells and place cells. During retrieval, sensory input does not influence the system, and head direction activity is determined internally. Awareness of this difference in dynamical state allows differentiation of retrieved events from current sensory input. The difference in dynamics could be determined by modulatory or attentional influences on the postsubiculum or deep entorhinal cortex determining the relative influence of different synaptic inputs. Encoding and retrieval of single associations or items have been modelled as occurring on different phases of each theta cycle (Hasselmo et al., 2002), but the sequential retrieval of a full trajectory requires updating of phase over multiple cycles, and might not be feasible to interleave with encoding on each cycle. This slower transition between encoding and retrieval could involve modulatory regulation of afferent versus feedback transmission by muscarinic acetylcholine receptors (Hasselmo, 2006).

Enhancement of trajectory retrieval by arc length cells

Trajectory retrieval can be greatly enhanced by combining the mechanism based on place cells p(t) with cells that code time intervals alone, or by cells that code arc length of the trajectory (Hasselmo, 2007). Cells with fixed differences in frequency will cause interference at a fixed time interval. In contrast, arc length cells will activate at a specific arc length (travel distance) along the trajectory from a given reference location. Both types of cells can be obtained in simulations by assuming that a specific item or location activates persistent spiking neurons in the entorhinal cortex. Persistent spiking neurons with fixed frequency will interfere with a baseline frequency at a specific time interval from their onset. Neurons involved in arc length could fire at a rhythmic rate that is modulated by speed but not by head direction. The modulation by speed drives neurons at frequencies that differ from the baseline frequency of other persistent spiking cells. The neurons receiving convergent input from these persistent spiking cells will fire dependent upon when the shift in frequency causes constructive interference with the baseline cells.

In mathematical terms, the mechanism of determining the activity a of arc length cells uses an interaction of two oscillations as follows:

$$a_i(t)=\mathrm{\Theta }[cos(f2\pi t)+cos((f2\pi (t+B\underset{0}{\overset{t}{\int }}s(\tau )d\tau )+{\varphi }_i(0))]$$ (11)

This resembles the model of grid cells, except that the interaction involves only two oscillations and the modulation of frequency depends on speed s(t) only rather than speed-modulated head direction. Note that each arc length cell with index ‘i’ will fire at an arc length dependent upon its initial phase ϕ_i(0). The threshold and frequency of arc length cells was set so that they would fire once during the trajectories studied here.

Simulations of arc length cells (Hasselmo, 2007) are able to replicate a number of features of the physiological data from the hippocampal formation, including the phenomenon of context-dependent “splitter” cells that fire selectively for right or left turn trials in continuous spatial alternation (Wood et al., 2000; Lee et al., 2006), the forward shifting of these splitter cells toward goal locations (Lee et al., 2006), and the context-dependent firing of neurons in a delayed non-match to position task (Griffin et al., 2007) or plus maze tasks (Ferbinteanu & Shapiro, 2003; Smith & Mizumori, 2006). A similar function could be obtained from cells with frequencies fixed in time that can code pure temporal intervals (Hasselmo et al., 2007).

A circuit composed of arc length cells, speed modulated cells and cells with oscillation frequencies modulated by speed can model sequential activation of arc length cells (Figure 1C). Analogous to the connection between place cells and head direction cells (W_PH), a connectivity matrix W_AS links the column vector a(t)^T representing arc length cell activity with the associated speed s(t) at each position along the trajectory.

$$W_{AS}=\sum _i{a}_i{(t)}^T{s}_i(t)$$ (12)

This process does not depend upon retrieval activating an accurate vector of head direction activity at each step. Instead, it only requires that retrieval activate a representation of speed. Thus, retrieval drives phase changes in one dimension along the trajectory instead of two dimensions. The activity a of arc length cells drives the activity of speed cells as follows:

$$s(t)=a(t)W_{AS}$$ (13)

Note that the arc length cell could be associated with the mean speed $S={\displaystyle \sum _{t_a}^{t_b}}s(t)/(t_b-t_a)$ on a segment of the trajectory rather than the instantaneous speed, as speed can vary considerably along a segment, and the total arc length A computed by the phase shift is a constant for each segment that results from proportional changes in mean speed and transition time, such that lower mean speed means longer transition time: A=tS.

Once an arc length cell has activated the appropriate mean speed during retrieval, the neurons representing the mean speed should modulate the oscillation frequency of another set of neurons, potentially the persistent firing cells in layer III of entorhinal cortex (Tahvildari et al., 2007). The change in frequency of these cells can update the phase of the interference giving rise to arc length cells. In simulations, the change in instantaneous phase of interference ϕ_a giving rise to arc length cell firing depends upon the speed modulation s(t) over each time interval Δt:

$$\mathrm{\Delta }{\varphi }_a(t)=\mathit{fBs}(t)2\pi \mathrm{\Delta }t$$ (14)

In addition to the associations with speed, arc length cells are concatenated with the place cell activity and represented together by the vector of place cell activity p(t) so they form associations with speed modulated head direction cells in the matrix W_PH created in equation 8. This forms associations between arc length cells and the action at the corresponding position on the trajectory. These cells and their phases are also associated with stimuli representing items or events as described in the next section.

During encoding, arc length cells i are created at regular intervals of arc length when the magnitude of interference in equation 11 crosses a threshold. In these simulations, the threshold and frequency shift of arc length cells were set so they would be active at a single contiguous segment on a trajectory. At the start of retrieval, the arc length phases are reset to the appropriate values and equation 11 is computed based on retrieved speed rather than external speed. This causes sequential activation of arc length cells to drive speed-modulated head direction and thereby drive the correct update of grid cell phase and place cell firing over time.

Associations with sensory stimuli representing items or events

The simulations included formation of associations between the place cell vector p(t) (which included the arc length vector) and a vector o(t) representing the stimulus features of individual objects or events experienced at specific positions on a trajectory. Individual objects were assigned locations near the trajectory, and the object vector was active when the agent was within a specific distance of the object location. During encoding, Hebbian modification of synapses W_PO formed associations between the stimulus feature vector o(t) (potentially arriving from the lateral entorhinal cortex) and the concatenated place cell vector p(t) (that included the arc length vector) as follows:

$$W_{PO}(t+1)=(W_{PO}(t)+\stackrel{\rightharpoonup }{p}{(t)}^T\stackrel{\rightharpoonup }{o}(t))/2$$ (15)

The retrieval of items shown in some figures resulted from the place cell vector p(t) (that included arc length cells) activating the stimulus feature vector o(t) according to:

$$\stackrel{\rightharpoonup }{o}(t)=\stackrel{\rightharpoonup }{p}(t)W_{PO}/\sum \stackrel{\rightharpoonup }{p}(t)$$ (16)

Because the place cell vector p(t) includes arc length cell activity, the matrix W_PO also allows arc length cells activated at a specific position along a trajectory to cue the retrieval of stimulus features associated with objects or events.

In some examples, retrieval was cued by a specific stimulus feature vector. This was done by using bidirectional Hebbian modification so that the inverse of W_PO would code associations between the object stimulus feature vector and the place cell vector (including arc length cells). In addition, a matrix coded associations between individual arc length activity and the vector of oscillation phases in the entorhinal grid cells. This allowed an individual stimulus feature vector to activate the associated pattern of place cells and arc length cells, and the arc length cell representation to activate the associated grid cell oscillation phase. This allowed cueing of retrieval from a specific stimulus or position along the trajectory.

Overview of simulations

The model presented here is effective for performing episodic encoding and retrieval of trajectories and items or events along the trajectory. Performance of the model was tested on a variety of trajectories. Some tests were performed with trajectories from experimental data in the Moser laboratory (Hafting et al., 2005), posted by Hafting and Fyhn on the web site at http://www.cbm.ntnu.no/. In this data, a rat moves along a winding, self-crossing trajectory as it forages for randomly scattered food pellets in a circular open field with diameter of 2 meters. In most simulations, simple trajectories were created by combinations of linear segments of movement in the environment.

At the start of retrieval, the simulation is cued with activation of the initial grid cell phase vector ϕ(0) associated with the start of the trajectory, or with a sensory stimulus that activates the grid cell and arc length cell phases at a particular point. This retrieval cue could be triggered by excitatory input from prefrontal cortex. Examples of trajectory retrieval are shown in the Figures.

RESULTS

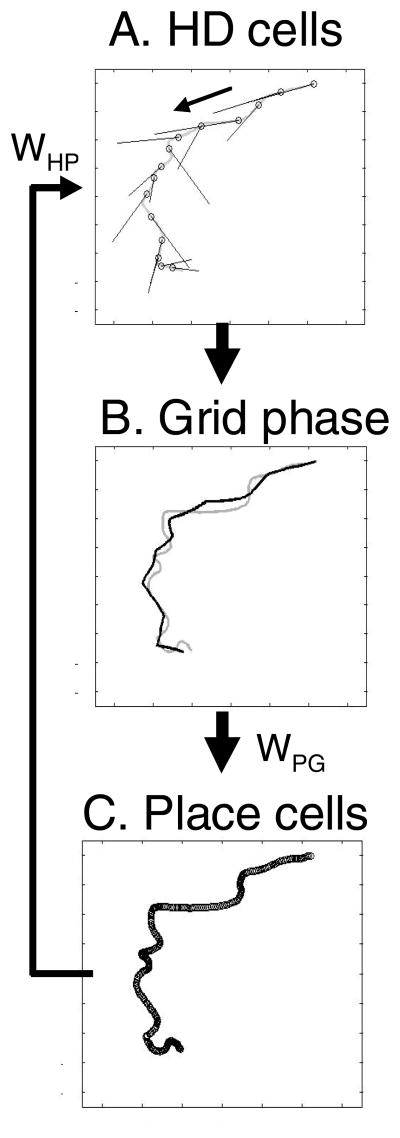
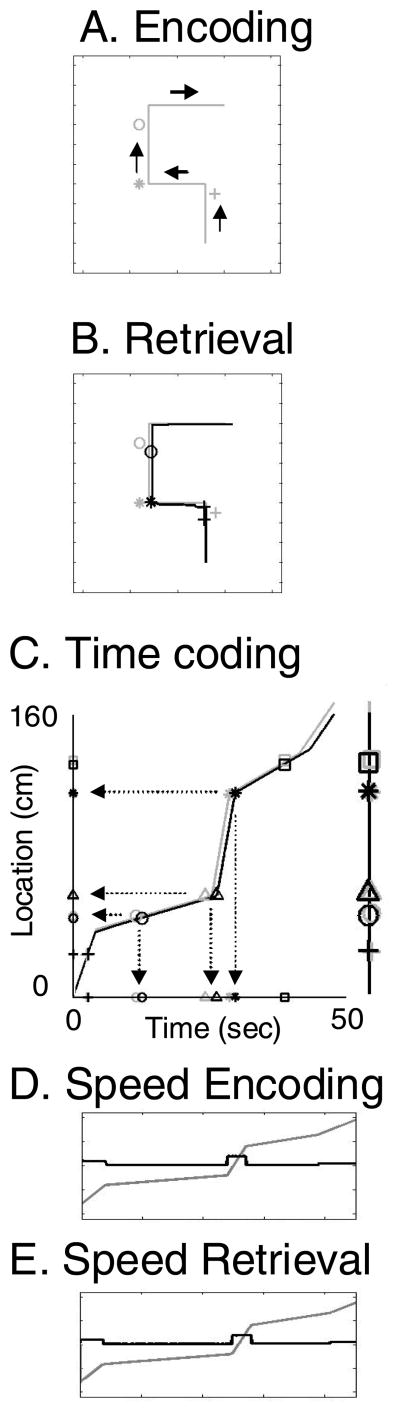
As shown in the figures, the model described here performs encoding and retrieval of complex spatial trajectories. Figure 4 illustrates the basic components of the trajectory retrieval, which includes head direction cell activity (4A), grid cell phase (4B), and place cell activity (4C). In the figure, the actual trajectory run by the rat is shown in gray. This trajectory is from experimental data obtained in the Moser laboratory (Hafting et al., 2005). The rat forages along a meandering trajectory through a circular open field environment. In Figure 4A, examples of head direction vectors activated by place cell activity at particular locations are shown as straight line segments. These head direction vectors guide the direction of shifts in grid cell phase shown by the black line in Figure 4B. The black line shows retrieval of the trajectory over the full period of retrieval, based on applying the inverse head direction transformation matrix to two components of the phase vector of an individual grid cell (corresponding to the internal representation of location during retrieval). In Figure 4C, the individual place cells activated by the phase change are shown as open circles. Each of these place cells activates an associated head direction vector shown in Figure 4A.

Figure 4.

Retrieval of a previously experienced trajectory (shown in gray). A. Examples of head direction activity vectors associated with specific locations along the trajectory during retrieval are shown as straight, black line segments. During retrieval place cells activate corresponding head direction vectors that drive the update of grid cell phase. (Arrow shows direction of trajectory). B. The location coded by the relative phase of modelled grid cells is plotted as a thick black line that follows the actual trajectory in gray. The inverse head direction transformation translates relative phase into Cartesian location. The relative phase shifts according due to the retrieved head direction vector until it activates new place cells that alter the head direction vector and change the direction of phase shift. C. The sequentially activated place cell representations are shown as open circles on the gray line representing the actual trajectory.

In simulations, during retrieval, the network can retrieve the full sequence from a cue consisting of just the initial grid cell phase representation (Figure 4B) of starting place along the trajectory (in simulations, the phase representing first location was presented using: ϕ(0) = Hx₀). This grid cell phase drives place cell activity (Figure 4C) that then activates the head direction vector h (Figure 4A) associated with that pattern of place cell activity. The head direction vector drives the update of the phase vector of the grid cells for a period of time. This occurs through the influence of the head direction activity on grid cell oscillation frequency. Eventually, the change in grid cell phase activates a new place cell representation (Figure 4C). Activation of new place cells activates the associated head direction neuron activity vector (Figure 4A), and this new head direction vector drives further update of the grid cell phase representing location. Thus, a recursive process allows place cell activity (state) to drive retrieval of the next action (speed modulated head direction) to update grid cell phase to activate the next place pattern (state) in a repetitive manner through the length of the trajectory.

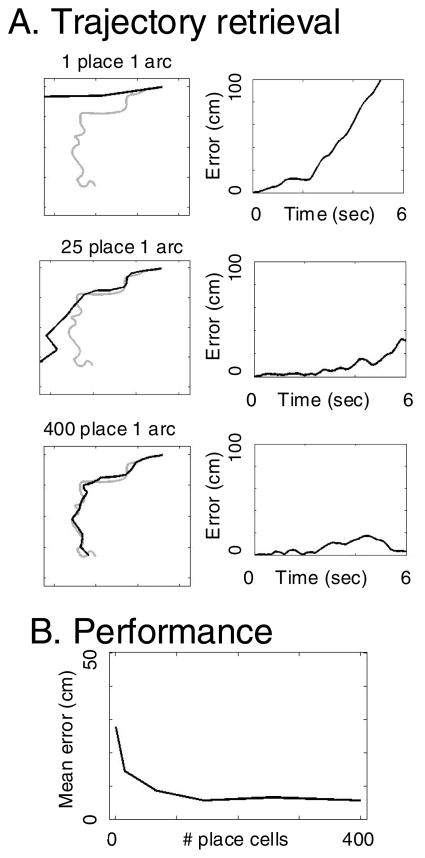
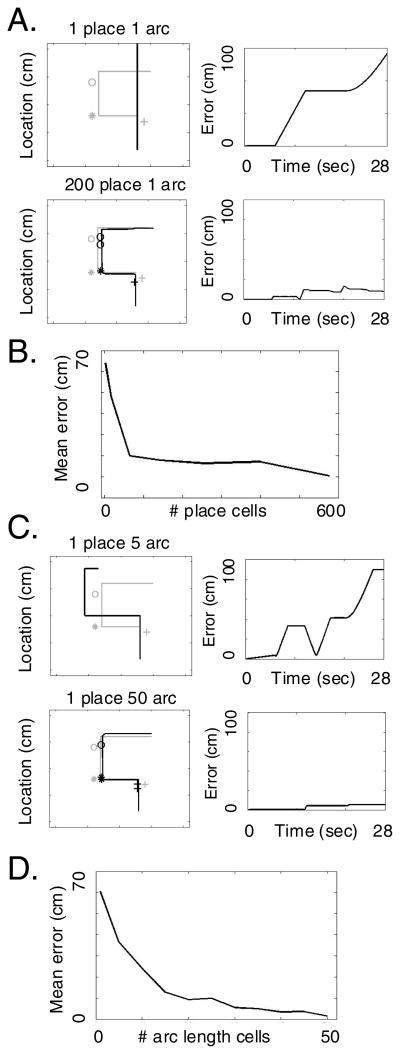
As shown in Figure 5, the network retrieves complex spatial trajectories with accuracy dependent upon the resolution of place cell representation. In the left column of Figure 5A, the black lines represents the change in grid cell phase that codes specific locations. Grid cell phase is continuous, so it does not limit resolution, but accuracy of retrieval is limited by the number of place cells. With 400 place cells, the network can retrieve the encoded trajectory reasonably well. For lower numbers of place cells, the network shows progressively poorer performance, and the internal representation of place deviates more from the actual trajectory. The right column of Figure 5A shows the error in performance over time for trajectory retrieval in each example shown on the left. Error is computed as the difference (in centimeters) between each time point of the encoded trajectory and the time point of the retrieved trajectory (note that this requires similar timing, as retrieval of the same trajectory at a different speed would cause a buildup of error). Note that with only one place cell, the trajectory rapidly deviates from the encoded trajectory, but with larger numbers the error increases more slowly. Figure 5B shows the mean error averaged across the full trajectory for different numbers of place cells (1, 16, 64, 144, 256, 400). Mean error is computed as the mean difference between each time point of the encoded trajectory and each time point of the retrieved trajectory. Mean error decreases with increasing numbers of place cells, due to the more accurate mapping between individual locations and the corresponding difference in speed-modulated head direction at each location.

Figure 5.

Trajectory retrieval with different numbers of place cells. A. Left column shows the location coded by grid cell phase during retrieval (thick black lines) relative to the actual trajectory during encoding (gray lines). Different rows show performance with different numbers of place cells along the full trajectory (for 1, 25 and 400 place cells). For fewer place cells, the retrieval diverges more from the actual trajectory. Right column shows distance over time between the retrieved and encoded trajectory. B. Mean error (distance between encoding and retrieved trajectory) plotted over time (6 secs) for different numbers of place cells in the simulation. Note the smaller error as the number of place cells increases (performance tested for 1, 16, 64, 100, 144, 256 and 400 place cells).

Figure 6 shows the encoding and retrieval of a simple trajectory with individual objects (or events) at individual points near the trajectory. In this simulation, individual items are located near specific points along the trajectory, as shown by the location of the gray symbols. The trajectory first passes the gray plus sign, then the gray asterisk, then the gray circle. During encoding, the pattern of place cell activity is associated with patterns representing individual items. During retrieval, the trajectory progressively activates place cell activity that activates vectors representing individual items. The locations where individual item representations are activated are shown with black symbols. Note that during retrieval, the network effectively retrieves first the black plus sign (at the first turn), then the black asterisk (at the second turn), and finally the black circle.

Figure 6.

Example of retrieval of events or items along simple trajectories. A. A four segment trajectory is shown as a gray line during encoding. The individual events or items experienced as sensory stimuli along this trajectory are shown as three different symbols (circle, asterisk, plus symbols) at different locations and times. B. The location retrieved by grid cell phase is plotted as a thick black line that matches the gray line showing location during encoding. Events or items are plotted as black symbols according to grid cell phase at time of retrieval, showing retrieval that matches location and time along the trajectory during encoding (plus, asterisk and circle symbols plotted in black). C. Encoding and retrieval of a separate one-dimensional trajectory (right) with five items at different locations during different running speeds (10 cm/sec to 1 cm/sec to 20 cm/sec to 2 cm/sec to 5 cm/sec). The trajectory is plotted versus location (y axis) and time (x axis). The circle and triangle are close in location, but slow running speed (1 cm/sec) means they are encoded and retrieved at a long time interval. The triangle and asterisk are far apart in location, but fast running speed (20 cm/sec) means they are encoded and retrieved at a short time interval. D.-E. The plot of running speed (black lines) during change in location (gray line) shows that running speed during encoding (D) is replicated during retrieval (E).

As shown for a different trajectory in Figure 6C, items or events can be retrieved based on the temporal intervals at which they were encountered. In this different trajectory example, five items are encountered during movement in one dimension. Because retrieval depends upon velocity, two items (circle and triangle) encountered at a slow velocity (1 cm/sec) are encoded and retrieved at a long temporal interval (12 sec, x axis) despite being close in space (12 cm, y axis). In contrast, two items (triangle and asterisk) encountered at high velocity (20 cm/sec) are encoded and retrieved at a short temporal interval (3–4 sec, x axis) despite being far apart in space (60 cm, y axis). As shown in Figures 6D and 6E, the model encodes the different velocities at different positions (going from 10 cm/sec to 1 cm/sec to 20 cm/sec to 2 cm/sec to 5 cm/sec), and effectively replicates these different velocities during retrieval. The Figure 6C simulation used 100 arc length cells. With 400 place cells, the temporal interval accuracy was similar for widely spaced items, but was poorer for the circle and triangle interval due to the resolution limit caused by place field size.

Figure 7 shows the performance for different numbers of place cells and arc length cells in this simulation. Again, increasing the number of place cells increases the performance. In addition, increasing the number of arc length cells results in better performance.

Figure 7.

A. Trajectory retrieval with different numbers of place cells. The left column shows the locations coded by grid cell phase during retrieval (black lines) relative to actual trajectory during encoding (gray lines) as well as the retrieved events (black symbols) relative to encoded events (gray symbols). Different rows show the phase performance with different numbers of place cells. Right column shows the distance between the retrieved trajectory and the encoded trajectory at each time point. B. Mean error (distance between encoding and retrieved trajectory) plotted for different numbers of place cells in the simulation. The mean error gets smaller with more place cells, but does not get better than 10. C. Trajectory retrieval with different numbers of arc length cells. D. Mean error for different numbers of arc length cells, showing better performance for high numbers of arc length cells relative to place cells.

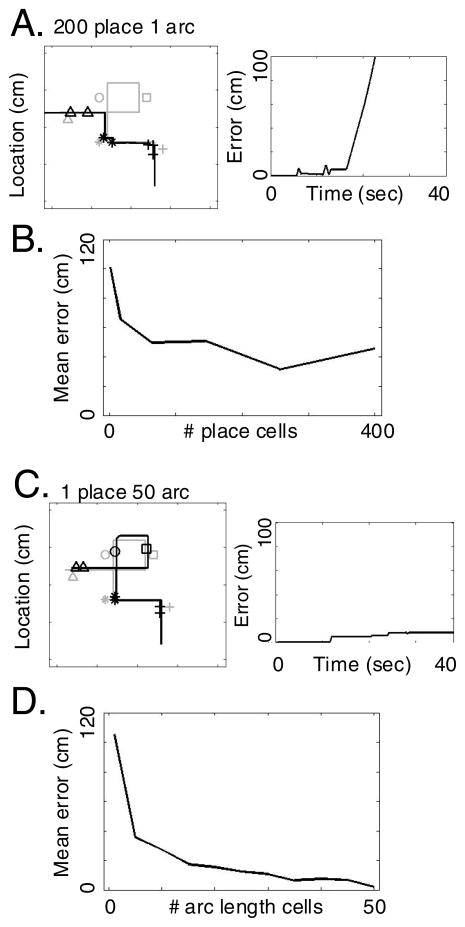
Figure 8 shows a problem faced by the encoding of the trajectory as a chain of associations between locations and actions. When there is ambiguity due to overlap in the location (state) representations, the network can miss segments of the trajectory or become trapped in loops. In Figure 8A, the network shows retrieval which misses a large loop in the upper right portion of the trajectory. This occurs because at the point of trajectory overlap, place cells are associated with two different actions (go North and go West) on the trajectory. In this example, the place cells activate the action (go West) associated with the later portion of the trajectory and causes retrieval to skip ahead to the last segment of the trajectory. Performance plotted in Figure 8B shows that this problem cannot be overcome by increasing the number of place cells. The mean error for place cells stays at a high level (poor performance) even for 400 place cells.

Figure 8.

Self-crossing trajectory. A. With place cells only, the phase representation of location (solid line on left) follows the actual trajectory (gray) until it encounters an self-crossing section. At this time, the place cells activate head direction cells going the wrong direction, missing a segment of the trajectory. On right, the performance of the network is plotted in the form of distance between transformed grid cell phase (solid line) and actual trajectory (gray) at each time point. B. Mean error with different numbers of place cells. Performance remains poor even with large numbers of place cells. C. With arc length cells, the network retrieves all components of the trajectory in order. On the left, the grid cell phase representation of location (solid line) effectively follows the full self-crossing trajectory. At the self-crossing location, arc length cells maintain context-dependent separation of the pathways because they respond to a one-dimensional measure of trajectory arc length instead of two-dimensional spatial coordinates. D. The performance of the network with different numbers of arc length cells shows much better performance than with place cells only.

Figure 8C shows a mechanism for overcoming the problem of trajectory overlap. This mechanism uses the arc length cells that provide a context-dependent signal for different portions of the trajectory, allowing differential representation of the same location depending on the preceding spatial locations. As described above, the arc length cells respond on the basis of the arc length along the trajectory rather than actual spatial position, thereby disambiguating overlapping locations occurring at different arc lengths along the trajectory. Each time a new arc length cell is activated, the arc cell activates the correct head direction cells and drives the grid cell phase to the correct spatial location. Figure 8C shows how retrieval of self-crossing trajectories is enhanced by inclusion of arc length cells. At the overlapping segment, the arc length cells activated for the early part of the trajectory are distinct from those coding the later segment, so they guide the grid cell phase through the overlapping segment and allow activation of the grid cell phase and place cells representing the loop in the upper right corner of the trajectory. Performance plotted in Figure 8D shows that mean error during retrieval with arc length cells reaches very small values when the number of arc cells reaches 50, indicating that retrieval very closely matches the originally encoded trajectory.

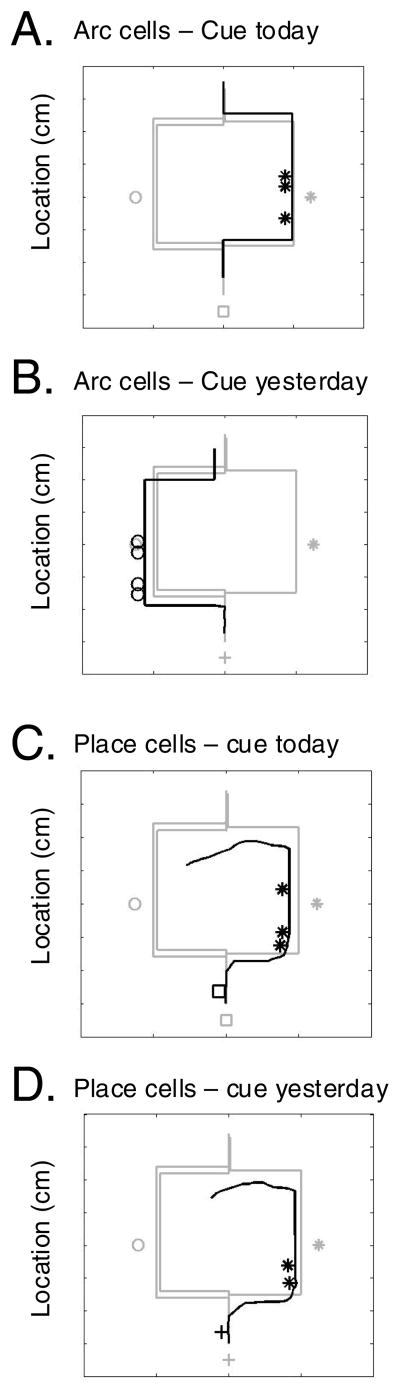
Figure 9 illustrates how the model presented here can be used to encode and retrieve common types of episodic memories, such as the location that one parks one’s car. The trajectories in Figure 9 illustrate the example of parking a car in the same parking lot on two different days. On the first day, the trajectory represents the car driving through the entrance (plus sign) and parking in a location to the left (circle). The trajectory continues with the driver walking into the building entrance (top) and later returning to the car on the left and driving back out the parking lot entrance from the left. On the second day, the trajectory represents the car driving through the same entrance but with a different cue indicating the second day (square symbol). This could indicate a different event or stimulus on that day. The trajectory then goes to a parking location on the right (asterisk). The trajectory continues with the driver walking into the building entrance (top).

Figure 9.

Episodic memory for parking location. The trajectory in gray shows the encoding of two consecutive days of parking in the same parking lot. A. Arc length cells allow selective retrieval of either day. When cued with a stimulus (square symbol) specific to only the 2nd day (cue today), the arc length cells effectively retrieve the correct 2nd day parking location (right side, asterisk symbol). B. When cued with a stimulus (plus sign) specific to only the 1st day (cue yesterday), the arc length cells effectively retrieve the correct 1st day parking location (left side, circle symbol). C. Place cells only retrieve the 2nd day. When cued with the location at the time of the 2nd day entrance to the parking lot (square symbol, cue today), the place cells effectively retrieve the 2nd day parking lot location (right side, asterisk symbol). D. When cued with the location at the time of the 1st day entrance to the parking lot (plus sign, cue yesterday), the place cells still retrieve the 2nd day parking lot location (right side, asterisk symbol), because of weakening of place to action associations with the first day trajectory.

Retrieval of the episodic memory is tested on the second day, as the driver comes back out of the building. In Figure 9A, the cue for memory retrieval is a specific event or stimulus (square symbol) that took place during the drive to the entrance on the second day (cue today). This activates reset of arc length cells that guide correct retrieval of the trajectory to the right side parking location (asterisks). Alternately, if necessary, the arc length cells can mediate retrieval of the parking location on the previous day (cue yesterday), as shown in Figure 9B. This uses a cue for memory retrieval in the form of a stimulus or event (plus sign) that took place during the drive to the entrance on the first day (yesterday). This activates reset of arc length cells that then guide retrieval of the trajectory to the left side parking location (circle).

Can the system work without arc length cells? Yes, but only for selection of the more recent trajectory. As shown in Figure 9C, a network without arc length cells, but with 400 place cells can be cued with an event from the current dat at the entrance of the parking lot, and can retrieve the recent episode (square symbol, cue today) of parking on the right (asterisk). However, a retrieval cue using an event at the entrance on the first day (plus sign, cue yesterday) does not retrieve the left side parking location (circle). Instead, the trajectory retrieval follows the recent trajectory to the right side (asterisk), as shown in Figure 9D. This occurs because the recent modification of synapses between place cells at the entrance and speed modulated head direction cells coding the right turn reduces the strength of previously modified synapses associated with the previous left turn. Thus, the entrance location is associated with the recent trajectory and cannot retrieve the older trajectory. Pure place to action associations represent temporal recency by differences in strength. In contrast, the arc length cells in this model allow distinct encoding and retrieval of the location that a car was parked on a previous day, as long as a distinct cue can be accessed to appropriately cue the reset of arc length cells.

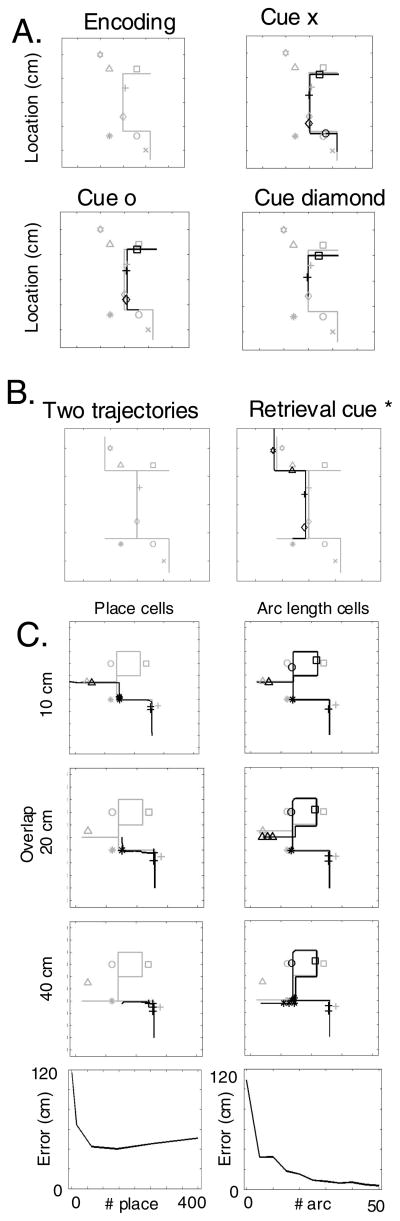
The sensory cueing of trajectory retrieval is demonstrated further in Figure 10A. This Figure shows examples of a trajectory passing multiple items. During retrieval, presentation of individual items as cues (such as the ‘x’, the ‘o’ and the diamond) can activate the associated phase and arc length cell activity, initiating retrieval of the remainder of the trajectory and subsequent items. As shown in Figure 10B, the arc length cell representation allows successful retrieval of one trajectory even if it has strong overlap with a different trajectory. The retrieval of pathways with different lengths of overlap has been addressed in Figure 10C, which shows that arc length coding is effective for retrieving trajectories that overlap for extended segments of 10 cm, 20 cm or 40 cm, whereas place cell coding breaks down for all types of overlap.

Figure 10.

A. Encoding and retrieval of a trajectory (gray line) passing multiple items (gray symbols). Sensory input vectors representing individual items (cue items ‘x’, ‘o’ or diamond) can cue initiation of retrieval at different points along the trajectory, after which the remainder of the trajectory and associated items are retrieved. B. The left side shows two overlapping trajectories learned by the network. The right side shows successful retrieval of one of these overlapping trajectories. C. Retrieval with different amounts of overlap of trajectories. Each row shows performance with 400 place cells or 50 arc length cells. Top row has overlap of 10 cm, middle is 20 cm and bottom is 40 cm overlap. Bottom plots show performance for 20 cm of overlap.

DISCUSSION

The model presented here uses grid cells, place cells, head direction cells and a set of context-dependent cells termed arc length cells to encode and retrieve neural activity associated with specific spatiotemporal trajectories through the environment. During encoding, external input drives head direction activity that drives entorhinal grid cell and hippocampal cell activity. Synaptic modification strengthens connections between hippocampal place cells and head direction cells. During retrieval, the phase of neural activity in grid cells represents the retrieved spatial state of the animal, which can be read out through the influence of grid cells on the activity of hippocampal place cells. The spread across modified synapses from place cells to head direction cells represents retrieval of the action associated with each state. In addition, the spread of activity from hippocampal place cells to neurons representing objects or events allows retrieval of the specific location and timing of each item or event. The temporally structured replay of memory shown here is an important property of episodic memory (Eichenbaum & Cohen, 2001; Tulving, 2002). Reminiscence reactivates the sequential events and locations in an episode with information about time intervals and relative spatial locations.

The model draws on recent physiological data to provide important functional components of the circuit. These mechanisms use phase coding that could arise from two different intrinsic cellular mechanisms in entorhinal cortex. The phase coding could depend upon shifting the baseline frequency of persistent spiking activity (Hasselmo, 2008a) that has been shown as an intrinsic mechanism of pyramidal cells in the entorhinal cortex (Egorov et al., 2002; Fransén et al., 2006; Tahvildari et al., 2007; Yoshida et al., 2008). The phase coding could also depend upon the phase of intracellular membrane potential oscillations that have been shown as an intrinsic mechanism in stellate cells in entorhinal cortex (Alonso & Llinas, 1989; Giocomo et al., 2007; Giocomo & Hasselmo, 2008b). In both cases, the voltage-dependent shift in frequency shifts the phase of grid cells, allowing continuous retrieval of a trajectory until the next closest spatial state is activated in the form of new place cell activity. As shown in the figures, complex trajectories can be encoded and retrieved accurately, depending on the resolution of the place cell representation.

This framework can be enhanced by the mechanism of arc length cells. Arc length cells respond on the basis of arc length of the trajectory from the most recent reset location. This allows disambiguation of retrieval at locations where trajectories overlap and more than one head direction (action) has been associated with a particular spatial state (place cell activity). In this case, the arc length activity drives the correct head direction activity or object representation dependent upon the arc length of that place from the location where arc length oscillations were most recently reset.

As shown in the figures, the model can retrieve multiple different events or items at particular positions along a trajectory, and individual events or items can cue retrieval from a particular position on the trajectory. The coding of associations with stimulus feature vectors representing items or events could depend upon convergence of two different pathways. The medial entorhinal cortex could provide a temporal and spatial context that can be associated with specific objects that arrive via input from the lateral entorhinal cortex and postrhinal cortex (Hargreaves et al., 2005; Eichenbaum & Lipton, 2008).

This model uses interference between different oscillations or rhythmic spiking activity with different phases to code the location or timing of individual movements on a trajectory and to encode associations to specific sensory stimuli. This use of oscillations has some similarities to the use of multiple oscillators for encoding the order of words in serial recall tasks (Brown et al., 2000). In addition, this use of oscillations resembles the use of oscillations for encoding temporal intervals in models of the timing of behavioural responses (Miall, 1989; Matell & Meck, 2004).

This model provides explicit physiological mechanisms for elements of episodic memory, including the perception of mental time travel during the retrieval of a prior episodic memory. The model presented here has the capacity to retrieve multiple continuous dimensions of an experience, including an explicit representation of the time duration during and between individual events in an episode, as well as the sense of spatial location, heading direction and movement speed. Though this has not been quantified extensively, subjective experience of episodic memories includes a sense of heading direction and movement speed. For example, the memory of a recent social event could include turning toward individual people, and moving through rooms with a particular direction and speed.

There are limits to the capacity of such a system to encode and retrieve multiple overlapping trajectories in the same environment. As shown in the figures, self-crossing trajectories cannot be accurately encoded by place cells, even when the number of place cells is large. Arc length cells can code self-crossing trajectories, but the number of arc length cells required will increase with the length of the trajectory. This suggests that trajectories are more effectively encoded in novel or distinctive environments, whereas in a highly familiar environment memory is usually best for the most recent trajectory or the earliest trajectories.

The use of oscillatory interference to encode episodes illustrates the strength of this mechanism for encoding a wide range of phenomena in continuous time and space. The same techniques could potentially be used for encoding of general perceptual features, such as computation and prediction of stimulus change (i.e. the trajectory of a baseball, or the frequency transitions in speech signals), or the proprioceptive tracking of limb movements. The baseline frequency used here is in the theta range, but similar mechanisms of oscillatory interference could function in other bands, such as the gamma frequency range.

As shown here, the cellular mechanism of persistent spiking (Egorov et al., 2002; Fransén et al., 2006; Tahvildari et al., 2007; Yoshida et al., 2008; Yoshida & Hasselmo, 2009) could contribute to the encoding and retrieval of episodes. Persistent spiking at stable frequencies (Egorov et al., 2002; Fransén et al., 2006) could hold states such as locations or items (Hasselmo, 2008a), allowing updating of these states by action inputs. Persistent spiking could also hold actions for updating of states (Hasselmo, 2008a). For example, persistent spiking in postsubiculum (Yoshida & Hasselmo, 2009) could hold head direction activity for updating of internal states. Functional imaging indicates a role for persistent activity in entorhinal and perirhinal cortex in the encoding of items for subsequent memory (Schon et al., 2004; Schon et al., 2005; Hasselmo & Stern, 2006).

The framework described here has advantages over models that encode trajectories or sequences as state to state associations. For example, several models replicate theta phase precession by strengthening excitatory synapses between place cells activated in a trajectory (McNaughton & Morris, 1987; Minai & Levy, 1993; Treves & Rolls, 1994; Jensen & Lisman, 1996a; b; Levy, 1996; Tsodyks et al., 1996; Wallenstein & Hasselmo, 1997; Hasselmo & Eichenbaum, 2005). These models can retrieve sequences, but they suffer from difficulties in timing the retrieval. The time scale of synaptic transmission is much faster than the time scale of initial activation of the neurons, resulting in very rapid sequence retrieval relative to behavioural time scales. In contrast, in this model, the state represented by place cells activates an action represented by persistent spiking in head direction cells (Yoshida & Hasselmo, 2009). This allows a transition in continuous phase space between discrete places, with variable timing of intervals between discrete locations. Thus, this network could provide temporally structured replay of neural activity.

The temporally structured replay shown in this model provides a potential mechanism for the neurophysiological evidence of temporally structured replay during rapid eye movement (REM) sleep (Louie & Wilson, 2001). In addition, this model generates the prediction that head direction cells during REM sleep should also show temporally structured replay of spiking activity observed previously during waking. This prediction has been tested in neural spiking in the postsubiculum during REM sleep. The model also predicts that replay of overlapping or self-crossing trajectories should show selectivity for the traversed pathway. Modulation of the magnitude of the synaptic strength W_HP or the frequency of oscillations could scale the intervals between sequential activation of discrete locations, allowing replay at fast rates as seen during slow wave sleep (Skaggs & McNaughton, 1996) or during waking (Foster & Wilson, 2006; Johnson & Redish, 2006; Diba & Buzsaki, 2007).

The simulations presented here provide a mechanism for retrieval of trajectories in continuous space that could be incorporated in models of memory guided behaviour. Previous work on memory guided behaviour in a spatial alternation task (Hasselmo & Eichenbaum, 2005) used episodic retrieval of sequences of discrete states (locations), due to associations between cells representing individual places. That model used retrieval at each location, but was extended with a model using selection of memory actions such as “encode” and “retrieve” to perform memory functions only when necessary for task performance (Zilli & Hasselmo, 2008c). The selection of memory actions could guide the selection of activity to initiate retrieval as used in the present paper. This framework could allow interaction of different types of memory for solution of tasks (Zilli & Hasselmo, 2008b; a). For example, the active maintenance of a phase representation can be seen as working memory. This active maintenance of phase could cue episodic retrieval (working memory cueing episodic memory), or could hold the output from prior episodic retrieval. The mechanisms presented here could also be used to integrate phase during the trajectory from a given place to a given goal. The integrated phase could be associated with specific place cells to code the head direction to the goal location from individual places (Hasselmo and Brandon, 2008).

This process is not necessarily limited to memory encoding and retrieval. If the actions are induced by prefrontal input rather than hippocampal feedback, then these mechanisms could allow mental time travel during planning of imaginary or future trajectories through a known environment. The process could also prove useful for building up a longer term semantic representation of a trajectory, such as a the route from home to work followed by a commuter. The mechanisms of encoding for a single trajectory shown here could build up over multiple experiences of the trajectory to provide progressively higher resolution memory for the trajectory.

In this framework, lesions of the hippocampus would impair the capacity for sequential retrieval of episodic memories. By preventing retrieval of previous trajectories, this could cause impairments in the 8-arm radial maze (Bunce et al., 2004), delayed spatial alternation task (Ennaceur et al., 1996) and the Morris water maze using a new platform location on each day (Buresova et al., 1986; Steele & Morris, 1999). Loss of entorhinal grid cells or postsubiculum head direction cells would prevent continuous update of spatial location during retrieval, thereby accounting for impairments of spatial behaviour after lesions of the entorhinal cortex (Steffenach et al., 2005) and postsubiculum (Taube et al., 1992).