Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2009 Nov 30;113(51):16384–16392. doi: 10.1021/jp9054582

Solvent Effects on Ionization Potentials of Guanine Runs and Chemically Modified Guanine in Duplex DNA: Effect of Electrostatic Interaction and Its Reduction due to Solvent

Satoshi Yokojima 1,†,‡, Norifumi Yoshiki 1,‡, Wataru Yanoi 1,‡, Akira Okada 1,*,‡
PMCID: PMC2825092  PMID: 19947608

Abstract

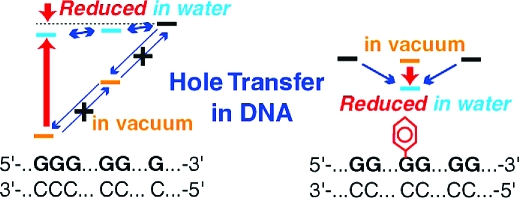
graphic file with name jp-2009-054582_0004.jpg

We examined the ionization potential (IP) corresponding to the free energy of a hole on duplex DNA by semiempirical molecular orbital theory with a continuum solvent model. As for the contiguous guanines (a guanine run), we found that the IP in the gas phase significantly decreases with the increasing number of nucleotide pairs of the guanine run, whereas the IP in water (OP, oxidation potential) only slightly does. The latter result is consistent with the experimental result for DNA oligomers in water. This decrease in the IP is mainly due to the attractive electrostatic interaction between the hole and a nucleotide pair in the duplex DNA. This interaction is reduced in water, which results in the small decrease in the IP in water. This mechanism explains the discrepancy between the experimental result and the previous computational results obtained by neglecting the solvent. As for the chemically modified guanine, the previous work showed that the removal of some solvent (water) molecules due to the attachment of a neutral functional group to a guanine in a duplex DNA stabilizes the hole on the guanine. One might naively have expected the opposite case, since a polar solvent usually stabilizes ions. This mechanism also explains this unexpected stabilization of a hole as follows. When some water molecules are removed, the attractive electrostatic interaction stabilizing the hole increases, and thus, the hole is stabilized. In order to design the hole energetics by a chemical modification of DNA, this mechanism has to be taken into account and can be used.

1. Introduction

It is important to understand the mechanism of the oxidatively generated damage to guanines in DNA. The reason is that the damage causes mutations and cancer, and it is an obstacle to use DNA as a molecular device.(1) In the case of the damage due to a one-electron oxidant, the reactions occur as follows. First, a hole is injected into DNA. It then migrates to a nearby guanine base, because a guanine base has the lowest ionization potential (IP) among the DNA bases. The trapped hole escapes to other guanine bases or triggers the chemical reactions which cause the damage to the guanine.2−8 It was found that the longer guanine run in a duplex DNA is damaged more than the shorter ones.9−17 It was also reported that the attachment of a phenyl group to a guanine suppresses the damage not only at the phenylated guanine but also at nearby guanines in the duplex DNA.(18) To understand the mechanism underlying these experimental results, we need to know how the hole transfer reactions occur in DNA. One of the important parameters determining the charge transfer rate is the free energy difference between the reactant and the product. Thus, in the present work, we theoretically analyzed the IP of duplex DNA corresponding to the free energy of the transferring hole on the duplex DNA. Since the above experiments were carried out in the presence of a solvent (water), we took into account the solvent; this turned out to be crucial to understanding the above experimental results.

One of our goals is to resolve the discrepancy between the theoretical results19,20 and the experimental one;(21) these results are about the free energy dependence of the transferring hole on the length of the guanine runs. The IPs (corresponding to the free energy of the hole) obtained by the ab initio Hartree−Fock (HF) molecular orbital (MO) calculations19,20 are smaller for the longer guanine run. These calculations were performed for the DNA oligomers without a backbone in the gas phase. This result of the IP is in qualitative agreement with the experimental results9−17 as follows. If the free energy of the hole on the longer guanine run is smaller, then the probability of the hole to be there is larger and thus the longer one is damaged more. However, the calculated IP difference between G and GG (GGG) of 0.47 (0.68) eV19,20 is too large compared to the corresponding free energy difference of 0.052 (0.077) eV obtained from the time-resolved data for DNA oligomers in water.(21) That is, if the previously calculated value was close to the real value, then the hole transfer from the longer guanine run to the shorter one hardly occurred and thus the distribution of the damage in the DNA would become considerably different from the real one. Here, we neglect the entropy difference in the free energy difference between the reactant and the product of the hole transfer reaction by assuming that the potential functions of the reactant and the product are harmonic around the equilibrium structures and their second derivatives are similar.

Another question to be answered in the present paper is about the effect of the chemical modifications of DNA oligomers on the hole transfer reactions. When a neutral functional group is attached to a guanine in a DNA oligomer in water, the nearby water molecules are removed. This removal was found to reduce the free energy of the hole on the guanine.(22) This might sound paradoxical. That is, since a polar solvent usually reduces the free energies of ions, the removal of nearby solvent molecules might be expected to increase the free energy of the hole. We will give the mechanism which explains this result. It will turn out that this mechanism also explains the discrepancy mentioned in the previous paragraph. The free energy reduction of the hole mentioned above was confirmed by the ab initio and the semiempirical HF calculations for various neutral functional groups, i.e., the phenyl, the benzyl, and the tert-butyl groups with the two structures of the typical B-DNA structures.(22) This free energy reduction was observed even when the phenyl group attached was replaced by an artificial H2 cluster mimicking the solvent-accessible surface of the phenyl group. Thus, it is considered that this free energy reduction is due to the removal of the solvent molecules.(22) This result agrees with the experimental one(18) that the damage to guanines near the phenylated guanine is suppressed as follows. The phenyl group attachment to a guanine reduces the free energy of the hole on it, and thus, the hole is trapped there; therefore, the guanines near the phenylated guanine are less damaged.

We briefly review the relevant works on the electrostatic interaction and the solvent effects on DNA, since they turned out to play crucial roles in the present cases. The electrostatic potential in DNA has been studied for many years in order to understand its reaction with other molecules.23,24 It was pointed out that the effect of the electrostatic interaction on the IP of a guanine doublet is important.(25) As for the solvent effects, the hydration effect on the IP of the small fragments of DNA, namely, the Watson−Crick (WC) base pairs, nucleotides, and a phosphorylated dinucleotide, was investigated.26−28 Recently, the solvent effects on the much-larger-sized DNA were investigated.29−34 These studies showed the importance of the solvent effects on DNA.

In the present work, we calculated and analyzed the IP of the duplex DNA by taking into account the solvent, where this IP corresponds to the free energy of the hole on the duplex DNA. On the basis of the same mechamism, we answer the above two questions as follows. Since the electrostatic interaction between the hole and a nucleotide pair in the duplex DNA is attractive, the IP of the longer guanine run is smaller than that of the shorter one. However, this attractive interaction is reduced in water, which results in the small difference of the IP between the longer guanine run and the shorter one in water. This mechanism explains why the theoretical results without taking into account the solvent19,20 were too large compared to the experimental one.(21) The effect of the chemical modification is understood as follows. A neutral functional group attached to a guanine in a duplex DNA in water expels the nearby water molecules which reduce the electrostatic interaction. Thus, the attractive electrostatic interaction stabilizing the hole on the guanine increases and the hole is stabilized. This is why the free energy of the hole decreases when nearby water molecules are removed. This is counterintuitive, since a polar solvent is usually expected to stabilize ions.

2. Methods

We calculated the IP of the duplex DNA oligomers in the gas phase and in water as follows.

We constructed the B-DNA structures with backbones using the 3DNA v1.5 program.35,36 We used the two structures of the typical B-DNA structures, namely, the 55th(37) and the 4th(38) fiber models, to ensure that the result is independent of the structure deviation within the B-DNA structure. Otherwise, we used only the 55th fiber model. The structural differences between the two models are mainly in the sugar−phosphate backbone. Their global structures are similar; the helical twists are 36° for both of the two models and the rises are 3.39 and 3.38 Å for the 55th and 4th fiber models, respectively. These model structures are determined by X-ray diffraction, and thus, the coordinates of the H atoms are missing. Therefore, we added these coordinates and optimized them using the electronic structure calculations described in the next paragraph. We calculated these optimized coordinates for DNA oligomers, which are in the neutral state in vacuum and in water, and in the ionic state in water.

We calculated the electronic structures using the Austin Model 1 (AM1) Hamiltonian(39) implemented in the MOPAC2002 v1.0 program.(40) (We did not use the linear scaling calculation program MOZYME.) We included the solvent as the dielectric continuum, namely, the conductor-like screening model (COSMO)41,42 with the dielectric constant of water, 78.4, and the vdW parameters optimized for the density functional theory.(42) These optimized parameters are expected to produce better results than the default ones implemented in the software;(43) this expectation was confirmed in the case of the IP of the nucleosides.(22) We calculated the IP as the difference between the total energies after and before one electron is removed. For these calculations, we used the unrestricted HF (UHF) method. There was no spin contamination in the case of an even number of electrons. In the case of an odd number of electrons, the spin contamination was less than about 3% and thus the error in the energy due to the spin contamination was calculated to be less than a few tenths of an eV. As for the IP in water, we calculated it for DNA oligomers in the neutral state and the ionic state; in the latter state, the phosphate backbones are completely ionized. The actual IP in water is considered to be between these IPs, since the ionic (neutral) state corresponds to the case when the counterions are far away from (very close to) the DNA oligomers.(22)

As for the validity of the method, we calculated the relative IPs of the nucleosides in water (the relative OPs), and compared them to the experimental result.(44) The root-mean-square (rms) deviation between the computational and the experimental result(44) was 0.14 V (Table 1), which is similar to the experimental error.(44) In addition, the method described here was successfully used to calculate the IPs and the electron affinities of nucleic acid bases in the gas phase,45,46 where the rms deviations between the computational results and the experimental ones47,48 are 0.12 and 0.20 eV, respectively. The IPs calculated by the method include the reorganization energies due to the relaxation of the solvent and H atoms of the solute but not that due to the relaxation of the heavy atoms of the solute. Our conclusions are not affected by this approximation, as will be discussed in section .

Table 1. OPs (V) of Nucleosides Relative to OP of Deoxyguanosine.

  AM1a experimentb
dA 0.23 0.47
dC 0.59 0.65
dT 0.63 0.62
Open in a new tab
a

The geometries are fully optimized.

b

In the experiment,(44) the solvent was acetonitrile. The solvation energy for the solvent change acetonitrile/H2O is calculated to be −0.02 eV using the Born equation,(44) and thus, the correction to the relative OP for the solvent change is negligible.

In order to interpret the IPs obtained by the electronic structure calculations, we used the net charges and dipoles of atoms and the electrostatic interaction calculated from them. We simply denote their distribution by the charge distribution. The charge distribution of the hole is defined as the difference in the charge distributions between after and before the removal of an electron.

3. Results

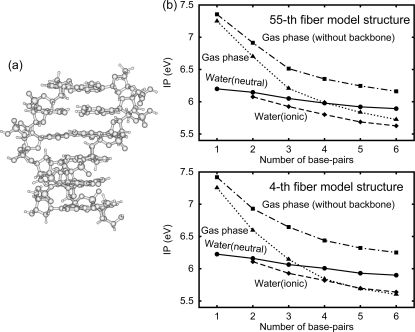
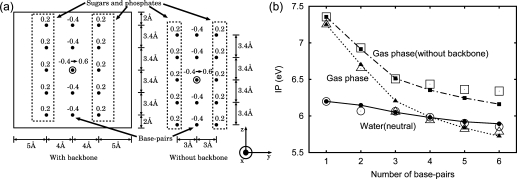
We calculated the IP of the DNA oligomer d[5′-(G)N-3′]·d[3′-(C)N-5′] (Figure 1a); we found that the IP in the gas phase significantly decreases with the increasing number of base pairs, N, whereas the IP in water (or OP) only slightly does (Figure 1b). The decrease in the IP in the gas phase from N = 1 to 3 is more than about 1 eV, but that in water is less than 0.2 eV. The latter result is consistent with the experimental result for the DNA oligomers in water.(21) The difference between the IP decreases in the gas phase and in water is much larger than the rms deviation (0.14 V) between the computational and the experimental results obtained in section . The values of the IPs in the gas phase rapidly decrease for N ≤ 3 and converge for N ≥ 5 or 6. The IP in the gas phase decreases more strongly than that without a backbone. About 90% of the charges of the hole is in a certain guanine and 5% is in the sugar covalently bonded to this guanine both in the gas phase and in water. We confirmed the above results using the two structures of the typical B-DNA structures. Note that the actual IP in water is between the solid and dashed lines, as described in section .

Figure 1.

Figure 1

Open in a new tab

(a) The structure of the duplex DNA d[5′-(G)6-3′]·d[3′-(C)6-5′]. (b) The IP of the DNA oligomer d[5′-(G)N-3′]·d[3′-(C)N-5′] as a function of the number N of base pairs for the 55th fiber model structure and the 4th fiber model structure, as indicated. Solid line with closed circles: the DNA oligomer in the neutral state in water. Dashed line with closed diamonds: the one in the ionic state in water. Dotted line with closed triangles: the one in the gas phase. Dot−dashed line with closed squares: the one without a backbone in the gas phase.

We calculated the IP of the DNA oligomers, d(5′-AAGAA-3′)·d(3′-TTCTT-5′) and d(5′-AGGGA-3′)·d(3′-TCCCT-5′), where the lengths of the guanine runs are different but the total number of base pairs is fixed; we again found that the IP difference between the two sequences in water, 0.11 (0.10) eV, is smaller than that in the gas phase, 0.21 (0.15) eV, for the 55th fiber model (the 4th fiber model).

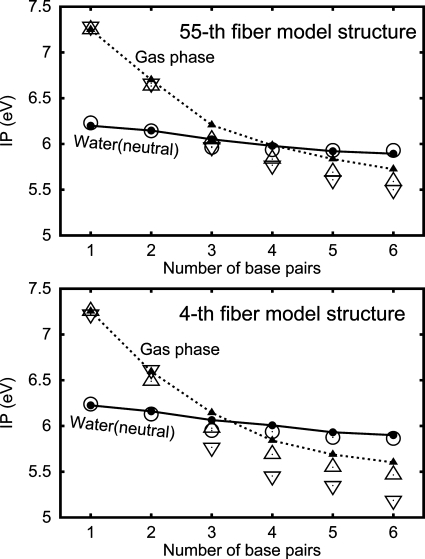
As shown in Figure 2, the IPs calculated above (the closed symbols) are close to the electrostatic energy of the hole both in the gas phase (the open triangles) and in water (the open circles). It is also shown that this energy in the gas phase decreases more strongly when we replace the charge distribution of the DNA oligomer in the gas phase by that in the neutral state in water (open inverted triangles). We define the electrostatic energy of the hole as the electrostatic interaction between the hole and all atoms except for the atoms of the guanine where the hole is localized plus a constant; this constant is such that the value of this electrostatic energy coincides with the IP in the gas phase for N = 1. In the case of the DNA oligomer in water, we added the electrostatic interaction between the hole and the water; we obtained this interaction as the dielectric energy,(49) which is considered to be the free energy but not the energy. We neglected the charge distribution of the hole outside the guanine where the hole is localized. We used the charge distribution after the removal of an electron as the charges which interact with the hole. We confirmed the above results using the two structures of the typical B-DNA structures.

Figure 2.

Figure 2

Open in a new tab

Comparison of the electrostatic energy of the hole (defined in the text) with the IP of the DNA oligomer d[5′-(G)N-3′]·d[3′-(C)N-5′] as a function of the number N of base pairs for the 55th fiber model structure and the 4th fiber model structure, as indicated. The symbols and lines are the same as those in Figure 1b except that the open symbols denote the electrostatic energy of the hole. Open circles: the one in the neutral state in water. Open triangles: the DNA oligomer in the gas phase. Open inverted triangles: the DNA oligomer in the gas phase but with the charge distribution of the DNA oligomer in the neutral state in water.

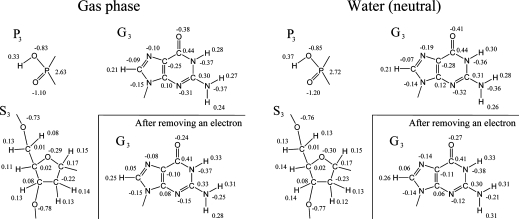
To understand the electrostatic interactions in the DNA oligomers, we calculated the charge distributions of the DNA oligomer d[5′-(G)5−3′]·d[3′-(C)5-5′] in the neutral state in the gas phase and in water (Figure 3); we found that the bases and sugars have negative partial charges and the phosphates have positive partial charges both in the gas phase and in water (Figure 4). (The phosphate backbones in the neutral state are not ionized.) About 90% of the charges of the hole is in a certain guanine both in the gas phase and in water, as described earlier. The DNA oligomer in water is more polarized than that in the gas phase. We observed the same features in other sequences of the DNA oligomers (not shown).

Figure 3.

Figure 3

Open in a new tab

Charge distributions in the DNA oligomer d[5′-(G)5-3′]·d[3′-(C)5-5′] in the neutral state in the gas phase and in water, as indicated. The numbers are the net charges (au) of atoms. G, C, S, and P denote guanine, cytosine, sugar, and a part of the phosphate, respectively. The subscripts are the residue sequence numbers.

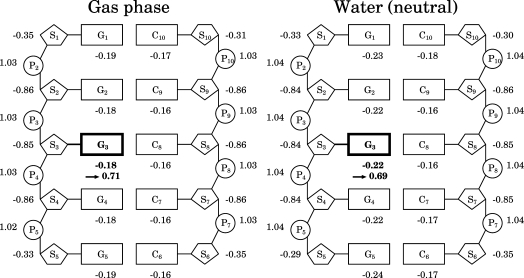
Figure 4.

Figure 4

Open in a new tab

Simplified charge distributions in the DNA oligomer d[5′-(G)5-3′]·d[3′-(C)5-5′] in the neutral state in the gas phase and in water, as indicated. Same as in Figure 3 except that the net charges of the fragments are shown. The fragment from which the largest fraction of an electron is removed is shown by the bold fonts and bold lines. The net charge of the fragment after removing an electron is indicated by an arrow. The fragments of sugars and bases are divided at the N9−C1′ bond for guanines and the N1−C1′ bond for cytosines. The fragments of the phosphates and sugars are divided at the P−O5′ and P−O3′ bonds. Thus, S2 and P2 denote C5H8O3 and PO2H, respectively.

We calculated the IP of the DNA oligomers with other sequences, where a guanine is embedded in the center of the contiguous adenines or thymines, and obtained the same result with that of d[5′-(G)N-3′]·d[3′-(C)N-5′] (Figure 5). That is, the IP significantly decreases with the increasing N in the gas phase, whereas it does only slightly in water. The values of the IP decreases are slightly smaller than the corresponding values of the contiguous guanines in Figure 1b, both in the gas phase and in water.

Figure 5.

Figure 5

Open in a new tab

IP of the DNA oligomers as a function of the number N of base pairs, where a guanine is embedded in the center of the contiguous adenines or thymines. The symbols and lines are the same as those in Figure 1b. (a) N = 1, 2, 3, 4, 5, and 6 are for d(5′-G-3′)·d(3′-C-5′), d(5′-AG-3′)·d(3′-TC-5′), d(5′-AGA-3′)·d(3′-TCT-5′), d(5′-AAGA-3′)·d(3′-TTCT-5′), d(5′-AAGAA-3′)·d(3′-TTCTT-5′), and d(5′-AAAGAA-3′)·d(3′-TTTCTT-5′), respectively. (b) Same as in Figure 5a except that A and T are exchanged in the sequences of the DNA oligomers.

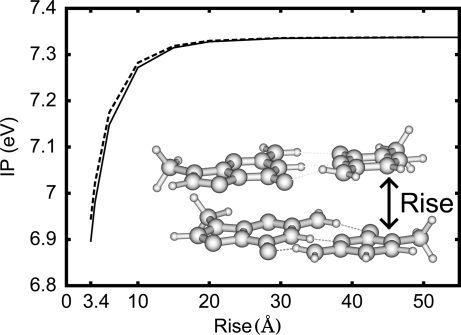
To understand the dependence of the obtained IPs on N, we calculated the IP of the system made of two G·C base pairs (the inset in Figure 6) as a function of the rise R; we found that the IP of this system (the solid line in Figure 6) is close to the IP of the single base pair plus the electrostatic interaction between the hole and the base pair where the hole does not reside (the dashed line in the same figure). The values of the IP rapidly increase for R ≤ 5 Å and converge for R ≥ 10 Å. We used the method described in section except that we removed the sugar−phosphate backbones (except the C1′ atom) from the structure of the DNA oligomer d(5′-GG-3′)·d(3′-CC-5′), capped the dangling bonds with the H atoms, and optimized the coordinates of H atoms for single base pairs. That is, the structure of the system in the cationic (neutral) state is made of the optimized structure of the G·C base pair of the 5′-side in the cationic (neutral) state and that of the G·C base pair of the 3′-side in the neutral state. We calculated the electrostatic interaction between the hole and the base pair where the hole does not reside; this interaction is the electrostatic interaction between one base pair in the cationic state and the other in the neutral state, minus that between the two base pairs both in the neutral state. We used single base pairs to calculate the charge distribution. More than 97% of the charges of the hole is in the guanine of the 5′-side in the calculated electronic structures of the system.

Figure 6.

Figure 6

Open in a new tab

IP of the two G·C base pairs as a function of the rise R. The inset shows the structure of the two G·C base pairs. Solid line: IP of the system made of the two G·C base pairs. Dashed line: IP of the single G·C base pair plus the electrostatic interaction between the hole and the base pair where the hole does not reside (defined in the text).

To understand the reduction in the IP decrease with the increasing N due to the solvent, we developed simple models of DNA oligomers (Figure 7a); we showed that these models reproduce the IPs of the DNA oligomer d[5′-(G)N-3′]·d[3′-(C)N-5′] (Figure 7b). In this figure, the open symbols are for the simple models and the others are the same as those in Figure 1b. The simple models are defined as follows. A duplex DNA oligomer is modeled as a box with the simplified charge distribution of a duplex DNA oligomer in the neutral state (the hole is localized on a certain guanine) and the water is replaced by a conductor (Figure 7a). The errors in the solvation energies caused by this replacement are less than 4%. The reason is that the dielectric constant of water is large (78.4) and the solvation energies of the dielectric continuum scale as (ϵ − 1)/(ϵ + x) with the dielectric constant ϵ, where 0 ≤ x ≤ 2.(50)

Figure 7.

Figure 7

Open in a new tab

(a) Charge distributions of the simple models for DNA pentamers with and without backbones, as indicated. The numbers above the filled circles are the assigned charges in au. One electron is removed from the filled circle marked by the outer circle, when the DNA is oxidized. The water is replaced by a conductor. The size of the box in the x- and y-directions is 18 Å. Charge distributions for DNA oligomers with different numbers of base pairs are defined in the same way as for the pentamers. (b) Comparison of the IPs of the simple models with those obtained by the MO calculations in section for the 55th fiber model structure (Figure 1b). The symbols and lines are the same as those in Figure 1b except that the open symbols are for the simple models of the DNA oligomers in the gas phase, those in water in the neutral state, and those without a backbone in the gas phase, as indicated.

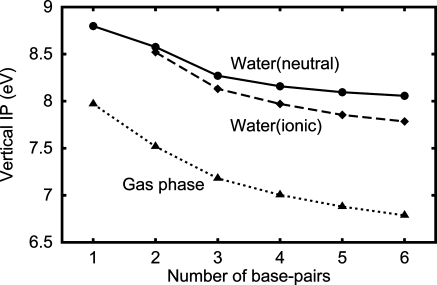
To discuss the obtained IPs, we calculated the vertical IP of the DNA oligomer d[5′-(G)N-3′]·d[3′-(C)N-5′] (Figure 8), and obtained a similar result with that of the IP (Figure 1b). That is, the vertical IP more significantly decreases with the increasing N in vacuum than in water. Since, by definition, the vertical IP does not include the reorganization energy, we obtained the vertical IP as the energy level of the highest occupied molecular orbital (HOMO) with the opposite sign using the restricted HF (RHF) method with Koopmans’ theorem.

Figure 8.

Figure 8

Open in a new tab

The vertical IP of the DNA oligomer d[5′-(G)N-3′]·d[3′-(C)N-5′] as a function of the number N of base pairs. The symbols and lines are the same as those in Figure 1b.

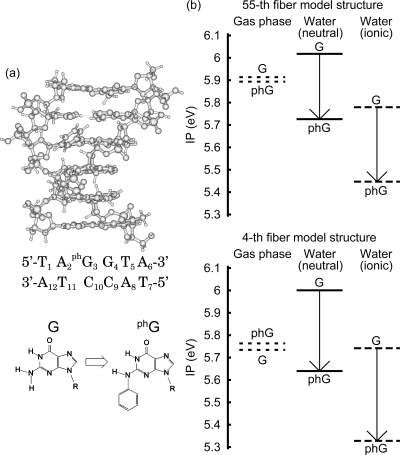
We calculated the IP of the modified nucleotide-containing DNA oligomer, d[5′-T1A2phG3G4T5A6-3′]·d[3′-A12T11C10C9A8T7-5′], where a phenyl group is attached to G3 (Figure 9a); we found that the attachment of a phenyl group reduces the IP in water but not in the gas phase (Figure 9b). For the phenylated DNA oligomer in water, the hole is always localized on the phenylated guanine phG3. We used the DNA sequence of the six base pairs around the phenylated guanine in the experiment.(18) We used the method described in section except that we optimized the coordinates of the phenyl group atoms by the electronic structure calculations. As for a single base, the OP of N2-phenyldeoxyguanosine phG relative to that of deoxyguanosine was 0.03 V in the experiment,(18) and the calculated one is 0.09 V, where the geometries are fully optimized. In the experiment,(18) the solvent was dimethylformamide (DMF); the solvation energy for the solvent change DMF/H2O is calculated to be −0.02 eV using the Born equation and thus the correction to the relative OP for the solvent change is negligible.

Figure 9.

Figure 9

Open in a new tab

(a) Structure of the modified nucleotide-containing DNA oligomer, d[5′-T1A2phG3G4T5A6-3′]·d[3′-A12T11C10C9A8T7-5′], where a phenyl group is attached to G3. The DNA sequence is the sequence of the six base pairs around the phenylated guanine in the experiment.(18) (b) The effect of the phenyl group attachment on the IP of the DNA oligomer in the gas phase, in the neutral state in water, and in the ionic state in water, for the 55th fiber model structure and the 4th fiber model structure, as indicated. The IPs before and after a phenyl group is attached are indicated by G and phG, respectively.

4. Discussion

Figure 1b shows that the large decrease (in the order of 1 eV) of the IP in the gas phase with the increasing DNA length is reduced to about a tenth of an eV in water. This reduction in the IP decrease is due to the solvent, since the computational error is less than about a tenth of an eV (section ). We can now understand why the calculated IP difference between G and GG (GGG) (in the order of 1 eV)9,19 is much larger than the experimental one (in the order of 0.1 eV).(21) This is because the solvent is not included in the calculations.9,19 In the present work, we used the two structures of the typical B-DNA structures, i.e., the 55th(37) and the 4th(38) fiber models. These models do not include the sequence dependence of the DNA structure; namely, the structure parameters of a base are independent of nearby bases. Since Figure 1b shows that the general features of the IPs are similar for both structures, we consider that the effect of the structure deviation within the B-DNA structure on the IP is minor and so is that of the sequence dependence of the DNA structure.

From Figure 2, it is clear that the decrease of the electrostatic energy of the hole causes the IP decrease with the increasing number of base pairs, N. Since the electrostatic energy of the hole decreases with the increasing N in Figure 2, the electrostatic interaction between the hole and a nucleotide pair is attractive in a duplex DNA; this nucleotide pair includes the two phosphates bonded to it. We now understand the obtained dependence of the IPs on N as follows. Because of the attractive interaction between the hole and a nucleotide pair, the IP in the gas phase decreases with the increasing N. This attractive interaction is reduced in water, and so is the IP decrease with the increasing N. When we replace the charge distribution of the DNA oligomer in the gas phase by that in the neutral state in water, the electrostatic energy of the hole in the gas phase decreases more strongly (Figure 2). The reason is that the polarization of the DNA oligomer is induced in water (Figure 4).

From the simplified charge distribution of the DNA oligomer in Figure 4, we understand why the electrostatic interaction between the hole and a nucleotide pair is attractive in the duplex DNA; this nucleotide pair includes the two phosphates bonded to it. The reason is that the hole is on a guanine and thus it is closer to nucleobases and sugars, which have negative partial charges, compared to phosphates, which have positive partial charges. We consider that the simplified charge distribution can be used to understand the above reason because the hole is delocalized over a guanine base and the rough electrostatic potential is smoothed. The miscellaneous points are as follows. The IP in the gas phase decreases more strongly than that without a backbone (Figure 1b), because the positive partial charges are separated more from the hole for the DNA oligomer with backbones compared to that without. In water, the IPs of the DNA oligomers in the ionic states are smaller than those in the neutral states (Figure 1b). This is because the Pn’s, which have positive partial charges in the neutral state of DNA oligomers, become almost neutral in the ionic state of the DNA oligomers and the repulsive interaction between Pn’s and the hole is reduced in the ionic state. The charge distribution of the DNA oligomer in Figure 4 is in accord with the result that the electrostatic potential around the guanine is lower in the interior than at the end of the sequence.(51)

Figure 5 shows that the similar dependence of the IP is observed also for the different sequences. We consider that the reason is the same as that for the DNA oligomer d[5′-(G)N-3′]·d[3′-(C)N-5′], since the charge distribution has the same features, as mentioned above.

Figure 6 shows that the attractive electrostatic interaction between the hole and a base pair causes the IP dependence of the rise R; this supports that this attractive interaction causes the dependence of the IP on N in Figure 1b. The IP in Figure 6 rapidly increases for R ≤ 5 Å and converges for R ≥ 10 Å. From this result, we can understand that the IPs in the gas phase in Figure 1b rapidly decrease for N ≤ 3 and converge for N ≥ 5 or 6 by considering that the hole is usually in the middle of the DNA oligomer and the rise in the duplex DNA is 3.4 Å.

The simple models of DNA oligomers (Figure 7a) illustrate that water molecules around the duplex DNA (but not between the base pairs) reduce the electrostatic interaction in the duplex DNA (Figure 7b).

As shown in Figure 8, the vertical IP more significantly decreases with the increasing N in vacuum than in water, similarly to the IP in Figure 1. This reason is also similar to that of the IP as follows. As for the dielectric shielding, when we use Koopmans’ theorem, the hole is not shielded by the solvent, but other charges are shielded, and thus, the attractive electrostatic interaction between them is reduced in water. The miscellaneous points are as follows. Unlike the IP, the vertical IP does not include the reorganization energy by definition. Thus, this reduction in the attractive electrostatic interaction leads to the result that the vertical IP in water is larger than that in the gas phase. Because of the reorganization energy, the IPs in water are more than a few eV smaller than the corresponding vertical IPs. The result of the IPs include the electronic energy reduction due to the charge redistribution in DNA after an electron is removed. However, that of the vertical IP does not. This is because we used Koopmans’ theorem to calculate the vertical IP. We also observed a slightly smaller decrease in the vertical IP in the gas phase with the increasing N and the slightly larger one in water compared to the corresponding IPs. These are understood as follows. The reorganization energy due to the relaxation of the DNA atoms and the electronic energy reduction mentioned above increase with the increasing N and these are included in the IPs but not in the vertical IPs. Thus, the IP in the gas phase decreases slightly more than the corresponding vertical IP. As for DNA in water, when N is increased, a part of the DNA replaces a part of the solvent, where the dielectric constant of the former is smaller than that of the latter, and thus, the total reorganization energy decreases. Therefore, the IP in water decreases less than the corresponding vertical IP. Since we did not include the reorganization energy due to the relaxation of the heavy atoms of DNA, the above decrease in the reorganization energy with the increasing N was overestimated. Thus, the decrease in the exact IP with the increasing N should be between those of the IP and the vertical IP obtained in the present work.

As shown in Figure 9, when the neutral functional group is attached to the guanine in the duplex DNA in water, the free energy of the hole on the guanine is reduced (but not in the gas phase). This result is counterintuitive, since the attached group expels the nearby water molecules, which are usually expected to stabilize ions. This result is understood as follows. Water molecules reduce the electrostatic interaction. Thus, when nearby water molecules are removed, the attractive electrostatic interaction stabilizing the hole increases. Therefore, the hole is stabilized. As for a single base, guanosine, the calculated OP of N2-phenyldeoxyguanosine phG relative to that of deoxyguanosine is small and positive, i.e., 0.09 V, which is close to the experimental value of 0.03 eV.(18) This means that the free energy of the hole (or OP) is not reduced by attaching the phenyl group. The reason is that there is no other bases and sugars which could attractively interact with the hole in the case of a single base. This result of the free energy reduction agrees with the previous one.(22) The difference between the former and the latter is that the former includes the reorganization energy due to the relaxation of the solvent but the latter does not. As already discussed,(22) this result is not changed by including this reorganization energy.

The stabilization of the guanine radical cation by the attached phenyl group similarly affects its chemical reactions, namely, the hydration and deprotonation processes,(52) as follows. This stabilization makes the possibility that the hole injected is on the phenylated guanine greater and that for guanines nearby less. Thus, the quantum yields of both of the chemical reactions of the nearby guanines decrease. In addition to that, this stabilization reduces the free energy of the initial state for both of the chemical reactions of the phenylated guanine radical cation. Thus, both of them become slower. This result agrees with the experimental result that the damage to the guanines near the phenylated guanine is suppressed.(18) Here, we have to be careful about the chemical yield data in the experiment(18) as follows. In this experiment, the hot piperidine treatment was used to detect damage. Thus, the product of the deprotonation was detected, but the products of the hydration processes, namely, 8-oxo-7,8-dihydroguanine (8-oxoGua) and 2,6-diamino-4-hydroxy-5-formanido phyrimidine (FapyGua) were not. The reason is that the latter products are stable under this treatment. The ratio of these two kinds of damage is sequence dependent,(53) and 8-oxoGua, which is the main product of the hydration process, is highly susceptible to secondary one-electron oxidation reactions.54,55 However, if the probability of the damage of one kind is larger (or smaller) at a site, then so is that for the other kind,(53) and this feature is not changed by the secondary one-electron oxidation reactions. Thus, if the probability of the damage of one kind is smaller at a site, then so is the other.

The miscellaneous points about the stabilization of the guanine radical cation by the attached phenyl group are as follows. According to the above mechanism, the IP of the modified nucleotide-containing DNA oligomer in the neutral state in water is supposed to be between the IP of the DNA not modified in the neutral state in water and that in the gas phase. However, it is not, as shown in Figure 9. One of the reasons is that when the nearby water molecules are removed, the IP of the modified nucleotide-containing DNA oligomer in the neutral state in water approaches not simply the IP of the DNA in the gas phase but that when the DNA is polarized by water. In water, the IP of the modified nucleotide-containing DNA oligomer in the ionic state is smaller than that in the neutral state. The reason is the same as that for the DNA oligomers which are not modified.

There are the computational results obtained by neglecting the solvent,56,57 where the IP dependences on the DNA sequence are smaller than those obtained by the ab initio HF MO calculations.19,20 For example, the calculated IP differences between the DNA oligomers, 5′-AGA-3′ and 5′-GGG-3′, are 0.1−0.2 eV,56,57 which are closer to the corresponding experimental result, 0.077 eV.(21) However, in the case of the different sequences, 5′-TGT-3′ and 5′-GGG-3′, the calculated IP differences are 0.3−0.5 eV,56,57 which are larger than the value(58) (less than 0.1 eV) calculated from the experimental results.59,60 In these computations,56,57 the semiempirical NDDO-G method(56) and the density functional theory(57) were used. In both of them, the backbones of the DNA oligomers were neglected; this makes the IP dependence on the DNA sequence smaller (Figure 1b). In the latter,(57) the charge distribution of the hole was calculated from the HOMO obtained by diagonalizing the reduced Hamiltonian with the elements ⟨ψi|h|ψj⟩, where h is the Kohn−Sham (KS) Hamiltonian, ψi and ψj are HOMOs of individual nucleobases, and the total system is made of the stacked three base pairs without a backbone. However, the vertical ionization potential was obtained not as the energy of the HOMO of the total system but as the diagonal element of the reduced Hamiltonian at the middle guanine site in the base pairs. The reason was not described.

About 90% of the charges of the hole is always in a certain guanine in our calculations. The inclusion of the neglected reorganization energy due to the relaxation of the heavy atoms of DNA will further localize the hole and not change the situation. The damage observed in the experiments9,4,14,61 is rather localized on a certain guanine in the G run. This fact also supports that the hole is localized. By neglecting the reorganization energy and the solvent effects, the following results were obtained. More than 95% of the charges of the hole is in a certain guanine for the stacked guanine bases and 70% is in a certain guanine for the stacked G·C base pairs.(19) More than 80% is in a middle guanine for the stacked three (N = 3) G·C base pairs with backbones, but it is delocalized over two guanines for N = 4.(51) The reason for the difference in the extent of the localization between these results and ours is mainly that the reorganization energy was neglected in these calculations.

We now discuss the solvent effects obtained by other people. The calculated IP of the stacked GA is smaller than that of G in the gas phase, and the difference between them is reduced in water.(27) This result is similar to that in Figure 1 and is understood in the same way. The calculated vertical IPs of the DNA tetramers with 65 water molecules are larger than those in the gas phase by a few eV,(34) where the B-DNA structure model is different from the ones used here. This result is similar to that in Figure 8 and is understood in the same way. Thus, it supports that the effect of the structure deviation within the B-DNA structure on the IP is minor and so is that of the sequence dependence of the DNA structure. It was discussed that the discrepancy between the theories and the experiment on the IP of the guanine run is reduced by taking into account the solvent effects;(29) in this work, the previously calculated IPs(19) were used as the values for the hole fully delocalized over the guanine run and this delocalization was assumed to be the origin of the IP dependence on N in vacuum. However, more than 95% of the hole is localized on a certain guanine in the results(19) used there, and the origin of the IP dependence on N is not the delocalization of the hole, as described above. This is known also from the computational results(19) as follows. If the origin of the IP dependence on N was the delocalization of the hole, the average of the HOMO and HOMO-1 of the guanine doublet was close to the HOMO of the single guanine. However, it is not.(19)

5. Conclusions

We examined the ionization potential (IP) corresponding to the free energy of a hole on a duplex DNA using the AM1 method(39) with COSMO.41,42 What we found is as follows. The electrostatic interaction between the hole and a nucleotide pair in the duplex DNA is attractive. Due to this attractive interaction, the IP in the gas phase significantly decreases with the increasing number of base pairs of the DNA oligomer. On the other hand, this attractive electrostatic interaction is reduced in water. Thus, this decrease in the IP is reduced in water. As for the guanine runs, this is the reason why this IP dependence calculated by neglecting the solvent(19) was much larger than that obtained from the time-resolved data.(21) Including the solvent makes this IP dependence consistent with the experimental result. As for the effect of the chemical modifications of DNA, when a neutral functional group is attached to a guanine in a DNA oligomer in water, nearby water molecules are removed; this removal was found to reduce the free energy of the hole on the guanine.(22) One might naively have expected the opposite case, since a polar solvent usually stabilizes ions. The above mechanism also explains this result as follows. When some water molecules are removed, the attractive electrostatic interaction stabilizing the hole increases, and thus, the hole is stabilized. In order to design the hole energetics by a chemical modification of DNA, this mechanism has to be taken into account and can be used.

Acknowledgments

This research is supported by “Research and Development for Applying Advanced Computational Science and Technology” of Japan Science and Technology Corporation (ACT-JST).

References

  1. Dekker C.; Ratner M. A. Phys. World 2001, 14, 29. [Google Scholar]
  2. a Grinstaff M. W. Angew. Chem., Int. Ed. 1999, 38, 3629. [DOI] [PubMed] [Google Scholar]; b Schuster G. B. Acc. Chem. Res. 2000, 33, 253. [DOI] [PubMed] [Google Scholar]; c Giese B. Acc. Chem. Res. 2000, 33, 631. [DOI] [PubMed] [Google Scholar]
  3. a Gasper S. M.; Schuster G. B. J. Am. Chem. Soc. 1997, 119, 12762. [Google Scholar]; b Hall D. B.; Holmlin R. E.; Barton J. K. Nature 1996, 382, 731. [DOI] [PubMed] [Google Scholar]; c Núñez M. E.; Hall D. B.; Barton J. K. Chem. Biol. 1999, 6, 85. [DOI] [PubMed] [Google Scholar]; d Nakatani K.; Dohno C.; Saito I. J. Am. Chem. Soc. 1999, 121, 10854. [Google Scholar]
  4. Yoshioka Y.; Kitagawa Y.; Takano Y.; Yamaguchi K.; Nakamura T.; Saito I. J. Am. Chem. Soc. 1999, 121, 8712. [Google Scholar]
  5. Tanielian C.; Kobayashi M.; Wolff C. J. Biomed. Opt. 2001, 6, 252. [DOI] [PubMed] [Google Scholar]
  6. a Kino K.; Saito I.; Sugiyama H. J. Am. Chem. Soc. 1998, 120, 7373. [Google Scholar]; b Cadet J.; Berger M.; Buchko G. W.; Joshi P. C.; Raoul S.; Ravanat J.-L. J. Am. Chem. Soc. 1994, 116, 7403. [Google Scholar]; c Vialas C.; Pratviel G.; Claparols C.; Meunier B. J. Am. Chem. Soc. 1998, 120, 11548. [Google Scholar]
  7. Oikawa S.; Tada-Oikawa S.; Kawanishi S. Biochemistry 2001, 40, 4763. [DOI] [PubMed] [Google Scholar]
  8. Candeias L. P.; Steenken S. J. Am. Chem. Soc. 1993, 115, 2437. [Google Scholar]
  9. Saito I.; Takayama M.; Sugiyama H.; Nakatani K.; Tsuchida A.; Yamamoto M. J. Am. Chem. Soc. 1995, 117, 6406. [Google Scholar]
  10. Iverson B. L.Ph.D. Thesis, California Institute of Technology, 1988.
  11. Fleisher M. B.; Mei H.-Y.; Barton J. K. In Nucleic Acids and Molecular Biology; Eckstein F., Lilley M. J., Eds.; Springer-Verlag: Berlin, 1988; Vol. 2, pp 65−84. [Google Scholar]
  12. Matsugo S.; Kawanishi S.; Yamamoto K.; Sugiyama H.; Matsuura T.; Saito I. Angew. Chem., Int. Ed. Engl. 1991, 30, 1351. [Google Scholar]
  13. Saito I. Pure. Appl. Chem. 1992, 64, 1305. [Google Scholar]
  14. Ito K.; Inoue S.; Yamamoto K.; Kawanishi S. J. Biol. Chem. 1993, 268, 13221. [PubMed] [Google Scholar]
  15. Takayama M.Ph.D. Thesis, Kyoto University, 1995.
  16. Breslin D. T.; Schuster G. B. J. Am. Chem. Soc. 1996, 118, 2311. [Google Scholar]
  17. Melvin T.; Plumb M. A.; Botchway S. W.; O’Neill P.; Parker A. W. Photochem. Photobiol. 1995, 61, 584. [DOI] [PubMed] [Google Scholar]
  18. Nakatani K.; Dohno C.; Saito I. J. Am. Chem. Soc. 2002, 124, 6802. [DOI] [PubMed] [Google Scholar]
  19. Sugiyama H.; Saito I. J. Am. Chem. Soc. 1996, 118, 7063. [Google Scholar]
  20. Saito I.; Nakamura T.; Nakatani K.; Yoshioka Y.; Yamaguchi K.; Sugiyama H. J. Am. Chem. Soc. 1998, 120, 12686. [Google Scholar]
  21. Lewis F. D.; Liu X.; Liu J.; Hayes R. T.; Wasielewski M. R. J. Am. Chem. Soc. 2000, 122, 12037. [Google Scholar]
  22. Yokojima S.; Yanoi W.; Yoshiki N.; Kurita N.; Tanaka S.; Nakatani K.; Okada A. J. Phys. Chem. B 2004, 108, 7500. [Google Scholar]
  23. Pullman A.; Pullman B. Q. Rev. Biophys. 1981, 14, 289. [DOI] [PubMed] [Google Scholar]
  24. Kovacic P.; Wakelin L. P. G. Anti-Cancer Drug Des. 2001, 16, 175. [PubMed] [Google Scholar]
  25. Prat F.; Houk K. N.; Foote C. S. J. Am. Chem. Soc. 1998, 120, 845. [Google Scholar]
  26. Colson A.-O.; Besler B.; Sevilla M. D. J. Phys. Chem. 1993, 97, 13852. [Google Scholar]
  27. Kim N. S.; Zhu Q.; LeBreton P. R. J. Am. Chem. Soc. 1999, 121, 11516. [Google Scholar]
  28. Kim N. S.; LeBreton P. R. J. Am. Chem. Soc. 1996, 118, 3694. [Google Scholar]
  29. Kurnikov I. V.; Tong G. S. M.; Madrid M.; Beratan D. N. J. Phys. Chem. B 2002, 106, 7. [Google Scholar]
  30. Starikov E. B. Phys. Chem. Chem. Phys. 2002, 4, 4523. [Google Scholar]
  31. Gervasio F. L.; Carloni P.; Parrinello M. Phys. Rev. Lett. 2002, 89, 108102. [DOI] [PubMed] [Google Scholar]
  32. Yoshioka Y.; Kawai H.; Sato T.; Yamaguchi K.; Saito I. J. Am. Chem. Soc. 2003, 125, 1968. [DOI] [PubMed] [Google Scholar]
  33. Reynisson J.; Schuster G. B.; Howerton S. B.; Williams L. D.; Barnett R. N.; Cleveland C. L.; Landman U.; Harrit N.; Chaires J. B. J. Am. Chem. Soc. 2003, 125, 2072. [DOI] [PubMed] [Google Scholar]
  34. Barnett R. N.; Cleveland C. L.; Landman U.; Boone E.; Kanvah S.; Schuster G. B. J. Phys. Chem. A 2003, 107, 3525. [Google Scholar]
  35. Lu X.-J.; Shakked Z.; Olson W. K. J. Mol. Biol. 2000, 300, 819. [DOI] [PubMed] [Google Scholar]
  36. Lu X.-J.; Olson W. K. Nucl. Acids Res. 2003, 31, 5108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Premilat S.; Albiser G. Nucl. Acids Res. 1983, 11, 1897. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. a Arnott S.Polynucleotide secondary structures: an historical perspective. In Oxford Handbook of Nucleic Acid Structure; Neidle S., Ed.; Oxford Press: New York, 1999; pp 1−38. [Google Scholar]; b Chandrasekaran R.; Arnott S. J. Biomol. Struct. Dyn. 1996, 13, 1015. [DOI] [PubMed] [Google Scholar]
  39. a Dewar M. J. S.; Zoebisch E. G.; Healy E. F.; Stewart J. J. P. J. Am. Chem. Soc. 1985, 107, 3902. [Google Scholar]; b Dewar M. J. S.; Jie C. THEOCHEM 1989, 187, 1. [Google Scholar]
  40. Stewart J. J. P.Fujitsu Limited, Tokyo, Japan, 2001. [Google Scholar]
  41. Klamt A.; Schüürmann G. J. Chem. Soc., Perkin Trans. 1993, 2, 799. [Google Scholar]
  42. Klamt A.; Jonas V.; Bürger T.; Lohrenz J. C. W. J. Phys. Chem. A 1998, 102, 5074. [Google Scholar]
  43. Klamt A. Personal communication. As for the vdW radius for the P atom, which was not reported in ref (42), the value 2.106 Å was suggested.
  44. Seidel C. A. M.; Schulz A.; Sauer M. H. M. J. Phys. Chem. 1996, 100, 5541. [Google Scholar]
  45. Zhang Q.; Chen E. C. M. Biochem. Biophys. Res. Commun. 1995, 217, 755. [DOI] [PubMed] [Google Scholar]
  46. Wetmore S. D.; Boyd R. J.; Eriksson L. A. Chem. Phys. Lett. 2000, 322, 129. [Google Scholar]
  47. Orlov V. M.; Smirnov A. N.; Varshavsky Y. M. Tetrahedron Lett. 1976, 48, 4377. [Google Scholar]
  48. Wiley J. R.; Robinson J. M.; Ehdaie S.; Chen E. C. M.; Chen E. S. D.; Wentworth W. E. Biochem. Biophys. Res. Commun. 1991, 180, 841. [DOI] [PubMed] [Google Scholar]
  49. Klamt A.; Baldridge K. J. Chem. Phys. 1997, 106, 6622. [Google Scholar]
  50. Jackson J. D.Classical Electrodynamics; Wiley: New York, 1975. [Google Scholar]
  51. Zhu Q.; LeBreton P. R. J. Am. Chem. Soc. 2000, 122, 12824. [Google Scholar]
  52. Steenken S. Chem. Rev. 1989, 89, 503–520. [Google Scholar]; Cadet J.; Delatour T.; Douki T.; Gasparutto D.; Pouget J.-P.; Ravanat J.-L.; Sauvaigo S. Mutat. Res. 1999, 424, 9–21. [DOI] [PubMed] [Google Scholar]
  53. Spassky A.; Angelov D. Biochemstry 1997, 36, 6571–6576. [DOI] [PubMed] [Google Scholar]
  54. Luo W.; Muller J. G.; Rachlin E. M.; Burrows C. J. Chem. Res. Toxicol. 2001, 14, 927–938. [DOI] [PubMed] [Google Scholar]
  55. Ravanat J.-L.; Saint-Pierre C.; Cadet J. J. Am. Chem. Soc. 2003, 125, 2030–2031. [DOI] [PubMed] [Google Scholar]
  56. Voityuk A. A.; Jortner J.; Bixon M.; Rösch N. Chem. Phys. Lett. 2000, 324, 430. [Google Scholar]
  57. Senthilkumar K.; Grozema F. C.; Guerra C. F.; Bickelhaupt F. M.; Siebbeles L. D. A. J. Am. Chem. Soc. 2003, 125, 13658. [DOI] [PubMed] [Google Scholar]
  58. Bixon M.; Jortner J. J. Phys. Chem. A 2001, 105, 10322. [Google Scholar]
  59. Meggers M.; Michel-Beyerle M. E.; Giese B. J. Am. Chem. Soc. 1998, 120, 12950. [Google Scholar]
  60. Giese B.; Wessely S.; Spormann M.; Lindemann U.; Meggers E.; Michel-Beyerle M. E. Angew. Chem., Int. Ed. Engl. 1999, 38, 996. [DOI] [PubMed] [Google Scholar]
  61. Saito I.; Nakamura T.; Nakatani K. J. Am. Chem. Soc. 2000, 122, 3001. [Google Scholar]

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES