Abstract
Although it is known that triglyceride concentrations increase with adiposity, whether the same increase applies for different percentiles of the triglyceride distribution has not been reported. Therefore, physican-supplied triglyceride concentrations from 7288 male and 2326 female runners were divided into strata according to the body mass index (BMI) and circumferences of the waist, hip and chest. The percentiles of the triglyceride distribution within each stratum were used to determine the cross-sectional regression slope between adiposity and triglyceride levels at each triglyceride percentile.
Compared to the 5th percentile of the triglyceride distribution, the rise in men's triglycerides at the 95th percentile per unit of adiposity was 14-fold greater for BMI, 7.8-fold greater for waist circumference, 3.6-fold greater for hip circumference, and 4.4-fold greater for chest circumference. The rise in women's triglyceride concentrations at the 95th percentile was 8-fold greater than at the 5th percentile for each kg/m2 increase in BMI.
These results suggest that the metabolic effects of adiposity on plasma triglycerides depend upon whether the concentrations are high or low. This contradicts statistical assumptions upon which prior studies of adiposity have based their analyses. We speculate that the reported greater increases in triglycerides per unit of adiposity in whites than blacks, in men than women, and in low-density lipoprotein (LDL) pattern B than A are all consistent with the relationships we observe. It remains to be verified whether these relationship also apply to less active populations.
Keywords: Triglycerides, Body mass index, Low-density lipoproteins, Waist, Hip, Chest, Regional adiposity
Introduction
Elevated plasma triglycerides increase the risk for cardiovascular disease directly [1–3], or indirectly by decreasing plasma high-density lipoprotein (HDL) cholesterol concentrations [4,5], increasing the levels of smaller, denser low-density lipoprotein (LDL) particles in plasma [6,7], or affecting other risk factors [8–11]. The plethora of published cross-sectional and longitudinal studies that have compared triglyceride levels to adiposity have led to some basic observations concerning their concordant relationship: (1) the relationships are strongest for central (visceral or male-type) obesity [12–23], which is most practically measured by waist circumference [24]; (2) the relationships are stronger in men than women [25,26], in whites than blacks [27–30], and in LDL phenotype B than A [31–33].
To our knowledge, the relationships of body fat with triglycerides have always been summarized by a single regression line or curve [34]. The curve represents the expected lipoprotein level at a given fatness, and deviations from the curve are presumed to represent random variation or error. If the assumption about the deviations (residuals) does not apply, the single regression curve may ignore important aspects of the relationships that are germane to their physiological understanding and public health significance.
This paper examines the relationship of adiposity to the distribution of plasma triglycerides (e.g., 5th, 10th, 25th, 50th, 75th, 90th and 95th triglycerides percentiles) in order to determine whether a single regression curve is sufficient for describing these relationships. The analyses are based on simple descriptive statistics (bivariate regression slopes) that are easily interpreted and dependent upon the fewest possible assumptions. In the discussion, we speculate that the findings may suggest a common interpretation for some of the differences cited above between races, sexes, and LDL phenotype pattern.
Methods
The design and subject characteristics of this cohort are described in detail elsewhere [35,36]. All participants received a two-page questionnaire as part of the National Runners' Health Study. The questionnaire solicited information on demographics, physical activity, weight history, diet, cigarette use, medical history and medications. Triglyceride values were obtained from the medical records of 7288 and 2326 nonvegetarian, nonsmoking men and women without prior history of heart disease or cancer and currently not using medications that might affect lipoprotein levels. Although these were presumably fasting (often but not always specifically stated in the data supplied), there is no separate verification of the fasting status.
Self-reported height, weight, and circumferences of the waist, hip and chest were obtained from the participant questionnaires. Body mass index (BMI) was calculated as weight in kilograms divided by height in meters squared. Two approaches were used to validate questions on anthropometric measurements from 116 men: (1) test–retest correlations from duplicate questionnaires and (2) correlations of clinical measurements of height, weight and circumference measurements with their self-reported values. Self-reported height and weight showed strong correspondence with the duplicate questionnaires (r = 0.98 and 0.97, respectively) and with the clinic measurement of these variables (r = 0.96 for both). There were reasonable but somewhat weaker test–retest correlations for self-reported waist circumference (r = 0.84), hip circumference (r = 0.79) and chest circumference (r = 0.93). Self-reported body circumferences also correlated reasonably with the clinic circumference measurements of the waist (r = 0.68), hip (r = 0.63) and chest (r = 0.77). The somewhat weaker reproducibility of the waist, hip and chest measurements signifies that the probability of a statistical type II error (false negative) will be greater for these variables than for height and weight, but this should not affect the probability of the type I statistical error (false positive) [37].
Statistical analyses
The statistical analyses are based on the cumulative distributions within each of five categories for BMI (men: <22.0, 22.0–23.5, 23.5–25.0, 25.0–26.5 and >26.5 kg/m2; women: <19.0, 19.0–20.5, 20.5–22.0, 22.0–23.5 and >23.5 kg/m2), waist circumference (men: <31, 31–33, 33–35, 35–37 and >37 in.; women: <24.5, 24.5–26, 26–27.5, 27.5–29 and >29 in.), hip circumference (men: <35, 35–36.5, 36.5–38, 38–39.5 and >39.5 in.; women: <34.5, 34.5–36.0, 36.0–37.5, 37.5–39 and >39 in.), and chest circumference (men: <38, 38–39.5, 39.5–41, 41–42.5 and >42.5 in.; women: <33.5, 33.5–34.5, 34.5–35.5, 35.5–36.5 and >36.5 in.). These categories were selected to cover comparable width intervals and to provide a sufficient number of observations for estimating percentiles. The intervals were defined prior to the analyses. Within each fatness category, we estimated the 5th through the 95th percentiles of the triglyceride distribution.
Simple least-squares regression analysis was used to estimate the rate of change at each triglyceride percentile across the five fatness categories. We applied simple linear regression to the five bivariate observations consisting of the average adiposity (independent variable) and the ith percentile of the triglyceride level within each fatness category (dependent variable) to estimate the change in triglycerides per unit of adiposity at the ith percentile. Since the usual underlying statistical assumptions presumably do not apply for percentiles (particularly those representing the tails of the distribution), we calculated the standard errors and significance levels with bootstrap resampling [38]. Bootstrap estimates were created for each sex as follows: (1) within each of the five fatness categories, sampling with replacement was used to create a bootstrap data set of adiposity and triglycerides; (2) within each fatness category, we then determined the average adiposity and triglycerides corresponding to the 5th, 10th, 25th, 50th, 75th, 90th and 95th percentiles for the bootstrap sample; (3) least squares regression was applied to estimate at each percentile the apparent change in triglycerides per unit of adiposity across the five fatness categories; (4) steps (1)–(3) were repeated 10,000 times. This yielded 10,000 regression slopes (one for each bootstrap sample). The average and the standard deviation of the 10,000 regression slopes provides the bootstrap estimate of the regression slope and its standard error at the ith percentile.
If adiposity causes the same triglyceride change regardless of whether the individual's triglycerides are relatively high or low, then the regression slopes for the 5th, 10th, 25th, 50th, 75th, 90th and 95th percentiles will be the same (i.e., parallel). Different (i.e., nonparallel) regression slopes could indicate that the metabolic processes associated with adiposity affect various portions of the triglyceride distribution differently. Bootstrap resampling was used to estimate the difference between two regression slopes (e.g., the 75% slope minus the 25% slope) and its corresponding standard error. Bootstrap resampling was also used to test whether the slopes increased or decreased progressively from the 5 to 95% of the triglyceride distribution. This was done by constructing a numerical contrast among the slopes that increased linearly across 7 percentiles (i.e., -45 × TG5% - 40 × TG10% - 25 × TG25% + 0 × TG50% + 25 × TG75% + 40 × TG90% + 45 × TG95%, where TGk% is the regression slope at the kth percentile of the triglyceride distribution).
Bootstrap estimates and standard errors for the regression slopes, differences in regression slopes, and linear contrasts across regression slopes were based on 10,000 bootstrap samples. Two-tailed significance levels were calculated as 2 × minimum(p, 1 - p), in which p is the proportion of times that the bootstrap slopes, difference in slopes, or linear contrasts were less than zero.
We verified that the statistics and software did not produce significant results due to statistical or programming artifacts. This was done by simulating data where the relationships of triglycerides to adiposity were given by their linear regression slope only (i.e., the same slope at all percentiles of the triglyceride distribution). Specifically, for the set of N observations, we: (1) estimated the simple linear relationship between triglyceride concentrations and adiposity by standard least squares regression on the complete data set, in order to estimate the predicted triglycerides based on adiposity; (2) created a data set of the N differences between the observed and the predicted triglycerides (i.e., the residuals); and (3) reconstructed a new set of observations by adding a randomly assigned residual to each predicted triglyceride level. If the statistics and program are correct, then the test statistic will be nonsignificant in all instances. In men, the test statistics for nonparallel slopes for the reconstructed triglyceride values were P = 0.68 for BMI, P = 0.87 for waist circumference, P = 0.99 for hip circumference, and P = 0.93 for chest circumference. The corresponding significance levels for women's reconstructed triglyceride values were P = 0.97, 0.85, 0.98 and 0.94, respectively. The distribution of the reconstructed data for men had essentially the same skewness (original versus reconstructed data: 2.91 versus 2.61) and kurtosis (15.39 versus 14.28) as the original data and parallel increases when plotted against BMI at all percentiles (P = 0.68 the test for different slopes across percentiles).
Results
The sample consisted of men and women who on average (mean±S.D.) ran 38.0±20.1 and 34.8±19.9 km per week, respectively. Correspondingly, they tended to have low BMI (men: 23.78 ± 2.47 kg/m2; women 21.30 ± 2.48 kg/m2), and narrow waist (men 0.850 ± 0.060 m; women 0.686 ± 0.069 m), hip (men 0.952 ± 0.071 m; women 0.919 ± 0.065 m;) and chest circumferences (men: 1.016±0.069 m; women 0.880±0.053 m). Twenty-six percent of the men and 6% of the women were at least moderately overweight (BMI ≥25 kg/m2). Mean plasma triglycerides concentrations were 1.16 ± 0.72 mmol/l in men and 0.92 ± 0.60 mmol/l in women.
Fig. 1 plots the cumulative percentiles of the men's triglyceride distribution versus the cumulative percentiles of the women's triglyceride distribution. The plotted values would lie along the diagonal if the distributions were the same for men and women. However, women have lower triglycerides then men at any given percentile and therefore the curve lies above the diagonal. For example, the 50th percentile of the men's triglyceride distribution (0.97 mmol/l) corresponds to the 66.4th percentile of the women's triglyceride distribution.
Fig. 1.
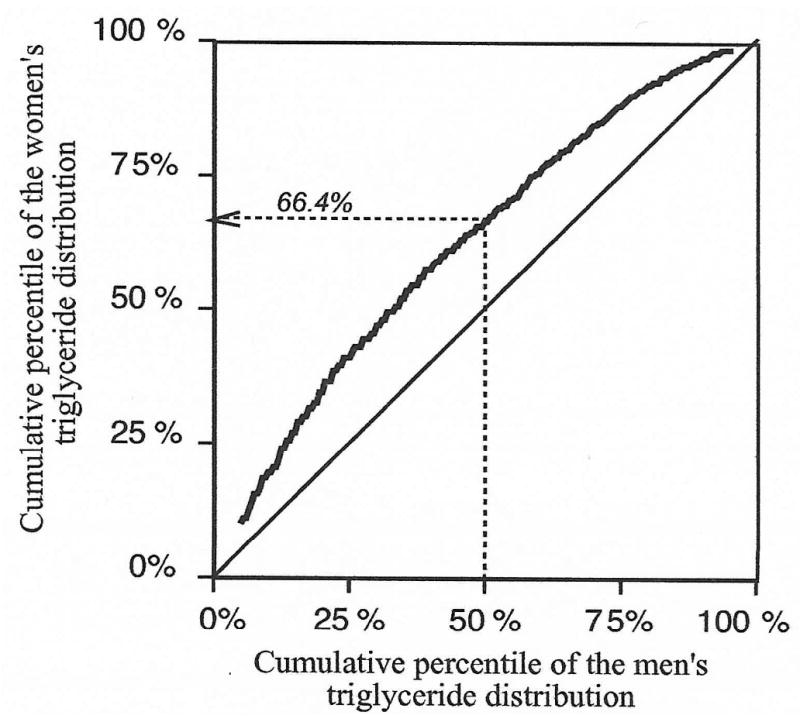
Correspondence between the cumulative triglyceride distribution of men and women (i.e., Q–Q plot). For example, 0.97 mmol/l corresponds to the 50th percentile of the men's triglyceride distribution and the 66.4th percentile of the women's triglyceride distribution.
Relationship of adiposity to percentiles of the triglyceride distribution
Table 1 displays the regression slopes (±S.E.) relating different percentiles of the plasma triglyceride distribution to BMI and circumferences of the waist, hip and chest. In men, the rises in triglyceride associated with BMI, waist circumference and hip circumference were all statistically significant for the 5th, 10th, 25th, 50th, 75th, 90th, and 95th percentiles of the triglyceride distribution. Men's triglycerides also increased in association with chest circumference for all percentiles except the 5th.
Table 1.
Regression slopes (±S.E.) for plasma triglycerides (mmol/L) vs. body mass index and circumferences of the waist, hip and chest in men and women for different percentiles of the triglyceride distribution.
| Body mass index (BMI) (mmol/L per kg/m2) |
Body circumferences (mmol/L per m) | |||
|---|---|---|---|---|
| Waist | Hip | Chest | ||
| Males | ||||
| 95% | 0.188 ±0.018‡ | 5.146 ±0.711‡ | 2.160 ±0.850† | 1.528 ±0.301‡ |
| 90% | 0.145 ±0.015‡ | 4.257 ±0.458‡ | 1.724 ±0.614† | 1.501 ±0.194‡ |
| 75% | 0.101 ±0.007‡ | 3.517 ±0.339‡ | 1.397 ±0.260‡ | 1.314 ±0.158‡ |
| 50% | 0.056 ±0.004‡ | 1.838 ±0.158‡ | 0.676 ±0.156‡ | 1.100 ±0.136‡ |
| 25% | 0.033 ±0.003‡ | 1.135 ±0.132‡ | 0.524 ±0.126‡ | 0.734 ±0.128‡ |
| 10% | 0.021 ±0.002‡ | 0.754 ±0.094‡ | 0.626 ±0.177‡ | 0.616 ±0.159‡ |
| 5% | 0.013 ±0.003‡ | 0.657 ±0.121‡ | 0.599 ±0.106‡ | 0.346 ±0.188 |
| Significance of trend (P) | <0.0001 | <0.0001 | 0.02 | 0.002 |
| Females | ||||
| 95% | 0.105 ±0.038‡ | 2.735 ±0.994† | 0.780 ±0.906 | 2.434 ±1.026* |
| 90% | 0.071 ±0.018‡ | 2.296 ±0.674‡ | 0.337 ±0.538 | 1.716 ±0.535† |
| 75% | 0.041 ±0.009‡ | 1.427 ±0.254‡ | 0.413 ±0.282 | 1.244 ±0.292‡ |
| 50% | 0.028 ±0.006‡ | 0.739 ±0.168‡ | 0.339 ±0.165* | 0.794 ±0.270‡ |
| 25% | 0.018 ±0.003‡ | 0.336 ±0.129† | 0.264 ±0.130* | 0.575 ±0.148‡ |
| 10% | 0.015 ±0.004‡ | 0.067 ±0.106 | 0.063 ±0.106 | 0.256 ±0.109* |
| 5% | 0.013 ±0.003‡ | −0.034 ±0.134 | 0.011 ±0.138 | 0.250 ±0.163 |
| Significance of trend (P) | <0.0001 | <0.0001 | 0.41 | 0.02 |
Sample sizes were 6677 men and 2163 women for body mass index, 6525 men and 2032 women for waist circumference, 3538 men and 1983 women for hip circumference, and 5732 men and 2048 for women for chest circumference. Estimated from 10,000 bootstrap samples. Significance levels from 10,000 permutations for slope not equal to zero coded:
P < 0.05;
< 0.01,
< 0.001.
For all four adiposity measurements, the rise in men's triglyceride at the 95th percentile was much greater than the rise at the 5th percentile (steeper slope). The statistical tests for progressive increases in slope from the smallest to largest percentiles were all significant (all P ≤ 0.0005 except hip circumference, which was P = 0.02). The rise in plasma triglycerides per kg/m2 of BMI was 14-fold greater at the 95th percentile than at the 5th percentile (slope ± S.E.: 0.188 ± 0.018 mmol/l versus 0.013 ± 0.003 mmol/l, Fig. 2). Per meter increase in body circumference, the apparent increases in plasma triglyceride concentrations at the 95th vis-a-vis the 5th percentile were 7.8-fold higher for waist, 3.6-fold higher for hip, and 4.4-fold higher for chest.
Fig. 2.
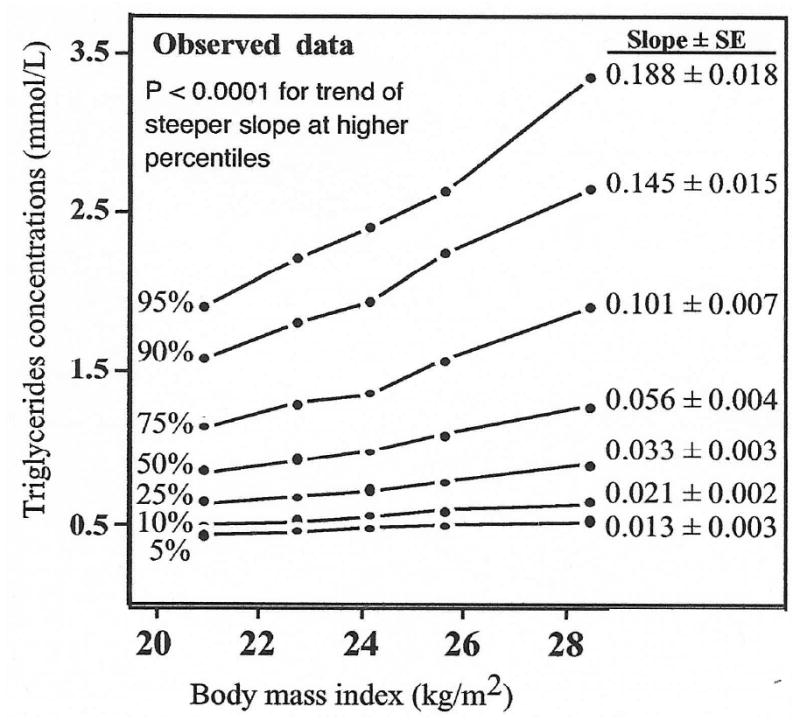
Rise in men's plasma triglyceride concentrations with increasing levels of body mass index at the 5th, 10th, 25th, 50th, 75th, 90th and 95th percentiles of the triglyceride distribution, showing a more pronounced increase at higher percentiles.
There were strong relationships between women's triglycerides and their BMI (P ≤ 0.001 at all percentiles), and somewhat weaker relationship with waist (P < 0.01 percentiles), and chest circumference (P < 0.05 between the 25th and 95th percentiles). The increase in women's triglycerides became progressively greater from the 5th through the 95th percentiles for both BMI and waist circumference (P < 0.0001). As a function of BMI, the increase in triglycerides was nearly 8-fold higher at the 95th percentile than at the 5th percentile. Waist circumference was unrelated to women's triglycerides at the 5th percentile, but exhibited a strong significant increase at the 95th percentile. Each meter increase in chest circumference was associated with 2.43 ± 1.03 mmol/l increase in women's triglycerides at the 95th percentile, which was nearly 10-fold greater than their increase at the 5th percentile. Women's hip circumferences were related to plasma triglyceride concentrations at the median (only marginally), but not other percentiles.
Tables 2 and 3 present the pairwise comparisons between slopes at different percentiles of the triglyceride distribution. For men's BMI, the slopes were always significantly greater for the higher percentiles than for all lower percentiles. The slopes for men's waistlines were also always significantly greater at the higher percentile with the exception of the extremes (90th versus 95th or 5th versus 10th). In women, slopes for BMI versus triglycerides above the median were always significantly greater than triglycerides at lower percentiles, except for the most proximal percentile. Women's waist circumferences showed a stronger relationship to plasma triglycerides above the triglyceride median than below. The slopes for chest circumferences reflected many of the same pairwise differences as noted for BMI and waistline. Pairwise comparisons among the slopes for hip circumference were only occasionally significant (men) or all nonsignificant (women).
Table 2.
In men, differences in the slopes (±S.E.) for percentiles of the triglyceride distribution (dependent variable) vs. body mass index and circumferences of the waist, hip and chest.
| Body mass index (BMI) (mmol/L per kg/m2) |
Body circumferences (mmol/L per m) | |||
|---|---|---|---|---|
| Waist | Hip | Chest | ||
| 95% vs. | ||||
| 90% | 0.043 ±0.014‡ | 0.889 ±0.526 | 0.436 ±0.640 | 0.027 ±0.227 |
| 75% | 0.086 ±0.016‡ | 1.629 ±0.661† | 0.763 ±0.787 | 0.214 ±0.282 |
| 50% | 0.131 ±0.017‡ | 3.308 ±0.695‡ | 1.484 ±0.829 | 0.428 ±0.301 |
| 25% | 0.155 ±0.017‡ | 4.011 ±0.706‡ | 1.636 ±0.844* | 0.794 ±0.312* |
| 10% | 0.167 ±0.018‡ | 4.392 ±0.709‡ | 1.534 ±0.859 | 0.912 ±0.331† |
| 5% | 0.174 ±0.018‡ | 4.488 ±0.715‡ | 1.561 ±0.851 | 1.182 ±0.349‡ |
| 90% vs. | ||||
| 75% | 0.044 ±0.013‡ | 0.740 ±0.394* | 0.327 ±0.515 | 0.188 ±0.168 |
| 50% | 0.088 ±0.015‡ | 2.420 ±0.435‡ | 1.048 ±0.583 | 0.401 ±0.196* |
| 25% | 0.112 ±0.015‡ | 3.122 ±0.452‡ | 1.200 ±0.604* | 0.768 ±0.212‡ |
| 10% | 0.124 ±0.015‡ | 3.503 ±0.457‡ | 1.098 ±0.623 | 0.886 ±0.238‡ |
| 5% | 0.132 ±0.016‡ | 3.600 ±0.464‡ | 1.125 ±0.616 | 1.155 ±0.261‡ |
| 75% vs. | ||||
| 50% | 0.045 ±0.006‡ | 1.680 ±0.287‡ | 0.721 ±0.216† | 0.214 ±0.142 |
| 25% | 0.069 ±0.007‡ | 2.382 ±0.323‡ | 0.873 ±0.253† | 0.580 ±0.172‡ |
| 10% | 0.081 ±0.007‡ | 2.763 ±0.335‡ | 0.771 ±0.291† | 0.698 ±0.204‡ |
| 5% | 0.088 ±0.007‡ | 2.860 ±0.345‡ | 0.798 ±0.270† | 0.967 ±0.232‡ |
| 50% vs. | ||||
| 25% | 0.024 ±0.003‡ | 0.702 ±0.140‡ | 0.152 ±0.140 | 0.366 ±0.129† |
| 10% | 0.036 ±0.004‡ | 1.084 ±0.157‡ | 0.050 ±0.202 | 0.484 ±0.174† |
| 5% | 0.043 ±0.005‡ | 1.180 ±0.176‡ | 0.077 ±0.170 | 0.754 ±0.207‡ |
| 25% vs. | ||||
| 10% | 0.012 ±0.003‡ | 0.381 ±0.115‡ | -0.102 ±0.157 | 0.118 ±0.147 |
| 5% | 0.020 ±0.004‡ | 0.478 ±0.141‡ | -0.075 ±0.136 | 0.388 ±0.187* |
| 10% vs. | ||||
| 5% | 0.008 ±0.003† | 0.096 ±0.096 | 0.027 ±0.162 | 0.269 ±0.158 |
Results from 10,000 bootstrap samples. Significance levels for the differences between two regression slopes are coded:
P < 0.05;
< 0.01,
< 0.001.
Table 3.
In women, differences in the slopes (±S.E.) for percentiles of the triglyceride distribution (dependent variable) vs. body mass index and circumferences of the waist, hip and chest.
| Body mass index (BMI) (mmol/L per kg/m2) |
Body circumferences (mmol/L per m) | |||
|---|---|---|---|---|
| Waist | Hip | Chest | ||
| 95% vs. | ||||
| 90% | 0.035 ±0.030 | 0.439 ±0.762 | 0.443 ±0.705 | 0.719 ±0.824 |
| 75% | 0.065 ±0.035* | 1.308 ±0.929 | 0.367 ±0.845 | 1.190 ±0.965 |
| 50% | 0.077 ±0.037† | 1.996 ±0.973* | 0.442 ±0.889 | 1.640 ±1.007 |
| 25% | 0.087 ±0.038‡ | 2.398 ±0.988* | 0.516 ±0.899 | 1.859 ±1.020 |
| 10% | 0.091 ±0.038‡ | 2.668 ±0.992† | 0.717 ±0.907 | 2.178 ±1.024 |
| 5% | 0.092 ±0.038‡ | 2.769 ±0.998† | 0.769 ±0.911 | 2.184 ±1.028 |
| 90% vs. | ||||
| 75% | 0.030 ±0.015 | 0.869 ±0.579 | -0.075 ±0.454 | 0.472 ±0.459 |
| 50% | 0.043 ±0.017* | 1.557 ±0.642* | -0.001 ±0.514 | 0.922 ±0.523 |
| 25% | 0.053 ±0.018† | 1.959 ±0.664† | 0.073 ±0.531 | 1.141 ±0.532* |
| 10% | 0.056 ±0.018‡ | 2.229 ±0.671‡ | 0.274 ±0.539 | 1.460 ±0.538† |
| 5% | 0.057 ±0.019‡ | 2.330 ±0.679‡ | 0.327 ±0.545 | 1.465 ±0.549† |
| 75% vs. | ||||
| 50% | 0.013 ±0.007 | 0.687 ±0.213‡ | 0.074 ±0.239 | 0.450 ±0.266 |
| 25% | 0.023 ±0.008† | 1.090 ±0.247‡ | 0.149 ±0.274 | 0.669 ±0.285† |
| 10% | 0.026 ±0.009‡ | 1.359 ±0.257‡ | 0.350 ±0.286 | 0.988 ±0.295‡ |
| 5% | 0.028 ±0.009‡ | 1.460 ±0.273‡ | 0.402 ±0.301 | 0.994 ±0.318† |
| 50% vs. | ||||
| 25% | 0.010 ±0.005* | 0.403 ±0.146† | 0.075 ±0.146 | 0.219 ±0.229 |
| 10% | 0.013 ±0.006* | 0.672 ±0.168‡ | 0.275 ±0.168 | 0.538 ±0.261* |
| 5% | 0.015 ±0.006* | 0.773 ±0.191‡ | 0.328 ±0.192 | 0.544 ±0.288* |
| 25% vs. | ||||
| 10% | 0.003 ±0.003 | 0.269 ±0.115* | 0.201 ±0.116 | 0.319 ±0.131* |
| 5% | 0.005 ±0.004 | 0.370 ±0.149* | 0.253 ±0.153 | 0.325 ±0.177 |
| 10% vs. | ||||
| 5% | 0.001 ±0.003 | 0.101 ±0.104 | 0.052 ±0.111 | 0.005 ±0.133 |
Results from 10,000 bootstrap samples. Significance levels for the differences between two regression slopes are coded:
P < 0.05;
< 0.01,
< 0.001.
Fig. 3 plots the regression slope for the rise in plasma triglyceride concentrations per unit of adiposity at every percentile between the 5th to the 95th percentile of the triglyceride distribution. In men, the slope for triglycerides versus BMI and chest circumferences increase linearly below the 64th and 69th percentile, and then accelerates rapidly for higher percentiles. The slope for women were the same as for men at the 5th percentile, but rose less rapidly than observed for men through the 84th percentile, after which there is also an accelerated increase. The slopes for triglycerides versus men's waist and chest circumference also rose linearly through the 63rd percentiles before acceleration. The corresponding plot for women's waists and chests were linear before the 86th percentile, and then accelerated.
Fig. 3.
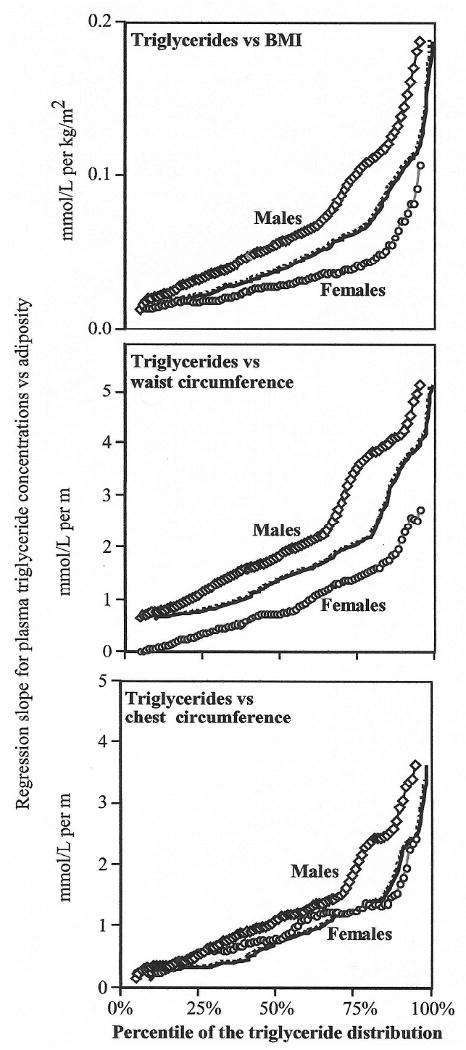
Plot of the regression slopes for plasma triglycerides (mmol/l) vs. BMI (kg/m2), waist circumference (m) and chest circumference (m) at all percentile of the triglyceride distribution in men and women (solid lines) and for the men's slopes adjusted to the women's cumulative distribution (dashed line).
Fig. 3 shows that the effects of BMI and waist circumference on plasma triglycerides are greater in men than women. The difference in slopes between sexes was significant between the 22nd and 93rd percentile for BMI and for all percentiles for waist circumference (analyses not displayed). The curves were generally not different for men's and women's chest circumferences. To test whether these differences in male and female curves are due to the fact that at any given percentile, women have a lower triglyceride value than men (Fig. 1), we replotted the male's curves to correspond to the female cumulative percentiles. For example, the 50th percentile of the men's triglyceride distribution corresponds to the 66.4th percentile of the female distribution. Therefore we replotted the men's slope for triglycerides versus BMI at the 50th percentile (0.057 mmol/l per kg/m2) at the 66.4th percentile to assess whether the shift in the women's distribution explained the differences between sexes. The replotted curves (dashed lines) suggest that the shift in the women's triglycerides towards smaller values accounted for approximately half of the difference between the male and female curves for BMI and waist, and all of the difference in the curves for chest circumferences.
Differences in slopes from the lowest to the highest triglyceride percentiles often persisted when the data were transformed into logarithms (Table 4). Waist circumferences in both men and women, and BMI and chest circumference in men continue to exhibit significant progressive increases in slope from the 5th through the 95th percentiles. However, logarithmic transformation eliminated both the difference in slope across percentiles for women's BMI, and also the marginally significant differences across percentiles for men's hip circumference and women's chest circumference.
Table 4.
Regression slopes (±S.E.) for log-transformed plasma triglycerides vs. body mass index and circumferences of the waist, hip and chest in men and women for different percentiles of the triglyceride distribution.
| Body mass index (BMI) (mmol/L per kg/m2) |
Body circumferences (mmol/L per m) | |||
|---|---|---|---|---|
| Waist | Hip | Chest | ||
| Males | ||||
| 95% | 0.074 ±0.006‡ | 2.093 ±0.260‡ | 0.867 ±0.342† | 1.530 ±0.301‡ |
| 90% | 0.070 ±0.006‡ | 2.107 ±0.200‡ | 0.860 ±0.304† | 1.503 ±0.193‡ |
| 75% | 0.068 ±0.004‡ | 2.370 ±0.194‡ | 1.008 ±0.183‡ | 1.316 ±0.160‡ |
| 50% | 0.054 ±0.003‡ | 1.806 ±0.137‡ | 0.698 ±0.162‡ | 1.099 ±0.137‡ |
| 25% | 0.043 ±0.003‡ | 1.495 ±0.154‡ | 0.743 ±0.181‡ | 0.734 ±0.130‡ |
| 10% | 0.036 ±0.004‡ | 1.304 ±0.158‡ | 1.199 ±0.377‡ | 0.614 ±0.160‡ |
| 5% | 0.027 ±0.006‡ | 1.294 ±0.225‡ | 1.349 ±0.233‡ | 0.346 ±0.188 |
| Significance of trend (P) | <0.0001 | <0.0001 | 0.41 | 0.0001 |
| Females | ||||
| 95% | 0.052 ±0.016‡ | 1.448 ±0.508† | 0.436 ±0.488 | 1.382 ±0.564* |
| 90% | 0.044 ±0.010‡ | 1.473 ±0.416‡ | 0.232 ±0.361 | 1.161 ±0.339† |
| 75% | 0.035 ±0.007‡ | 1.282 ±0.227‡ | 0.375 ±0.257 | 1.090 ±0.246‡ |
| 50% | 0.033 ±0.006‡ | 0.922 ±0.207‡ | 0.425 ±0.207* | 0.986 ±0.325‡ |
| 25% | 0.028 ±0.004‡ | 0.547 ±0.202† | 0.440 ±0.209* | 0.923 ±0.230‡ |
| 10% | 0.028 ±0.007‡ | 0.139 ±0.217 | 0.135 ±0.220 | 0.511 ±0.220* |
| 5% | 0.029 ±0.006‡ | -0.081 ±0.313 | 0.030 ±0.322 | 0.552 ±0.368 |
| Significance of trend (P) | 0.12 | 0.002 | 0.62 | 0.12 |
Sample sizes were 6677 men and 2163 women for body mass index, 6525 men and 2032 women for waist circumference, 3538 men and 1983 women for hip circumference, and 5732 men and 2048 for women for chest circumference. Estimated from 10,000 bootstrap samples. Significance levels from 10,000 permutations for slope not equal to zero coded:
P < 0.05;
< 0.01,
< 0.001.
Discussion
When the relationship between triglycerides and adiposity is described by a single regression slope, correlation coefficient, partial correlation, or adjusted regression slope, an assumption is being made that this relationship is consistent throughout the range of triglycerides values. The deviations from the standard least-squares fit are presumed to be due to random variations or other factors that do not systematically affect the relationship between the variables. Although minor departures from these assumptions are expected and probably don't greatly affect the conclusion reached, major departures from the underlying statistical model could undermine much that is presumed true.
Results presented in this paper suggest that the departures from the classical assumptions are not minor when triglycerides are compared to adiposity. Compared to the 5th percentile, the rise in men's triglycerides at the 95th percentile per unit of adiposity was 14-fold greater for BMI, 7.8-fold greater for waist circumference, 3.6-fold greater for hip circumference, and 4.4-fold greater for chest circumference. The rise in women's triglyceride concentrations at the 95th percentile was 8-fold greater than at the 5th percentile for each kg/m2 increase in BMI. If the increase in plasma triglycerides with adiposity is substantially different for different percentiles of the triglyceride distribution, then simple conclusions, such as whether triglycerides are more strongly related to waist circumference in men than women, become complex. Fig. 3 shows that BMI has a stronger apparent effect on triglycerides at higher percentiles of the triglyceride distribution, but this is less true for the lower percentiles. The sexual difference is also diminished when the regression slopes are matched on the basis of their triglyceride levels rather than percentile. The regression slope for triglycerides versus BMI is the same for women at the 59th percentile of their triglyceride distribution (0.033 ± 0.007 mmol/l per kg/m2) and men at the 25th percentile of their distribution (0.033 ± 0.003 mmol/l per kg/m2). Thus, whether adiposity has a greater effect on triglycerides in men then women depends upon the percentile of their triglyceride distribution. This is never the case under the classical assumption of parallel slopes (i.e., the difference in the apparent effect is assumed to be always the same).
The traditional regression slope overestimated the effect of adiposity at the lower portions of the triglyceride distribution and underestimates the effect at higher portions. Moreover, Fig. 3 shows that the traditional estimate does not characterize the association for the average person but rather is influenced more strongly by the relationship in individuals with elevated triglycerides. The traditional regression slope for the increase in men's triglycerides per kg/m2 of BMI was 0.070±0.003 mmol/l, which Fig. 3 shows corresponds to the calculated increase at the 63rd percentile of the triglyceride distribution (the rate of increase for median triglycerides was 0.057 ± 0.004 mmol/l or 19% lower). The standard (traditional) regression slopes for triglycerides versus men's waist (2.349 ± 0.145 mmol/l per m), hip (0.968 ± 0.169 mmol/l per m) and chest (1.520 ± 0.136 mmol/l per m) all correspond to the rates for percentiles falling above the median (64th, 62nd and 71st percentiles, respectively). The women's standard regression slopes for triglycerides versus BMI (0.031 ± 0.004 mmol/l per m), waist (1.046 ± 0.157 mmol/l per m), and chest (0.864 ± 0.257 mmol/l per m) correspond to the rates for percentiles falling slightly above the median (56th, 60th and 53rd percentiles, respectively).
We speculate that the dependence we observed between the slope of the triglyceride–adiposity relationship and the percentile of the triglyceride distribution may explain in part the stronger triglyceride–adiposity relationships observed in whites than blacks. Specifically, whites have higher plasma triglyceride concentrations than blacks [30,39,40], and based on the progressive increase in the regression slopes for increasing percentiles of the triglyceride distribution we would expect a greater triglyceride increase per unit of adiposity in whites than blacks. Correspondingly, others report that the increase in triglycerides associated with skinfold thicknesses is 2- to 3-fold greater in white than in black adults [27]. The stronger association of relative weight with triglycerides in white than black children reported by Frerichs et al. might also be attributed in part to the higher triglyceride levels of the white children [28]. The 2- to 6-fold difference in the relations of waist girth to plasma triglyceride and large VLDL concentrations between white and black children may also be in part the consequence of their 25 mg/dl difference in triglyceride concentrations [29]. In another study, waist circumference was associated with triglycerides in white males (whose mean triglycerides were 135 mg/dl) but not black males (whose mean triglycerides were 114 mg/dl) [30]. The racial differences described in these reports may reflect in part the properties of the triglyceride–adiposity relationship and the race-specific triglyceride levels (this does not preclude other metabolic differences in the triglyceride–adiposity relationships between blacks and whites).
We also speculate that the dependence between the slope of the triglyceride–adiposity relationship and the percentile of the triglyceride distribution may also explain in part the stronger triglyceride-waist circumference relationships observed in LDL pattern B women vis-a-vis LDL pattern A women [31]. Plasma triglyceride levels were 35% higher in the pattern B (133.8 mg/dl) than pattern A women (98.9 mg/dl). Katzel et al. also reported a greater triglyceride increase with increasing percent body fat in LDL pattern B (whose mean triglycerides was 1.76 mmol/l) than pattern A men (mean triglycerides of 1.03 mmol/l) [32]. The dependence may also explain in part why a 10 kg weight loss produced greater triglyceride reductions in obese pattern B men (34% reduction) than pattern A men (15% reduction) [33].
Plasma triglyceride concentrations are not normally distributed; they exhibit a strong degree of skewness in both men and women (in women, a skewness of 10.74 and a kurtosis of 255.59). However, we have demonstrated that nonnormality (skewness and kurtosis) does not explain why the regression slopes at different percentiles of the triglyceride distribution were not parallel (i.e., the nonsignificant test statistic for the reconstructed data described in Section 2). Table 4 shows that the logarithmic transformation does not eliminate many of the differences in the regression slope between the 5th, 10th, 25th, 50th, 75th, 90th and 95th percentiles of the triglyceride distribution.
In this paper, we have shown that the relationship of plasma triglycerides to adiposity varies depending upon whether the plasma concentrations are high or low relative to others in the population. Standard statistical techniques such as multiple regression analyses assume that the same relationship applies throughout the distribution. If it does not, then the usual description of the of the triglyceride–adiposity relationship by a single regression slope or correlation coefficient becomes insufficient, as does comparisons between sexes (or other groups), and the meaning of statistical adjustment becomes problematic (there are three relationships that go into estimating the independent effects of waist circumference and BMI on triglycerides, and our unpublished data suggests that all three appear to deviate significantly from the classical model).
We recognize that runners are not typical of the general population, and the results may not be representative of a more sedentary population. However, the sample includes both moderately overweight and overweight individuals, and we expect that the biological causes that link adiposity to triglycerides in physically active individuals may be relevant to those less active. Our study suggests that triglyceride concentrations are significantly associated with circumferences of the waist and hip and BMI even in lean, physically active men and women. It remains to be verified whether the relationship described in this paper for different percentiles of the triglyceride distribution also apply to less active populations.
Acknowledgments
Supported in part by grant HL-45652 and from the National Heart Lung and Blood Institute, and was conducted at the Lawrence Berkeley Laboratory (Department of Energy DE-AC03-76SF00098 to the University of California).
References
- 1.Tanne D, Koren-Morag N, Graff E, Goldbourt U. Blood lipids and first-ever ischemic stroke/transient ischemic attack in the bezafibrate infarction prevention (BIP) registry. High triglycerides constitute an independent risk factor. Circulation. 2001;104:2892–7. doi: 10.1161/hc4901.100384. [DOI] [PubMed] [Google Scholar]
- 2.Hokanson JE, Austin MA. Plasma triglyceride level is a risk factor for cardiovascular disease independent of high-density lipoprotein cholesterol level: a meta-analysis of population-based prospective studies. J Cardiovasc Risk. 1996;3:213–9. [PubMed] [Google Scholar]
- 3.Jeppesen J, Hein HO, Suadicani P, et al. Triglyceride concentration and ischemic heart disease: an eight-year follow-up in the Copenhagen Male Study. Circulation. 1998;97:1029–36. doi: 10.1161/01.cir.97.11.1029. [DOI] [PubMed] [Google Scholar]
- 4.Austin MA. Plasma triglyceride and coronary heart disease. Arterioscler Thromb. 1991;11:2–14. doi: 10.1161/01.atv.11.1.2. [DOI] [PubMed] [Google Scholar]
- 5.NIH Consensus Development Panel on Triglyceride, High-Density Lipoprotein, and Coronary Heart Disease. JAMA; Proceedings of the NIH Consensus Conference on Triglyceride, High-Density Lipoprotein, and Coronary Heart Disease; 1993. pp. 505–10. [PubMed] [Google Scholar]
- 6.Williams PT, Vranizan KM, Krauss RM. Correlations between plasma lipoprotein concentrations and low-density lipoprotein subfractions by particle diameter in men and women. J Lipid Res. 1992;33:765–74. [PubMed] [Google Scholar]
- 7.Austin MA, Breslow JL, Hennekens CH, et al. Low-density lipoprotein subclass patterns and risk of myocardial infarction. JAMA. 1988;260:1917–22. [PubMed] [Google Scholar]
- 8.Valabhji J, Donovan J, McColl AJ, et al. Rates of cholesterol esterification and esterified cholesterol net mass transfer between high-density lipoproteins and apolipoprotein B-containing lipoproteins in Type 1 diabetes. Diabet Med. 2002;19:424–8. doi: 10.1046/j.1464-5491.2002.00714.x. [DOI] [PubMed] [Google Scholar]
- 9.Byberg L, Siegbahn A, Berglund L, et al. Plasminogen activator inhibitor-1 activity is independently related to both insulin sensitivity and serum triglycerides in 70-year-old men. Arterioscler Thromb Vasc Biol. 1998;18:258–64. doi: 10.1161/01.atv.18.2.258. [DOI] [PubMed] [Google Scholar]
- 10.Metha J, Mehta P, Lawson D, Saldeen T. Plasma tissue plasminogen activator inhibitor levels in coronary heart disease: correlation with age and serum triglyceride concentrations. J Am Coll Cardiol. 1987;9:263–8. doi: 10.1016/s0735-1097(87)80373-x. [DOI] [PubMed] [Google Scholar]
- 11.Reaven GM. Role of insulin resistance in human disease. Diabetes. 1988;37:1595–607. doi: 10.2337/diab.37.12.1595. [DOI] [PubMed] [Google Scholar]
- 12.Despres JP, Prud'homme D, Pouliot MC, Tremblay A, Bouchard C. Estimation of deep abdominal adipose-tissue accumulation from simple anthropometric measurements in men. Am J Clin Nutr. 1991;54:471–7. doi: 10.1093/ajcn/54.3.471. [DOI] [PubMed] [Google Scholar]
- 13.Pouliot MC, Despres JP, Lemieux S, et al. Waist circumference and abdominal sagittal diameter: best simple anthropometric indices of abdominal visceral adipose tissue accumulation and related cardiovascular risk in men and women. Am J Cardiol. 1994;73:460–8. doi: 10.1016/0002-9149(94)90676-9. [DOI] [PubMed] [Google Scholar]
- 14.Ferland M, Despres JP, Tremblay A, et al. Assessment of adipose tissue distribution by computed axial tomography in obese women: association with body density and anthropometric measurements. Br J Nutr. 1989;61:139–48. doi: 10.1079/bjn19890104. [DOI] [PubMed] [Google Scholar]
- 15.Lear SA, Chen MM, Frohlich JJ, Birmingham CL. The relationship between waist circumference and metabolic risk factors: cohorts of European and Chinese descent. Metabolism. 2002;51:1427–32. doi: 10.1053/meta.2002.34042. [DOI] [PubMed] [Google Scholar]
- 16.Rheeder P, Stolk RP, Veenhouwer JF, Grobbee DE. The metabolic syndrome in black hypertensive women-waist circumference more strongly related than body mass index. S Afr Med J. 2002;92:637–41. [PubMed] [Google Scholar]
- 17.Halkes CJ, Castro Cabezas M, van Wijk JP, Erkelens DW. Gender differences in diurnal triglyceridemia in lean and overweight subjects. Int J Obes Relat Metab Disord. 2001;25:1767–74. doi: 10.1038/sj.ijo.0801831. [DOI] [PubMed] [Google Scholar]
- 18.Hernandez-Ono A, Monter-Carreola G, Zamora-Gonzalez J, et al. Association of visceral fat with coronary risk factors in a population-based sample of postmenopausal women. Int J Obes Relat Metab Disord. 2002;26:33–9. doi: 10.1038/sj.ijo.0801842. [DOI] [PubMed] [Google Scholar]
- 19.Van Pelt RE, Evans EM, Schechtman KB, Ehsani AA, Kohrt WM. Waist circumference vs. body mass index for prediction of disease risk in postmenopausal women. Int J Obes Relat Metab Disord. 2001;25:1183–8. doi: 10.1038/sj.ijo.0801640. [DOI] [PubMed] [Google Scholar]
- 20.Ohrvall M, Berglund L, Vessby B. Sagittal abdominal diameter compared with other anthropometric measurements in relation to cardiovascular risk. Int J Obes Relat Metab Disord. 2000;24:497–501. doi: 10.1038/sj.ijo.0801186. [DOI] [PubMed] [Google Scholar]
- 21.Gustat J, Elkasabany A, Srinivasan S, Berenson GS. Relation of abdominal height to cardiovascular risk factors in young adults: the Bogalusa heart study. Am J Epidemiol. 2000;151(1):885–91. doi: 10.1093/oxfordjournals.aje.a010292. [DOI] [PubMed] [Google Scholar]
- 22.Onat A, Sansoy V, Uysal O. Waist circumference and waist-to-hip ratio in Turkish adults: interrelation with other risk factors and association with cardiovascular disease. Int J Cardiol. 1999;1(70):43–50. doi: 10.1016/s0167-5273(99)00049-2. [DOI] [PubMed] [Google Scholar]
- 23.Caprio S, Hyman LD, McCarthy S, et al. Fat distribution and cardiovascular risk factors in obese adolescent girls: importance of the intraabdominal fat depot. Am J Clin Nutr. 1996;64:12–7. doi: 10.1093/ajcn/64.1.12. [DOI] [PubMed] [Google Scholar]
- 24.Bouchard C, Bray GA, Hubbard VS. Basic and clinical aspects of regional fat distribution. Am J Clin Nutr. 1990;52:946–50. doi: 10.1093/ajcn/52.5.946. [DOI] [PubMed] [Google Scholar]
- 25.Heitmann BL. The effects of gender and age on associations between blood lipid levels and obesity in Danish men and women aged 35–65 years. J Clin Epidemiol. 1992;45:693–702. doi: 10.1016/0895-4356(92)90046-p. [DOI] [PubMed] [Google Scholar]
- 26.Wing RR, Jeffery RW. Effect of modest weight loss on changes in cardiovascular risk factors: are there differences between men and women or between weight loss and maintenance? Int J Obes Relat Metab Disord. 1995;19:67–73. [PubMed] [Google Scholar]
- 27.Folsom AR, Burke GL, Byers CL, et al. Implications of obesity for cardiovascular disease in blacks: the CARDIA and ARIC studies. Am J Clin Nutr. 1991;53(Suppl):1604S–11S. doi: 10.1093/ajcn/53.6.1604S. [DOI] [PubMed] [Google Scholar]
- 28.Frerichs RR, Webber LS, Srinivasan SR, Berenson GS. Relation of serum lipids and lipoproteins to obesity and sexual maturity in white and black children. Am J Epidemiol. 1978;108:486–96. doi: 10.1093/oxfordjournals.aje.a112647. [DOI] [PubMed] [Google Scholar]
- 29.Freedman DS, Bowman BA, Otvos JD, Srinivasan SR, Berenson GS. Differences in the relation of obesity to serum triacylglycerol and VLDL subclass concentrations between black and white children: the Bogalusa Heart Study. Am J Clin Nutr. 2002;75:827–33. doi: 10.1093/ajcn/75.5.827. [DOI] [PubMed] [Google Scholar]
- 30.Frontini MG, Srinivasan SR, Elkasabany A, Berenson GS. Distribution and cardiovascular risk correlates of serum triglycerides in young adults from a biracial community: the Bogalusa Heart Study. Atherosclerosis. 2001;155:201–9. doi: 10.1016/s0021-9150(00)00538-4. [DOI] [PubMed] [Google Scholar]
- 31.Maki KC, Davidson MH, Cyrowski MS, Maki AC, Marx P. Low-density lipoprotein subclass distribution pattern and adiposity associated dyslipidemia in postmenopausal women. J Am Coll Nutr. 2000;19:23–30. doi: 10.1080/07315724.2000.10718910. [DOI] [PubMed] [Google Scholar]
- 32.Katzel LI, Krauss RM, Goldberg AP. Relations of plasma TG and HDL-C concentrations to body composition and plasma insulin levels are altered in men with small LDL particles. Arterioscler Thromb. 1994;14:1121–8. doi: 10.1161/01.atv.14.7.1121. [DOI] [PubMed] [Google Scholar]
- 33.Katzel LI, Coon PJ, Rogus E, Krauss RM, Goldberg AP. Persistence of low HDL-C levels after weight reduction in older men with small LDL particles. Arterioscler Thromb Vasc Biol. 1995;15:299–305. doi: 10.1161/01.atv.15.3.299. [DOI] [PubMed] [Google Scholar]
- 34.Mamalakis G, Kafatos A, Manios Y, Kalogeropoulos N, Andrikopoulos N. Adipose fat quality vs. quantity: relationships with children's serum lipid levels. Prev Med. 2001;33:525–35. doi: 10.1006/pmed.2001.0930. [DOI] [PubMed] [Google Scholar]
- 35.Williams PT. Relationship of distance run per week to coronary heart disease risk factors in 8283 male runners. The National Runners' Health Study. Arch Inter Med. 1997;157:191–8. [PMC free article] [PubMed] [Google Scholar]
- 36.Williams PT. High-density lipoprotein cholesterol and other risk factors for coronary heart disease in female runners. N Engl J Med. 1996;334:1298–303. doi: 10.1056/NEJM199605163342004. [DOI] [PubMed] [Google Scholar]
- 37.Fuller WA. Measurement error models. New York: Wiley; 1987. p. 4. [Google Scholar]
- 38.Efron B. The Jackknife, the bootstrap and other resampling plans. Philadelphia, PA: Society for Industrial and Applied Mathematics; 1982. pp. 1–92. [Google Scholar]
- 39.Tyroler HA, Hames CG, Krishan I, et al. Black-white differences in serum lipids and lipoproteins in Evans County. Prev Med. 1975;4:541–9. doi: 10.1016/0091-7435(75)90040-7. [DOI] [PubMed] [Google Scholar]
- 40.Zoratti R. A review on ethnic differences in plasma triglycerides and high-density-lipoprotein cholesterol: is the lipid pattern the key factor for the low coronary heart disease rate in people of African origin? Eur J Epidemiol. 1998;14:9–21. doi: 10.1023/a:1007492202045. [DOI] [PubMed] [Google Scholar]


