Temperature response in electrosensors and thermal voltages in electrolytes

Abstract

Temperature sensation is increasingly well understood in several model organisms. One of the most sensitive organs to temperature changes is the functional electrosensor of sharks and their relatives; its extreme thermal responsiveness, in excised preparations, has not been mechanistically described. In recent years, conflicting reports have appeared concerning the properties of a hydrogel that fills the ampullae of Lorenzini. The appearance of a thermoelectric effect in the gel (or, using different methods, a reported lack thereof) suggested a link between the exquisite electrosense and the thermal response of the electroreceptors (or, alternately, denied that link). I review available electrophysiology evidence of the organ’s temperature response, calculate a theoretical gel signal prediction using physical chemistry, analyze the strengths and weaknesses of the existing gel measurements, and discuss broader implications for the ampullae and temperature sensation.

Introduction

Recent advances have brought increasing clarity to temperature sensation, and the key molecular substrates exhibit conservation across a wide range of species [1]. In particular, transient receptor potential (TRP) channels are strongly implicated in thermosense for both mammals and flies. TRPs in general enjoy a quickly expanding profile in sensation [2].

An outlier in temperature response is found in the elasmobranchs. Sharks and their relatives are known to possess an exquisite sensitivity to small environmental electric signals. Hundreds of electrosensors, the ampullae of Lorenzini, work in concert to provide sensitivity to electric field fluctuations as small as 1 nV/cm (Kalmijn, measured behaviorally) [3]. These electrosensors also consistently exhibit exquisite sensitivity to temperature changes. While no functional role for this response is known, and evidence for temperature sensitivity in natural conditions has not been recorded (contrasting the well-established function of the electric sensitivity), electrophysiology has shown the organs to be incredibly sensitive to abrupt temperature changes. This paper will focus on the possible mechanism by which the organ transduces temperature changes, with the hope of enriching the larger conversation of temperature transduction; it will not treat functional implications, or a lack thereof, for the elasmobranchs themselves.

The ampullae are described in detail elsewhere [4]. In brief, the ampullae are small multi-chamber bulbs, with the sensory epithelium containing tens of thousands of sensing cells that amplify electrical fluctuations via a mechanism involving both apical and basal ion channels [5]. In marine species, thin canals ranging from 1 to 20 cm in length connect the ampullae to surface pores (see Fig. 1). Each ampulla-canal system is filled with a uniform hydrogel that has approximately the same ion content and conductivity as seawater. Studies suggest a salt content identical to that of seawater, a glycoprotein structure of the underlying polymers [6], little variation in properties between species, strongly temperature-dependent electrical conductivity [7], and much greater impedance to alternating currents than seawater [8].

Fig. 1.

Diagram of single ampulla of Lorenzini with associated canal and nerve fibers. The ampulla-canal system features a remarkably thick, high-resistance wall, containing a uniform extracellular gel approximating the electrical properties of seawater. Point P denotes the pore, while points A₁ and A₂ frame the sensory ampulla, with associated nerve fibers, to reference the array of measurements in the literature (see text)

The gel properties originally motivated thermoelectric measurements. With a base conductivity and temperature-dependent conductivity that match natural silicon samples, a phenomenological similarity to semiconducting behavior has been noted [7], and semiconducting materials, including some organic semiconductors [9, 10], are known to exhibit strong thermoelectric signals.

Thermoelectric tests of the gel are also logically recommended by the unique electrophysiology data collected from the ampullae. Though confirmed as electroreceptors, the organs exhibit sensitivity to multiple stimuli. Sand originally noted thermal and mechanical sensitivity, and for several decades, the organs were thought to be temperature sensors [11]. Murray noted sharp mechanical, thermal, electrical, and chemical sensitivity [12–14]. The ampullae are also, not surprisingly, sensitive to changes in salinity.

I first review the electrophysiology literature for the ampullae, with a particular focus on temperature sensitivity. Subsequent sections treat the notion of thermal voltages in the shark gel from a theoretical standpoint and discuss the attempted measurements.

Electrophysiology literature

Starting with Sand’s work in 1938, the ampullae have consistently demonstrated acute sensitivity to temperature and particularly temperature fluctuations [11].

Murray’s first investigations of the ampullae noted “anomalous responses to temperature change” [12]. He reported several experiments with interwoven electrical and thermal stimuli and found that in combination, “thermal stimulation is equivalent to electrical; the one is as effective in the presence of the other as in its absence.” He did not propose a mechanism for the temperature sensitivity. He considered and tried to rule out the idea that thermal gradients within the ampullae were involved; he applied temperature gradients perpendicular to the canal (gradients applied from point A₁ to A₂ in Fig. 1) and found no link between such applied gradients and the response of the organ.

Another test of temperature gradients in the ampullae appeared in the work of Hensel, as he applied temperature and electric stimuli to ampullae from the dogfish [15]. Temperature gradients had no substantial effect on firing. Once more, the gradients were only applied perpendicular to the gel-filled canals (Fig. 1, from point A₁ to A₂).

Nier, Hensel, and Bromm repeated some of the early measurements of Murray, combining electrical and thermal stimuli to ampullae of dogfish [16]. Again, they observed that an electrical stimulus strongly affected the ampullary sensitivity to temperature, and they noted a “possible interaction of the two types of stimulation” [16].

Broun, Govardovskii, and Zhadan measured the effect of temperature on firing rates in the ampullae of skates, with simultaneous measurements of transepithelial voltages [17]. They suggested that temperature stimulation effects “reflect changes in the potential difference on the basal membrane of the receptor cells (related to) Goldman’s equation.” Goldman’s equation, derived from the Nernst equation, relates electric potentials in different regions to ionic concentrations via basic physical chemistry. Broun and Govardovskii returned to this explanation for the ampullary temperature sensitivity in further skate measurements [18].

Akoev et al. carried out an extensive battery of electrophysiology measurements on ampullae in anesthetized skates [19]. Varying salinity and temperature, along various locations in the ampulla-canal system, provided some of the most comprehensive (and in the intervening years, arguably the most overlooked) thermosensitivity data for the electrosensors. By referencing Fig. 1, their results are summarized in Table 1. Akoev et al. found complete reversals of inhibition/excitation when moving a given stimulus to different points along the canal or sensory bulb. Of particular relevance to temperature sensitivity, the act of increasing localized temperature inhibited nerve firing when applied to the ampulla directly, while the same stimulus, applied to the midpoint of the canal (point M in Fig. 1), excited firing. In both cases, the overall temperature of the preparation increased; yet, the stimulus effect was inverted by altering stimulus placement.

Table 1.

Summary of Localized Stimuli. Summary of stimuli on electroreceptors and effects on associated nerve fiber firing from Akoev et al., 1980 [19]

Stimulus and location producing transient excitation	Stimulus and location producing transient inhibition
Salinity increase (+), A	Salinity increase (+), P
Salinity decrease (–), P	Salinity decrease (–), A
Temperature increase (+), M	Temperature increase (+), A
Temperature decrease (–), A	Temperature decrease (–), M

Location designations relate to points shown in ampullary diagram of Fig. 1

A ampulla, P pore, M midpoint of canal

Akoev et al. also found that temperature changes at the pore had no appreciable effect on the associated ampullae; while this observation may suggest the ampullae do not sense water temperatures in natural conditions, it is of little relevance to a discussion of the thermoelectric mechanism. Given a canal length of 10 cm, the temperature gradients (and hence thermoelectric signals) from pore heating or cooling were presumably confined to regions of the canal far from the electrosensitive ampulla.

The effect of temperature on the midpoint and ampulla was effectively mimicked by altering the salt content of nearby fluids. By washing the ampulla in a solution with an increased NaCl concentration, the resulting firing excitation was roughly equivalent to that seen in response to a sudden temperature decrease. When washing the pore with a solution of increased salinity, however, firing was inhibited.

Further linking thermal and electrical sensitivity, Akoev et al. observed that the transient response to temperature change was directly dependent on the electrical sensitivity of a given ampulla [19]. The most electrically sensitive ampullae were those displaying the most dramatic transient responses to temperature changes; a single receptor that had shown a sensitivity threshold that was 1.5% the threshold of a neighboring receptor displayed a dynamic temperature response 30 times greater than the neighbor’s response to the same temperature stimulus.

The effect of salinity matched the observations of Lowenstein and Ishiko, who in early ampulla experiments, found that salinity changes at the pore could immediately effect the firing of the associated receptor, with a 10% salinity change having exactly the effect of a direct 1.5 nA current [20]. The authors noted that normal diffusion through the gel would take roughly 2 h to render a significant change in concentration of sodium above the receptor epithelium; they concluded that the change in concentration, at a distance of 1 to 2 cm, created an immediate electrical effect within the ampulla.

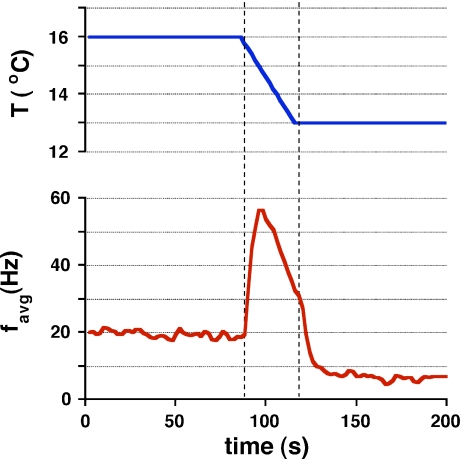
Wissing et al. exposed excised ampullae from the dogfish to electrical and thermal stimuli [21]. The baseline firing rate of the ampullae showed a dependence on the ambient temperature. However, abrupt temperature changes induced dramatic transient firing responses (up to 300% excitation over baseline firing rates, as shown in Fig. 2). The transient spiking rate effect (lasting less than 10 s) was independent of the total magnitude of the temperature change, ΔT, and relatively insensitive to the speed of temperature change dT/dt, but the effect was directly linked to the acceleration of temperature change, d²T/dt². In addition, the transients in many cases opposed the overall ambient effect of the temperature change. (In Fig. 2, an excitatory transient presages an overall inhibitory response to the temperature decrease.)

Fig. 2.

The response of an excised dogfish electrosensor to temperature change (reference [21], reprinted with permission)

Later, the same group again studied excised ampullae from dogfish, exposing the organs to thermal and electrical stimuli, but this time paying particular attention to the inter-spike intervals (ISI) [22]. While electrical currents and increased temperatures both affected the average firing rates of associated afferents, the ISI profiles clearly distinguished the effects of the stimuli. Ambient temperature affected the actual oscillation period (hence, the fundamental frequency) of the associated primary afferents, while electrical stimuli affected the probability of afferent firing. Most notably, the transient (and again dramatic) spiking events that accompanied temperature acceleration were shown to only affect spiking probability, with no affect on the intrinsic firing frequency. Hence, the act of abruptly changing temperature creates a transient firing effect in the ampullae that is coded as an electrical event, as opposed to a thermal event.

In summary, I focus on the transient firing responses to abrupt temperature changes. Of all observations, the following are the most provocative for an ampulla-canal system responding to temperature fluctuations.

1. An acceleration of temperature change directly affects the magnitude of the transient response.

2. Temperature gradients induced across a single ampulla, orthogonal to the canal, do not affect firing.

3. In spike trains, the transient response is encoded in the exact manner of electrical events. Each type of stimulus (thermal fluctuation or electrical current) affects spike probability, while ambient temperature affects the underlying firing frequency.

4. The polarity of the transient response has shown dependence on the direction of an induced thermal gradient parallel to the canal. Two heating events gave opposite transient responses based on the polarity of the applied thermal gradient in the ampulla-canal system.

5. Effects of temperature gradients are equivalent to the effects of salinity gradients.

One assumes that each abrupt temperature change leads logically to a temporary temperature gradient, where some parts of the ampulla-canal system are cooler or warmer than other areas. It is also reasonable to assume that the most abrupt temperature changes (i.e. largest ΔT for the ampulla-canal system) give rise to the most significant thermal gradients. If a thermal gradient leads to a thermoelectric voltage within the hydrogel or some other part of the system [23], this induced voltage could make significant strides in accounting for the observations listed here.

Theoretical predictions for gel thermoelectricity

Does one expect an electrical response to a temperature gradient in a system like shark gel? All solid systems possess some measure of thermoelectricity. The Seebeck effect describes the appearance of an electric field within a material in response to a temperature gradient. The inverse phenomenon, called the Peltier effect, is also observed, and this is the basis of thermoelectric cooling systems, etc. The interplay of temperature and electric potential gradients are fairly well understood in condensed matter [24]. Charge carriers possess temperature-dependent free energies. When a charge carrier encounters a temperature gradient, it automatically encounters a free energy gradient; an asymmetry of charge carrier density logically follows, leading to an electric field and a measurable voltage between the relatively warm and relatively cool areas of the system. The open questions for a given material do not involve the existence of the effect but rather the measurement technique and the effect’s magnitude.

Strongly temperature-dependent conductivity, which the gel exhibits [8], is a typical harbinger of strong thermoelectric signals in solids. From that basis, a negligible signal from the gel would be surprising. For the acutely sensitive ampullae, thermoelectric effects of even 1–10 nV/K would be relevant.

The extent to which such a condensed matter physics viewpoint is relevant to a hydrogel is questionable. The shark gels are 97% water by mass [6]. While structurally stiff, they arguably have more in common with aqueous electrolytes than with solids. Therefore, the chemistry of thermal diffusion provides an arguably more appropriate theoretical framework.

At the most simple level, an aqueous electrolyte system with a temperature gradient possesses a corresponding chemical potential gradient, and ion migration follows [25]. Phenomenologically, differential ion content in temperature gradients is well established in fluids via the Soret effect [26]. Theoretical treatments are non-trivial [27–29], but the observed effect and its implications are straightforward.

The Soret coefficient σ (in K^− 1) describes the extent to which a given component’s concentration changes with temperature. According to Agar and Turner,

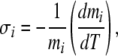where i is an index for the electrolyte, and m is the concentration in mol/kg [26]. Typical values of σ for dilute electrolytes in solution range in magnitude from 0.001 to 0.015 K^− 1 [26]. However, coefficients depend strikingly on the presence of other components; binary and tertiary systems for a given salt (e.g., NaOH) yield coefficients that are notably different from single-component systems [30]. In addition, note that much larger effects have been reported for mixtures of soft matter [29, 31], an observation of potential relevance to gels.

Like the simple picture of charge carrier density gradients described above for condensed matter physics, the Soret effect naturally leads to charge imbalances and inherent electric fields. In fact, measuring the e.m.f. of a non-isothermal cell is one method used for measuring Soret coefficients [30]. Since thermoelectricity is inseparable, in origin, from temperature-dependent conductivity, one can also take the approximate analogy of laboratory engineering: changing the temperature of part of the gel changes its resistance, thereby changing the system impedance and the standing DC voltage of the open circuit.

So what order of magnitude Seebeck coefficient, in volts/Kelvin, would one predict for shark gel based on the Soret effect? Here, I estimate the Soret-based voltage arising in an isothermal solution, containing seawater concentrations of Na⁺ and Cl⁻ (as sodium and chloride are the dominant the ionic species in the ampullary gel and seawater). Soret values for binary and ternary mixed electrolytes, including mixes of NaCl and NaOH, range from magnitudes of 1 × 10^− 3 to 20 × 10^− 3 K^− 1 [30]; in general, the Soret coefficient varies with concentration and the presence of other salts, with higher values being recorded for ternary versus binary mixtures. NaCl, most relevant to seawater and the ampullary gel, showed Soret coefficients of approximately −0.005 K^− 1 at a concentration of 0.015 mol/kg, in the presence of NaOH.

To translate Soret coefficients into induced voltages in a temperature gradient, one can compute the relative concentration difference between two regions that differ in temperature by one degree Kelvin. Rearranging Eq. 1 expresses the concentration gradient with respect to temperature:

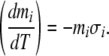These Soret-induced concentration differences can then inform the familiar membrane-type Goldman–Hodgkin–Katz (GHK) equation to find the electric potential difference developing across a sample, in the presence of a temperature gradient. Where, for a membrane, the GHK equation gives the voltage measured inside versus outside a neuron, here the expression measures voltage for the warm region versus the cold region. A theoretical electric potential for NaCl in solution results, arising in the presence of a temperature gradient:

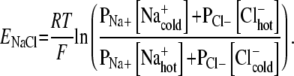Note the use of one mean T here to facilitate the combination of logarithmic terms. Given a room temperature of 293 K, the averaging of T has introduced 0.3% error in this calculation; given the other assumptions made, this is insignificant.

Equations 2 and 3 are now used in concert to estimate an electric potential difference, based on the Soret coefficient for NaCl. In seawater (and shark gel), the concentrations of Na and Cl are 0.469 and 0.546 mol/kg, respectively. Using a Soret coefficient of approximately −0.005 K^− 1 means, via Eq. 2, that the concentrations of ions on the “warm” side of the sample are slightly higher than the concentrations on the “cold” side. The natural log term is then positive in Eq. 3. Assuming that the permeabilities for sodium and chloride ions are equivalent in the seawater or gel media, E_NaCl = 58 μV for a T gradient of 1 K. This figure is roughly five orders of magnitude above the sensitivity threshold for the electrosensory system. The estimated value is suppressed by the conservative assumption that P_Na + = P_Cl −. There is strong evidence that, in systems such as the sulfate-rich shark gels, cations like Na⁺ experience sharply depressed diffusion and, hence, lower permeability values than anions like Cl⁻ [31]. If, for instance, P_Na + = (0.5) P_Cl −, then E_NaCl = 151 μV for a T gradient of 1 K; a polymer with repeated negative charge centers has shown that it can decrease cation permeability to 25% its normal value [32].

The estimate computed here assumes: (1) liquid system Soret coefficients are relevant to hydrogel systems; (2) the Soret coefficient of NaCl in shark gel is equivalent to that measured in laboratory synthesized NaCl + NaOH ternary systems; (3) the Soret coefficients of NaCl measured at concentrations of 0.015 mol/kg is equivalent to those at about 0.5 mol/kg (shark gel and seawater concentration levels); (4) the role of other ionic species in the shark gel (e.g., potassium, calcium, etc.) is negligible; and (5) the GHK equation can be used at such high ionic concentrations, treating the concentrations of all other ions as constant, while sodium and chloride ions are allowed to vary. These are significant assumptions and recommend taking the computed number as a proof-of-principle exercise.

Caveats accepted, the Soret effect could easily lead to electric signals in an electrolyte system on the order of those reported for shark gels. Without invoking any special physics or notions of solid state “thermoelectricity,” electric voltages logically arise from the fundamental considerations of electrolyte chemistry. A zero result would be unlikely, unless all the individual Soret coefficients for different salts in the gel happen to precisely cancel one another’s voltage effects.

Note that a Soret-based source of thermal voltages is consistent with the observations of salinity sensitivity in the ampulla. As referenced earlier, Akoev et al. found that a salinity change at the pore of the canal immediately induced a transient firing response in the receptor [19]; this was reported as surprising, as ion diffusion had been measured as particularly slow in the gel [20]. However, the immediate response is not surprising for physical chemistry, since ion concentration gradients lead to electric fields before substantial current flows.

I now review the three existing attempts to measure a thermoelectric signal in the ampullary gel.

Thermoelectric data

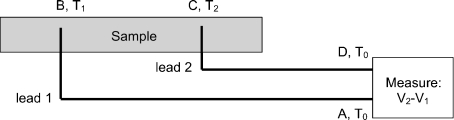
Most thermoelectric measurements rely on an “open circuit” format, meaning that instead of a truly closed conduction loop, a partial loop terminates at the inputs of a voltage measurement device [33, 34] (Fig. 3). T₀ marks an ambient temperature for the voltmeter, which must have both terminals at a constant temperature. T₁ marks, for instance, the cooler end and T₂ marks the warmer end within a sample. In each case, the associated electrical lead is only relevant if it is in thermal contact with T₁ or T₂. (In some cases, with localized heating or cooling, either T₁ or T₂ may be very close to T₀. This is fine as long as T₁ is not equal to T₂).

Fig. 3.

Basic open-circuit thermoelectric measurement. Via heating or cooling, a temperature gradient is created within the sample, with T₂ differing from T₁ at points where electrical leads then measure a corresponding voltage difference, V₂ versus V₁. The labels A–D are given for reference to the text. The measurement’s open loop runs A to D through points B and C. Temperature gradients also necessarily exist between the measurement lead and the voltage recording instrument, which sits at a temperature T_o. Resulting measured voltage for a temperature gradient corresponds to the difference in thermopower between lead material and sample material

In any such measurement, once a temperature gradient exists in the sample, if the leads are placed relevantly, at least one of them will also experience a temperature gradient. In the figure, one lead experiences a change of T₀ to T₁ somewhere along its length (probably close to the sample), and the other lead experiences a gradient of T₂ back to ambient T₀. The lead length is not relevant, as long as the measuring instrument is far from the heat source.

To compute the Seebeck coefficent (or thermopower), S, of the sample, one integrates the thermoelectric contributions around the entire open circuit, from one measurement terminal to the other [33]:

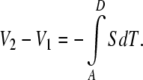Referencing Fig. 3, this path integral breaks down into three distinct components: lead one from A to B, the sample from B to C, and lead 2 from C to D [33]:

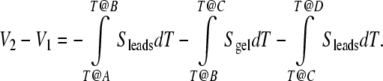Assuming homogeneous sample material and homogeneous lead material, standard simplification follows:

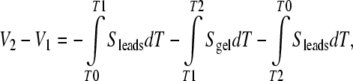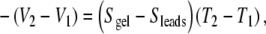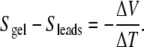The first attempted measurements found ΔV/ΔT of −238 μV/K for a white shark gel and −372 μV/K for a black-tip reef shark’s gel. Using Eq. 4.e, and silver’s Seebeck coefficient, these corresponded to S = + 240±50 and 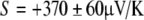, respectively [23].

Silver artifact concerns were communicated to us soon after publication, with electrochemists recommending confirmation with platinum leads [35]. Experiments were run again using braided platinum leads [25]. A response of −295 μV/K for white shark gel with platinum leads supported the gel’s thermoelectricity (corresponding to a Seebeck value of + 290). We ran further trials with white shark gel, seawater, and lab-synthesized collagen gels and discussed electrode issues, with observations suggesting that artifacts do not dominate the measurement signals [25]. Note that the measurements employing platinum, housed in a thick Lucite chamber, match exactly Leaist’s method for measuring Soret coefficients via voltage signals [27]. If the metal lead measurements of shark gel are dominated by artifacts then one must conclude a significant portion of physical chemistry’s Soret literature is similarly stained.

Fields et al. reported gel thermoelectricity measurements, from skates, using salt bridge leads and carbon leads [36]. The authors noted artifact concerns with silver electrodes used by Brown in 2003. Using agar-filled salt bridges and temperature gradients in skate gels, they reported 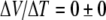. They also reported a result of 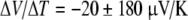from carbon-based leads (data not shown). They duplicated the Brown ΔV/ΔT signal using silver leads, −281 μV/K and by comparing this result to the salt bridge data, they concluded that thermoelectric signals from silver leads are entirely artifactual in nature, the result of temperature-dependent electrode potentials that are independent of sample properties.

I now step through the strengths and weaknesses of the three published measurements.

Metals are known to exhibit contact potentials in electrolytes, and these contact potentials are usually temperature dependent; the magnitudes of temperature dependence can be on the order of the gel thermopower values reported, raising the question of whether the entire signal collected from silver leads could be a systematic artifact, unrelated to the gel’s properties. Detailed tables of cell potentials and their temperature coefficients do not include seawater, let alone gel [37]. AgCl oxidization, the most likely culprit for an artifact for the Ag electrodes, exhibits a +316 μV/K temperature coefficient in a 1M HCl solution [37]. The gel ΔV/ΔT signals from metal electrodes are of the opposite sign. An oceanographic work cites a temperature coefficient for an Ag/AgCl electrode in seawater [38]. The lead author relays that, consistent with the HCl result above, the coefficient approaches +315 μV/K for relevant temperature gradients (0.1– 0.2 K) [39].

Platinum lead measurements exhibited linear shark gel signals, independent of heating speed, gradient size and gradient direction [25]. However, seawater signals were non-linear, hysteretic and of opposite sign from shark gels. For platinum, all listed temperature coefficients involve the oxidation of species that are formed with platinum by applying 0.8 V or more versus a standard electrode [36]. The platinum leads were never exposed to applied voltages, as the open-circuit technique is non-Faradaic [25]. For synthetic collagen gels, the Seebeck-like signal during heating depended only weakly on seawater concentration, though one would expect strong ion concentration dependence for electrode artifacts.

In sum, unquantified electrode artifacts presumably affected the silver electrode gel data. However, references to similar systems show temperature coefficient artifacts of a sign opposing the reported signals; at this time, the existence of thermoelectric signals is more bolstered than overturned [35]. For the platinum work, temperature-dependent electrode reactions in the absence of applied voltages are not listed; no clear candidates for temperature-dependent lead voltages present themselves, but they have not been systematically ruled out.

The measurements of Fields et al., when viewed from the fundamental position of thermoelectric measurement practice, do not support the authors’ position [36]. While salt bridges remain the reliable tool of choice for a great span of electrophysiology, they present an unintentionally complicated tool for thermoelectric measurements. Measurements require homogeneous electrodes with small, precisely known self signals (hence, the use of metals). As described above, it is not possible to induce thermal gradients in a sample without having equal and opposite gradients in the leads, and a sample’s thermopower value is derived by equating the measured voltage to the careful sum of all contributions [33, 34]. A thermopower signal S is derived from ΔV/ΔT using Eq. 4.e above.

Fields et al. do not address the thermoelectric contribution of their leads [36]. They set the sample thermopower to the measured ΔV/ΔT trace, instead of using the standard expression 4.e. In this context, their Fig. 1c (a flat ΔV/ΔT trace showing zero slope), can only strictly mean that a thermoelectric signal within the salt bridge leads (S_leads) opposes an equivalent signal in skate gel (S_sample). Since the authors also use silver leads to measure the same non-zero signal for a salt bridge (Fig. 1d) as skate gel (Fig. 1a), their salt bridge measurements are consistent with building a “null thermocouple” from two very similar materials and measuring the expected null signal (their Fig. 1c; see [33] for a null thermocouple diagram). Put another way, if agar gel and skate gel have the same thermoelectric properties, the measurement will necessarily give zero voltage at the ambient T₀ terminals. For the skate gel’s signal to be zero, an argument must be made for both the skate gel and agar gel to have exactly zero thermoelectric response.

Fields et al. relay a result using carbon electrodes of 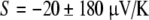but do not show the raw data. The uncertainties of this result encompass the calculated theoretical values of a thermoelectric effect in NaCl solution, and are over one half the signal reported using Ag leads. As with the salt bridge data, Fields et al. neglect the necessary contribution of the leads. Bulk carbon has an attractively low Seebeck coefficient, but carbon electrode contributions will depend on the forms of carbon present, the surface treatment (e.g., glassy), the types and locations of metal present within the electrode, and the exact location of thermal gradients.

Discussion

It must be clearly stated that the current work seeks neither to suggest that the ampullae of Lorenzini are functional temperature sensors, nor to overturn the established function of the ampullae as electrosensors. Whether sharks use the striking temperature sensitivity of their electrosensors is not known. The effect could be more an annoyance than a benefit, like wind affecting a mammalian eye. It could also be true that in natural conditions, the embedded ampullae are not exposed to significant temperature gradients. The question of interest here is simply one of underlying transduction mechanism.

Electrophysiology data from the ampullae consistently exhibit sharp responses to abrupt temperature change. The dynamic overshoots do not always match the excitatory/inhibitory pattern of the static response to temperature change (e.g., see Fig. 2), and this distinguishes the organs from the majority of cold receptors, for instance [40]. Many authors have suggested that the transient dynamic response is somehow intertwined with the organ’s electric sensitivity. Particularly compelling are the reports that: (a) ISIs of the transient feature are coded exactly like electrical events; (b) the magnitude of the dynamic feature depends sharply on the electrical sensitivity of the ampulla; (c) salinity stimuli produce the same effects as abrupt temperature changes; and (d) changing the position of a temperature stimulus or a salinity stimulus along the length of an ampullary canal reverses the firing effect of that stimulus. While perpendicular temperature gradients show no appreciable effect on the firing rate, one would not expect an effect in that geometry from a thermoelectric mechanism in the lumen.

Underlining that the response to temperature changes is localized to the lumen and sensing cells, further electrophysiology has shown that blocking synaptic transmission from the receptive cells to the afferent fibers completely removes the transient response, but not the tonic shift with ambient temperature [41]. There are ever-fewer candidates to explain the strong link of the electric sensitivity to the transient temperature sensitivity.

The extent to which TRP channels could account for the electrophysiology data of the ampullae of Lorenzini has not been explored. The facts that TRPs appear in a wide variety of species are increasingly linked to temperature sensation and appear to play a great role in sensory systems in general recommend the channels as a candidate for further exploration in the ampullae. Some TRPs exhibit gating Q10 values (a measure of thermal sensitivity) 3–5 times greater than other channels [42], and that a subset of the TRP family has shown very flexible voltage sensitivity [2]. Whether or not TRPs are expressed in the elasmobranchs, and the ampullae in the particular, is not currently known.

As for the gel itself, the arguments above support the notion that these gels show “no unusual” thermoelectric character [36]; neither physics nor physical chemistry would find signals in these systems surprising. A general theoretical treatment based on the Soret effect predicts significant thermoelectric signals for aqueous electrolytes like seawater, and for systems like the shark and skate gels. The lack of such an effect could apparently only follow from an exact cancellation of multiple contributions to the Soret effect from various salts. Given the range of ions present in the gel, and given the range of Soret values observed for these different salts on their own, an exact cancellation is unlikely. Without a greater knowledge of Soret coefficients in seawater and shark gel, and without an exact knowledge of permeabilities or diffusion constants for the major ionic species in such samples, calculations cannot progress beyond the general treatments presented here. In the end, the notion of the Soret effect fits electrophysiology data very nicely. In particular, it would insist that salinity stimuli mimic the effects of abrupt temperature changes.

The gel thermoelectric measurements displayed in the literature to date are not quantitatively conclusive. While all estimates of possible artifacts for the silver metal leads oppose the signals measured, they still have a questionable final magnitude. Platinum metal leads, with zero applied voltage, do not have obvious artifacts, but temperature dependent contact potentials have not been conclusively ruled out via systematic measurement. In sum, worries of temperature-dependent metal lead potentials are not dismissed. The Seebeck coefficient values for shark gels are, on average, 2–5 times the magnitude of Seebeck coefficients computed theoretically. This is not too meaningful, given the number of assumptions underlying the calculation. Meanwhile, experiments using agar-filled salt bridges failed to characterize thermoelectric contributions from the leads; these measurements deviated from measurement protocol and fail to support the authors’ claims. In those measurements, a skate gel signal of zero follows if and only if agar gel also has a zero thermoelectric signal; as shown above, this is highly improbable, due to the Soret effect.

Two ways forward could help resolve the controversy of thermoelectric temperature transduction. A measurement with small, single-material, well-characterized carbon electrodes, if possible, would be the best recommendation for further gel measurement work. In addition, a straightforward electrophysiology trial is needed, where a temperature gradient is set up between the ampulla and some point along the canal (A gradient could occur in a region as small as the ampulla itself; the canal allows for the possibility of substantial gradients, and the majority of electrophysiology trials maintain at least some if not the entire canal structure.). Precise knowledge of such a gradient, involving multiple thermometers and simultaneous spike train measurements could either strongly support or refute the thermoelectric hypothesis. The only suggestively similar trial, from Akoev et al., noted an opposite effect for an abrupt heating event localized at the receptor and a similar one localized in the canal, 2–4 cm from the ampulla [19].

Thermal voltages in biology could have applications beyond the ampullae of Lorenzini. The basic physical chemistry of the Soret effect demonstrates that electrolyte systems will typically generate internal voltages in response to temperature gradients. Since any abrupt temperature change in a biological system will result in temporary temperature gradients, the related electrical effects could play a role in certain cases of temperature sensation. However, the theoretical and experimental values described above, all well below 500 μV/K, would fall below most channel gating voltages, suggesting thermoelectric relevance in only remote cases. Large, abrupt temperature changes, presumably relevant to thermal nociception, would lead to significant local temperature gradients; such cases would be the most likely candidates for thermoelectric relevance, beyond the ampullae of Lorenzini.